Семина Лилия Анатольевна 2010- 2011 уч год пояснительная записка

Вид материала

Содержание

Основная цель курса –
Составлен: учащимися 9 класса
Алгебраические уравнения
Исторические задачи.
Решить уравнение с параметром
Задания для самостоятельного решения.
Р е ш е н и е : ( 2+x)² - 3x(2 + x) + x + 11= 0
Составлен: учащимися 10 класса

Подобный материал:

Муниципальное образовательное учреждение

«Средняя общеобразовательная школа д. Шибково»

Искитимского района Новосибирской области

Рассмотрено Согласовано Утверждаю

на заседании МО учителей Зам. директора по УВР Директор МОУ «СОШ д. Шибково»

_______________________________ __________ ____________ ___________ ________________

Протокол №___от

«___» сентября 20___г. «___» сентября 20___г. «___» сентября 20___г.

Руководитель МО

____________ ___________________

Рабочая программа

элективного курса по математике

«Уравнения и параметры»

для_10_класса

Учитель:Семина Лилия Анатольевна

2010- 2011 уч. год

Пояснительная записка.

Решение уравнений занимает в математическом образовании огромное место. Умение решать уравнения с параметром дает возможность учащимся:

получить представления об уравнениях как математическом аппарате решения разнообразных задач из математики, смежных областей знаний и практики,
овладеть понятием “ параметр, усвоить понятие равносильность уравнений,
получить начальные представления о задаче решения уравнений с параметром и научиться решать уравнения с параметрами, сводящиеся к линейным и квадратным,
использовать для описания математических ситуаций графический и аналитический языки, применять геометрические представления для решения и исследования уравнений и систем.

Курс «Уравнения и параметры» рассчитан на учащихся 10 класса, которые стремятся повысить свои знания. Учитывая математическую подготовку учащихся 10 класса, я разработала программу данного курса.

Основная цель курса – обобщить и систематизировать имеющиеся у учащихся сведения об уравнениях с параметром, усвоить общую схему решения уравнений, систем уравнений с параметром, дать возможность ученику проявить себя и добиться успеха.

Актуальностью данного курса является:

инвариантность: применимость для учащихся с различными уровнями развития,
дифференцируемость: по способам выполнения учебных заданий, характеру познавательной деятельности,
направленность на развитие познавательного интереса к математике (привлекательность, реальность, включение исторических сведений, личностная значимость для учащихся)

В связи с этим я ставлю следующие задачи:

знать алгоритм решения уравнений с параметром,
формирование умений решать уравнения с параметрами, сводящиеся к линейным и квадратным,
развитие логического мышления, навыков работы с дополнительными источниками информации, навыков работы с компьютером.

Данный курс в базовой программе представлен односторонне, понятие «параметр» упоминается вскользь. Вместе с этим, вступительные экзамены в техникумы, колледжи, институты предусматривают овладение учащимися навыков решения уравнений с параметром.

На протяжении всей работы курсов учащиеся работают в группах, индивидуально, по парам, учатся работать с дополнительной литературой, развивают навыки работы с компьютером. Курс обеспечен материалами фонда библиотеки, современными источниками информации.

Формы контроля:

подготовка и оформление презентации «Уравнения и параметры»,
подготовка сообщений из истории математики:
- алгебраические уравнения,
- Диофантовые уравнения,
- Карл Гаусс,
- Георг Крамер,
- Франсуа Виет,
составление справочника «Уравнения»,
составление решебника «Уравнения с параметром».
оформление буклета «Элективный курс»

Результатом работы является создание презентации «Уравнения и параметры», буклета «Элективный курс», составление справочника «Уравнения», решебника «Уравнения с параметром».

Календарно-тематическое планирование

1 час в неделю, 36 часов

№ п/п	тема	кол-во часов	дата
Линейное уравнение (9 часов)
1 2 3 4 5 6 7 8 9	Определение. Диофантовые уравнения. Алгебраические уравнения. Исторические задачи. Решение линейных уравнений повышенной сложности. Параметр. Линейные уравнения с параметром. Решение уравнений с параметром, приводимых к линейным. Создание справочного материала из истории математики: алгебраические уравнения, Диофантовые уравнения, Карл Гаусс, Георг Крамер, Франсуа Виет,	3 2 4
Системы линейных уравнений (8 часов)
10 11 12 13 14 15 16 17	Уравнение с двумя переменными. К. Гаусс. Матрица. Метод Гаусса. Определитель. Г. Крамер. Правило Крамера. Экзаменационные задания повышенного уровня сложности. Решение экзаменационных заданий повышенного уровня сложности (по материалам ГИА-9) Создание справочного материала. Создание решебника. Решение систем уравнений методом Гаусса. Решение систем уравнений по правилу Крамера.	3 2 3
Системы линейных уравнений с параметром (6 часов)
18 19 20 21 22 23	Системы линейных уравнений с параметром. Алгоритм решения. Разбор заданий вступительных экзаменов. Создание справочного материала. Создание решебника. Системы линейных уравнений с параметром. Системы линейных уравнений с параметром.	3 3
Квадратные уравнения с параметром (8 часов)
24 25 26 27 28 29 30 31	Ф. Виет. Теорема Виета. Дробно-рациональные уравнения. Квадратные уравнения с параметром. Уравнения, сводящиеся к квадратным. Разбор экзаменационных заданий (по материалам ГИА-9). Создание справочного материала. Создание решебника. Квадратные уравнения с параметром. Уравнения, сводящиеся к квадратным.	2 2 1 3
Итог работы (6 часов)
32 33 34 35 36	Работа по созданию презентации. Работа по созданию проекта. Работа по созданию буклета. Работа по созданию УМП. Итоговое занятие. Защита проекта, представление УМП «Уравнения и параметры»

Данный курс можно продолжить в 11 классе, рассмотрев темы «Тригонометрические уравнения с параметром», «Показательные и логарифмические уравнения с параметром».

Литература для учащихся.

Энциклопедический словарь юного математика.- М., Педагогика, 1989 г.
Детская энциклопедия, т. 2
Кузнецова Л. В. и другие. « Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы». - M., Просвещение, 1987г.
Гиндикин С. Г. «Рассказы о физиках и математиках». М., Наука, 1985г.
Рыбников К.А. «Возникновение и развитие математической науки». - М., Просвещение, 1987г.
Абрамович М. И., Стародубцев М. Т. «Математика и элементарные функции».- М., Высшая школа, 1976г.

Литература для учителя.

Симонов А. Я., Бакаев Д. С., Эпельман А.Г. и другие. « Система тренировочных упражнений по математике». – М., Просвещение 1991 г.
Абрамович М. И., Стародубцев М.Т. Математика. « Алгебра и элементарные функции».- М., Высшая школа,1976г.
Каганов Э. Д. « 400 самых интересных задач с решениями (6-11кл.)». В помощь школьнику. – М., ЮНВЕС,1997г.
Математика. Приложение к газете «1 сентября».
Выгодский М. Я. «Справочник по элементарной математике». – М., Наука,1979г.
Выгодский М. Я. «Справочник по высшей математике». – М., Наука,1977г.

МОУ «Средняя общеобразовательная школа д.Шибково»

Справочник

Уравнения.

Составлен:

учащимися 9 класса

2009 – 2010 уч. год

Диофантовое уравнение.

Диофантовыми уравнениями называют алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные корни. Диофантовые уравнения имеют, как правила, много решений, поэтому их называют неопределенными уравнениями.

Например:3х + 5х = 7, х + у = z, 3x + 4y = 5z.

Названы они по имени греческого математика Диофанта, жившего в III веке до н.э. Его книга содержала большое количество интересных задач, ее изучали математики всех поколений. Книга сохранилась до наших дней.

К диофантовым уравнениям относятся задачи, по смыслу которых неизвестные величины могут быть только целыми числами, например,

формулы для нахождения целочисленных сторон прямоугольного треугольника (т.е. для решений уравнений х + у = z).

Даже при n=3 диофантовы уравнения подаются решению с большим трудом, при чем ответы могут быть самыми разными. 3х + 4у = 5z: такие уравнения совсем не имеют решений в целых числах, которые легко найти. х + у = 2z: имеет конечные число решений в целых числах, которые легко найти. х + у = 9z: имеет бесконечно много целочисленных решений, однако, написать для них формулы далеко не просто.

Среди 23 проблем, выделенных Диофантом, третья проблем ставила вопрос об эквивалентности понятий, десятая проблема была посвящена вопросам разрешимости диофантовых уравнений и.т.д.

Диофант рассматривал задачи из неопределенного анализа. Он отыскивал рациональные решения таких систем алгебраических уравнений, в которых число неизвестных превышает число уравнений. В системе современной математической науки она расположена на стыке теории чисел и алгебраической геометрии: ее теперь называют диофантовым анализом.

«Арифметика» Диофанта состояла из 13 книг (частей), но сохранились только 6 «первых» книг. В начале сочинения введена алгебраическая символика и определен способ подхода к решению задач, характерный для алгебры. В «Арифметике» величины обозначены порядковыми буквами греческого алфавита, введены специальные символы для неизвестной и для первых ее шести степеней. Показатели степеней у Диофанта не только положительные, но и отрицательные. Имеются специальные обозначения для свободного члена, для знака вычитания и знака равенства. Для сложения специального знака еще нет, слагаемые просто пишутся рядом. Явно сформулированы правила алгебраических операций, в том числе правило умножения и деления степеней неизвестной, правило перенесения членов уравнения с одной стороны знака равенства членов на другую и другие.

Алгебраические уравнения.

Алгебра выросла из арифметики, и вычислительной практики людей. Тенденции роста, которые можно отнести к алгебраическим, появились очень рано. Они в начале представляли собой стремление группировать однотипные задачи и формулировать, возможно, более общие правила их решения. У них была общая особенность: неизвестная, которое требуется отыскать по условию задачи, получало свое особое название, а затем обозначалось специальным символом. Основополагающим сочинением по алгебре был трактат узбекского математика и астронома IX века аль Хорезми «Китаб аль Джебр Валь Мукабала». Название в переводе означает: книга об операциях «Джебр (восстановления) и Кабала (приведения)».

Уравнение вида ах = b, где х - переменная, a и b некоторые числа, называются линейными уравнением с одной переменной. Например, 5x = - 4, -0.2x = 0. В первом уравнении а = 5, b = - 4.

Решить уравнение с одной переменной - значит найти все его корни или доказать, что корней нет. Уравнения с одной переменной, имеющие одни и те же корни, называются равносильными.

Алгебраические уравнения – уравнения вида Р [х₁,…,х_n] = 0, где Р – многочлен от переменных х₁, …,х_п. Эти переменные называют неизвестными. Упорядочный набор чисел [а₁,…,а_n] удовлетворяет этому уравнению, если при замене х₁ на а₁, х₂ на а₂ и т.д. получаются верное числовое равенство [напр.: упорядочная тройка чисел [3,4,5] удовлетворяет уравнению х²+у²=z² , поскольку 3²+ 4²= 5²]. Число, удовлетворяющее алгебраическому уравнению с одним неизвестным, называют корнем этого уравнения. Два алгебраических уравнения, имеющие одно и тоже множество решений, называют равносильными. Степень многочлена P называется степенью уравнения P(x₁, …., x_n) = 0, например, 3x -5y +z = c – уравнение I степени, называется также линейным , x²+ y²= z² – уравнение II степени, x⁴-3y³+1 = 0 – уравнение IV степени.

Исторические задачи.

Многие задачи, решаемые алгебраически, могут быть решены и без помощи уравнений. Люди умели это делать задолго до возникновения алгебры, потому что им это было нужно для жизни и работы. Не случайно задачи на сообразительность имеются в фольклоре, сказках и легендах разных народов. Вот несколько таких задач.

Задача Пифагора ( Πΰωάχοράζ , ок. 570 – ок. 500 г.до н.э.) .

Учителя спросили: «Скажи, о великий Пифагор, сколько у тебя учеников?» И он ответил: «Половина изучает математику, четверть – музыку, седьмая часть пребывает в молчании и, кроме того, есть еще три женщины». Узнайте число учеников Пифагора.

Одна из известных русских задач.

Летела стая гусей, а навстречу им летит один гусь и говорит: «Здравствуйте, сто гусей!» - «Нас не сто гусей, - отвечает вожак,- если бы нас было столько, сколько теперь, да еще столько, да полстолька, да четверть столька, да еще ты, гусь, с нами, так тогда нас было бы сто гусей» Сколько гусей было в стае?

Задача из «Арифметики» Магницкого.

«Послан человек из Москвы на Вологду, и велено ему в хождении своем совершати на всякий день по 40 верст; потом другий человек в другий день послан вслед его, и велено ему идти за день 45 верст, и ведательно есть, в коликий день постигнет второй первого?»

Задача Диофанта.

Найти три числа, чтобы большее превышало среднее на третью часть наименьшего, среднее было бы больше наименьшего на третью часть большего, наименьшее же на 10 превышало третью часть среднего.

Р е ш е н и и е.

Задача Пифагора. Пусть х- число учеников, тогда

х + х + х + 3 =х,

Ответ: 28 учеников.

Одна из известных русских задач. Пусть х – число гусей в стае, тогда

х + х + 0,5х + 0,25х + 1 = 100,

Ответ: 36 гусей. .

Задача из «Арифметики» Магницкого.

1 верста = 500 саженям = 1500 аршинам = 3500 футам = 1,0668 км.

Ответ: через 8 дней.

Задача Диофанта. Пусть 3х среднее, тогда третья часть будет х,

наименьшее – ( х + 10).

1 х + 10

3х – (х + 10) = — (3х + ——— ).

3 3

Ответ: среднее – 37,5; наименьшее – 22,5; наибольшее – 45.

Уравнение с параметрами.

Параметр – это постоянная величина в уравнении или неравенстве, обозначенная буквами.

Решить уравнение с параметром - это значит:

- выразить неизвестные величины через параметр,

- исследовать найденное выражение в зависимости от значения параметра на предмет существования решений и их видов.

Линейное уравнение с параметром.

Решите уравнение:

(а-2)*х=4

Решение: 1) а -2 = 0, 2) а≠ 2 ,

а = 2,

0*х = 4, корней нет. 4

х= ────, ед. решение.

а - 2

Ответ: при а = 2: корней нет,

4

при а ≠ 2: х = ──── - ед. решение.

а – 2

Уравнение такого вида может иметь специфику.

(а – 3)*х = 0

Решение: 1) а -3 = 0 , 2) а ≠ 3,

а = 3 , х = 0, ед решение.

0*х = 0, х € R.

Ответ: при а = 3: х – любое,

при а ≠ 3: х = 0 , ед. решение.

Возможны все три ситуации.

(а² - 1)х = 3а² + 2а – 5

Решение: 1) а² - 1= 0, 2) а ≠ 1, а ≠ - 1

а² = 1, 3а² +2а – 5 3а + 5

а = 1 или а = -1. х = ─────── = ─────, ед. реш.

а) а = 1, б) а = -1 , а² - 1 а + 1

0*х = 3 + 2 -5, 0*х = 3 -2 -5, D = 4-4*3*(-5) = 64

0*х = 0, 0*х = -4, а = 1, а = -1⅔,

х € R. корней нет

Ответ: при а = 1: х € R,

при а = -1: корней нет,

3а +5

при а ≠ 1, а ≠ - 1: х = ────, ед. решение.

а + 1

6 (ах -1) = 2(а + х) – 7.

Решение: 6ах – 6 = 2а + 2х - 7,

6ах - 2х = 2а – 7 + 6,

(6а - 2)*х = 2а - 1.

1) 6а - 2 = 0, 2) 6а – 2 ≠ 0,

а = ⅓ , а ≠ ⅓,

0*х = -1, корней нет. 2а - 1

х= ─────, ед. решение.

6а - 2

Ответ: при а = ⅓: корней нет,

2а - 1

при а ≠ ⅓: х= ────, ед. решение.

6а – 2

Задания для самостоятельного решения.

1). 1 m

m + 1 = ─── + ───────,

m + 1 (m +1)x

2). 3ax 7

──── = 2 *(x + 1) + ─── ,

a – 1 a - 1

3). X – 5 2 1

──── + ──── = ────────── .

x + 2 d + 1 (d + 1)(x + 2)

Уравнения, приводимые к линейным.

Решите уравнения:

3ах + 5 3а + 11 2х + 7

─────── + ──── = ──── .

(а + 1)(х + 3) а + 1 х + 3

Решение: 1) а = - 1, решений нет,

х = - 3, решений нет.

2) а ≠ - 1, х ≠ - 3.

3ах + 5 3ах + 11х +9а + 33 = 2ах + 7а + 2х + 7 ,

4ах +9х = - 2а – 31,

(4а + 9)х = - 2а – 21. 2а + 31

а) 4а + 9 = 0, б) а ≠ - 2,25: х = ─ ─────, ед.реш.

а = - 2,25, 4а + 9

0х = - 2 *(- 2,25) – 31, решений нет. Проверим условие х ≠ - 3.

2а + 31

───── = 3

4а + 9

а = 0,4 – исключить, т.к. х ≠ - 3.

Ответ: при а = 0,4: решений нет,

при а = - 1: решений нет,

при а = - 2,25: решений нет, 2а + 31

при а ≠ 0,4, а ≠ - 1, а ≠ - 2,25: х = ─ ─────, ед. решение.

4а + 9

2в 1 1

─── = ──── - ────

х а – в а + в

Решение. 2в 2в

─── = ────

х а² - в²

1) х ≠ 0, а² - в² ≠ 0.

а) в = 0: 0 0 б) а² - в² = 0:

─ = ──── , а = ± в, решений нет.

х а² - в²

0 0

── = ── ,

х а²

0 = 0, х € R; x ≠ 0.

Ответ: при а = ±в: решений нет,

при а² ≠ в², в = 0: х € R, х ≠ 0.

при а² ≠ в², в ≠ 0: х = а² - в².

Квадратные уравнения с параметром.

Решите уравнения:

mx² + 3mx –(m +2) = 0.

Решение. а) m = 0: - 2 = 0, решений нет.

б) m ≠ 0: Д = в² - 4ас, Д = 9m² + 4m(m + 2) = 9m² + 4m² + 8m = m(13m + 8)

1) Д = 0: m(13m + 8) = 0,

8 3m

m = ─ ─── , х= ─ ──, ед. решение

13 2

8 - 3m ± √13m² + 8m

2) Д > 0: m < - ── и m > 0, х = ──────────── ,

13 2m

8

3) Д < 0: m € (- ── , 0), решений нет.

13

Ответ: 8

при m € (- ── , 0), решений нет.

13

8 - 3m ± √13m² + 8m

при m < - ── и m > 0, х = ──────────── ,

13 2m

8 3m

при m = ─ ─── , х= ─ ──, ед. решение.

13 2

Уравнения, сводящиеся к квадратным.

Решите уравнения:

х 2 3 - а²

────── - ────── = ─────────.

а( х +1 ) х + 2 а( х + 1)( х + 2 )

Решение.

а = 0: решений нет,

a) а ≠ 0, х ≠-1, х ≠ 2:

x² + 2x - 2xа – 2а = 3 - а²,

x² + 2( 1-а )x – а² – 2а – 3 = 0,

D=(1-а)² - (а² – 2а – 3) = 1 – 2а + а² - а² + 2а + 3 = 4

- (1-а ) ± 2

х

= , х₁ = а - 1 + 2 = а + 1,

1

х₂ = а – 1 – 2 = а – 3.

х₁= - 1, а -3 = -1 х₁= - 2 , а -3 = - 2

а = 2 а = 1

х₂ = - 1, а +1 = - 1 х₂ = - 2 а +1 = - 2

а= - 2 а = - 3.

Ответ: при а = 0: решений нет,

при а = 2: х₁ = 3 ,

при а = 1: х₂ = 2 ,

при а = -2: х₃ = - 5,

при а = - 3: х₄ = - 6 ,

при а ≠ 0, а ≠ 2, а ≠ 1, а ≠ - 2, а ≠ - 3: х₅ = а – 3, х₆ = а + 1.

( с + 2)х² 2сх 5 12 - с - с²

──────── - ──────── = ───── + ─────────

( с + 2)(х – 2) (с – 1)( х – 2) с² - 1 (с² - 1)( х – 2)

Решение.

Р

ассмотрим уравнение при условии с ≠ ± 1, х ≠ 2.

(с + 2)x²( с -1) – 2с( с +1)x = 5( x – 2) + 12 –с - с² ,

(с - 1)( с + 2)x² - (2с² + 2с +5)x – 2 + с + с² = 0,

(с – 1 )(с + 2)x² - (2с² + 2с + 5)x + (с - 1)(с + 2) = 0.

Рассмотрим случай

1) с = - 2: -9x = 0,

x₁= 0.

2) с ≠ 1, k ≠ - 2. Разделим на (с - 1)(с + 2).

с² + 2с + 5

x² - ────── x +1 = 0.

(с - 1)(с + 2)

Если с = 1, то корни взаимообратные ,

с – 1 с + 2

тогда x₁ = ─── и x₂ = ──── .

с + 2 с - 1

Если х₁ + х₂ = 2с² + 2с + 5 , то х₁ и х₂ имеют одинаковые знаки._

Из условия x = 2 имеем:

с - 1 с + 2

─── = 2, ─── = 2,

с + 2 с - 1

с – 1 = 2с+ 4, с + 2 = 2с – 2,

с = - 5, х = 0,5. с = 4, х = 0,5.

Ответ: при с ≠ ± 1: решений нет,

при с = - 2: х = 0 ,

при с = - 5: х = 0,5,

при с = 4: х = 0,5 ,

при с ≠ - 2, с ≠ -5, с ≠ - 4: с – 1 с + 2

x₁ = ─── и x₂= ──── .

с + 2 с – 1

При каких значениях параметра р оба корня уравнения

2x² +3px + (p² +1) будут меньше 0?

Решение.

1) D = 9p² - 4*2(p² +1) = 9p² - 8p² - 8 = p² - 8.

Так как уравнение имеет 2 корня, то D > 0: p² - 8 > 0

р € (-∞, -√8) (2√2, ∞)

Если х₁и х₂- корни уравнения, то х₁*х₂ = 0,5(p² + 1), поэтому х₁ и х₂ имеют одинаковый знак.

Если х₁ < 0 и х₂ < 0, то х₁+ х₂ < 0, т.е. (по т. Виета) – 1,5p < 0 , р > 0.

Ответ: уравнение будет иметь 2 различных отрицательных корня

при p € (2√ 2; ∞).

Г) При каких значениях параметра m уравнение x² + (m+2) x + (m+1) = 0 имеет 2 различных корня. Найти корни.

Решение. По теореме, обратной теореме Виета, х₁+х₂ = m+2,

х₁*х₂ = m+1.

Если х₁ и х₂ корни, то х₁ = - (m +1), х₂ = -1.

Необходимо, чтобы D = (m + 2)² - 4(m + 1) = m² + 4m + 4 - 4m + 4 = m²,

D > 0 при любых m.

Уравнение будет иметь 2 различных корня, если m ≠ 0, тогда х₁= - m – 1,

х₂ = - 1.

Ответ: при m ≠ 0: х₁= - m – 1, х₂ = - 1.

Примеры решений экзаменационных задач.

1) При каких значениях с уравнение х² + 2х + с = 0 не имеет корней?

Укажите одно из таких значений с.

Р е ш е н и е: x² + 2x +c = 0.

Квадратное уравнение не имеет корней, если Д <0.

Д=4 - 4с , Д < 0,

4 - 4c < 0,

-4c < - 4,

c > 1.

Ответ: при с > 1 уравнение корней не имеет, с = 2.

2) При каких значениях k уравнение 16х² + kх +1 = 0 не имеет корней? Имеет ли уравнение корни при k = 0,03; при k = -20,4?

Р е ш е н и е: 16х² + kx +1 = 0.

Уравнение корней не имеет, если Д <0.

Д = k² - 4*16*1, Д = k² - 64,

( k – 8 ) ( k + 8 ) < 0,

Ответ: при k Î (-8;8) уравнение не имеет корней.

k = 0,03Î (-8;8) – да, k = - 20,4Ï (-8;8) – нет.

3) При каких значениях с уравнение 0,25x² + cx +11 = 0 имеет 2 корня?

Р е ш е н и е: Уравнение имеет 2 корня, Д > 0.

Д = c² - 4*0,25*11, Д = с² – 11,

(c –√ 11)(c +√ 11) > 0,

Ответ: при с € (- ∞, –√ 11 ) ( √ 11, ∞ )

4) При каких значениях а уравнение ах ² + х -3 = 0 имеет 2 корня? Из

чисел –1/6, -1/20, 1/6, 1/20 выберите те, которые удовлетворяют этому условию.

Решение: Уравнение имеет 2 корня, Д > 0.

Д = 1 -4*а(-3), Д = 1+12а,

а > - 1/12.

Ответ: при а € ( - 1/12; ∞), -1/6 > -1/12 - ложно,

-1/20 > - 1/12 – верно,

1/6 > - 1/12 – верно,

1/20 > - 1/12 - верно.

Системы алгебраических уравнений.

Линейное уравнение имеет вид ах + в = 0, а ≠ 0, а, в € R. Оно имеет единственное решение х = -в/а.

С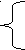истемой двух линейных уравнений с двумя неизвестными называется система вида : ах +ву = с,

ах +ву = с.

Все коэффициенты системы предполагаются вещественными.

Исследование линейной системы уравнений проводится с помощью следующих утверждений:

1.Система двух линейных уравнений с двумя неизвестными имеет единственное решение тогда и только тогда, когда

а/а = в/в.

При этом, если хотя бы один из знаменателей равен нулю, то последнее неравенство надо понимать как

а*в = а*в.

2. Система двух линейных уравнений с двумя неизвестными не имеет решений тогда и только тогда, когда

а/а = в/в = с/с.

3. Система двух линейных уравнений с двумя неизвестными имеет бесконечно много решений тогда и только тогда, когда а/а = в/в = с/с.

Каждое уравнение системы определяет некоторую прямую на координатной плоскости. Если система имеет единственное решение, то прямые, задаваемые первым и вторым уравнениями, пересекаются. Если система имеет бесконечно много решений, то прямые совпадают. Если система не имеет решения, то прямые параллельны.

Системы алгебраических уравнений.

Р

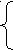ешите системы уравнений:

1. y - 3xy + x – y + 9 = 0,

y – x = 2.

Р е ш е н и е : ( 2+x)² - 3x(2 + x) + x + 11= 0,

4 + 4x + x² - 6x - 3x² + x + 11= 0,

-x² - 2x + 15 = 0,

х² + 2х + 15 = 0,

Д = 4 -4115 = 64,

- 2+ 8 - 2-8

х

= = 3; х= = - 5.

2 2

Найдём y:

1)если х = 3, то у = 5, 2) если х = - 5, то y = - 3.

Ответ: (-5;- 3), ( 3; -5).

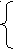
2. xy + y² + x = 5y,

x² + xy = 6y.

Р е ш е н и е: 1) Вычтем из второго уравнения первое:

х² – y² – x = y,

x² – y² = x + y,

(x + y) (x - y) = x + y,

(x + y) (x - y) - (x + y) = 0,

(x + y) (x – y - 1) = 0.

x = - y или x = y + 1.

Подставим выражение x:

- y² + y² = 6y или (y + 1)² + y(y + 1) = 6y,

0 = 6y, y² + 2y + 1+ y² + y = 6y,

у = 0. 2y² - 3y + 1 = 0,

Д = 9 - 4*2*1 = 1,

у = 1, у = 0,5.

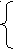
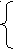
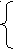3) Найдём x:

у = 1, у = 0,5, у = 0,

х = - 1. х = - 0,5. х = 0.

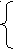
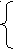
у = 1, у = 0,5, у = 0,

х = 2. х = 1,5. х = 1.

Ответ: (0, 0), (- 0,5, 0,5), (-1, 1), (1, 0), (1,5, 0,5), (2, 1).

Задания для самостоятельного решения.

Решите системы уравнений:

1 1 3

1

) y -3xy + x – x + y + 9 = 0, 2) + = 3) ху = 24,

x y 8 .

y – x = 2. х + у = 12. (х+1)(у-20)=20.

Системы линейных уравнений с параметром.

Р

ешить систему уравнений:

х + ау = 2,

2х + 5у = 7.

Решение. Умножим первое уравнение на 2 и вычтем из него второе

уравнение, получим

(2а - 5)у = - 3.

1) 2а = 5, 2) а ≠ 2,5.

а = 2,5. 3

0 * у = - 3, решений нет. у = ─────, х = 2 – ау,

5 – 2а 10 – 7а

х = ─────.

5 – 2а

Ответ: при а = 2,5: решений нет,

10 – 7а

при а ≠ 2,5: х = ─────.

5 - 2а

2х + ау = а + 2,

3х – у = 2.

Решение. Умножим первое уравнение на 3, а второе на (-2) и сложим

полученные уравнения: (3а + 2)у = 3а + 6 – 4,

(3а + 2)у = 3а + 2

3а + 2 = 0, 2) 3а + 2 ≠ 0,

а = -⅔, а ≠ - ⅔ ,

0 * у = 0, 2 + у у = 1, х = 1.

у € R, х = ───.

3

2 2 + у

Ответ: при а = ──: х = ───, у € R,

3 3

2

при а ≠ ──: х = 1, у = 1.

3

(а + 2)х + (а + 3)у = 4,

2х + 3у = 4.

Решение. а) а + 2 ≠ 0,

а ≠ - 2.

У

множим второе уравнение на (а + 2), первое на (- 2):

- 2 (а + 2)х – 2(а + 3)у = - 8,

2 (а + 2)х – 3(а + 2)у = 4(а + 2).

Решим систему способом сложения: ау = 4а,

2х + 3у = 4.

а = 0, 2) а ≠ 0,

* у = 0, у = 4,

у € R, х = 2 – 1,5у. х = 2 – 1,5у , х = - 4.

б) а = - 2,

у = 4,

х = - 4.

Ответ: при а = 0: х = 2 – 1,5у, у € R,

при а ≠ 0: х = - 4, у = 4.

ах + 3у = 4,

2х + ау = 3.

Р

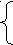ешение. а) а ≠ 0, тогда ах + 3у = 4, │*(- 2)

2х + ау = 3; │*а.

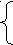- 2ах – 6у = - 8,

2ах + а²у = 3а;

а

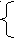х + 3у = 4,

(а² - 6)у = 3а - 8;

а² - 6 = 0, 2) а² - 6 ≠ 0,

а = √ 6 или а = - √ 6, 3а – 8 4 – 3у

0* у =3√ 6 – 8 или 0* у = -3√ 6 – 8; у = ────, х = ────,

а² - 6 а

4а² - 24 – 9а + 24

х = ───────────,

а( а² - 6)

4а - 9

х = ──── .

а² - 6

б

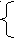) а = 0, тогда 3у = 4, При подстановке а = 0 получаем

2х = 3;

3 4

х = ─, у = ─.

2 3

Ответ: при а = ± √ 6: решений нет,

4а – 9 3а - 8

при а ≠ ± √ 6: х = ────, у = ────.

а² - 6 а² - 6

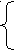
2х + 3у = 4 + а,

2х + 3у = 4.

Решение. Умножим второе уравнение на (- 1) и сложим его с первым

уравнением:

2

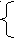х + 3у = 4.

0 = а. 4 – 2х

1) а = 0: у = ────, х € R.

3

а ≠ 0: решений нет.

4 – 2х

Ответ: при а = 0: у = ────, х € R.

3

при а ≠ 0: решений нет.

Задания для самостоятельного решения.

Решите системы уравнений:

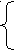ах + 3у = 2, 2 - х

2х + 6у = 4. Ответ: при а = 1: х € R, у = ────,

3

2

при а ≠ 0: х = 0, у = ─.

3

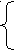3х - 2у = 1,

ах + 2у = 2. Ответ: при а = - 3: решений нет,

3 6 - а

при а ≠ - 3: х = ───, у = ────.

3 +а 6 + 2а

(а + 1)х +2у = 4,

3х +ау = 4. Ответ: при а = - 3: решений нет,

4 – 2у

при а = 2: х = ───, у € R,

3

4 – 3а - 4

при а ≠ - 3, а ≠ - 2: х = ───, у = ───.

а + 3 а + 3

2х + ау = 4,

ах + 5у = 7. Ответ: при а = ±√ 10 : решений нет,

7а – 20 4а - 14

при а ≠ ±√ 10 : х = ────, у = ────.

а² - 10 а² - 10

МОУ «Средняя общеобразовательная школа д.Шибково»

Решебник

Уравнения с параметром.

Составлен:

учащимися 10 класса

2004 – 2005 уч. год

Способы решения систем линейных уравнений.

В курсе алгебры ученики 7 класса научились решать системы линейных уравнений способом подстановки и способом сложения. На одном из занятий элективного курса я познакомила ребят еще с двумя способами решения систем линейных уравнений: алгоритм Гаусса и правило Крамера. Это очень удобный и часто используемый в самых разнообразных исследованиях математический аппарат.

Рассмотрим применение матриц и определителей к исследованию системы трех уравнений первой степени с тремя неизвестными x, y, z :

а₁x + b₁y + c₁z = h₁,

a₂x + b₂y + c₂z = h₂, (1)

a₃x + b₃y + c₃z = h₃.

(коэффициенты а₁, а₂, а₃, в₁, в₂, в₃, с₁, с₂, с₃ и свободные члены h₁, h₂, h₃ считаются заданными).

Определитель ∆ называется определителем системы (1). Определители ∆x, ∆y, ∆z получаются из определителя системы ∆ заменой свободными членами элементов соответственно первого, второго и третьего столбцов.

Если определитель ∆ системы (1) отличен от нуля, то существует, и притом единственное, решение этой системы, и оно выражается формулами Крамера: ∆х ∆у ∆z

х = ── , у = ── , z = ──. (2)

∆ ∆ ∆

В дальнейшем основную роль будут играть следующие четыре определителя:

а₁ в₁ с₁ h₁ в₁ с₁ а₁ h₁ с₁ а₁ в₁ h₁

∆ = а₂ в₂ с₂ , ∆x = h₂ в₂ с₂ , ∆y= а₂ h₂ с₂ , ∆z = a₂ в₂ h₂ .

а₃ в₃ с₃ h₃ в₃ с₃ а₃ h₃ с₃ а₃ в₃ h₃

Алгоритм Гаусса. Нахождение множества решений системы линейных уравнений основывается на том, что от заданной системы с помощью эквивалентных преобразований переходят к равносильной системе, которая решается «проще», чем исходная система. Эквивалентными преобразованиями системы линейных уравнеий

являются:

перемена местами двух уравнений в системе,
умножение какого-либо уравнения системы на действительное число с ≠ 0,
прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Формулы Крамера для решения систем линейных уравнений.

Рассмотрим пример. Найти все решения системы :

x + 2y +z = 4,

3x - 5y +3z = 1,

2x + 7y – z = 8.

Решение. 1 2 1

∆ = 3 -5 3 = 1*(-5)*(-1) + 3*7*1 + 2*3*2 – 2*1*(-5) – 1*3*7 – 3*2*(-1) = 33,

2 7 -1

4 2 1

∆х = 1 -5 3 = 4*(-5)*(-1) + 1*7*1 + 2*3*8 – 1*(-5)*8 – 4*3*7 – 1*2*(-1) = 33,

7 -1

1 4 1

∆у = 3 1 3 = 1*1*(-1) + 3*8*1 + 4*3*2 – 1*1*2 – 4*3*(-1) – 1*3*8 = 33,

8 –1

∆z = 3 -5 1 = 1*(-5)*8 + 3*7*4 + 2*2*1 – 2*(-5)*4 – 1*7*1 – 3*2*8 = 33.

2 7 8

Т.к ∆ = 33 ≠ 0, то данная система имеет единственное решение, определяемое формулами:

∆х 33 ∆у 33 ∆z 33

х = ── = ── = 1, у = ── = ── =1, z = ── = ── = 1.

∆ 33 ∆ 33 ∆ 33

Ответ: (1, 1, 1)

2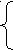x + y + 3z = 9,

x - 2y + z = -2,

3x + 2y + 2z = 7.

Р

ешение.

2 1 3 9 1 3 2 9 3 2 1 9

∆ = 1 -2 1 = 13, ∆х = -2 -2 1 = - 13, ∆у = 1 -2 1 = 26, ∆z = 1 -2 -2 = 39.

3 2 2 7 2 2 3 7 2 3 2 7

∆х 13 ∆у 26 ∆z 39

х = ── = ── = - 1, у = ── = ── = 2, z = ── = ── = 3.

∆ - 13 ∆ 13 ∆ 13

Ответ: (-1, 2, 3)

Метод Гаусса.

Рассмотрим несколько примеров.

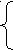x + 2y +z = 4,

3x - 5y +3z = 1,

2x + 7y – z = 8.

Решение. 1 2 1 4 1 2 1 4 1 2 4 4 1 2 4 4

3 -5 3 1 ~ 0 -11 0 -11 ~ 0 1 0 1 ~ 0 1 0 1

2 7–1 8 0 3 –3 0 0 1-1 0 0 0 –1 1

z = 1, y = 1, x = 1.

Ответ: (1, 1, 1).

2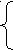x + y + 3z = 9,

x - 2y + z = -2,

3x + 2y + 2z = 7.

Решение.

2

1 3 9 1 -2 1 -2 1 -2 1 -2 1 -2 1 -2

1 -2 1 -2 ~ 2 1 3 9 ~ 0 5 1 13 ~ 0 1 0,2 2,6 ~

3 2 2 7 3 2 2 7 0 8 –1 13 0 8 -1 13

1 -2 1 -2 1 -2 1 -2 z = 3,

~ 0 1 0,2 2,6 ~ 0 1 0,2 2,6 y = 2,6 - 0,2* 3 = 2

0 0 -2,6 7,8 0 0 1 3 x = - 2 + 4 – 3 = -1.

Ответ: (- 1, 2, 3).

Содержание.

Диофантовые уравнения.
Алгебраические уравнения.
Исторические задачи (математика для ленивых).
Системы алгебраических уравнений.
Способы решения систем линейных уравнений.

Содержание.

Уравнения с параметрами.

Линейное уравнение.
Уравнения, приводимые к линейным.
Квадратные уравнения.
Уравнения, сводящиеся к квадратным.

Примеры решения экзаменационных задач.
Системы алгебраических уравнений.

Системы линейных уравнений с параметром.
Формулы Крамера.
Метод Гаусса.

Задания для самостоятельного решения

(a + 5)*x = -10,
(-2a+6)*x = 5,
(3a²-7a + 4)*x = -3
(-a²+3a+5)*x = 7

Blog

Семина Лилия Анатольевна 2010- 2011 уч год пояснительная записка

Содержание

Справочник

Составлен:

учащимися 9 класса

Р е ш е н и е : ( 2+x)² - 3x(2 + x) + x + 11= 0,

х² + 2х + 15 = 0,

Д = 4 -4*1*15 = 64,

Составлен:

учащимися 10 класса

Решение. 1 2 1

Д = 4 -4115 = 64,