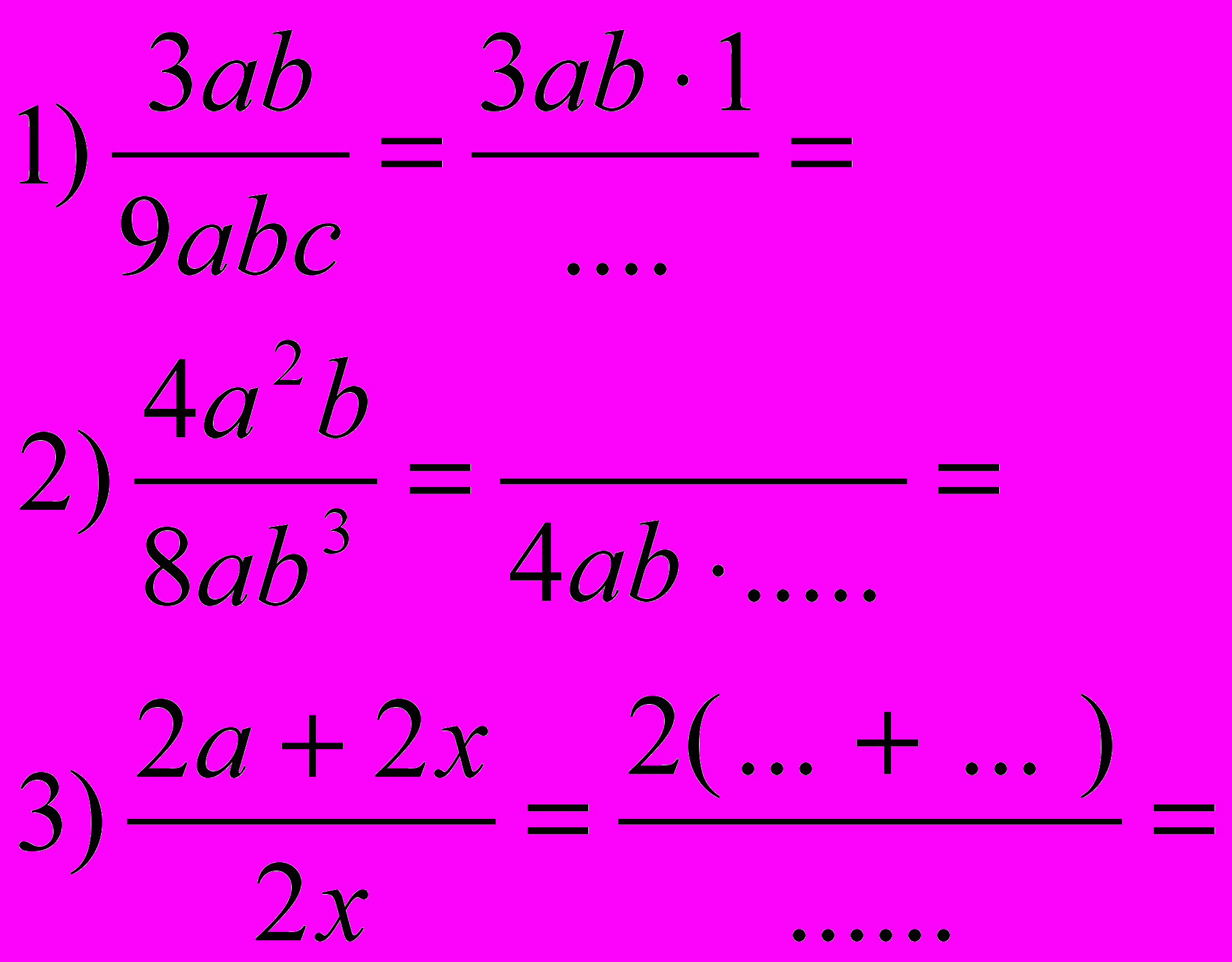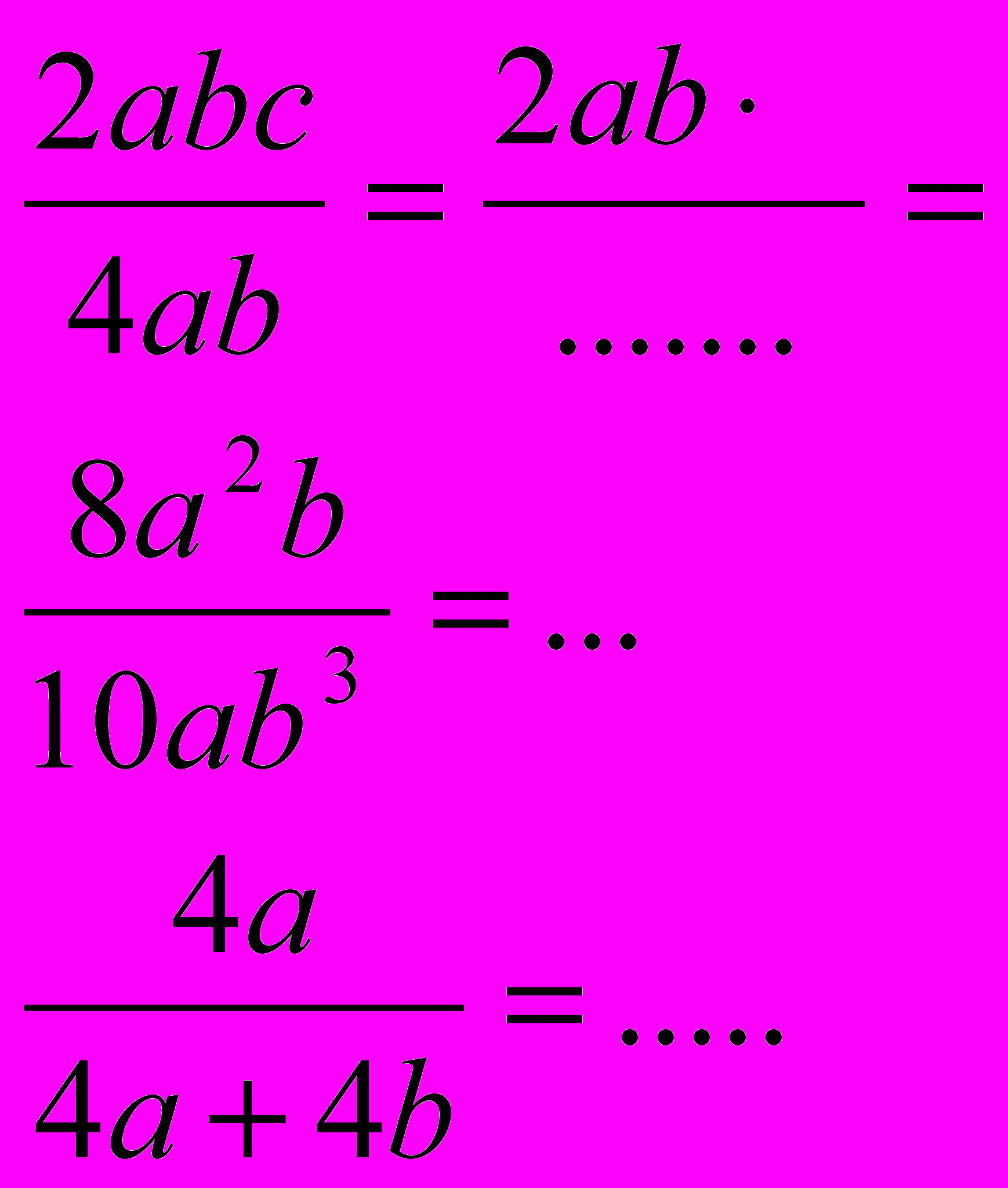Разложение многочлена на множители

Вид материала

Документы

Содержание Выделение полного квадрата

Подобный материал:

• План-конспект урока-путешествия в 7-м классе учителя математики Боярович В. С. по теме, 42.45kb.
• План-конспект открытого урока по теме: «Разложение многочленов на множители», 74.23kb.
• Урок по алгебре в 7 классе на тему: «Применение различных способов для разложения, 194.49kb.
• Изучение алгебры и теории чисел с помощью системы компьютерной алгебры gap, 88.13kb.
• Разложение многочленов на множители” (7 класс), 38kb.
• Кейс по алгебре №1 для 7 класса по теме «математический язык, математическая модель», 257.87kb.
• Разложение на множители суммы и разности кубов, 43.62kb.
• Календарно-тематический план учебная дисциплина: «Математика», 31.74kb.
• Счисления. Римская нумерация. Арифметические действия над натуральными числами. Степень, 88.12kb.
• I I. Действия над многочленами. III. Комплексные числа >IV. Разложение многочленов, 201.14kb.

Разложение многочлена на множители

1) вынесение общего множителя за скобки

Правило: для того чтобы вынести за скобки общий множитель, надо:

– выделить наибольший общий делитель коэффициентов

– выделить буквы в наименьшей степени

– вынести общий множитель за скобки, в скобках будет столько,

сколько было слагаемых в условии.

3х − 3у = 3 ∙ х − 3 ∙ у = 3(х − у)

aх + ab = a ∙ x + a ∙ b = a(x + b)

2a − 10 = 2 ∙ a − 2 ∙ 5 = 2 (a − 5)


a² − a = a ∙ a − a ∙ 1 = a (a −1)


3(a+b) + x(a+b) = (a+b)(3+x)

(х − у)² + (х − у) = (х − у)(х − у) + 1 ∙ (х − у) = (х − у)(х − у + 1)


2(а − b) − a(b − a) = 2(a − b) + a(a − b) = (a − b)(2 + a)

(a − b) = − (b − a) − смена знака


3xy² + 9x²y³ −12x³y⁴ =

− выделяем общий множитель для чисел (коэффициентов) − наибольший общий делитель − НОД(3;9;12) = 3

− выделяем общий множитель среди степеней с одинаковым основанием − степень с наименьшим показателем − x¹y²


= 3xy² ∙ 1 + 3xy² ∙ 3ху − 3xy² ∙ 4х²у² = 3xy² (1 + 3ху −4х²у²)




3xy² 9x²y³ 12x³y⁴


2) применение ФСУ.

a² − b² = (a − b)(a + b) − разность квадратов

a² −2ab + b² = (a − b)² − квадрат разности

a² +2ab + b² = (a + b)² − квадрат суммы

3) способ группировки


а ²+ аx + 2a + 2x = (a² + аx) + (2a + 2x) = a(а+ x) + 2(a + x) = (a + x)(a + 2)


Выделение полного квадрата




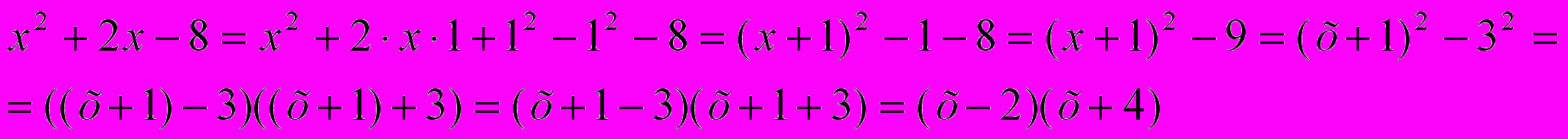
Сокращение алгебраических дробей

Допустимые значения алгебраической дроби – значения буквы, входящей в дробь, при которых знаменатель не равен нулю.



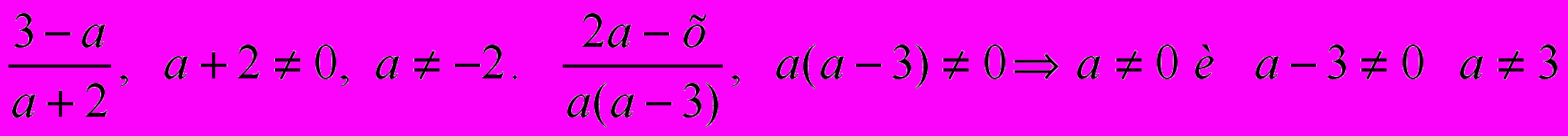
Все значения а, кроме а =-2 все значения а ,кроме 0 и 3

Дробь можно сократить только на общий множитель, входящий одновременно и в числитель и в знаменатель дроби.

Основное свойство дроби: величина дроби не изменится если числитель и знаменатель разделить или умножить на одно и то же число.



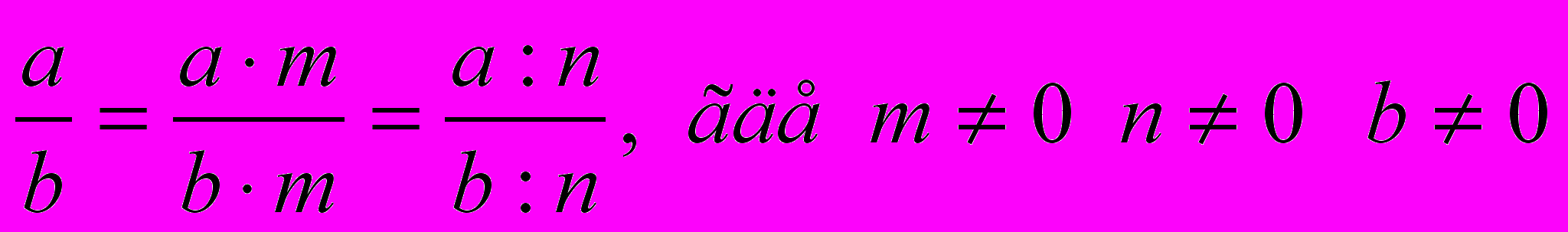
Чтобы сократить дробь надо:

1) выделить общий множитель для числителя и знаменателя

2) разделить числитель и знаменатель на общий множитель



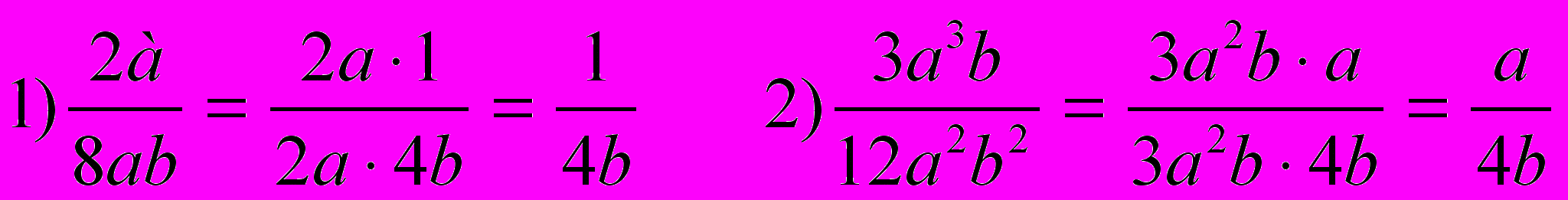
3) если числитель и знаменатель алгебраические суммы,

то необходимо разложить их на множители

4) разложение выполнять по алгоритму 1) 2)




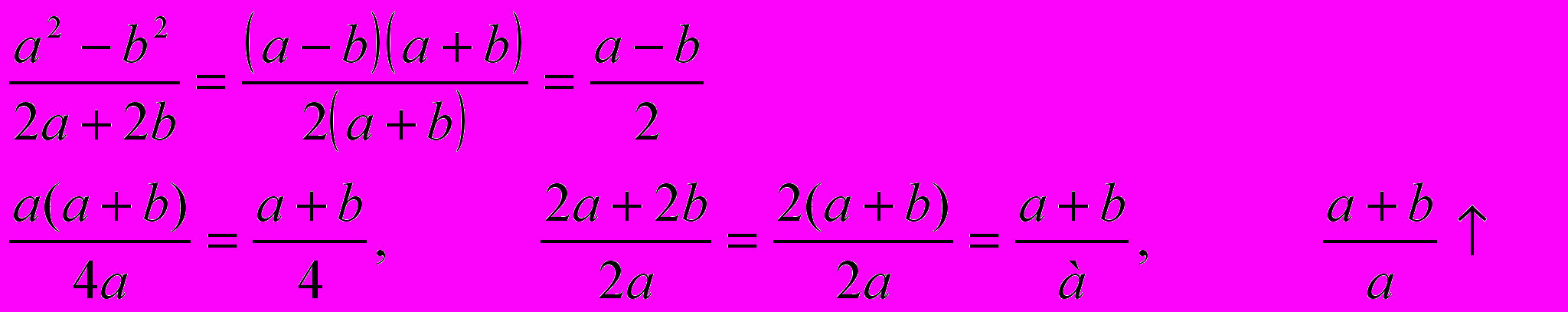
Сократить нельзя


Сам-но с проверкой у учителя самостоятельно