Активізація пізнавальної діяльності учнів

Вид материала

Урок

Содержание Найпростіше доведення 2.Доведення Евкліда Алгебраїчне доведення CD із вершини прямого кута С Sabed= (de+ab)*ad/2.

Подобный материал:

• Активізація навчально-пізнавальної діяльності учнів на уроках математики, 19.25kb.
• Активізація пізнавальної діяльності учнів на уроках хімії, 98.22kb.
• Активізація пізнавальної діяльності учнів на уроках географії, 30.16kb.
• Активізація пізнавальної діяльності шляхом впровадження інтерактивних технологій, 185.2kb.
• Компанієць А. Г, 27.85kb.
• Розвиток пізнавальної активності учнів на уроках математики, 12.55kb.
• Василя Симоненка Черкаської міської ради. Проблема досвіду: Активізація пізнавальної, 83.7kb.
• План. І. Вступ. ІІ. Шляхи І методи активізації розумової діяльності учнів на уроках, 183.28kb.
• Методичні рекомендації для вчителів початкових класів щодо стимулювання навчально-пізнавальної, 114.31kb.
• З м І с т № з/п Найменування теми Стор. Введення 2 1 Активізація розумової діяльності, 151.32kb.

Активізація пізнавальної діяльності учнів

на уроках математики.

Лукова С.М.- вчитель

математики ЗОШ-2

Що найцінніше для людини? «Здоров’я», - не задумуючись відповість кожний. А мені хочеться додати: «Думка». Настільки дивна захоплююча наука математика. Як сказав американський фізик Р. Фейнман:

«Математика – це мова плюс міркування, це наче мова і логіка

разом.

Математика – це знаряддя для міркування. У ній концентровані

мислення багатьох людей.»

Це відкриття слід донести учням якнайраніше. Ось чому провідна ідея в педагогіч-ній і методичній практиці – максимально розкрити перед учнем спектр застосування математичних знань, передати своє захоплення предметом вихованцям.

Працюючи в школі, визначила, що навчання – це систематична праця вчителя і учня. Сьогодні важливо обирати оптимальні варіанти організації навчального процесу, адже освіта повинна бути орієнтована на формування розумової діяльності, щоб сформувати особистість, яка обов’язково знайде своє місце у житті.

Школа не в змозі дати учневі таку суму знань, яка необхідна йому на все життя. Але вона може навчити його вчитися, керувати своєю діяльністю

Саме в цьому аспекті навчання я застосовую принцип свідомості, активності і самостійності навчання.

Цей принцип полягає в цілеспрямованому сприйнятті явищ, що вивчаються, їх осмисленні, творчій переробці й застосуванні.

Найголовнішою формою навчання завжди був і залишається урок-чітко продуманий, організований, цікавий, де кожен учень залучений до активної пізнавальної діяльності. Викладаючи математику, вчителю необхідно шукати у своїй творчій скарб -ниці важелі емоційного впливу на свідомість учнів, які сприяли б активізації пізнава -льних факторів дитячого сприйняття, всебічному засвоєнню складного матеріалу, кращому узагальненню вивченого, застосуванню нових прийомів, створенню атмосфери співробітництва, нестандартності та не типовості. Це налаштовує дітей на спокійний емоційний настрій сприйняття, підвищує інтерес до всього. Засвоювання дитячої уваги на тривалий період дає змогу отримати бажаний результат уроку.

Для того, щоб підвищилась ефективність уроків я вважаю доцільним :

• зробити мету уроку – метою учнів
  
• учити дитину позитивно ставитись до себе
  
• створити атмосферу зацікавленості для кожного учня, можливості реалізувати себе у навчанні.
  

Відомо, що діти йдуть до школи за спілкуванням з друзями і учителем.

Життя – одне і ці 45 хвилин ніколи не повторяться. Найбільшу радість і задоволення учні отримують від роботи на уроці. Це дозволяє відкрити себе та свої здібності. Очі у дітей загоряються в той момент, коли їх навчають чомусь значному, важливому в житті, а не для отримання оцінок.

Розкрити особистість учня можливо, якщо вчитель йтиме на урок не тільки зі знанням навчального матеріалу. Методів і прийомів навчання чи набором красивих задач і вмінням їх майстерно розв’язувати, а тоді коли застосовує різноманітні цікаві способи і прийомами організації праці учнів.

Багато традиційних методів викладання на сьогоднішній день малоефективні і не допомагають розвивати інтерес до вивчення математики.

Ігрові методи і форми навчання суттєво відрізняються від традиційних тим, що дають змогу учню безпосередньо стати учасником ситуації чи події.

На мою думку, майбутнє за системою навчання, що вкладається в схему « учень – технологія – учитель ».

Процес навчання потребує напруженої розумової роботи і власної активної участі в цьому процесі. Пояснення і демонстрація, самі по собі ніколи не дадуть справжніх, стійких знань.

Цього можливо досягти тільки за допомогою інтерактивного навчання, яке дозволяє учням самостійно брати участь в отриманні знань.

Самостійність – це властивість особистості діяти самій, без сторонньої допомоги або керівництва , здатність на незалежні усвідомлені дії та вчинки.

Відомо, що будь-яка риса особистості розвивається в процесі відповідної діяльності. В навчальному процесі на уроці самостійність може розвиватися в учнів лише під час виконання самостійних робіт. Без самостійної роботи учнів не можна виробити в них жодних навчальних і життєво-практичних вмінь та навичок. Психологи вважають, що найбільшу цінність становлять ті знання, які досягнуті власною працею, тобто в процесі самостійної роботи.

Кожен учень – це особистість, і яким він у майбутньому буде, залежить від нас, вчителів. Одним математика дається легко, іншим – ні. Ті , хто якимось чином пристосувались до вимог і темпу учителя, - гарні учні, а хто ні – невдахи. А як навчати так , щоб усі без винятку накопичували тільки успіх?

Технології інтерактивного навчання:

• кооперативне навчання;
  
• колективно – групова робота;
  
• ситуативне моделювання;
  
• дискусійне навчання.
  

Саме до технологій ситуативного моделювання відносять гру. Навчально – ігрове спілкування важливе тим, оскільки виконує такі функції:

• виховну – розкривається почуття колективізму, сміливості, рішучості,
  

виховуються морально-етичні якості;

• пізнавальну – розвиток пізнавальної активності, збагачення знань
  

новою інформацією;

• гедонічну – переживаються раніше невідомі відчуття, формується
  

оптимальний життєрадісний настрій;

• компенсаторну – через гру знімається психогенне і фізичне
  

напруження, підвищується загальний тонус,

з’являється почуття розкутості.

Дітям подобаються такі форми і методи вивчення математики, коли складні задачі стають зрозумілими, а процес вивчення цікавим, захоплюючим, творчим.

Щоб зацікавленість учнів до вивчення математики не знижувалась, намагаюсь проводити ігри з використанням інтерактивних технологій.

Тема	Клас	Гра
«Натуральні числа»	5 кл	«Козацькому роду нема переводу»
«Подільність чисел»	6 кл	«Подорож у країну ознак подільності»
«Звичайні дроби»	6 кл	«Подорож з дробами» Магічні квадрати
«Відношення і пропорції»	6 кл	Кросворд, естафета
«Додавання»	6 кл	«Математичний хокей»
«Вирази та рівняння»	7 кл	«Сім чудес світу»
«Трикутник»	7 кл	«Магія трикутника»
«Многочлен»	7 кл	«Подорож країною динозаврів»
«Квадратні рівняння»	8 кл	«Сім чудес України»

Розробка нової гри, ігрової ситуації не викликає труднощів, за основу беруться будь-які відомі ігри і змінюються відповідно до вимог потрібної теми. Наприклад ігри: «30 сек на роздуми», «Знайди помилку», «Поле чудес»

Батьки відмічають, що таке вивчення математики є легшим, цікавішим. Діти із захопленням розповідають про такі уроки. [Додаток 1: Гра].

Пригадаємо вислів Яна Снядецького:

«Математика – цариця всіх наук.

Її улюблениця – істина,

її вбрання – простота і ясність.»

На жаль не завжди у процесі викладання учні чітко усвідомлюють можливості проникнення математики до інших наук, не підозрюють між предметні зв’язки.

(слайди уроку «Козацькому роду нема переводу»)

Як приклад застосування: 5 клас, урок «Козацькому роду нема переводу» був проведений під час тижня математики. На ньому були присутні не тільки математики, а й вчителі історії, української літератури, українознавства.

Ще одним способом активізації пізнавальної діяльності учнів є націлювання їх на розв’язування однієї і тієї ж задачі кількома способами.

Так, у 7 класі під час вивчення теми «Розкладання многочленів на множники» маємо:

І спосіб: ab + ac + xb + xc = ( ab + ac) + ( xb +xc) = a ( b + c ) + x ( b + c )

= ( b + c ) ( a + x)

ІІ спосіб: ab + ac + xb + xc = ( ab + xb ) + ( ac + xc ) = b (a + x ) + c ( a + x )

= ( a + x ) ( b + x )

Великий інтерес викликає в учнів 8 класу доведення теореми Піфагора кількома способами:

1. Найпростіше доведення
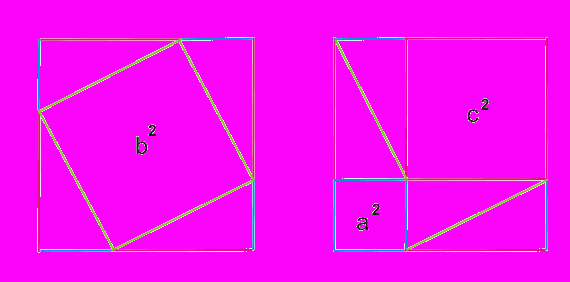
   Розглянемо квадрат, показаний на рисунку.
   Сторона квадрата рівна
   

a + c.

В першому випадку (зліва) квадрат розбито на квадрат зі стороною b і чотири прямокутних трикутника з катетами a і c.

В другому випадку (справа) квадрат розбито на два квадрата зі сторонами a і c і чотири прямокутних трикутника з катетами a і c.

Таким чином, одержуємо, що площа квадрата зі стороною b рівна сумі площ квадратів зі сторонами a і c.

2.Доведення Евкліда

Дано: ABC-прямокутний трикутник

Довести: SABDE=SACFG+SBCHI

Доведення:

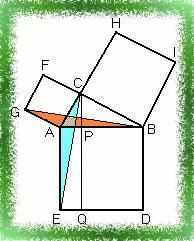
Нехай ABDE-квадрат, побудований на гіпотенузі прямокутного трикутника ABC, а ACFG і BCHI-квадрати, побудовані на його катетах. Опустимо із вершини C прямого кута перпендикуляр CP на гіпотенузу і продовжимо його до перетину зі стороною DE квадрата ABDE в точці Q; з’єднаємо точки C і E, B і G.

Очевидно, що кути CAE=GAB(=A+90°); звідси випливає, що трикутники ACE і AGB (зафарбовані на рисунку) рівні між собою (за двома сторонами і кутом, між ними). Порівняємо трикутник ACE і прямокутник PQEA; вони мають спільну основу AE і висоту AP, опущену на цю основу, звідси SPQEA=2SACE

Точно так само квадрат FCAG і трикутник BAG мають спільну основу GA і висоту AC; отже, SFCAG=2SGAB

Звідси і з рівності трикутників ACE і GBA випливає що прямокутник QPBD і квадрат CFGA - рівновеликі; аналогічно доводиться що прямокутник QPAE і квадрат CHIB -рівновеликі. А звідси випливає, що квадрат ABDE рівний сумі квадратів ACFG і BCHI, тобто теорема Піфагора.

2. Алгебраїчне доведення
   

Дано: ABC-прямокутний трикутник

Довести: AB2=AC2+BC2

Доведення:


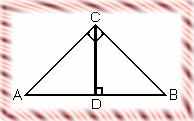
1) Проведемо висоту CD із вершини прямого кута С.
2) За означенням косинуса кута соs А= AD:AC= AC:AB, звідси випливає AB ∙AD=AC.

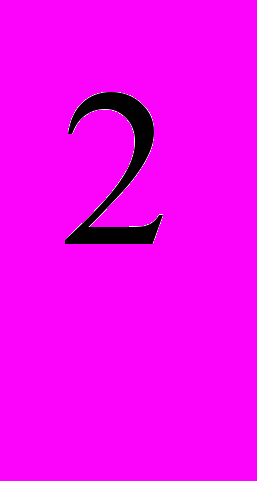3) Аналогічно соsВ =BD:BC=BC:AB, отже AB ∙ BD=BC.

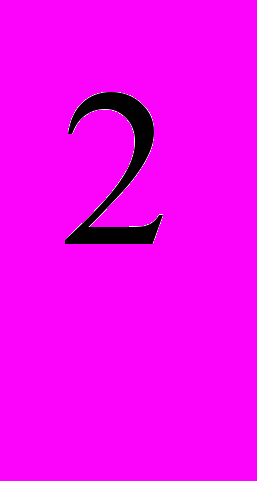4) Додавши отримані рівності почленно, одержимо:

AC2+BC2=АВ*(AD + DB)

AB2=AC2+BC2.

Що і потрібно було довести.

3. Геометричне доведення
   

Дано: ABC-прямокутний трикутник

Довести: BC2=AB2+AC2

Доведення:


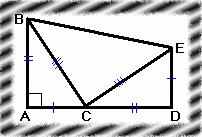
1) Побудуємо відрізок CD рівний відрізку AB на продовженні катета AC прямокутного трикутника ABC. Опустимо перпендикуляр ED до відрізка AD, рівний відрізку AC, з’єднаємо точки B і E.
2) Площу фігури ABED можна знайти, якщо розглядати її як суму площ трьох трикутників:

SABED=2*AB*AC/2+BC2/2

3) Фігура ABED являється трапецією, отже, її площа дорівнює:

SABED= (DE+AB)*AD/2.

4) якщо прирівняти ліві частини знайдених виразів, то одержимо:

AB*AC+BC2/2=(DE+AB)(CD+AC)/2

AB*AC+BC2/2= (AC+AB)2/2

AB*AC+BC2/2= AC2/2+AB2/2+AB*AC

BC2=AB2+AC2.

   Це доведення було опубліковано в 1882 році Герфілдом.

Ще один спосіб за допомогою якого можна підвищити інтерес учнів до математики – це вправи з набором відповідей, тобто тести.

Про результати роботи над цією темою я доповідала на засіданні метод об’єднанні: «Шляхи підвищення методичного викладання математики». Де ми з колегами обговорювали доцільність застосування ігрових методів навчання на уроках математики.

Одне з головних завдань вчителя математики – навчити учнів самостійно працювати, оскільки темпи надходження наукової інформації надзвичайно зросли. Тому при організації самостійної роботи дуже важливо допомогти учням самостійно впоратися із завданням і в результаті побачити на його обличчі посмішку. Працюючи самостійно, учні, як правило, глибше вдумуються у зміст матеріалу, що опрацьовується, краще зосереджують свою увагу. Тому знання, уміння і навички, набуті учнями в результаті самостійної роботи, бувають міцнішими і ґрунтовнішими. Крім того, в процесі самостійної роботи в учнів виховуються наполегливість, уважність, витримка.

Моє завдання - допомогти учневі скласти з окремих відомих фактів цілісну систему, сприяти формуванню власної думки. Учень ніколи не піднімається до рівня знань вчителя, якщо постійно буде відчувати його перевагу. Тому запровадження нового і цікавого, творчий пошук – основний зміст сучасної роботи, багатьох проблем сучасної методики важливою і актуальною є формування пізнавальних інтересів школярів. Адже там , де є інтерес до предмета, матеріал засвоюють глибше, повніше і міцніше, а де навчання ґрунтується на принципах примусу, панують пасивність, які зводять нанівець продуктивність навчальної діяльності.

Практично кожній людині, яка хоче мати роботу та продуктивно працювати, потрібно весь час оновлювати свої знання, а то й переучуватись, а це можливо за наявності умінь і навичок самостійної роботи.

Кожний вчитель любить свій предмет і вважає його найголовнішим у навчальному плані. Я теж вважаю, що таким предметом є математика. Тому на уроках я вчу дітей , що математика є основою сучасного виробництва, є основою розвитку науки і техніки, нових технологій, що її розвиток сприяє покращенню добробуту людей, підвищенню інтелектуального розвитку суспільства, допомагає розуміти світ і своє призначення в ньому. І тому її треба вчити всім , щоб відчувати щасливим себе і бажати зробити щасливими інших.

Ви побачили, почули творчі пошуки, спроби їх реалізації. Праця вчителя – постійний творчий пошук Математику люблять одиниці, хочуть знати десятки, а навчити треба всіх.

Я бажаю всім вам :

- натхнення;

- стійкості;

- творчих злетів;

- постійного пошуку;

- активних зацікавлених учнів;

- високих результатів праці.