Урок по геометрии преподаватель математики
| Вид материала | Урок |
- Урок общественная лекция по теме : «Развитие геометрии как науки экскурс в историю», 48.39kb.
- Урок по геометрии и русскому языку на тему «Четырехугольники», 85.99kb.
- Программа курса повышения квалификации учителей математики, 15.17kb.
- Урок усвоения новых знаний Учитель математики Чурсинова, 108.42kb.
- Тема: Геометрия на службе архитектуры, 341.17kb.
- Базовая учебная программа дисциплины «Основания геометрии» для студентов специальности, 51.22kb.
- Урок «Путешествие в музей геометрии» Тип, 151.51kb.
- Ерилова Г. Ф., учитель математики моу сош №33 г. Томска Нетрадиционные формы контроля, 248.47kb.
- Задачи преподавания геометрии в школе. Различные способы построения школьного курса, 75.88kb.
- Математики история, 1398.68kb.
ОТКРЫТЫЙ УРОК ПО ГЕОМЕТРИИ

Преподаватель математики:
Максимова Светлана Владимировна
Введение.
Применение информационно-коммуникационных технологий в обучении математике, как, наверное, и любого другого предмета, объясняется необходимостью решения проблемы поиска путей и средств активизации познавательного интереса учащихся, развития их творческих способностей, стимуляции умственной деятельности. Новые технологии обучения на основе информационных и коммуникационных позволяют интенсифицировать образовательный процесс, увеличить скорость восприятия, понимания и глубину усвоения огромных массивов знаний.
Воздействие учебного материала на учащихся во многом зависит от степени и уровня иллюстративности учебного материала. Визуальная насыщенность учебного материала делает его ярким, убедительным, способствует лучшему его усвоению и запоминанию.
Данная обучающая программа может быть использована при изучении в 10 классе темы «Построение сечений многогранников», входящей в раздел «Параллельность прямых и плоскостей». Этот блок уроков последний по теме «Тетраэдр и параллелепипед», поэтому необходимо начинать с повторения пройденного теоретического материала, что в свою очередь приведёт к осмысленному построению сечений многогранников и усвоению всей темы.
При работе с демонстрациями наиболее целесообразна работа в едином темпе. Поэтому выбираемая в данном случае фронтальная форма обучения предполагает работу всего класса по реализации конкретной дидактической задачи, достижение которой становится возможным при активном взаимодействии учащихся друг с другом и с учителем. При этой форме организации обучения ученики выполняют общее для всех задания в едином, усредненном темпе.
Предлагаемый урок предусматривает самостоятельную работу учащихся по отработке и закреплению нового материала с использованием раздаточного материала, содержащий рисунки многогранников, с последующей проверкой. В конце урока подводится итог урока – повторение нового изученного материала и оценка своей практической работы на уроке, для осознанного выполнения работы над ошибками и домашнего задания в целом.
Тип урока: Урок объяснения новой темы
Цель урока: Сформировать умение строить сечения многогранников плоскостью, проходящей через три заданные точки на примере тетраэдра и параллелепипеда.
Задачи урока:
- Обучающие:
- ввести определение секущей плоскости и сечения многогранника плоскостью;
- сформулировать алгоритм построения точки пересечения прямой и плоскости;
- сформулировать алгоритм построения сечение многогранников плоскостью.
- Развивающие:
- продолжить формирование пространственного воображения и математической речи;
- развивать аналитическое мышление при выработке алгоритма построения точки пересечения прямой и плоскости и сечение многогранников.
- Воспитывающие:
- вырабатывать умение осознанно трудиться над поставленной целью;
- воспитание культуры общения.
Приемы учебной деятельности:
- Применение знаний и способов деятельности в новой ситуации
- Самоконтроль
Материально-техническое обеспечение урока:
Интерактивная доска, компьютер, раздаточный материал, интерактивная доска SMART Board (программное обеспечение Notebook),программное обеспечение Microsoft PowerPoint для просмотра слайдов.
Формы обучения: Сочетание фронтальной и индивидуальной форм при повторении и актуализации знаний и умений.
Методы обучения: Методы диагностики, методы повторения, актуализации, проверки и самопроверки знаний и умений. Наглядные методы.
План урока
| Этап урока | Содержание | Слайды | Время (мин) |
| 1) Организационный этап | Включение всех учащихся в работу. Сообщение темы и цели урока. | 2 | 2 |
| 2) Этап повторения. Подготовки учащихся к активному усвоению знаний | Повторение теоретического материала. | 3-4 | 33 |
| 3) Этап изучения новой темы. | Знакомство с новыми понятиями. Составление алгоритма действий, используя знания и навыки в новой ситуации. | 5-6 (презентация) | |
| 4) Этап отработки полученных знаний | Разъяснения и пояснения нового материала в процессе выполнения упражнений и самостоятельной работы. | 6 (презентация) | 40 |
| 5) Подведение итогов урока | Анализ достижения цели урока. Домашнее задание | 6-7 (презентация) | 5 |
Ход урока
1) Организационный этап Презентация
Слайд1

Природа говорит языком математики:
буквы этого языка – круги, треугольники
и иные математические фигуры
Галилей
Геометрия представляет собой могущественный инструмент познания природы и создания техники. В основе всей техники, так или иначе, лежит геометрия, потому что она появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров.
Посмотрите, многогранники вокруг нас. На предыдущих уроках мы начали знакомство с ними на примерах тетраэдра и параллелепипеда. Сегодня мы познакомимся с аксиоматическим методом построения сечения многогранников плоскостью, проходящих через три точки, не лежащих на одной прямой. Будьте внимательны и постарайтесь в ходе урока выяснить все непонятные для вас моменты. И так, тема урока.
Слайд 2 Запишите в тетрадях число и тему урока. Какие же задачи мы должны с вами решить? На какие вопросы должны ответить? Постановка целей урока
2) Этап повторения. Подготовки учащихся к активному усвоению знаний
Слайд 3.Повторение с помощью кроссворда.
Слайд 4 Вспомним необходимый теоретический материал для выполнения построений. По данным рисункам сопоставьте аксиому или теорему с чертежом.

3) Этап изучения новой темы.
Слайд 5 Введем определение секущей плоскости и сечения многогранника с плоскостью. Что же нужно уметь для построения сечения? (Ответы учащихся.) Необходимо научиться строить точку пересечения прямой и плоскости.
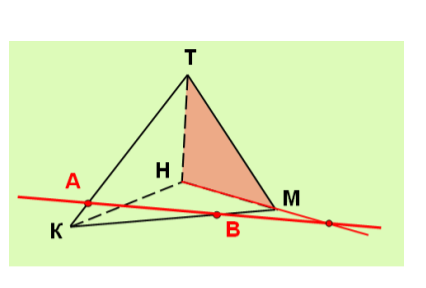
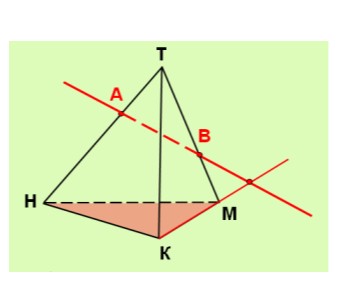
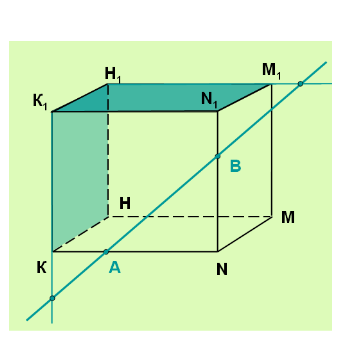
Слайд 6 Задание № 1. Постройте точку пересечения прямой с выделенной плоскостью. (Фронтальная работа с классом по составлению алгоритма построения искомой точки.) Где лежит выделенная прямая? Где должна лежать общая точка и почему? Укажите план построения. Запишите план построения. Сформулируйте алгоритм построения точки пересечения прямой с выделенной плоскостью.
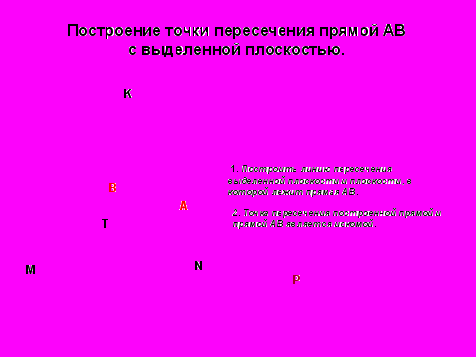
Задание № 2 (устно). Проверьте правильность построения точки, укажите ошибку, если есть и предложите свой план построения точки.
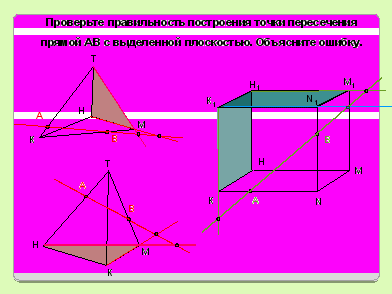
4) Этап отработки полученных знаний
Задание № 3 (самостоятельная работа). Постройте точку пересечения прямой с выделенной плоскостью. (Во время проведения самостоятельной работы, для тех, кто затрудняется, на экране высвечивается алгоритм построения точки)
Проверьте правильность построения точки, исправьте ошибку, оцените свою работу (Без ошибок – 5, 1 ошибка – 4, 2 ошибки – 3).
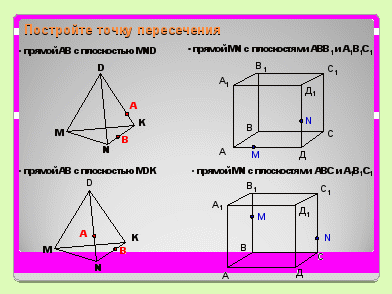
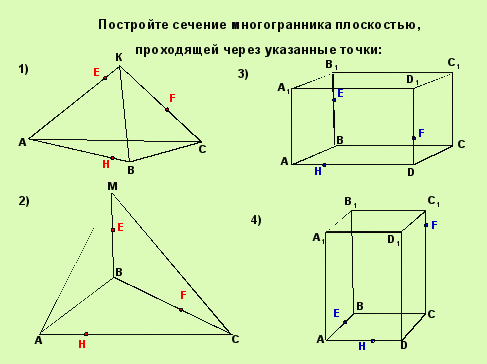
Задание № 4. Постройте сечение многогранника с плоскостью, проходящего через три выделенные точки. (Фронтальная работа с классом по составлению алгоритма построения искомого сечения.) Какие отрезки сечения можно провести и почему? Как построить общую точку сечения и нижней грани? и.т.д. Укажите план построения. Запишите план построения. В чем особенность построения сечения параллелепипеда, какую теорему нужно использовать?
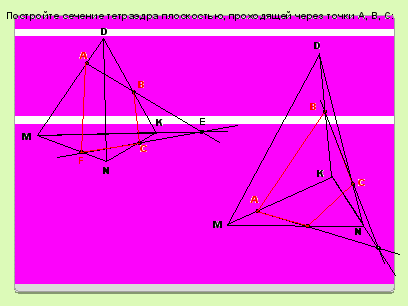
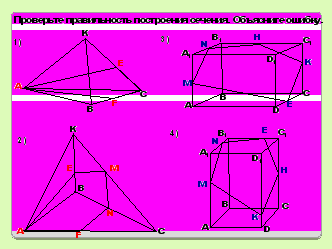
Задание № 5 (устно). Проверьте правильность построения сечения, укажите ошибку.
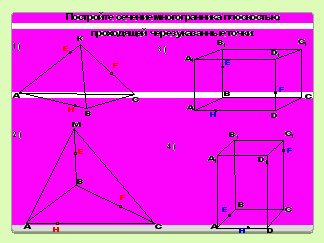
Задание № 6 (самостоятельная работа). Постройте сечение многогранника с плоскостью, проходящего через три выделенные точки.Проверьте правильность построения сечения, исправьте ошибку, оцените свою работу (Без ошибок – 5, 1 ошибка – 4, 2 ошибки – 3).
5) Подведение итогов урока
Подведение итогов урока. Выставление оценок. (В журнал выставляются только оценки «5» и «4».)
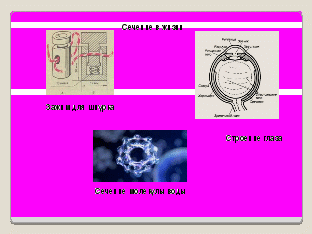
Слайд 7 Сечения в жизни.

Приложение 1
Приложение 2
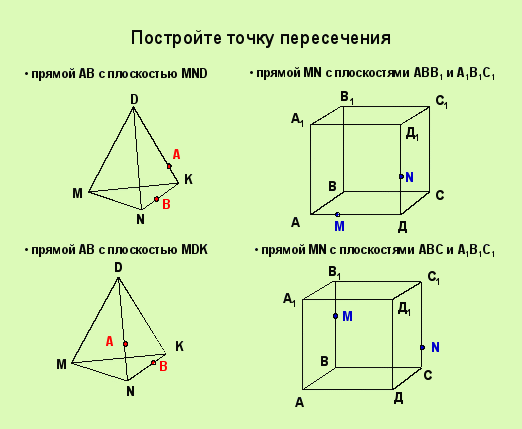
Приложение 3
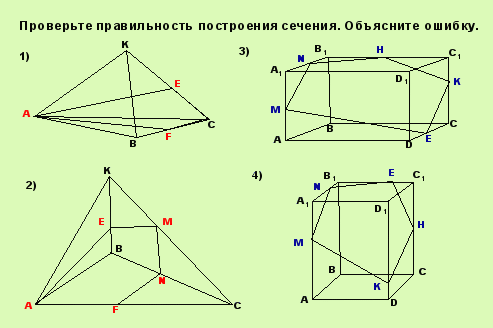
Приложение 4