«Российский государственный педагогический университет им. А. И. Герцена»

Вид материала

Автореферат

Содержание В четвертом и пятом параграфах Парадоксальность физического мышления В шестом параграфе Во второй главе Развитие математического моделирования Выбор языка описания, т.е. набора физических величин и понятий В третьей главе В третьей главе В пятой главе Шестая глава На уровень овладения методологией На общий уровень освоения предметных знаний Деятельностно-коммуникативная составляющая) Положительная динамика проявления познавательных интересов Положительная динамика проявления интереса у обучающих

Подобный материал:

• «Российский государственный педагогический университет им. А. И. Герцена», 374.58kb.
• «Российский государственный педагогический университет им. А. И. Герцена», 586.79kb.
• «Российский государственный педагогический университет им. А. И герцена», 581.63kb.
• Утверждаю первый проректор гоу впо российский государственный педагогический университет, 4472.86kb.
• Вуза: Российский государственный педагогический университет имени А. И. Герцена,, 154.47kb.
• Четвертая всероссийская научно-практическая конференция с международным участием «здоровье, 77.66kb.
• Российский государственный педагогический университет им. А. И. Герцена, 24.03kb.
• «Российский государственный педагогический университет имени А. И. Герцена», 601.25kb.
• «Российский государственный педагогический университет имени А. И. Герцена», 1893.4kb.
• На правах рукописи, 865.61kb.

В третьем параграфе анализируется научное мышление, соотношение логики и интуиции. Приступая к более подробному анализу научного мышления, в качестве отправной точки были выбраны слова А. Эйнштейна: «Самое непостижимое в мире то, что он постижим». Парадоксальный характер этого выражения задает тон и направление исследования специфических черт научного мышления, того, что отличает это мышление от мышления вообще. В современном мире значение точного научного знания, существенно опирающегося на формальную логику, выросло настолько, что формально-логические методы часто фетишизируются. Между тем, полное постижение как материального, так и духовного мира, требует использования и дискурсии (лат. discursus – рассуждение, дискурсивный – рассудочный, логический), и интуиции. Соотношение дискурсивного и интуитивного в научном мышлении не есть постоянная величина, оно постоянно изменяется как у отдельного исследователя, так и у всего сообщества ученых.

Овладение логическим мышлением порождает особый стиль творческой деятельности, без которого наука невозможна. Этот стиль характеризуется именно осознанием необходимости как можно дольше придерживаться именно строгого логического метода и выходить из него только при крайней необходимости. Когда создатели основ точных наук – математики и физики – решались высказать новое обобщающее (т.е. основанное на интуиции) суждение по принципиальным проблемам, это всегда происходило после титанических усилий обойтись без него, остаться на почве прежних, уже устоявшихся и проверенных аксиом и строго логических следствий из них.

Говоря о роли внелогических элементов мышления именно в развитии физической науки, А. Эйнштейн писал: «Высшим долгом физика является поиск тех общих элементарных законов, из которых путем чистой дедукции можно получить картину мира. К этим законам ведет не логический путь, а только основанная на проникновении в суть опыта интуиция».

В четвертом и пятом параграфах рассматриваются математические и физические корни парадоксального характера мышления.

Понятие парадоксальности физического мышления, настолько многогранного, что было бы бессмысленно пытаться дать ему формальное определение; более естественно раскрывать суть этого понятия на конкретных примерах. Это свойство мышления напрямую связано с интуицией, с внелогическими элементами, о чем образно сказал Л. Ландау, что, раскрыв законы атомного мира, создав квантовую механику, человек познал то, что невозможно себе представить. Одна из поразительных особенностей природы – это многообразие всевозможных схем ее истолкования. Принцип толерантности стал в настоящее время одним из основных методологических принципов физики. Но при всех возможных вариациях в любой физической теории неизменной остается одна фундаментальная черта – в ней обязательно присутствует математика. И в этом одна из основных особенностей языка физики.

Одним из самых выразительных примеров успешного применения математического мышления в физике является теория гравитации А. Эйнштейна (общая теория относительности). В качестве рабочего материала была взята неевклидова геометрия – теория искривленных многомерных пространств. Эйнштейн отождествил физическое пространство – время (связанное в единый континуум уже в специальной теории относительности) с искривленным неевклидовым пространством. В результате физические законы превратились в утверждения геометрии, принципиально отличающейся от классической геометрии плоского евклидового пространства.

Парадоксальность физического мышления заключается в необходимости понимания и корректного использования математического аппарата и умения подняться выше этого математического аппарата при физической интерпретации полученных результатов. Исключительная роль парадоксальности физического мышления, заключается в способности и склонности не следовать формальным требованиям математической строгости, а попытке поиска возможных путей обобщения полученного результата и возможности его различной трактовки в рамках исследованной математической модели явления.

Парадоксальность физического мышления проявляется в рамках двух разных моделей иерархической цепочки, моделей, основанных на взаимоисключающих предположениях, а также в различной трактовке одних и тех же математических выражений.

В работе рассмотрен парадоксальный характер физических представлений, не связанных напрямую с используемым математическим аппаратом. Наши знания о природе не априорны, а вытекают из анализа и обобщения опыта, поэтому проникновение человеческого разума в новую, неизведанную область явлений влечет необходимость периодического коренного пересмотра и обобщения основных понятий и представлений физики. При этом с каждым новым шагом выявляются и уточняются границы применимости понятий и законов, которые ранее считались универсальными, вскрываются закономерности более общего характера.

В шестом параграфе анализируется вопрос, почему именно физическое мышление в настоящее время является эталоном научного мышления. Точность знаний – вот характерная черта физики, выделяющая ее из всего ряда естественных наук. Но «…сама по себе ученость не научает, как применять ее – на то есть мудрость особая, высшая, которую приобрести можно только опытом». Это известное высказывание Ф. Бэкона проливает свет на рассматриваемую проблему, поскольку специфика научной деятельности может быть понята в результате анализа ее метода. Объект исследования физики  это явление материального мира в строго учитываемых условиях. Математика является «языком» современной физики, с помощью которого формулируются физические теории и выражаются результаты эксперимента. Автор большого числа уникальных математических моделей В.П. Маслов так характеризует эту ситуацию: «Мне кажется, что на самом деле современная математика и физика … с достаточно глубокой физико– математической точки зрения – просто одна и та же наука». В настоящее время выдающимся математиком В.И. Арнольдом высказывается хоть и крайняя, но весьма показательная точка зрения о том, что «Математика, подобно физике, – экспериментальная наука, отличающаяся от физики лишь тем, что в математике эксперименты очень дешевы … Математика является экспериментальной наукой – частью теоретической физики и членом семейства естественных наук…».

Говоря о проблемах образования в свете обсуждаемых вопросов, Р. Фейнман считает, что «Мы обязательно должны допускать возможность сомнения, иначе нет прогресса и нет никакого истинного обучения. Невозможно обучать, не разрешая задавать вопросы. А вопрос для своего появления требует сомнения. Людям свойственно стремиться к определенности. Но полной определенности никогда нет. Большинство наших действий основывается на неполном знании». И далее: «Необходимо учить, как принимать, так и отрицать прошлое знание с определенным балансом, что требует заметного искусства».

Логика определения содержания учебного предмета, разумеется, руководствуется логикой развития основных категорий и понятий данной науки, учитывает возрастные особенности освоения материала и «организации на его основе как восхождения от абстрактного к конкретному, так и от конкретного к абстрактному». Характерной особенностью развития физического знания является обилие парадоксов, причем каждый парадокс соответствует неожиданному повороту науки с присущим ему методом решения. С одной стороны, парадокс – это источник новых приобретений в знаниях, а с другой – источник развития физического мышления.

Парадоксы – это краеугольные камни на пути развития физического знания, нередко оказывавшие и оказывающие в настоящее время, решающее влияние на развитие науки. Недооценка роли парадоксов приводит к задержке развития науки, поэтому они должны входить в методологическую основу системы обучения физике и широко использоваться в учебном процессе. Приведенный анализ показывает, что умение анализировать парадоксы составляет обязательный компонент физического мышления, и выработка способности производить такой анализ должна составлять доминирующий аспект физического образования.

Отвечая на вопрос, почему же именно физическое мышление может в настоящее время рассматриваться как эталон научного мышления, приходим к выводу об универсальном характере развитого физического мышления, которое отличается исключительно широким диапазоном черт и компонентов – от формально - логического до образно - эмоционального. Этот диапазон определяется не свойствами отдельных личностей, занятых добыванием новых знаний в области физической науки, а объективными обстоятельствами, связанными с методологией современной физики, отличающейся исключительным богатством и разнообразием методов исследования явлений природы. Здесь и сбалансированное соответствие между качественными и количественными методами, причем сами качественные методы анализа выступают как внутри используемого математического аппарата, так и вне его. Формулировка общих фундаментальных законов, справедливых всегда и везде в рамках доступных границ представлений о Вселенной, и частных законов, относящихся к строго определенным реальным явлениям, протекающим в строго учитываемых условиях; и, что особенно важно для понимания уровня развития физического знания, и установление внутренних, глубинных связей между фундаментальными и частными законами. Здесь и выход на новые, обсуждавшиеся выше формы представления научных данных, не обязательно в виде аналитических выражений и формул; формы, которые могут оказаться единственно приемлемыми в некоторых других естественных и гуманитарных науках. Наконец, обилие парадоксов, являющихся исключительно эффективным средством развития физического мышления и уровня понимания при их разрешении, позволяет сводить воедино различные, подчас прямо противоположные подходы и требует проявления парадоксальности мышления, обеспечивая тем самым высокий эмоциональный накал творческой работы.

Правильная организация обучения физической науке, отражающая перечисленные и многие другие компоненты физического мышления, приводит к тому, как показывает мировой опыт, что физическое образование оказывается наиболее востребованным в плане широты диапазона областей деятельности, подчас весьма далеких от физики

Во второй главе «Принципы построения методической системы по развитию парадоксальности мышления в средней школе» обсуждаются теоретические положения, которые необходимо учитывать для адекватного педагогического проектирования и конструирования процесса обучения физике в средней школе. Методическая система по развитию парадоксальности мышления представляет собой совокупность компонентов (цель, содержание, методы, средства и формы), которые в своем взаимодействии образуют единое целое.

Обсуждение принципов построения методики развития парадоксальных черт мышления при обучении физике, и выяснения влияния общих психолого-педагогических аспектов на этот процесс, уместно начать с краткого анализа стиля мышления, некоторых выдающихся физиков-теоретиков, научные результаты которых существенно повлияли на последующее развитие физической науки.

Акцент внимания на распознании этих черт в стиле мышления отдельных ученых, поможет целенаправленно сформулировать определенные требования к методике обучения физике, ориентированной на развитие парадоксальности мышления.

Прежде всего, следует отметить, что развитие парадоксального характера мышления обучаемых, отнюдь не отменяет все остальные цели обучения физике, начиная от усвоения определенной совокупности конкретных физических знаний, овладения основными методологическими принципами физики и ее математическим аппаратом, развития высшей степени физического понимания и т.д. Напротив, выработка парадоксального характера мышления производится именно на основе этих фундаментальных моментов физического образования и параллельно с ними, представляя собой, восхождение на вершину, которая включает в себя все эти моменты. Фактически это последний штрих в полноценном физическом образовании, знаменующий становление компетентности ученого как исследователя природы.

Говоря о методологии физики как науки и обсуждая методику обучения физике, следует ясно понимать, что, в конечном счете, парадоксальность мышления как его доминирующая черта должна быть развита и направлена таким образом, чтобы обеспечивать возможность наиболее эффективного проникновения в тайны природы. В первую очередь это связано с неординарностью мышления, определенной непредсказуемостью ходов и действий. Роль психологии и педагогики здесь заключается в установлении того, что именно и на каком уровне может быть практически реализовано на различных этапах обучения физике.

Исключительно полезным для анализа обсуждаемой проблемы является изучение научного и педагогического наследия Л.И. Мандельштама, который был не просто ученым, а мыслителем, для которого физика была путем к пониманию «природы вещей». Мандельштам принадлежал к редкому типу физиков, соединявших в себе теоретика, экспериментатора, инженера – изобретателя, педагога и философа. Как педагог-ученый он не только был блестящим лектором, но и создал мощную школу теоретической физики.

В проведенном исследовании рассмотрены основные принципы построения методической системы, поскольку они определяют основную «философию» методики обучения физике, целью которого является выработка такого парадоксального характера мышления. Совершенно очевидно, что этого можно добиться только на пути реализации непрерывного обучения, начиная от курса физики средней школы вплоть до изучения теоретической физики в вузах, где физика определяет профессиональную направленность образования.

Развитие мышления – это сугубо индивидуальный процесс, определяемый способностями, характером и другими психологическими чертами личности. Этот процесс сам по себе парадоксален, поскольку в свете сформулированной задачи подразумевается одновременное развитие противоположных черт психики. Развитие парадоксальности мышления требует определенного смещения акцентов и введения ряда новых компонентов в методику обучения, ориентированную на развитие высшей степени физического понимания. Одним из таких новых компонентов является прослеживание преемственности в рассмотрении родственных физических явлений на разных этапах изучения физики с учетом особенностей возрастной психологии.

Развитие мышления происходит в процессе самостоятельной деятельности, связанной с анализом физических явлений, т.е. в конечном счете, с решением задач в широком смысле понимания этого вопроса. Это, разумеется, не означает, что на теоретических занятиях, посвященных изучению нового материала, преподаватель не должен заострять внимание обучаемых на определенных моментах, связанных с критическим анализом, как используемых методов, так и получаемых результатов. Напротив, именно на теоретических занятиях, излагая фундаментальные и частные физические законы, необходимо демонстрировать учащимся значимость постоянного сомнения и проверки правильности производимых действий, стимулируя развитие критичности мышления. Однако сама по себе критичность мышления является только первым шагом на пути становления его парадоксального характера. Парадоксальность мышления, разумеется, включает в себя такое свойство, как критичность, т.е. способность и потребность к логическому отрицанию, парадоксальность характеризуется, прежде всего, способностью и нацеленностью на получение положительных результатов на основе самых разных, в том числе и внелогических действий.

Особое значение, парадоксальный характер физического мышления приобретает в свете развития информационной методической системы обучения физике на всех уровнях физического образования. Широкое внедрение персонального компьютера, как в систему научных исследований, так и в среду образования, означает открытие еще одного мощного потока получения информации, напрямую не связанного с традиционными классическими методами. Установление соответствия между результатами, полученными классическими и новыми методами, зачастую представляет собой более сложную задачу, чем само получение результата и, соответственно, требует более высокого уровня парадоксальности мышления.

Развитие математического моделирования, которое в настоящее время выступает как новый универсальный компонент методологии любой науки, в том числе и физики, вносит ряд новых принципиальных моментов в проблему развития физического мышления.. Понятый и до конца осознанный модельный характер наших знаний о природе привел к кардинальной перестройке психологии исследовательской деятельности. Появились и приобрели определенный смысл такие фундаментальные понятия математического моделирования, как адекватность математических моделей изучаемому явлению, их универсальность, иерархичность, оснащенность, нелинейность, численная реализация и т.д.

Обучение основам математического моделирования при изучении физики подразумевает не просто усвоение определенных правил и способов действия, а именно развитие своеобразного стиля мышления, отличного от того, который формировался при классическом подходе к изучению физики. Иерархичность различных моделей одних и тех же явлений, изучаемых на разном уровне, может быть аккуратно отслежена на целом ряде конкретных примеров. Это, как показывает опыт обучения, позволяет добиваться успеха при овладении наиболее трудным этапом моделирования реальных процессов – построением вербальной модели явления и переводом этой модели на математический язык.

Выбор языка описания, т.е. набора физических величин и понятий, в терминах которых описывается явление, устанавливает место данной модели в иерархической цепочке. При этом парадоксальность мышления исследователя может проявляться в постоянной психологической готовности к такой ситуации, когда достаточно простые математические модели весьма сложных систем могут дать удовлетворительное, хорошее, а иногда даже лучшее описание исследуемых процессов, чем более сложные и изощренные модели. Возможность уверенного ориентирования в таких ситуациях, определяется умением анализировать характерные временные масштабы, характеризующие процессы в изучаемой системе, и оценивать возможности натурного эксперимента с точки зрения разрешающей способности используемых измерительных устройств.

Парадоксальность мышления проявляется в понимании места данной модели в общей иерархии возможных моделей системы. Что позволяет в ряде случаев заранее устанавливать границы применимости модели, ориентироваться в возможности обобщения или конкретизации модели при движении по иерархической цепочке по принципу «сверху вниз» или «снизу вверх» и, в конечном счете, предсказывать или, по крайней мере, понимать причины и условия появления физических парадоксов при исследовании математических моделей реальных явлений. Вычислительный эксперимент, представляющий собой определенный этап математического моделирования, в ряде случаев является единственным средством получения научного знания в связи с принципиальной невозможностью натурного эксперимента либо из-за масштаба явления, либо из-за невозможности воспроизвести необходимый диапазон физических характеристик. Такая ситуация имеет место с крупномасштабными экологическими экспериментальными, глобальными климатическими изменениями, изучением эволюции галактик. Очень важным моментом с точки зрения особенностей физического мышления здесь является тот факт, что «экспериментатор – вычислитель» может делать то, чего не сможет сделать ни теоретик, ни физик – экспериментатор: он может проверять, как на данное явления влияет в отдельности каждое из независимых упрощающих предположений. И здесь открываются новые возможности по сравнению с «классической» ситуацией в физике, очень метко охарактеризованной В. Паули, – « …лишь в исключительных случаях появляется готовая теория и ее оправдание или опровержение, что так охотно предполагается в теоретико-познавательных исследованиях. В общем случае появляются эмпирические результаты, обработанные с помощью уже известных теорий, но выходящие за пределы объяснимого этими теориями. Так сами будни физика выдвигают в физике на передний план аспект развития, становления …».

Развитие парадоксального характера мышления в процессе изучения физики должно опираться на опыт выдающихся ученых-педагогов, оставивших многочисленные примеры неординарного, иногда нелогичного подхода к изложению некоторых принципиальных вопросов; изложения, которое, как оказалось впоследствии, помогало вскрывать самые тонкие моменты в сути физических явлений и используемых для их описания понятий. В этом отношении весьма показательна педагогическая деятельность Л.И. Мандельштама, не всегда правильно понимавшаяся некоторыми его коллегами при всем в целом положительном и даже восторженном отношении к этой его деятельности.

Следует различать понятия парадоксальности определенной физической ситуации или результатов ее анализа и парадоксальности физического мышления. В ряде случаев эти понятия оказываются действительно тесно связанными, и для объяснения определенного физического парадокса необходимо проявление именно парадоксальных черт мышления. Но бывает и наоборот: парадоксальная ситуация получает объяснение в результате обычных «непарадоксальных» рассуждений, проведенных на строгом уровне с исследованием всех существенных обстоятельств, а обычная, непарадоксальная, но в целом неясная ситуация требует для объяснения неординарного, парадоксального подхода. При разработке методической системы, обеспечивающей развитие парадоксального характера физического мышления, целесообразно особо подчеркивать сходство и различие отмеченных моментов, по возможности отмечать тип «парадоксальности», встречающейся в каждом рассматриваемом случае.

Значение парадоксальности мышления исследователя для развития физической науки прекрасно передается словами Л. де Бройля о методологическом значении теории относительности: «Она показала нам, что можно преодолевать кажущиеся неприступными препятствия и открывать неожиданные точки зрения, стоит только отказаться от предвзятых мнений, которые считаются справедливыми скорее в силу привычки, чем логики. Теория относительности была великолепным средством упражнять дух физиков». Средством такого упражнения «духа физиков» должен стать каждый конкретный пример, требующий неординарного подхода для своего разрешения.

В третьей главе «Методическая система по развитию парадоксальности мышления в средней школе» и четвертой главе «Методическая система по развитию парадоксальности мышления при углубленном изучении предметов физико-математического цикла в средней школе» излагаются принципы построения методической системы, ориентированной на развитие парадоксальности мышления, на двух уровнях изучения физики  физика в средней школе обычной и специализированной, с углубленным изучением предметов физико-математического цикла. Излагаемый материал, соответствующий каждому из перечисленных уровней обучения, группируется по принципу разделов физики, а не по подуровням обучения (классы в средней школе). Подробно обсуждаются те конкретные компоненты парадоксального характера мышления, которые могут вырабатываться при изучении соответствующего материала с учетом особенностей возрастной психологии.

В третьей главе излагается материал для учителя физики средней школы, который можно использовать для целенаправленного развития парадоксальности мышления учащихся. На этом этапе обучения учащиеся еще, как правило, неспособны к последовательному проявлению парадоксального характера мышления, прежде всего, к поиску неординарных, неожиданных идей. При изучении курса физики в школах с углубленным изучением предметов физико-математического цикла (четвертая глава) ситуация уже иная. И хотя учитель по-прежнему может сыграть исключительную роль именно в развитии мышления обучаемых, наступает пора, когда учащийся может вполне самостоятельно обращать внимание на необходимость развития парадоксальности своего мышления, проявляющейся в различных формах.

Соответственно изменяется и подбор материала по главам. В третьей главе это более или менее последовательный анализ развития мышления при изучении всего школьного курса физики. В четвертой главе это, прежде всего, разбор некоторых наиболее сложных физических понятий, фигурирующих во всех курсах физики, адекватное понимание которых является необходимым условием развития мышления. Отбор материала производился в соответствии с принципом непрерывного образования, когда прослеживался путь изучения одних и тех же физических систем и теорий на разных этапах образования. И, наконец, даже разнообразные примеры подбирались таким образом, чтобы материал, изложенный в одном из них, находил применение при анализе других вопросов.

Изложение основано на разборе конкретных физических явлений, теорий и методов, причем степень детализации изложения определяется, новизной излагаемого материла в методической литературе по физике. При конкретных методических разработках отдельных вопросов и тем на основе изложенных принципов, прежде всего, следует обратить внимание на правильную формулировку задачи или задания, которые с самого начала стимулировали бы развитие или проявление определенных «положительных» моментов мышления.

Выработку парадоксального характера физического мышления следует начинать с первых шагов обучения физике, четко определяя при этом педагогическую задачу – какую именно черту парадоксальности следует подчеркивать, разбирая тот или иной конкретный вопрос. Остановимся на гидростатических явлениях, которые обеспечивают ряд парадоксальных ситуаций, связанных с законом Паскаля. Разбор стандартных гидростатических парадоксов, основанный на использовании выражения для давления в жидкости

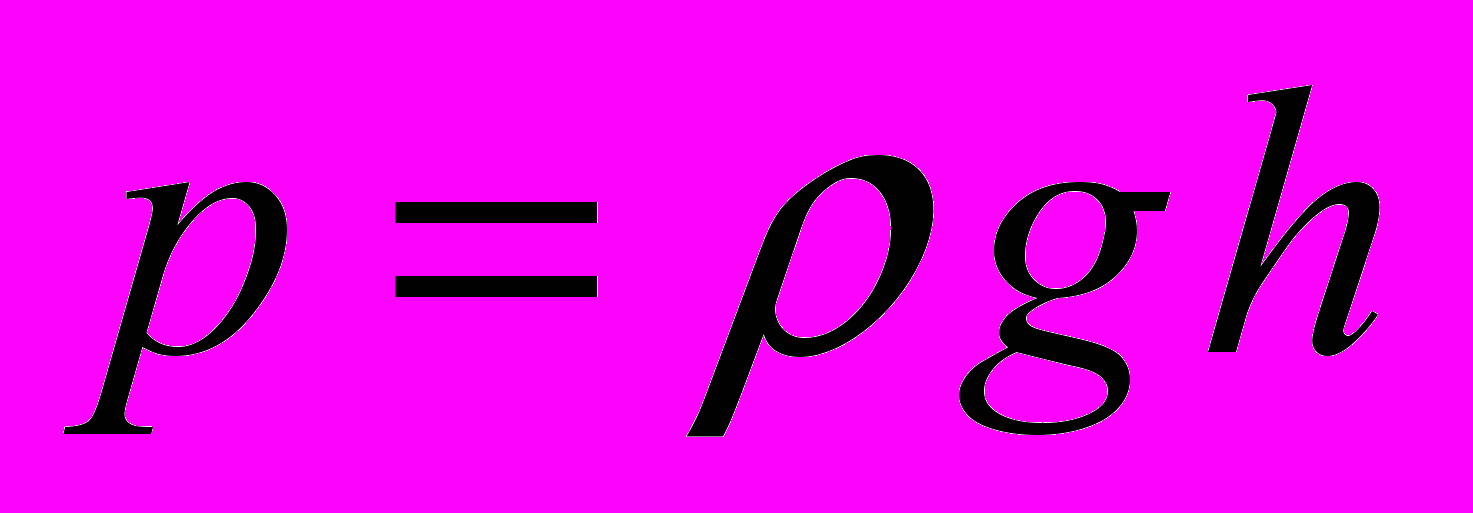(1)

целесообразно продолжить анализом более сложных ситуаций, когда прямое использование соотношения (1) приводит к необходимости проведения громоздких математических расчетов, выходящих за пределы компетентности учащихся средней школы. Парадоксальность мышления при этом проявляется в способности так перестроить рассуждения, чтобы, не меняя их физической основы, т.е. физических законов, описывающих рассматриваемое явление, обойти математические трудности путем привлечения некоторых дополнительных физических соображений, напрямую не относящихся к рассматриваемому вопросу.

П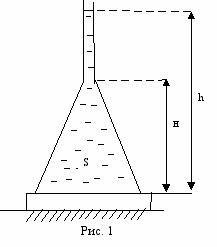роиллюстрируем сказанное конкретным примером. Перевернутая тяжелая коническая воронка поставлена на ровную горизонтальную поверхность, покрытую куском резины, чтобы обеспечить плотный контакт воронки с поверхностью, на которой он стоит.

Узкое отверстие воронки заканчивается тонкой трубкой, через которую внутрь воронки можно наливать воду. Вода начинает вытекать из–под воронки, когда высота уровня воды в трубке становится равной h. Какова масса воронки m, если площадь сечения ее широкого отверстия равна S, а высота воронки равна H?

Разбирая этот опыт, учащиеся обычно довольно легко приходят к выводу, что вода начинает вытекать из-под воронки, когда воронка приподнимается и между ней и куском резины образуется просвет. Так же легко они устанавливают и причину того, что воронка начинает приподниматься вследствие сил давления воды, действующей на боковую поверхность воронки: равнодействующая этих сил, как ясно из соображений симметрии, направлена вертикально вверх. Когда величина этой равнодействующей сравняется с действующей на воронку силой тяжести, воронка перестанет давить на горизонтальную подставку и начнет приподниматься. Однако столь же легко учащиеся приходят и к выводу, что прямой расчет равнодействующей сил давления воды на воронку находится за пределами их возможностей.

Нужен некий парадоксальный на первый взгляд ход, который может быть основан только на привлечении новой физической идеи. Психологическая трудность, которую необходимо преодолеть в сознании учащихся, заключается в осознании необходимости проявить какой-то новый взгляд на ситуацию, когда с принципиальной физической точки зрения все уже ясно, и дело заключается только в преодолении математических трудностей. Таким неожиданным новым ходом является мысленное помещение всей рассматриваемой системы на весы. Подчеркнем чисто физический характер этой идеи, которая, не меняя физического характера явления, сразу открывает возможность его новой математической интерпретации. Расчеты по-прежнему будут основываться на использовании соотношения (1) для гидростатического давления, но теперь, вместо подсчета равнодействующей сил давления на боковую поверхность, необходимо будет найти силу давления воды на горизонтальную подставку в условиях, когда воронка приподнимается и перестает давить на подставку. Парадоксальность мышления здесь проявляется именно в способности найти эти условия и заменить громоздкое и недоступное на уровне элементарной математики вычисление результирующей сил давления воды, действующих на боковую поверхность, вычислением силы давления на подставку, что представляет собой тривиальную математическую операцию. Схема рассуждений по замене одной ситуации на другую здесь выглядит следующим образом.

Очевидно, что показания весов определяются суммой масс воронки и налитой в нее через трубку воды. Когда вода начинает вытекать из-под воронки, а воронка соответственно перестает давить на подставку, эти показания весов определяются силой давления столба воды высотой h и площадью S на подставку:

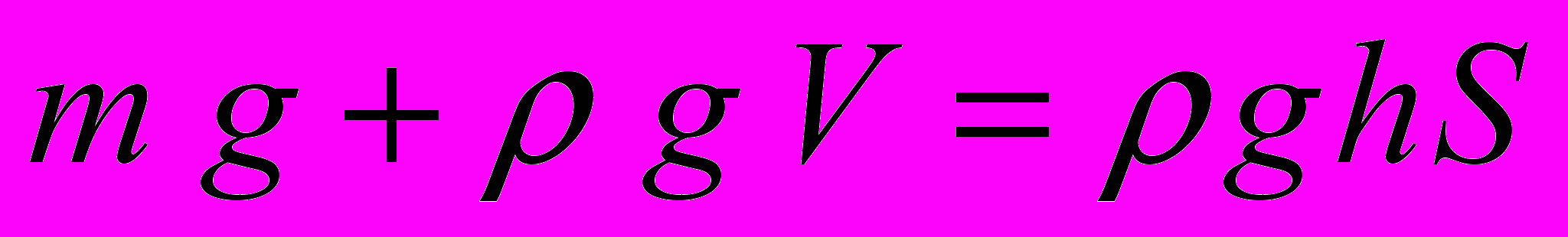, (2)

где 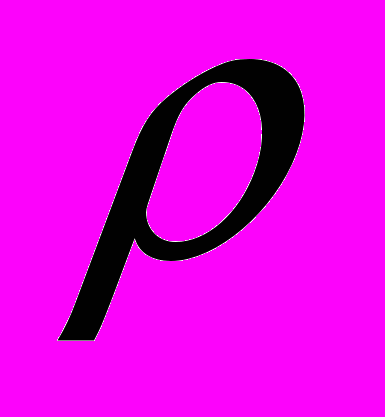— плотность воды, а V – объем воды в воронке и трубке. Если трубка тонкая, то объемом заполненной водой части трубки можно пренебречь по сравнению с объемом самой воронки. В этом случае 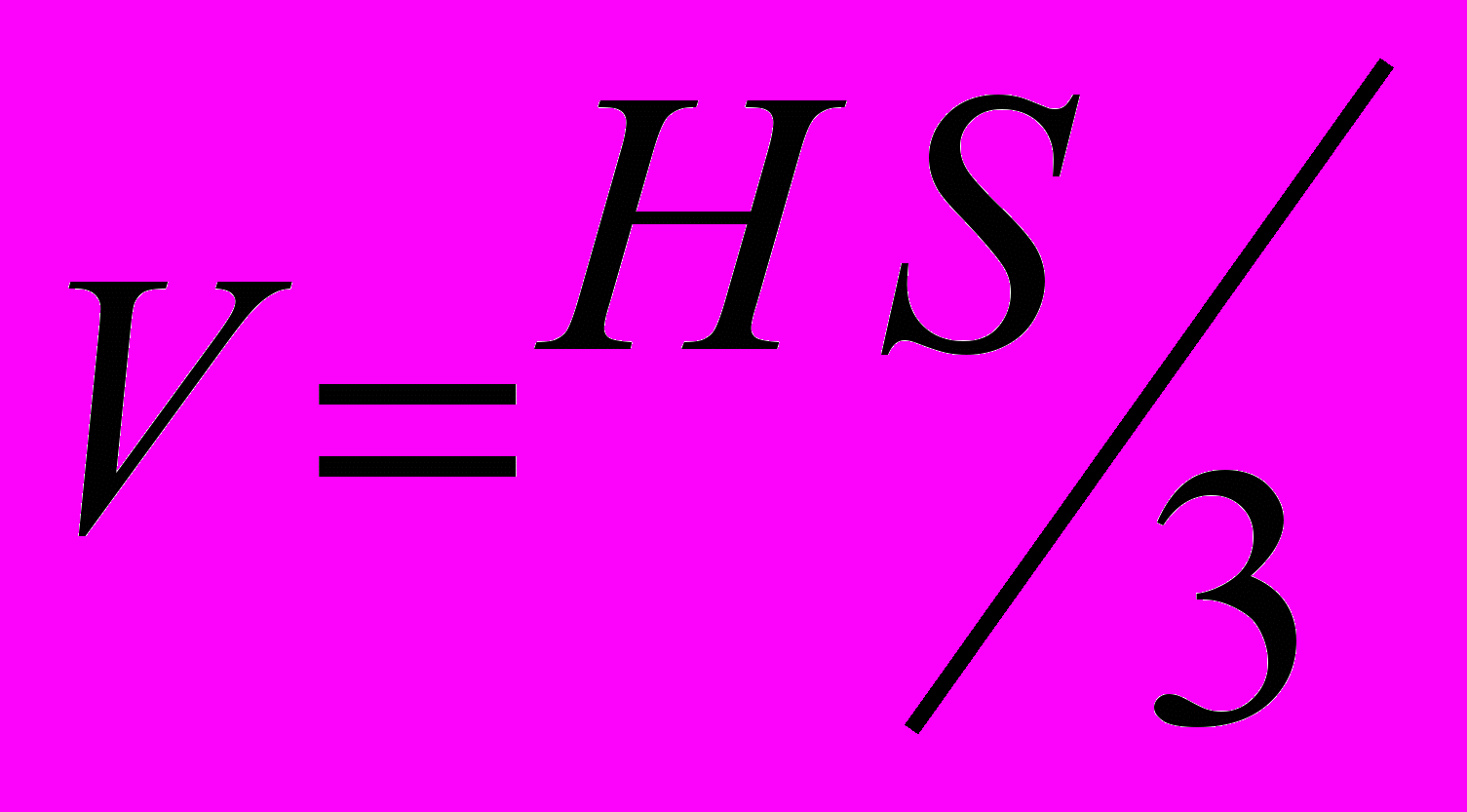, и из уравнения (2) получаем для массы воронки: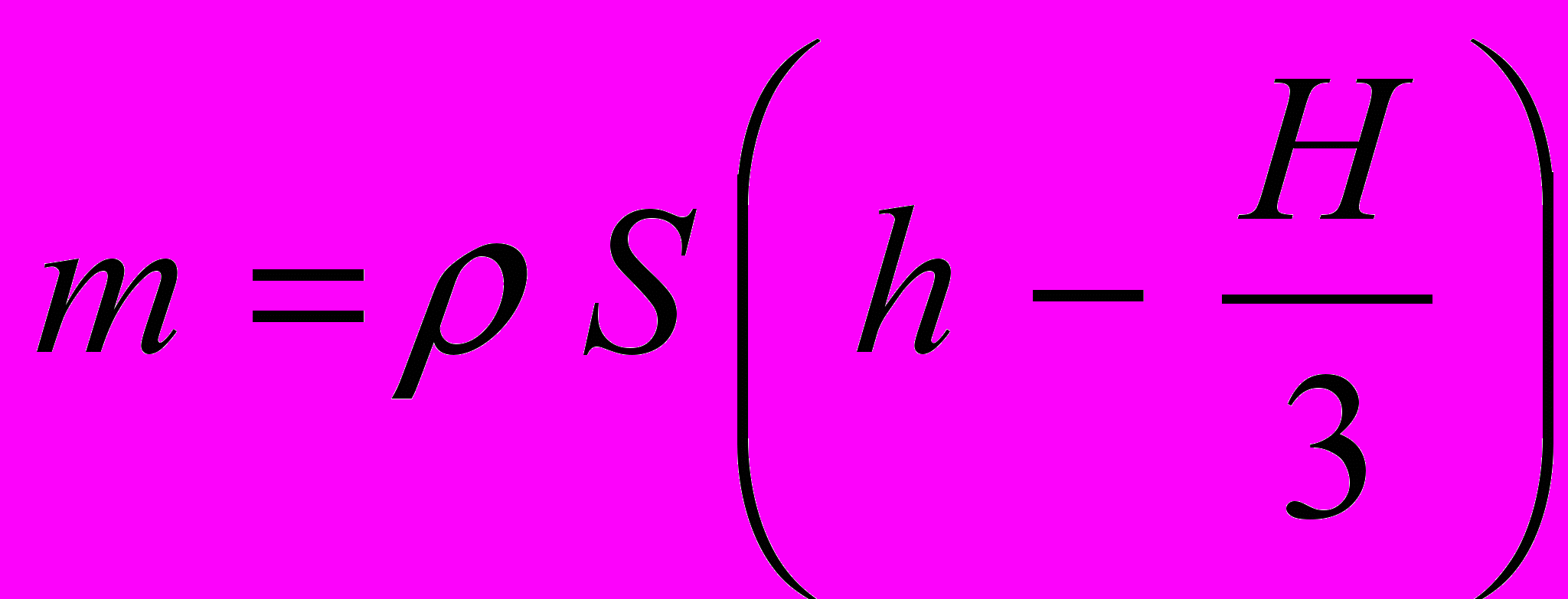

(3)

Если трубка достаточно широкая, то можно легко учесть объем находящейся в ней воды.

Подчеркнем, что к описанной выше идее замены одной ситуации на другую можно придти, если предварительно рассмотреть один из стандартных гидростатических парадоксов, связанный с возможным отличием силы давления жидкости на дно сосуда от действующей на эту жидкость силы тяжести.

Исследовав формулу (3), придем к выводу, что в наблюдаемых условиях воронка должна быть достаточно тяжелой – ее масса должна вдвое превышать массу воды в объеме воронки. Если масса воронки была бы меньше, чем 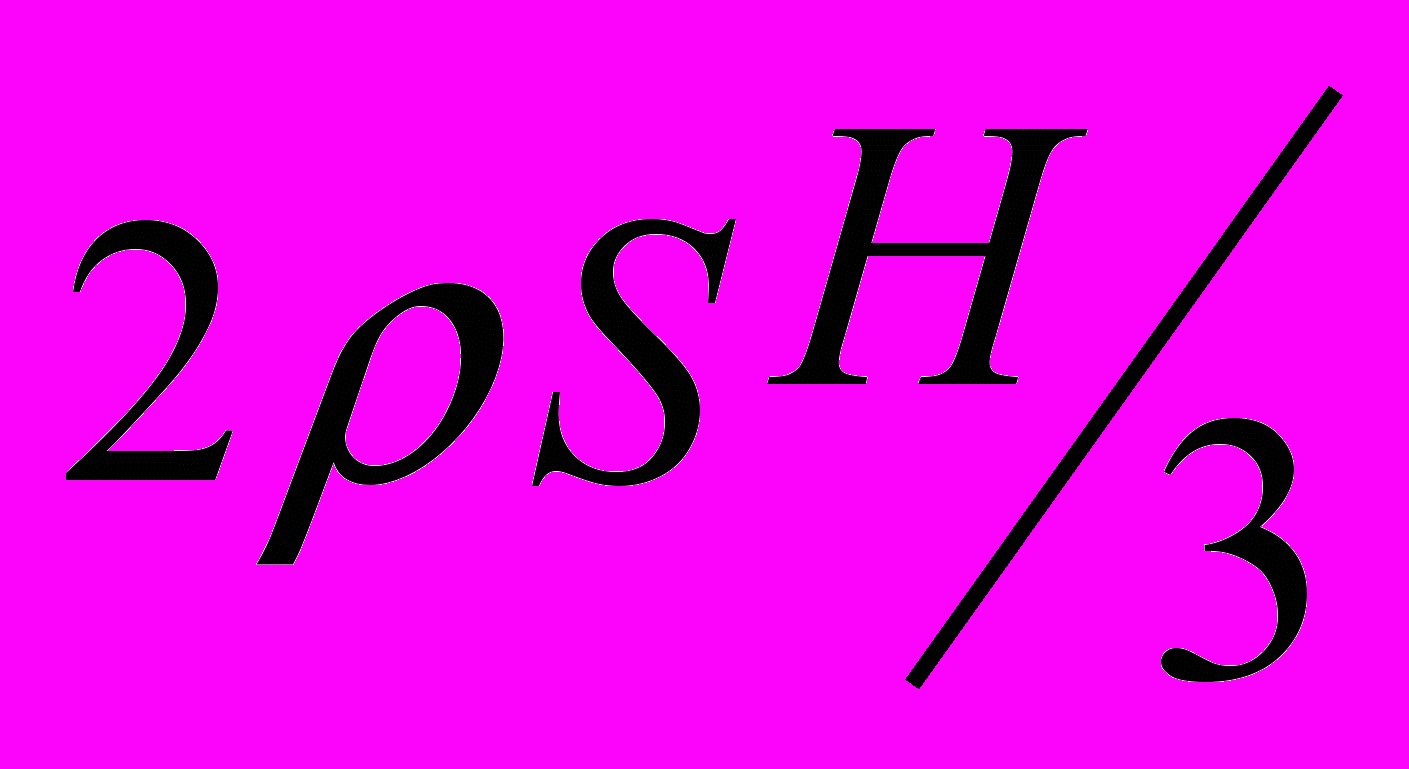, то при наливании воды через трубку воронка начала бы отрываться от подставки еще до того момента, как вода заполнила всю воронку. Здесь открывается хорошая возможность обсуждения вероятности экспериментального наблюдения рассмотренного явления. Далее, необходимо добиться, чтобы учащиеся осознали, что уравнение (2) остается справедливым и в тех случаях, когда воронка имеет более сложную, а не коническую форму.

Парадоксальность физического мышления в рассмотренном случае проявляется в том, что находится иная математическая трактовка явления в рамках использования того же самого физического закона, описываемого формулой (1). Для нахождения этой новой трактовки нужна, однако, новая физическая идея о других условиях проявления закона (1).

В пятой главе «Физические парадоксы как средство развития парадоксальных черт мышления» проанализированы причины и неизбежность появления парадоксов в физике, методика использования физических парадоксов при обучении физике в средней школе. Под парадоксом мы дальше будем понимать ситуацию, в которой обнаруживается кажущееся или действительное противоречие, возникающее в рамках принятой системы понятий.

Нужно отметить важный момент, что любое развитие физической теории, как системы взглядов и представлений об окружающем мире в той или иной степени связано с использованием математического аппарата. Поэтому в физике, последовательно используя математические методы, мы никогда не застрахованы от появления противоречий (парадоксов), не связанных с какими - то ни было непоследовательностями в рассуждениях или расчетах в рамках выбранной физической модели. Невозможно построить физическую теорию, использующую математический аппарат, в которой можно было бы в принципиальном плане исключить появление парадоксов.

В практическом плане гораздо вероятнее ожидать появление парадоксов, связанных с внутренней противоречивостью используемой модели или выходом за рамки ее применимости. Поэтому правильной представляется точка зрения, согласно которой парадокс является непременным атрибутом любой конкретной физической теории, и вопрос может стоять только о педагогической и методической целесообразности явного представления этого парадокса, или его устранения путем перехода к более общей модели или выбора более адекватных методов рассмотрения.

Подлинный парадокс необычен и странен, более того, он даже невероятен, однако предстает как убедительное для нашего ума доказательство, и потому он соответствует высшей степени образования. Отличительная особенность физических парадоксов, рассчитанных на творческое мышление и исследовательский подход, заключается в том, что в задачах творческого характера ставится проблема, которую нужно решить, и не приводится никаких указаний на те физические законы, которыми следует воспользоваться для решения этой проблемы. Анализируя физические парадоксы, учащиеся прогнозируют, а тем самым сознательно осваивают этапы научного познания. В процессе обучения физике учитель должен готовить учащихся к оценке парадоксальности физических теорий систематическим включением физических парадоксов в практику преподавания.

В работе рассмотрена классификация физических парадоксов, определены основные причины возникновения парадоксов в учебном процессе и требования к выбору физических парадоксов.

Обобщая все выше сказанное, можно сделать вывод о том, что, проявляя интерес к физике, особенностям ее структуры и методологии, социальному месту науки, нужно следить не только за ее успехами. Современное положение достигло того момента, когда для понимания сути науки ее нужно изучить изнутри, осознать причины, возникающих в ней противоречий, учиться преодолевать их.

Шестая глава «Методика проведения и результаты педагогического эксперимента» посвящена описанию организации педагогического эксперимента, который являлся неотъемлемой и органичной частью всего проведенного исследования. Он продолжался практически 10 лет, начиная с 1997г., и закончился в 2008 г. При окончательном подведении итогов исследования и формулировании выводов по результатам работы. Текущий анализ результатов выполнял функцию обратной связи и в ряде случаев заставлял вносить серьезные коррективы в теоретические построения и методику их реализации на практике.

Эксперимент проводился в три этапа: констатирующий (1997 - 2000 гг.), поисковый (2000 - 2004 гг.) и формирующий (2004 – 2008 гг.). На различных этапах к эксперименту привлекались около 1000 учащихся общеобразовательных школ и колледжей и 500 студентов, 20 преподавателей вузов и 90 учителей.

Основной целью констатирующего эксперимента является определение состояния развития парадоксальности мышления, и обучения решению физических парадоксов в современной школе, выявление трудностей, возникающих в процессе решения физических парадоксов, определение роли физических парадоксов в обучении и отношение к ним учителей, учащихся, выяснение возможности повышения эффективности обучения физике и качества физического образования, развития парадоксальности мышления учащихся на основе использования физических парадоксов.

Методика массового анкетирования и опроса преподавателей и учителей физики позволила выявить и обобщить их мнения по следующим блокам вопросов:

• отношение учителей к понятию физического мышления; парадоксальности физического мышления, понятию физического парадокса;
  
• отношение учителей к повышению своего педагогического мастерства в области развития физического мышления;
  
• степень удовлетворенности учителей методическим обеспечением по развитию парадоксальности физического мышления, использованию физических парадоксов в учебном процессе по физике;
  
• трудности, возникающие в процессе развития парадоксальности мышления школьников и использования физических парадоксов при обучении физике.
  

Отвечая на вопрос: «Для каких целей нужно развивать парадоксальность физического мышления?» – учителя отметили следующие: для умения анализировать различные явления, умения решать физические задачи, для реализации компетентностного подхода в общем образовании, для постановки физического образования на качественно новую ступень. Более 50 % учителей осознают большое значение использования физических парадоксов при обучении физики, но используют их редко, и лишь 9 % опрошенных учителей используют парадоксы как средство развития парадоксальности мышления на уроках физики систематически. Среди причин не использования физических парадоксов в процессе обучения физике учителя отметили сложность подготовки и подбора задач-парадоксов, большие затраты времени для разрешения парадокса, низкий уровень подготовки школьников, недостаток знаний. Подготовка, подбор задач-парадоксов требует дополнительного времени от учителей, дополнительных знаний от учащихся, а, следовательно, обращения к дополнительной литературе. А, как выяснилось, 81 % учителей не имеют информации о такой литературе, отмечают отсутствие методической литературы по данной теме.

На рис. 2 представлено сравнение ответов учителей и учащихся на вопрос анкеты, связанный с пониманием роли физических парадоксов в изучении физики.

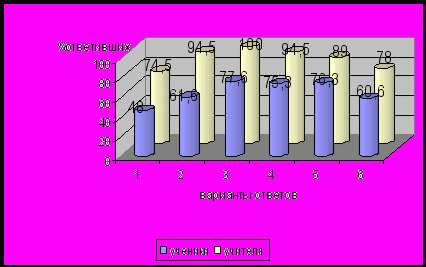	1. – четко помогает представить физические явления 2. – повышают научный уровень физики 3. – способствуют развитию парадоксального характера физического мышления 4. – активизируют учебную деятельность, развивают познавательный интерес 5. – создают проблемные и творческие ситуации 6. – помогают решать задачи.
Рис. 2 Результаты анкетирования по выяснению роли физических парадоксов при изучении физики

Предложенные преподавателями пожелания и замечания были учтены при разработке методических рекомендаций.

В результате опытно-поисковой работы на втором этапе педагогического эксперимента была создана методическая система развития парадоксального характера мышления, разработаны методические рекомендации по ее использованию, разработана методика последовательного использования физических парадоксов. Для более детального, но, в то же время, комплексного оценивания влияния методической системы развития парадоксальности мышления через использование физических парадоксов на качество образования была выбрана следующая система критериев.

I. Позитивное влияние предлагаемого подхода, оцениваемое по двум аспектам:

А) На уровень овладения методологией.

Вводится четырехуровневая оценка практических знаний и умений:

1) Знает, умеет (владеет) – 1,0 (обходится без преподавателя).

2) Частично знает, умеет – 0,8 (не требует принципиальных содержатель­ных подсказок).

3) Частично знает, умеет – 0,5 (требует принципиальных содержательных подсказок).

4) Справляется при постоянном участии преподавателя – 0,2.

Б) На общий уровень освоения предметных знаний при обучении физике.

1) По результатам комплексных контрольных работ (Предметная составляющая).

2) По оценке результатов разрешения парадоксов ( Деятельностно-коммуникативная составляющая).

– высказывание своей точки зрения (уровень знания);

– объяснение выбора плана решения, его логичности (уровень понимания);

– стиль речи, участие в диалоге (уровень применения);

– аргументированность ответов (уровень анализа);

– оценка разных подходов к проблеме, самооценка (уровень синтеза и оценки).

Использовалась карта-анкета, заполняемая преподавателем (учителем) или совместно.

II. Положительная динамика проявления познавательных интересов у обучаемых. Этот параметр, на наш взгляд, характеризует способность и возможность для самовыражения (самореализации) в рамках и средствами предмета. Он отслеживался по следующим позициям:

а) Активизация учебно-познавательной деятельности;

б) Усиление интереса к решению физических парадоксов (и расширение их содержания);

в) Участие студентов и школьников в творческих конференциях, конкурсах и олимпиадах, «Днях науки».

III. Положительная динамика проявления интереса у обучающих:

а) Интереса и стремления к освоению методики последовательного использования физических парадоксов в процессе обучения физике в педагогической практике у учителей физики и студентов (на педагогической практике);

б) Уровня профессиональной компетентности учителей физики.

Последние два критерия оценивались на основе анкетирования обучаемых и обучающих, наблюдения за учебным процессом.

На поисковом этапе было подтверждено положительное влияние разработанной методической системы на эффективность проведения учебно - воспитательного процесса при обучении физике и опробованы критерии проверки ее эффективности. Также было подготовлено все необходимое учебно-методическое обеспечение для организации и проведения формирующего этапа педагогического эксперимента.

Формирующий педагогический эксперимент представлял собой по существу совокупность независимых экспериментальных исследований. Первое проводилось на базе физического, математического факультетов ИвГУ и инженерно-физического факультета ИГЭУ, в Ивановском государственном институте противопожарной безопасности, в течение пяти лет. Второе – на базе педагогического и промышленно-экономического колледжа г. Иваново. Третье проводилось с учащимися и учителями восьми общеобразовательных школ города Иваново и Ивановской области.

Каждый год в каждом из вузов в эксперименте было задействовано по две группы (экспериментальная и контрольная), данные приведены в таблице 1.

Таблица 1

Численный состав участников первого исследования

Группы	Число студентов
	1 год	2 год	3 год	4 год	5 год	Общее
Эксперимент.	51	52	53	52	53	530
Контрольн.	52	55	53	55	54

Каждый раз перед включением в эксперимент проводили входной контроль степени развития предметно-информационной составляющей образованности студентов путем сравнения средних оценок по группам за предыдущее время обучения, проведения общеобразовательного теста (естественнонаучной направленности) и экспертных оценок, даваемых преподавателями. Придерживались правила – контрольные группы по результатам входного контроля должны иметь показатели не ниже, чем аналогичные показатели экспериментальных групп. Проводились также заседания экспертных советов, в которые входили преподаватели (учителя) дисциплин естественнонаучного цикла, с целью более адекватного определения степени развития деятельностно-коммуникативной составляющей образованности.

Для чистоты проведения эксперимента была достигнута договоренность об одинаковом (во времени) прохождении изучения учебного материала и синхронности в проведении текущих и итоговых контрольных мероприятий. Были также согласованы материалы контрольных работ, входных и выходных предметных тестов.

После проведения очередного контрольного задания и заседания экспертного совета данные собирались и анализировались путем:

1. Сравнения результатов заданий в экспериментальных и контрольных группах (классах);

2. Сравнения экспертных оценок, присваиваемых студентам (учащимся) экспериментальных и контрольных групп (классов) экспертным советом;

3. Анализа динамики получаемых результатов для контрольных и экспериментальных групп (классов) в отдельности;

4. Сопоставления результатов выполнения заданий и экспертных оценок с динамикой изменения интереса к предмету.

Для определения степени развития предметно-информационной составляющей образованности (уровень обученности) использовали результаты проведения однотипных контрольных работ и (или) письменных тестов. После изучения и опробования ряда методик, мы пришли к выводу, что, они дают максимально объективную информацию и, кроме того, такая форма контроля результатов обучения является общепринятой и не приводит к дополнительным затратам учебного времени.

В соответствии с методикой оценивания, основанной на работе В.П. Беспалько, все участники эксперимента по результатам испытаний были распределены на четыре группы: первая – достигшие отличного уровня по результатам обучения, вторая – хорошего, третья – удовлетворительного и четвертая – неудовлетворительного (низкого). Для сопоставления результатов полученных в экспериментальных и контрольных группах, т.е. двух статистически независимых выборках, использовался стандартный статистический метод Пирсона χ² .


Таблица 2

Результаты оценки развития уровня сформированности

предметной составляющей образования для первого исследования

	fe	fk	fe (%)	fk (%)	fe – fk	(fe – fk)2	(fe – fk)2 /fk
Низкий	21	34	8,05	12,64	- 4,59	21,07	1,67
Удовлетворит.	59	82	22,61	30,48	- 7,87	61,94	2,03
Хороший	130	123	49,81	45,72	4,09	16,73	0,37
Отличный	51	30	19,54	11,15	8,39	70,39	6,31
ВСЕГО	261	269	100 %	100 %	0	χ2 = 10,38

Уровень сформированности предметно-информационной составляющей образования в экспериментальных группах оказался выше, чем в контрольных, что следует объяснить использованием в экспериментальных группах разработанной нами методики.

Коммуникативные умения и навыки формируются у обучаемых в процессе учебной деятельности и должны оцениваться как компонент результата образования – деятельностно-коммуникативная составляющая образованности выпускника. Исходя из оценки показателей данного критерия, составлялась карта-анкета, заполняемая на каждом контрольном срезе экспертным советом, в который входили преподаватели (учителя) дисциплин естественнонаучного цикла, работающие в экспериментальных и контрольных группах (классах).

Первый срез проводился при включении группы в эксперимент, а последний – по окончании этапа. Сводные результаты для студентов первого исследования представлены в таблице 3.

Таблица 3

Результаты оценки динамики уровня сформированности деятельностно-коммуникативной составляющей образования первого исследования

Группы	Число студентов	Уровень сформированности
		Входной контроль	Выходной контроль
Эксперимент.	261	45,4 %	74,6 %
Контрольн.	269	46,8 %	54,8 %

Данные, представленные в таблице, подтверждают позитивное влияние предлагаемого подхода на общий уровень освоения предметных знаний.

Во втором исследовании в эксперимент были включены учащиеся педагогического и промышленно-экономического колледжа первого и второго курсов (по две группы каждый год в течение четырех лет проведения эксперимента). Общая численность участников эксперимента равнялась 319 человек. Аналогичное исследование проводилось с учащимися 10 – 11 классов общеобразовательных школ. Общая численность участников эксперимента - 408 человек.

Методика проведения эксперимента и критерии, используемые для оценки качества образования, оставались неизменными. Качественно был получен тот же результат.

Экспертные оценки эффективности методики развития парадоксальности мышления через последовательное использование физических парадоксов при обучении физике формализованы по следующей шкале.

Шкала формализации экспертных оценок:

0 – методика не эффективна; 1 – эффективность методики низкая; 2 – по эффективности данная методика не отличается от существующих, основанных на традиционном дидактическом принципе учета индивидуальных особенностей учащихся при обучении физике; 3 – эффективность данной методики незначительно выше существующих, основанных на традиционном дидактическом принципе учета индивидуальных особенностей учащихся при обучении физике; 4 – эффективность методики высокая; 5 – эффективность методики очень высокая.

Результаты экспертных оценок первой и второй групп экспертов единодушно оценили эффективность предложенной методики по предложенной шкале в 4 балла.

На основании результатов формирующего эксперимента выявлено, что выбранная нами методика обучения учащихся разрешению физических парадоксов и последовательного их использования на всех этапах обучения физике развивает парадоксальный характер мышления и физическое понимание учащихся, преодолевая формальное её понимание, повышает эффективность обучения физике, что обеспечивает качество физического образования.

В целом по материалам, представленным в шестой главе, можно сделать вывод: педагогический эксперимент, проведенный на широкой экспериментальной базе, подтвердил эффективность разработанной методической системы и позволил оценить ее положительное влияние на развитие предметно-информационной и деятельностно-коммуникативной составляющих образованности учащихся общеобразовательных школ, средних специальных учреждений и студентов высших учебных заведений.