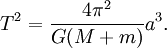Законы Кеплера законы движения планет
| Вид материала | Закон |
- Законы сохранения и принципы симметрии, 283.17kb.
- Законы Кеплера, 12.41kb.
- Направление: Искусство и гуманитарные науки, 1316.91kb.
- Тема: Введение в гидравлику Лекция, 328.7kb.
- Программа профильного курса для 10-11-х классов средней общеобразовательной школы Ивлев, 503.96kb.
- Лекция №8 Построение математических моделей технологических объектов и систем аналитическим, 98.99kb.
- Связанные с механическим движением жидкости в различных природных и техногенных условиях, 1539.22kb.
- Законы делимости (дискретности) в мире животных и растений. Законы наследственности, 276.87kb.
- Авторское право. Терминология, 213.44kb.
- Задачи работы: 1 Изучить особенности строения и климата, условия движения, состав атмосферы, 340.41kb.
Законы Кеплера - законы движения планет
В формулировке Ньютона законы Кеплера звучат так:
- первый закон: под действием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе. Надо сказать, что он справедлив для всех тел, между которыми действует взаимное притяжение.
- формулирование второго закона Кеплера не дана, так как в этом не было необходимости.
- третий закон Кеплера сформулирован Ньютоном так: квадраты сидерических периодов планет, умноженные на сумму масс Солнца и планеты, относятся как кубы больших полуосей орбит планет.
Первый закон Кеплера (Закон эллипсов)
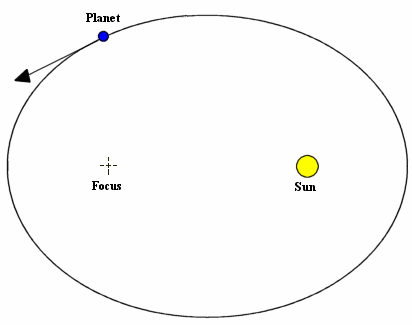
Первый закон Кеплера.
Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.
Форма эллипса и степень его сходства с окружностью характеризуется отношением
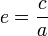 , где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.
, где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.Доказательство первого закона Кеплера
Закон всемирного тяготения Ньютона гласит, что «каждый объект во вселенной притягивает каждый другой объект по линии соединяющей центры масс объектов, пропорционально массе каждого объекта, и обратно пропорционально квадрату расстояния между объектами». Это предполагает, что ускорение a имеет форму
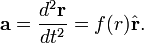
Вспомним, что в полярных координатах
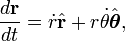
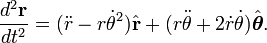
В координатной форме запишем
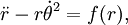
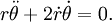
Подставляя
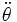 и
и 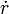 во второе уравнение, получим
во второе уравнение, получим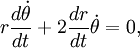
которое упрощается
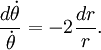
После интегрирования запишем выражение
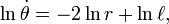
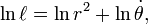
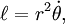
для некоторой константы
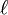 , которая является удельным угловым моментом (
, которая является удельным угловым моментом (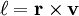 ).Пусть
).Пусть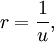
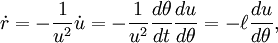
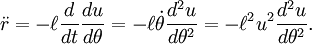
Уравнение движения в направлении
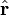 становится равным
становится равным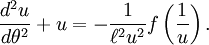
Закон всемирного тяготения Ньютона связывает силу на единицу массы с расстоянием как
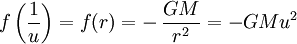
где G — универсальная гравитационная константа и M — масса звезды.
В результате
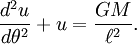
Это дифференциальное уравнение имеет общее решение:
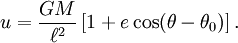
для произвольных констант интегрирования e и θ0.
Заменяя u на 1/r и полагая θ0 = 0, получим:
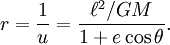
Мы получили уравнение конического сечения с эксцентриситетом e и началом системы координат в одном из фокусов. Таким образом, первый закон Кеплера прямо следует из закона всемирного тяготения Ньютона и второго закона Ньютона.
Второй закон Кеплера (Закон площадей)
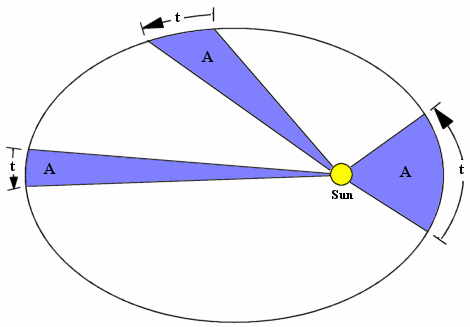
Второй закон Кеплера.
Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные времена радиус-вектор, соединяющий Солнце и планету, заметает сектора равной площади.
Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кепплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии бо́льшую линейную скорость, чем в афелии.
Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца по эклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.
Доказательство второго закона Кеплера
По определению угловой момент
 точечной частицы с массой m и скоростью
точечной частицы с массой m и скоростью 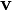 записывается в виде:
записывается в виде: .
. где
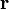 - радиус-вектор частицы а
- радиус-вектор частицы а 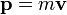 - импульс частицы.
- импульс частицы.По определению
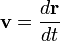 .
. В результате мы имеем
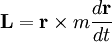 .
. Продифференцируем обе части уравнения по времени
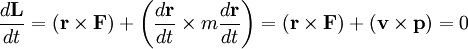
поскольку векторное произведение параллельных векторов равно нулю. Заметим, что F всегда параллелен r, поскольку сила радиальная, и p всегда параллелен v по определению. Таким образом можно утверждать, что
 - константа.
- константа.Третий закон Кеплера (Гармонический закон)
Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей орбит планет.
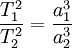 , где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.
, где T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.Ньютон установил, что гравитационное притяжение планеты определенной массы зависит только от расстояния до неё, а не от других свойств, таких, как состав или температура. Он показал также, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:
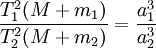 , где M – масса Солнца, а m1 и m2 – массы планет.
, где M – масса Солнца, а m1 и m2 – массы планет.Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.
Доказательство третьего закона Кеплера
Второй закон Кеплера утверждает, что радиус-вектор обращающегося тела заметает равные площади за равные промежутки времени. Если теперь мы возьмём очень малые промежутки времени в момент, когда планета находится в точках A и B (перигелий и афелий), то мы сможем аппроксимировать площадь треугольниками с высотами, равными расстоянию от планеты до Солнца, и основанием, равным произведению скорости планеты на время.
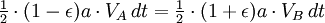
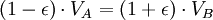
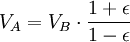
Используя закон сохранения энергии для полной энергии планеты в точках A и B, запишем
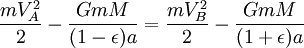
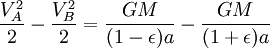

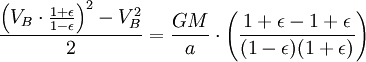
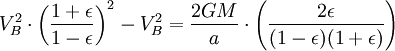
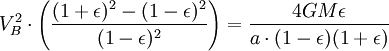
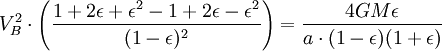
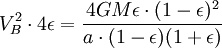
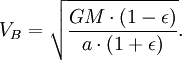
Теперь, когда мы нашли VB, мы можем найти секториальную скорость. Так как она постоянна, то можем выбрать любую точку эллипса: например, для точки B получим
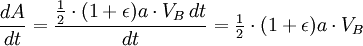
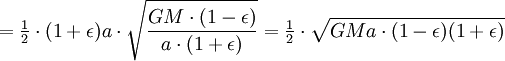
Однако полная площадь эллипса равна
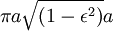 (что равно πab, поскольку
(что равно πab, поскольку 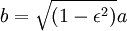 ). Время полного оборота, таким образом, равно
). Время полного оборота, таким образом, равно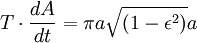
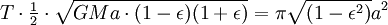
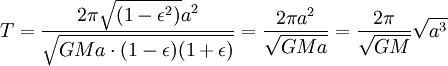
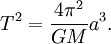
Заметим, что если масса m не пренебрежимо мала по сравнению с M, то планета будет обращаться вокруг Солнца с той же скоростью и по той же орбите, что и материальная точка, обращающаяся вокруг массы M + m (см. приведённая масса). При этом массу M в последней формуле нужно заменить на M + m: