Ф-рабочая программа по дисциплине утверждено ученым советом факультета математики и информационных технологий

Вид материала

Содержание

Рабочая программа
Специальность (направление): 010100 Математика
Цели и задачи изучения дисциплины. 2
4.Темы практических занятий 6
Цели и задачи изучения дисциплины.
Требования к уровню освоения дисциплины
Объем дисциплины и виды учебной работы
Всего по плану
Распределение часов по темам и видам учебной работы
Название и разделов и тем
Аудиторные занятия
Темы практических занятий
Примерный перечень контрольных вопросов по подготовке к зачетам и экзаменам
Экзаменационная программа
Учебно-методическое обеспечение дисциплины.

Подобный материал:

Федеральное агентство по образованию Ульяновский государственный университет	Форма
Ф-Рабочая программа по дисциплине

УТВЕРЖДЕНО

Ученым советом факультета математики и информационных технологий

Протокол №________ от «____»_________20___ г.

Председатель __________________

(подпись, расшифровка подписи)

Рабочая программа

Дисциплина:	Математический анализ

Кафедра:	Алгебро-геометрических вычислений ____(АГВ)____ (аббревиатура)

Специальность (направление): 010100 Математика

(код специальности (направления), полное наименование)

Дата введения в учебный процесс УлГУ: «_____» ___________ 20___ г.

Сведения о разработчиках:

ФИО	Аббревиатура кафедры	Ученая степень, звание
Кругликова Ольга Петровна	АГВ	к.ф.м.н.

	Заведующего кафедрой
	Мищенко С.П. /_____________/ (ФИО) (Подпись) «______»__________ 20___ г.

2

Оглавление 2

ЦЕЛИ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ. 2

1.1.Цели 2

1.2.Задачи 2

2.ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ ДИСЦИПЛИНЫ 3

3.1.Объем дисциплины и виды учебной работы: 3

3.2.Распределение часов по темам и видам учебной работы: 3

3.СОДЕРЖАНИЕ 5

4.ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ 6

5.ПРИМЕРНЫЙ ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ ВОПРОСОВ ПО ПОДГОТОВКЕ К ЗАЧЕТАМ И ЭКЗАМЕНАМ 7

6.УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ. 9

ЦЕЛИ И ЗАДАЧИ ИЗУЧЕНИЯ ДИСЦИПЛИНЫ.

Данная программа определяет объем знаний по курсу математического анализа для студентов II курса механико-математического факультета

Пpогpамма pассчитана на 136 учебных часов.

Предусматривается проведение двух коллоквиумов, двух контpольных pабот и двух домашних контрольных работ (типовые расчеты).

Обучение пpоводится в третьем семестpе.

Учебная дисциплина «Математический анализ» (3семестр) является продолжением одной из фундаментальных математических дисциплин, изучаемых студентами первого и второго курсов, обучающихся на специальностях математического профиля.

Дисциплина «Математический анализ» (3 семестр) базируется на знаниях и умениях, полученных студентами в школьном курсе математики и при изучении этой дисциплины в 1 и 2 семестрах.

Целью курса является научное обоснование важнейших понятий математического анализа: числовых и функциональных рядов, рядов Фурье, несобственных и собственных интегралов, зависящих от параметра, сходимости, равномерной сходимости, операций предельного перехода, дифференцирования и интегрирования функциональных последовательностей и функциональных рядов.

Курс имеет образовательное и прикладное значение.

На практических занятиях вырабатываются умения и навыки решения задач.

Цели

Целями учебной дисциплины являются:

овладение начальными знаниями по теории рядов и несобственных интегралов, необходимыми для изучения других дисциплин специальности
развитие навыков решения задач по теории рядов и несобственных интегралов.

Задачи

Основными задачами учебной дисциплины являются:

формирование у будущих математиков знаний …
приобретение студентами навыков и умений по решению задач по теории рядов и несобственных интегралов.

ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ ДИСЦИПЛИНЫ

В результате изучения дисциплины «Математический анализ» (3 семестр) студенты должны

знать:

понятие несобственных интегралов на бесконечном промежутке и от неограниченной функции
понятие числового ряда, функциональной последовательности и функционального ряда
основы теории рядов и несобственных интегралов

уметь:

решать задачи на вычисление и исследование сходимости несобственных интегралов
решать задачи на исследование сходимости числовых и функциональных рядов

Объем дисциплины и виды учебной работы:

Вид учебной работы	Количество часов (форма обучения очная__)
	Всего по плану	В т.ч. по семестрам
	Всего по плану	1	2	3
1	2	3	4	5
Аудиторные занятия:	136			136
Лекции	68			68
практические и семинарские занятия	68			68
Самостоятельная работа	68			68
Всего часов по дисциплине	204			204
Текущий контроль (количество и вид, контрольные работы)	2			2
Курсовая работа
Виды промежуточной аттестации (экзамен, зачет)	зачет, экзамен			зачет, экзамен

Распределение часов по темам и видам учебной работы:

Форма обучения ___очная____

Название и разделов и тем	Всего	Виды учебных занятий
		Аудиторные занятия		Самостоятельная работа
		лекции	практические занятия, семинар	Самостоятельная работа
1	2	3	4	10
1. Несобственные интегралы	36	12	12	12
2. Числовые ряды	66	16	28	22
3. Функциональные последовательности и ряды	66	22	22	22
4. Ряды Фурье	36	18	6	12

Итого	204	68	68	204

СОДЕРЖАНИЕ

Тема 1 : Несобственные интегралы.

Несобственные интегралы по бесконечному промежутку и их вычисление.

Замена переменной, интегрирование по частям.

Несобственные интегралы от неограниченных функций и их вычисление.

Замена переменной, интегрирование по частям

Признаки сходимости несобственных интегралов. Абсолютная и условная сходимость

Тема 2: Числовые ряды.

Понятие числового ряда. Частичные суммы числового ряда. Сходящиеся числовые ряды. Геометрическая прогрессия. Гармонический ряд. Необходимое условие сходимости числового ряда. Критерий Коши сходимости числовых рядов.

Понятие знакоположительного ряда. Необходимое и достаточное условие сходимости знакоположительного ряда. Признаки сходимости знакоположительных рядов (признак сравнения, признак Даламбера, радикальный признак Коши, интегральный признак Коши-Маклорена, признак Раабе, признак Гаусса).

Знакочередующиеся ряды. Теорема Лейбница. Абсолютно и условно сходящиеся ряды. Признаки Абеля, Дирихле.

Арифметические операции над сходящимися рядами. Бесконечные произведения и их сходимость. Двойные и повторные ряды. Суммирование числовых рядов.

Тема 3: Функциональные последовательности и ряды.

Функциональные последовательности. Поточечная и равномерная сходимость функциональных последовательностей. Критерий Коши равномерной сходимости функциональных последовательностей. Теоремы о непрерывности предельной функции, почленное интегрирование и дифференцирование функциональных последовательностей.

Функциональные ряды. Равномерная сходимость функциональных рядов. Достаточные условия равномерной сходимости функциональных рядов (признак Вейерштрасса, признаки Абеля и Дирихле).

Степенные ряды. Интервал и радиус сходимости степенного ряда. Теорема Абеля о степенных рядах. Разложение функций в степенной ряд.

Ряд Тейлора. Достаточное условие разложения функции в степенной ряд. Разложение основных элементарных функций в ряд Тейлора.

Применение рядов в приближенных вычислениях.

Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.

Тема 4. Ряды и интегралы Фурье.

Ортонормированные системы функций. Ряды Фурье по ортонормированным системам. Неравенство Бесселя. Замкнутость и полнота ортонормированных систем. Равенство Парсеваля. Тригонометрическая система и её замкнутость.

Тригонометрический ряд Фурье. Условия равномерной сходимости и сходимости в точке. Условия почленного дифференцирования и интегрирования.

Преобразование Фурье. Свойства преобразования Фурье. Понятие об обратном преобразовании Фурье. Интеграл Фурье.

ТЕМЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

Несобственные интегралы по бесконечному промежутку и их вычисление
Замена переменной, интегрирование по частям.
Несобственные интегралы от неограниченных функций и их вычисление.
Замена переменной, интегрирование по частям
Признаки сходимости несобственных интегралов.
Абсолютная и условная сходимость. Признаки Абеля, Дирихле.
Числовой ряд и его сумма. Исследование сходимости числовых рядов по определению.
Необходимое условие сходимости. Критерий Коши сходимости рядов.
Признаки сходимости знакоположительных рядов. Признак сравнения.
Признак Даламбера. Радикальный признак Коши.
Признак Раабе. Признак Гаусса.
Интегральный признак Коши-Маклорена сходимости знакоположительных рядов.
Другие признаки сходимости знакоположительных рядов (признак сравнения Коши, логарифмический признак и т.д.).
Оценка остатка знакоположительного ряда.
Знакопеременные ряды. Признак Лейбница. Оценка остатка знакочередующегося ряда.
Признак Абеля, признак Дирихле.
Умножение и деление рядов.
Бесконечные произведения
Решение задач по теме «Числовые ряды».
Контрольная работа 1 по теме «Числовые ряды».
Функциональные последовательности. Поточечная и равномерная сходимость функциональных последовательностей.
Функциональные ряды. Поточечная и равномерная сходимость функциональных рядов.
Степенные ряды. Область сходимости.
Решение задач.
Интегрирование и дифференцирование степенных рядов.
Ряд Тейлора. Разложение функций в ряд Тейлора.
Разложение функций в ряд Тейлора.
Суммирование степенных рядов.
Вычисление сумм числовых рядов.
Итоговое занятие по теме «Функциональные последовательности и ряды».
Контрольная работа 2 по теме «Функциональные последовательности и ряды».
Ряды Фурье
Ряды Фурье.
Итоговое занятие.

ПРИМЕРНЫЙ ПЕРЕЧЕНЬ КОНТРОЛЬНЫХ ВОПРОСОВ ПО ПОДГОТОВКЕ К ЗАЧЕТАМ И ЭКЗАМЕНАМ

Требование к зачету

Вычисление несобственных интегралов. Исследование несобственных интегралов на сходимость.
Исследование числовых рядов на сходимость.
Исследование функциональных рядов на сходимость.
Почленный переход к пределу, почленное интегрирование и дифференцирование функциональных рядов.
Разложение функций в ряд Тейлора.
Вычисления со степенными рядами.
Разложение функций в тригонометрический ряд Фурье.

ЭКЗАМЕНАЦИОННАЯ ПРОГРАММА

Тема 1. Несобственные интегралы.

1.Несобственные интегралы 1 и 2 рода, их основные свойства. Вычисление

несобственных интегралов.

2.Несобственные интегралы от неотрицательных функций. Признак

сравнения несобственных интегралов.

3.Критерий Коши сходимости несобственных интегралов.

4.Абсолютная и условная сходимость несобственных интегралов. Признаки

Абеля и Дирихле сходимости несобственных интегралов.

Тема 2. Числовые ряды.

Сходимость числового ряда. Гармонический ряд. Геометрическая прогрессия. Остаток числового ряда. Необходимое условие сходимости числового ряда. Действия над рядами.
Критерий Коши сходимости числового ряда.
Признак сравнения знакоположительных рядов. Следствия.
Признак Даламбера сходимости знакоположительного ряда.
Радикальный признак Коши сходимости знакоположительного ряда.
Признак Раабе сходимости знакоположительного ряда.
Признак Куммера сходимости знакоположительного ряда.
Признак Гаусса сходимости знакоположительного ряда.
Интегральный признак Коши-Маклорена сходимости знакоположительного ряда.
Знакопеременные и знакочередующиеся ряды. Теорема Лейбница. Теорема об остатке знакочередующегося ряда.
Абсолютно и условно сходящиеся ряды. Теорема о сходимости абсолютно сходящегося ряда.
Формулы дискретного преобразования Абеля.
Признаки Абеля и Дирихле сходимости числовых рядов.
Перестановка членов ряда. Теорема Дирихле о перестановке членов абсолютно сходящегося ряда. Теорема Римана о перестановке членов условно сходящегося ряда.
Группировка членов ряда.
Умножение рядов. Теорема о произведении абсолютно сходящихся рядов. Теорема Мертенса.

Теоремы о сходимости двойных и повторных рядов.
Бесконечные произведения и их сходимость. Признак абсолютной сходимости бесконечного произведения.

Тема 3. Функциональные последовательности и ряды.

Сходимость и равномерная сходимость функциональных последовательностей и рядов.
Критерий равномерной сходимости функциональных последовательностей и рядов.
Критерий Коши равномерной сходимости функциональных последовательностей и рядов.
Достаточные условия равномерной сходимости функциональных рядов (признак Вейерштрасса, признаки Абеля и Дирихле).
Свойства равномерно сходящихся функциональных последовательностей: предельный переход в функциональных последовательностях, условие коммутирования двух предельных переходов, непрерывность предельной функции.
Достаточное условие равномерной сходимости функциональной последовательности. Теорема Дини.
Свойства равномерно сходящихся функциональных рядов: предельный переход, непрерывность суммы равномерно сходящегося ряда. Теорема Дини.
Предельный переход под знаком интеграла, почленное интегрирование функциональных последовательностей и рядов.
Предельный переход под знаком производной, почленное дифференцирование функциональных последовательностей и рядов.
Сходимость в среднем функциональных последовательностей
Равностепенная непрерывность последовательности функций. Теорема Арцела.
Степенные ряды. Теорема Абеля. Радиус сходимости, интервал сходимости степенного ряда. Теорема Коши-Адамара.
Равномерная сходимость степенных рядов. Вторая теорема Абеля.
Разложение элементарных функций в ряд Тейлора.
Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.

Тема 4. Ряды Фурье.

1. Ортогональные системы функций. Ряды Фурье по ортогональным

системам.

2. Ортонормированные системы функций. Неравенство Бесселя.

3. Ряды Фурье по ортонормированным системам. Сходимость ряда Фурье в

среднем. Равенство Парсеваля.

4. Свойства рядов Фурье (экстремальное свойство, единственность ряда

Фурье).

5. Теорема о свойствах замкнутых ортонормированных систем.

6. Свойства рядов Фурье. Теорема Рисса-Фишера.

7. Полнота тригонометрической системы в R([-,]).

8. Периодические функции и их свойства.

9. Тригонометрический ряд и его свойства.

10.Тригонометрический ряд Фурье. Ряды Фурье четных и нечетных

функций. Ряд Фурье функции, интегрируемой на отрезке [-l,l].

11.Неравенство Бесселя для тригонометрической системы функций.

12.Экстремальное свойство тригонометрических рядов Фурье.

13.Ряды Фурье в комплексной области.

14.Интегральное представление частичной суммы ряда Фурье.

15. Ядра Дирихле и их свойства.

16.Сходимость ряда Фурье в точке.

17.Достаточные условия сходимости ряда Фурье в точке.

18.Суммирование рядов Фурье методом средних арифметических. Ядра

Фейера и их свойства.

19.Теорема Фейера.

20.Теорема Вейерштрасса о равномерном приближении непрерывной

функции тригонометрическим многочленом.

УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ.

7.ЛИТЕРАТУРА

7.1.ОСНОВНАЯ

Зорич В.А. Математический анализ.Учебник .Ч.II  М.: Наука,1984.  640с.
Камынин Л.И. Курс математического анализа.Т.II. Учебник.  М.: Издво МГУ, 1995.  624с.
Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ. Продолжение курса. Под ред. А.Н.Тихонова.  М.: Изд-во МГУ, 1987.  358 с.
Кудрявцев Л.Д. Курс математического анализа ( в двух томах). М.: Высшая школа,1981. т. I  ;т.II – 584 с.
Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу: Учебник для университетов и педвузов. М.: Высшая школа, 1999. 695 с.
Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.:Наука,1987.
Виноградова И.А.,Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. В 2 кн. Кн. 2. Ряды, несобственные интегралы, кратные и поверхностные интегралы. М.: Высшая школа, 2000.  712с.

7.2. ДОПОЛНИТЕЛЬНАЯ

Ильин В.А., Позняк Э.Г. Основы математического анализа. 

М.: Наука,1982, ч.1; 1983, ч.2.

Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ.

Начальный курс. Под ред. А.Н.Тихонова.  М.: Изд  во МГУ,

1985.  662 с.

Задачник по курсу математического анализа под ред. Н.Я.Виленкина.

М.:Просвещение,1971, ч.12.

Фихтенгольц Г.М. Основы математического анализа.  М.:

Наука,1967, т.12.

Никольский С.М. Курс математического анализа.  М.: Наука,1973,

т.12.

Райков Д.А. Одномерный математический анализ.  М.: Высшая

школа, 1982.

Зорич В.А. Математический анализ.  М.: Наука,1982, ч.1.
Будак О.М. ,Фомин С.В. Кратные интегралы и ряды. М.: Наука,

1967.  608 с.

Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник

задач по математическому анализу. Интегралы. Ряды. М.: Наука,1986.

10. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М.И. Сборник

задач по математическому анализу. Функции нескольких

переменных.  М.: Наука,1995.

Контрольные вопросы к коллоквиуму по теме «Несобственные интегралы»

Привести пример непрерывной на промежутке [1; +) функции, для которой несобственный интеграл на этом промежутке сходится.

Привести пример непрерывной на промежутке [1; +) функции, для которой несобственный интеграл на этом промежутке расходится.

Привести пример неограниченной на промежутке [1;b) функции, для которой несобственный интеграл на этом промежутке сходится.

Привести пример неограниченной на промежутке [1;b) функции, для которой несобственный интеграл на этом промежутке расходится.

Привести пример сходящегося на интервале [0; +) несобственного интеграла, подынтегральная функция которого не ограничена на любом интервале вида [а; +), где а > 0.

Доказать, что если функция f(x) непрерывна при х  0 и существует конечный предел, то .
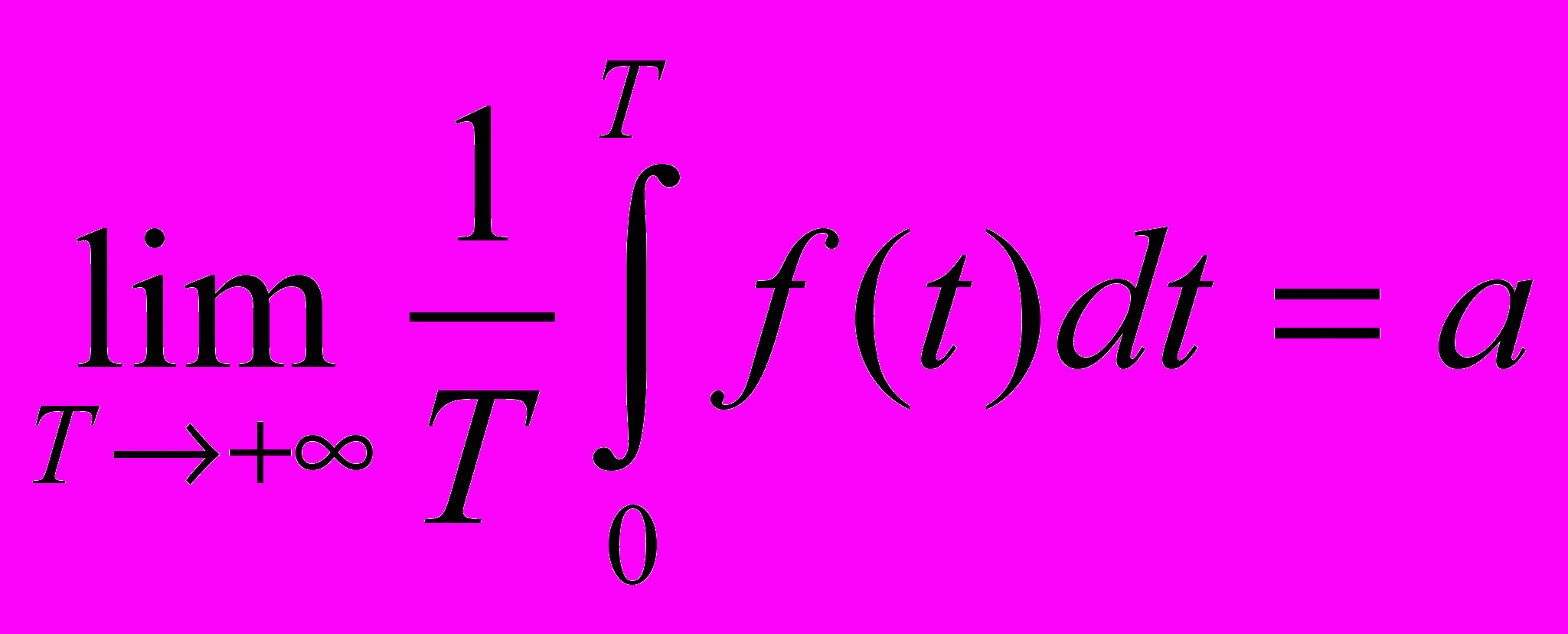Если 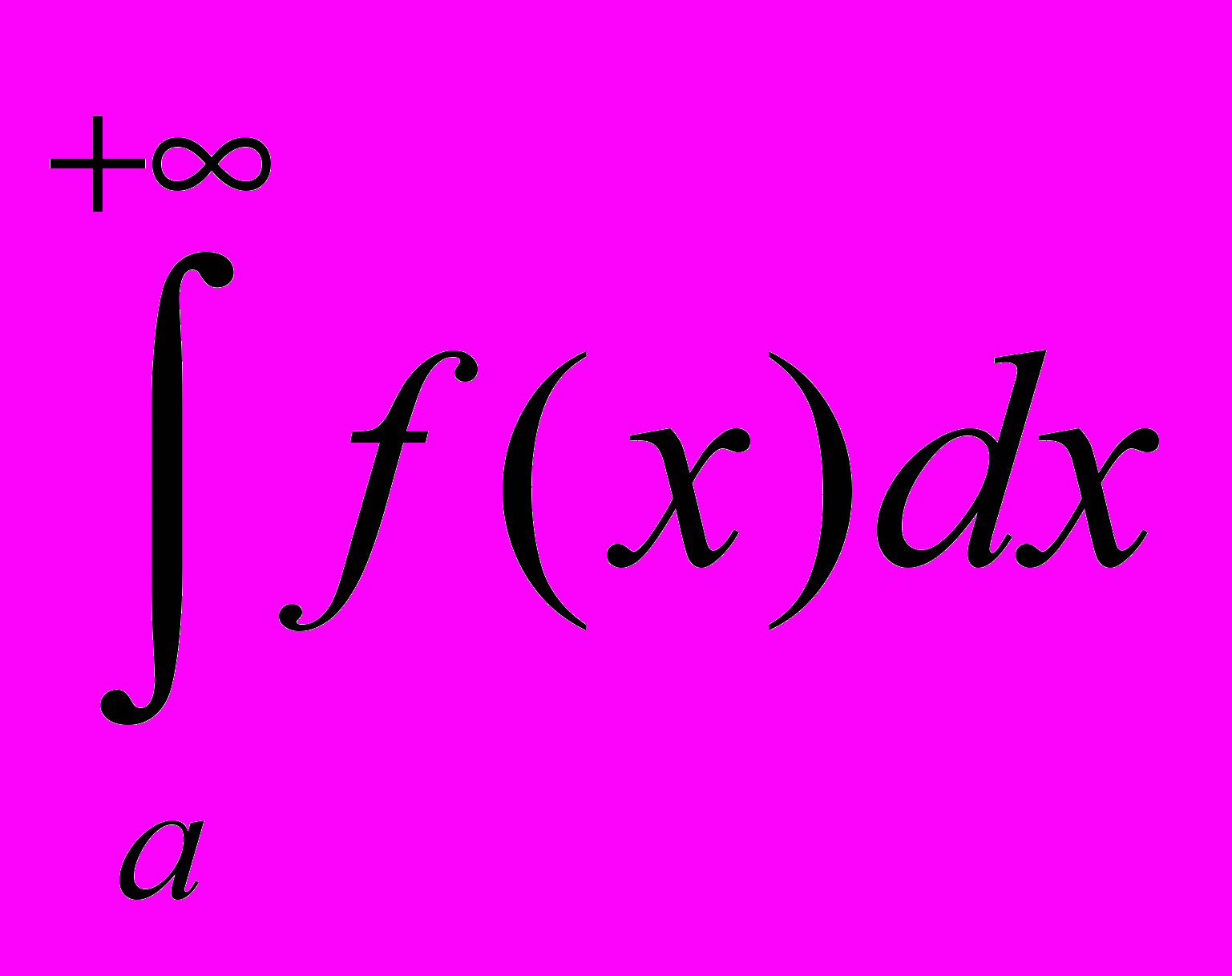сходится, то обязательно ли f(x) 0 при х  +.
Функция f(x) непрерывна на [а; +) и 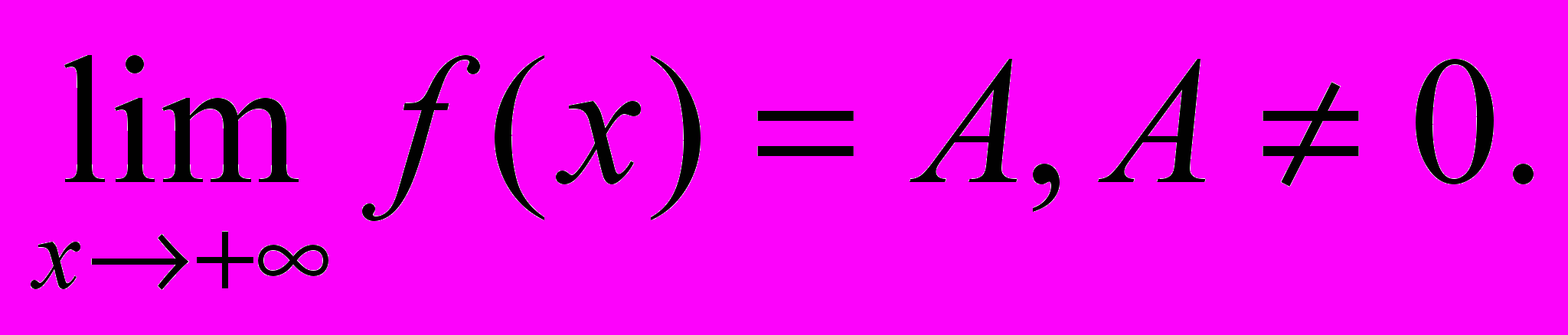Может ли интеграл

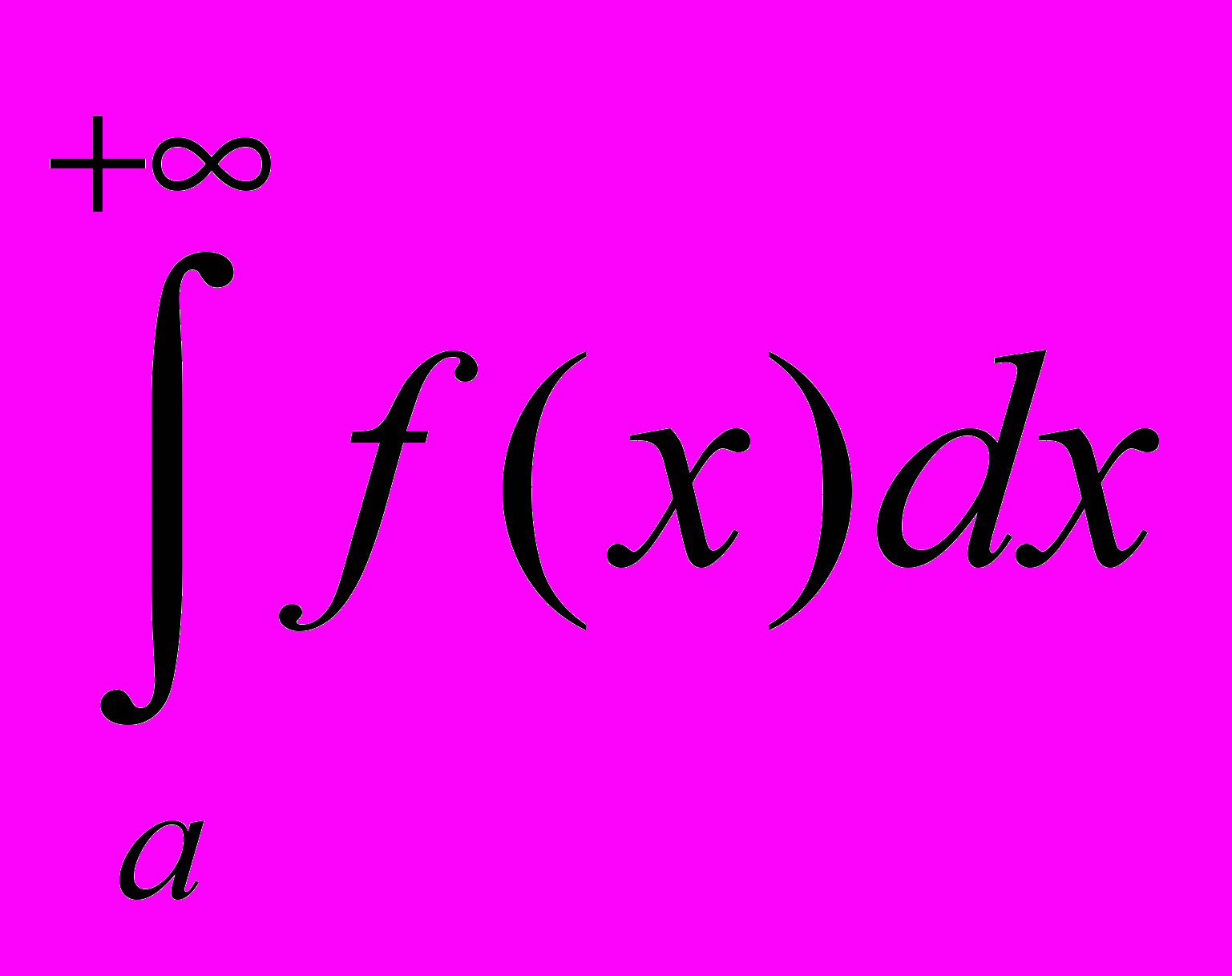сходиться?

Доказать, что

если

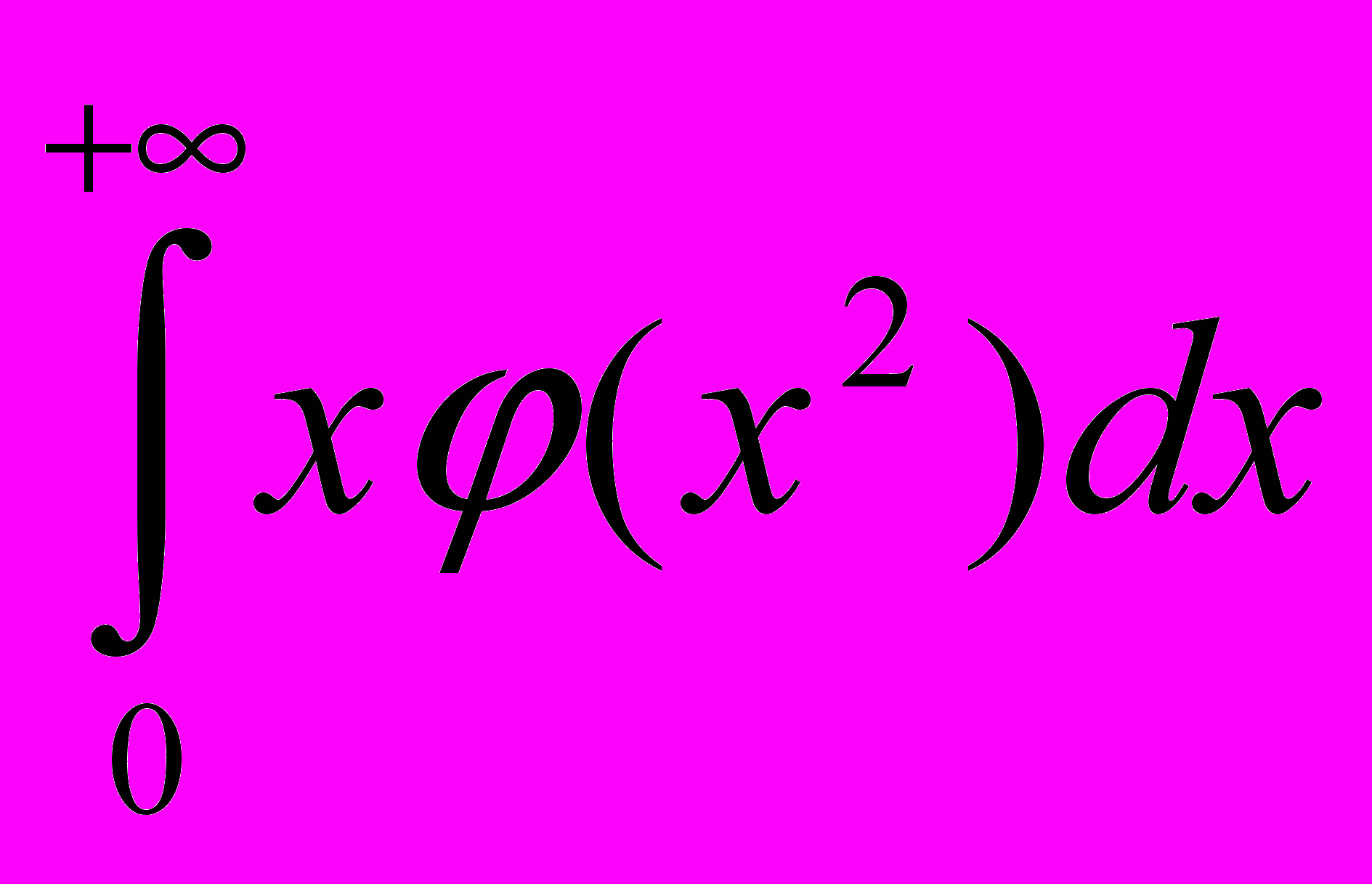сходится, то

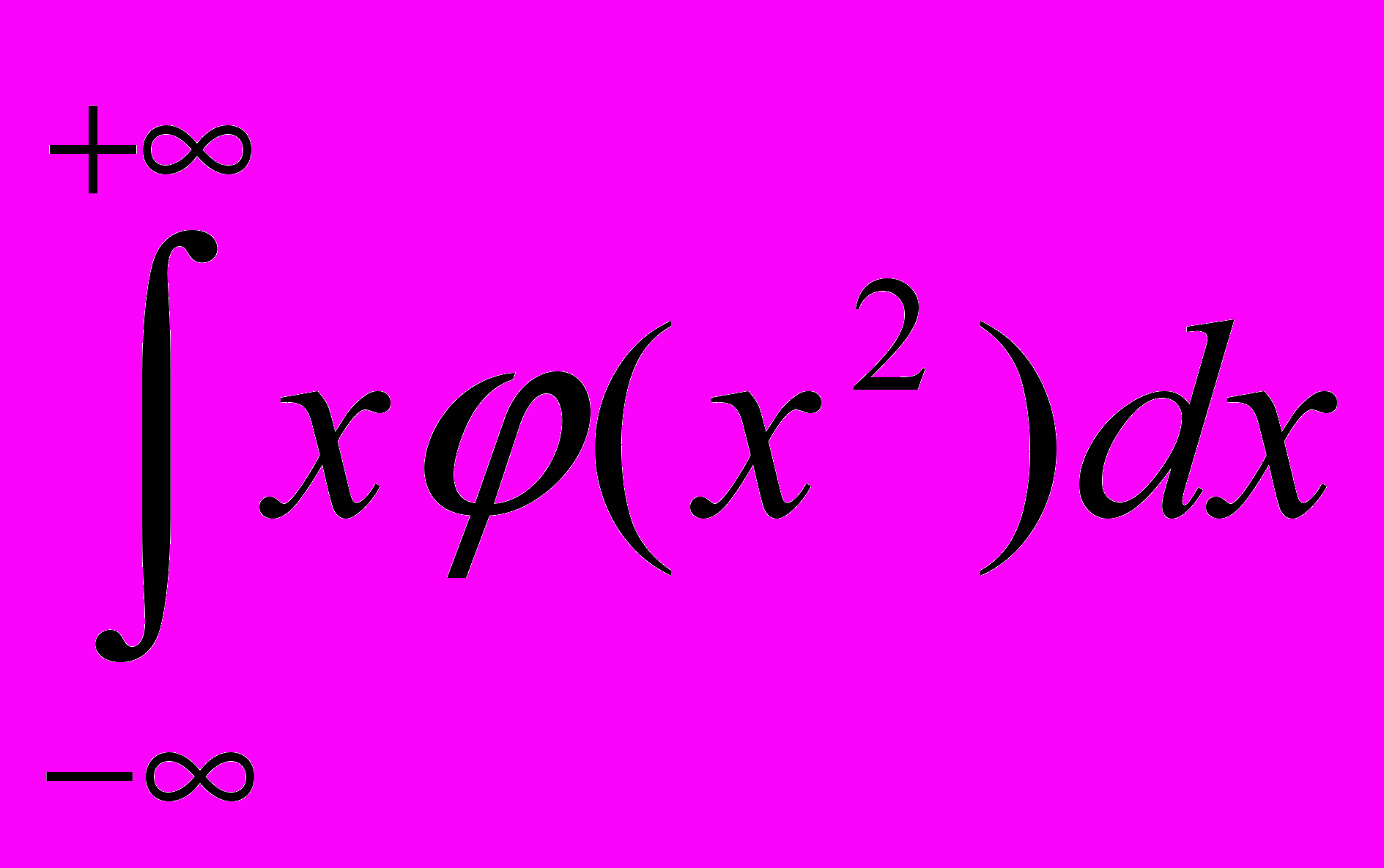=0.

Доказать, что

если

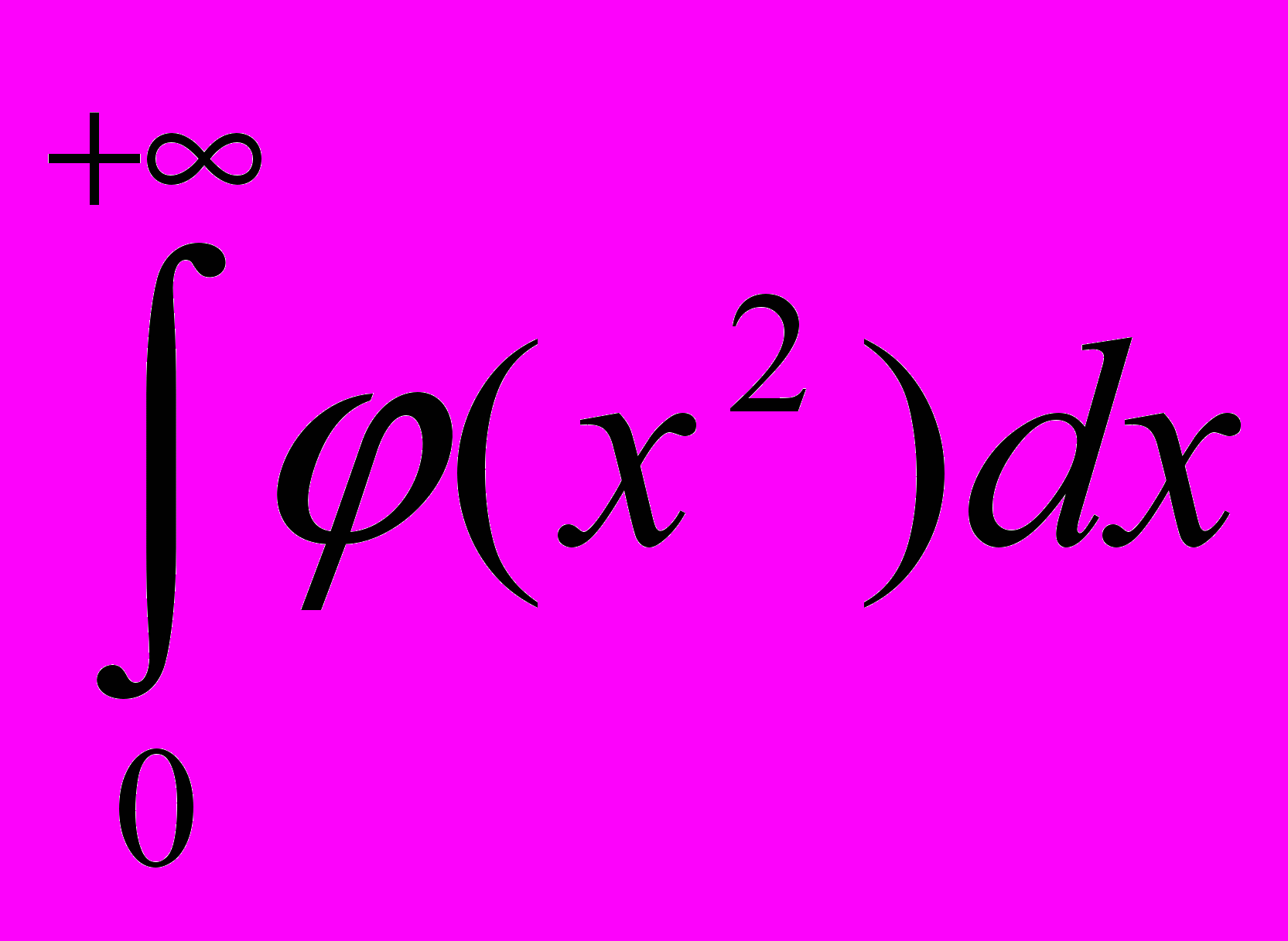сходится, то

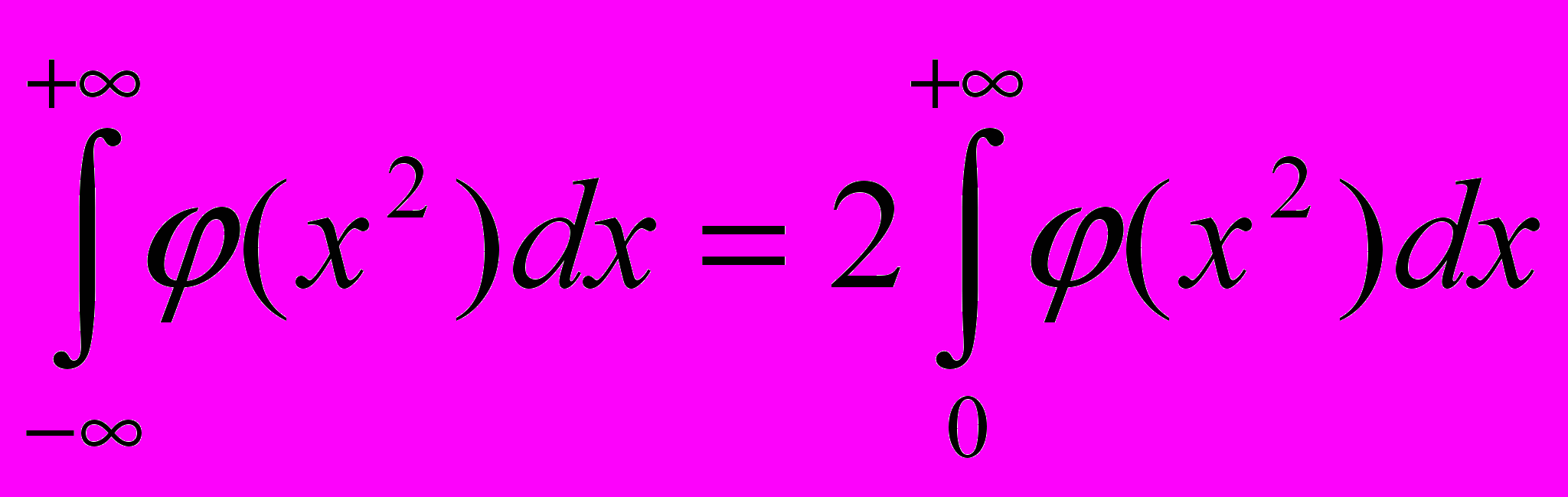Доказать, что если функция f(x) положительна и монотонно убывает, а интеграл 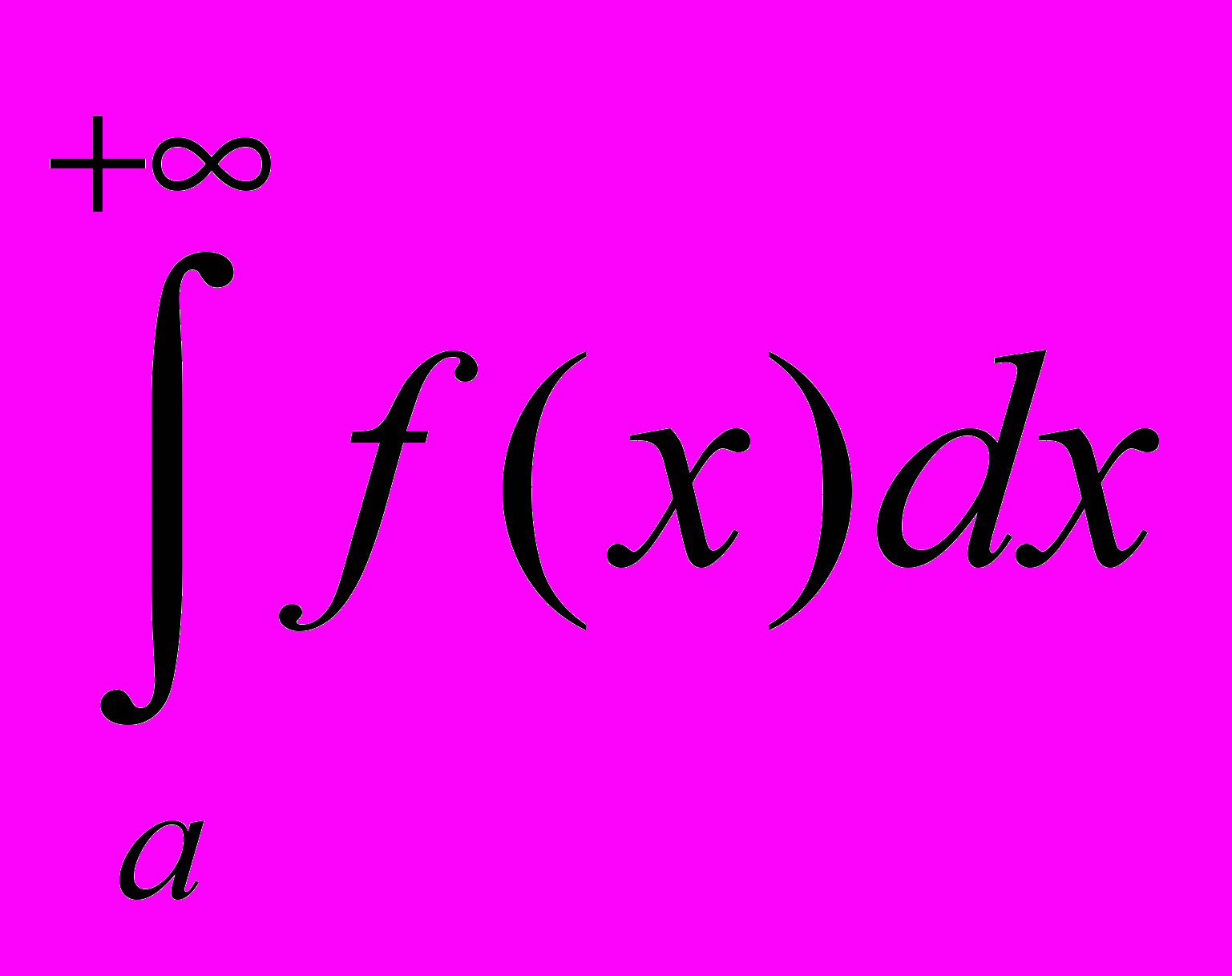сходится, то .
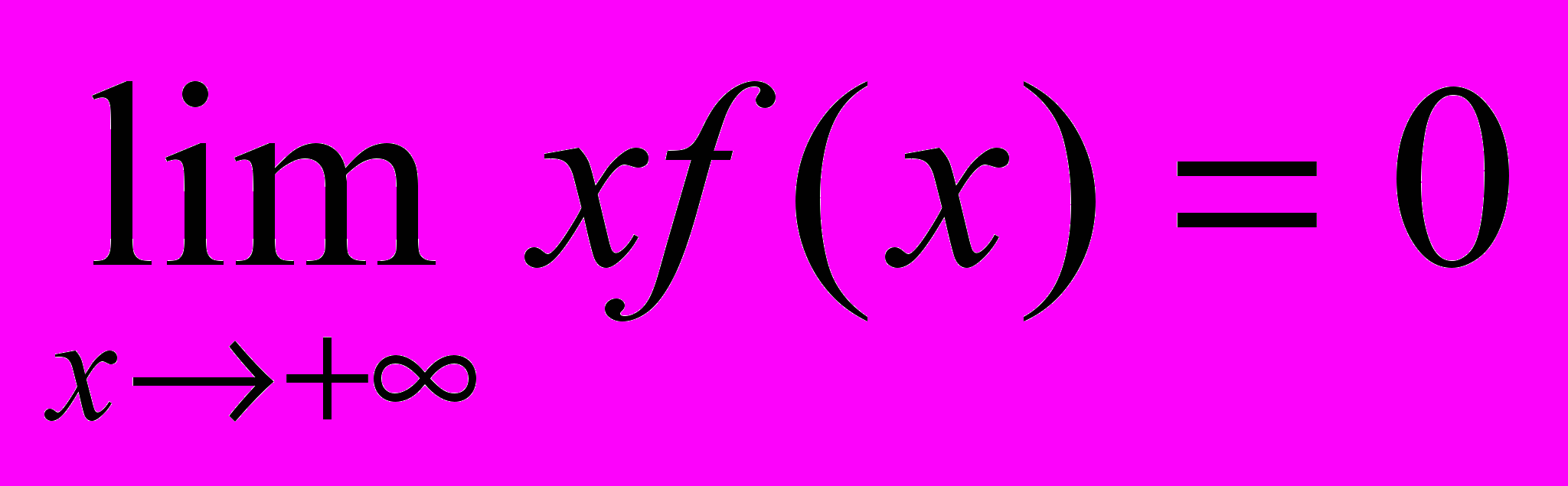Доказать, что если функция f (x) абсолютно интегрируема на промежутке (а; +), то она интегрируема на этом промежутке.

Доказать, что если функция f (x) абсолютно интегрируема на промежутке [а; +) и φ (x)- ограниченная функция, интегрируемая на каждом конечном отрезке, то

функция φ (x) f (x) абсолютно интегрируема промежутке (а; +).

Утверждение перестаёт быть верным, если функция f (x) интегрируема на промежутке (а; +), но не абсолютно.

Функция f (x) абсолютно интегрируема на промежутке (а; +). Всегда ли f ² (x) также интегрируема на этом промежутке?

Всегда ли произведение двух абсолютно интегрируемых функций на бесконечном промежутке абсолютно интегрируемо?

Привести пример функции, интегрируемой на бесконечном промежутке, квадрат которой интегрируем на этом промежутке.

Доказать, что функция

f (x) =

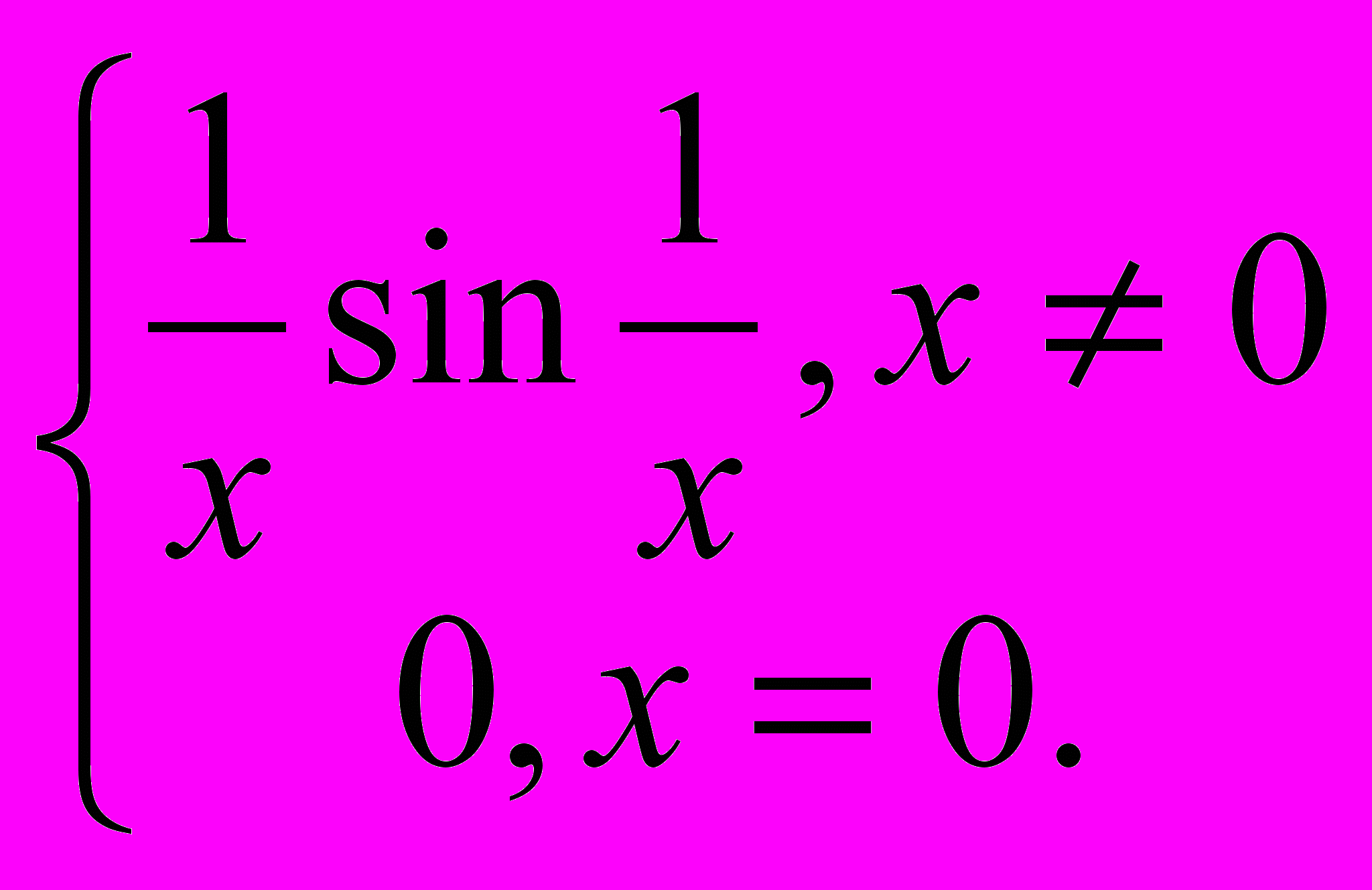
имеет на отрезке [0 ;1] конечный несобственный интеграл, но не является

абсолютно интегрируемой на этом отрезке.

Доказать, что

функция f (x) =

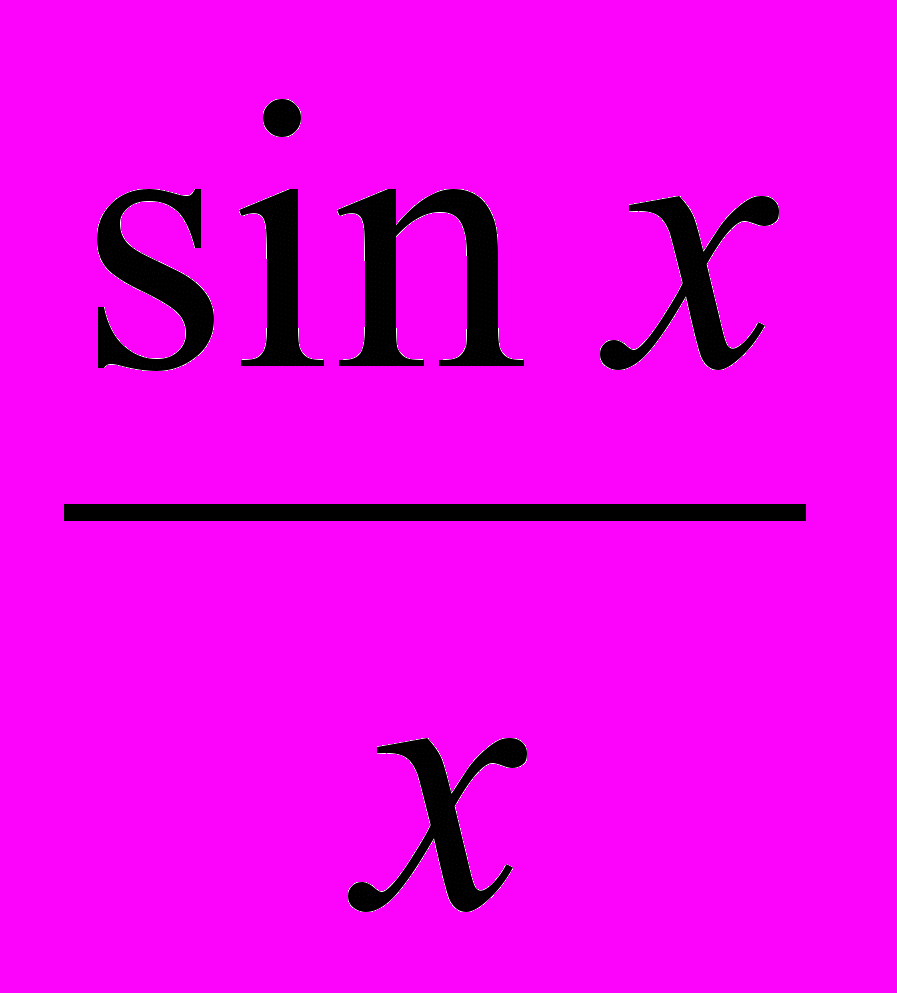интегрируема на промежутке (а; +), а >0, но не

интегрируема абсолютно на этом промежутке.

Привести пример функции f (x), имеющей конечный несобственный интеграл на

[a ;b], для которой функция |f (x)| не интегрируема на этом отрезке.

Привести пример функции f (x), имеющей конечный несобственный интеграл на [a ;b], квадрат которой f ² (x) не интегрируем на этом отрезке.

Всегда ли функция f (x), абсолютно интегрируемая на отрезке [a ;b], интегрируема на этом отрезке?

Функция f (x) абсолютно интегрируема на отрезке[a ;b]. Всегда ли квадрат её интегрируем на этом отрезке?

Доказать, что если существует несобственный интеграл функции f (x) на отрезке[a ;b], то существует интеграл этой функции в смысле главного значения.

Доказать, что

если функция функции f (x) имеет только одну особую точку на отрезке[a ;b],

совпадающую или с точкой а или с точкой b, то её интеграл в смысле главного

значения совпадает с несобственным интегралом.

Привести пример функции f (x), интегрируемой на отрезке [a ;b] в смысле главного значения и не имеющей конечного несобственного интеграла на этом отрезке.

Привести пример функции f (x), интегрируемой на отрезке [a ;b] в смысле главного значения и не интегрируемой в этом же смысле на некотором отрезке [ ;], а   <   b.

Доказать, что если функция f (x) положительна (отрицательна) и имеет на [a ;b] конечный несобственный интеграл, то она абсолютно интегрируема на этом отрезке.

Доказать, что

если функция f (x) ограничена снизу (сверху) на отрезке [a ;b] и имеет на этом

отрезке конечный несобственный интеграл, то она абсолютно интегрируема на

этом отрезке.

Контрольные вопросы к коллоквиуму по теме «Числовые ряды»

Доказать, используя критерий Коши сходимости рядов, что сумма двух сходящихся рядов есть ряд сходящийся.
Доказать критерий Лейбница сходимости знакочередующегося ряда, используя критерий Коши сходимости рядов.
Доказать, что сумма двух абсолютно сходящихся рядов есть ряд абсолютно сходящийся.
Вывести из критерия Коши сходимости рядов необходимое условие сходимости ряда.
Убедиться, что признак Даламбера - следствие признака Раабе .
Используя критерий Коши сходимости рядов доказать расходимость гармонического ряда.
Исследовать на сходимость ряд .
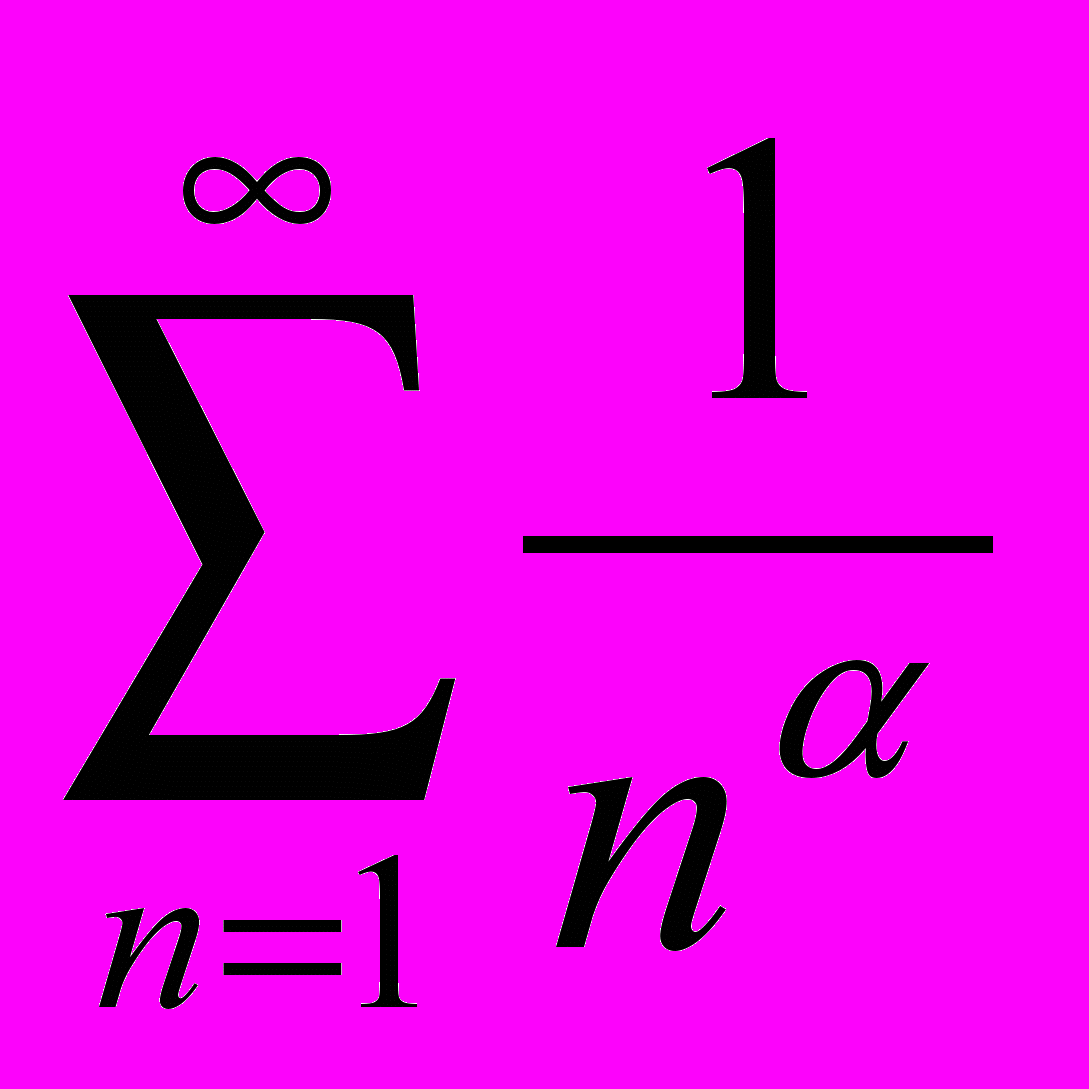Доказать, что если для знакоположительного ряда 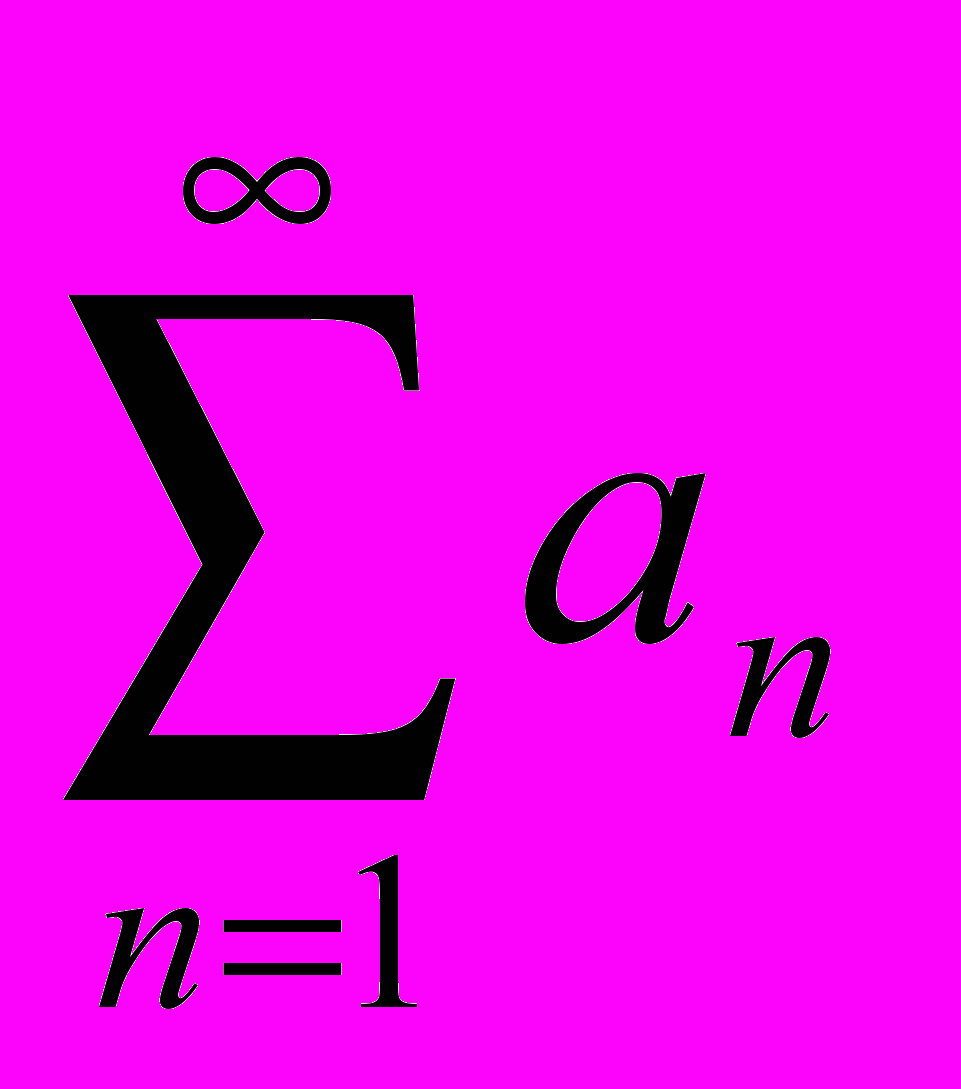существует 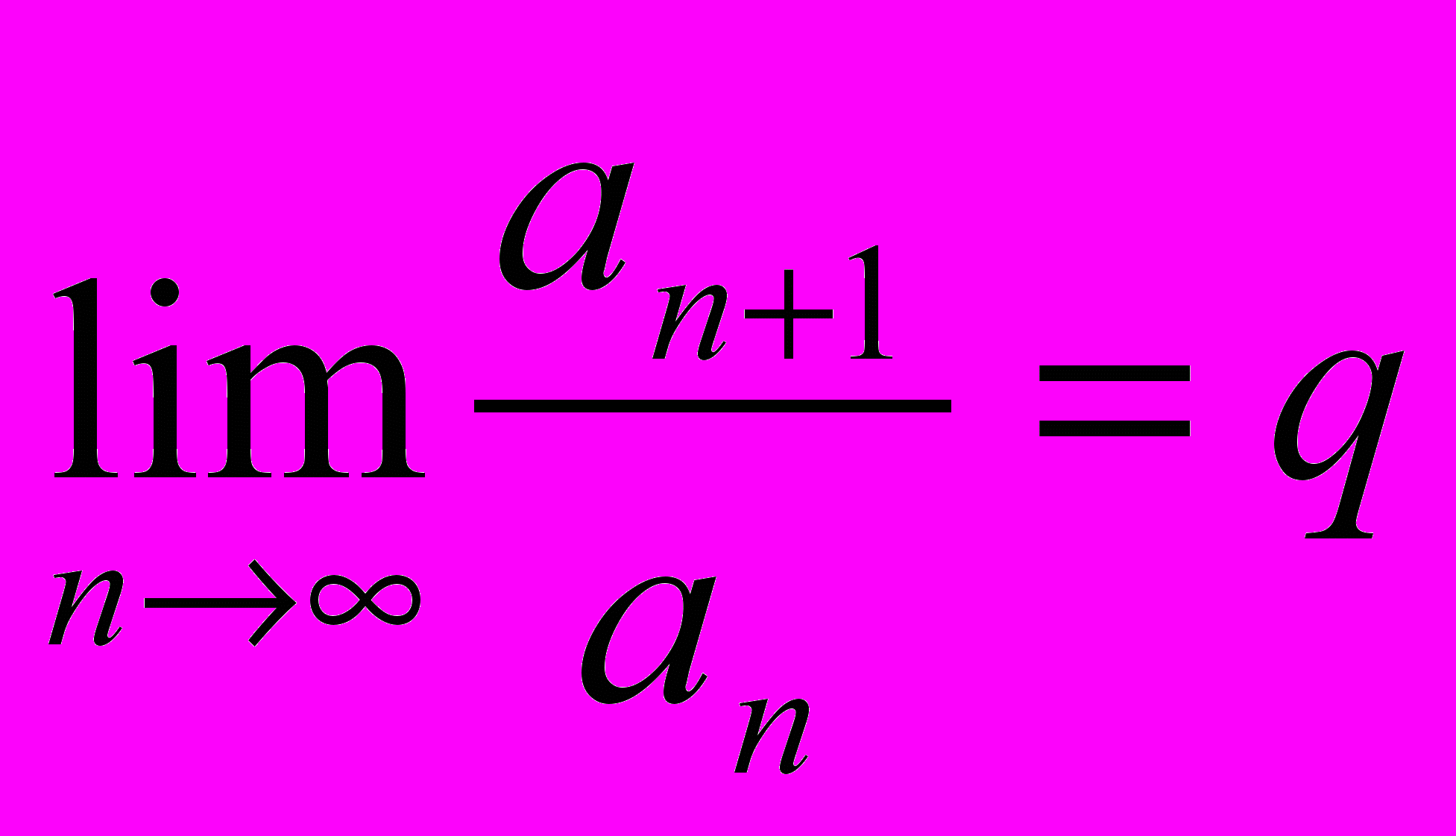, то существует также 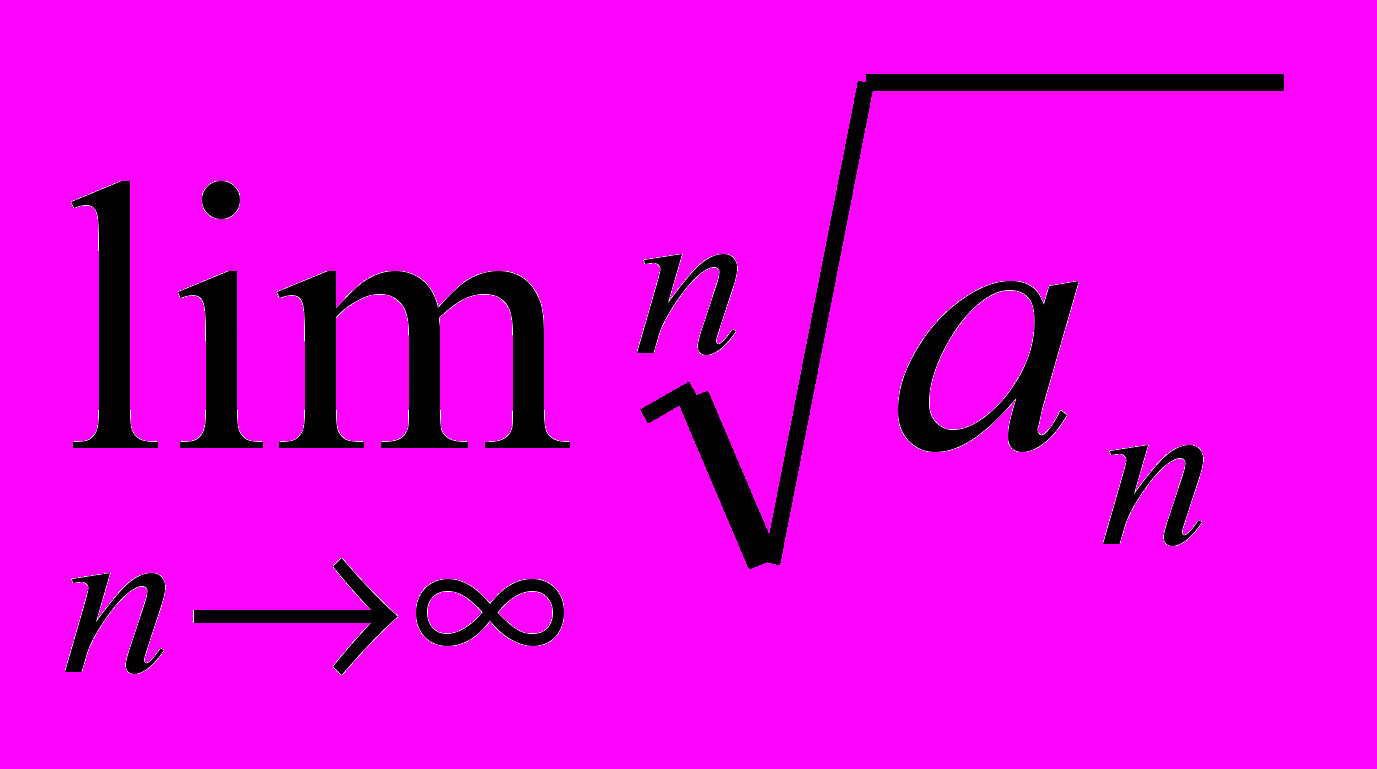= q. Верно ли обратное утверждение?
Доказать, что ряд чисел, обратных членам арифметической прогрессии, расходится.
Исследовать сходимость ряда а)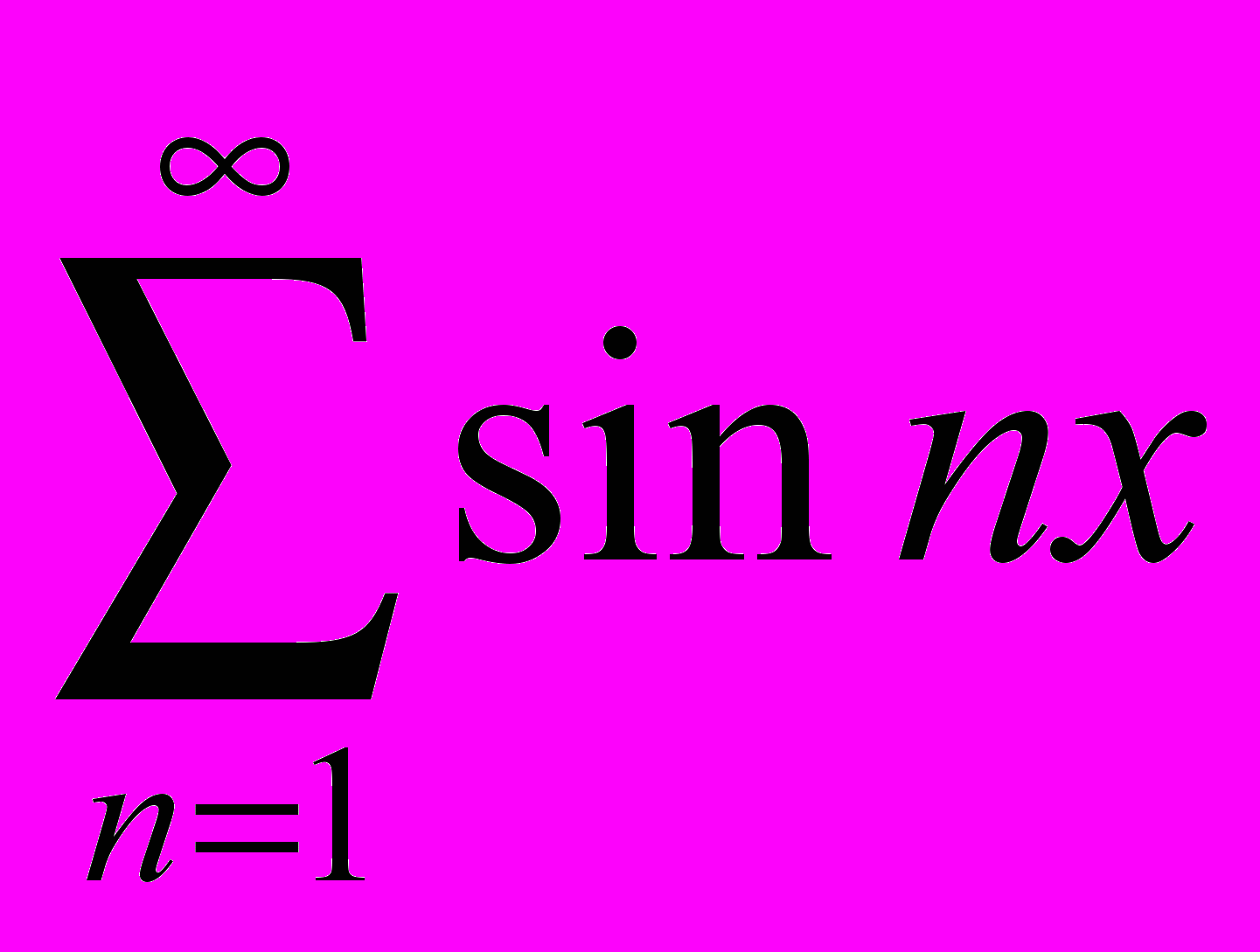; б).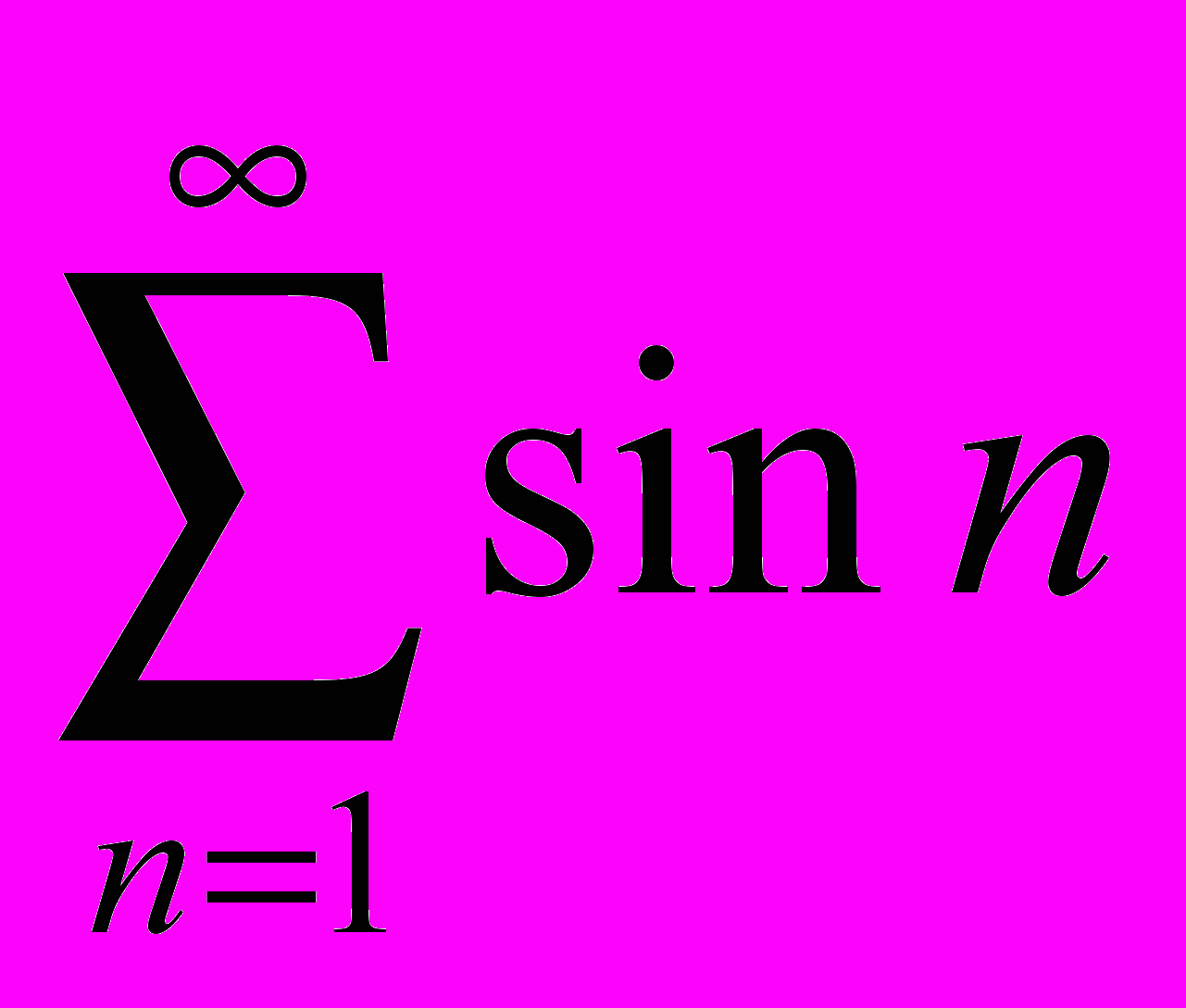
Доказать, что ряд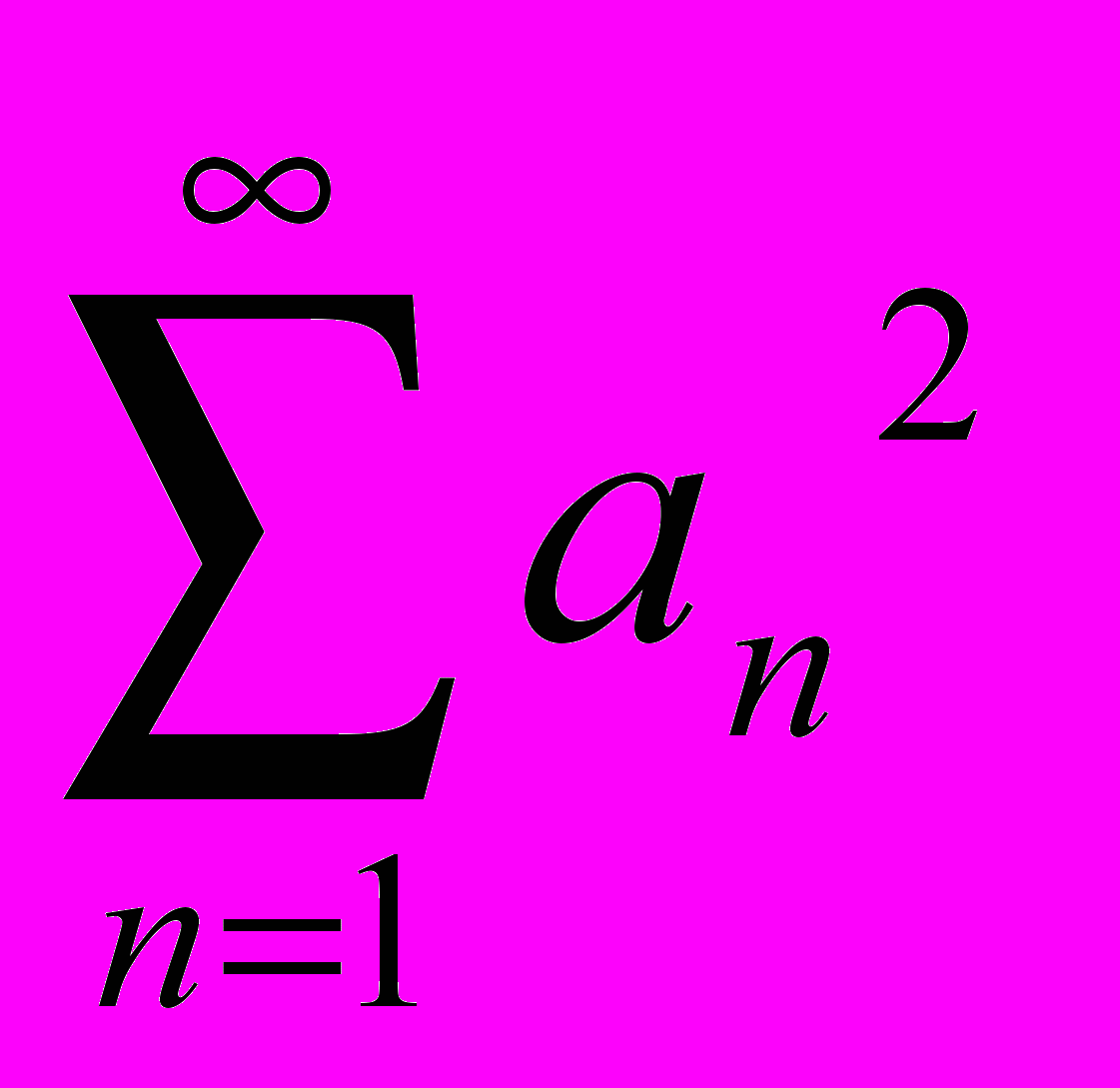сходится, если знакоположительный ряд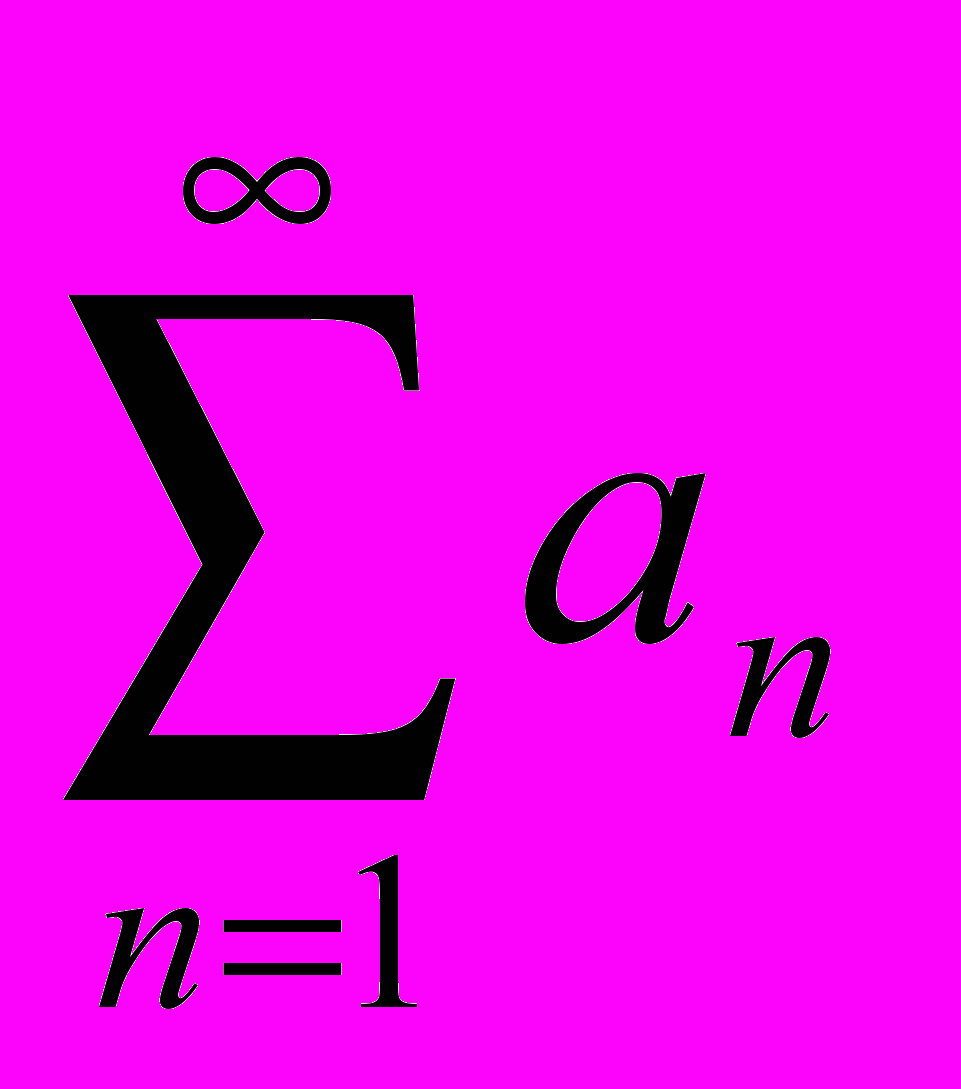сходится. Верно ли обратное утверждение?
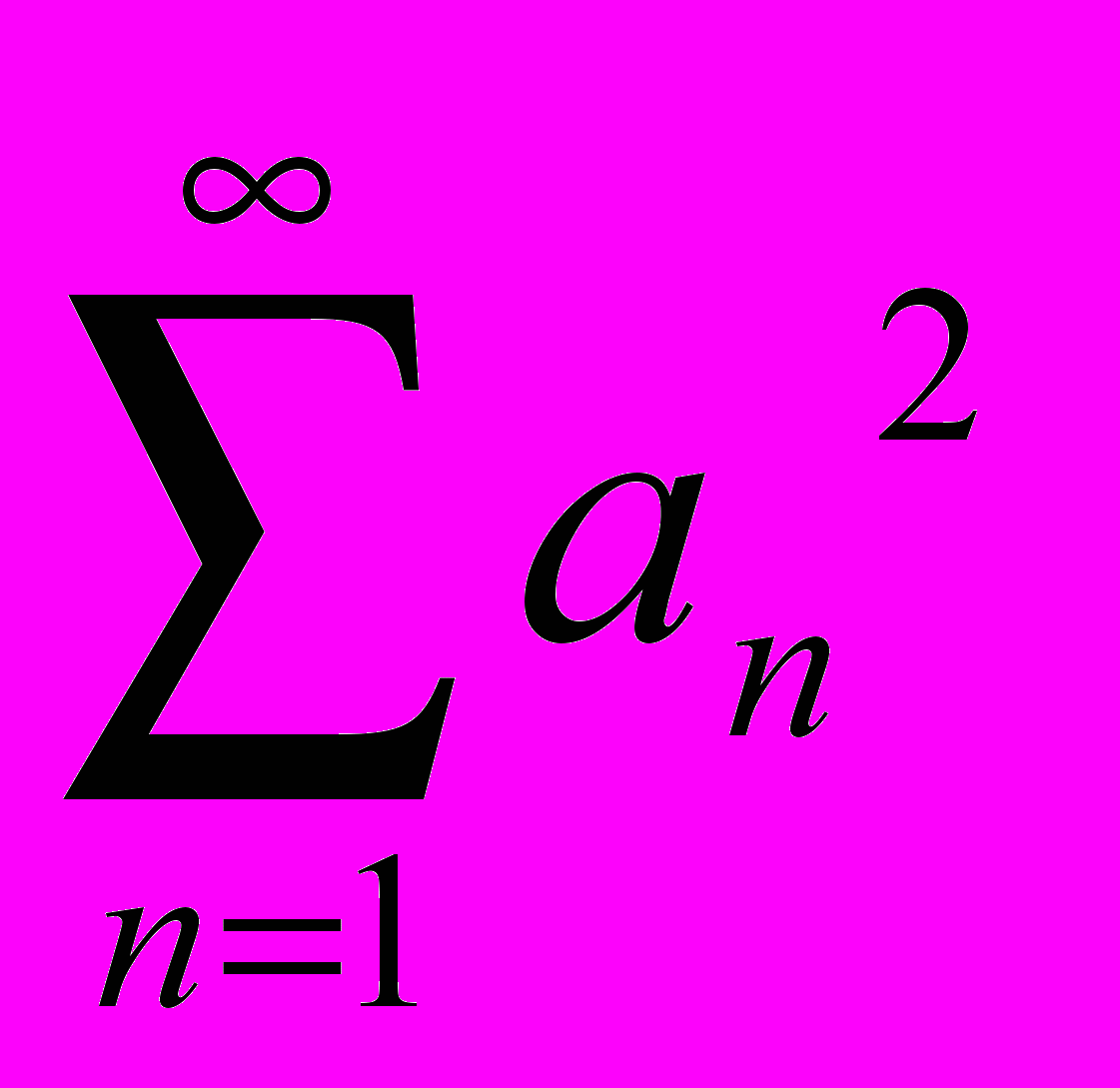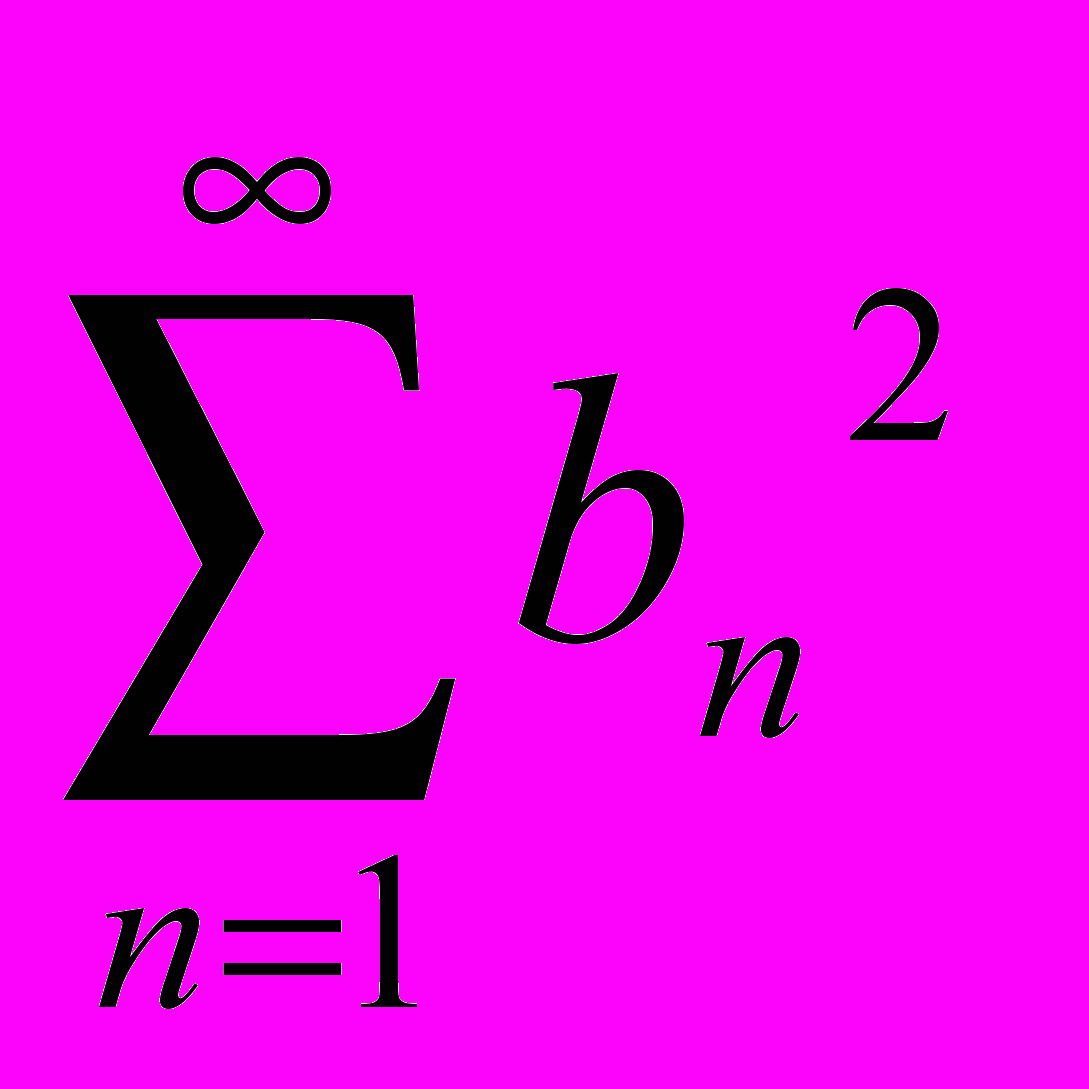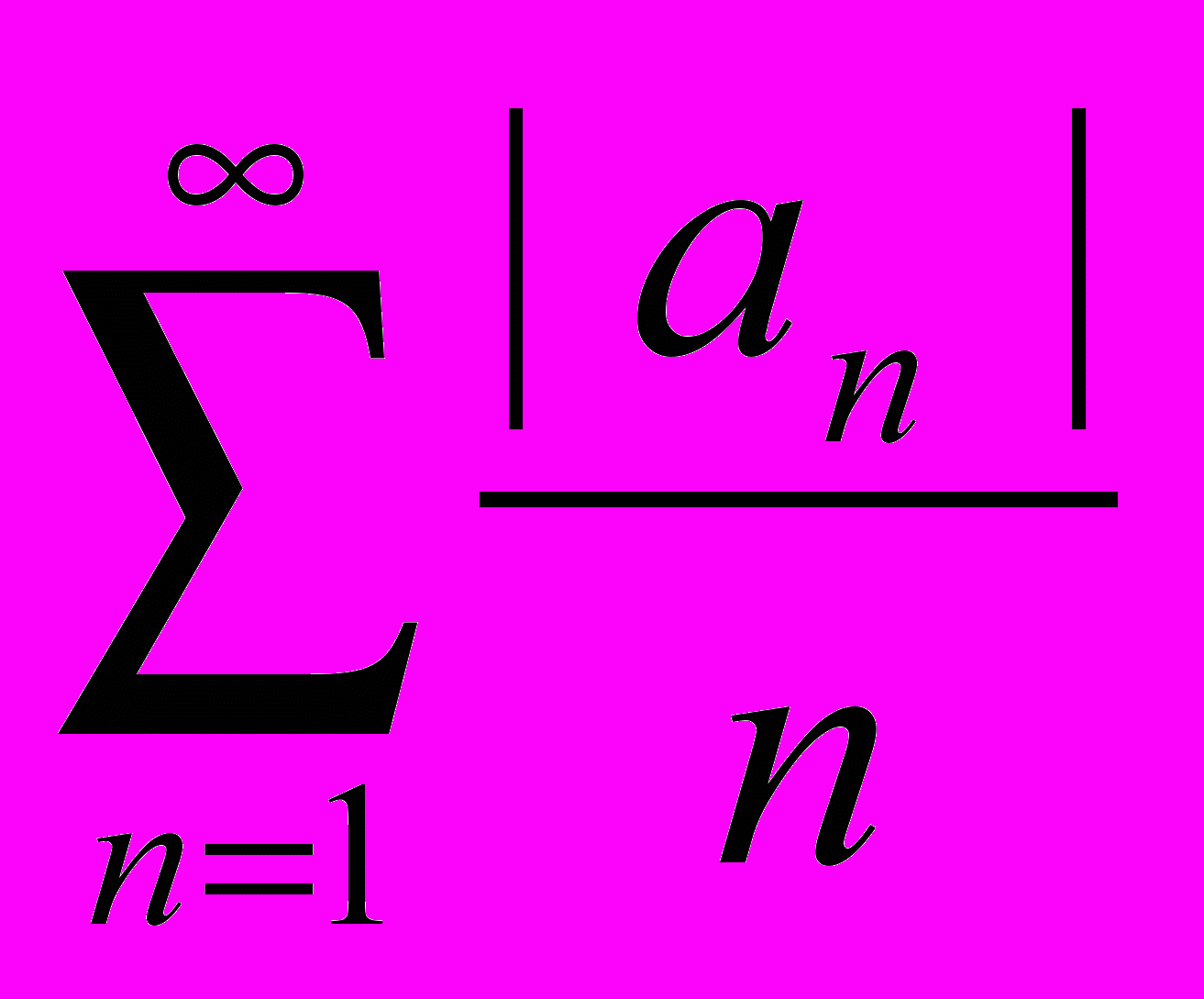
Доказать, что если ряды исходятся, то ряды ; 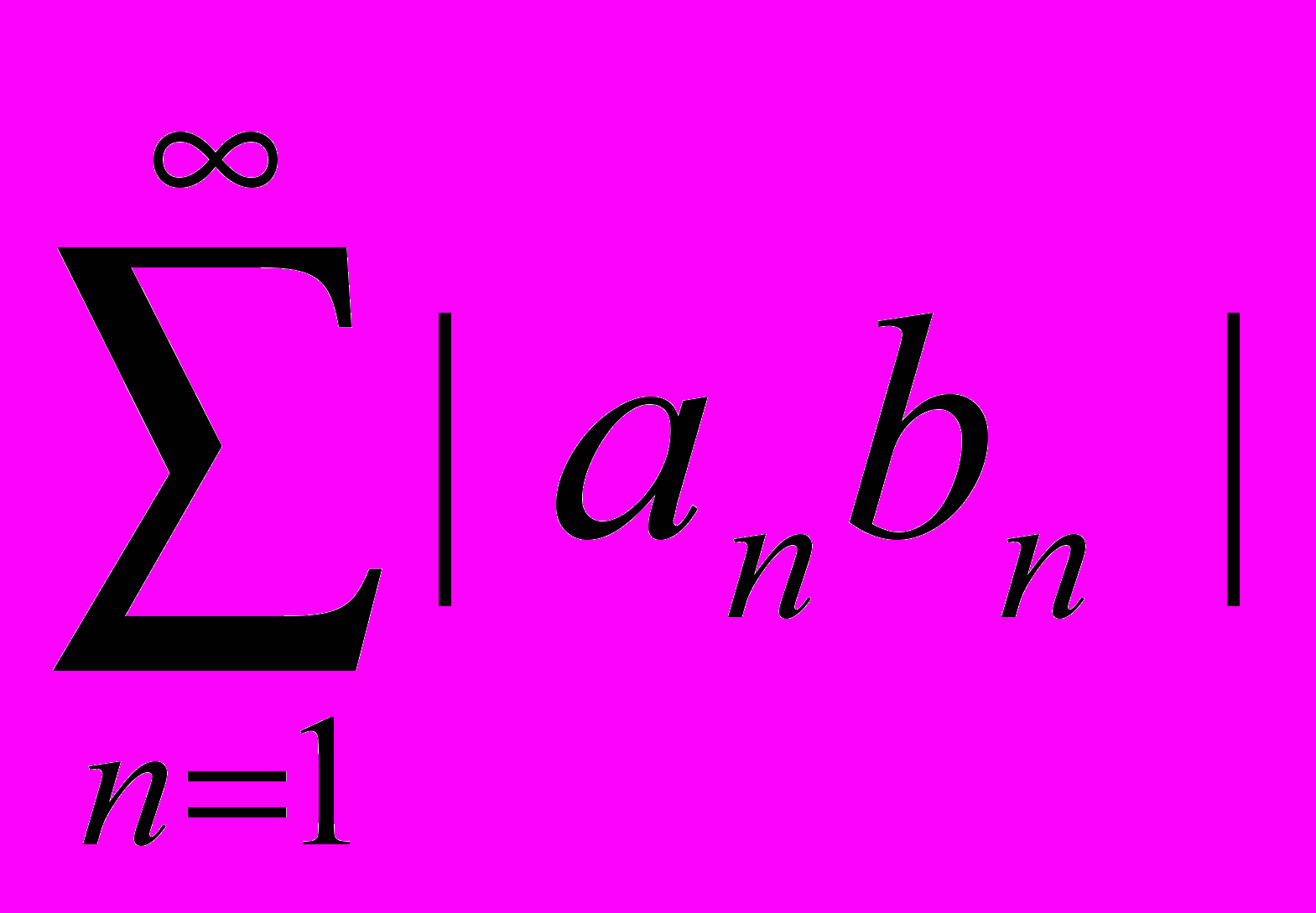сходятся.

Доказать, что если 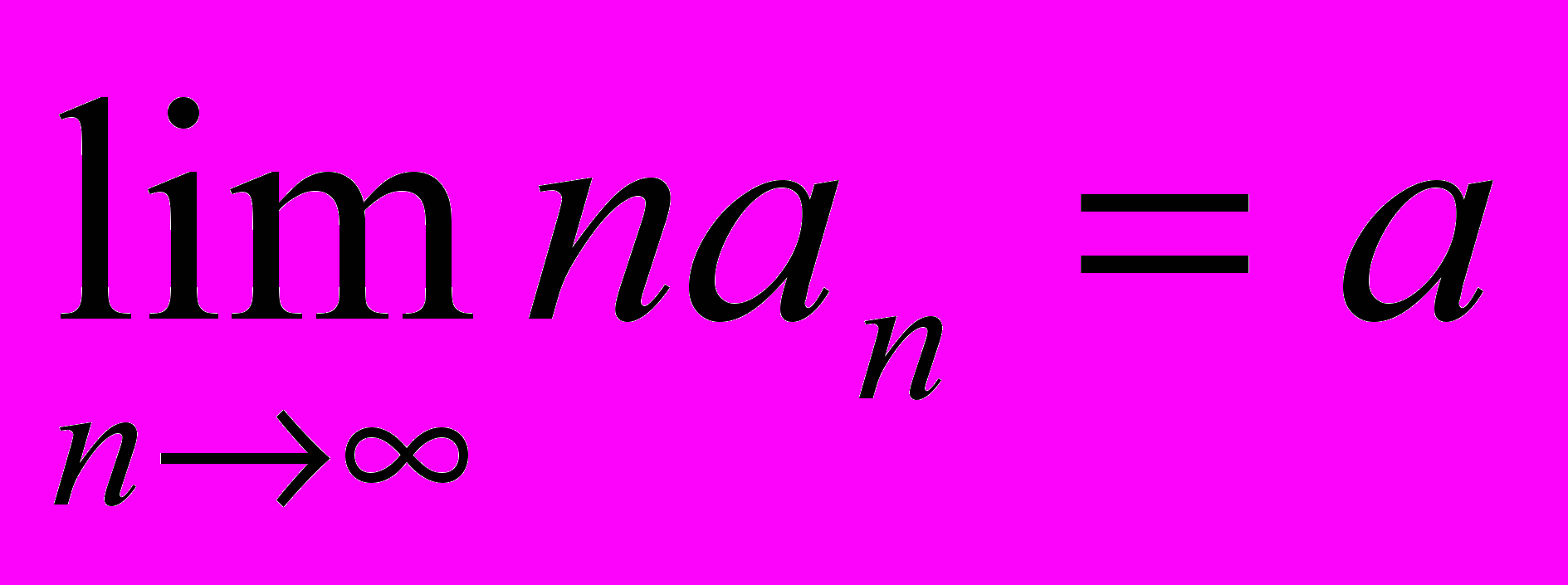, а ¹ 0, то ряд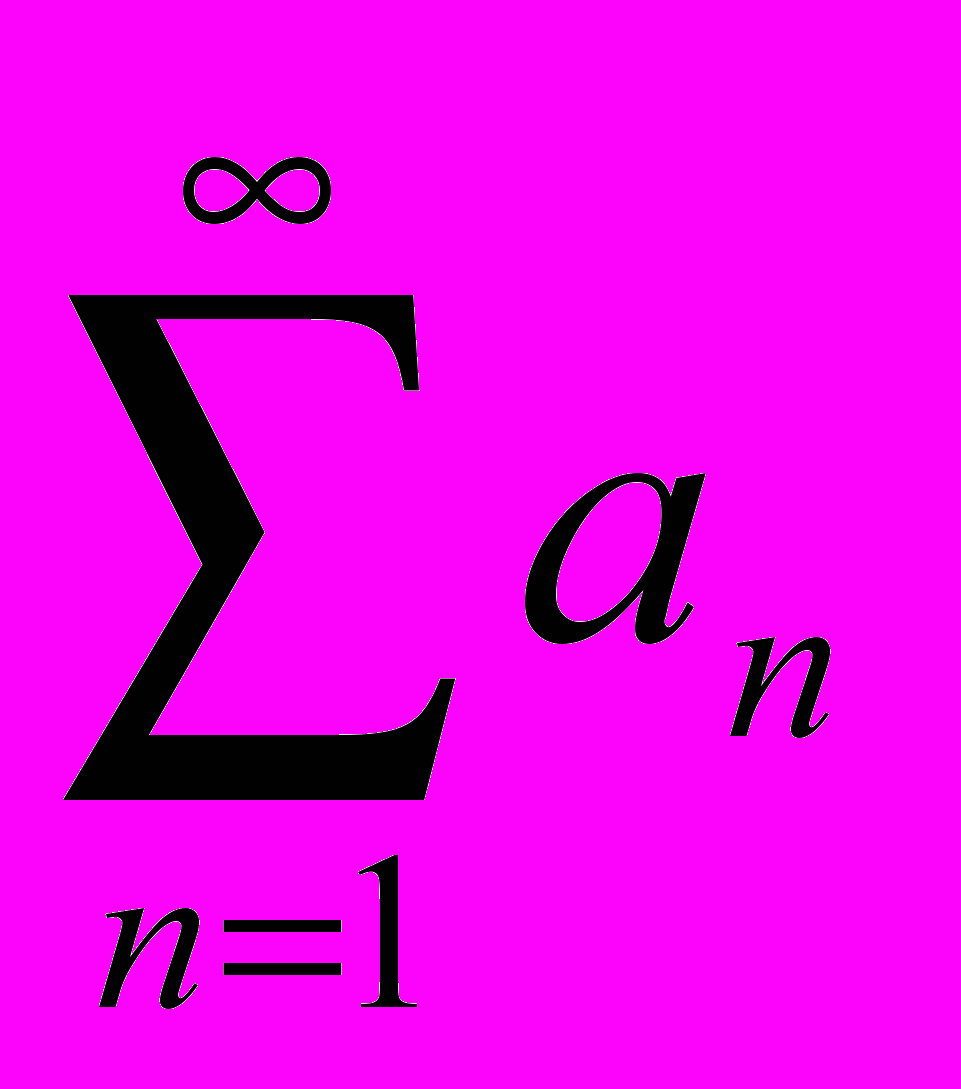расходится.
Доказать, что если знакоположительный ряд 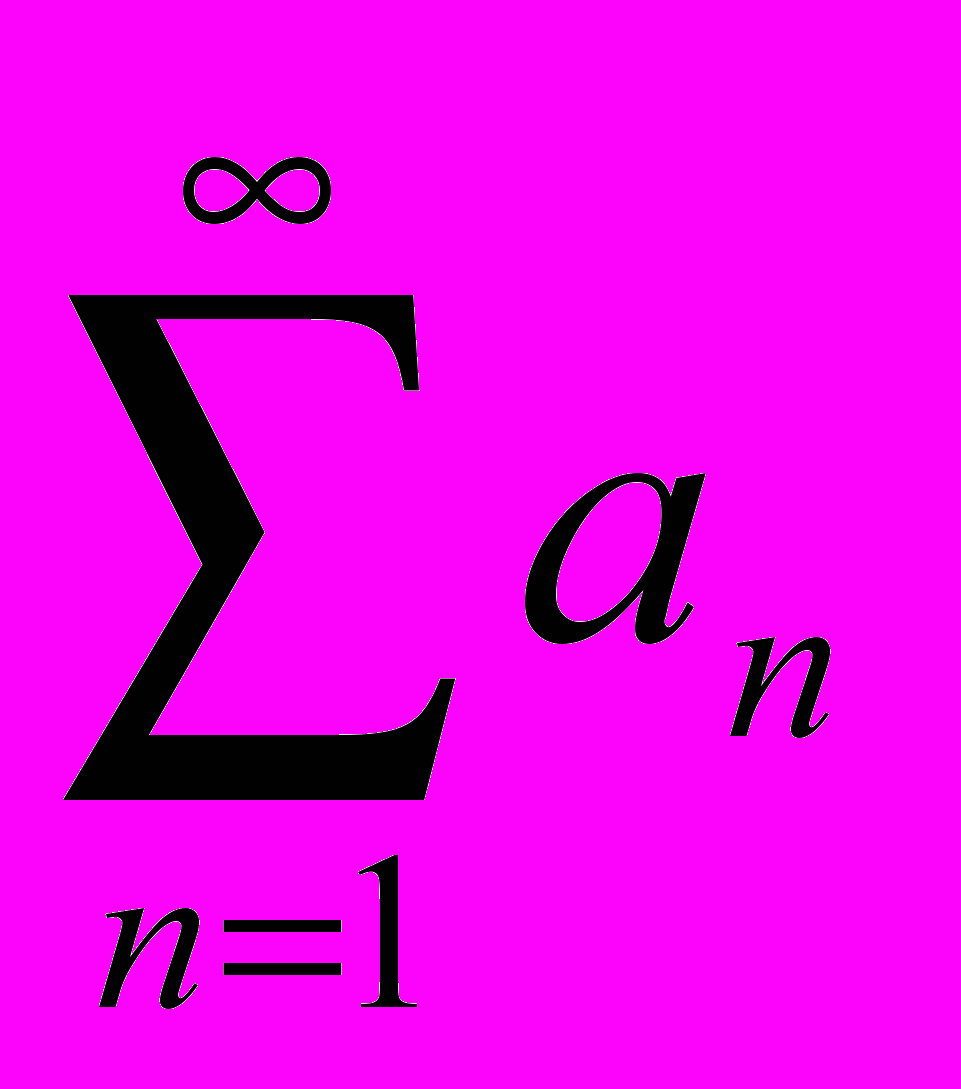сходится, причем последовательность ( 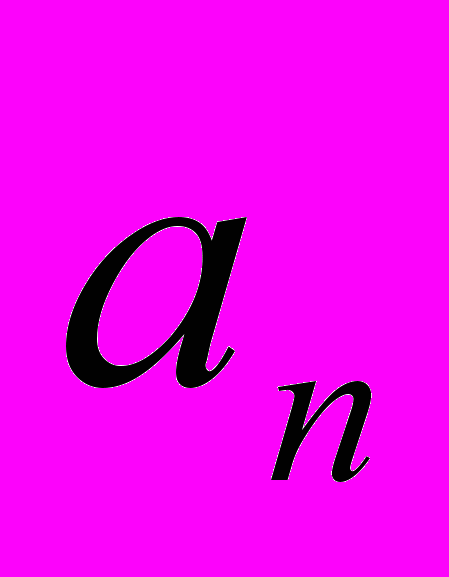) монотонно убывает, то .
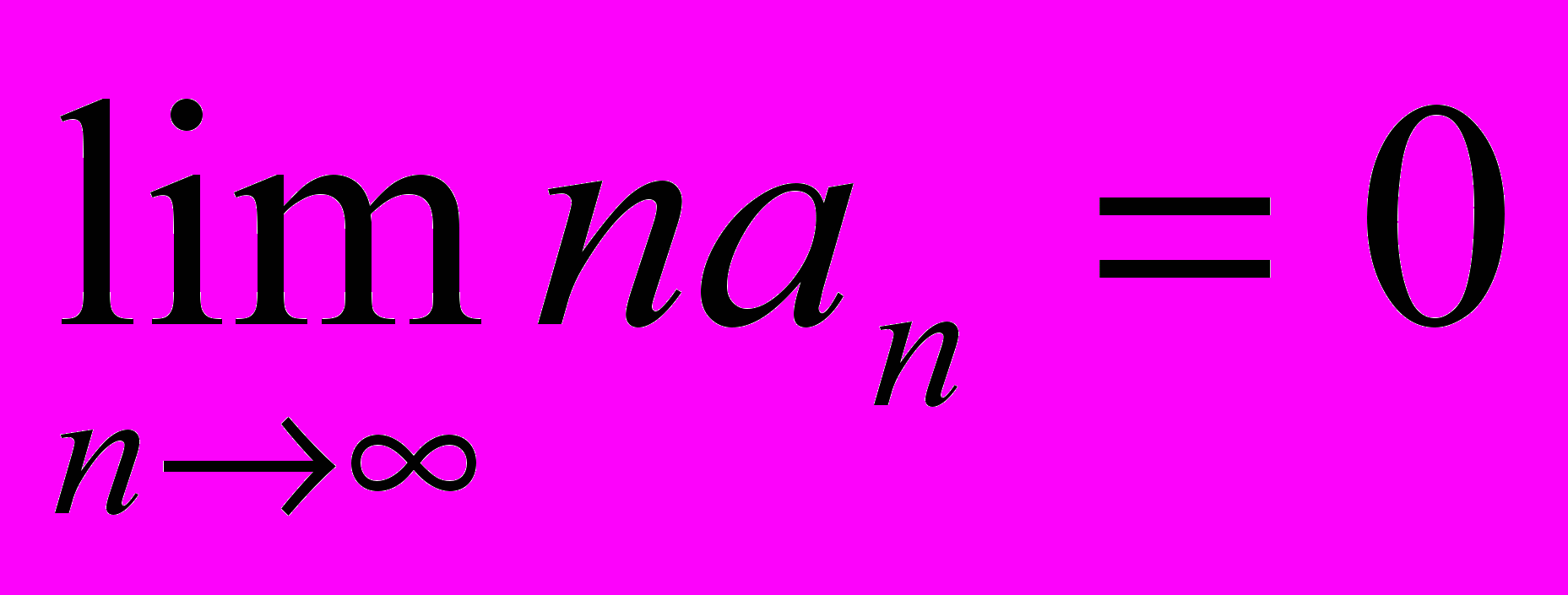Является ли сходящимся ряд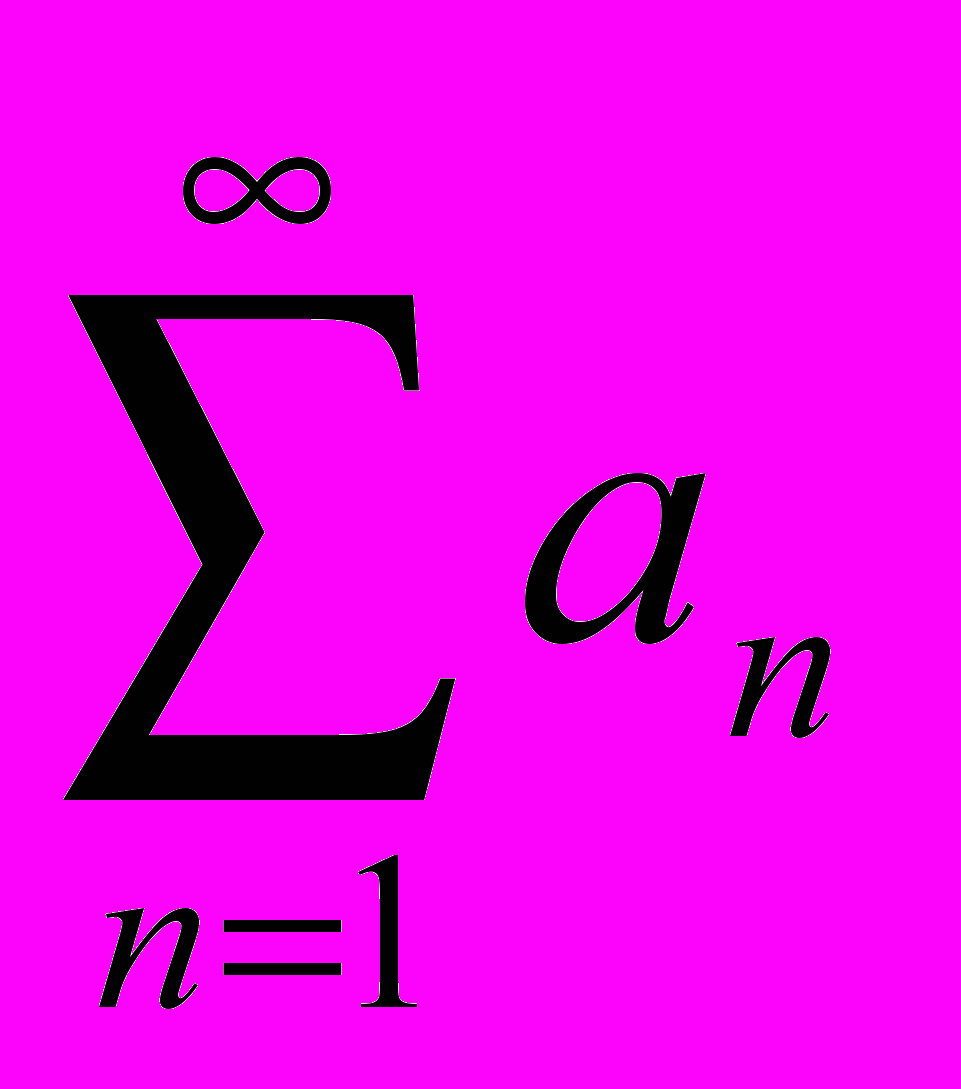, если 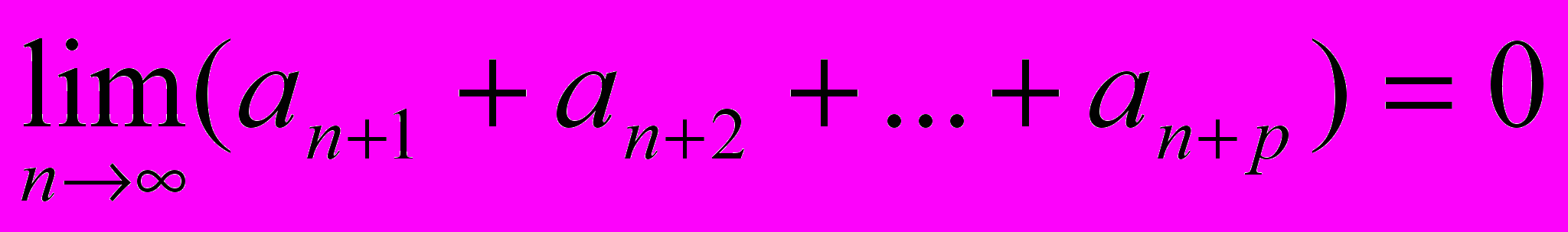при р = 1,2,3, …?
Можно ли утверждать, что ряд 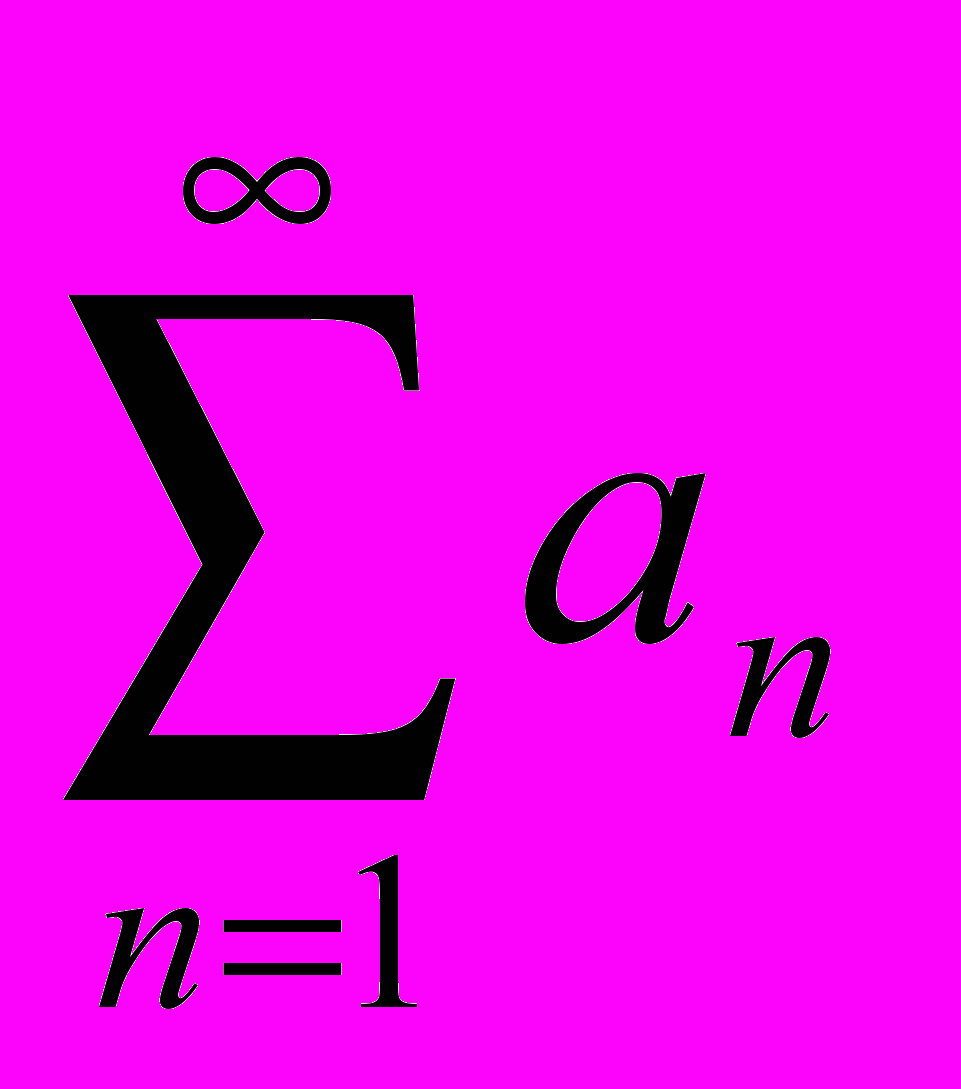расходится, если а) по признаку Даламбера ряд 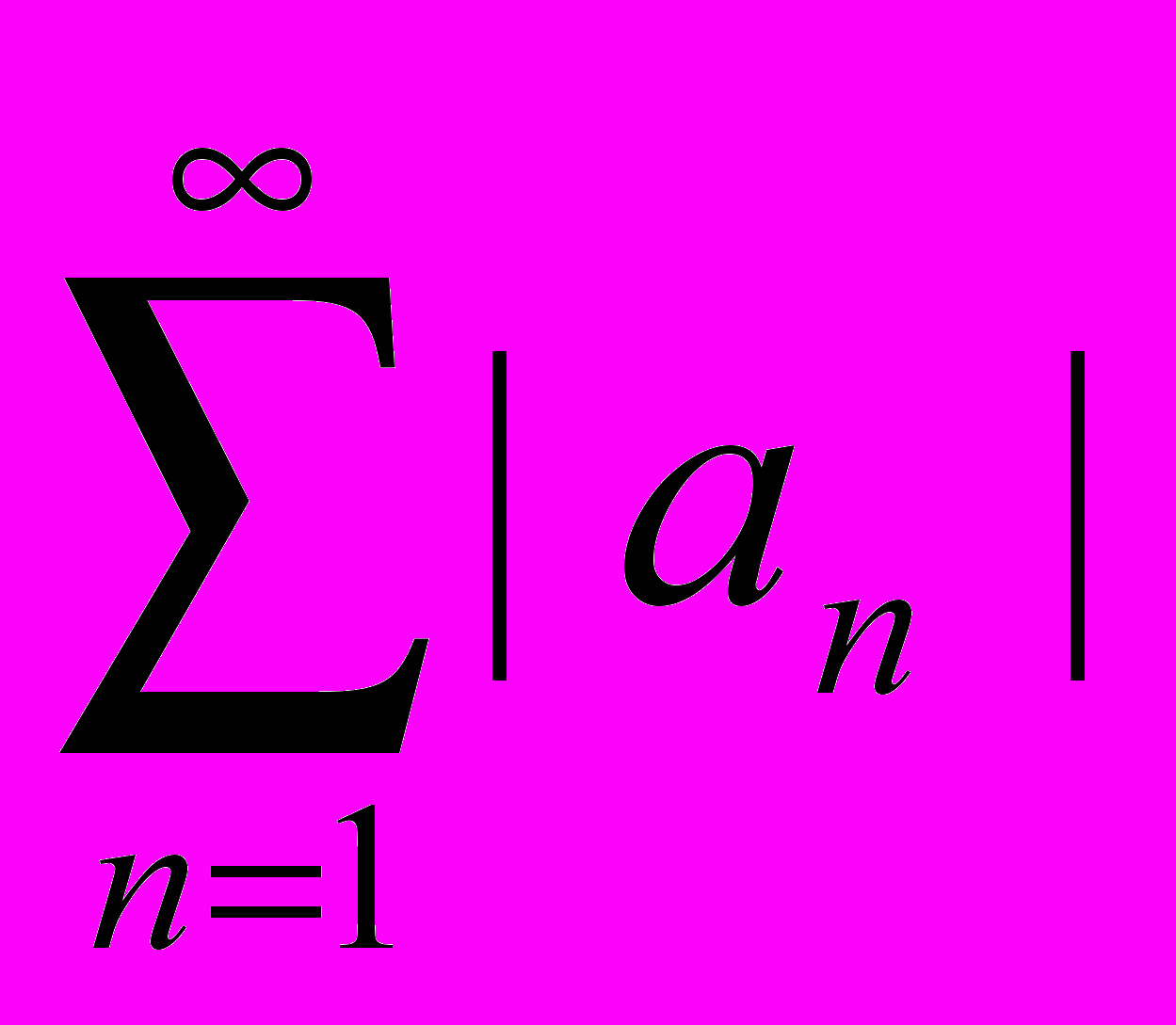расходится? б) по радикальному признаку Коши ряд 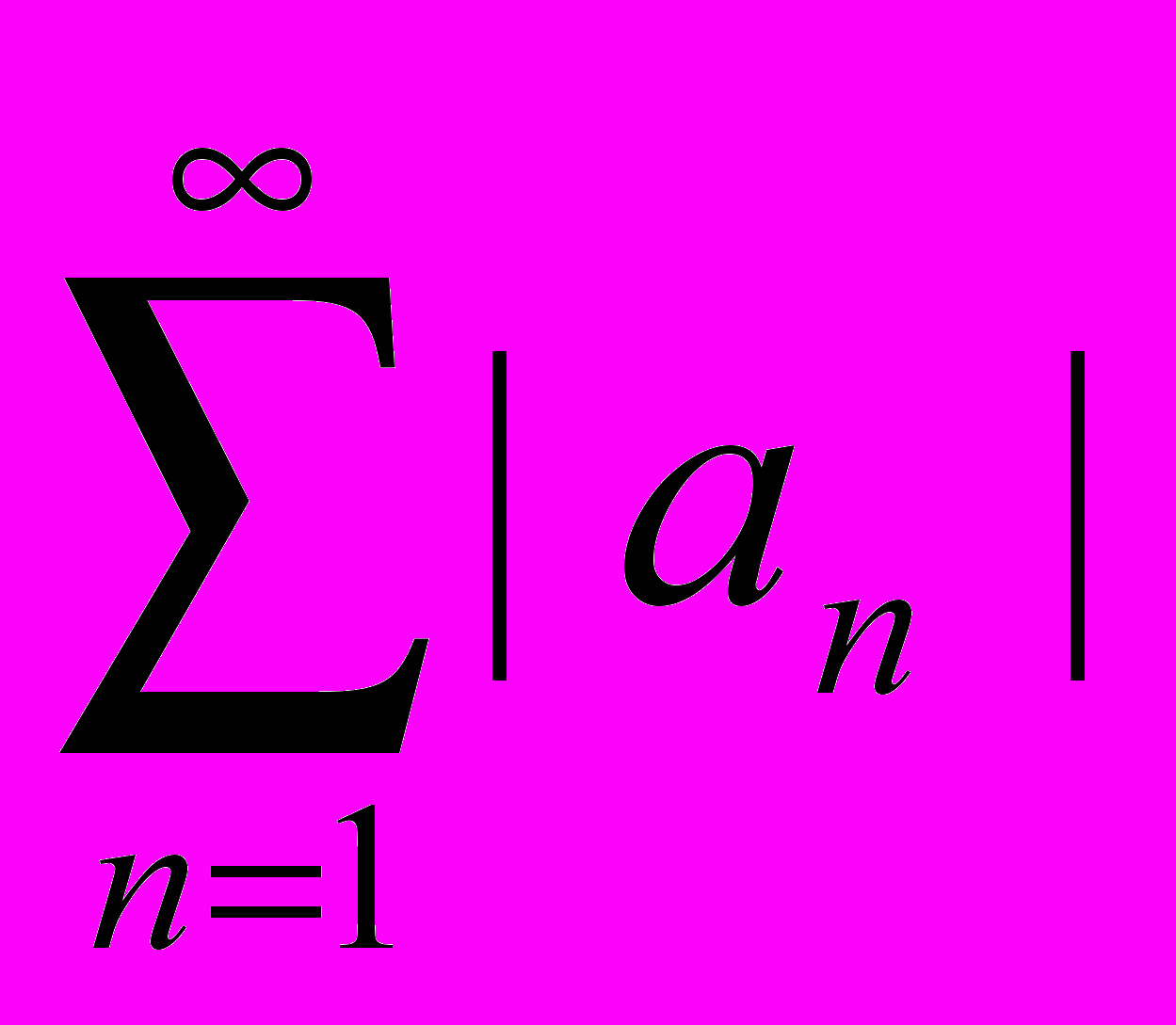расходится?
Может ли разность двух расходящихся рядов сходиться ?
Какие признаки сходимости рядов основаны на сравнении ряда с геометрической прогрессией?
Может ли расходиться последовательность сумм остатков сходящегося ряда?
Привести пример сходящегося знакоположительного ряда, для которого ряд 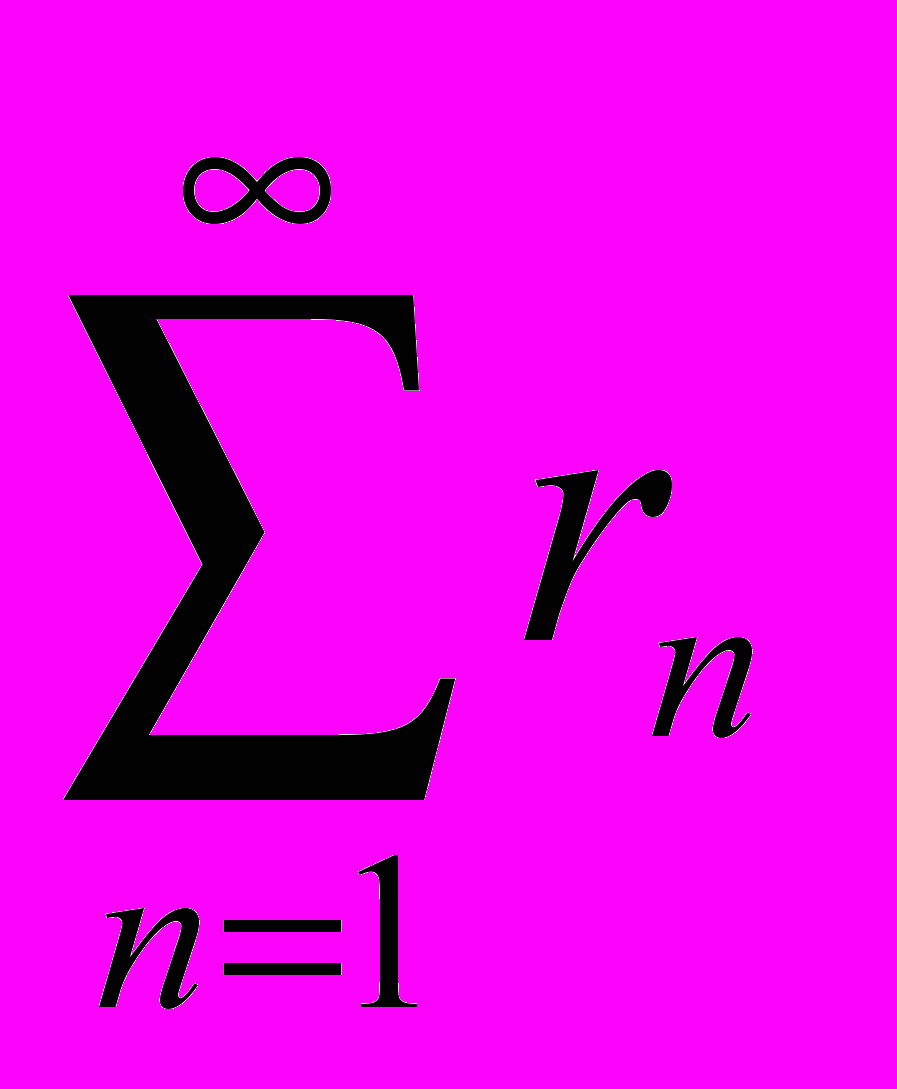сходится.
Может ли ряд 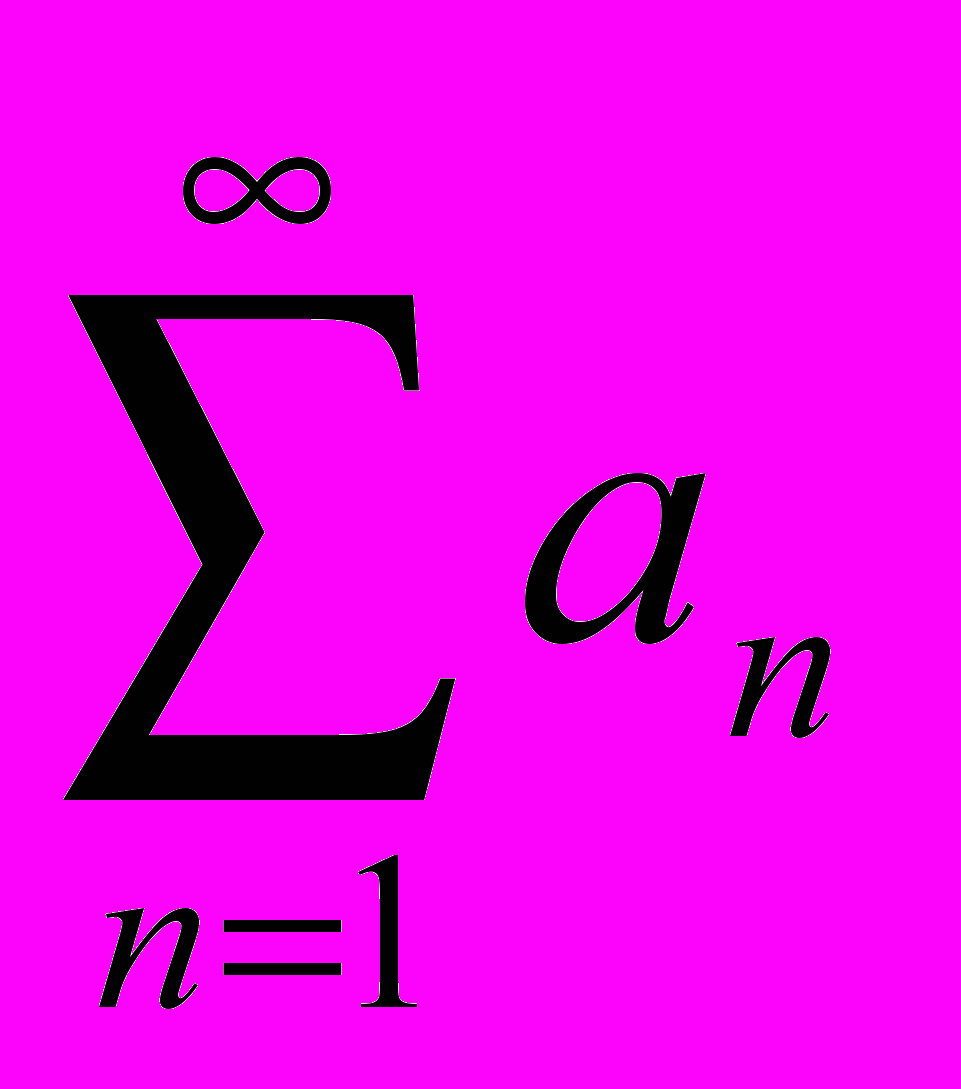сходиться, а ряд 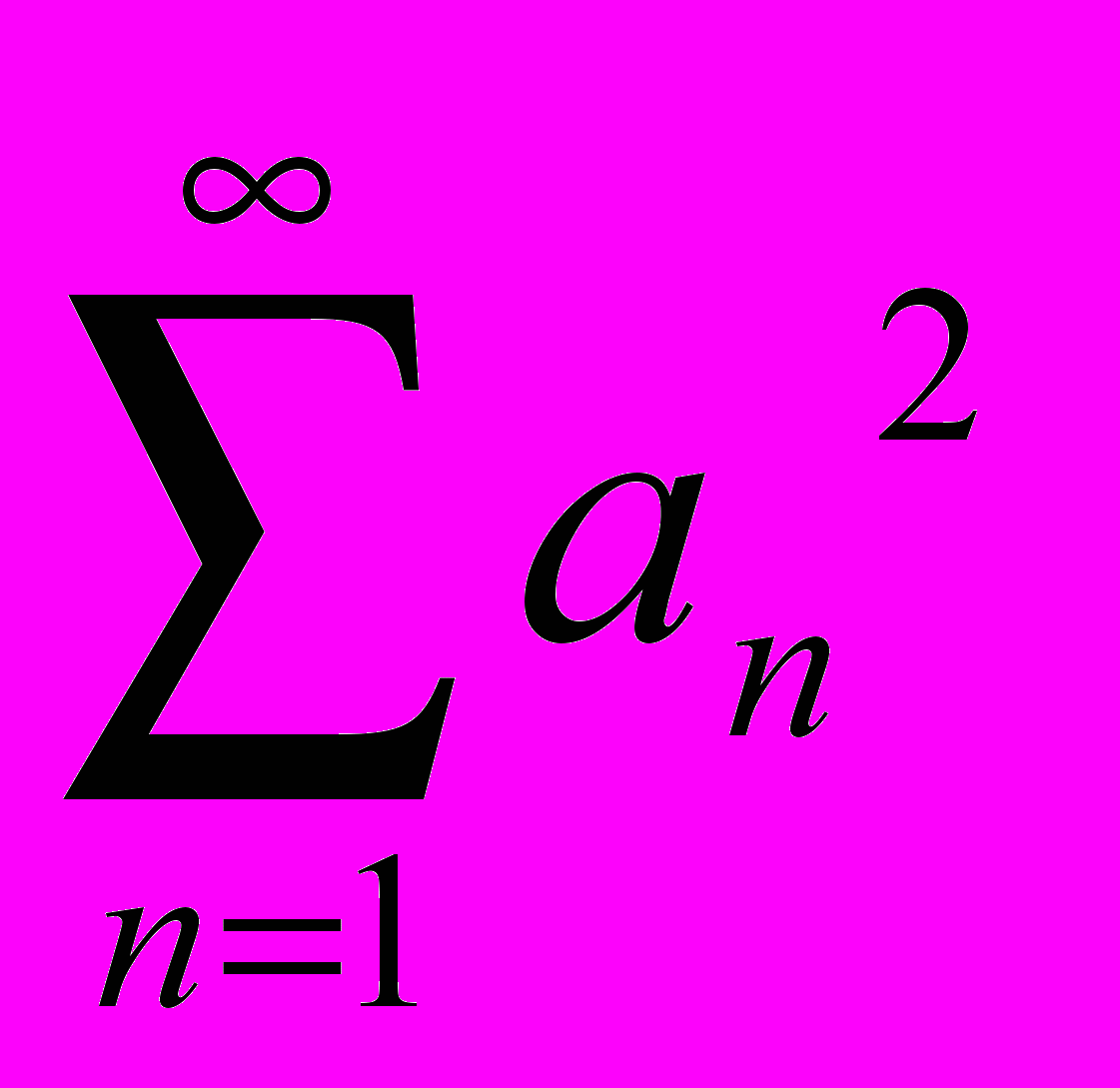расходиться?
Может ли знакочередующийся ряд, общий член которого стремится к нулю, расходиться ?
Если в абсолютно сходящемся ряде изменить знаки на противоположные у произвольного числа членов, то нарушится ли при этом абсолютная сходимость ряда?
В сходящемся знакопостоянном ряде у бесконечного множества членов изменили знаки на противоположные. Будет ли сходиться полученный таким образом ряд?
Ряд сходится условно. Изменится ли его сумма, если в нем поменять местами конечное число членов?
Из гармонического ряда убрали все дроби, содержащие 9 в знаменателе. Будет ли оставшийся ряд сходиться?
Приведите пример расходящегося ряда, который можно превратить в сходящийся путем расстановки скобок.
Дан сходящийся ряд 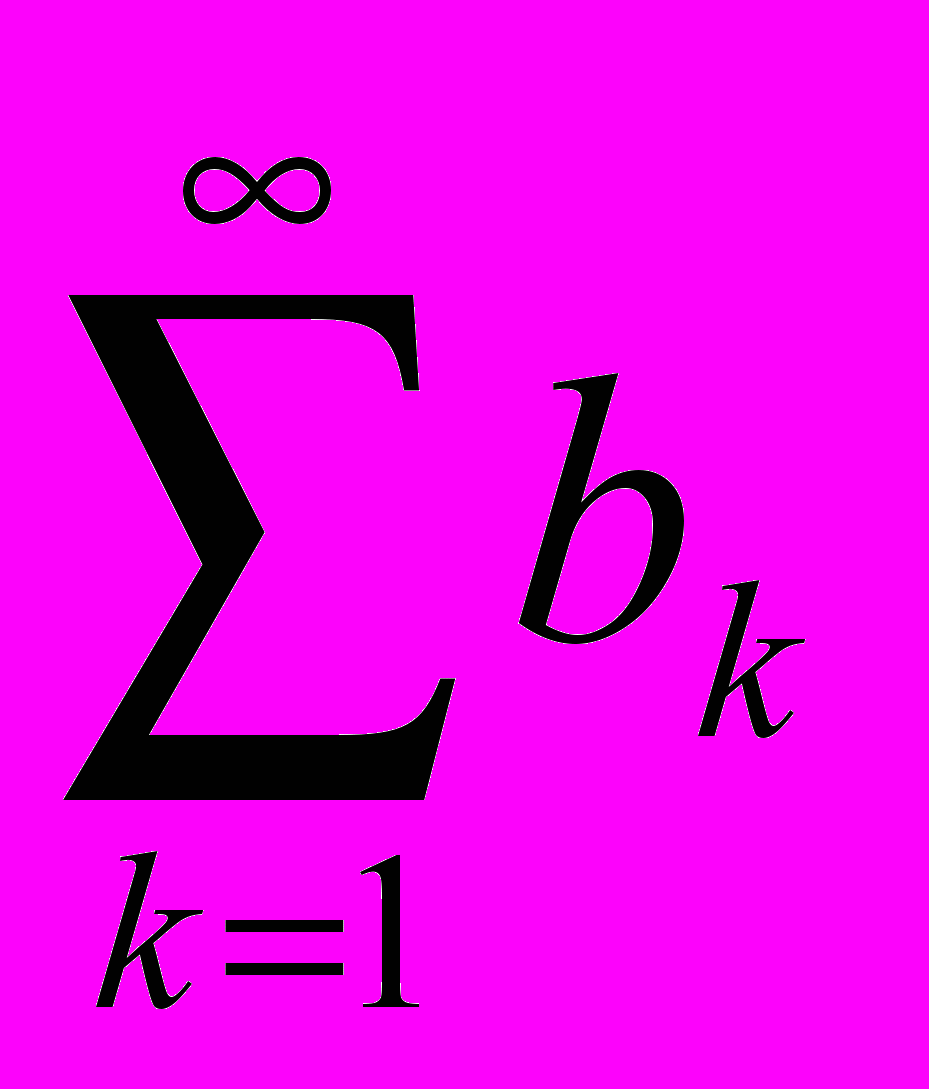. Каждый член ряда представляет собой сумму конечного числа слагаемых: 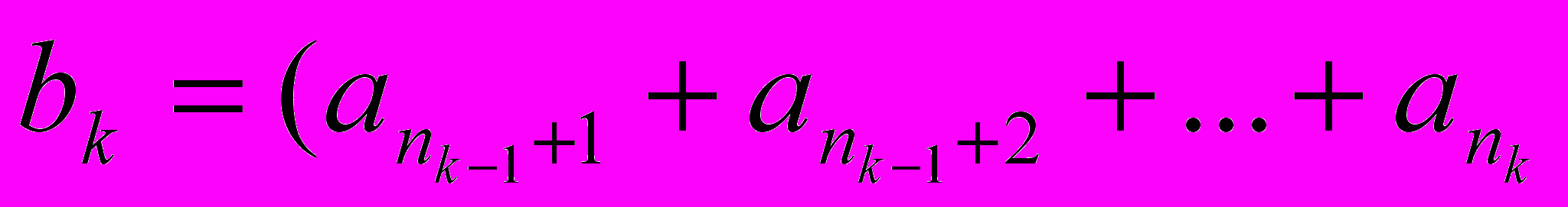), причем внутри каждых скобок все числа одного знака. Можно ли в этом ряде раскрыть скобки?
Сходится ли ряд, составленный из всех положительных членов условно сходящегося ряда?
Сходится ли ряд, составленный из всех отрицательных членов абсолютно сходящегося ряда?
Сходится ли ряд, составленный из всех положительных членов абсолютно сходящегося ряда?
Сходится ли ряд, составленный из всех отрицательных членов условно сходящегося ряда?
Всегда ли сходится произведение двух условно сходящихся рядов?
Всегда ли сходится произведение двух сходящихся рядов?
Почему отбрасывание или добавление конечного числа слагаемых к данному ряду не влияет на его сходимость?
Почему признак Даламбера только достаточное условие сходимости ряда?
Даны два знакоположительных расходящихся ряда. Что можно сказать о сходимости рядов: а) 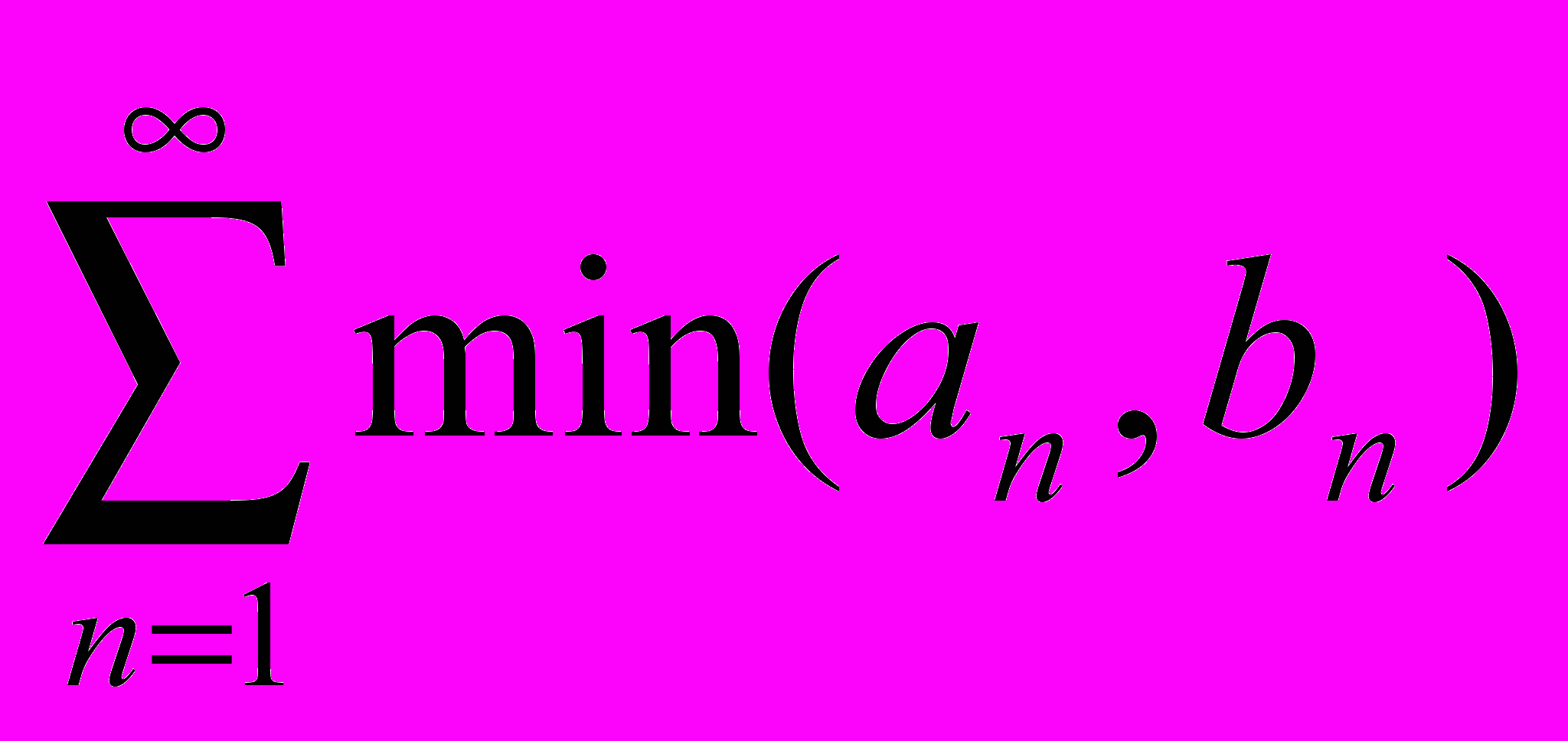, б).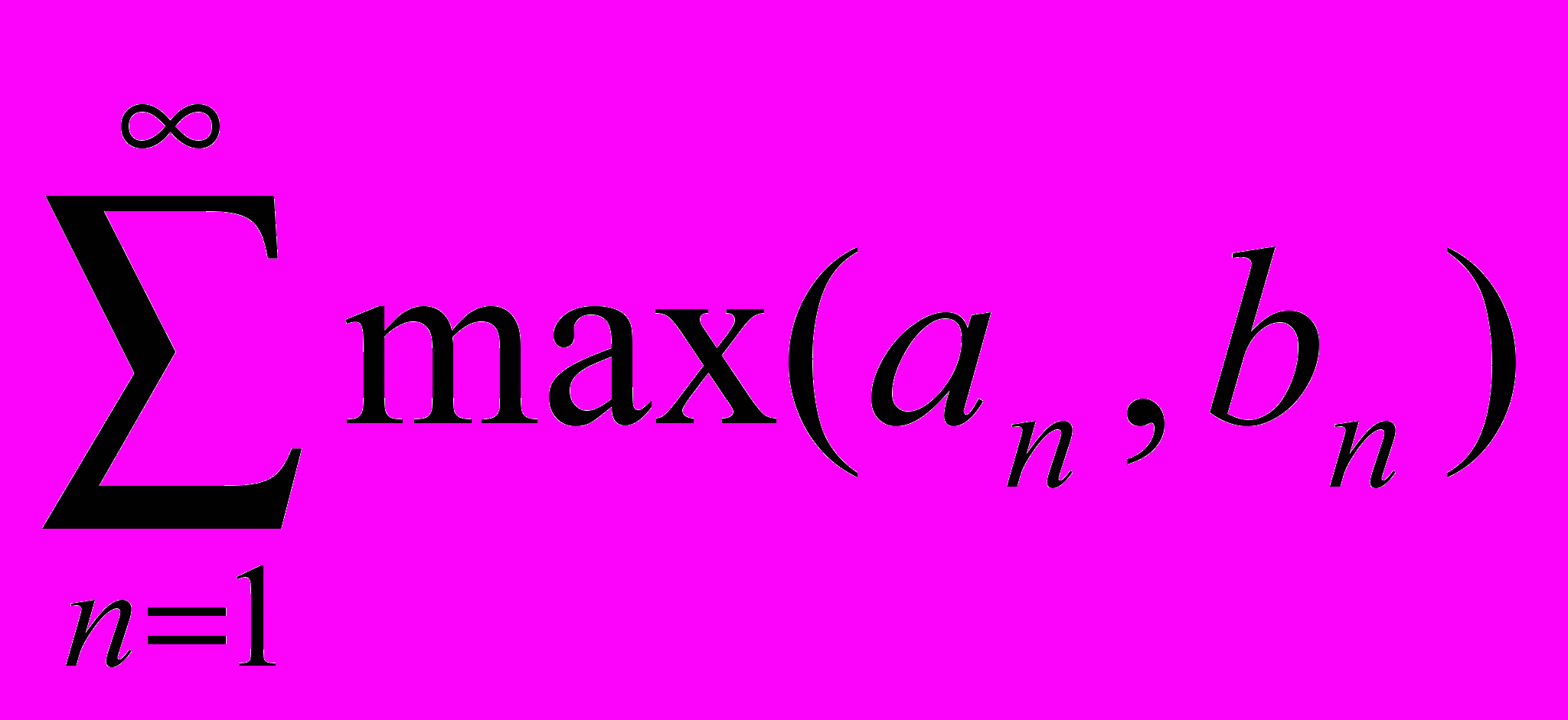
Можно ли для установления абсолютной сходимости пользоваться признаками Даламбера и Коши?
Доказать, что члены условно сходящегося ряда можно без перестановки сгруппировать так, что полученный новый ряд будет абсолютно сходящимся.
Верно ли, что разность двух абсолютно сходящихся рядов есть ряд абсолютно сходящийся?
Некоторый ряд остается сходящимся при любой перестановке его членов. Что можно сказать о характере сходимости?
Можно ли из условно сходящегося ряда путем перестановки его членов получить расходящийся ряд?
Гипотенуза равнобедренного прямоугольного треугольника равна 1. На его катете как на гипотенузе строится подобный ему треугольник. Исследовать на сходимость ряд, составленный из длин катетов этих треугольников.
В прямой круговой конус, радиус которого R, а высота H, последовательно вписаны шары. Найти длины радиусов этих шаров и составить из них ряд. Найти сумму объемов всех шаров и сравнить с объемом конуса.
Криволинейная фигура ограничена дугами касающихся окружностей радиуса 1 и прямой, касающейся этих окружностей. В эту фигуру последовательно вписываются окружности максимально возможного радиуса. Очевидно, что длины диаметров этих окружностей образуют ряд, сумма которого равна 1. Написать этот ряд.
Каков должен быть знаменатель прогрессии с первым членом 1, чтобы ряд, составленный из остатков её имел сумму, равную 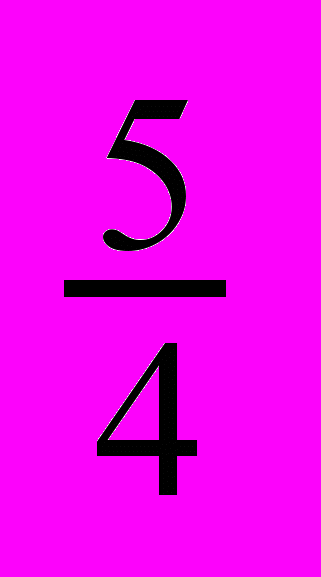? Покажите, что если остатки ряда образуют геометрическую прогрессию, то и сам ряд является геометрической прогрессией.