Лекция 22 Несобственные интегралы на неограниченном промежутке

Вид материала

Лекция

Содержание Критерий коши сходимости интеграла. Теорема сравнения 1. Теорема сравнения 2.

Подобный материал:

• Лекция 17. Несобственные интегралы, 16.57kb.
• Программа дисциплины «Математический анализ», 500.52kb.
• Программа дисциплины «математический анализ», 432.47kb.
• Программа обсуждена на заседании кафедры Математики фнти, 28.33kb.
• «Социальная стратификация и социальная мобильность», 46.19kb.
• Исследование функций на монотонность и экстремумы. Построение графиков, 13.79kb.
• Реферата по математической статистике, 169.6kb.
• Ооо «Виртэк» 603014, г. Нижний Новгород, пр-кт Гагарина, 14.7kb.
• «Неопределенные и определенные интегралы», 13.17kb.
• Неопределенный интеграл, 106.73kb.

Лекция 22 Несобственные интегралы на неограниченном промежутке.

П.1 Несобственные интегралы по неограниченному промежутку.

Пусть функция 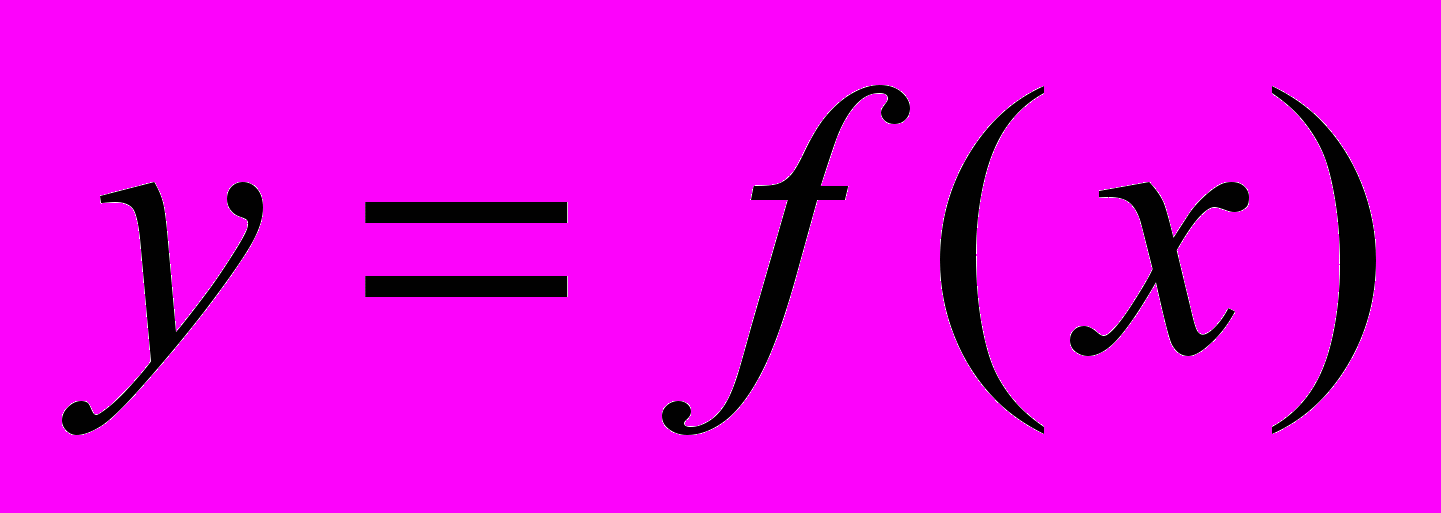непрерывна на полуоси .

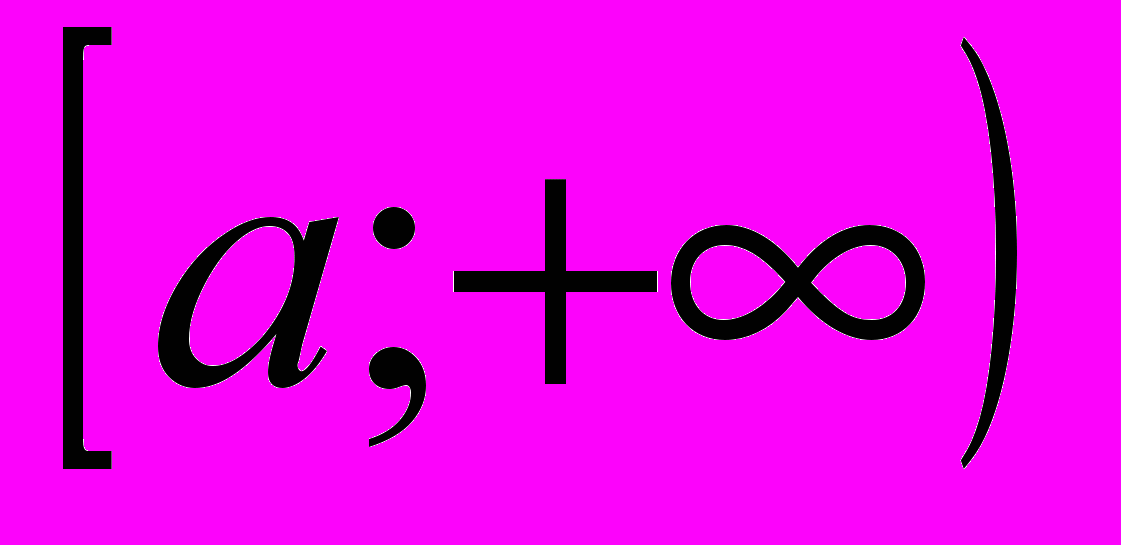ОПР. Несобственным интегралом функции на 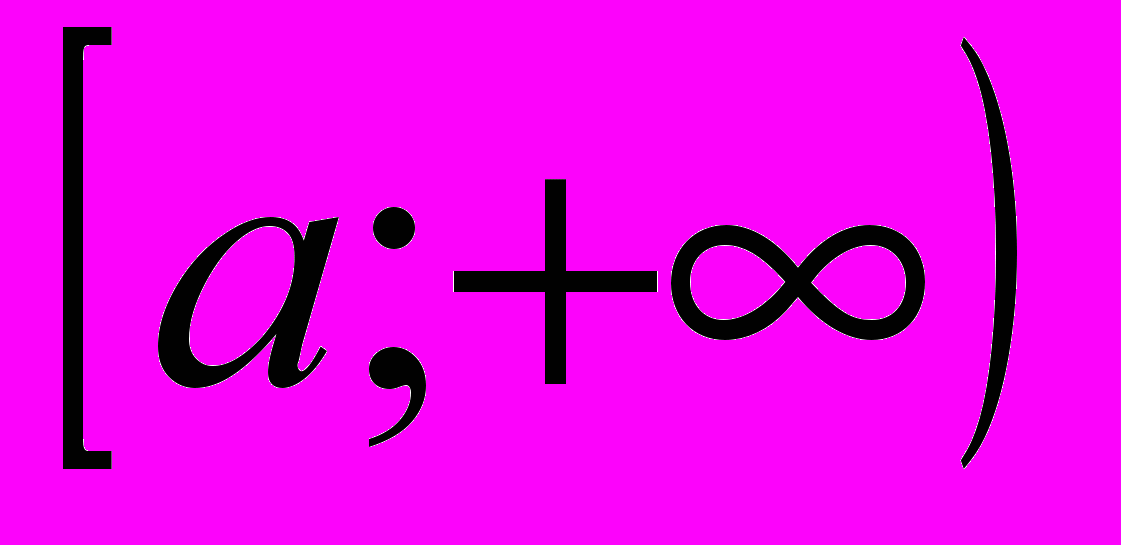называется число

.

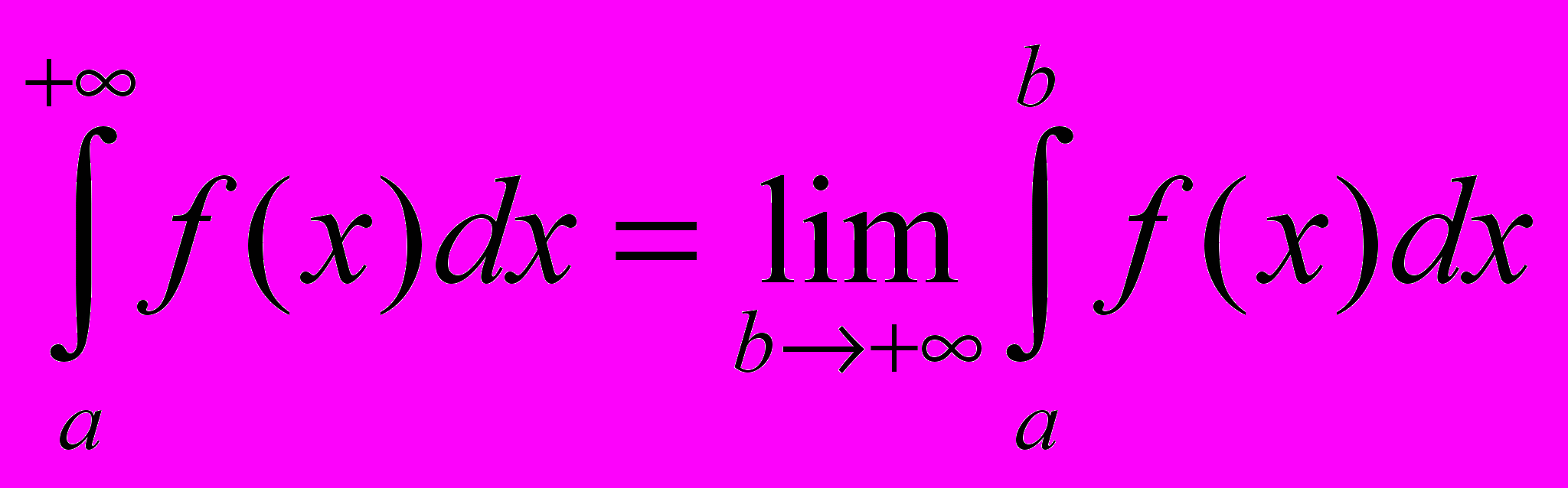Если предел существует, то интеграл 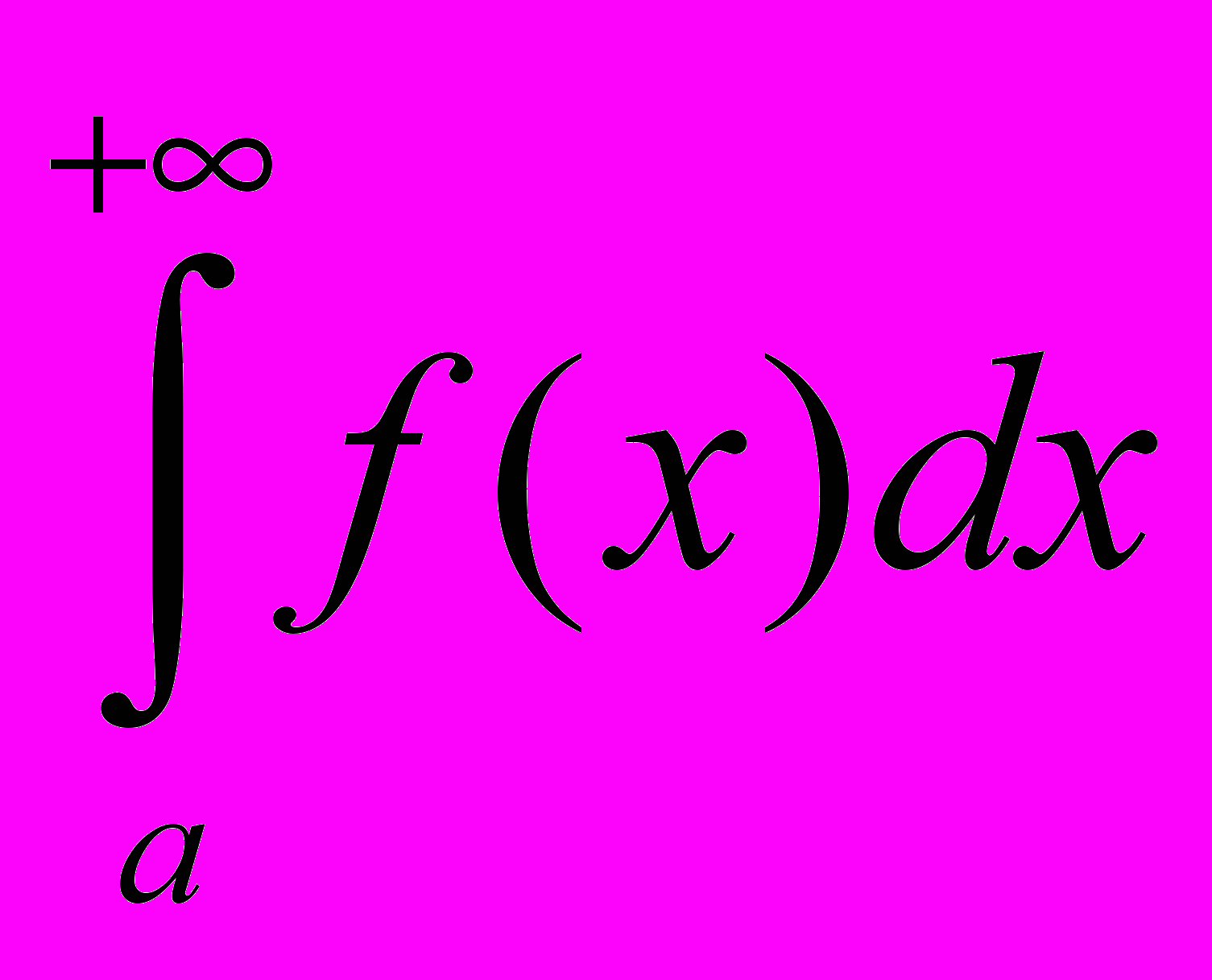называется сходящимся, в противном расходящимся.

ПРИМЕР 1 Исследовать на сходимость интеграл 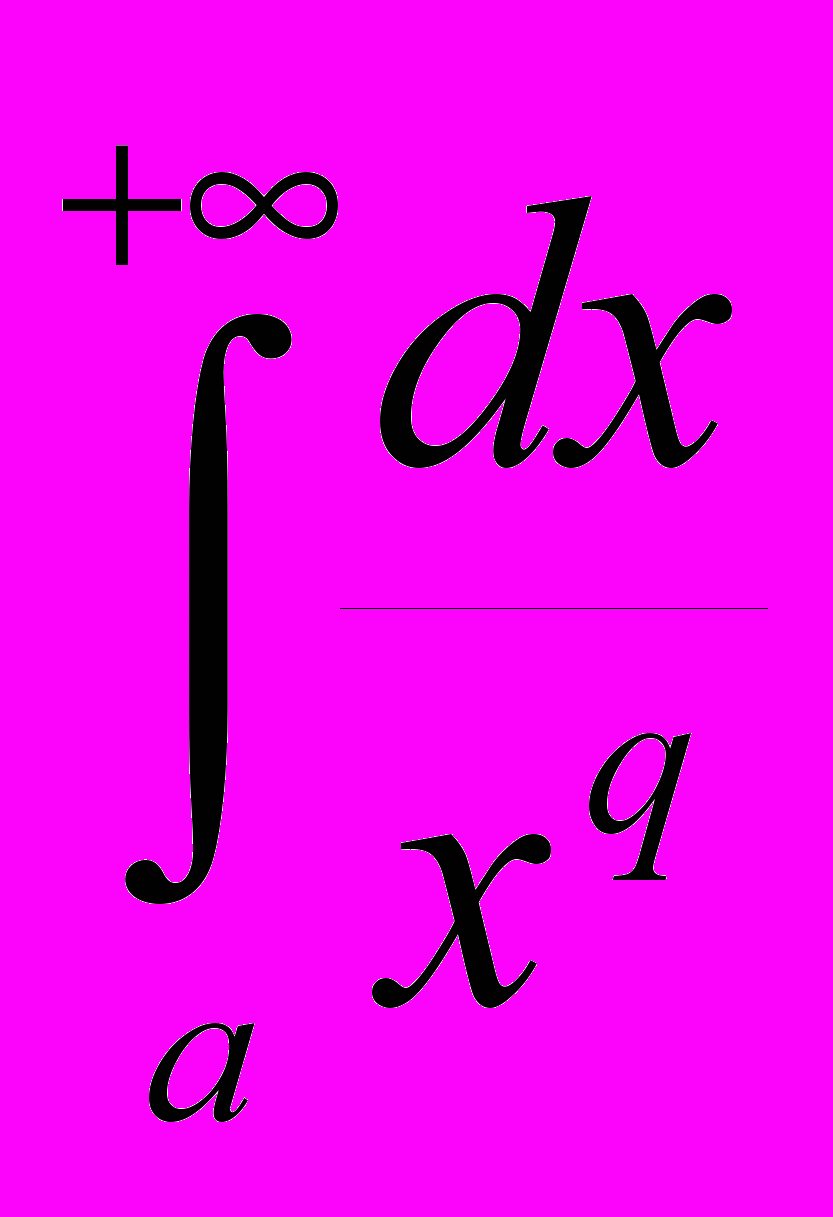в зависимости от q .

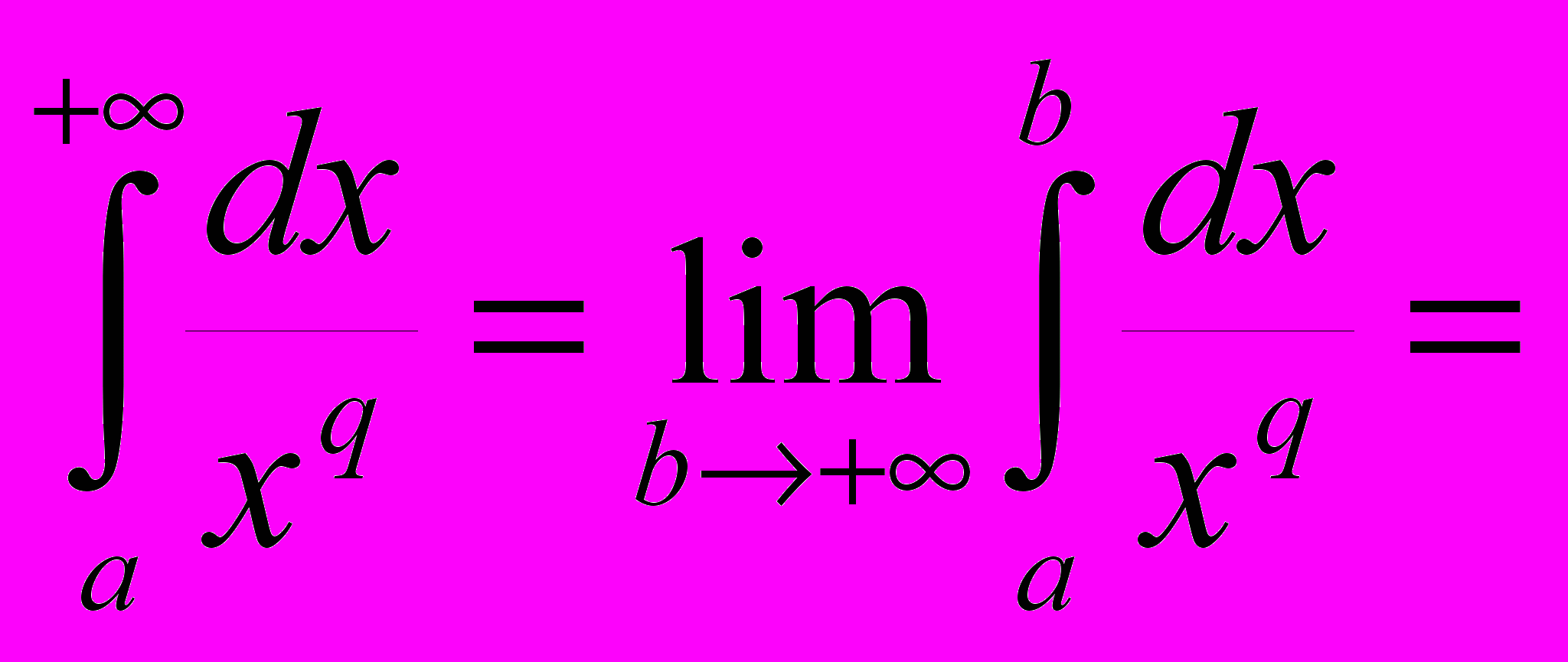
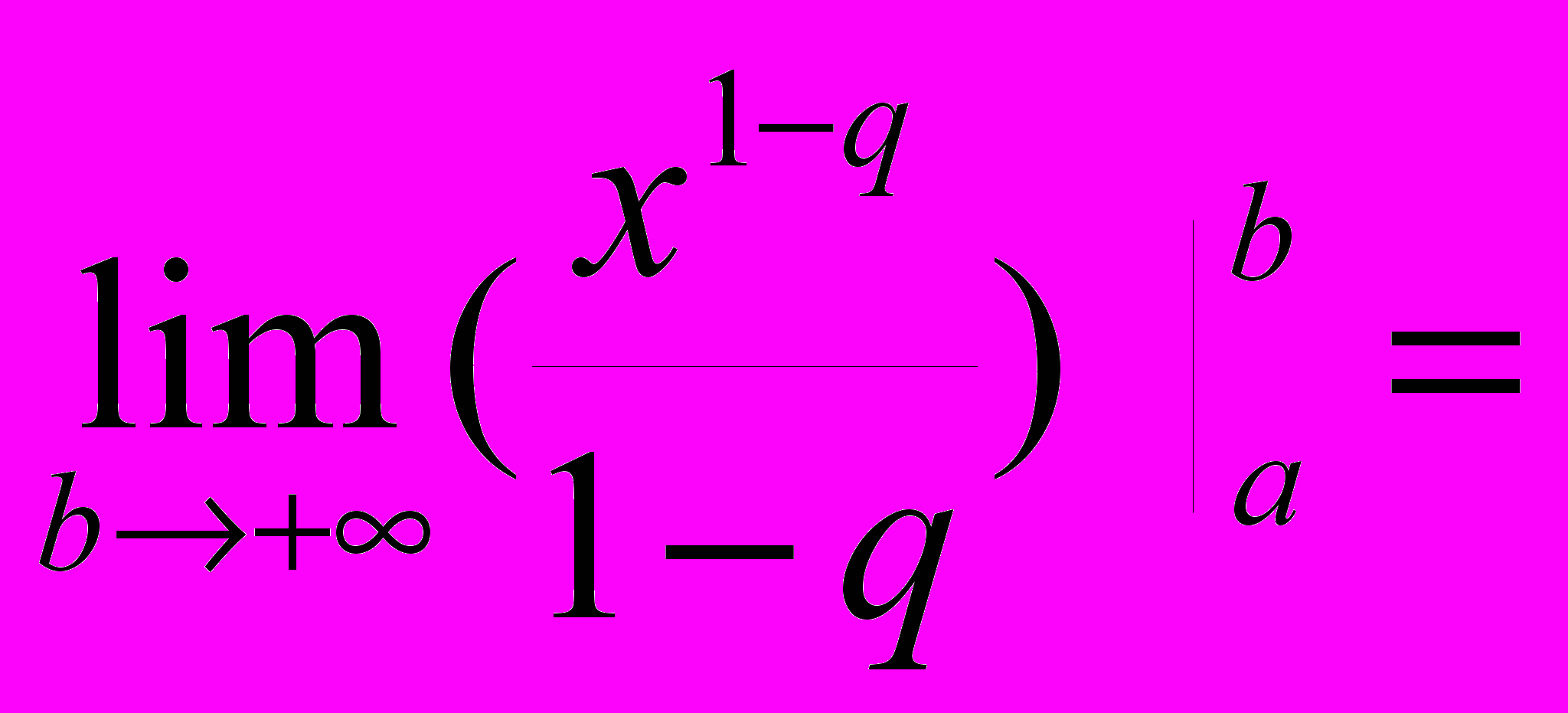
РЕШЕНИЕ. 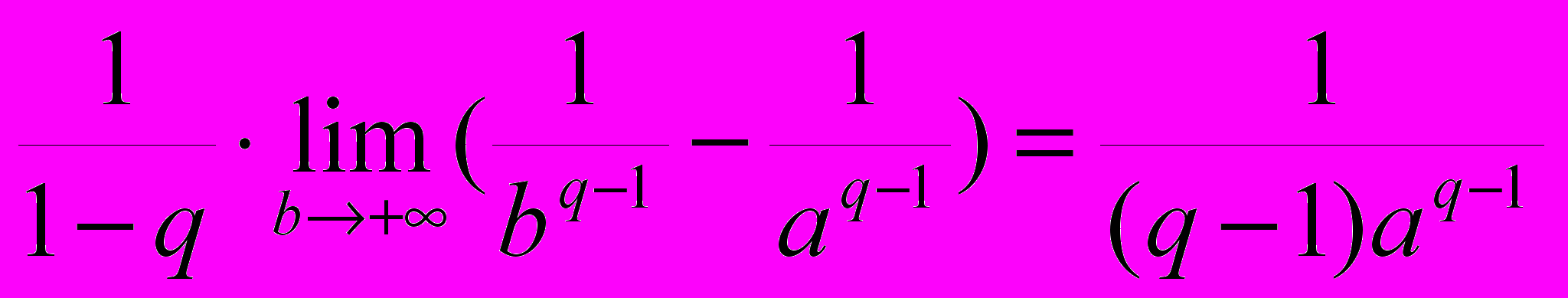, есл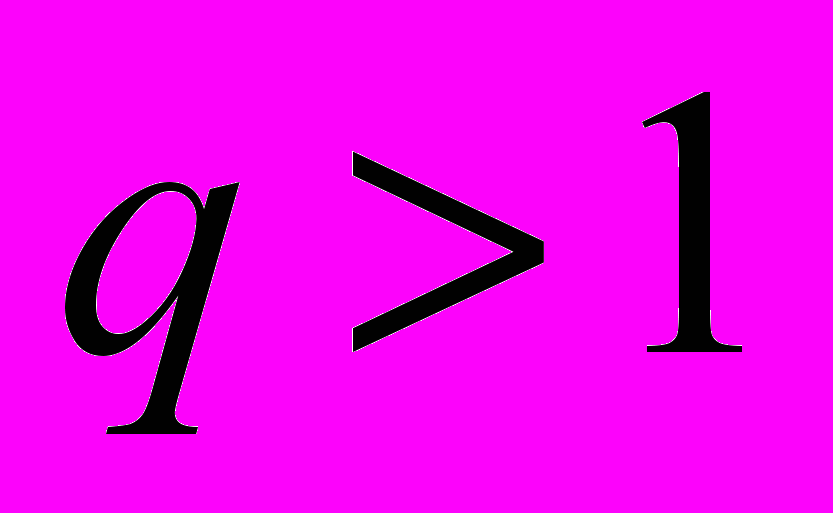и . При 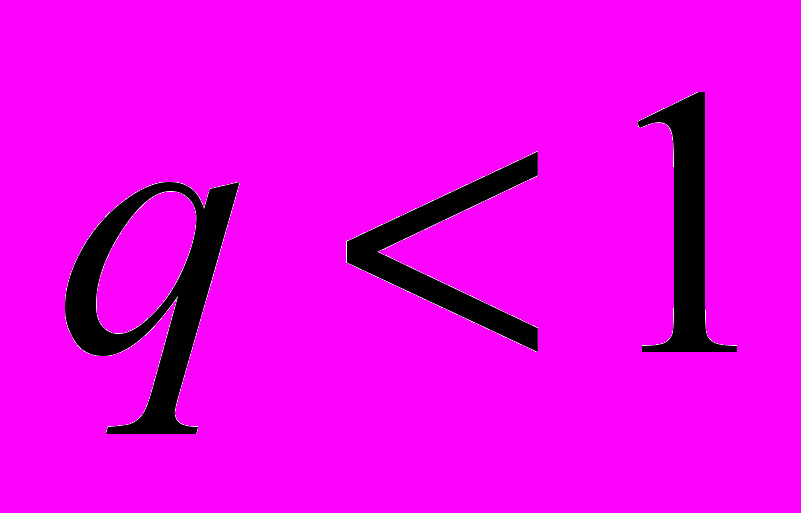конечного предела нет и интеграл расходится. При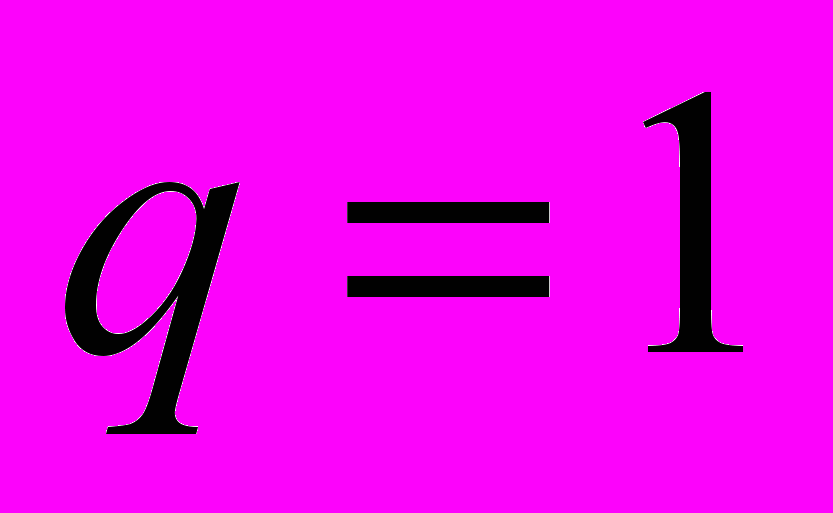 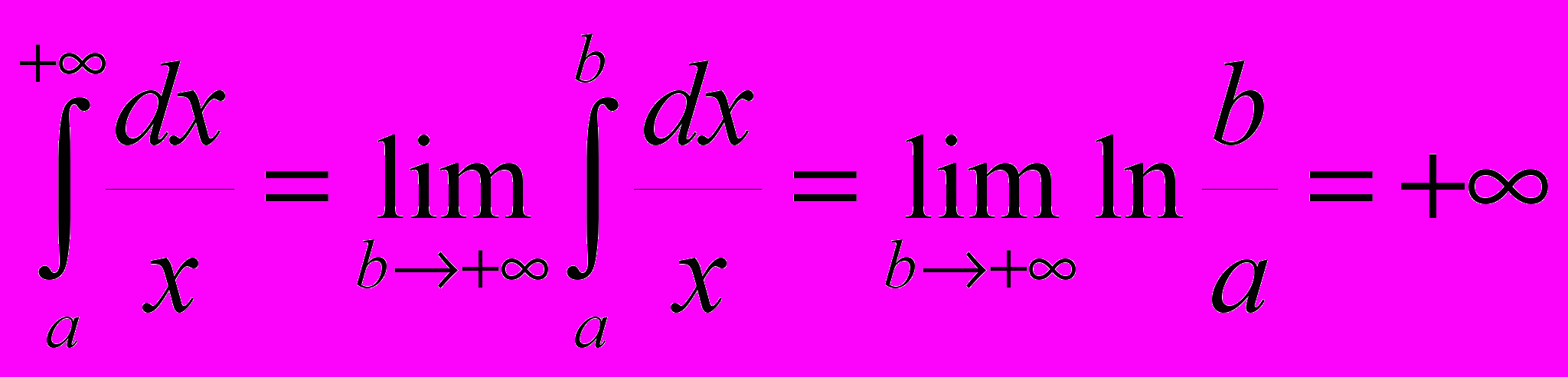и интеграл также расходится.

Для несобственных интегралов на полуоси справедливы свойства 1-5 с заменой

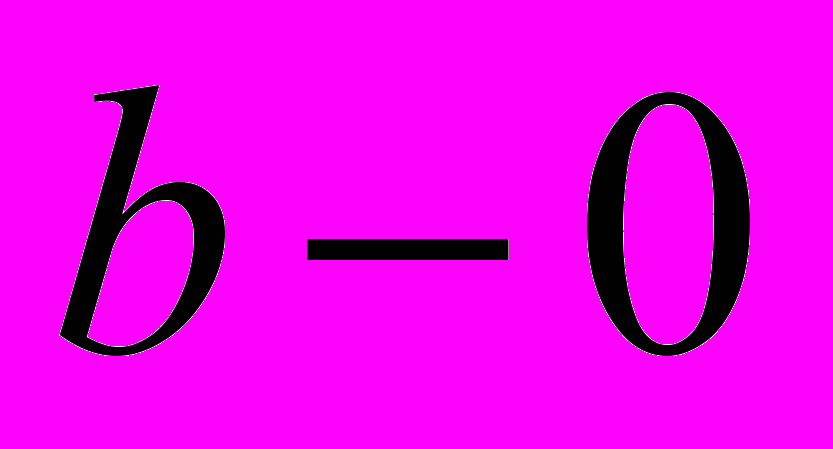
на .

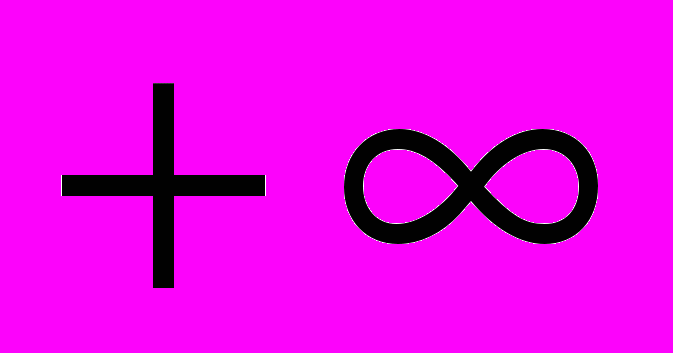КРИТЕРИЙ КОШИ СХОДИМОСТИ ИНТЕГРАЛА.

Для сходимости интеграла 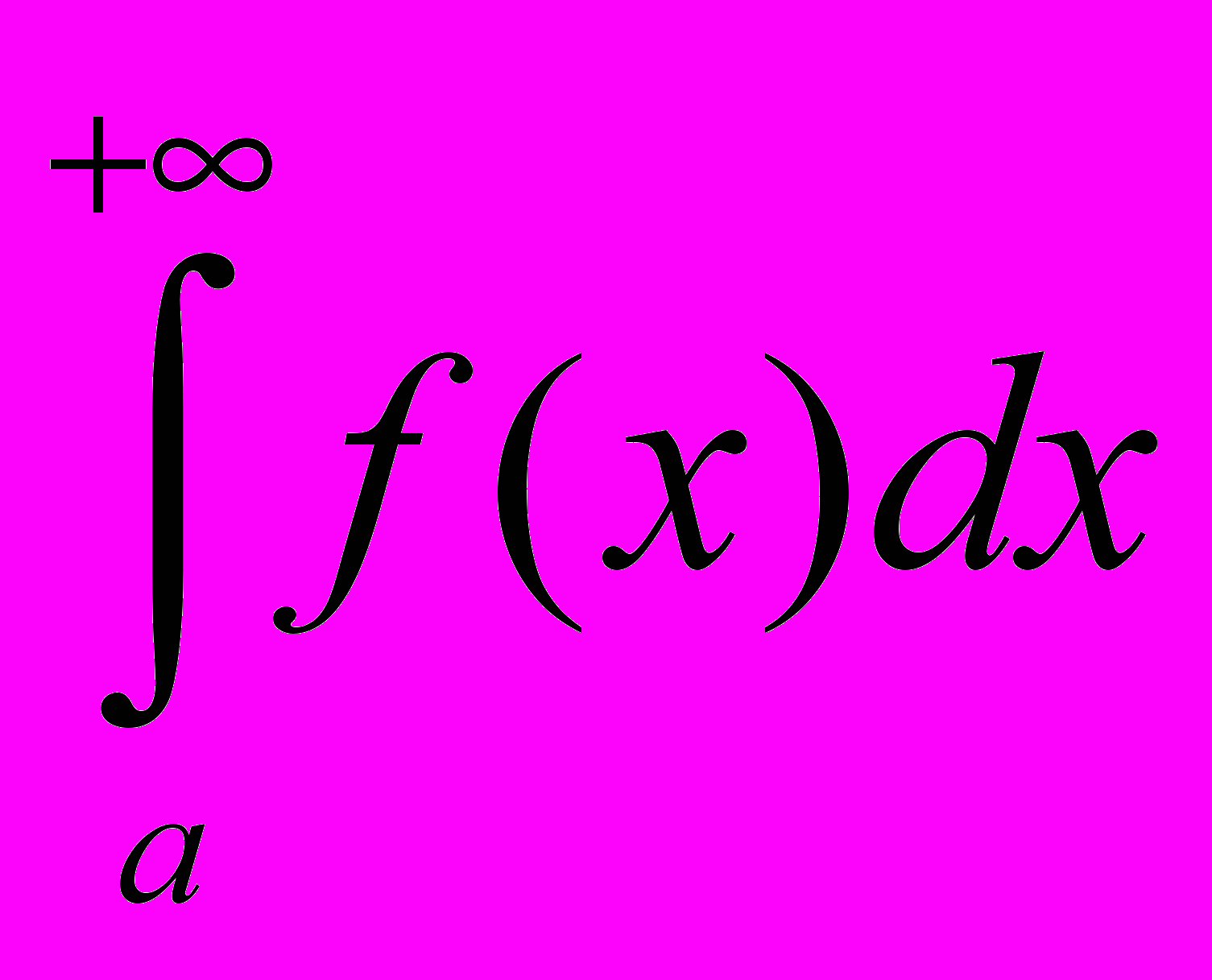необходимо и достаточно выполнения условия :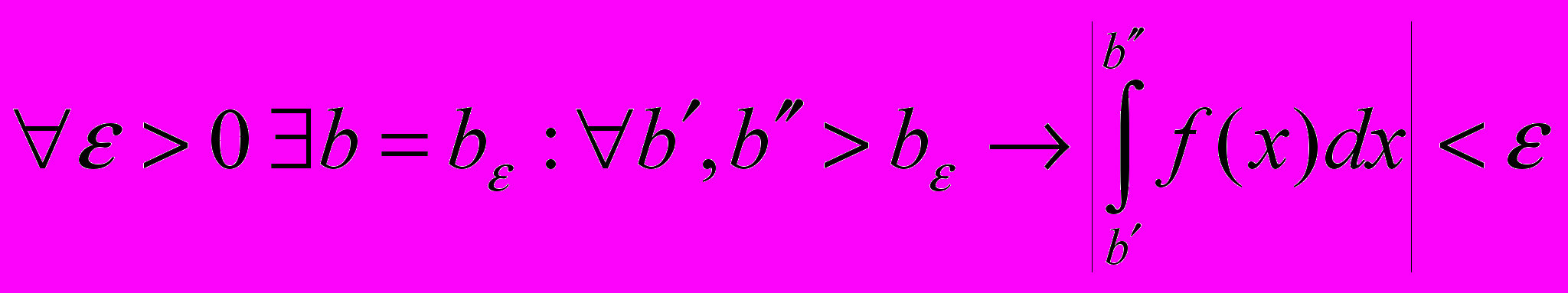



ДОК. Сходимость интеграла равносильна существованию предела , где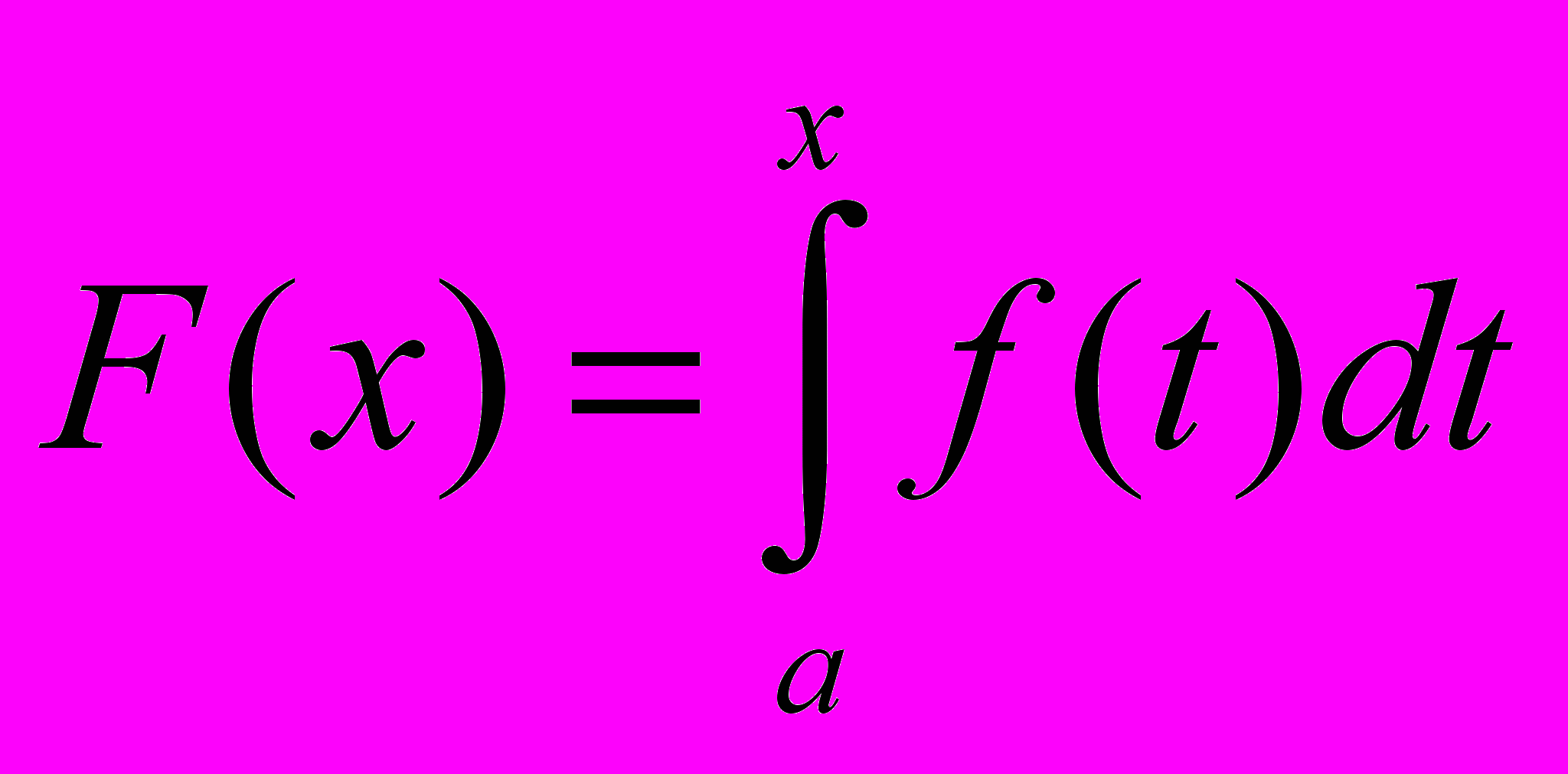

- первообразная функции 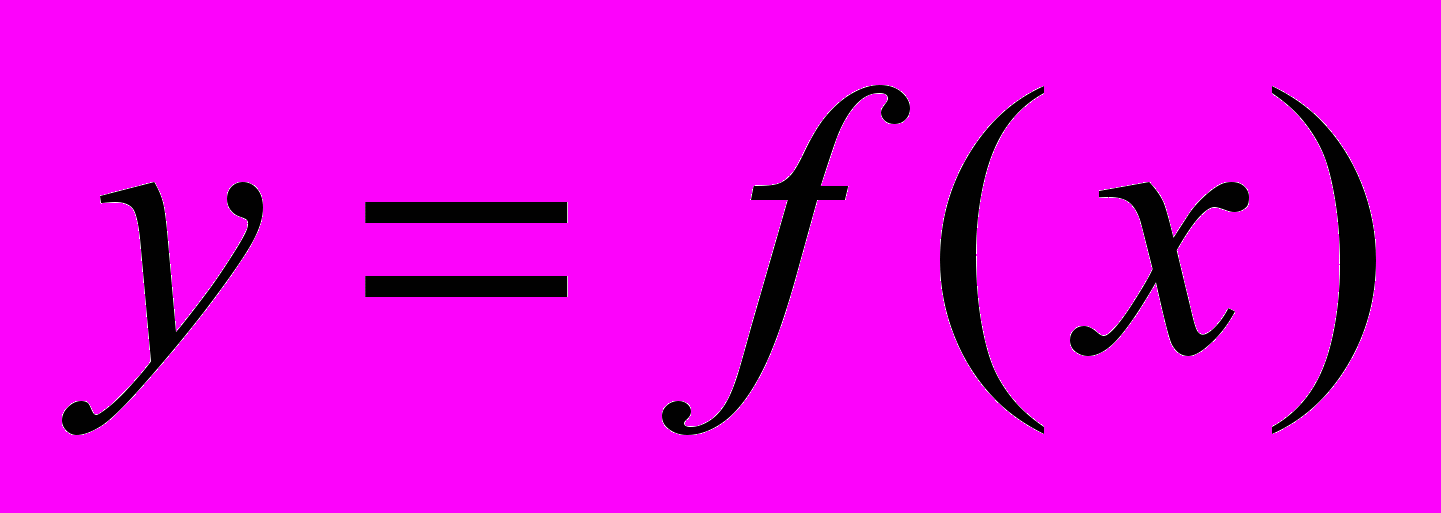на 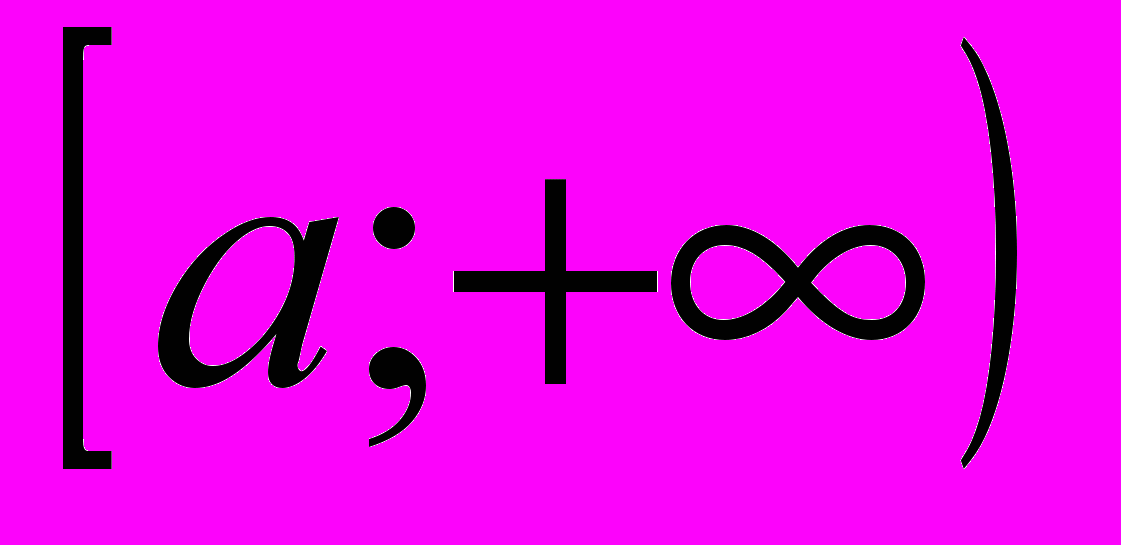. Для существования необходимо и достаточно по критерию Коши для предела функции, чтобы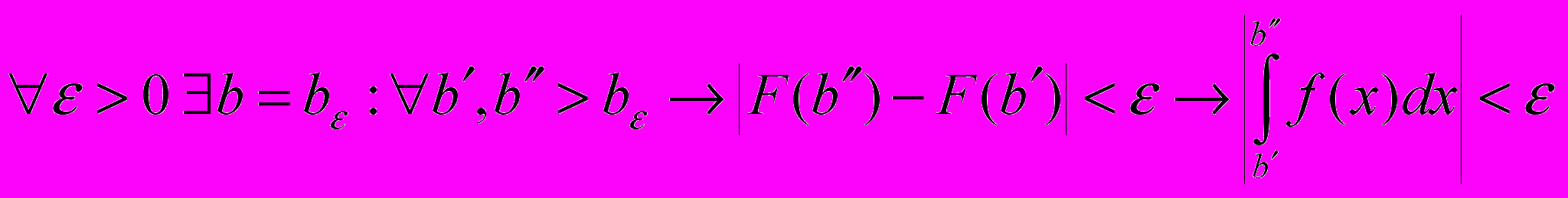

.

Сформулируем теоремы сравнения 1 и 2 для несобственных интегралов от на .

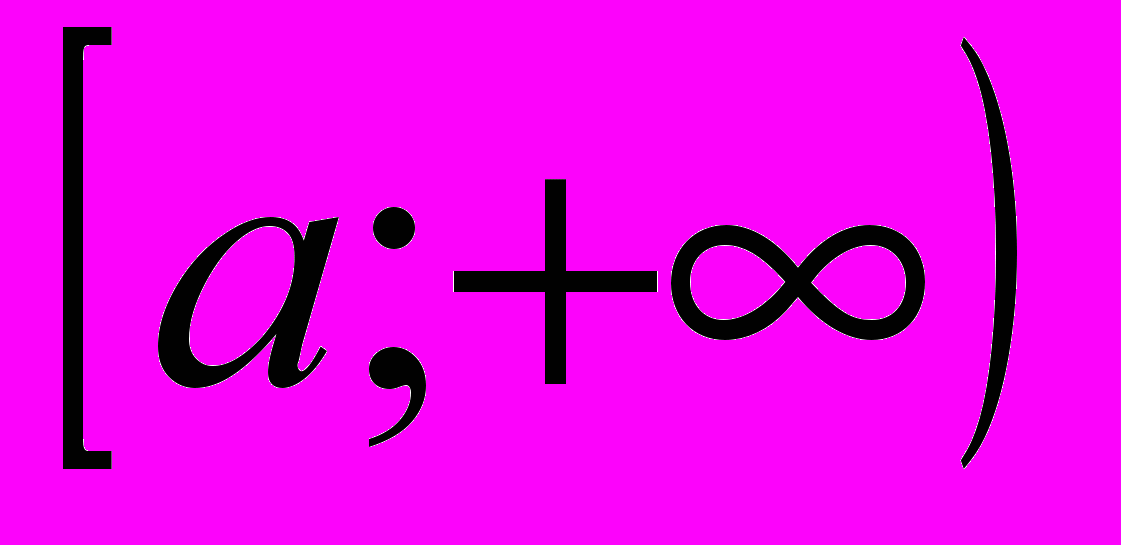ТЕОРЕМА СРАВНЕНИЯ 1.

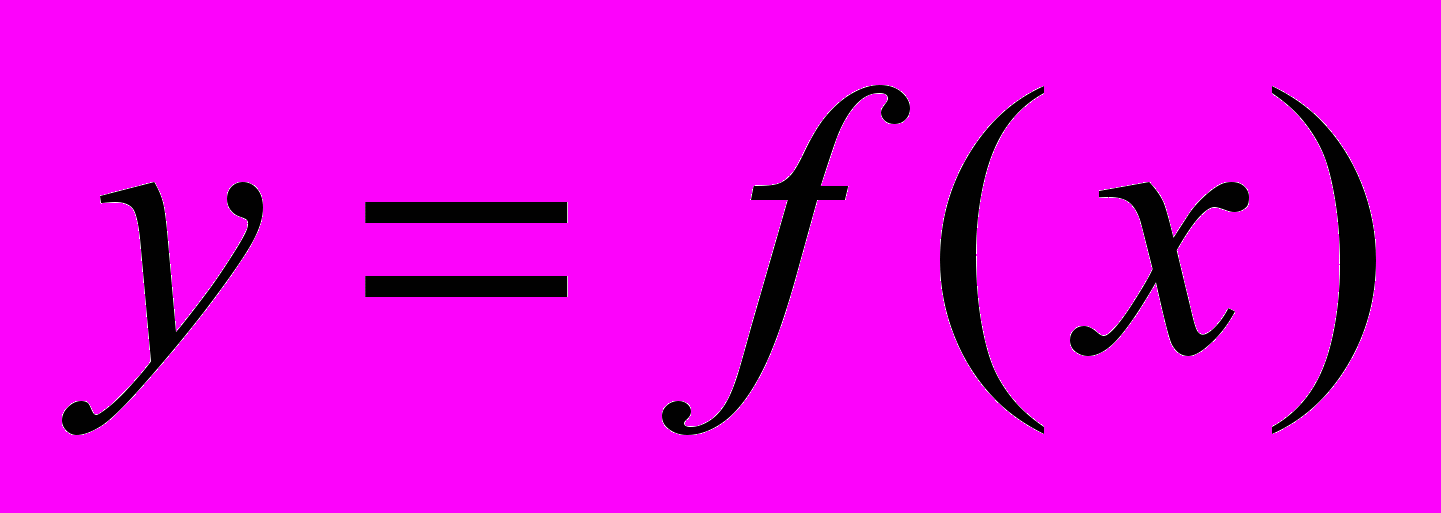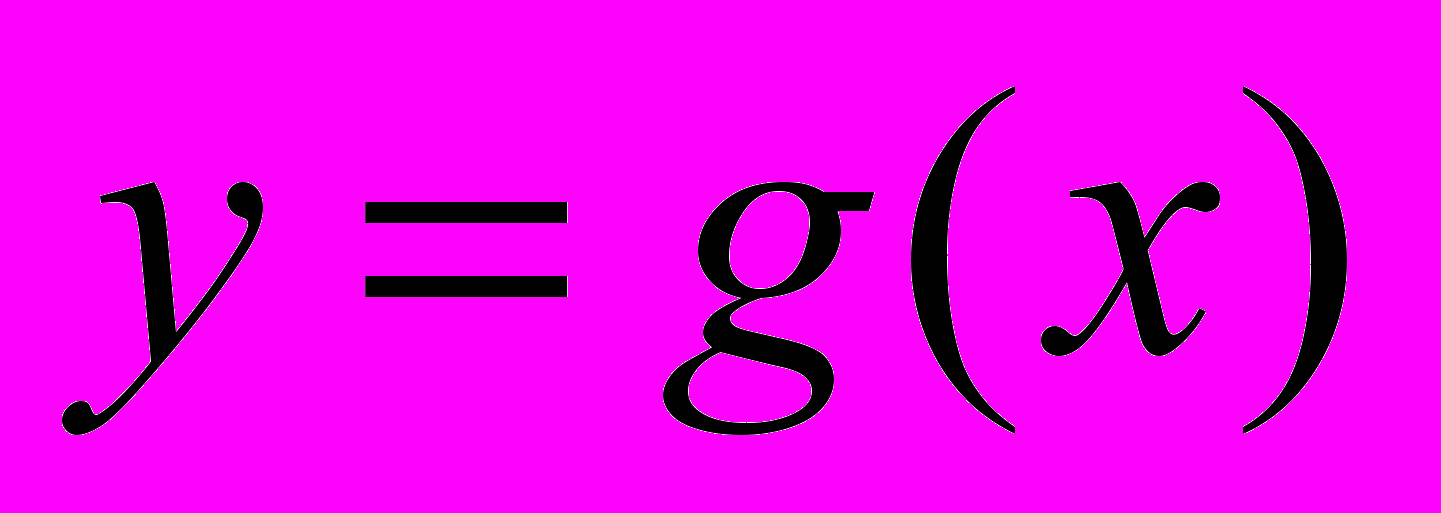Если непрерывные функции и удовлетворяют условию 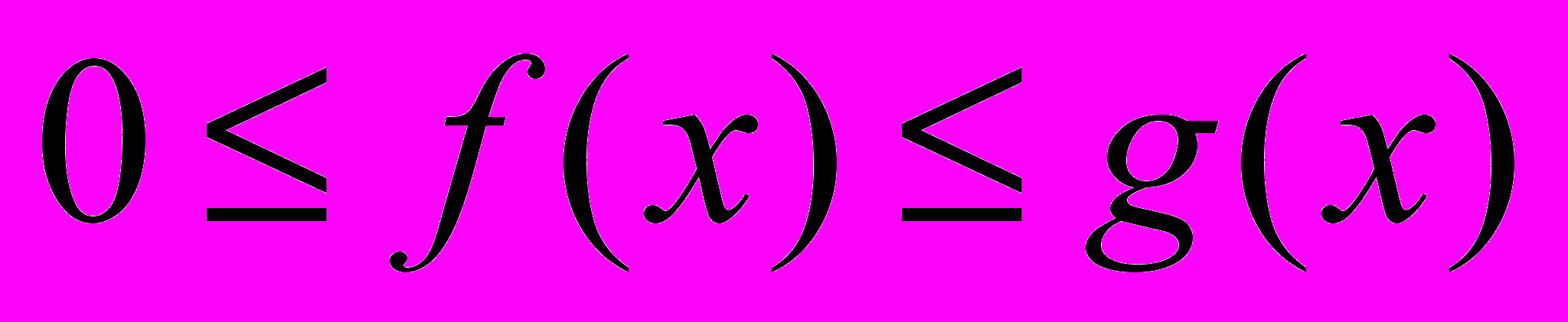для 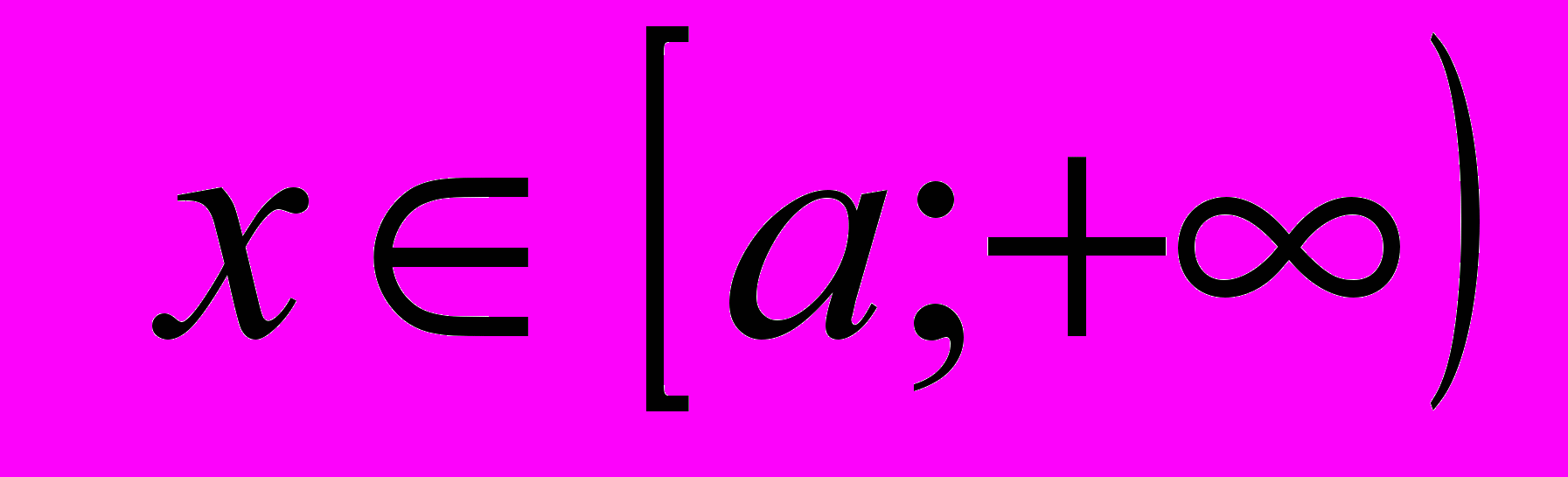и интеграл 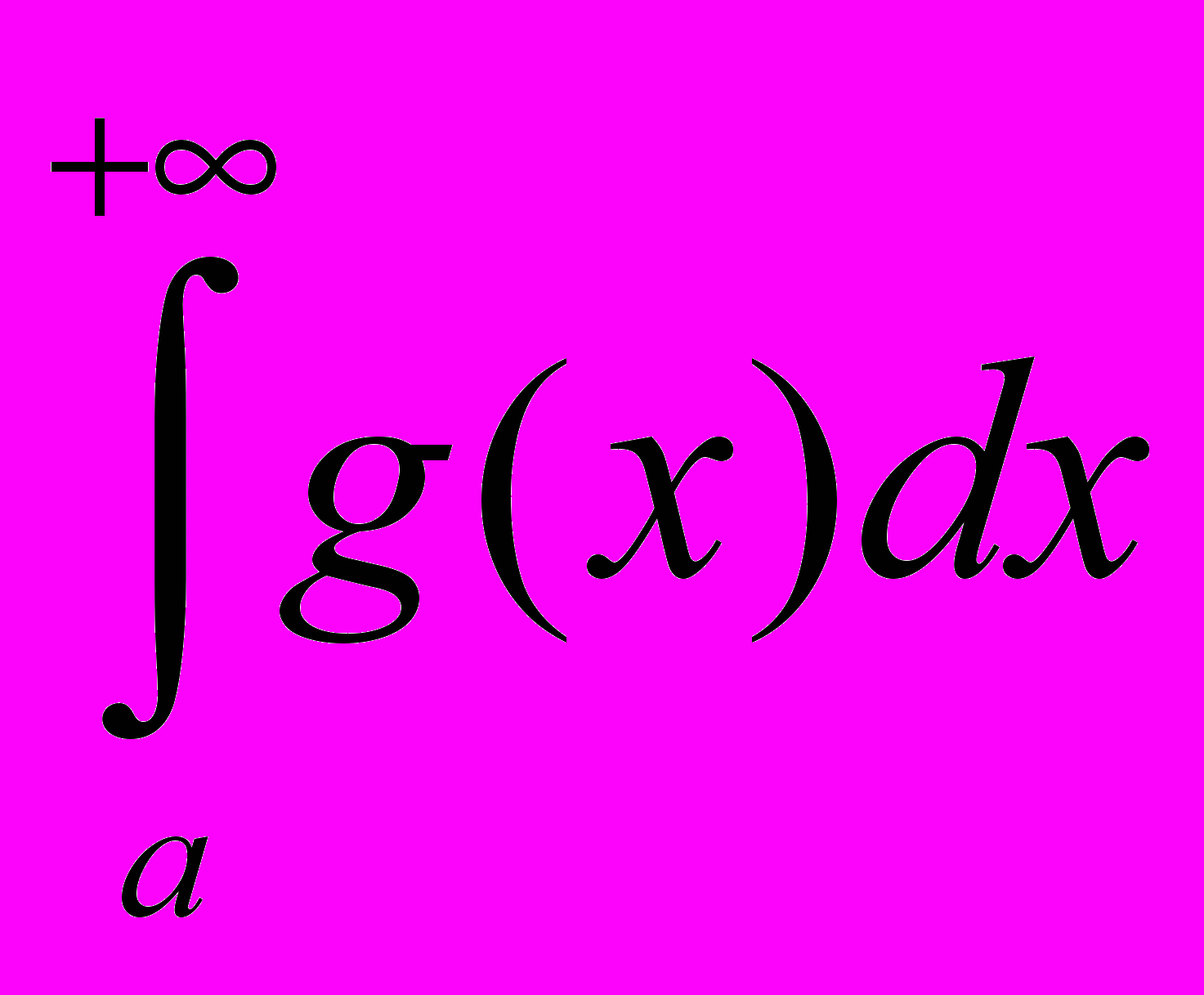сходится, то сходится интеграл 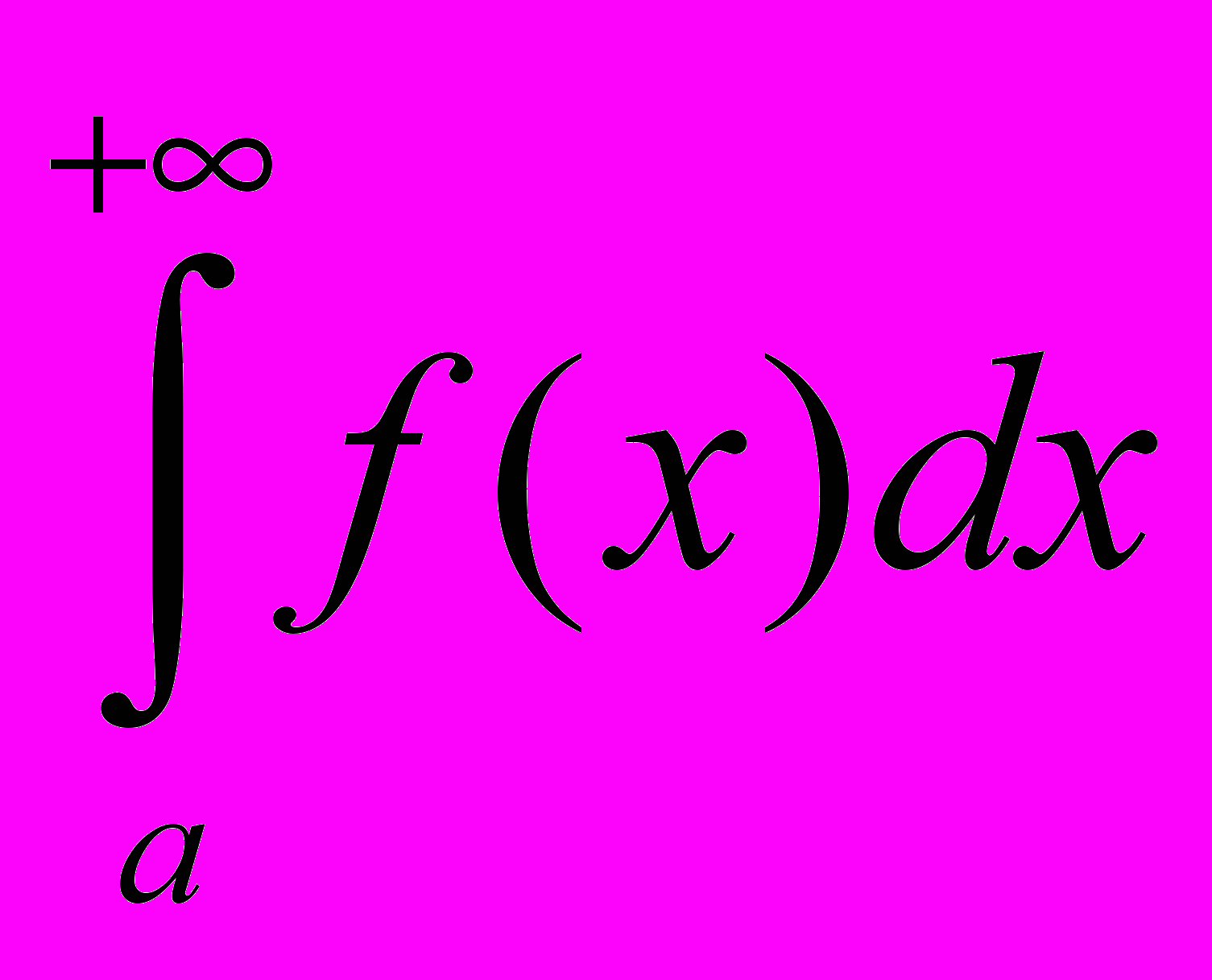. Если интеграл 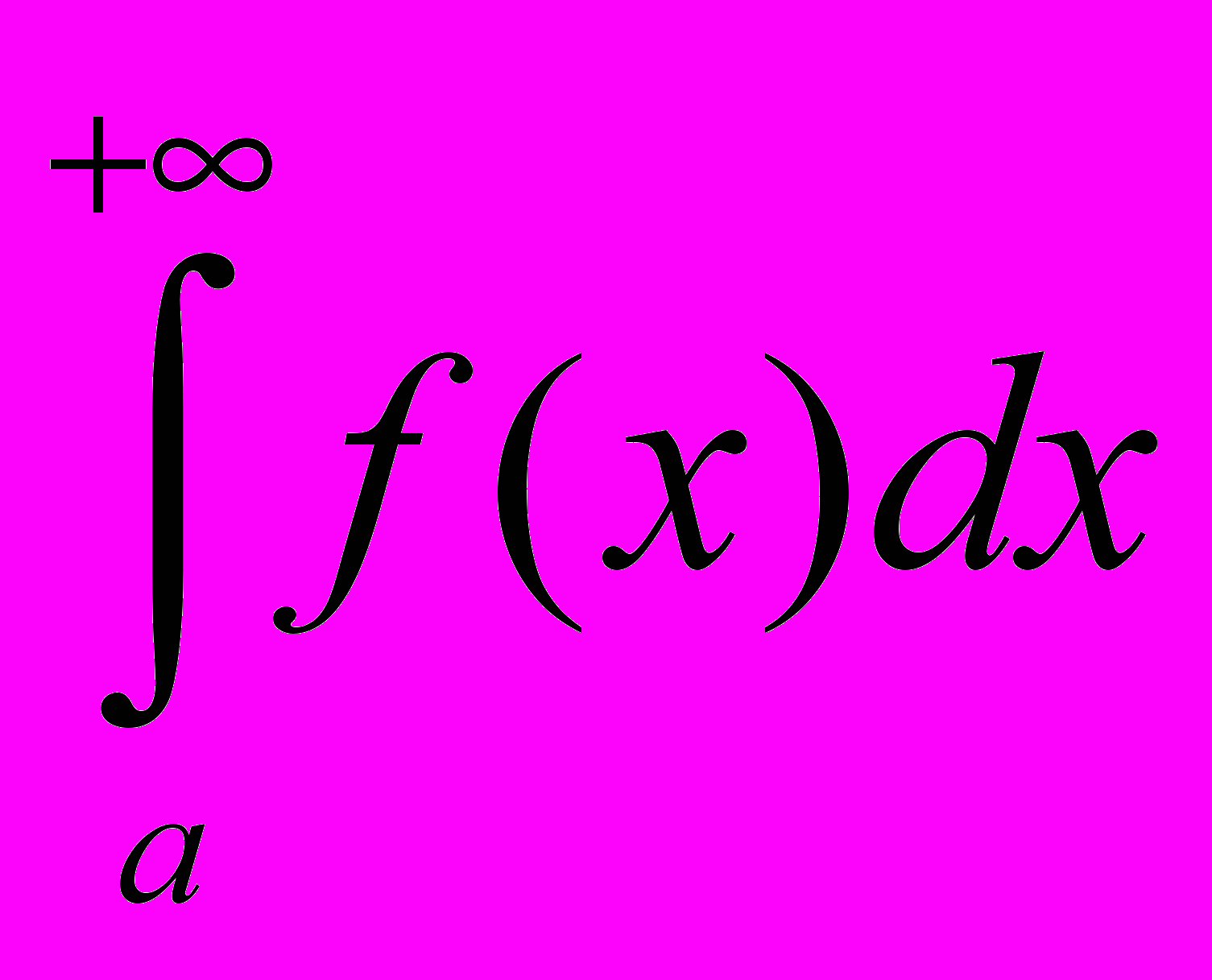расходится, то расходится интеграл .

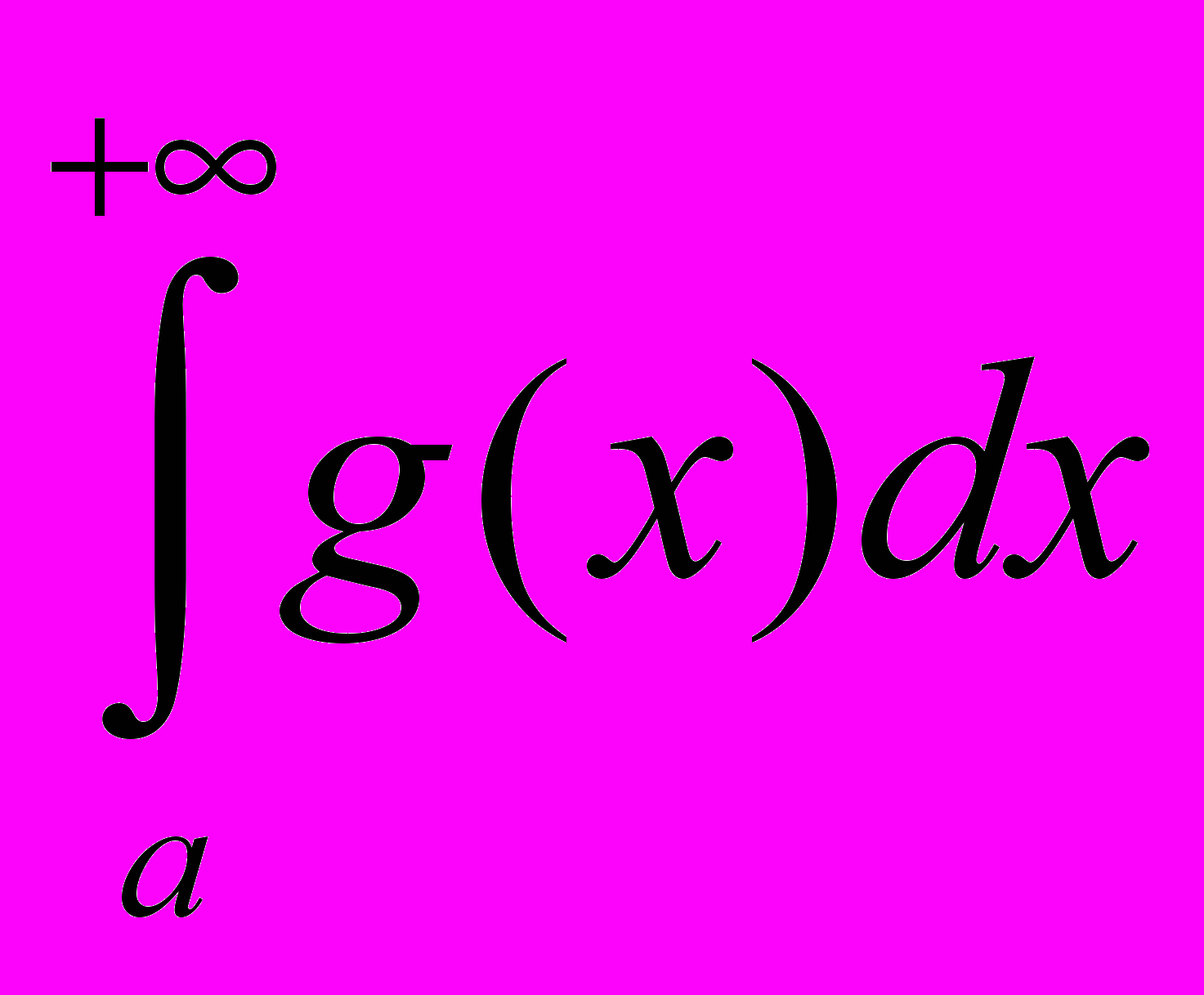ДОК. Проводится аналогично доказательству теоремы для несобственных интегралов

от неограниченных функций.


ТЕОРЕМА СРАВНЕНИЯ 2.

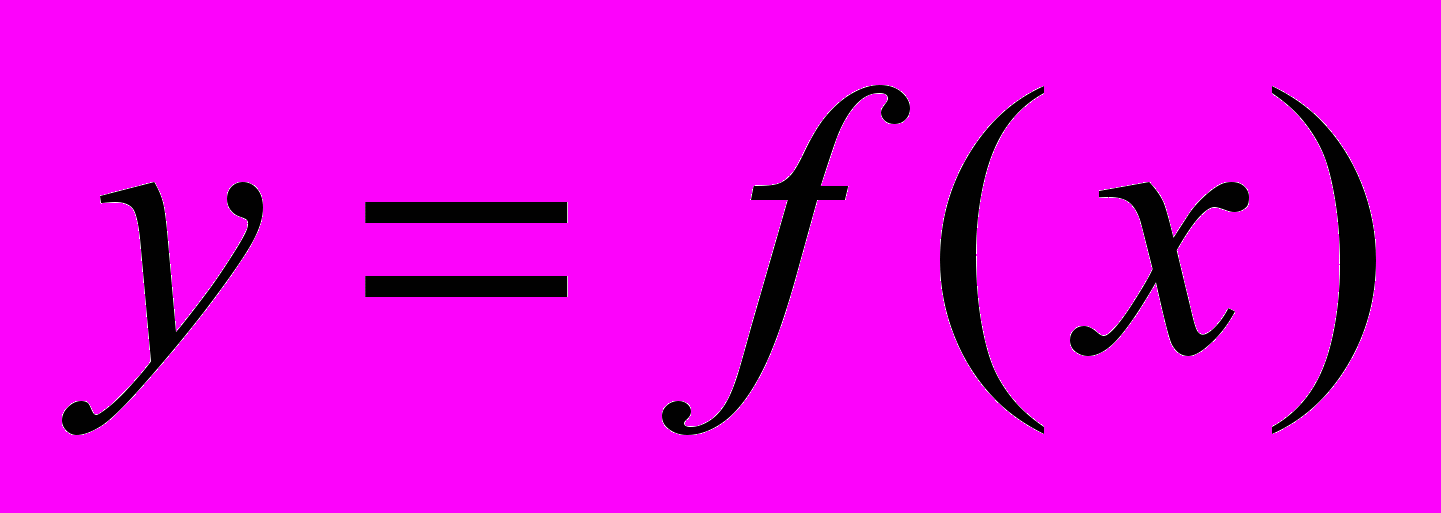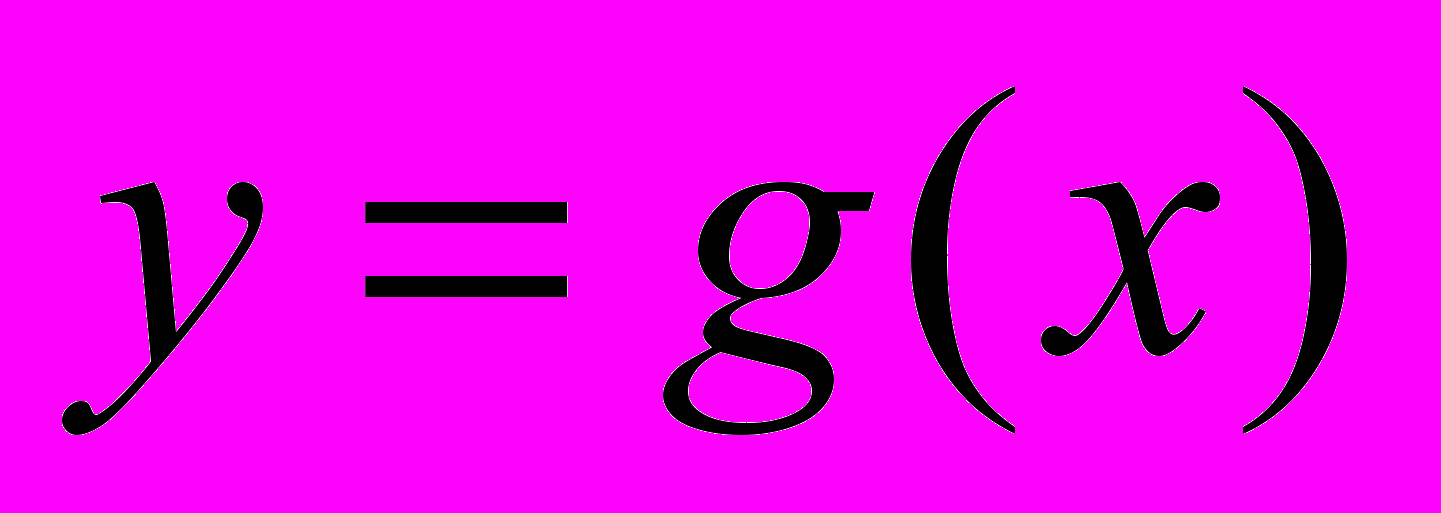Если непрерывные функции и удовлетворяют условию 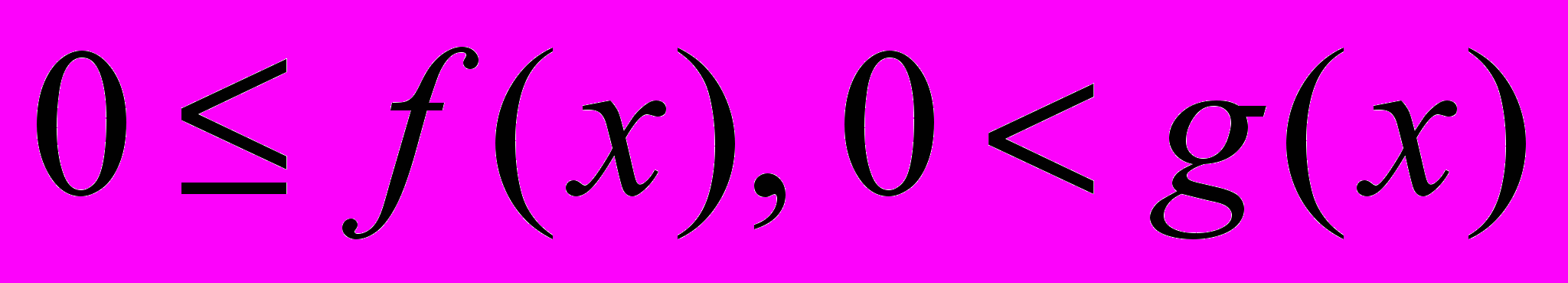для 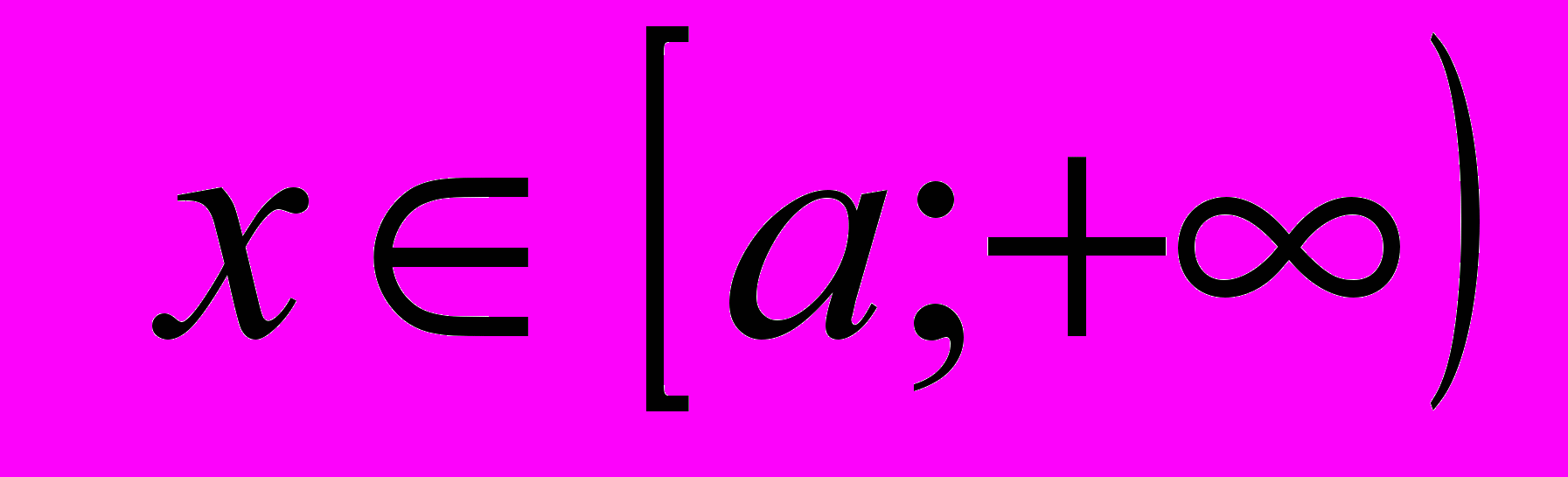и существует 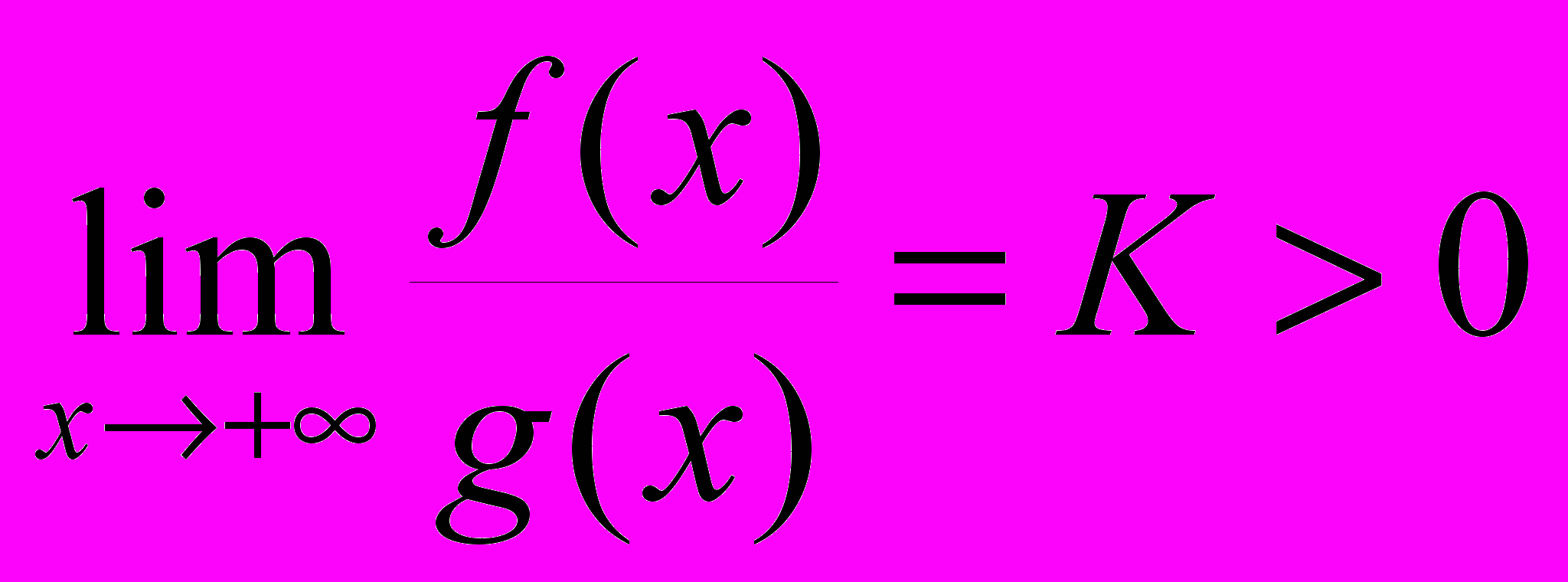, то сходимость и расходимость интегралов 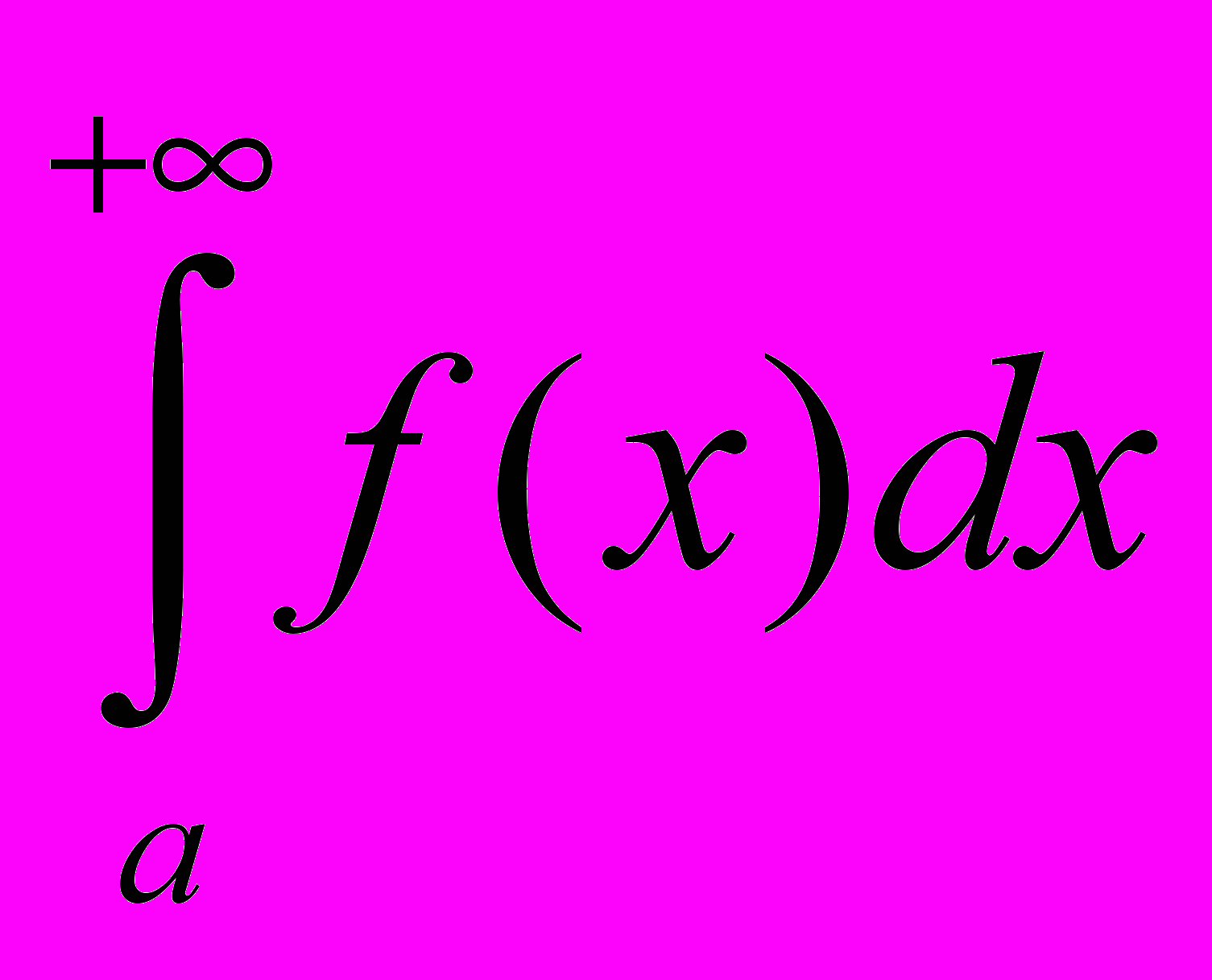и 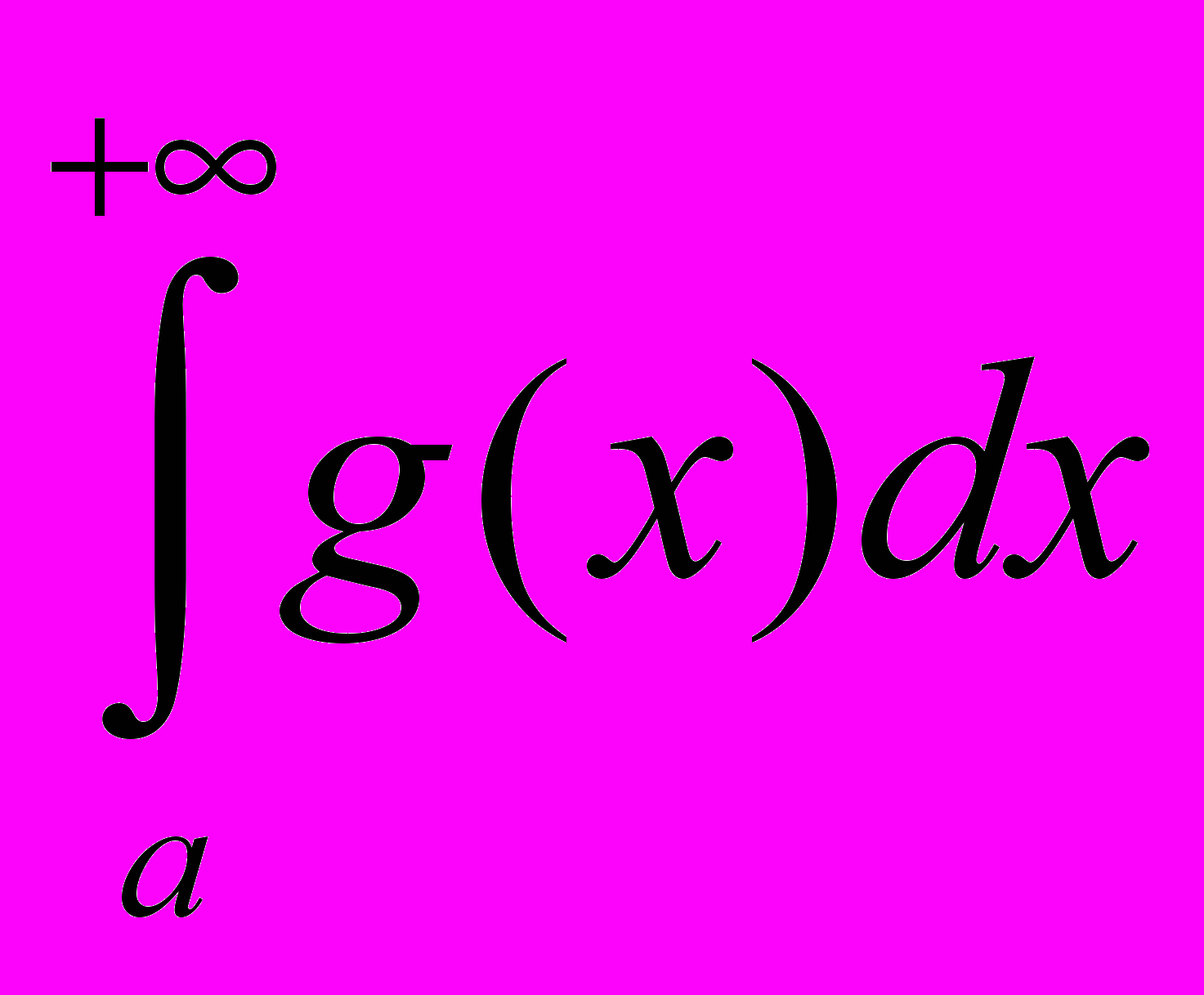одновременная . Если 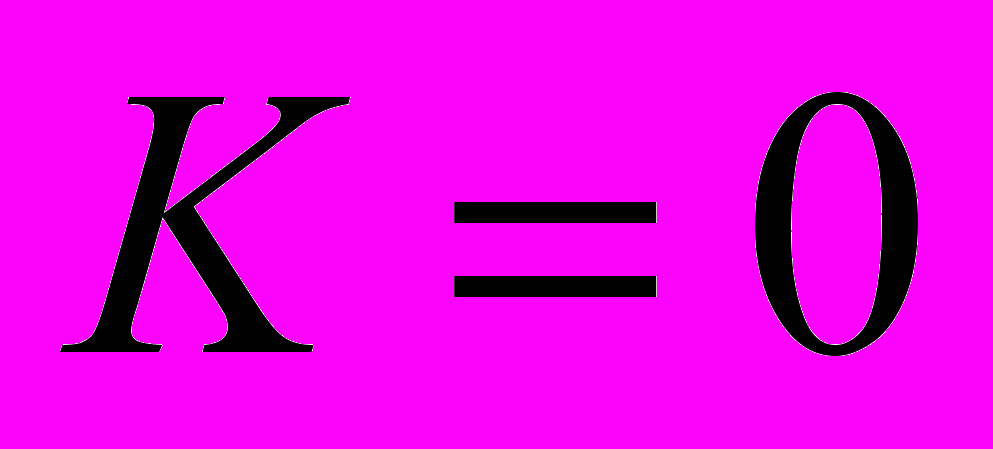, то из сходимости интеграла 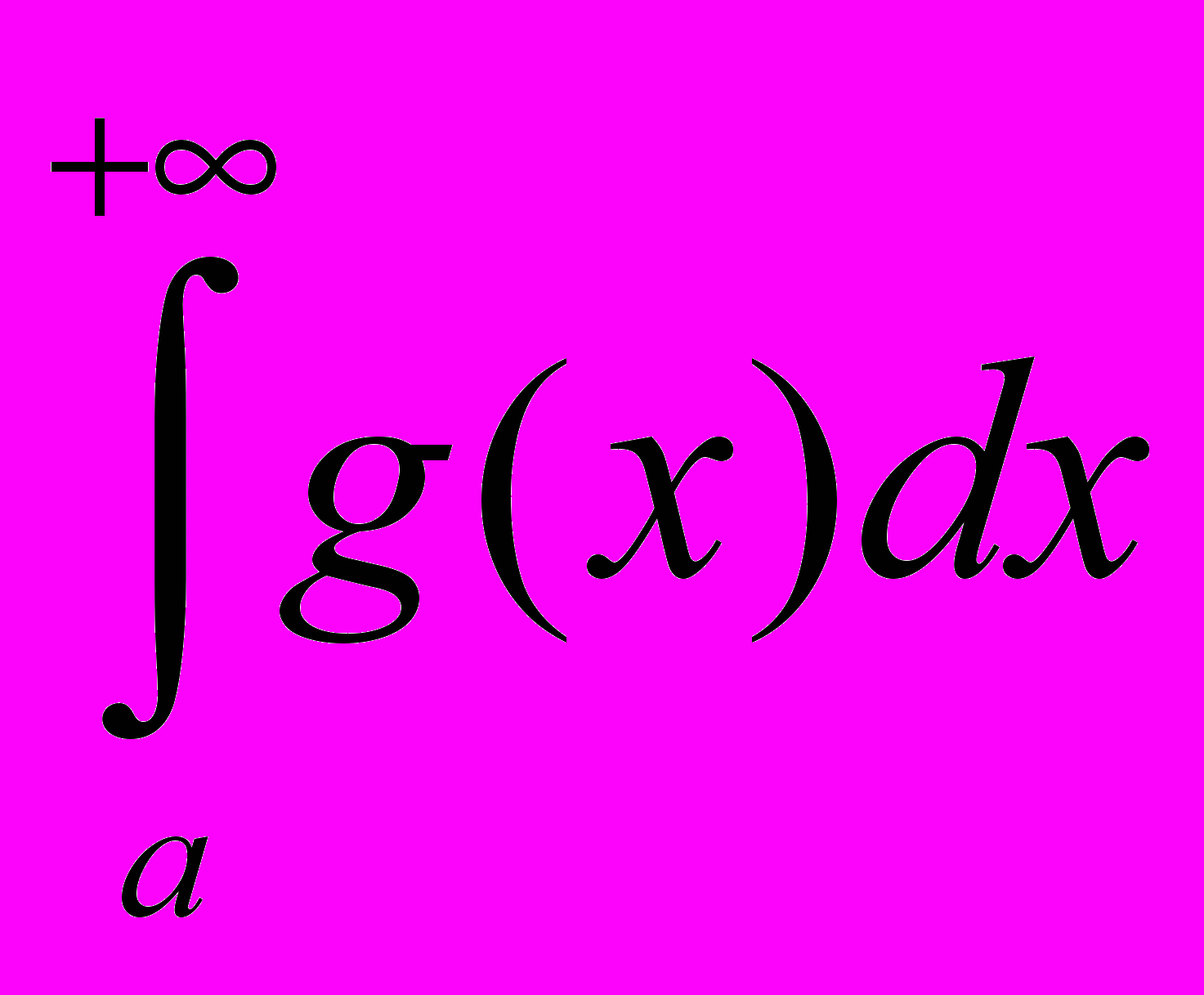следует сходимость интеграла 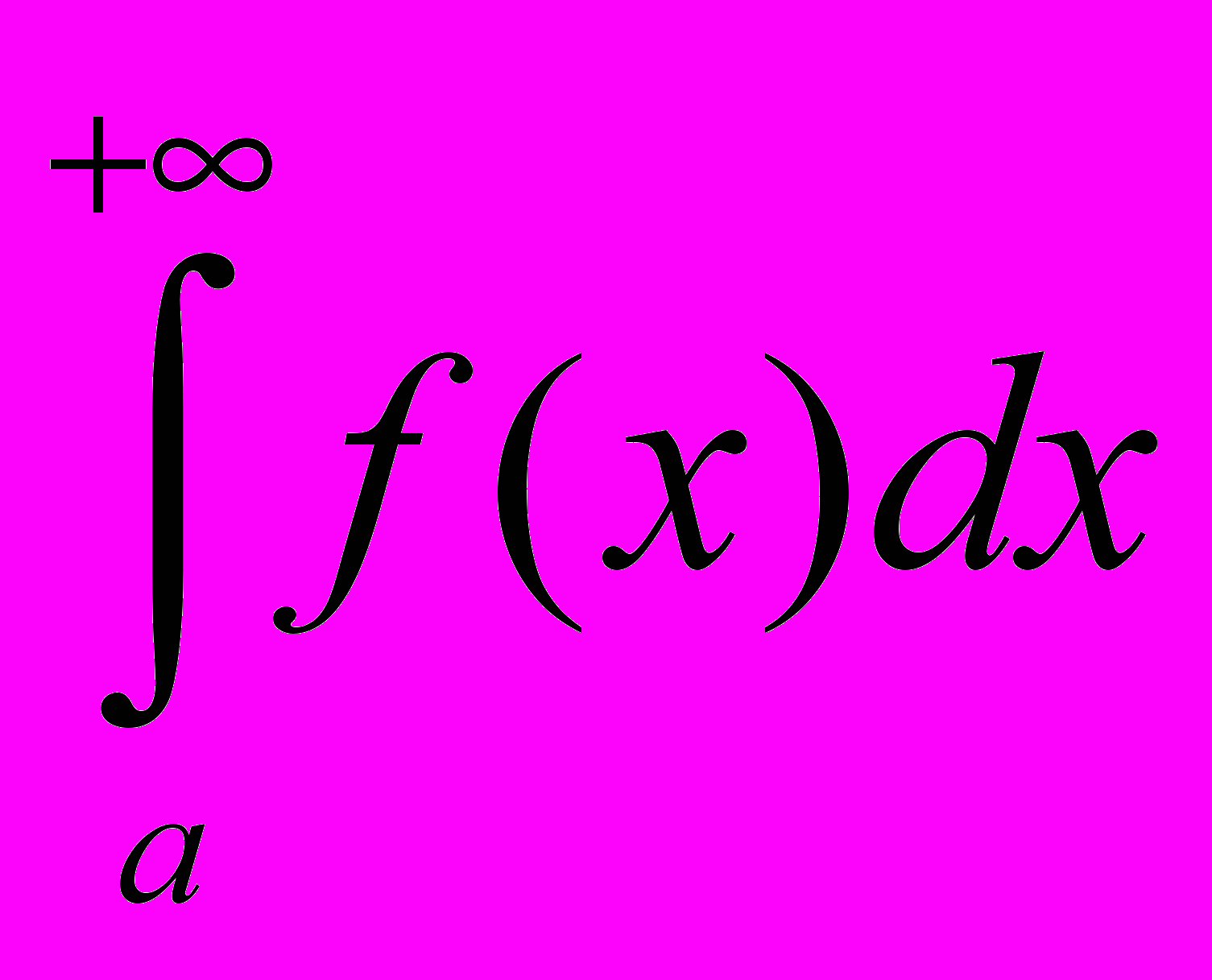и из расходимости интеграла 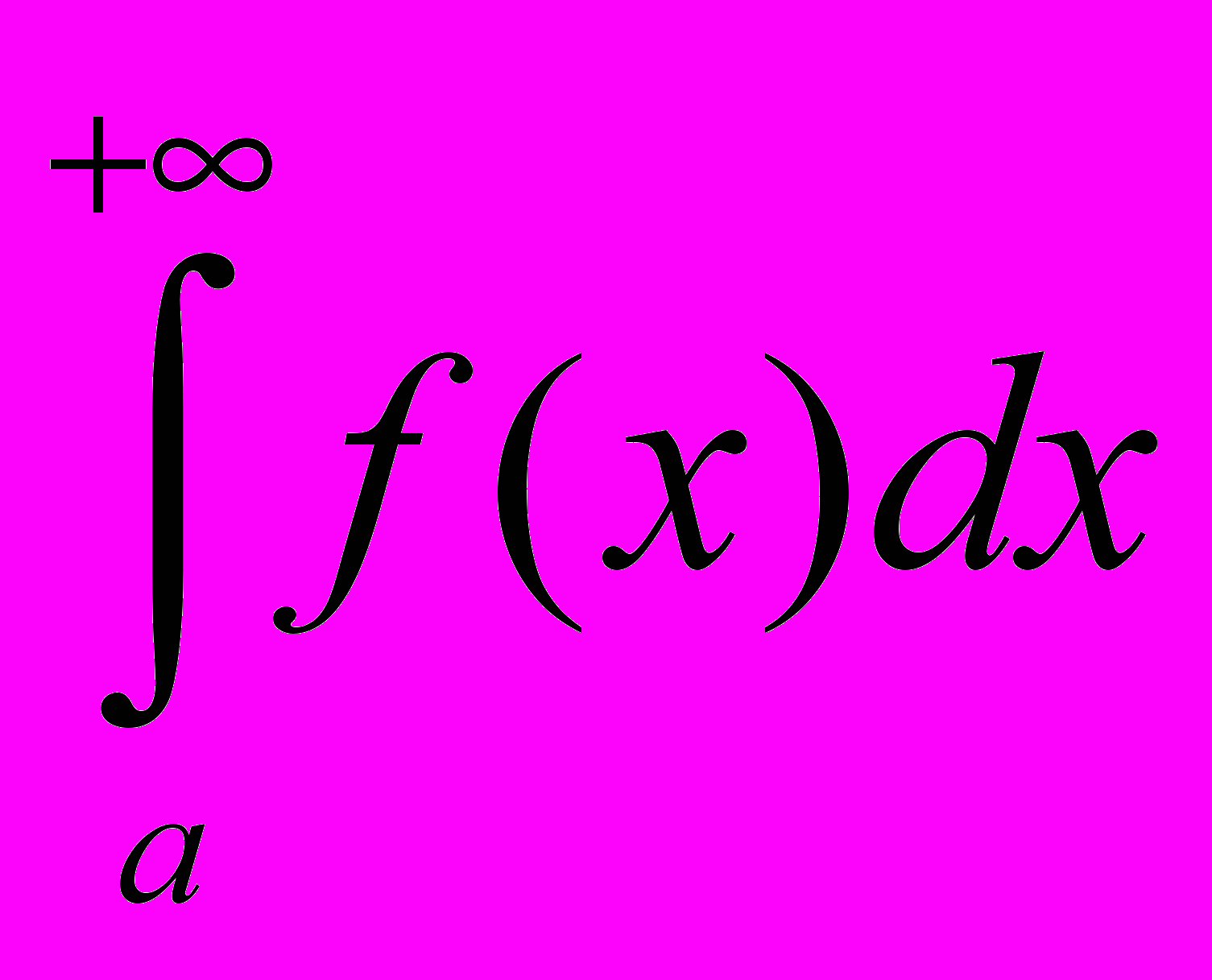следует расходимость интеграла .

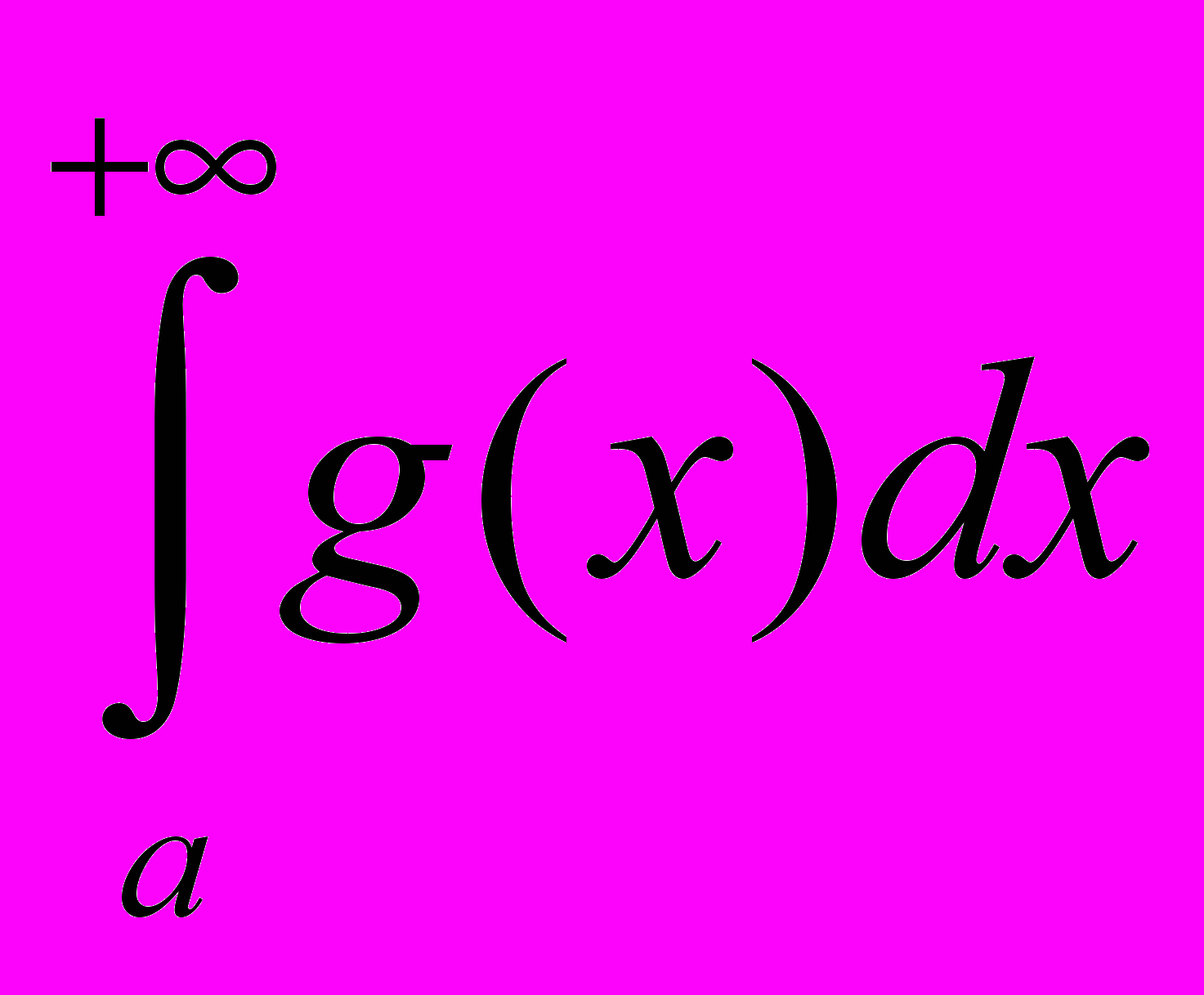ДОК. Аналогично доказательству теоремы сравнения 2 для неограниченных функций.

П.2 Абсолютная сходимость интегралов.

ОПР. Интеграл 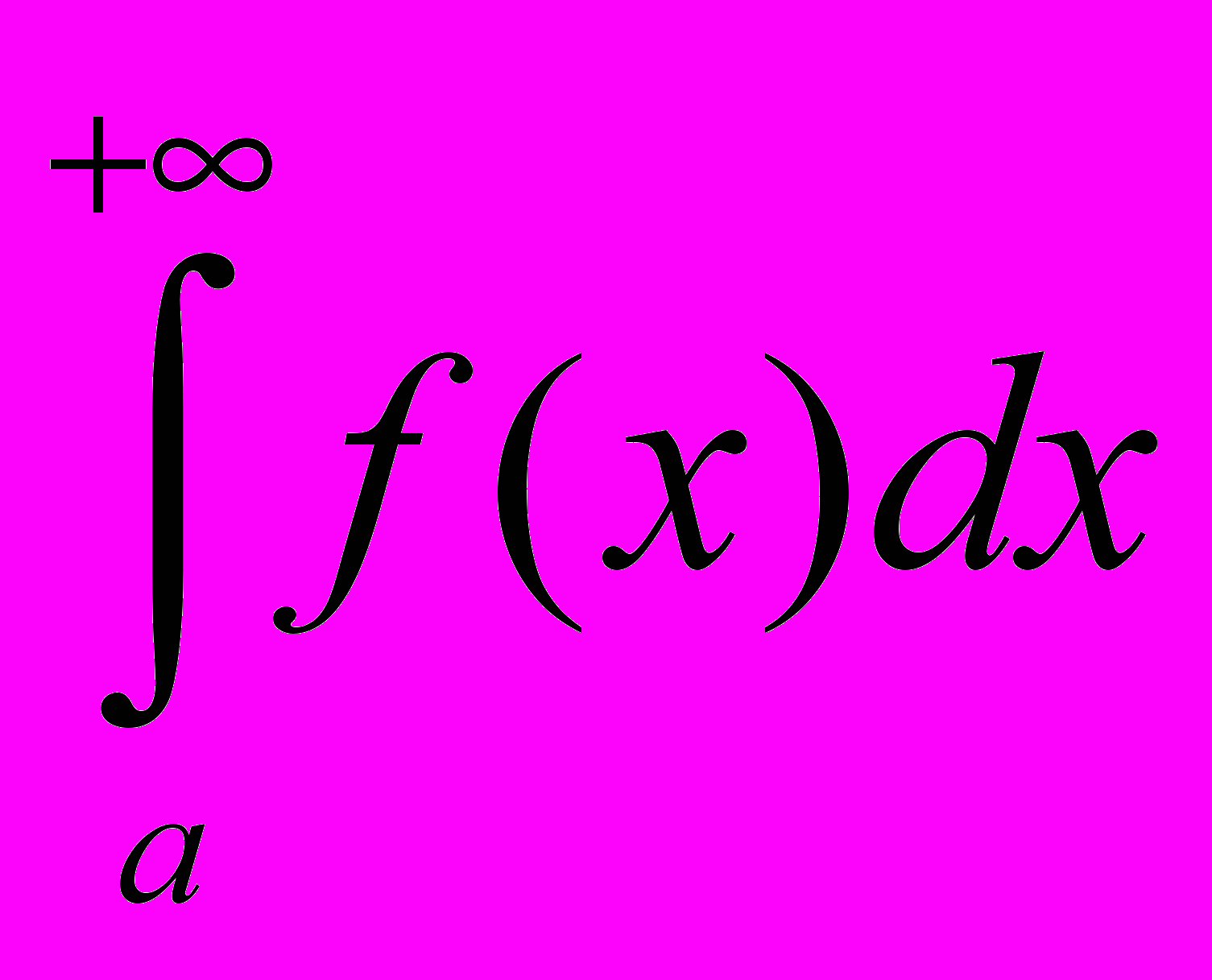называется абсолютно сходящимся, если сходится

интеграл .

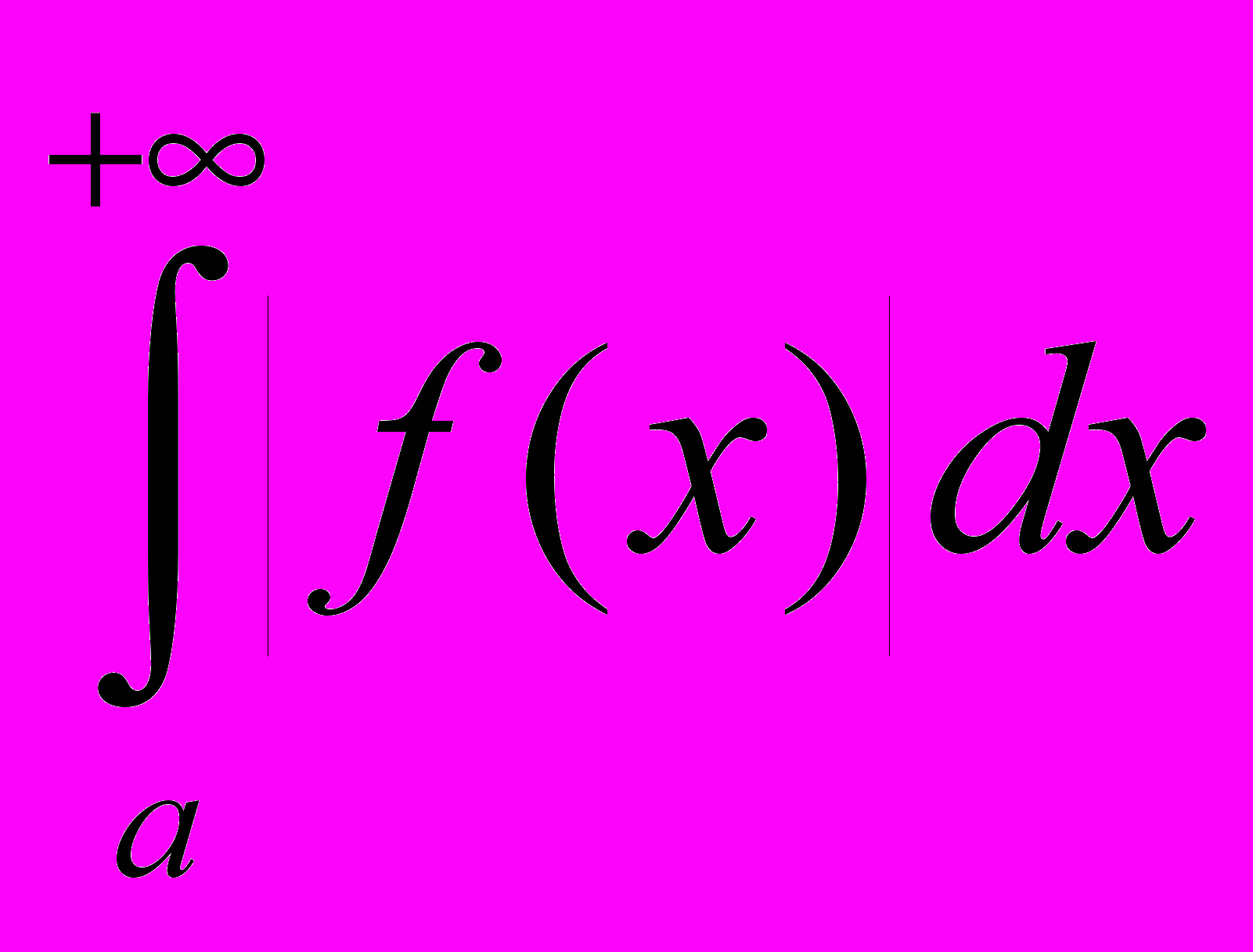ТЕОРЕМА ( о сходимости абсолютно сходящегося интеграла)

Если функция интегрируема на каждом конечном отрезке полуоси 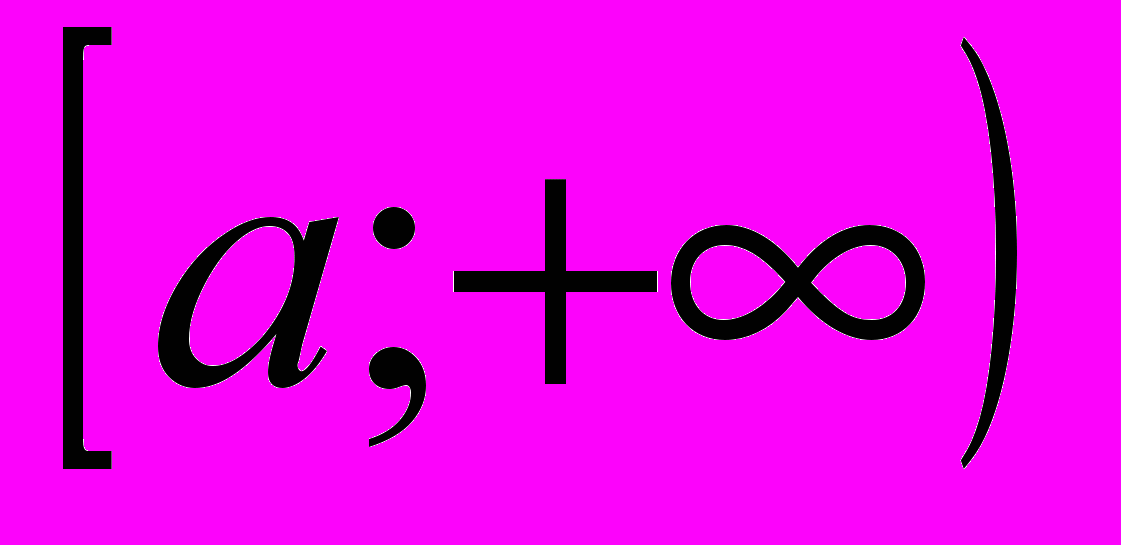и

интеграл 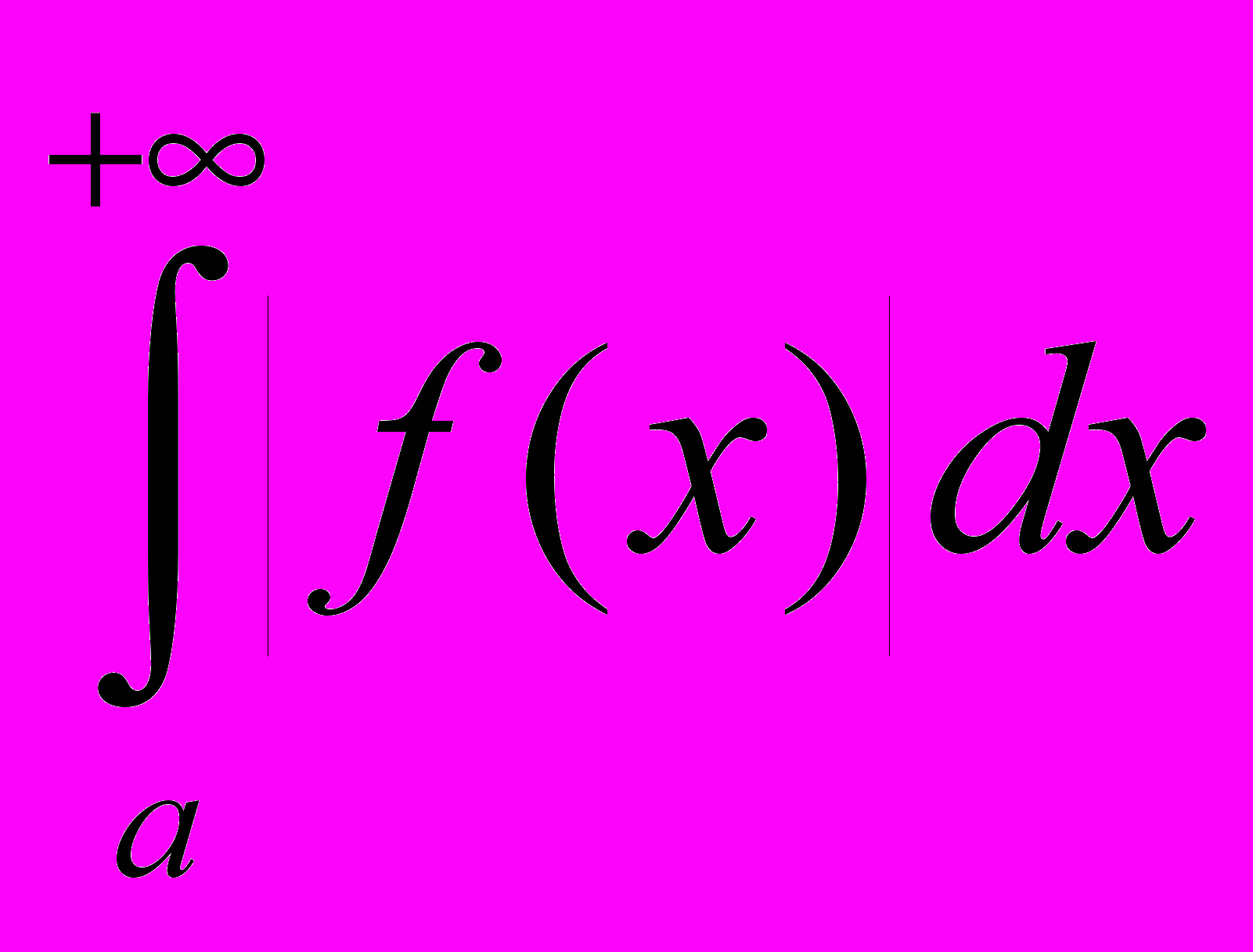сходится, то 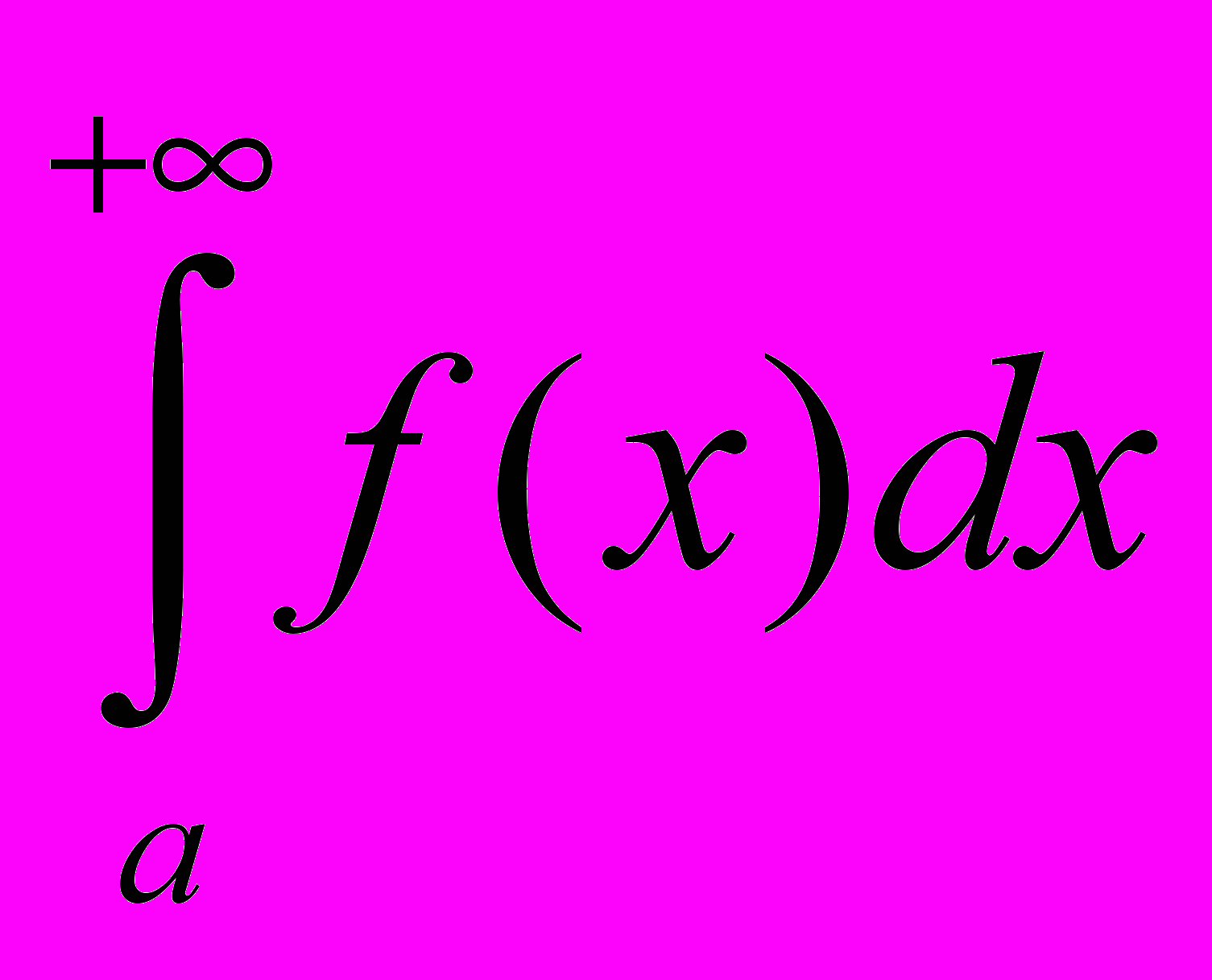также сходится.

ДОК. Из сходимости 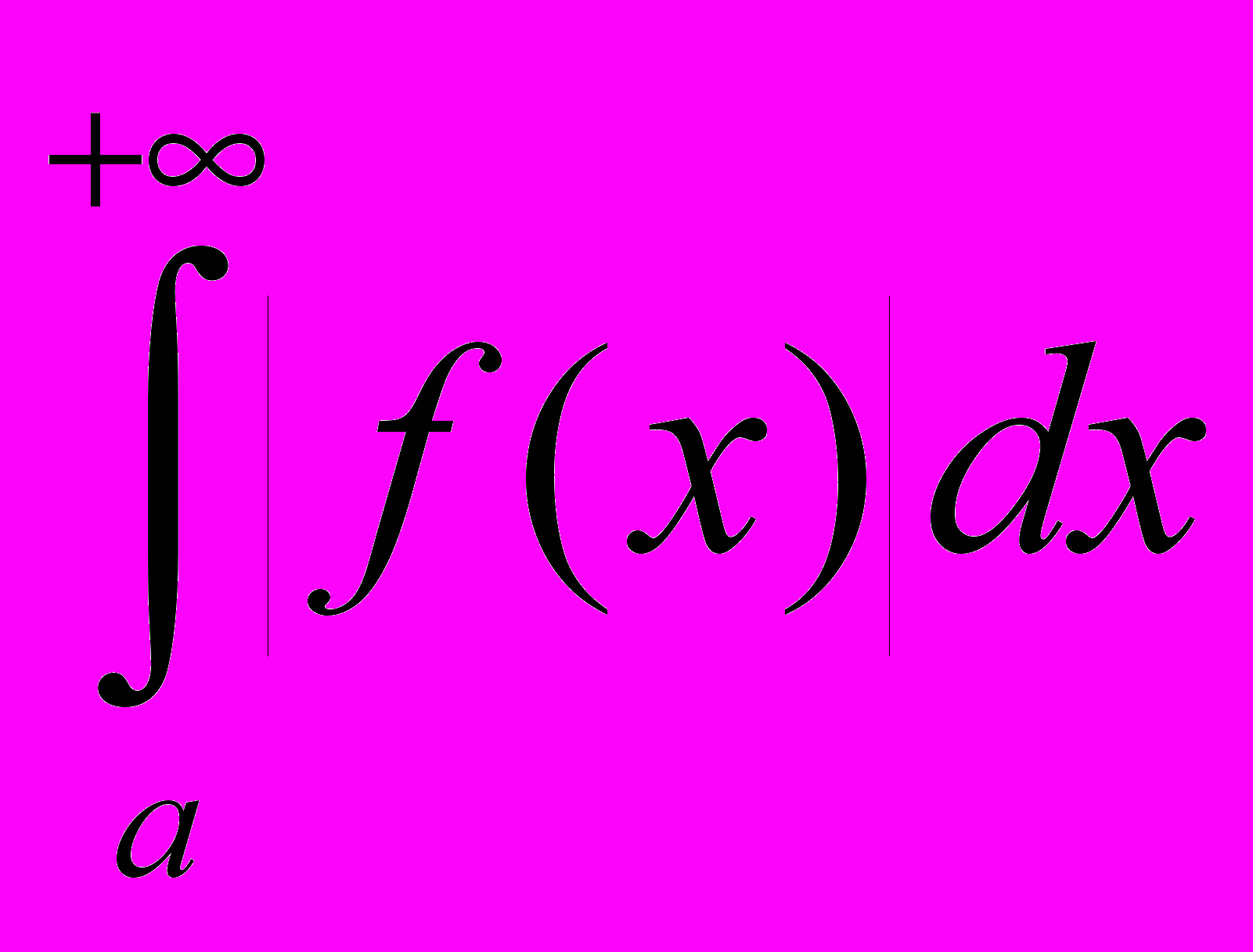по критерию Коши следует, что 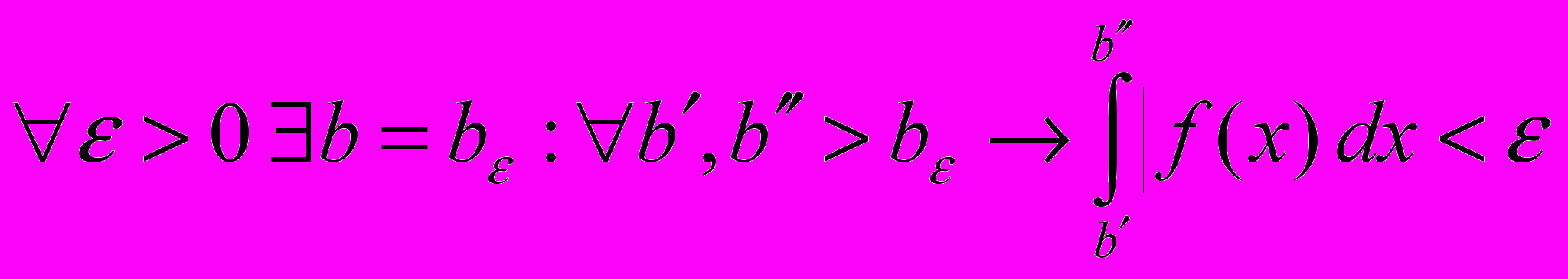. Для завершения доказательства осталось заметить, что .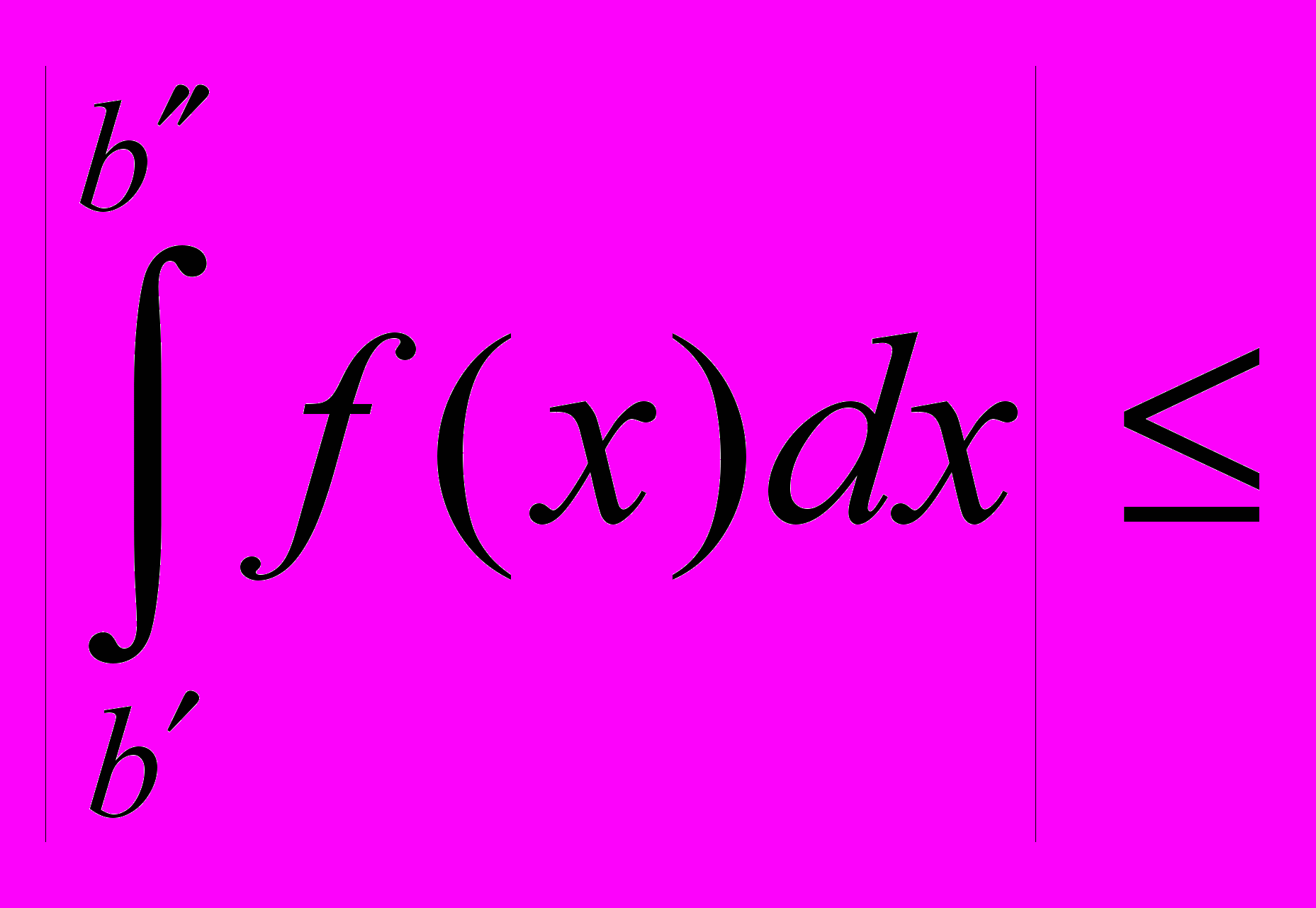

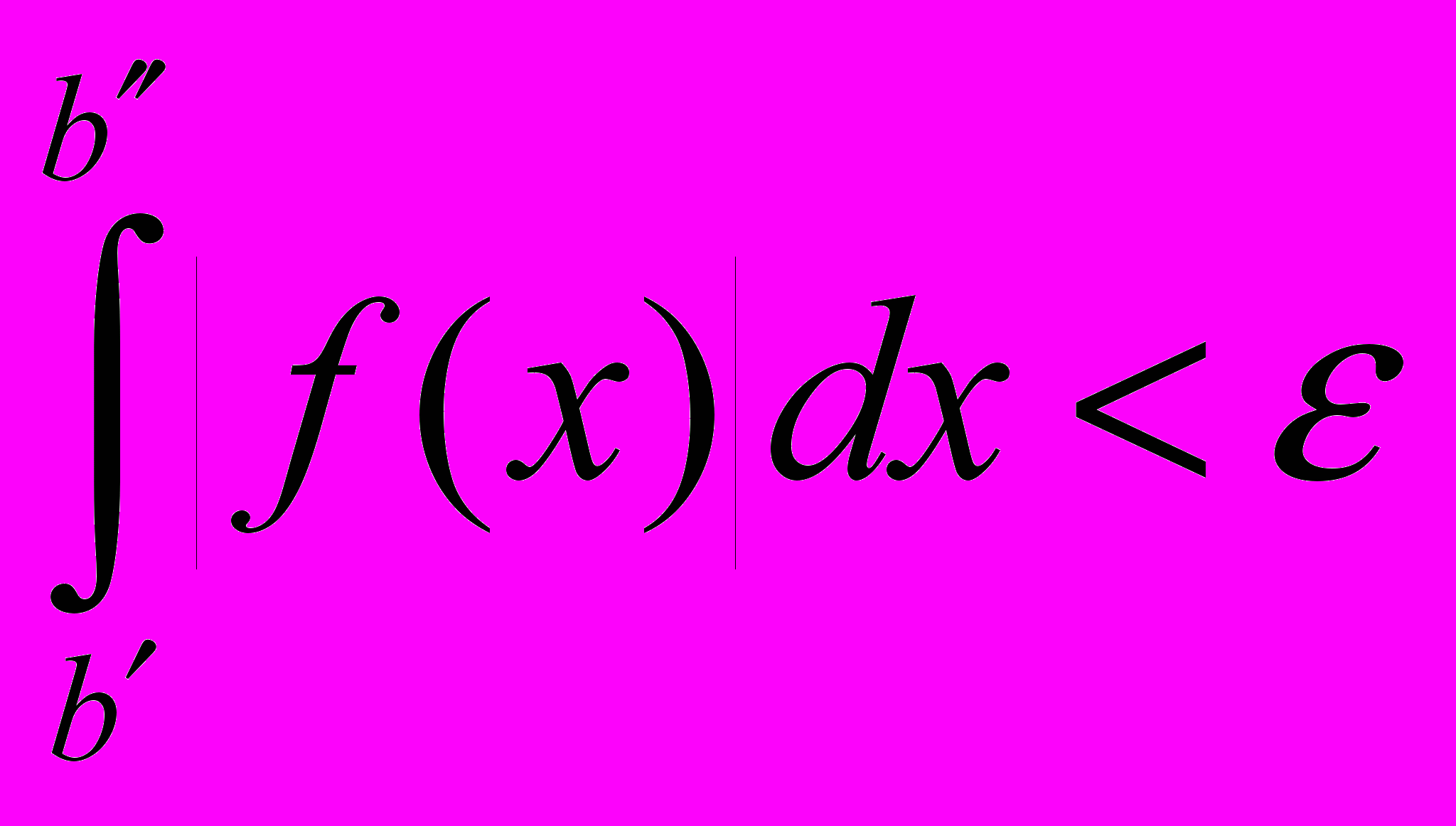Требование интегрируемости функции существенно для справедливости утверждения теоремы.

ПРИМЕР 2. Функция 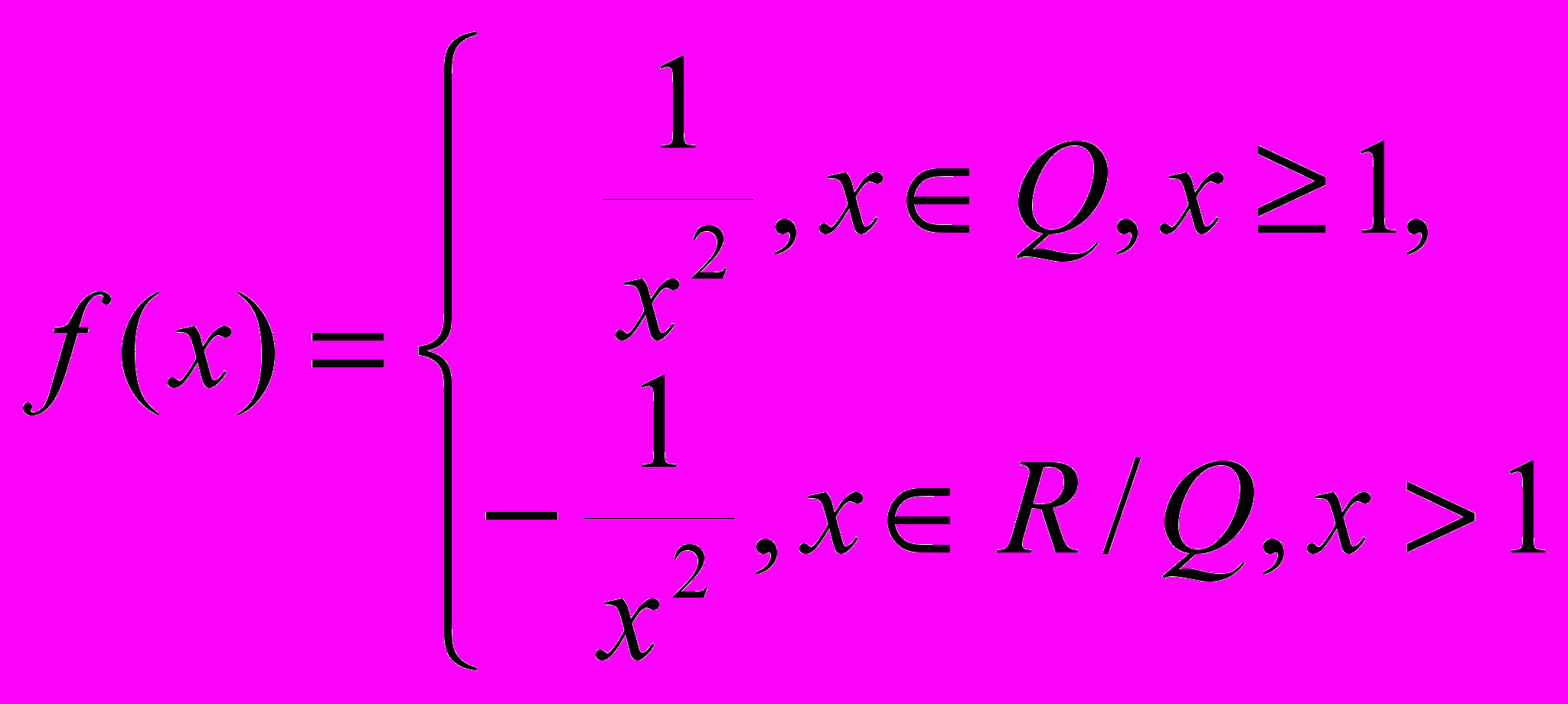не интегрируема на любом конечном отрезке полуоси 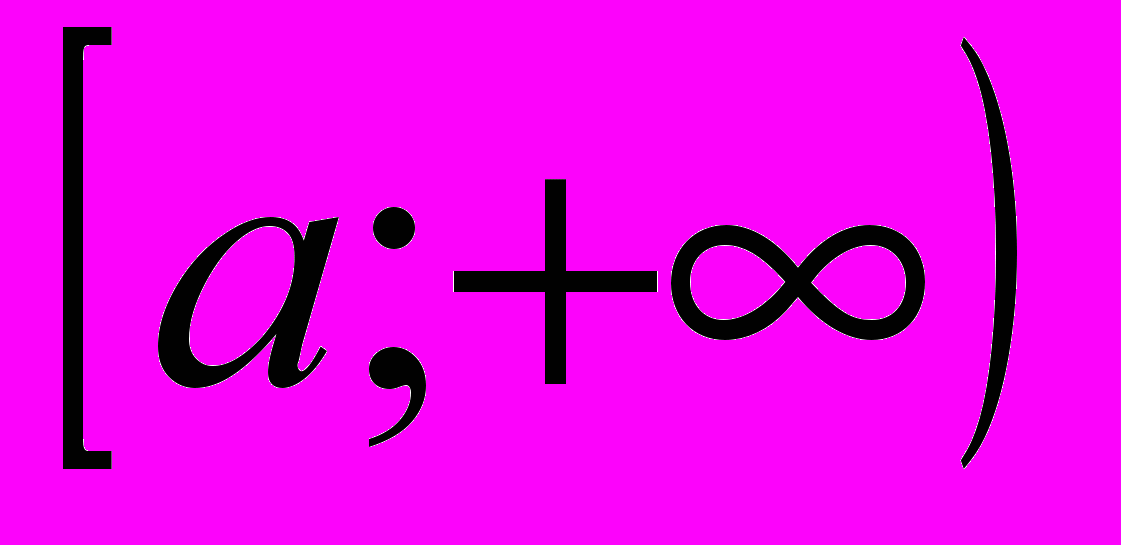, поэтому 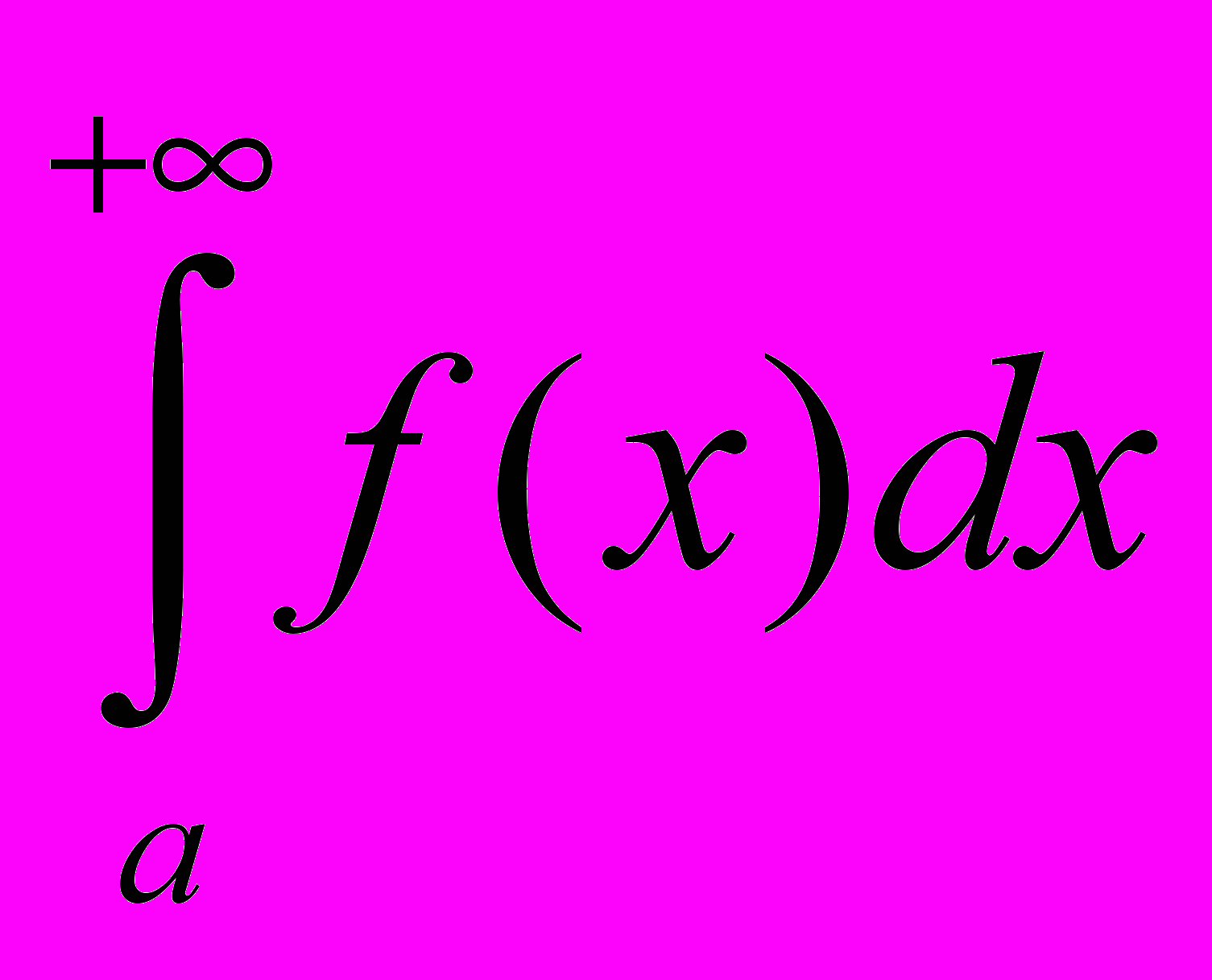расходится. Однако, функция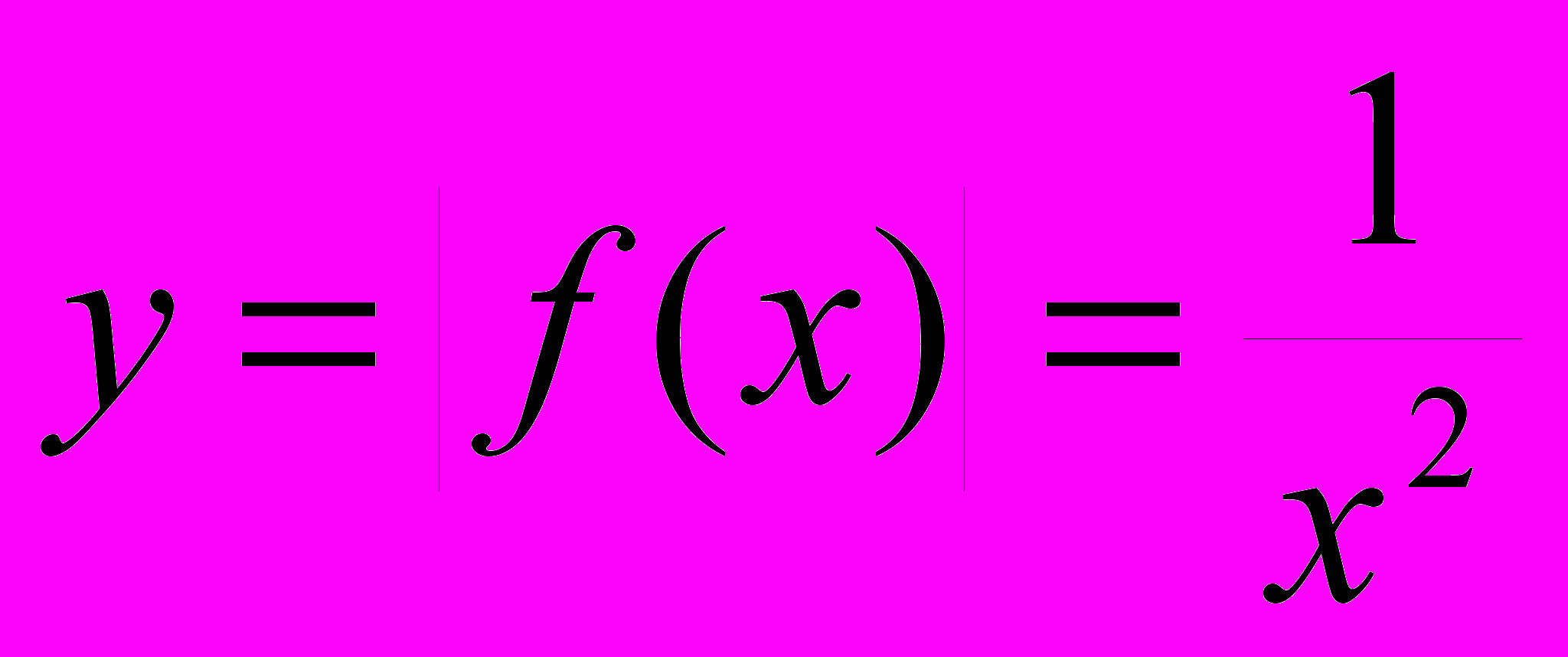

интегрируема и 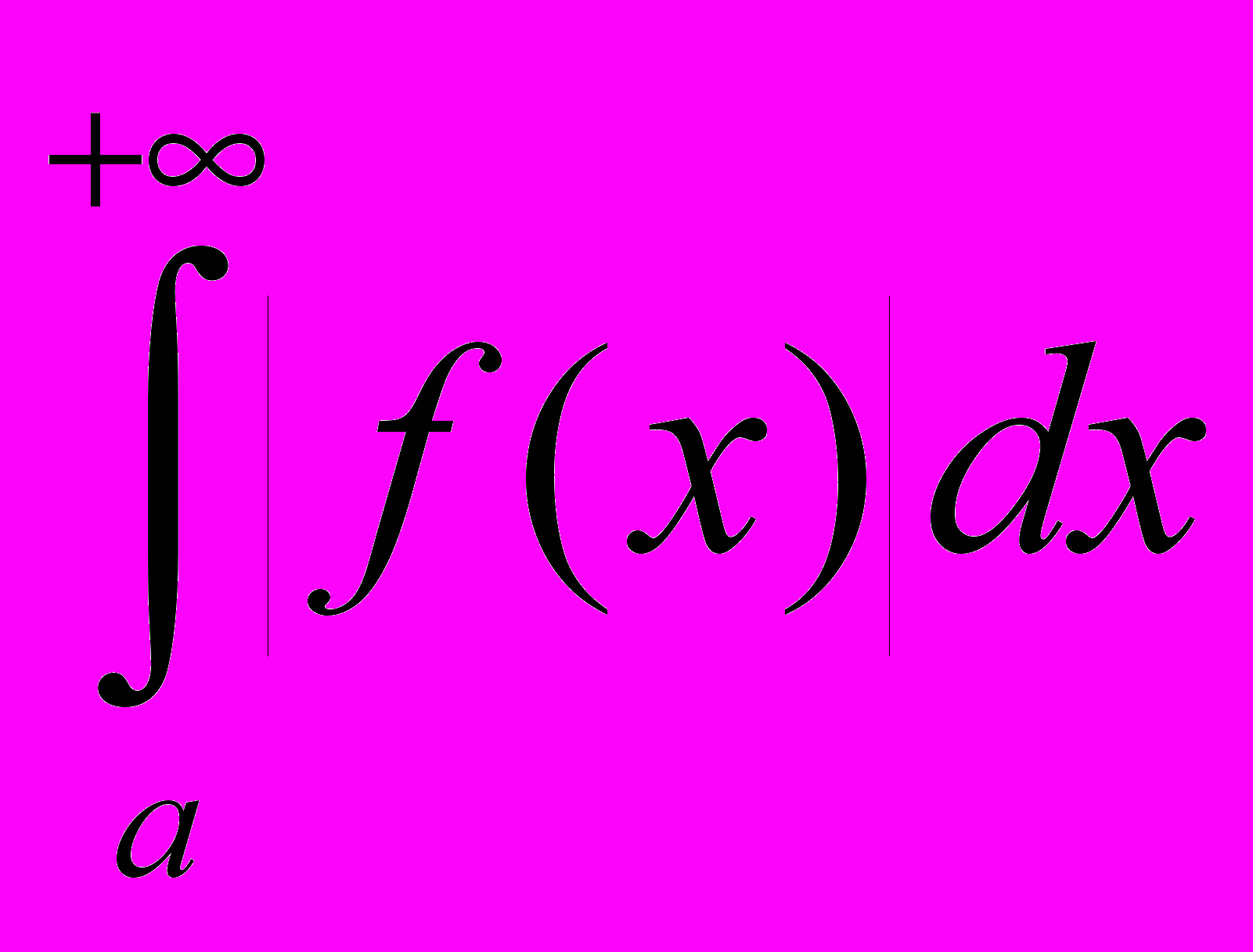сходится.

ПРИЗНАК АБЕЛЯ-ДИРИХЛЕ для сходимости несобственных интегралов .

Если функция 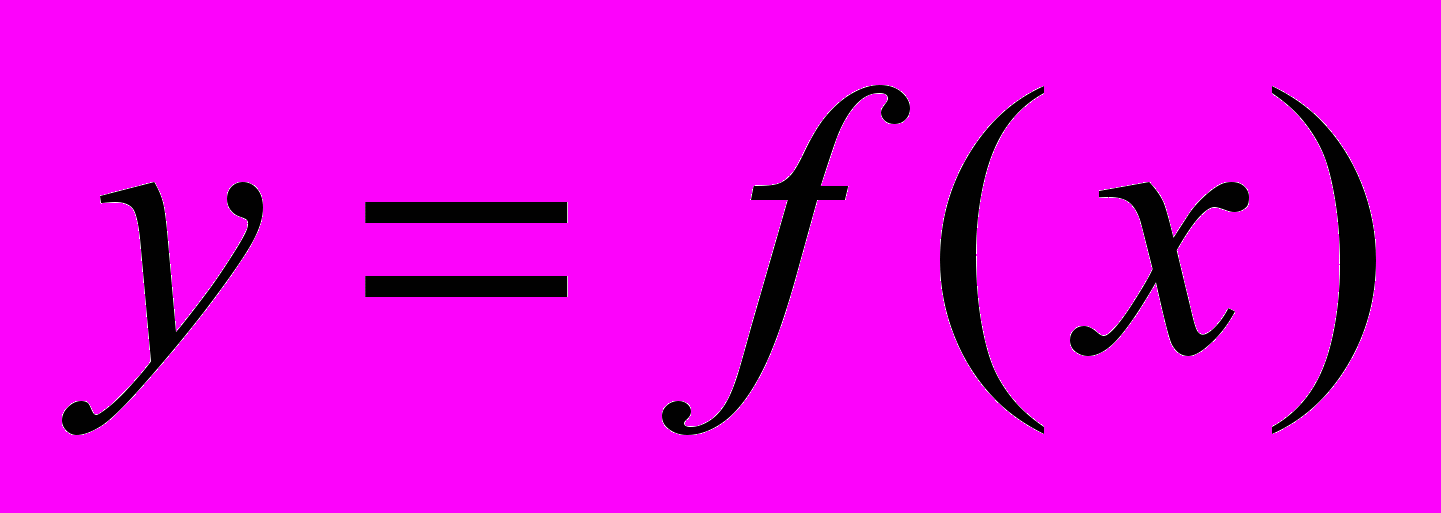непрерывно дифференцируема на 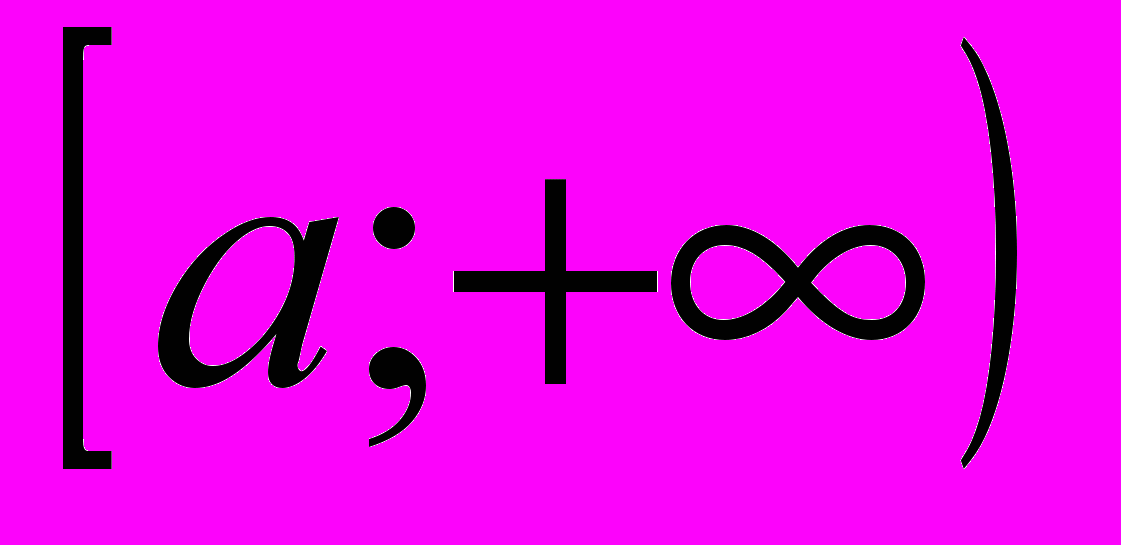, функция 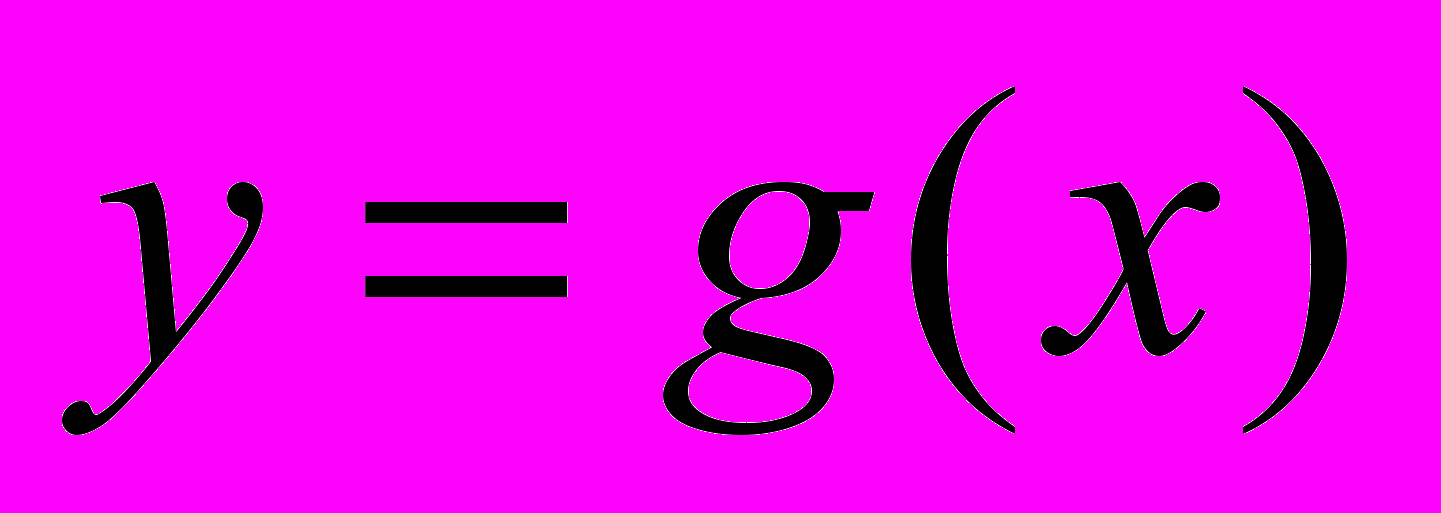непрерывна на 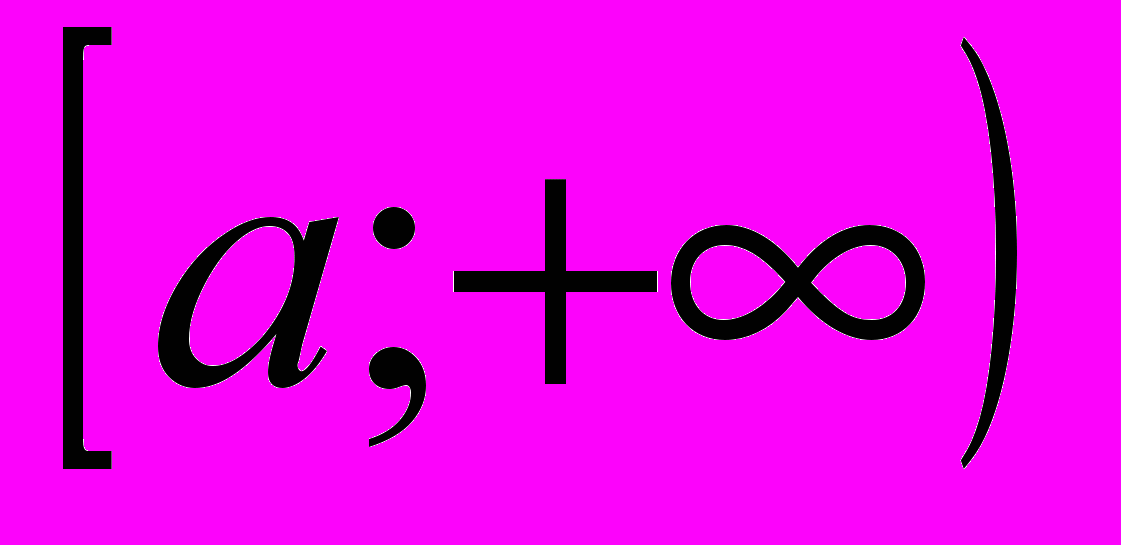и 1) 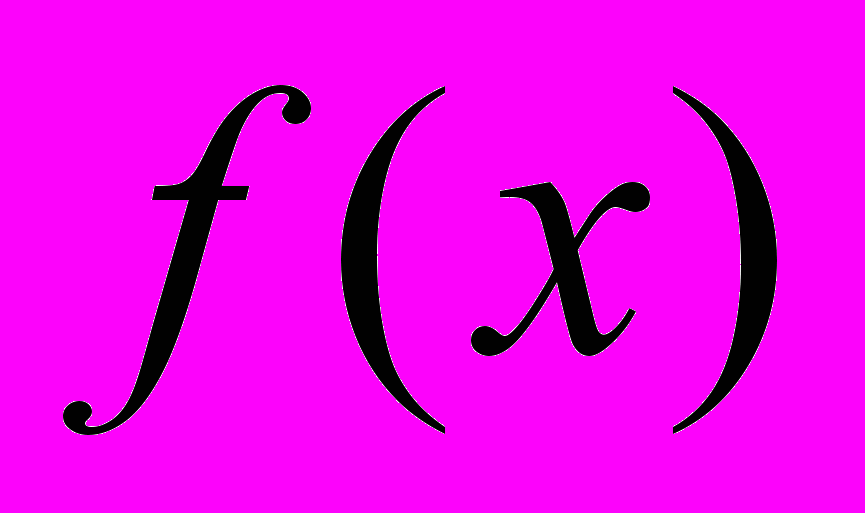монотонно убывает и ,

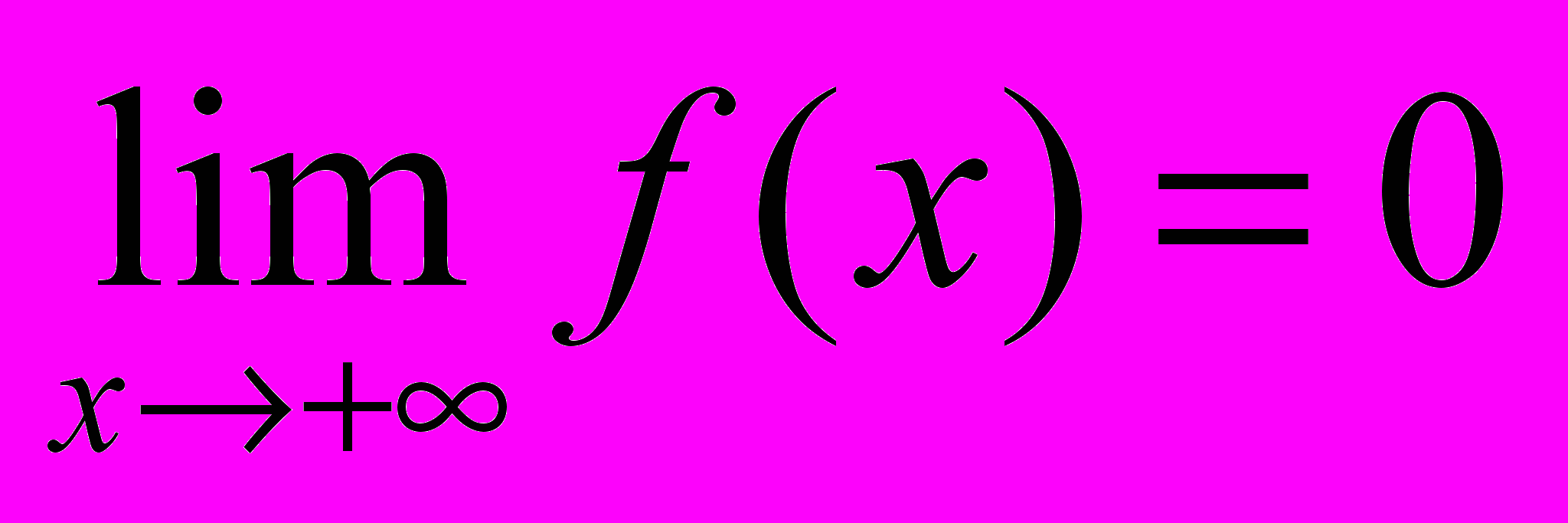2) 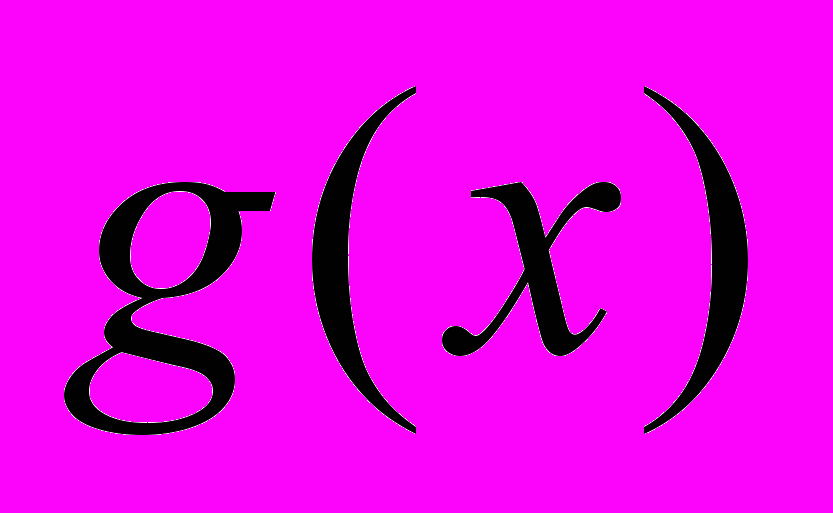имеет ограниченную первообразную : .

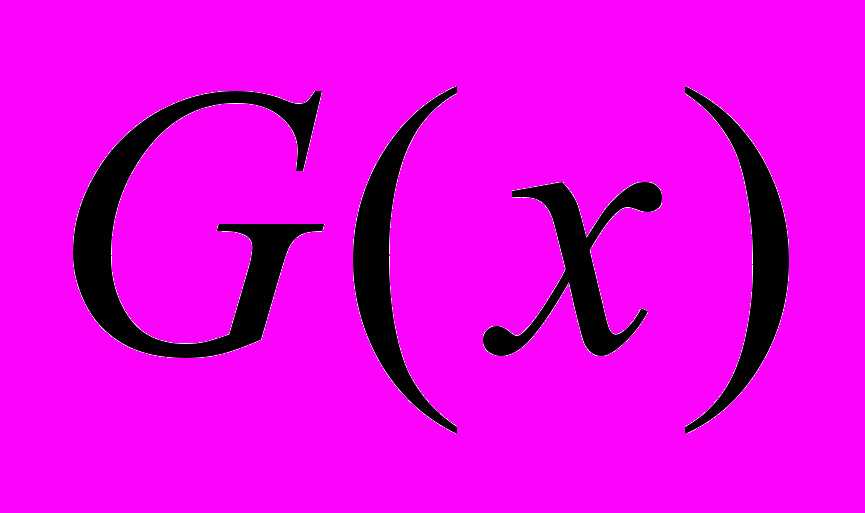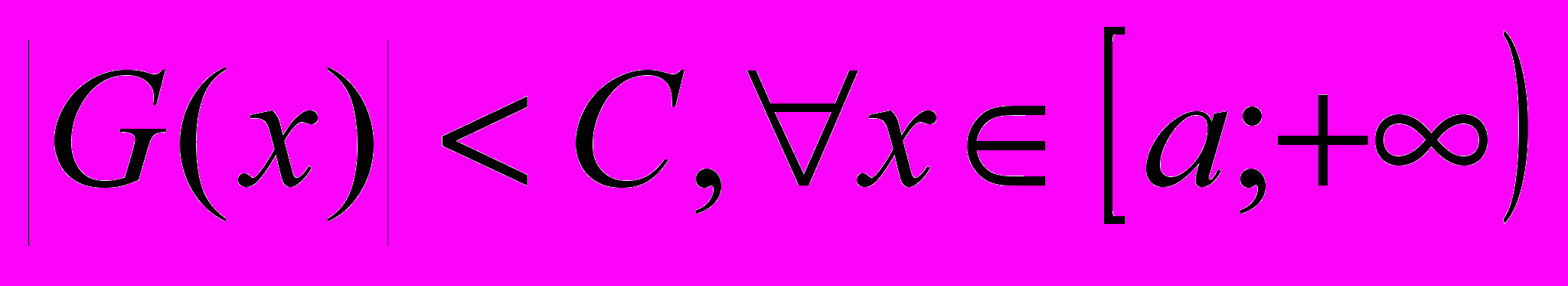Тогда интеграл 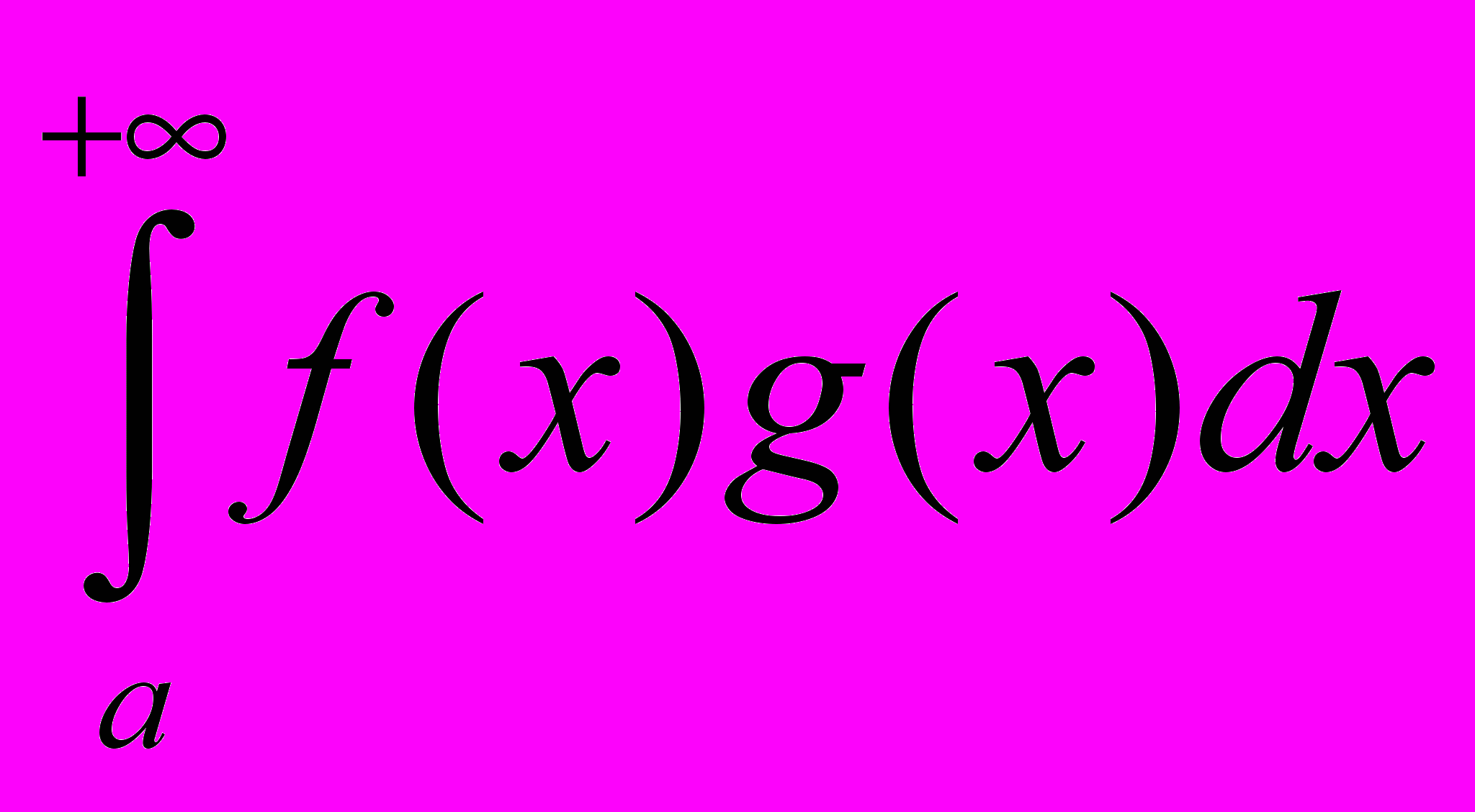сходится.

ДОК.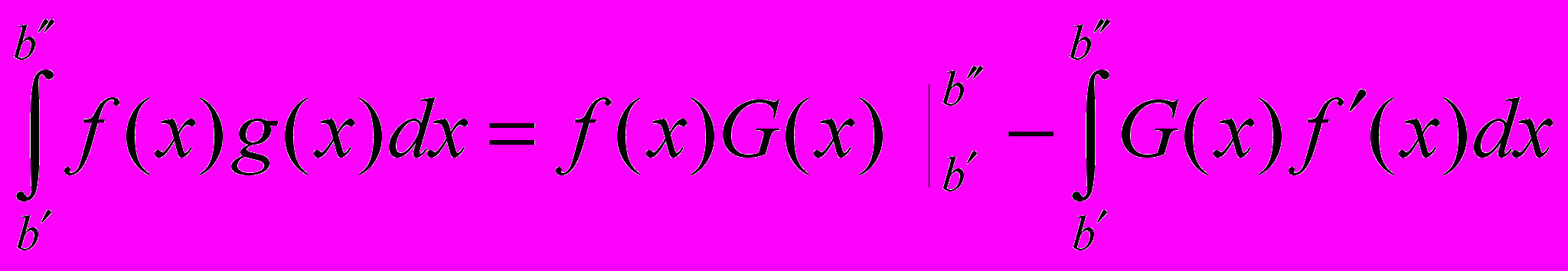. Из условия 1), 2) теоремы следует,что

для любого .

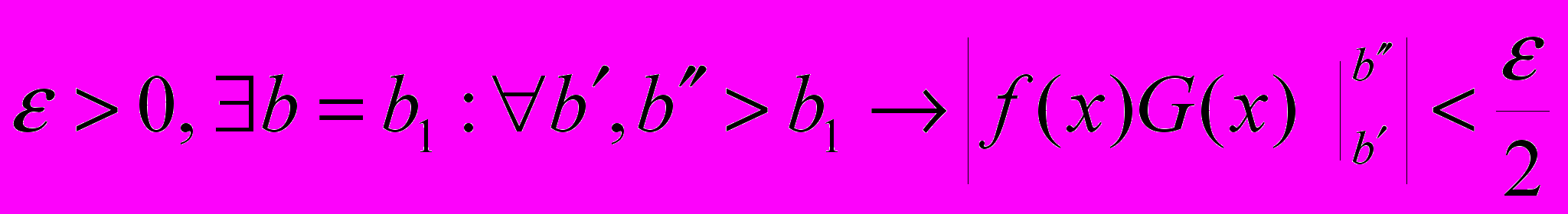Для второго слагаемого .

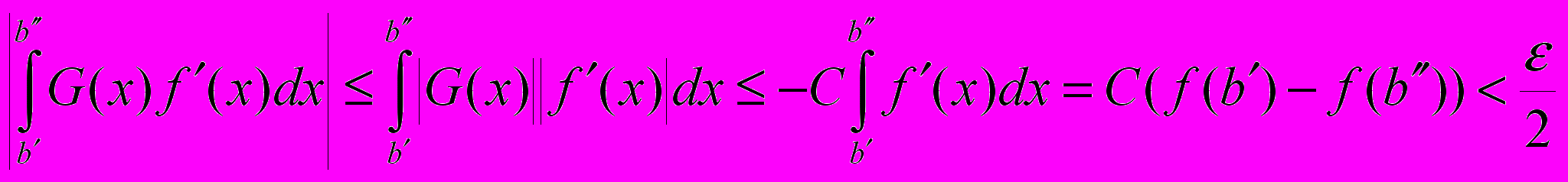Тогда .

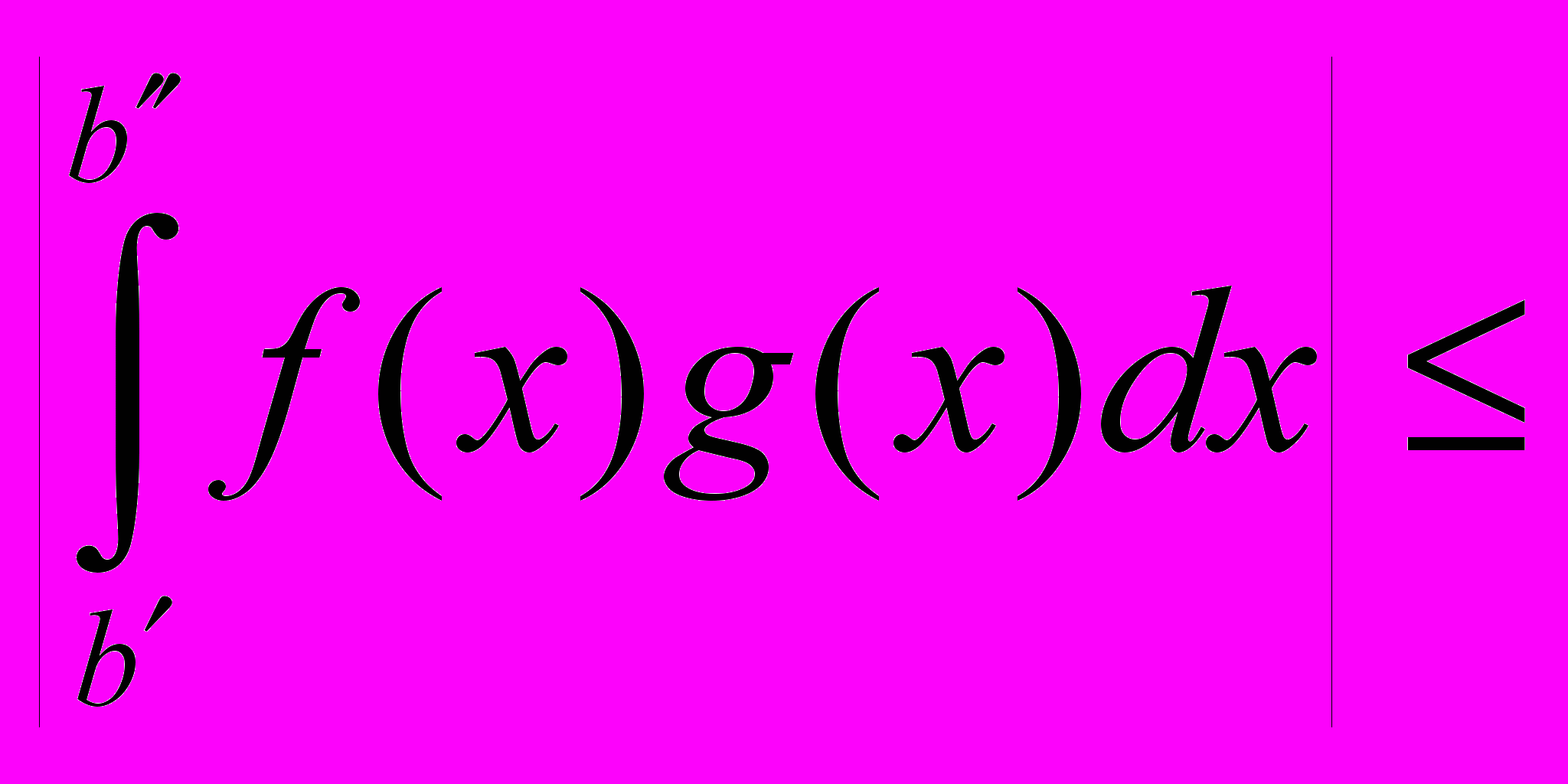
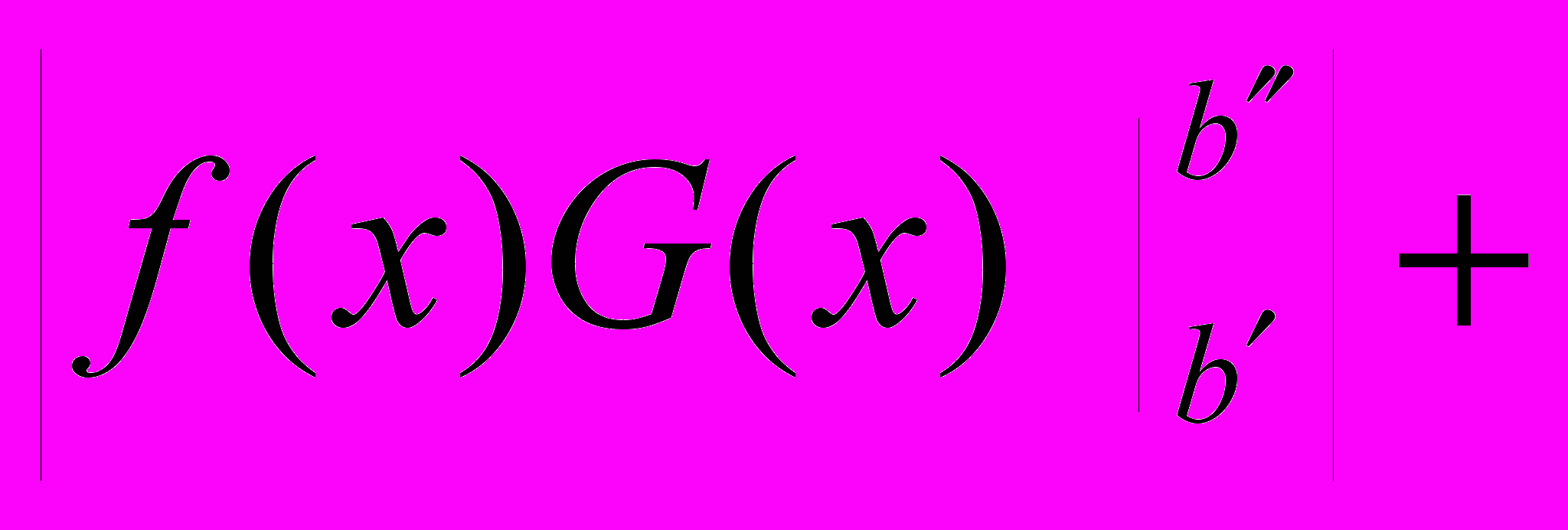
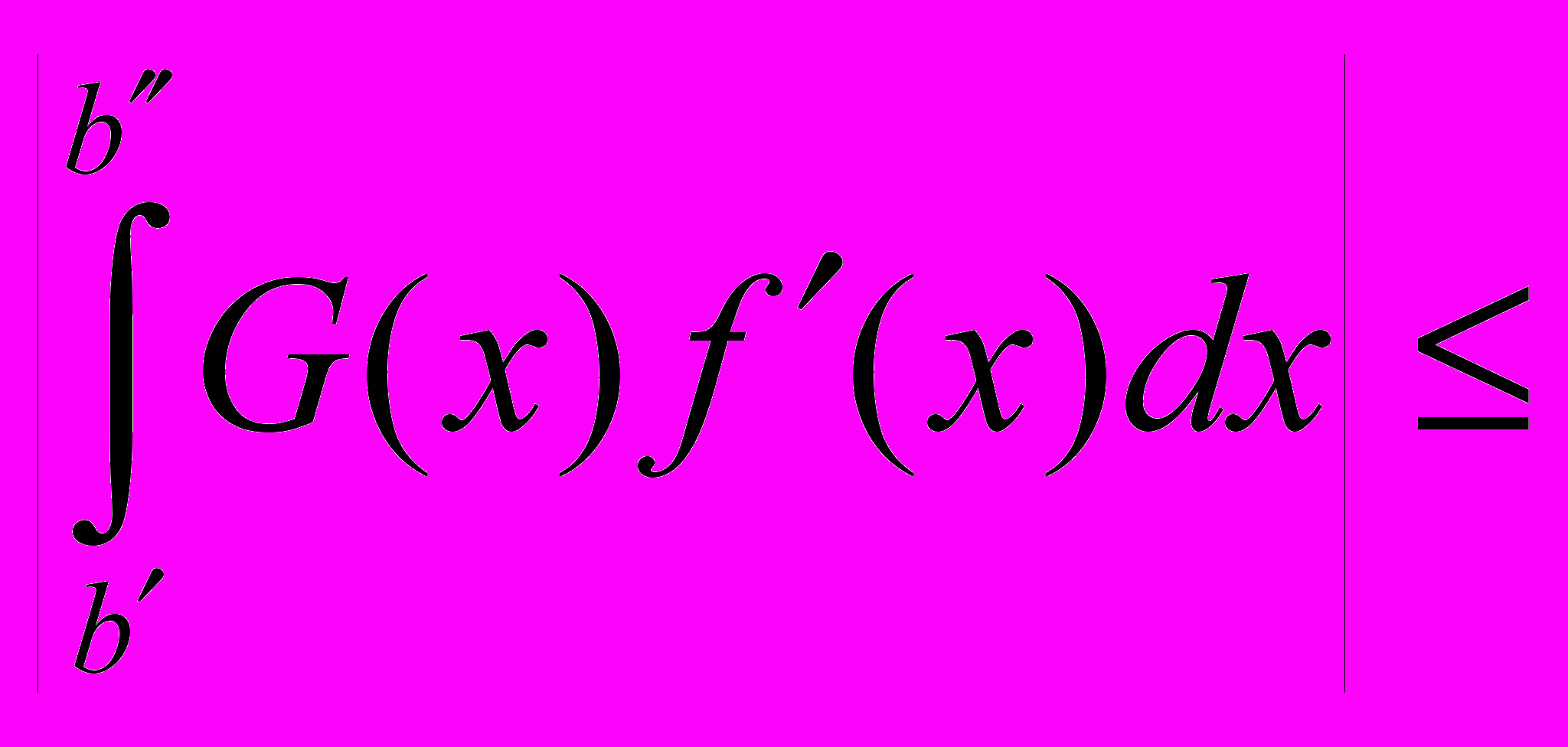
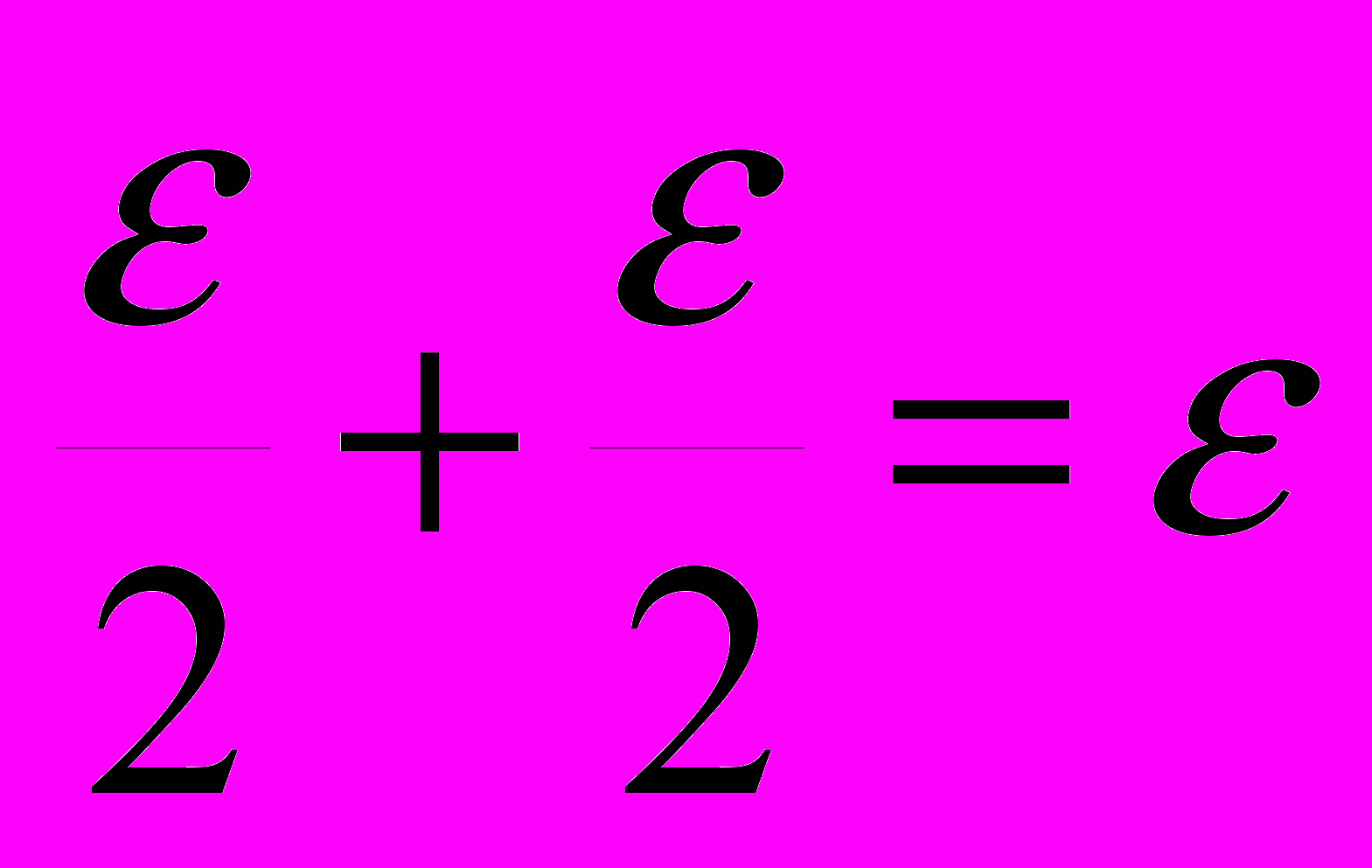ПРИМЕР 3 . Интеграл 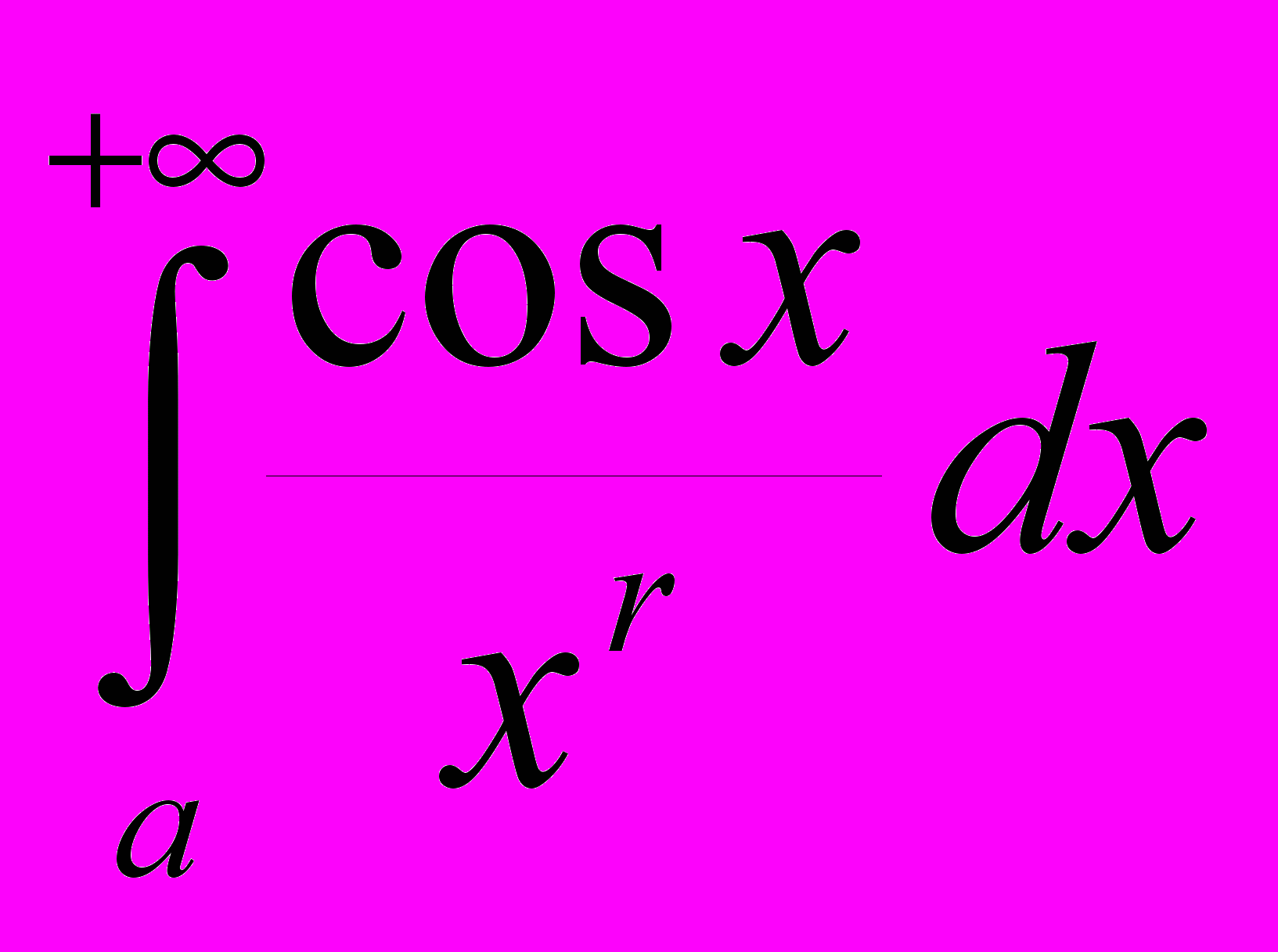сходится при .

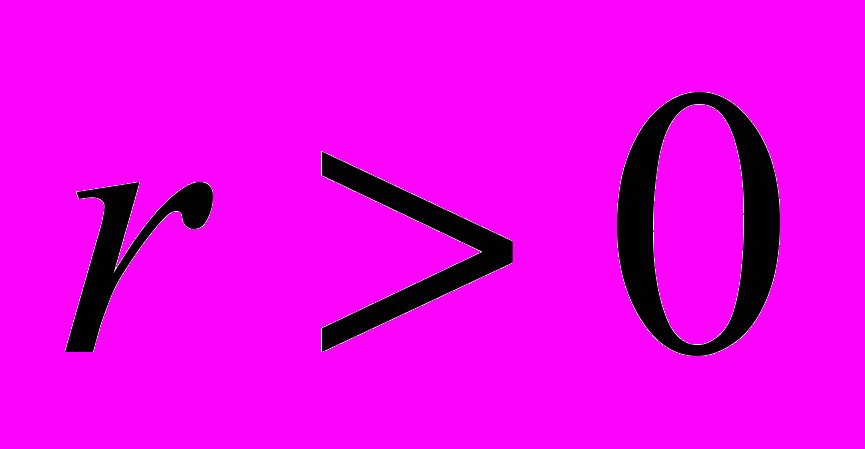РЕШЕНИЕ. Функция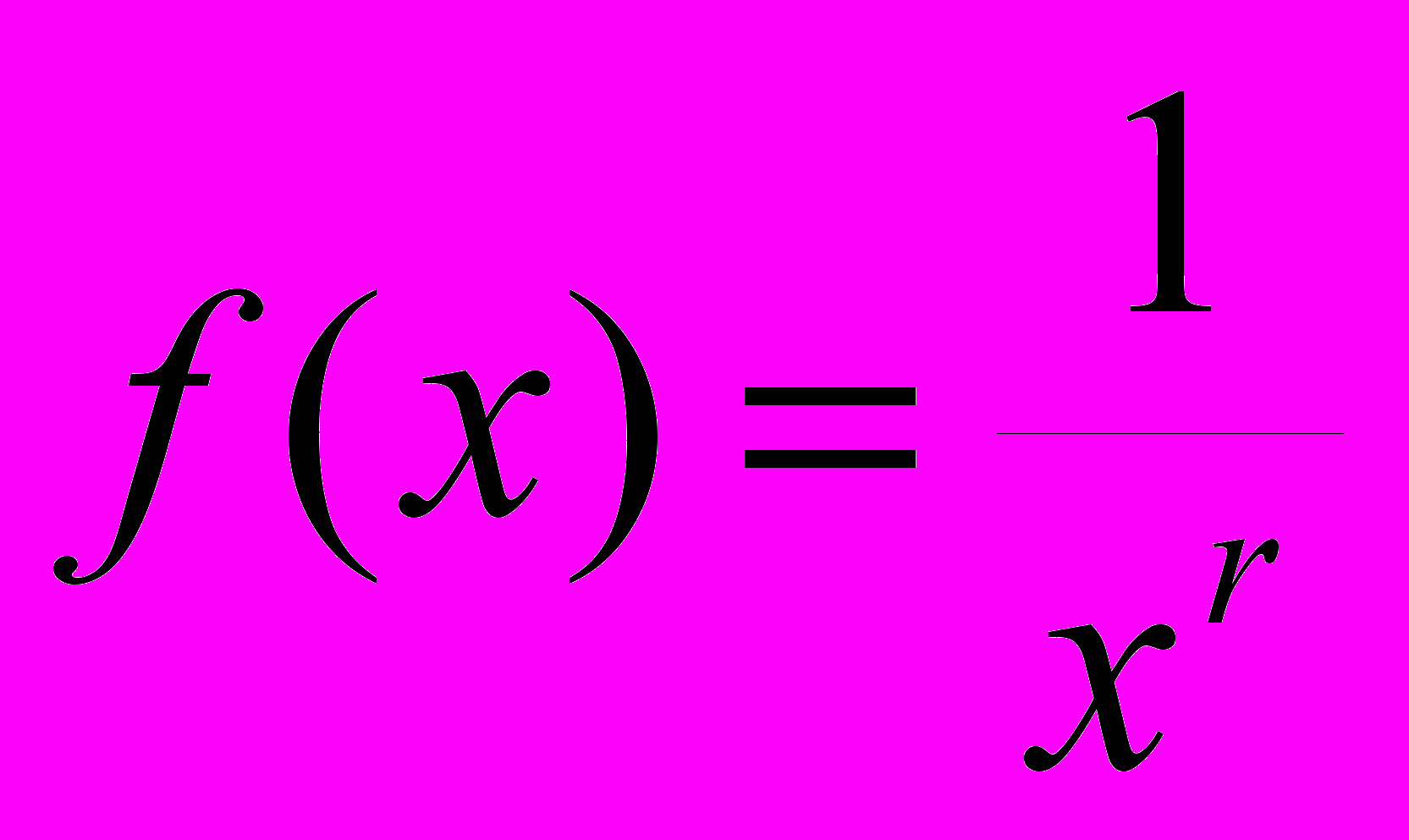убывает на 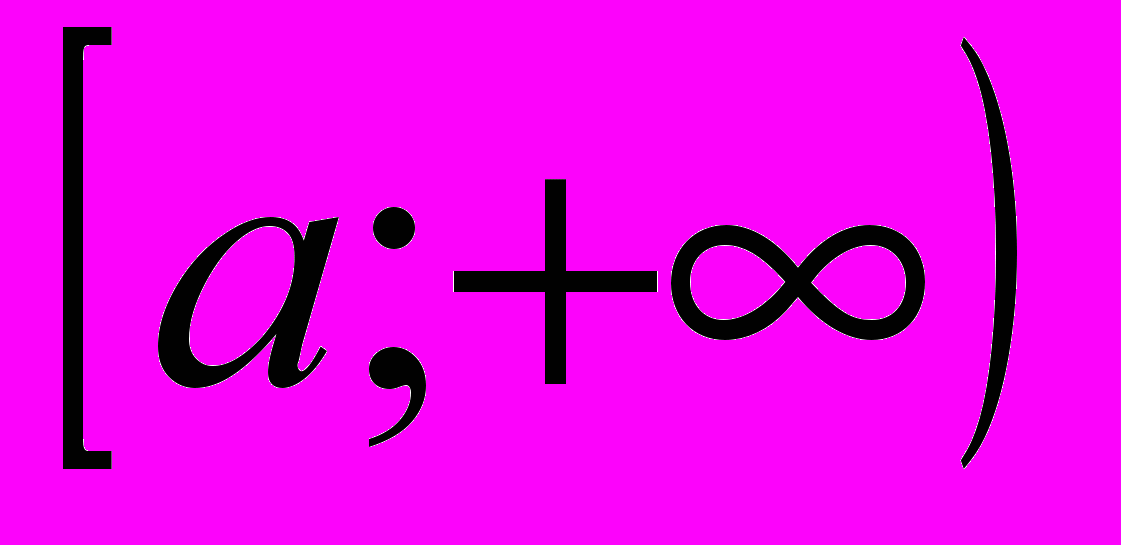, 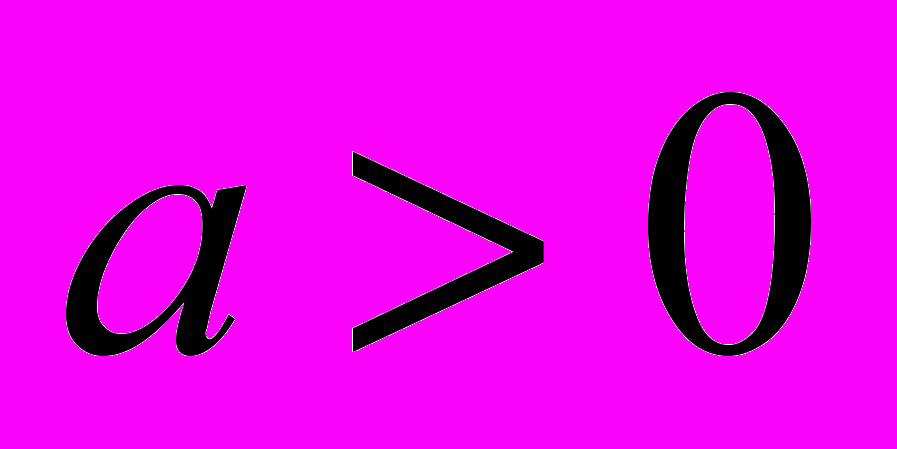. Первообразная функции 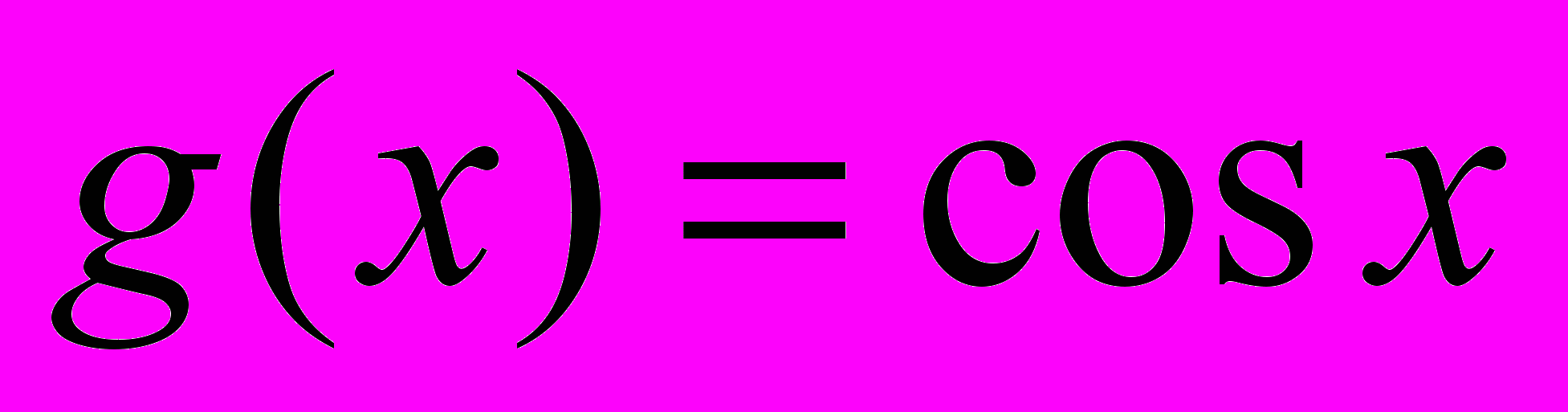равна 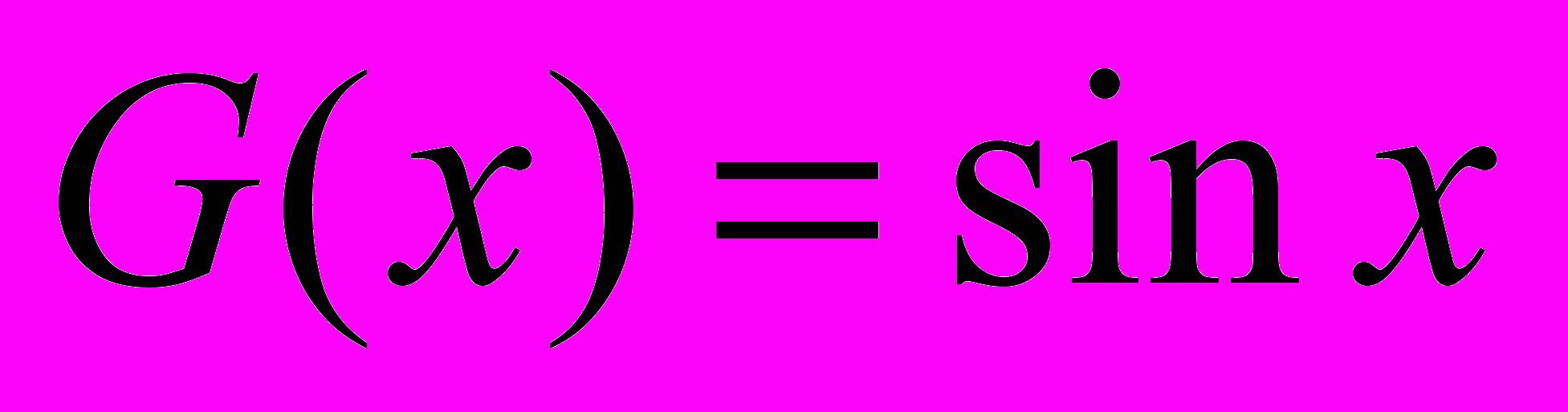и ограничена на 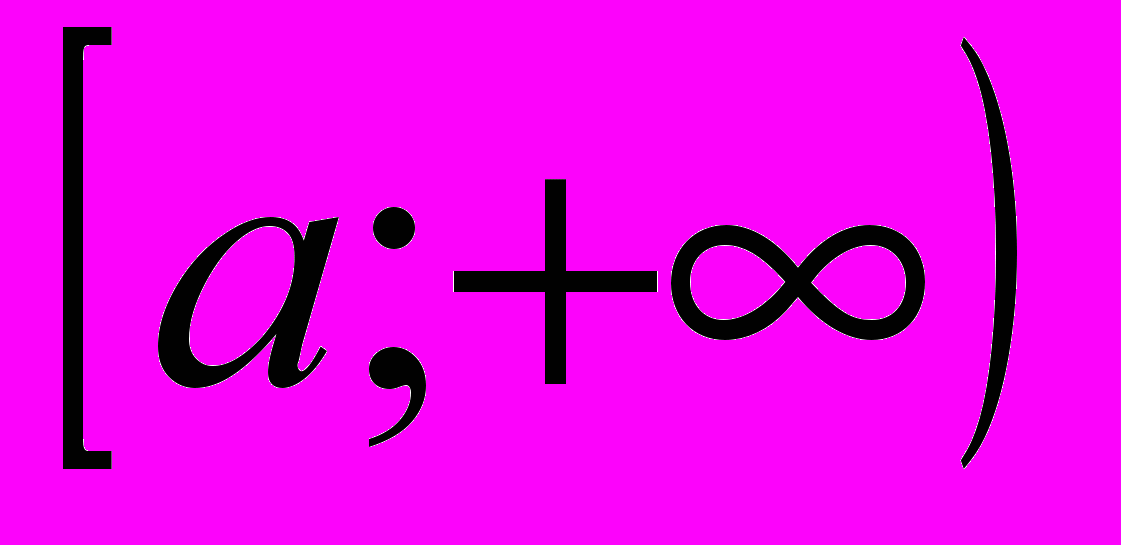и по признаку Абеля интеграл сходится .

ВОПРОСЫ К ЭКЗАМЕНУ.

1) Понятие несобственного интеграла на бесконечном промежутке. Критерий Коши сходимости интеграла.

2) Теоремы сравнения для несобственных интегралов на неограниченном промежутке.

3) Понятие абсолютной сходимости несобственных интегралов. Теорема о сходимости

абсолютно сходящихся интегралов.

4) Критерий Абеля- Дирихле сходимости несобственных интегралов.