«Неопределенные и определенные интегралы»
| Вид материала | Документы |
- Неопределенные местоимения (indefinite pronouns), 225.16kb.
- Неопределенные местоимения (indefinite pronouns), 67.39kb.
- Программа обсуждена на заседании кафедры Математики фнти, 28.33kb.
- «Алгоритмизация и решение физических задач на эвм», 391.8kb.
- Р. Бендлер и Д. Гриндер, 2635.29kb.
- Правила и решения 5 4 3 2 1 Внимательно анализирует ответ, полученный в ходе решения, 127.87kb.
- Местоимение (The Pronoun), 187.47kb.
- Лекция 22 Несобственные интегралы на неограниченном промежутке, 30.33kb.
- Вводный курс нлп тренинга. (Из лягушек в принцы) январь 1978, 2576.27kb.
- Риск-менеджмент Лекция Троицк, 211.92kb.
РГР № 2
«Неопределенные и определенные интегралы»
Теоретические вопросы:
- Неопределенный интеграл, его основные свойства.
- Понятие первообразной функции. Теоремы о первообразных.
- Понятие определенного интеграла, его основные свойства и геометрический смысл.
- Замена переменной в неопределенном и определенном интегралах.
- Интегрирование по частям в неопределенном и определенном интегралах.
- Интегрирование рациональных функций.
- Интегрирование выражений, содержащих тригонометрические функции.
- Интегрирование иррациональных выражений.
- Вычисление площадей плоских фигур.
- Вычисление длины кривой, объемов тел вращения.
- Теорема о среднем, оценка определенного интеграла.
Теоретические упражнения:
- Доказать, что если
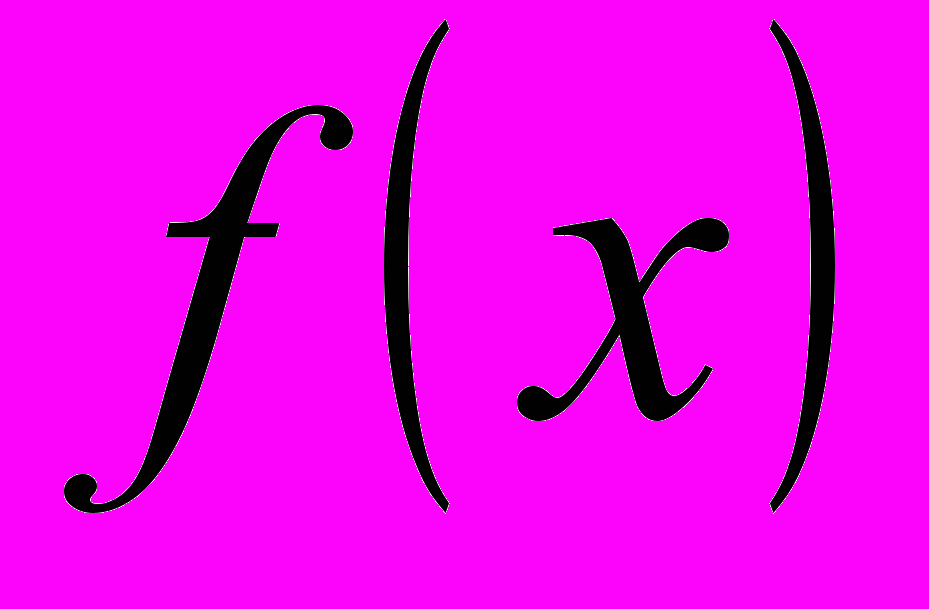 - четная функция, то
- четная функция, то
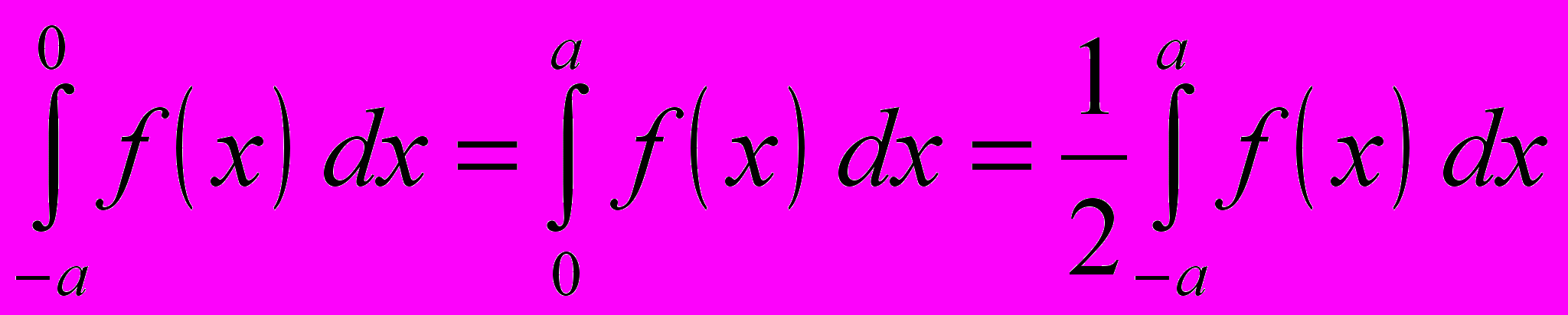 .
.- Доказать, что для нечетной функции справедливы равенства
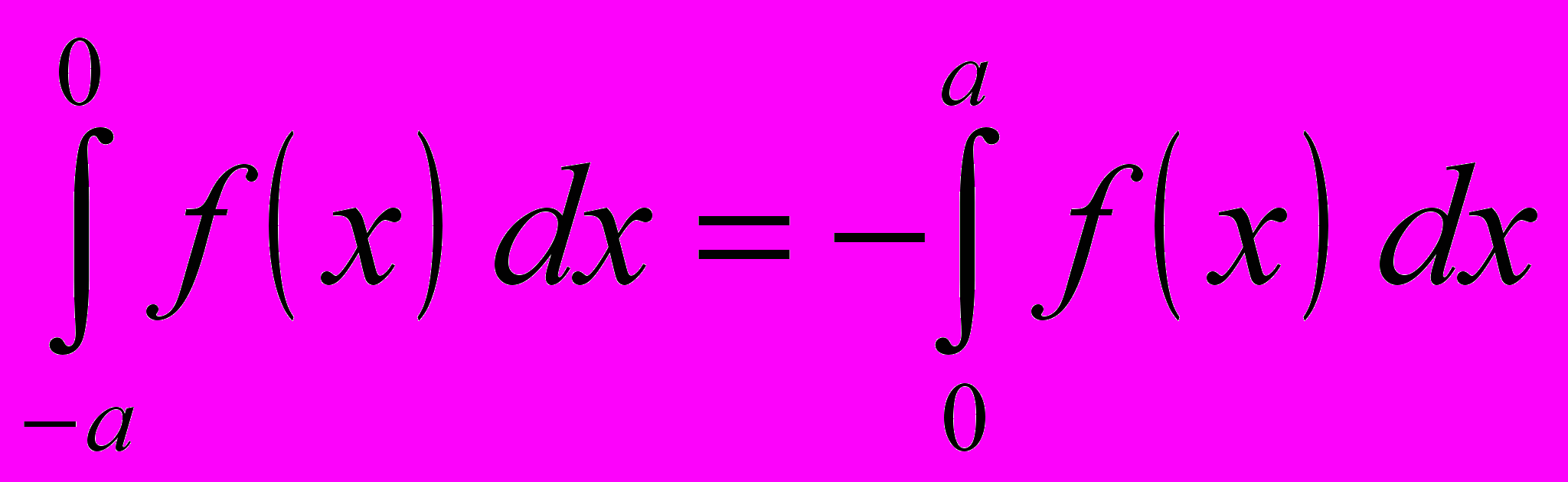 и
и 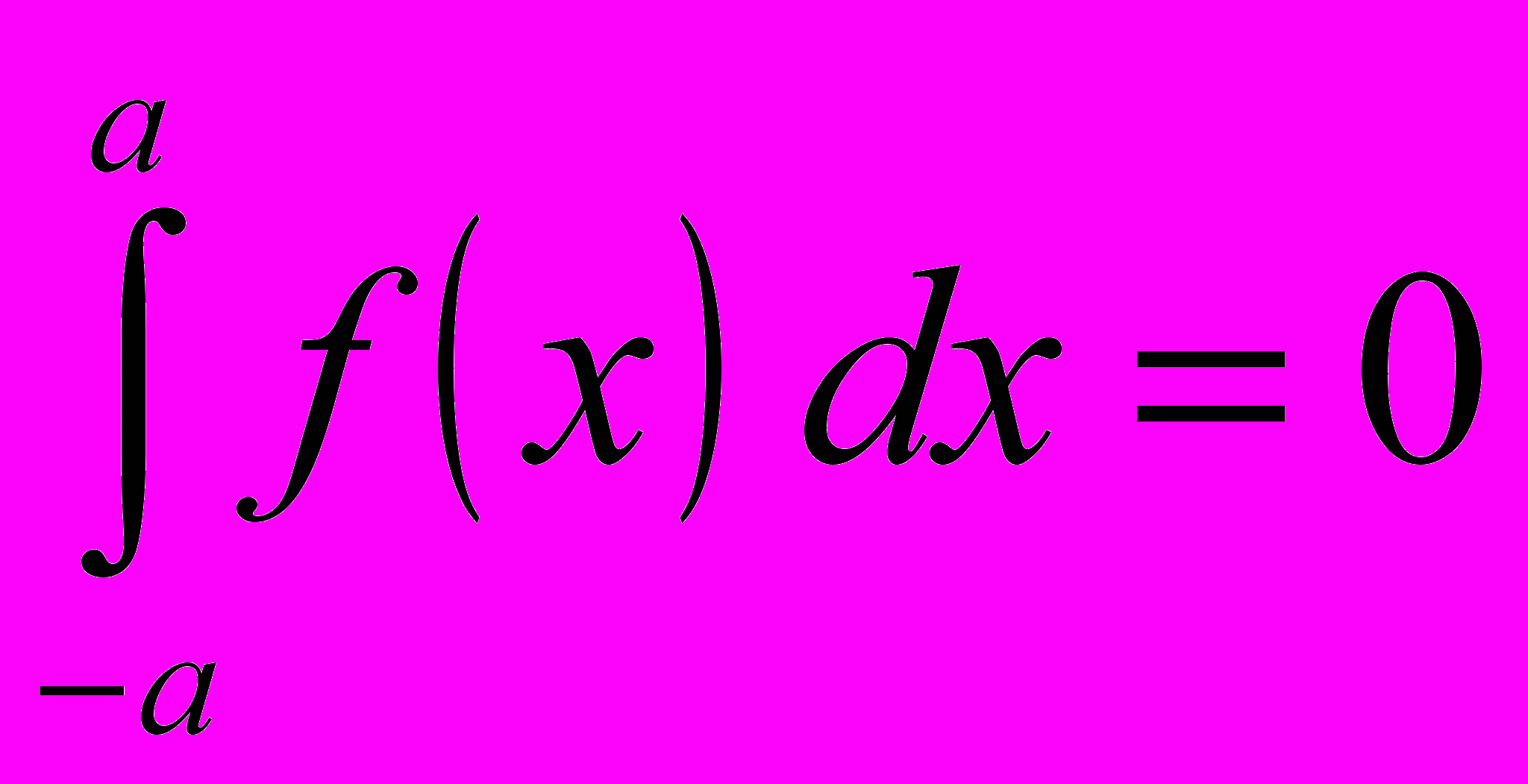 .
.- Какой из интегралов больше
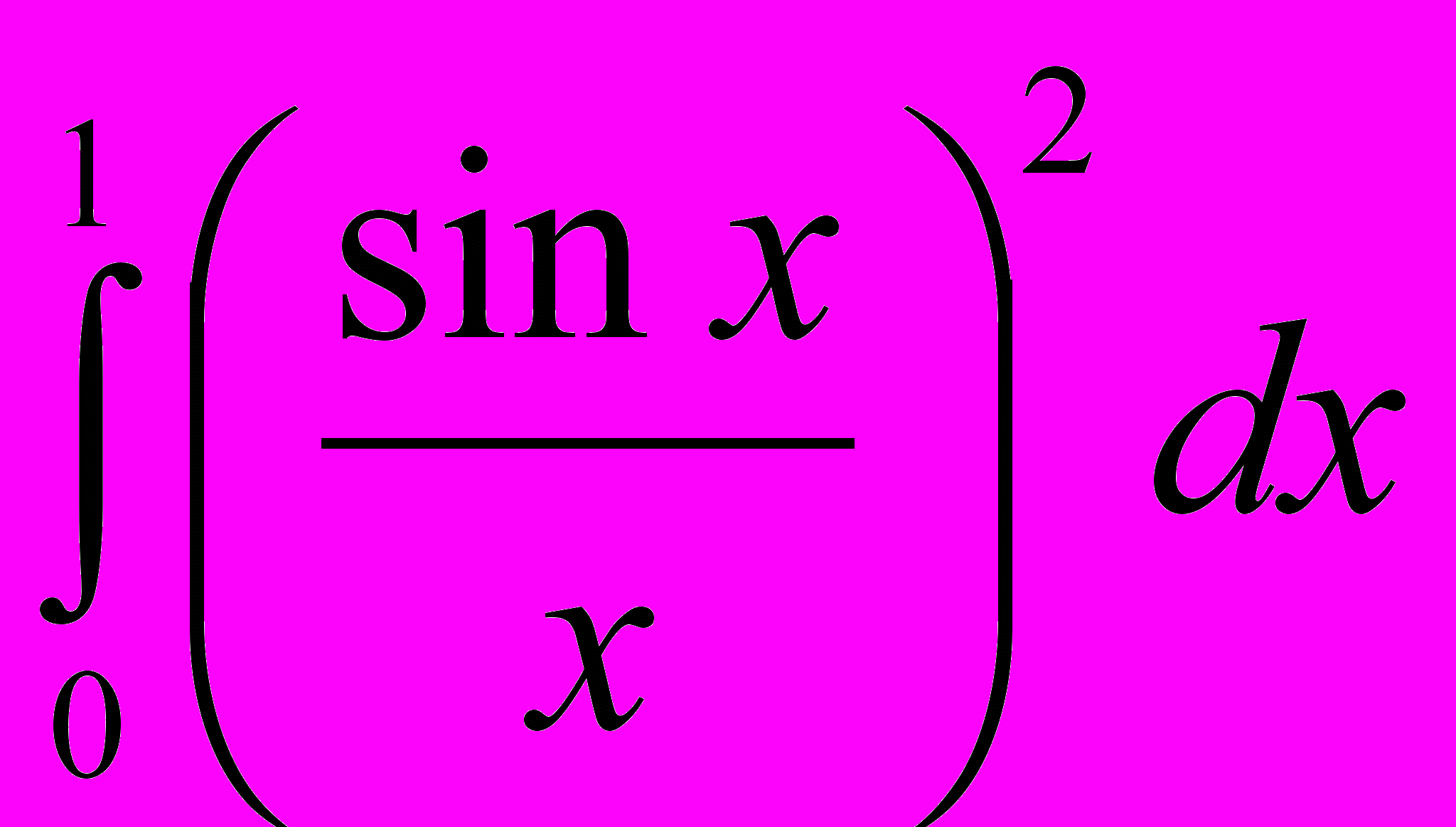 или
или 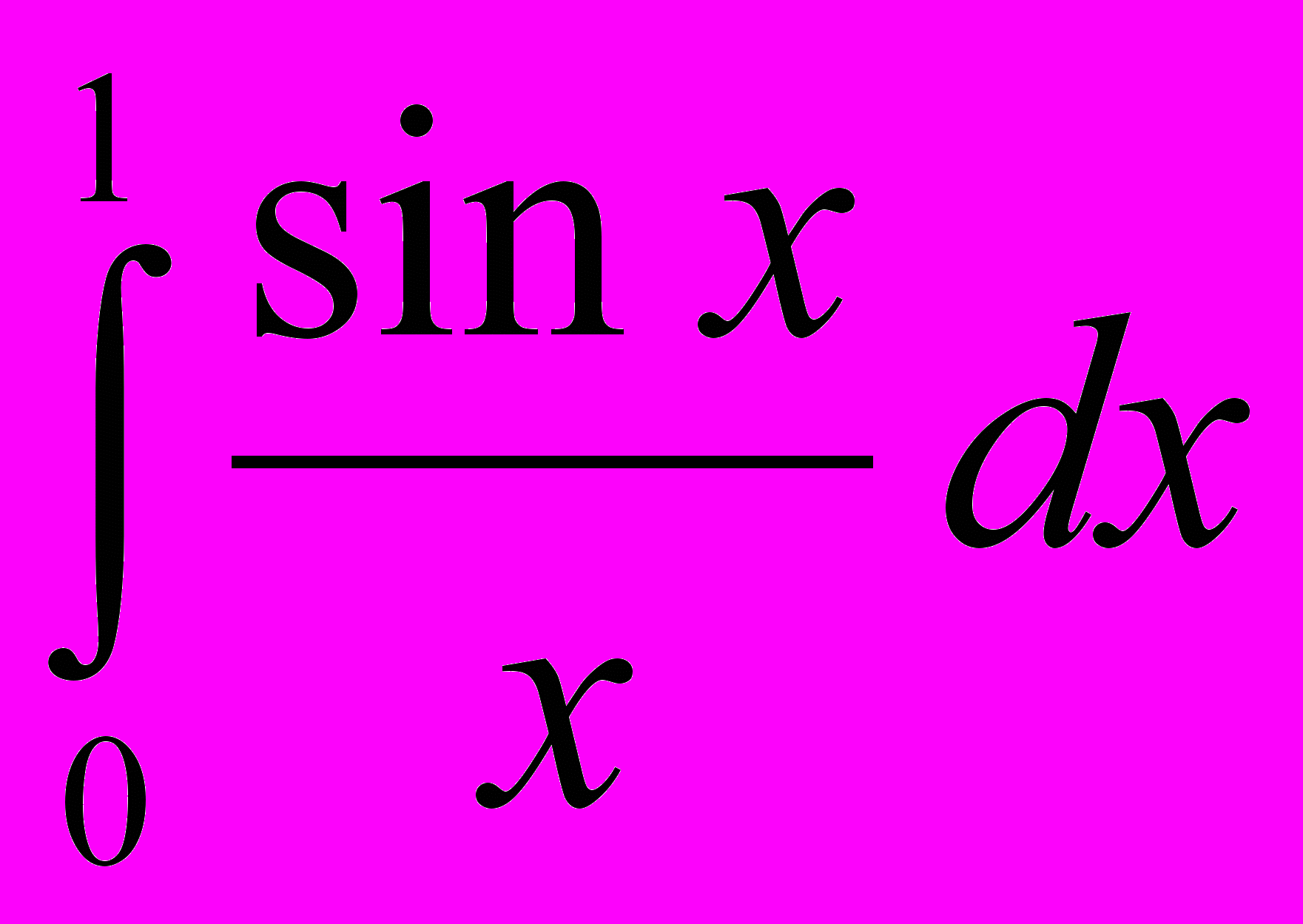 ?
?- При каких целых значениях
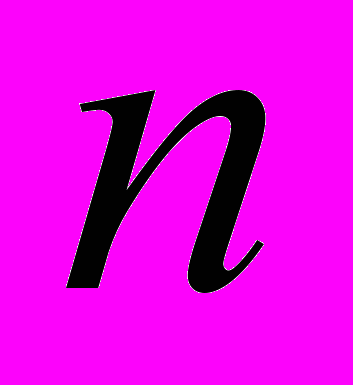 интеграл
интеграл 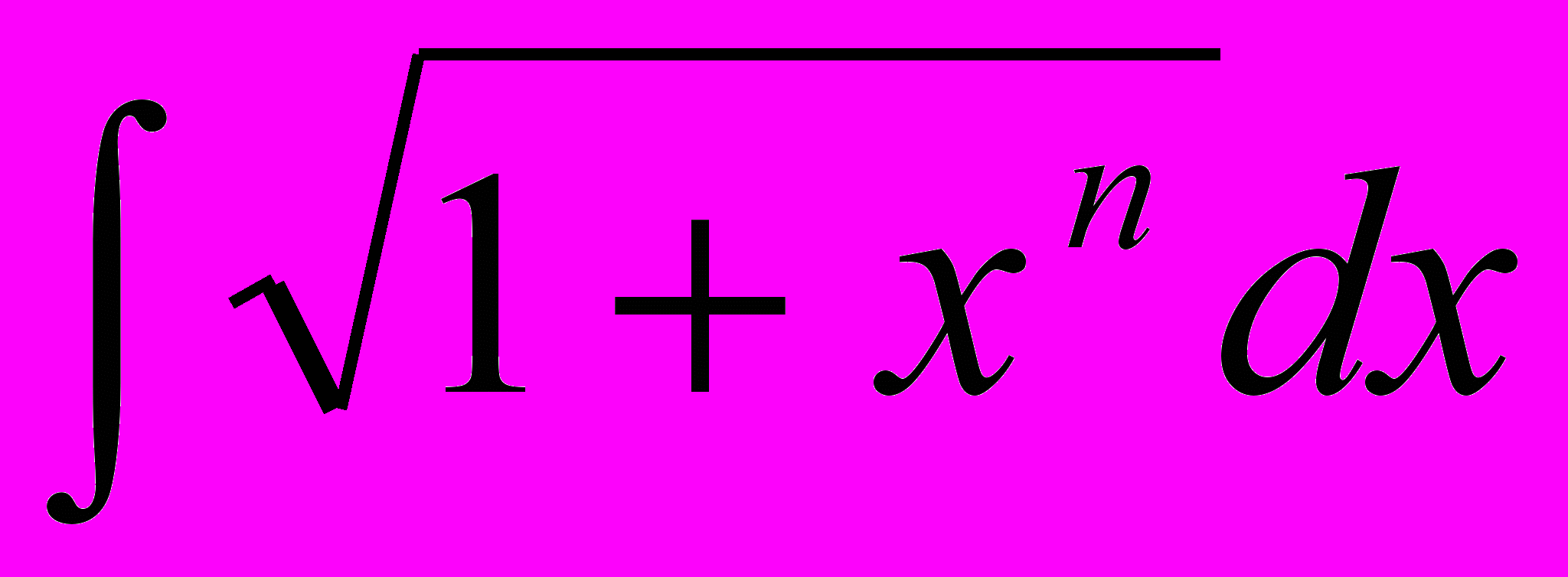 выражается в элементарных функциях?
выражается в элементарных функциях?
- Оценить интеграл
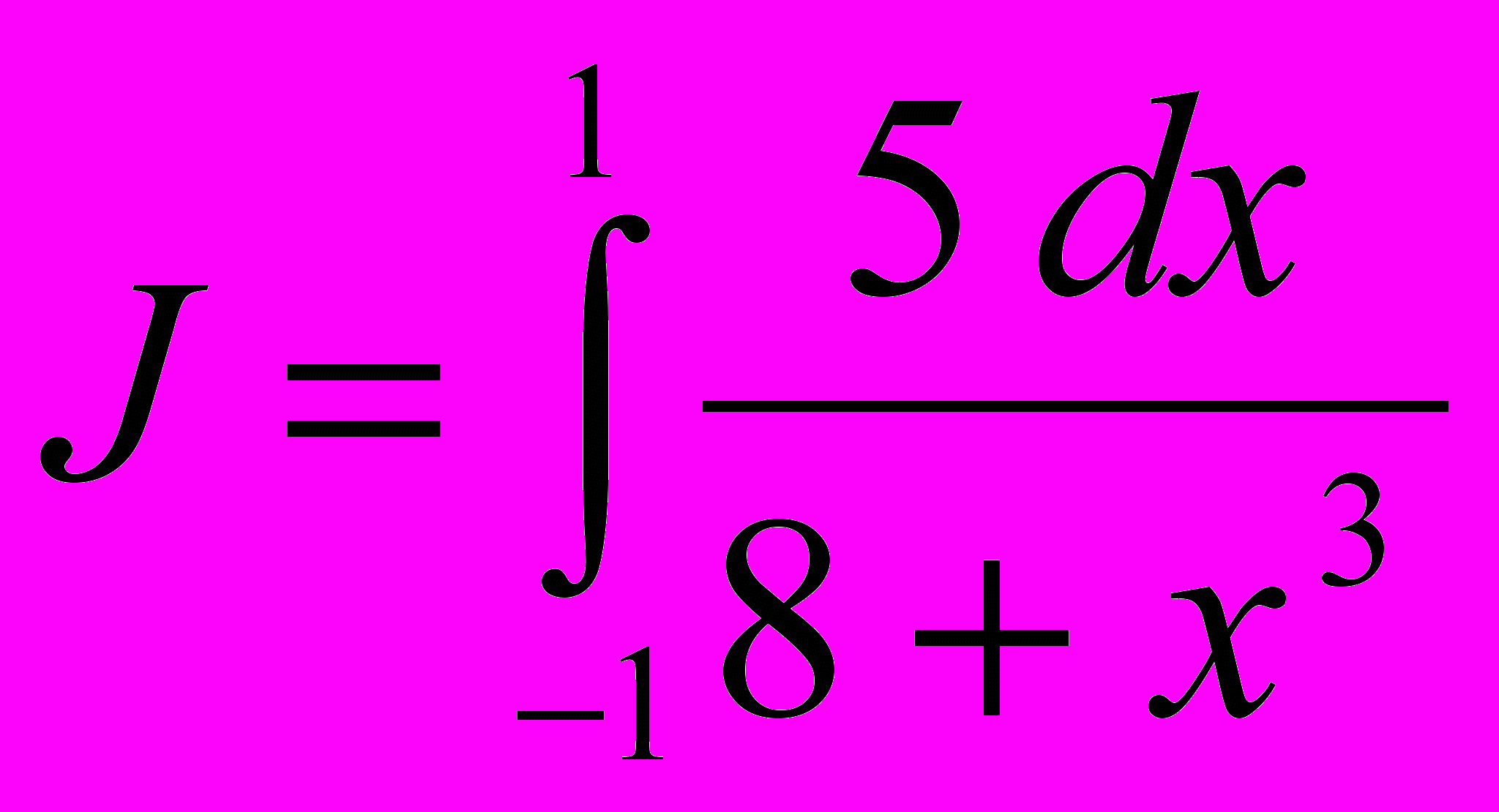 .
.
- Найти точки экстремума функции
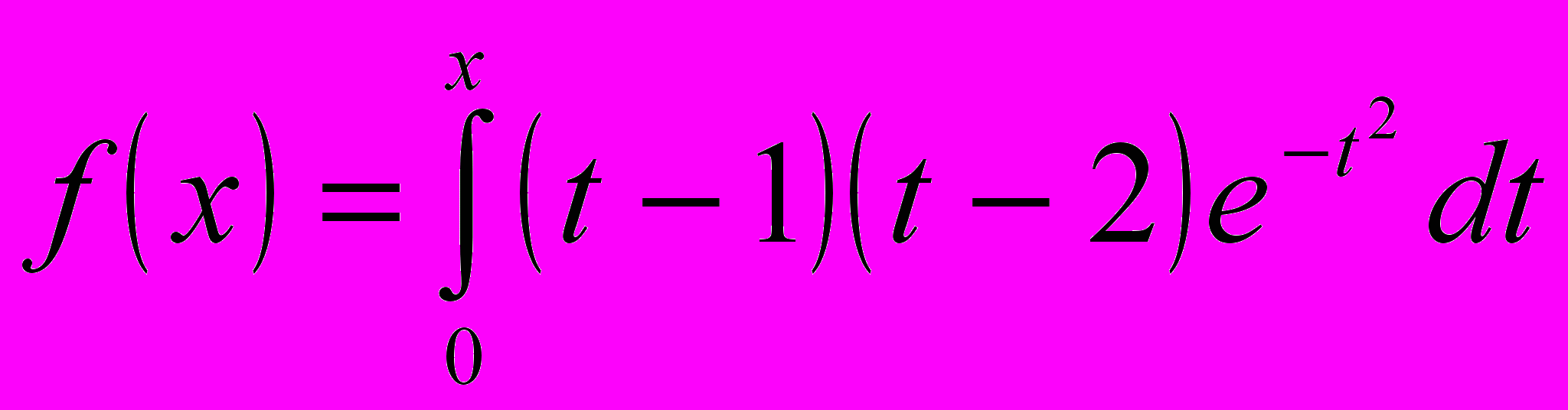 .
.
Задания:
- Найти интегралы:
а)
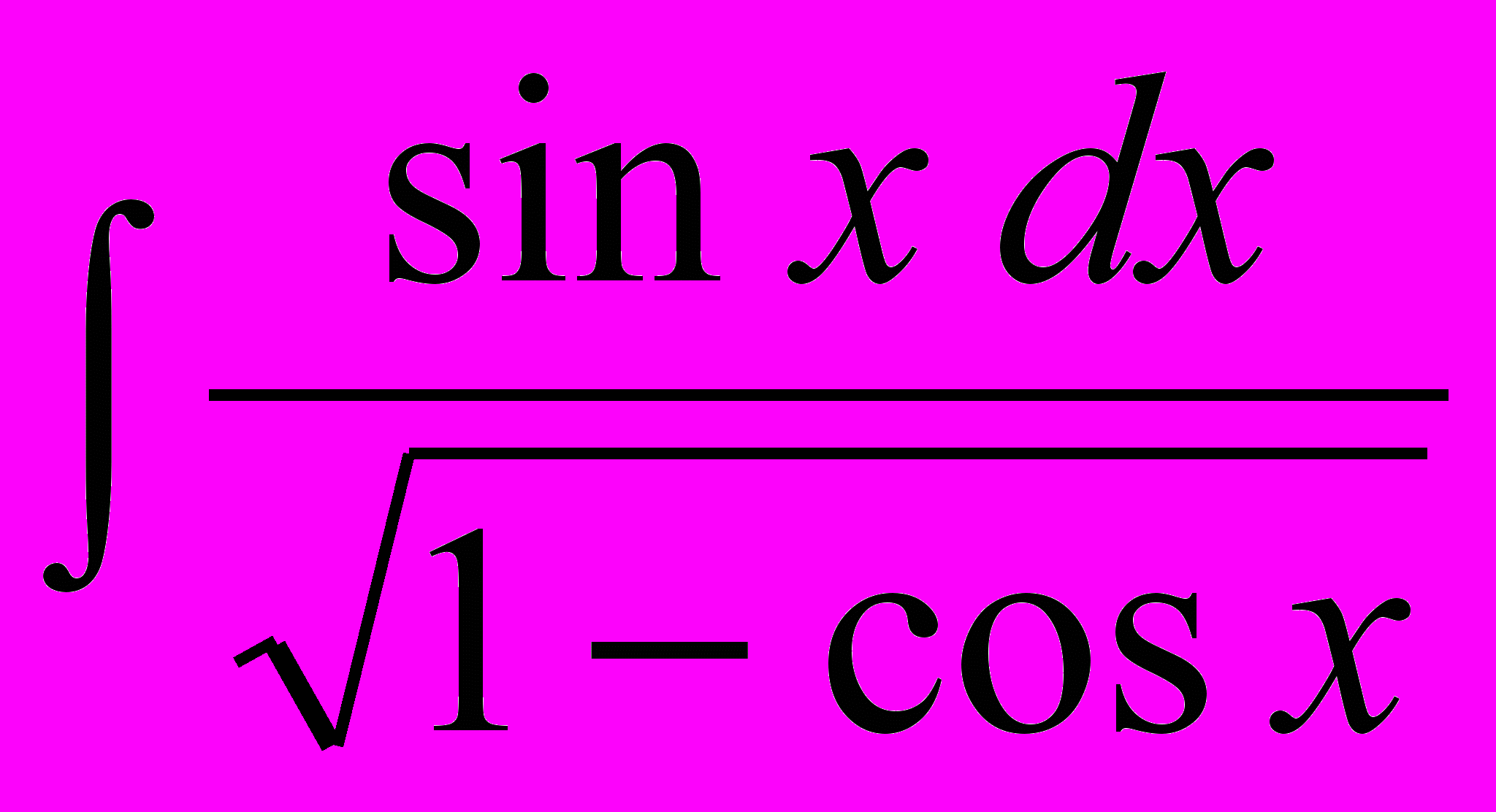 ; б)
; б) 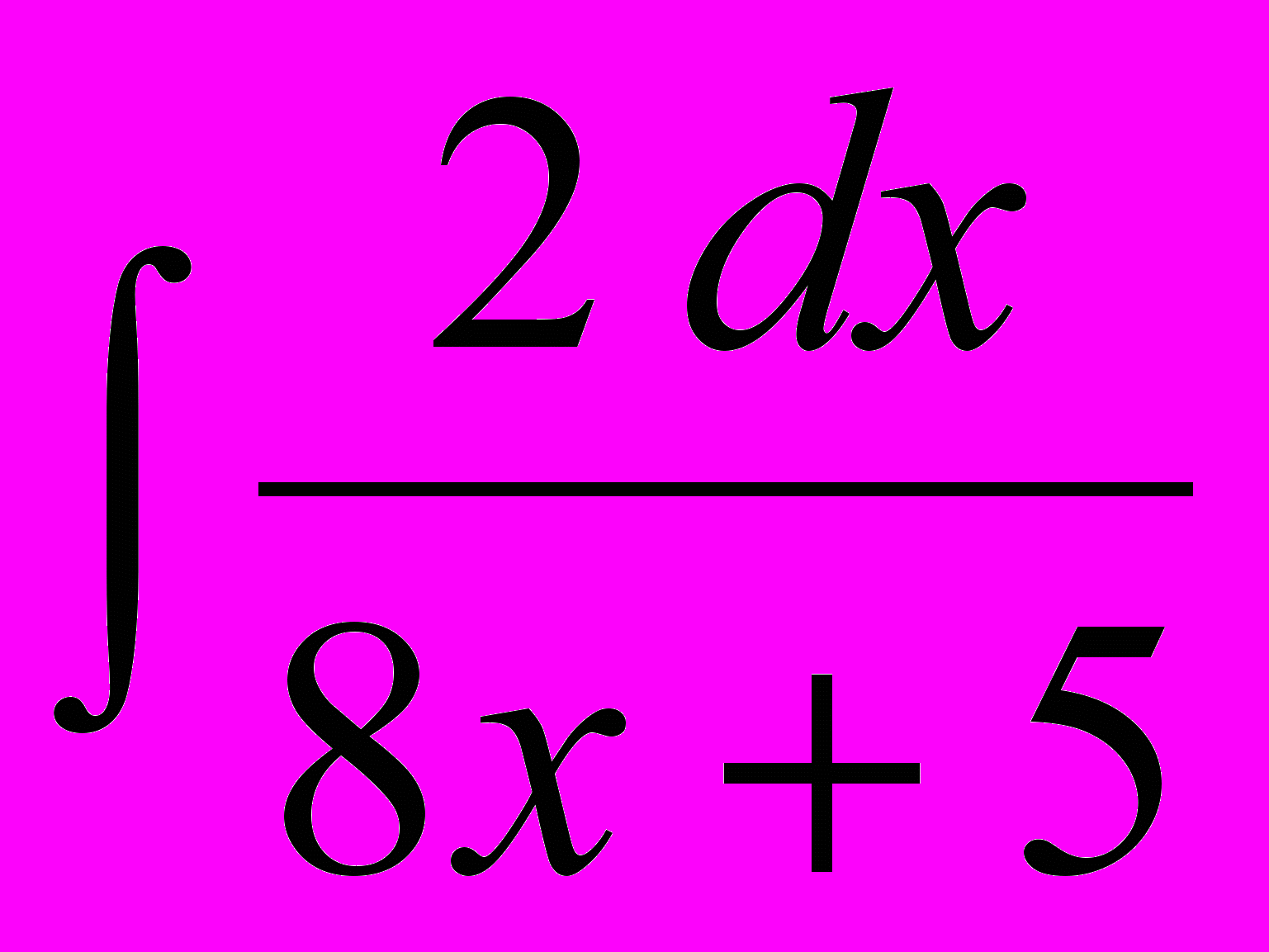 ; в)
; в) 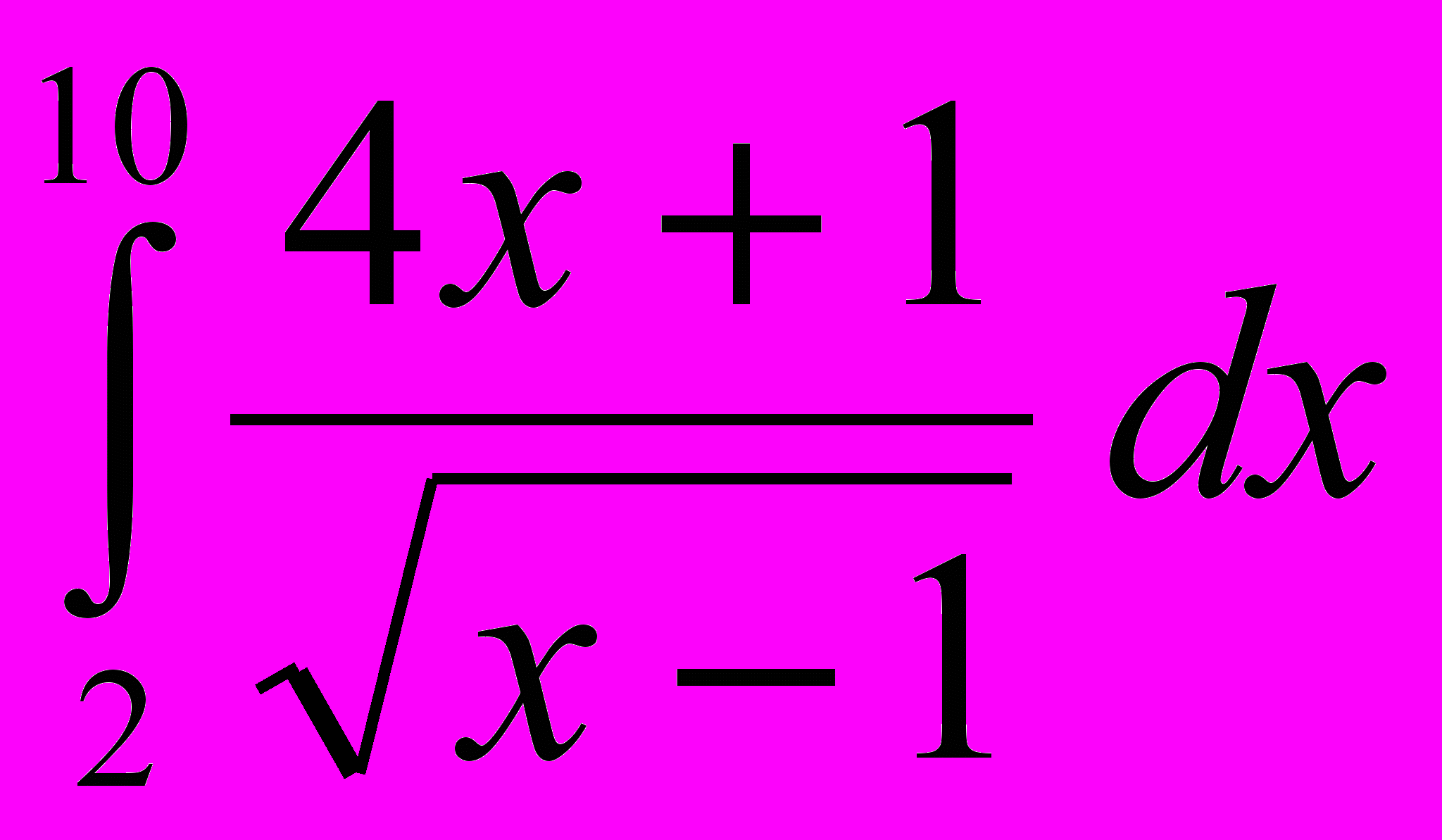 ;
;г)
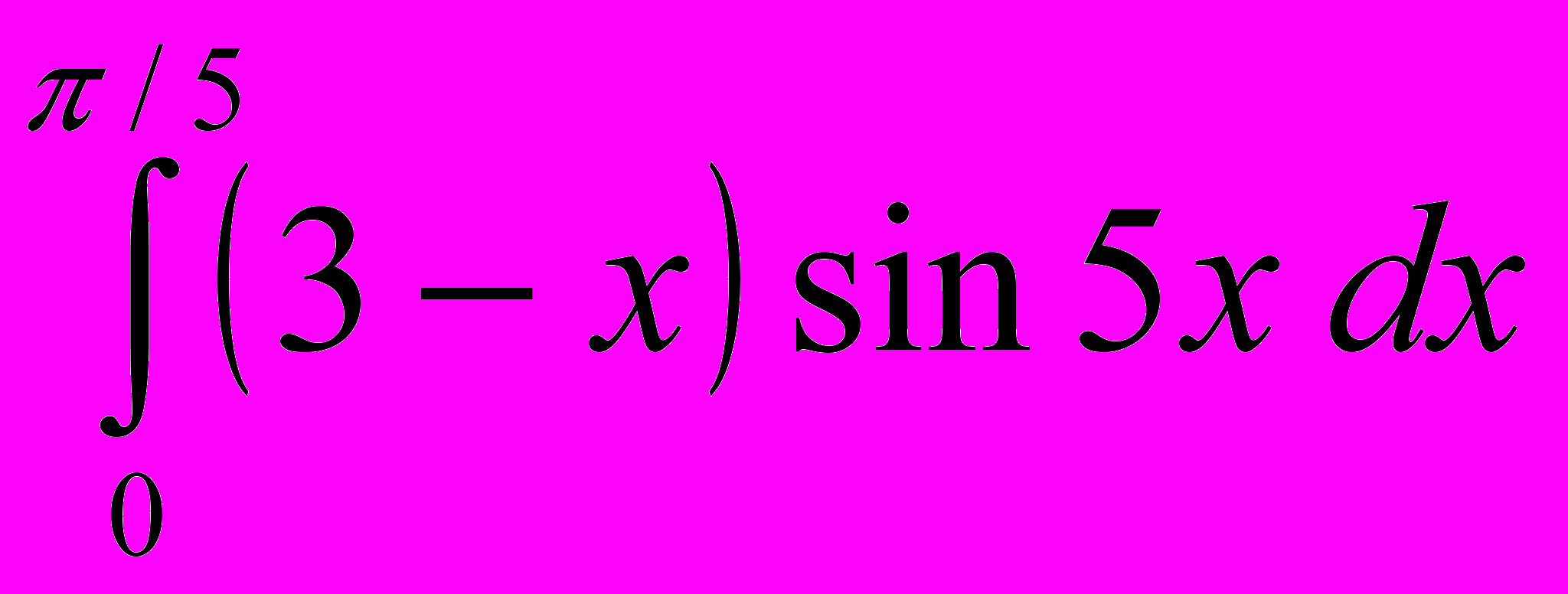 ; д)
; д) 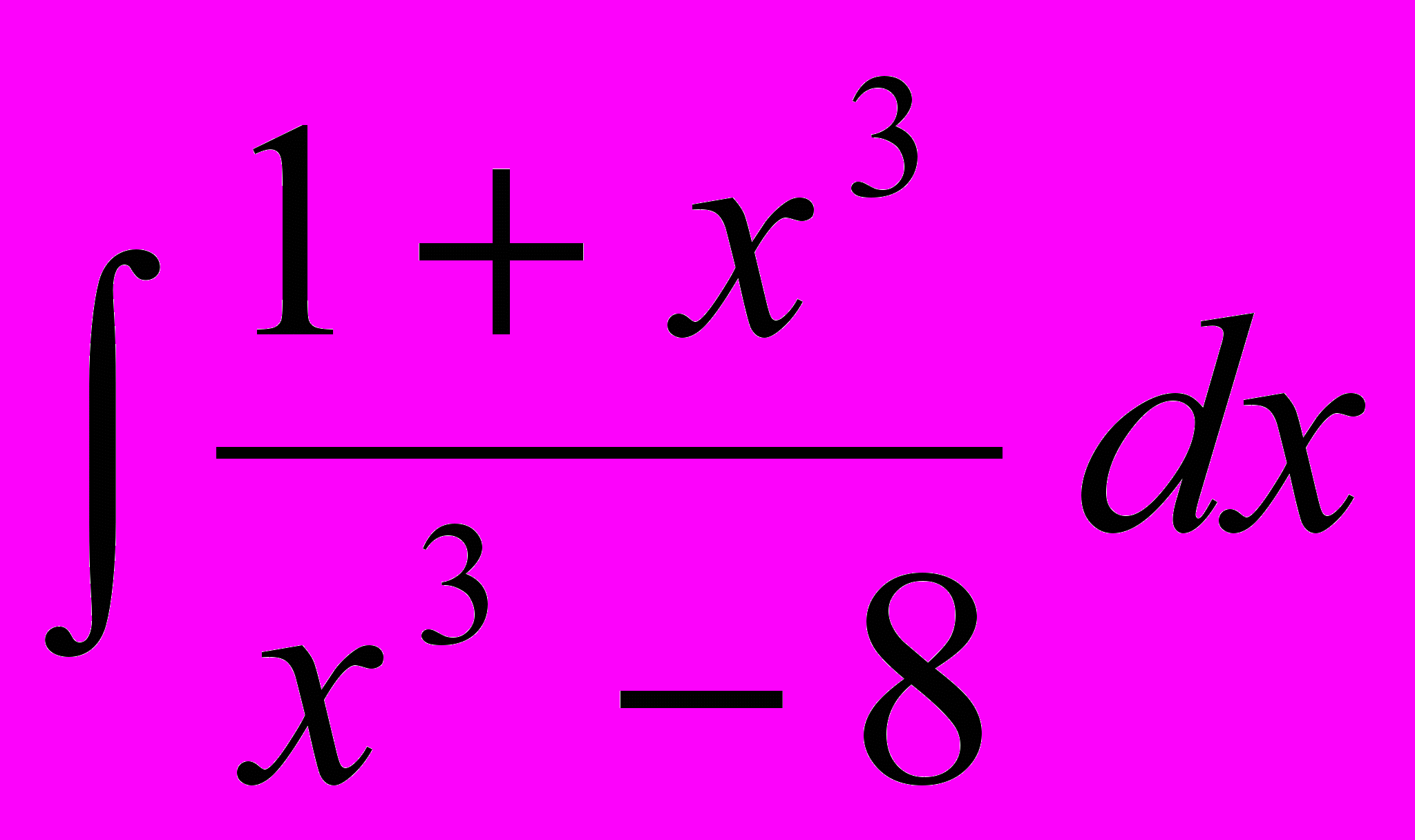 ; е)
; е)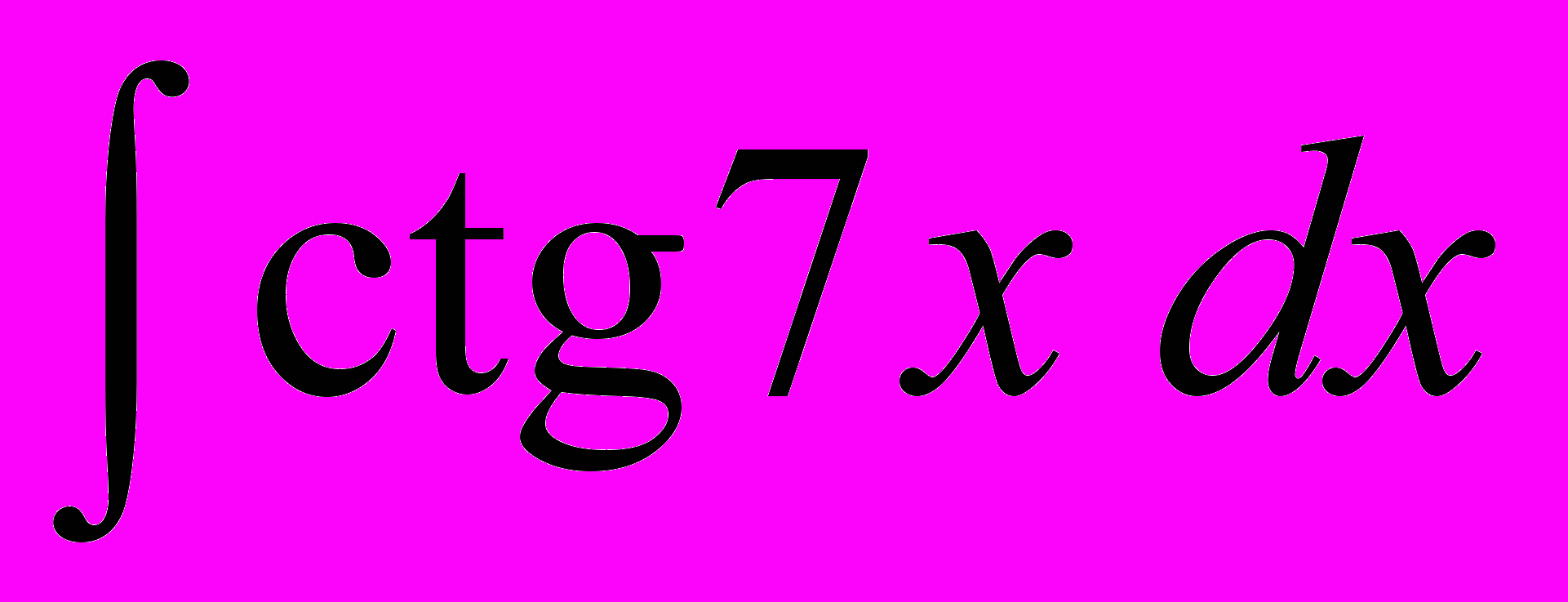 .
.- Вычислить объем тела, полученного вращением вокруг оси
 фигуры, ограниченной
фигуры, ограниченной 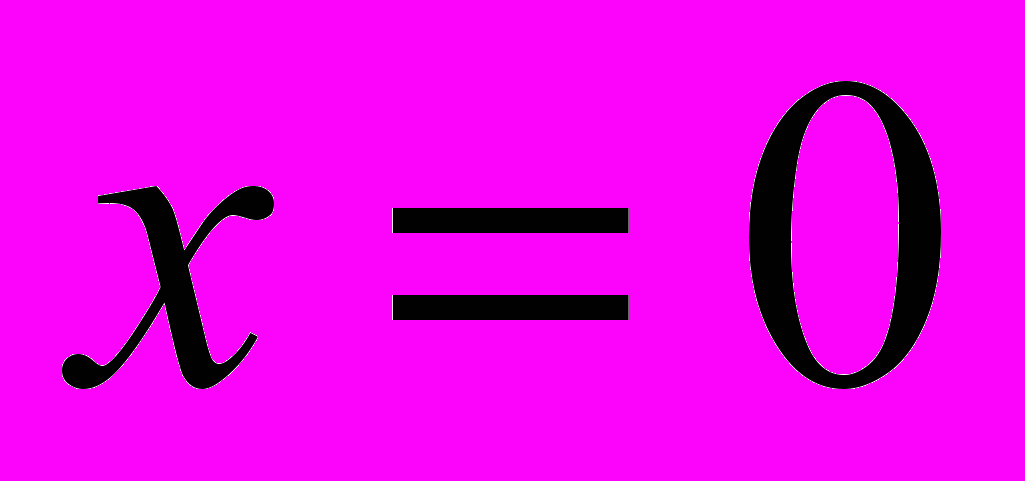 ,
, 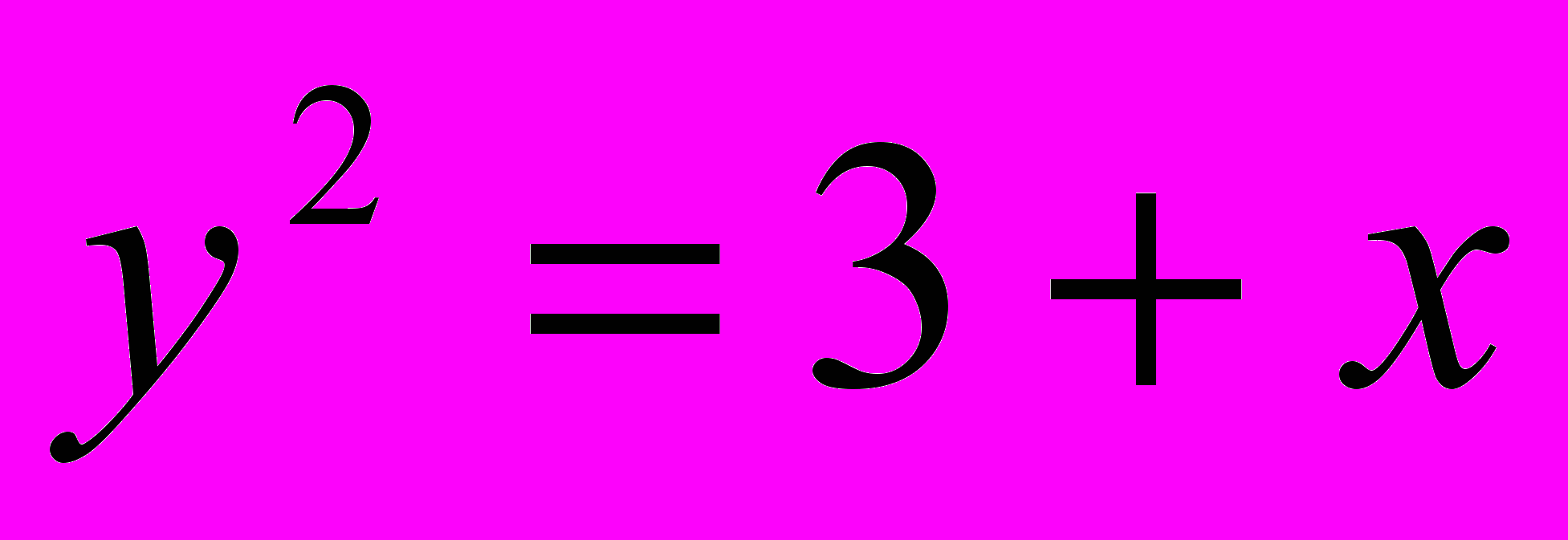 . Сделать чертеж.
. Сделать чертеж.
- Найти длину одной арки кривой
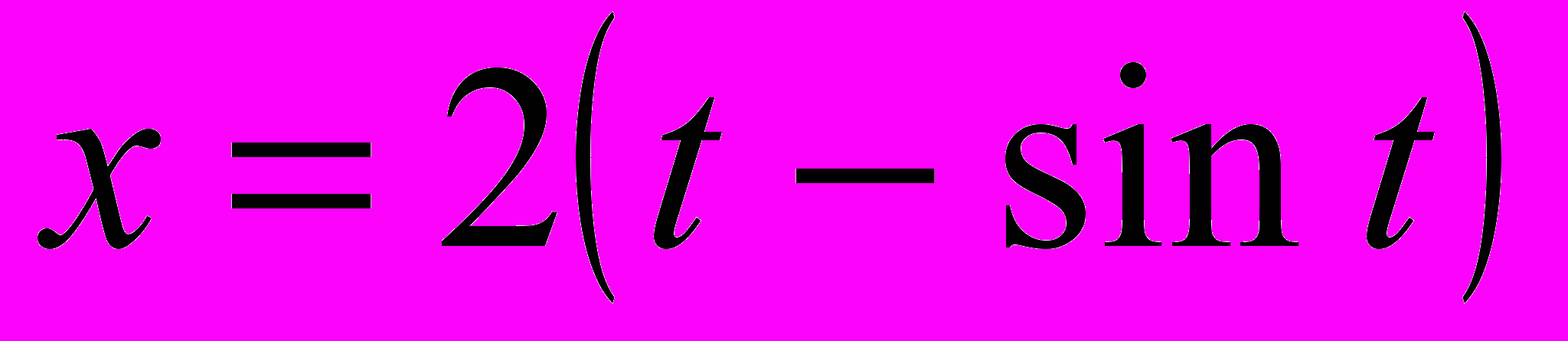 ,
, 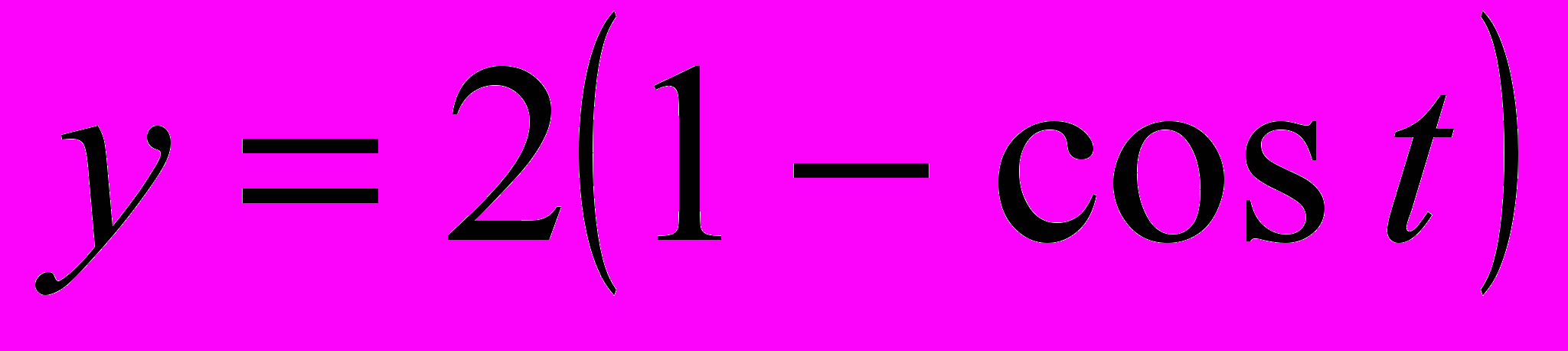 . Сделать чертеж.
. Сделать чертеж.
- Найти среднее значение функции
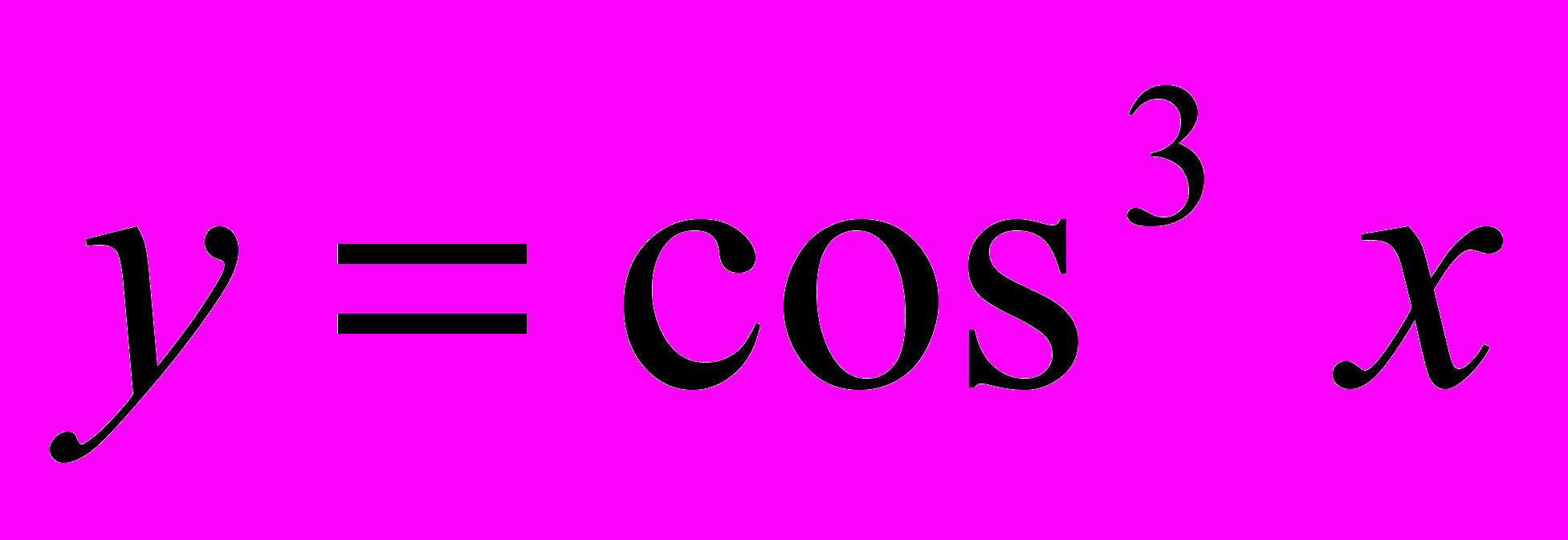 на
на 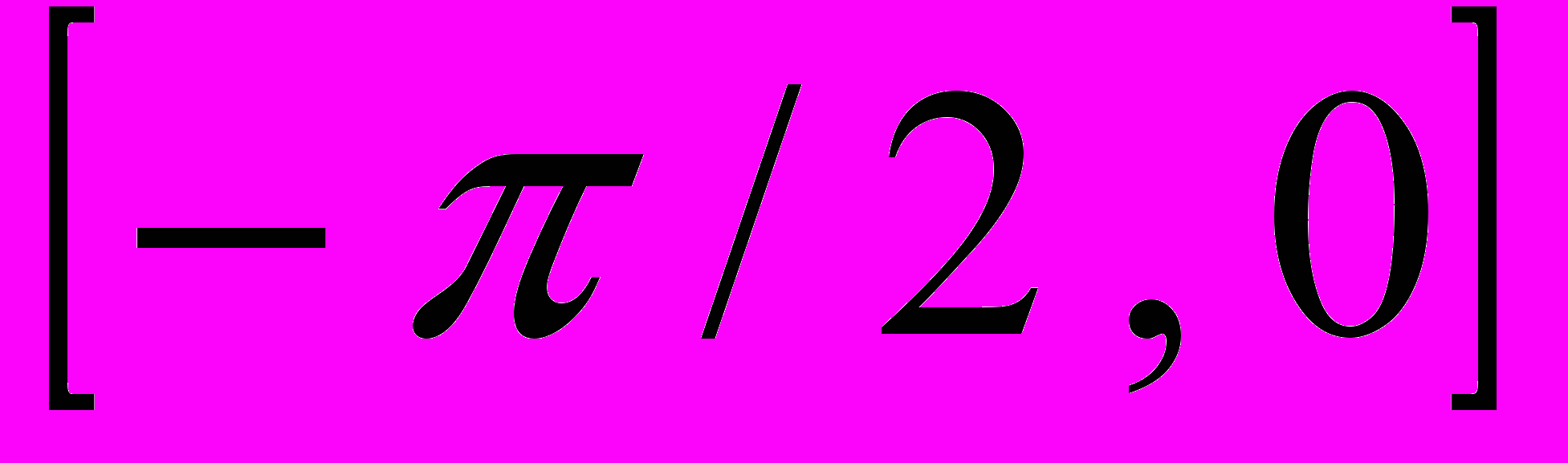 .
.
- Найти площадь фигуры, ограниченной кривой
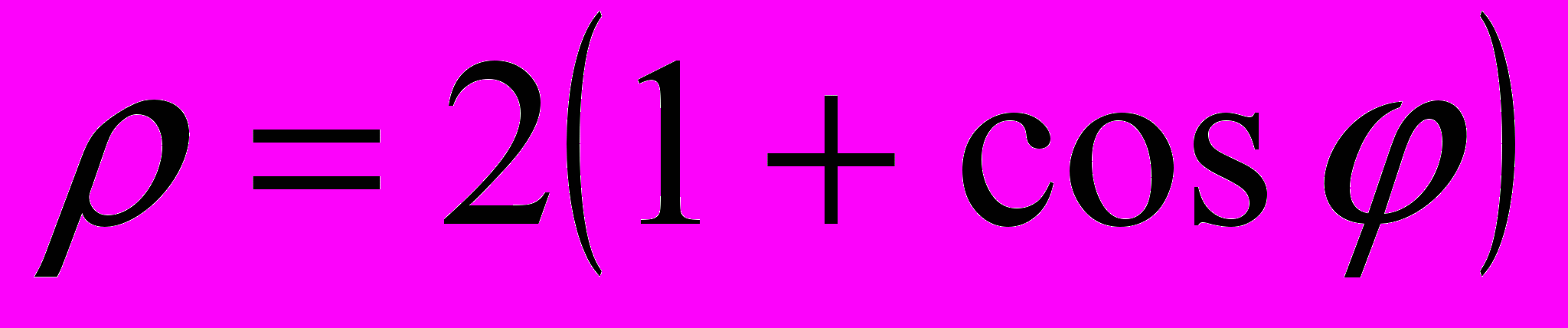 .
.
