Лекция 14. Неопределенный интеграл
| Вид материала | Лекция |
- Задачи, приводящие к понятию определенного интеграла. Определенный интеграл и его свойства., 79.79kb.
- Интегральное исчисление неопределённый интеграл § Первообразная функция и неопределённый, 83.07kb.
- Лекция 12. Первообразная и неопределённый интеграл, 41.05kb.
- Домашнее задание №2 Неопределенный интеграл Составили дз №2 Хомутова Л. Ю., Мишина, 22.72kb.
- Правила дифференцирования, исследование функций; ( в 1 сем) основы интегрального исчисления:, 10.67kb.
- Неопределенный интеграл, 106.73kb.
- Первообразная. Неопределённый интеграл, 21.22kb.
- Анализа и теории функций календарныйпла нучебных занятий по дисциплине "Высшая математика", 54.18kb.
- Лекция 26. Неопределённый интеграл или свойства первообразных Вматематике как и в жизни, 140.32kb.
- Лекция 15. Определённый интеграл, 71.1kb.
Лекция 14. Неопределенный интеграл
П.1 Понятие неопределенного интеграла.
ОПР. Пусть задана функция
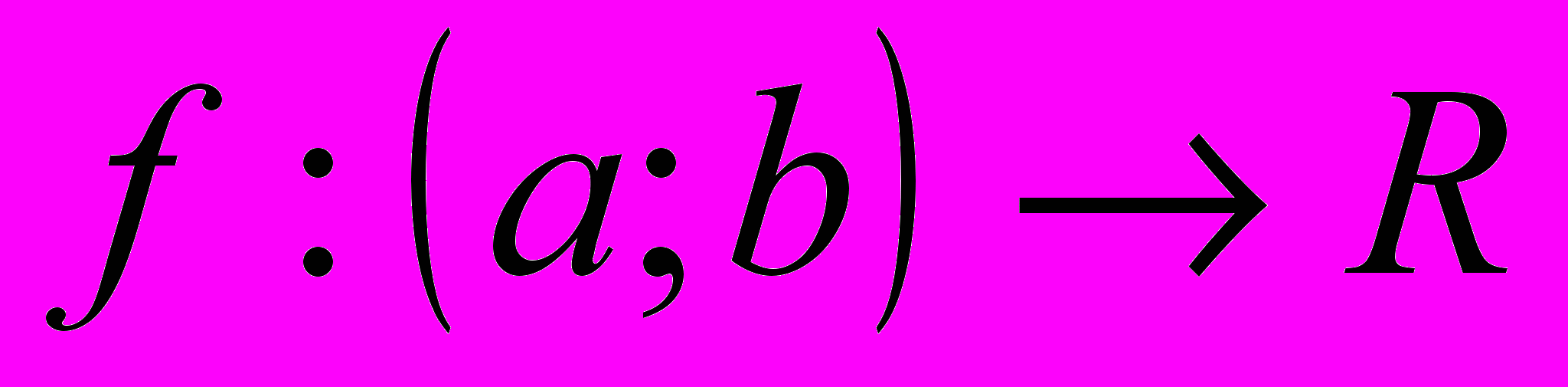 . Функция
. Функция 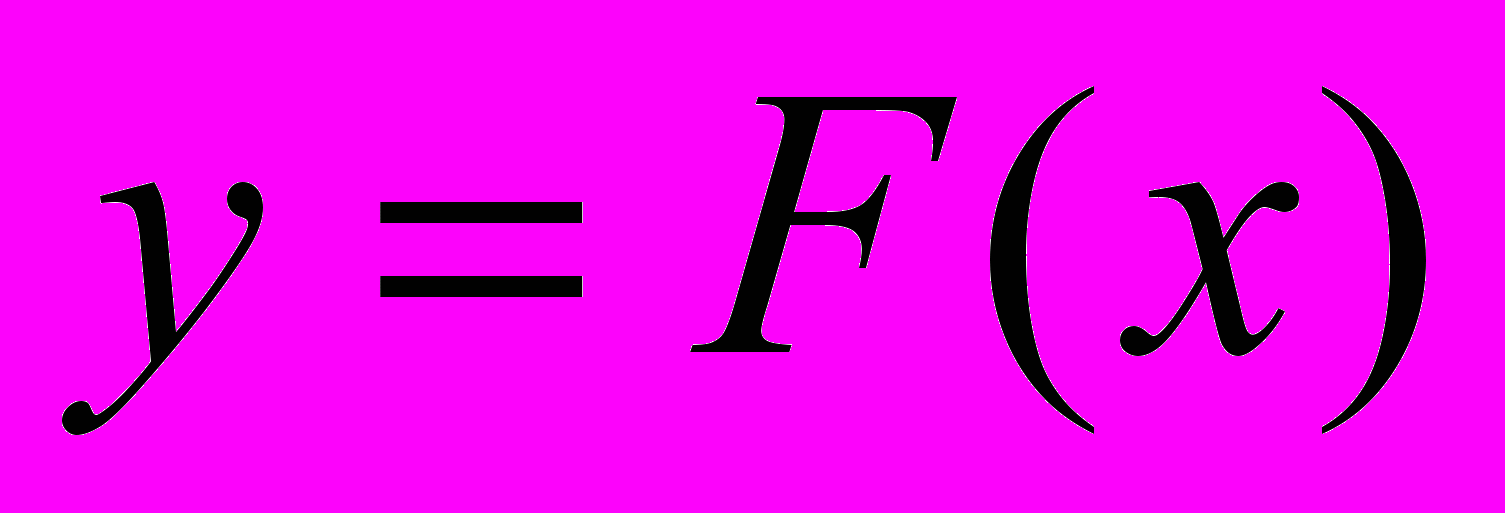 называется первообразной функции
называется первообразной функции 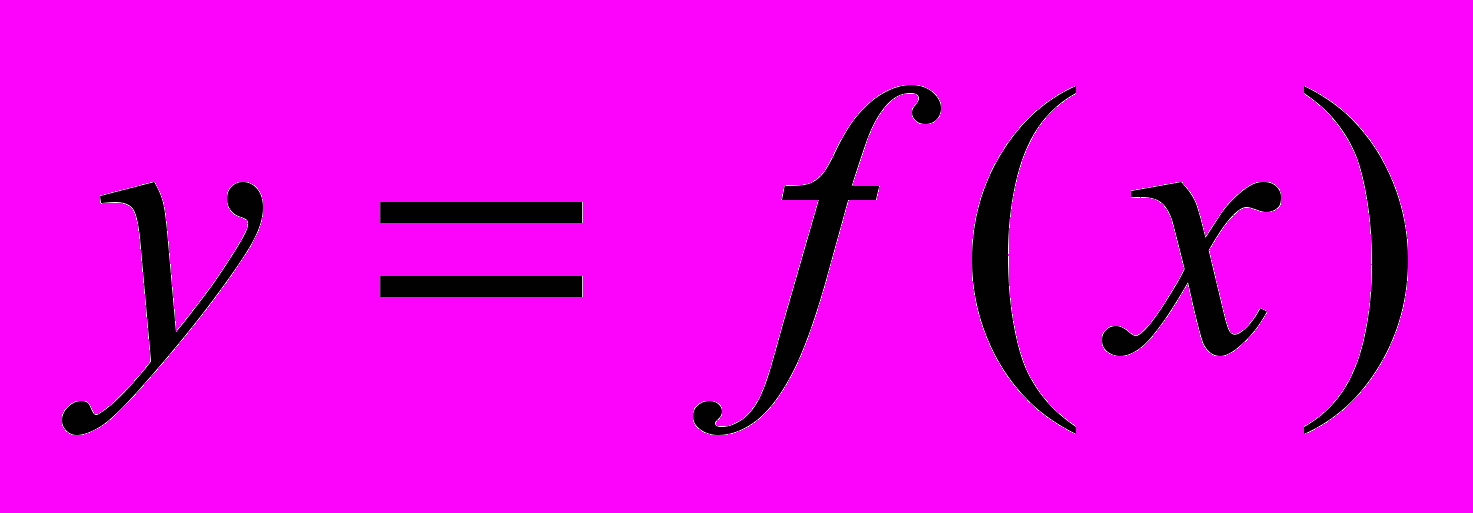 на
на 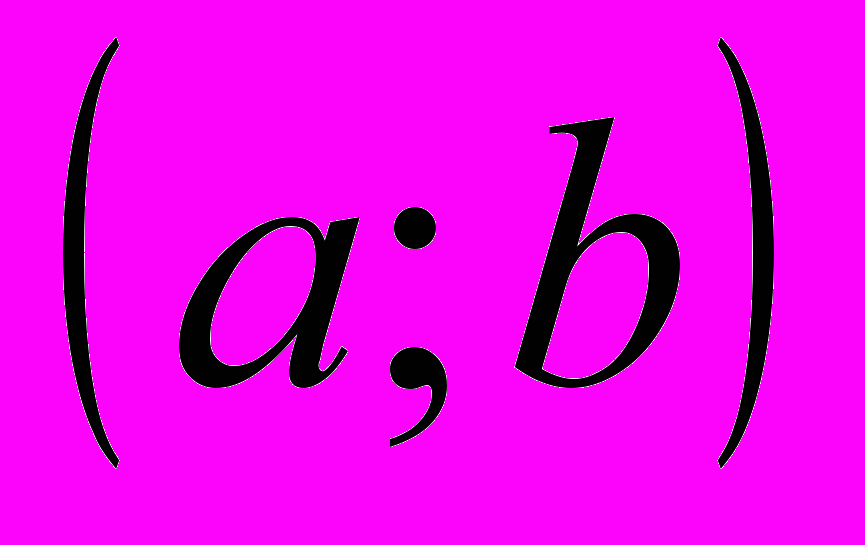 , если
, если 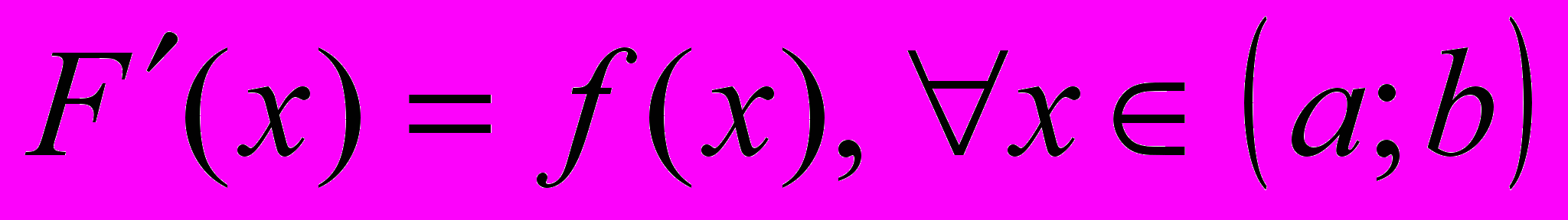 .
.У функции
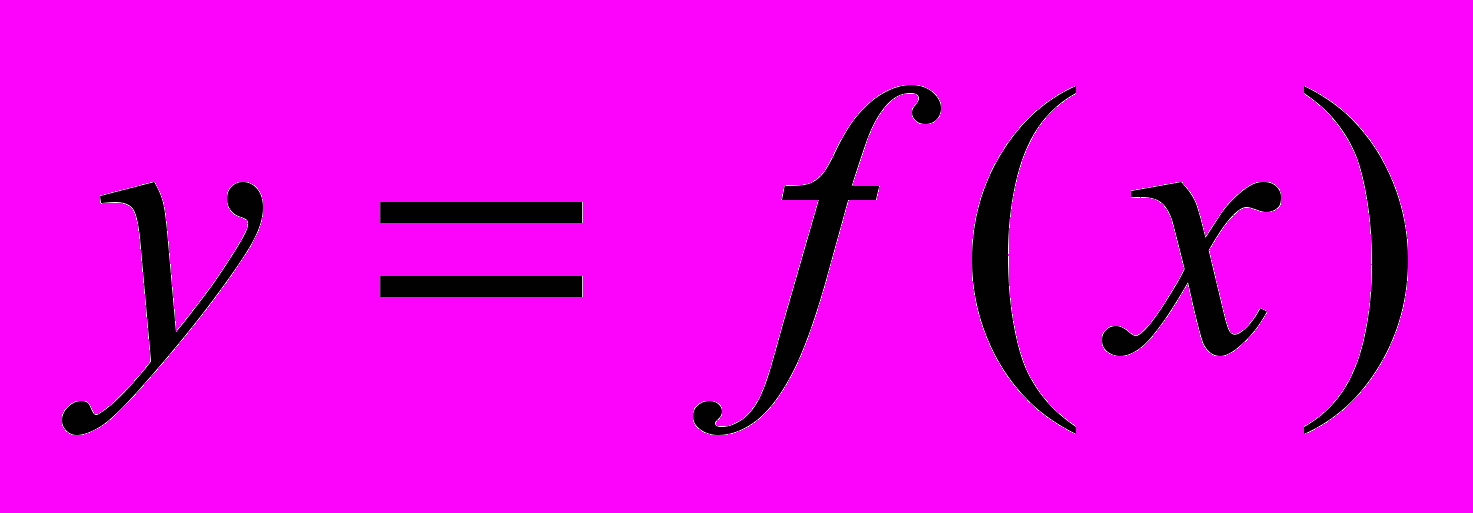 может существовать много первообразных . Например, функции
может существовать много первообразных . Например, функции 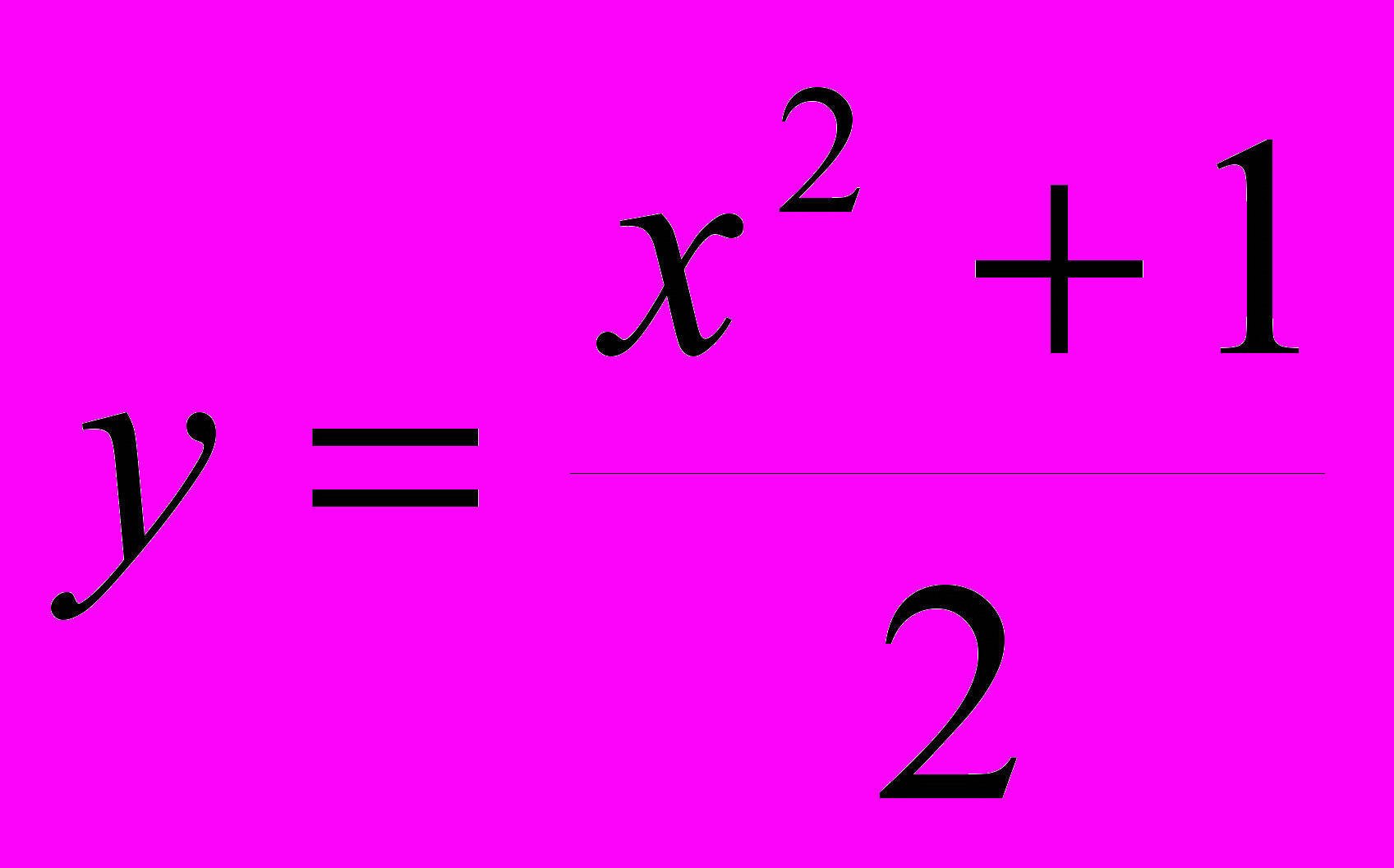 и
и 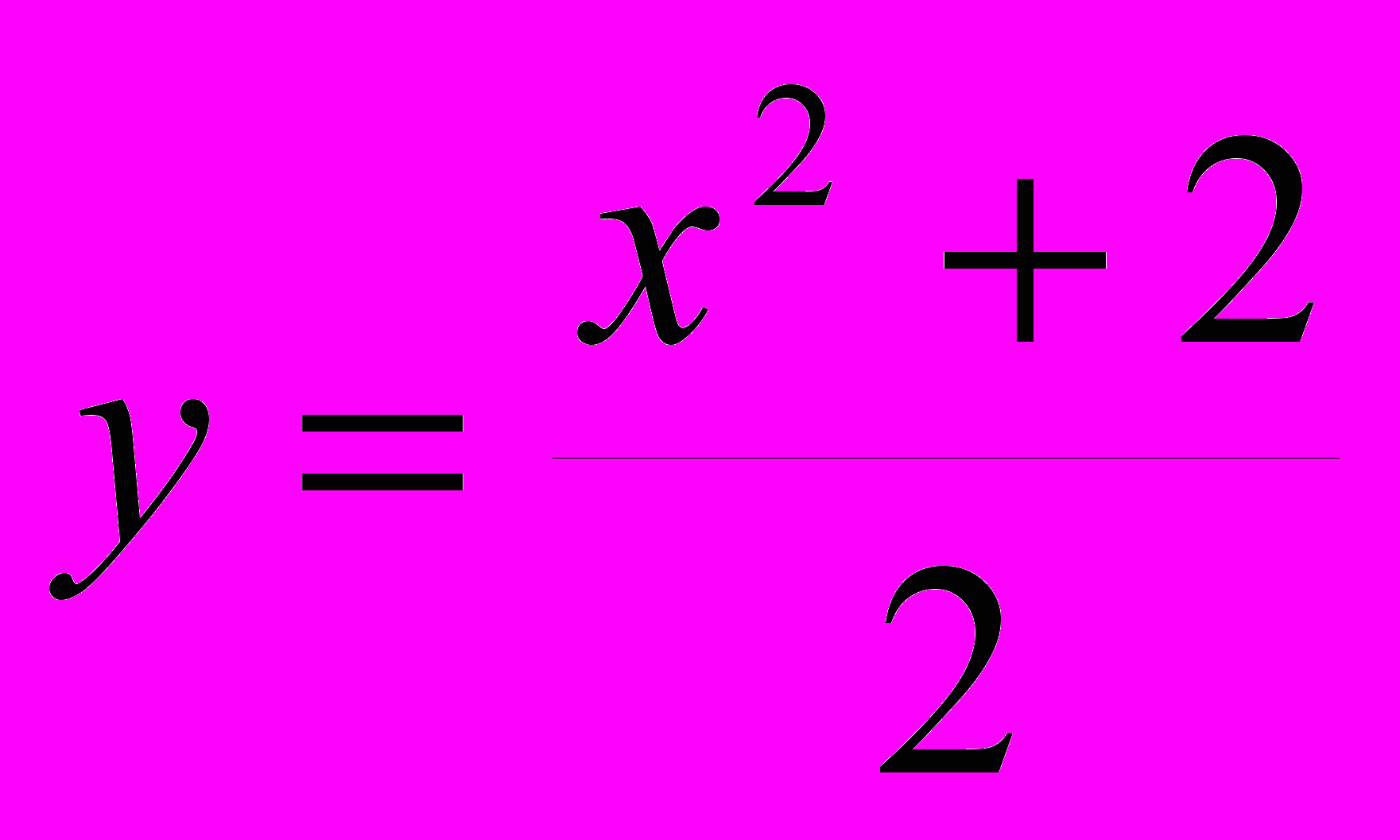 являются первообразными функции
являются первообразными функции 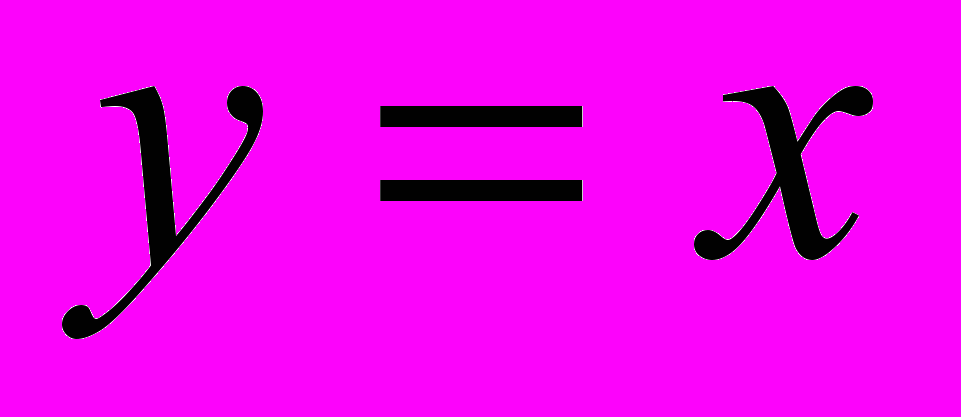 .
.ТЕОРЕМА 1 (о структуре множества первообразных)
Пусть
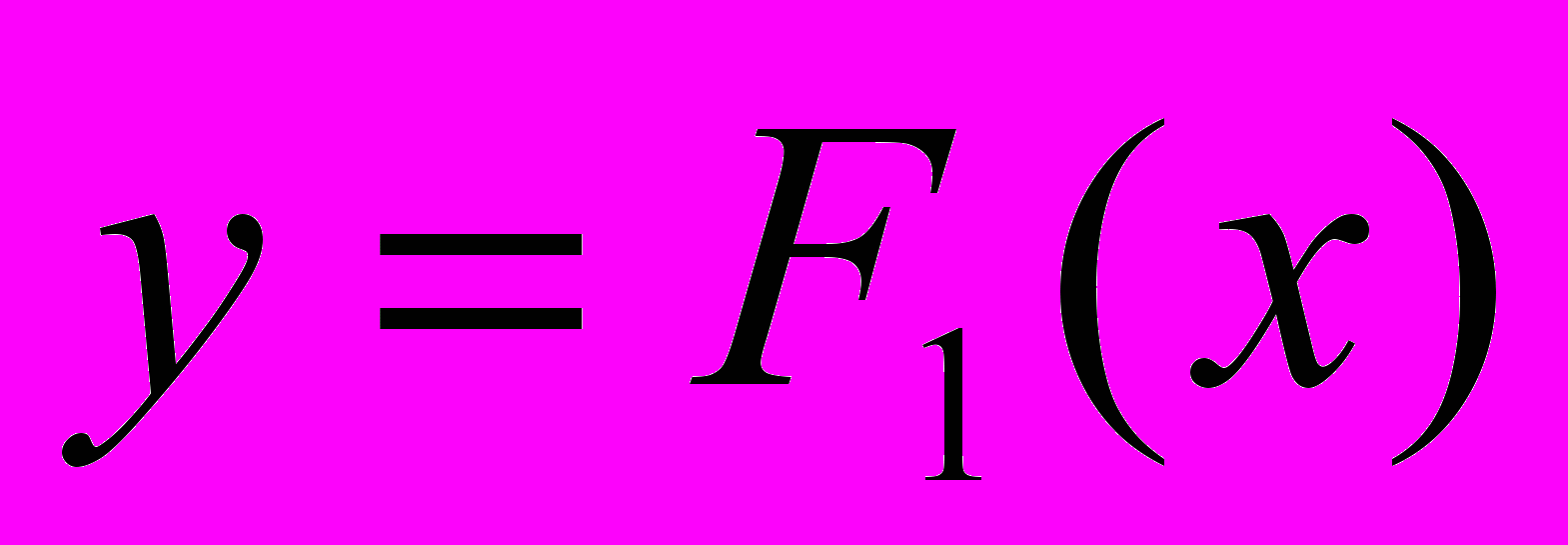 и
и 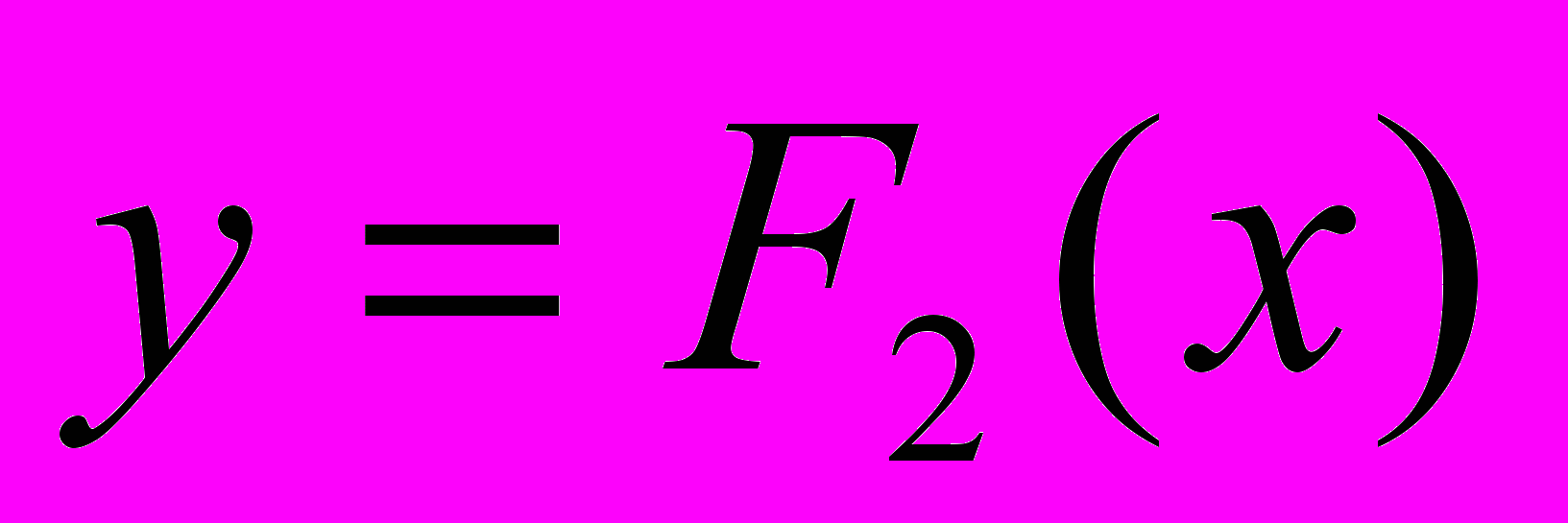 две первообразные функции
две первообразные функции 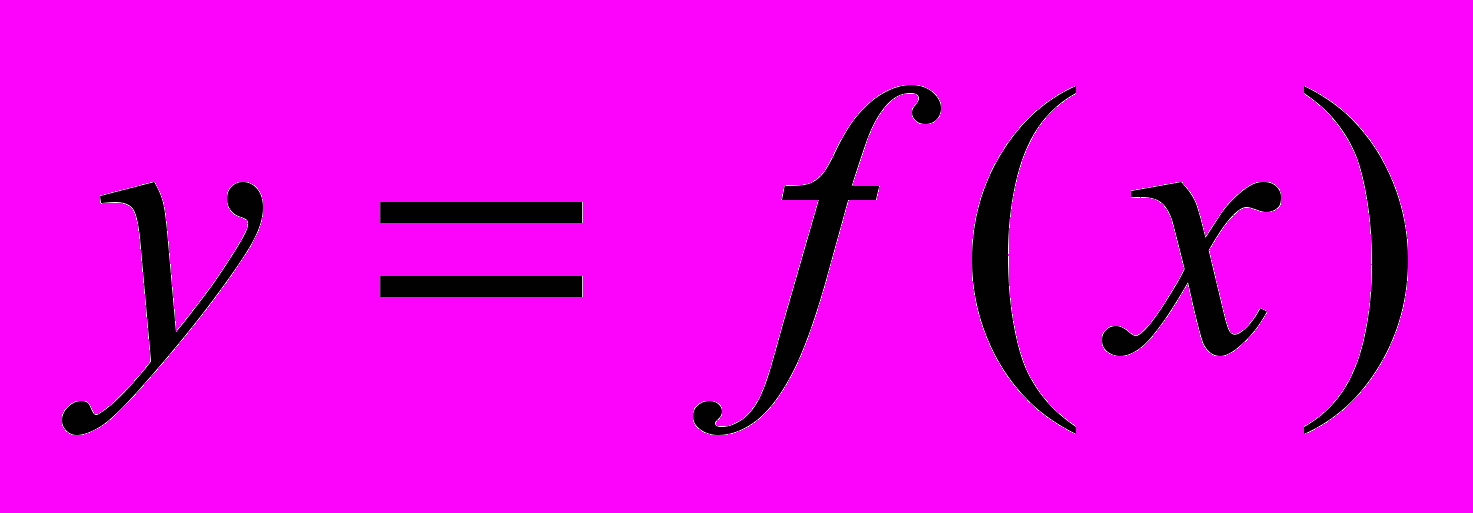 на
на 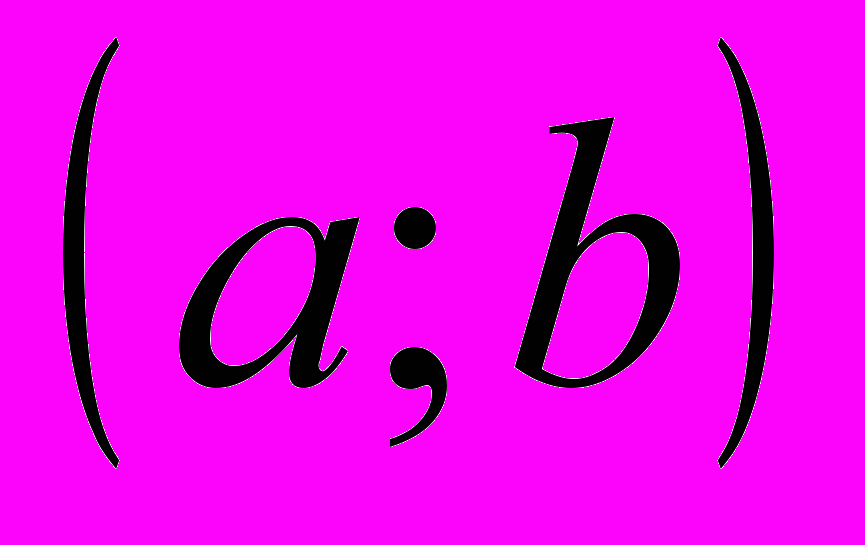 . Тогда
. Тогда 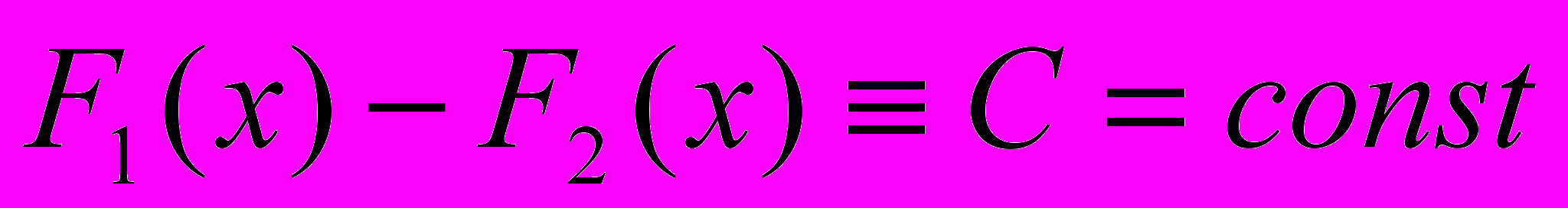 .
.ДОК. Предположим противное :
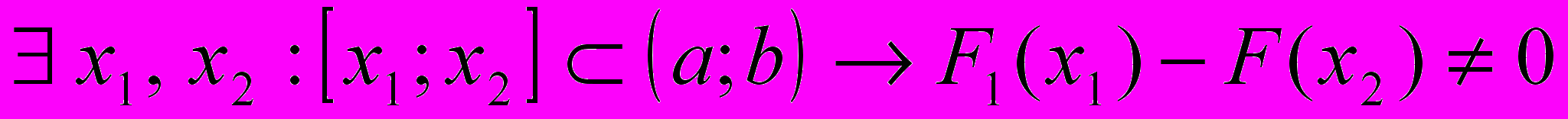 . Тогда на
. Тогда на отрезке
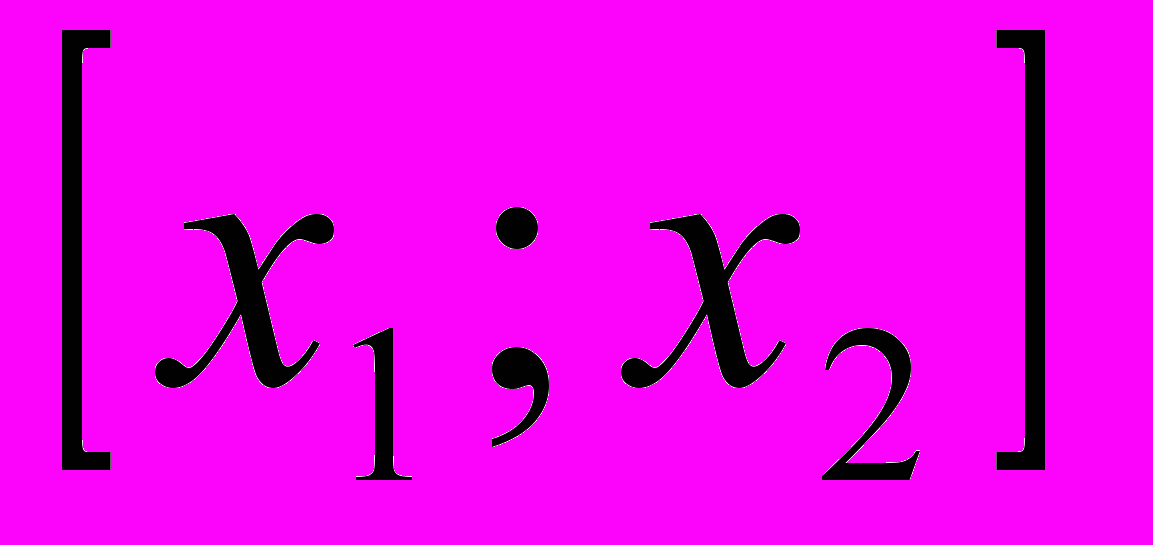 для функции
для функции 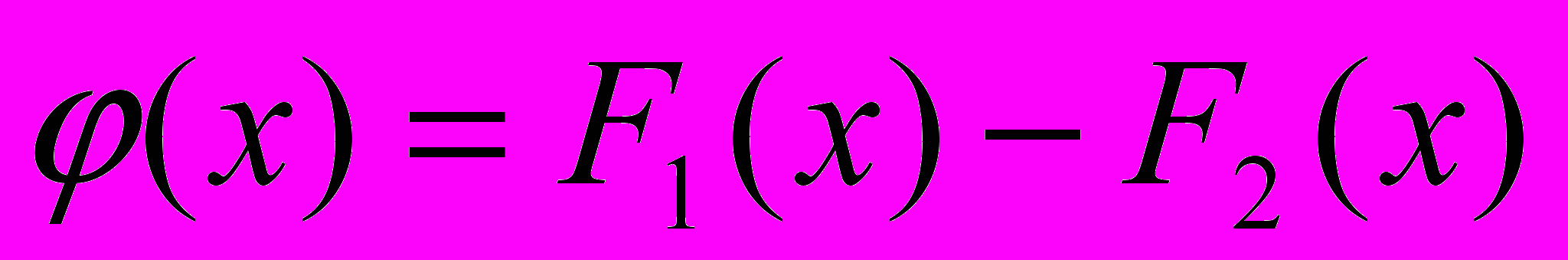 справедлива теорема Лагранжа :
справедлива теорема Лагранжа : 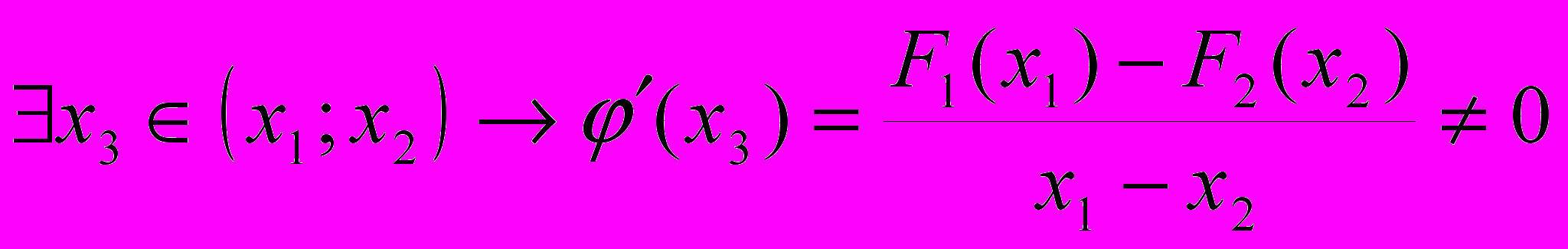 . Последнее противоречит условию того, что
. Последнее противоречит условию того, что 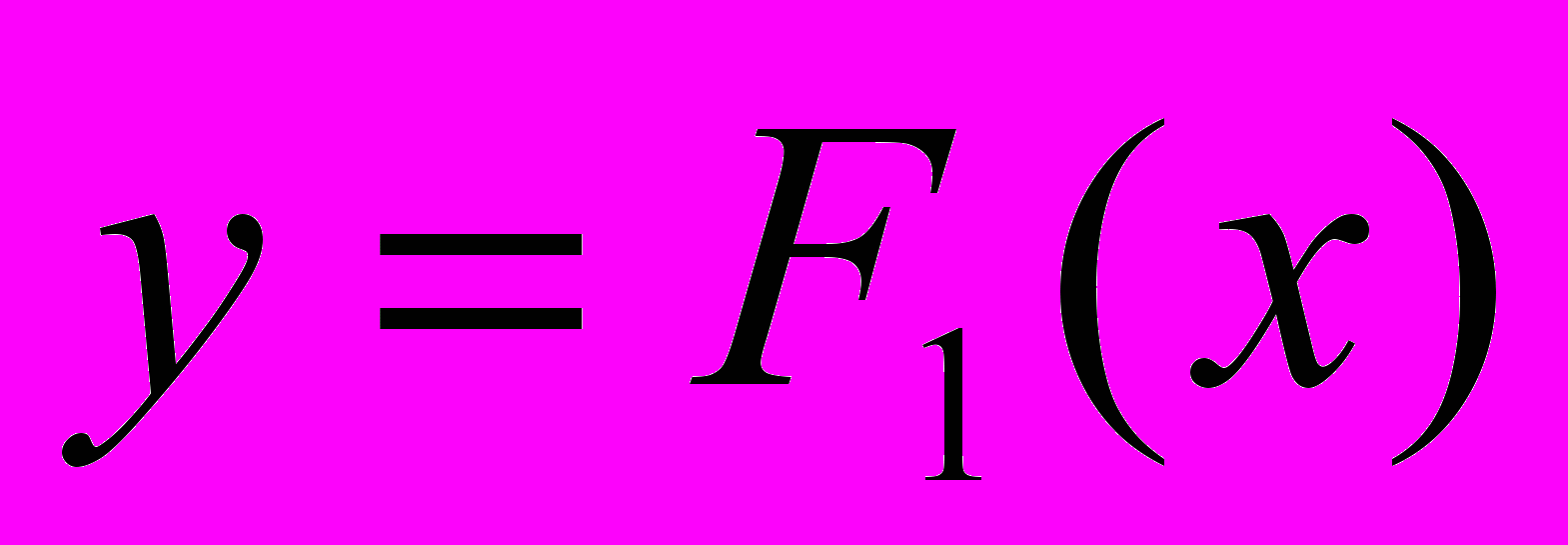 и
и 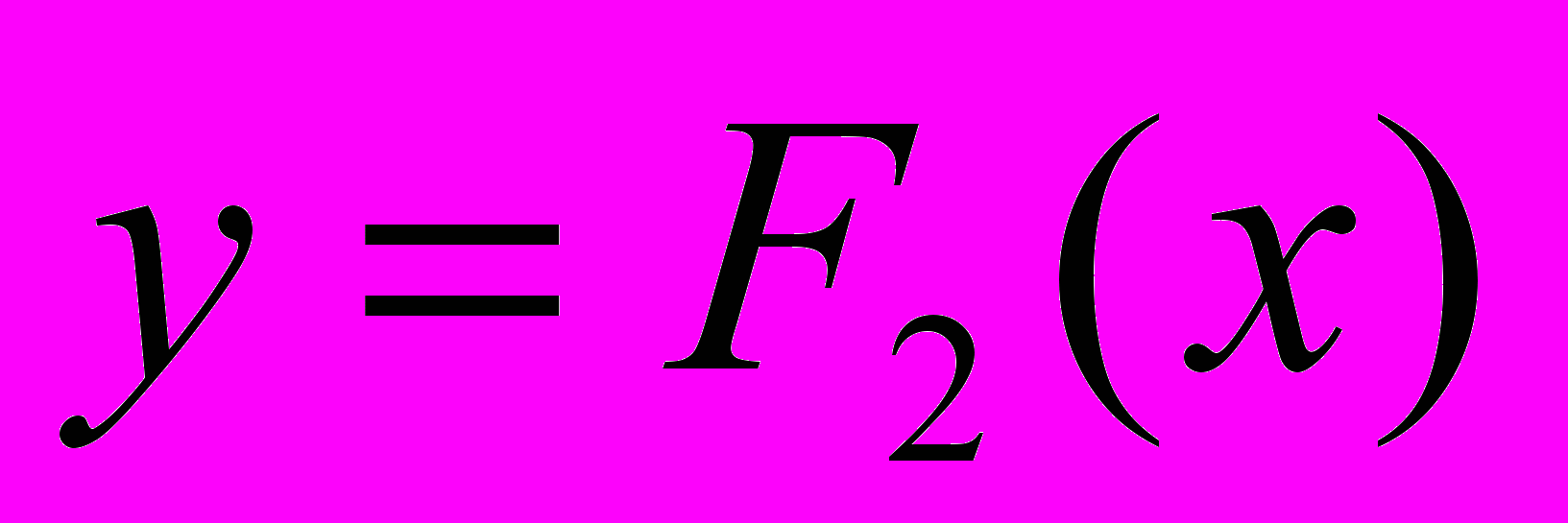 две первообразные функции
две первообразные функции 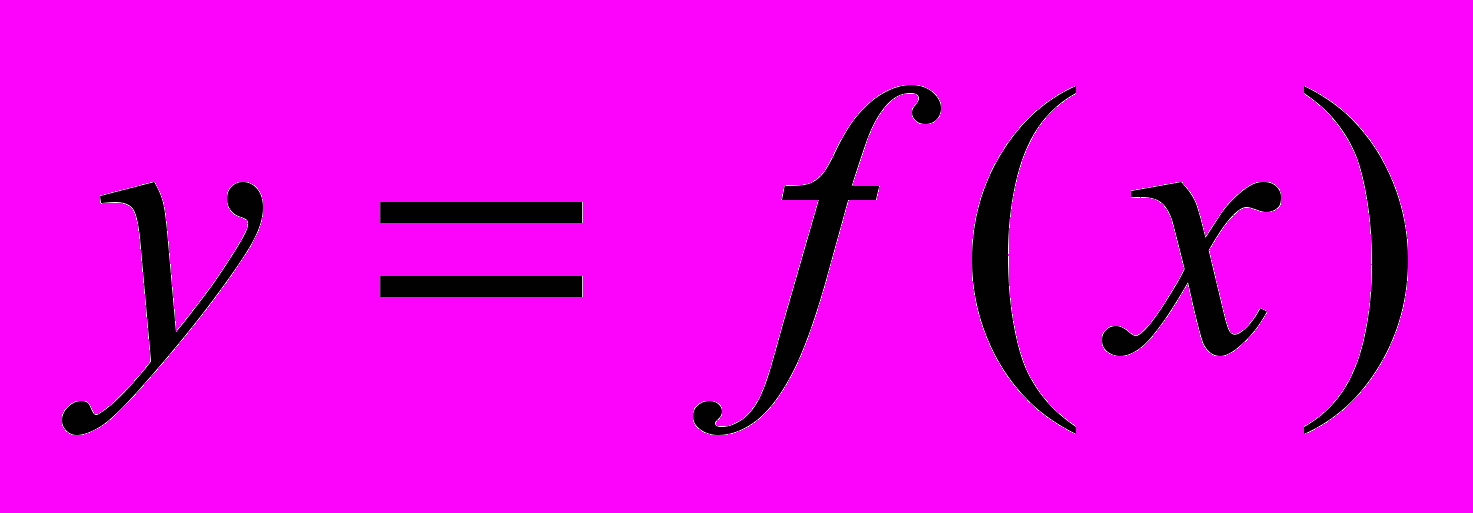 на
на 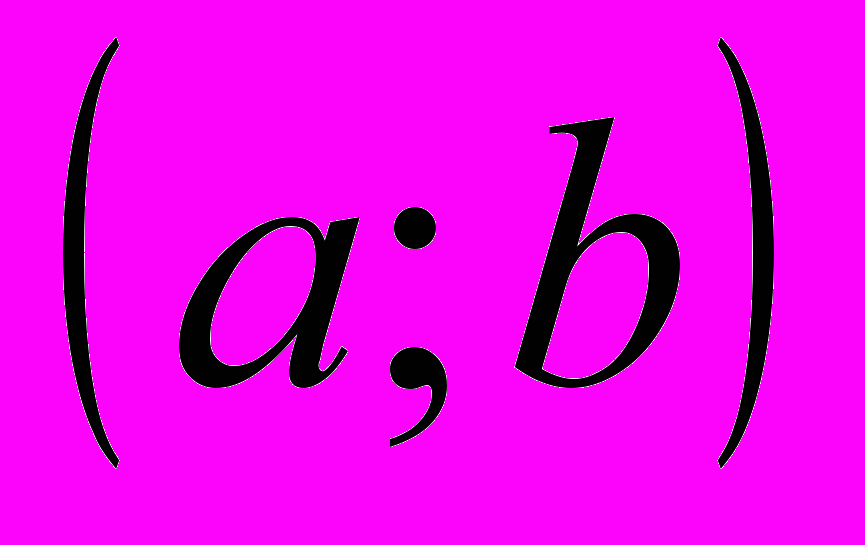 , поскольку
, поскольку 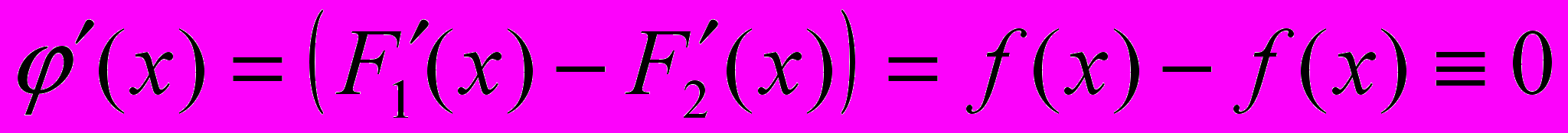 на
на 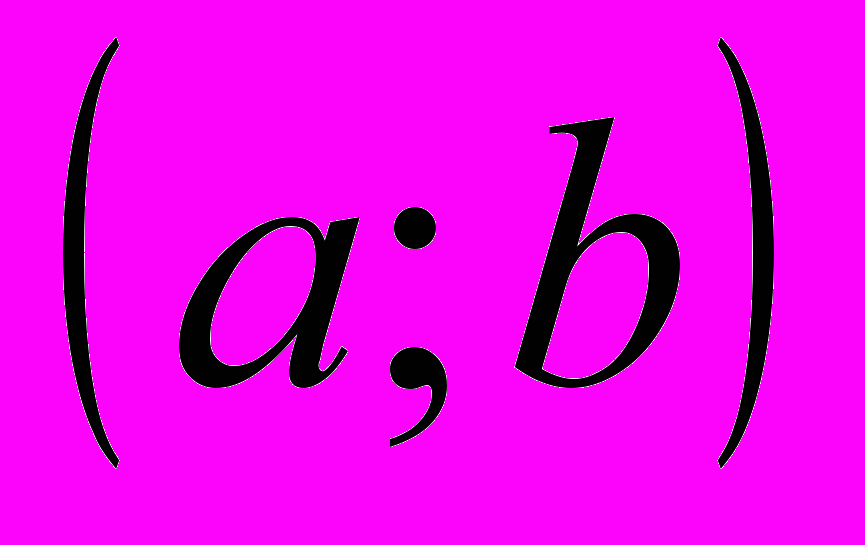 .
.ОПР. Неопределенным интегралом функции
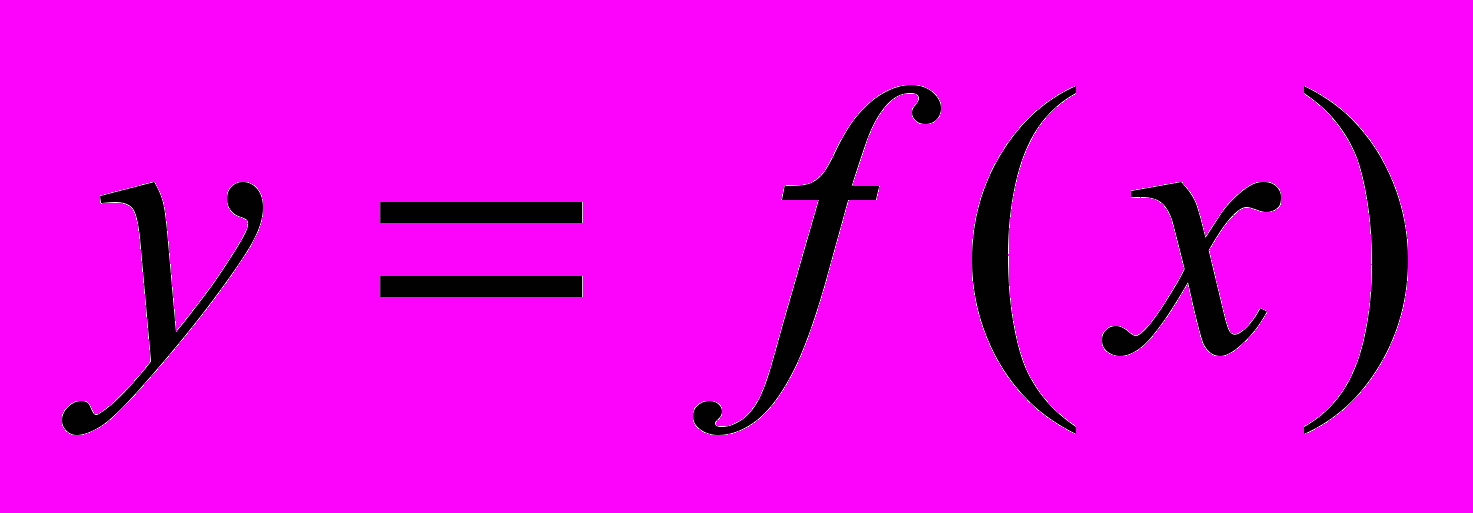 на
на 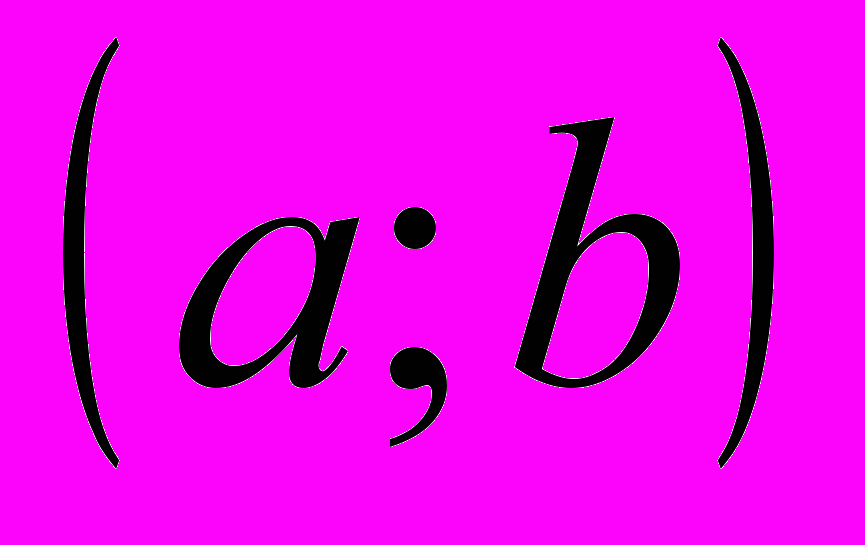 называется множество всех
называется множество всехпервообразных функции
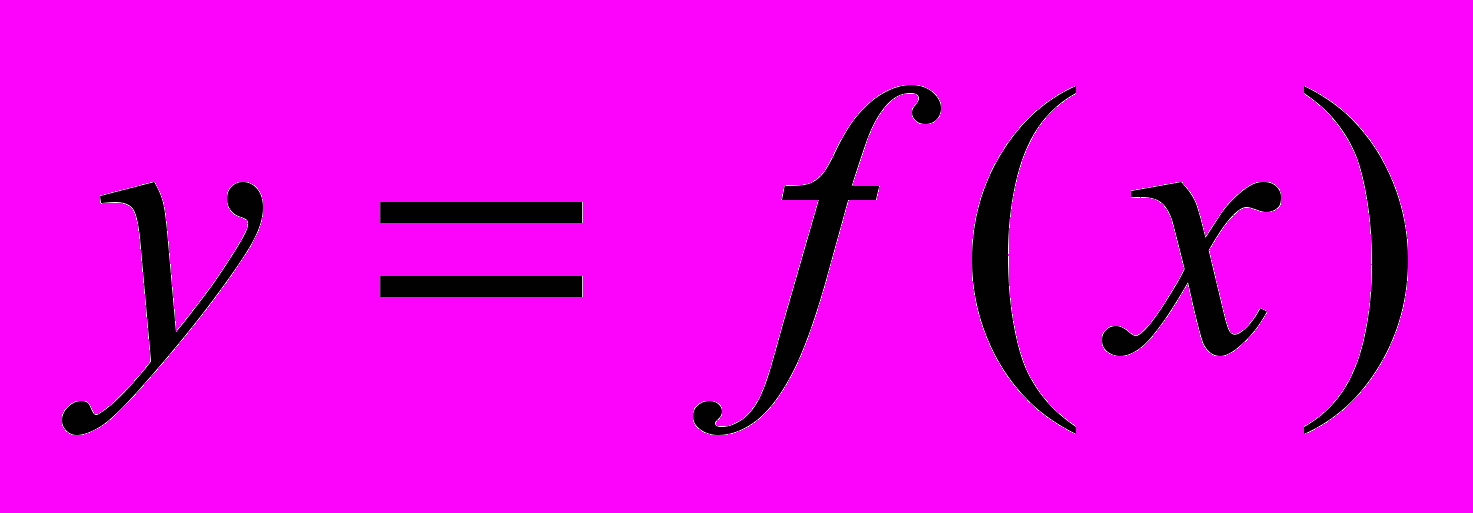 на
на 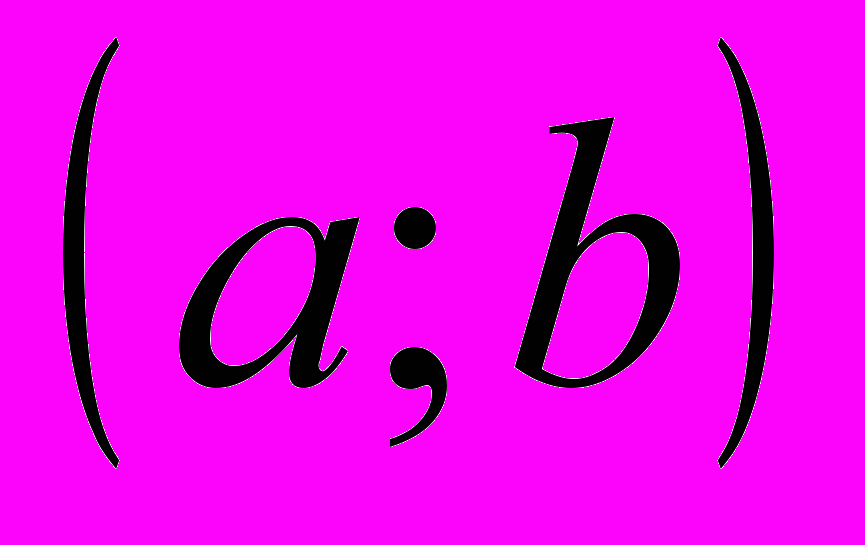 . Обозначение :
. Обозначение : 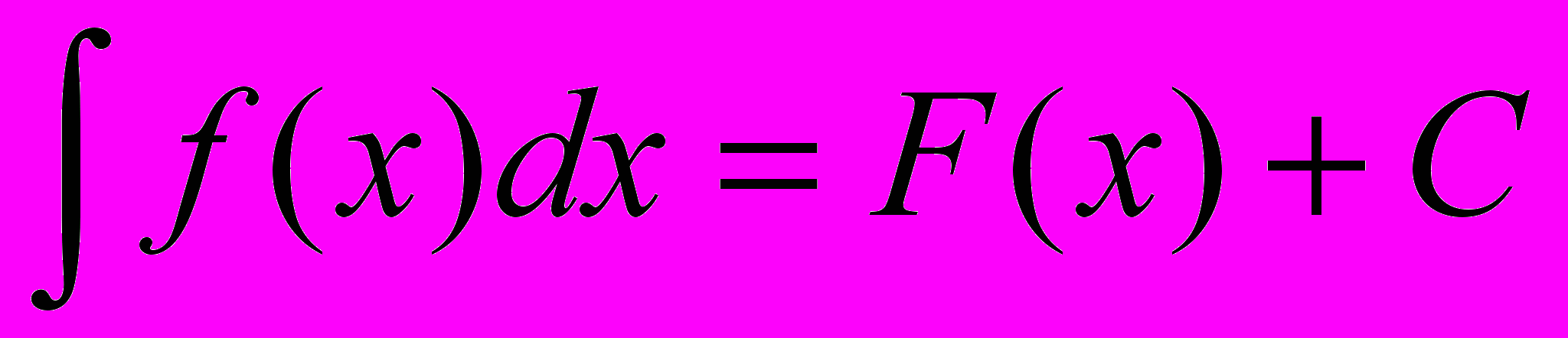 .
.Операции дифференцирования и интегрирования обратные в том смысле, что
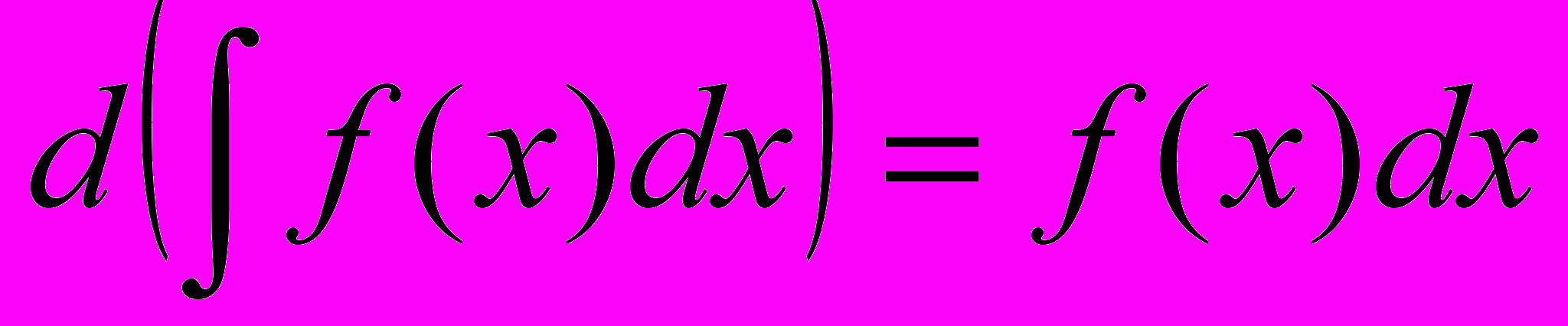 и
и 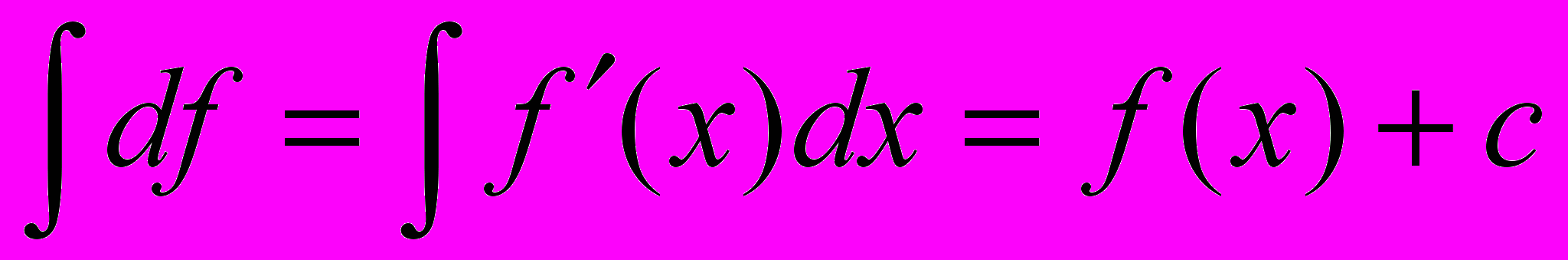
Доказательство этих формул находится на уровне определений понятий дифференциала функции и неопределенного интеграла (самостоятельно). Таким образом, значки d и
стоящие рядом друг друга уничтожают.
В качестве простейших свойств интеграла, вытекающий из его определения, следует отметить его линейность :
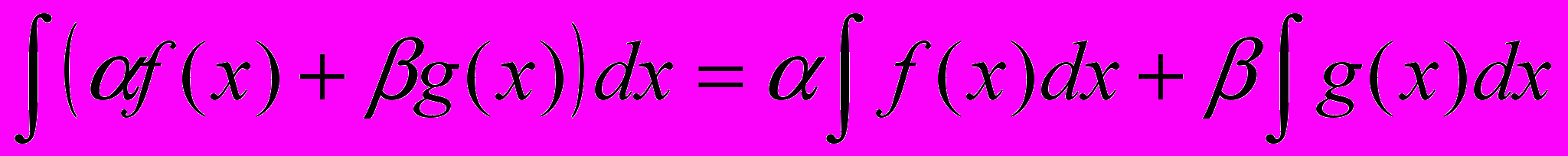 .
.П.2 Техника неопределенного интегрирования.
А. Замена переменной.
ТЕОРЕМА 2.( о замене переменной в неопределенном интеграле)
Пусть функция
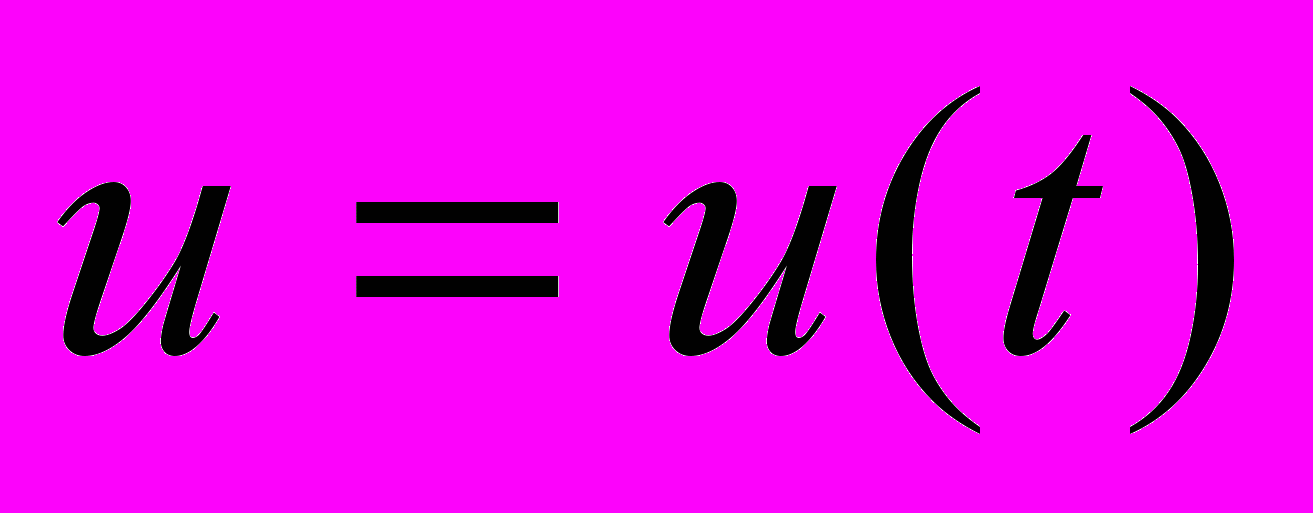 имеет непрерывную производную на отрезке
имеет непрерывную производную на отрезке 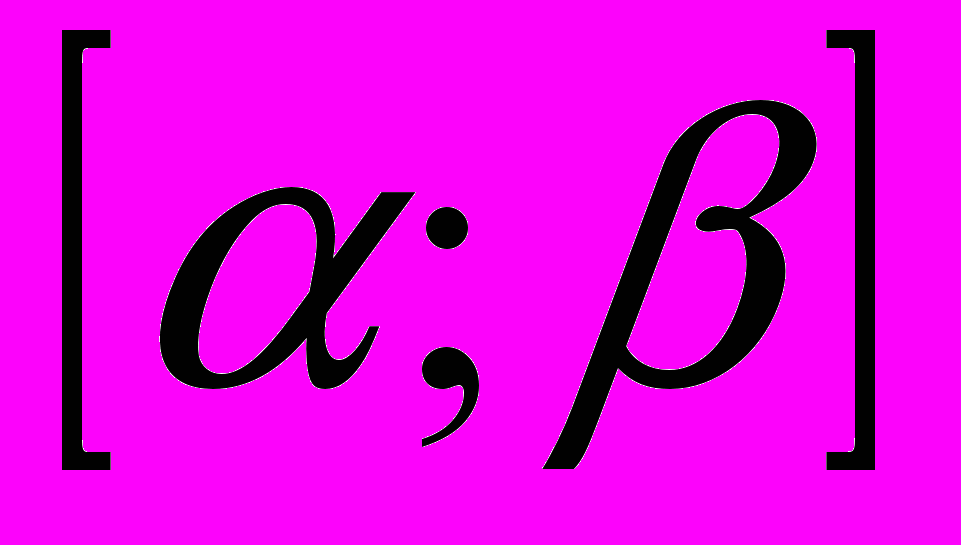 и
и  ,
,а функция
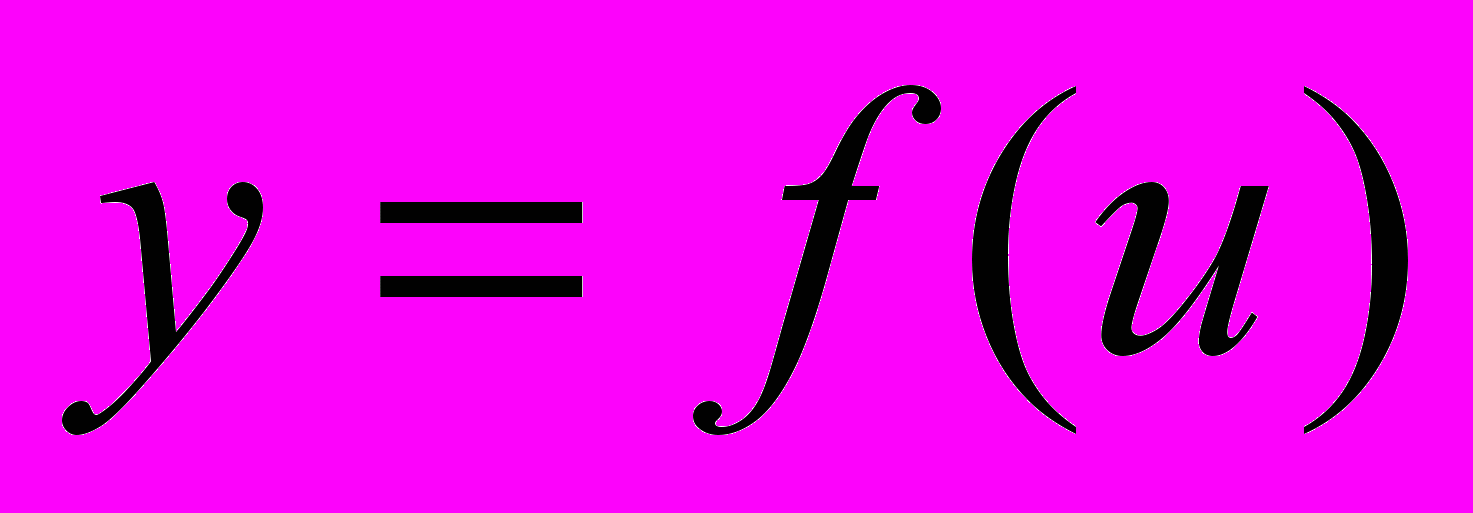 непрерывна на
непрерывна на 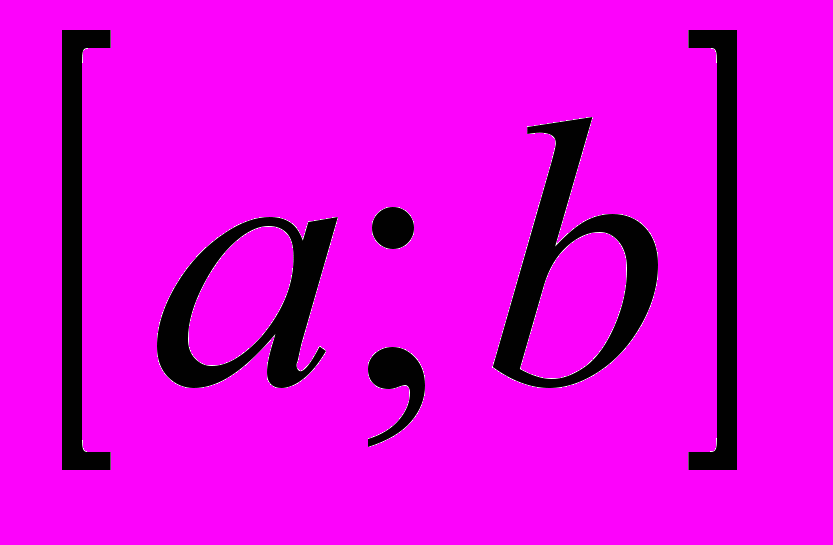 . Рассмотрим две первообразных
. Рассмотрим две первообразных 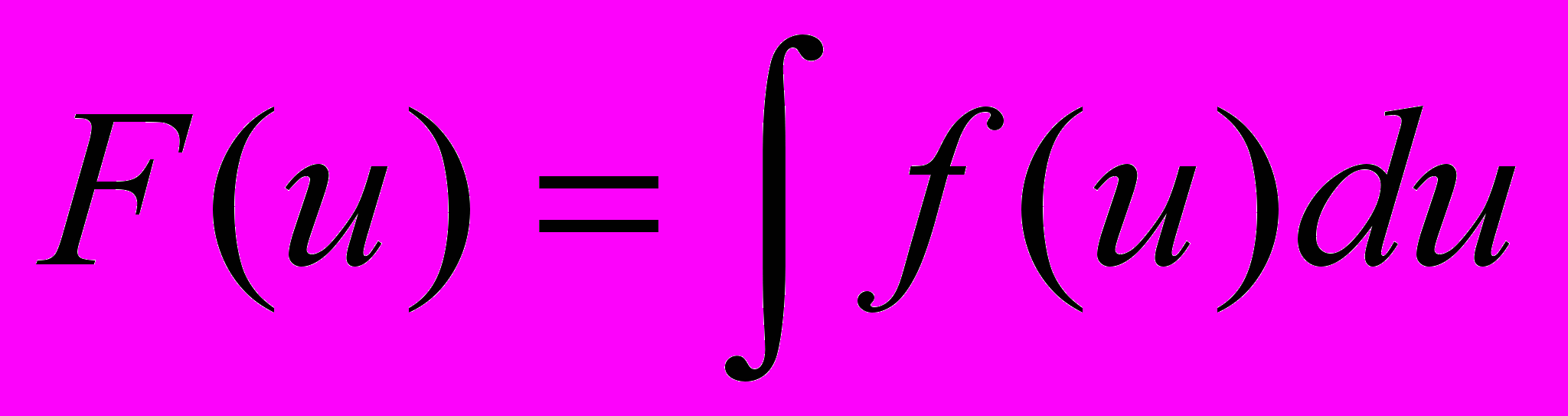 и
и 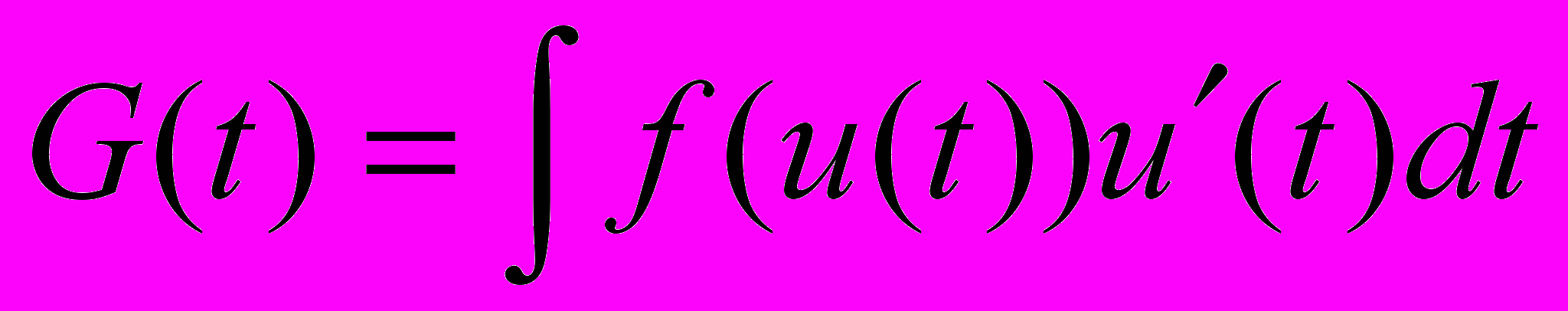 .Тогда справедлива формула
.Тогда справедлива формула 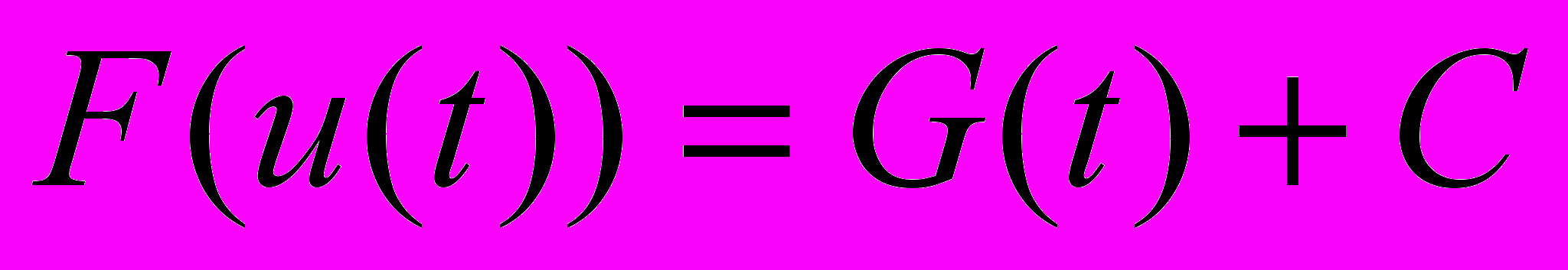 .
.ДОК.
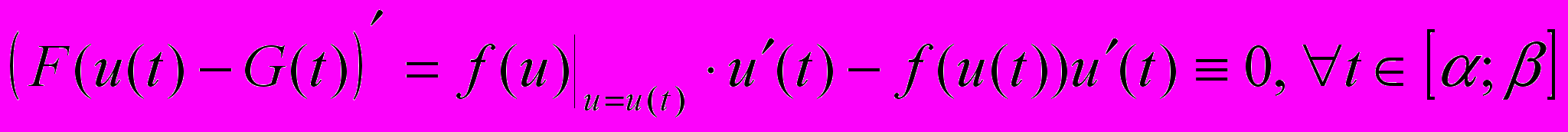 . Тогда
. Тогда 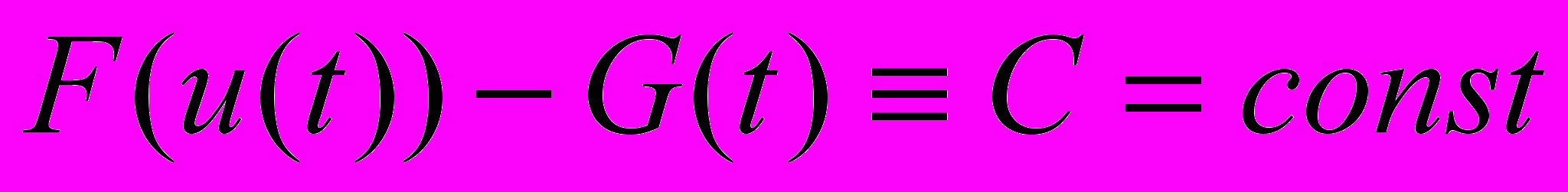 .
.Пример. Найти интеграл
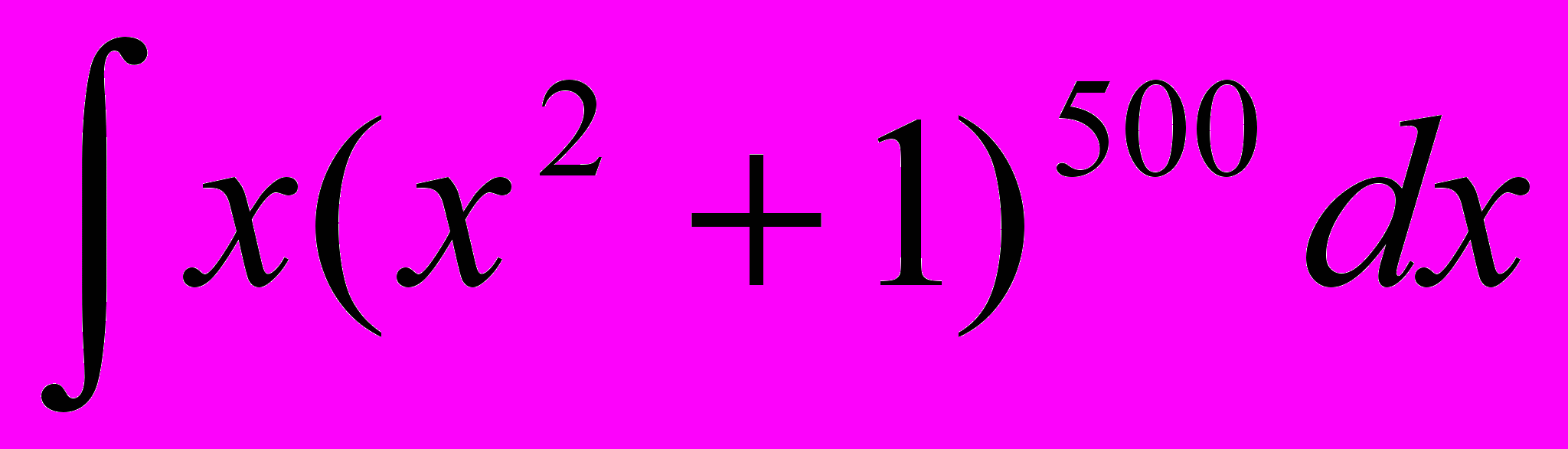 .
.РЕШЕНИЕ. Делаем замену
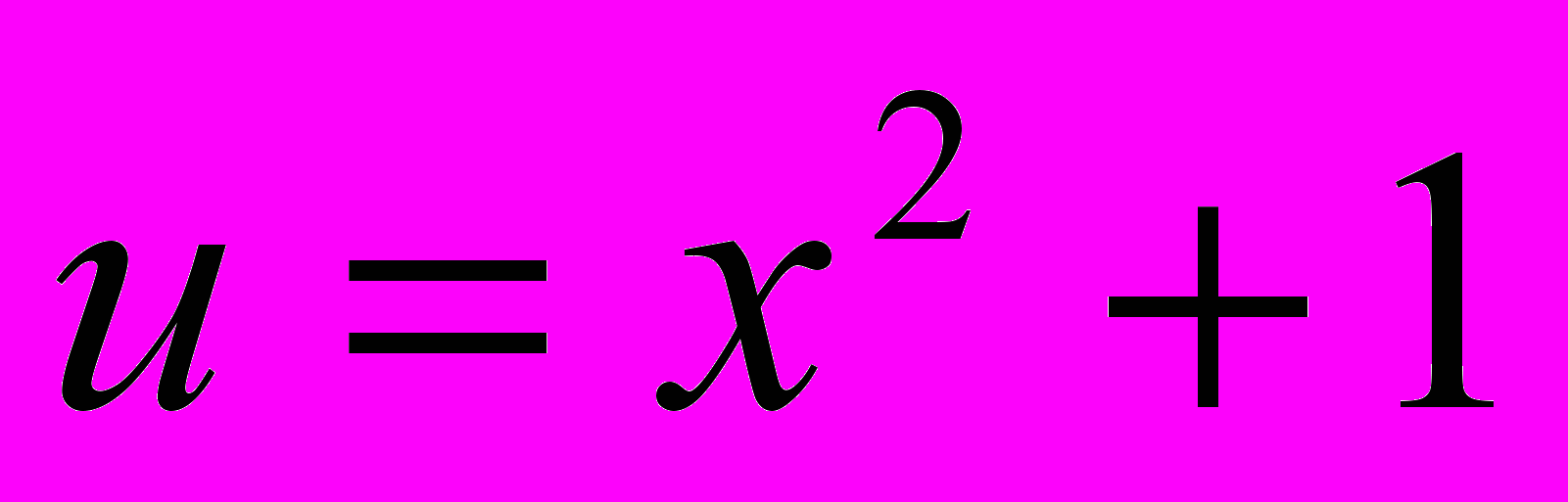 . Тогда
. Тогда 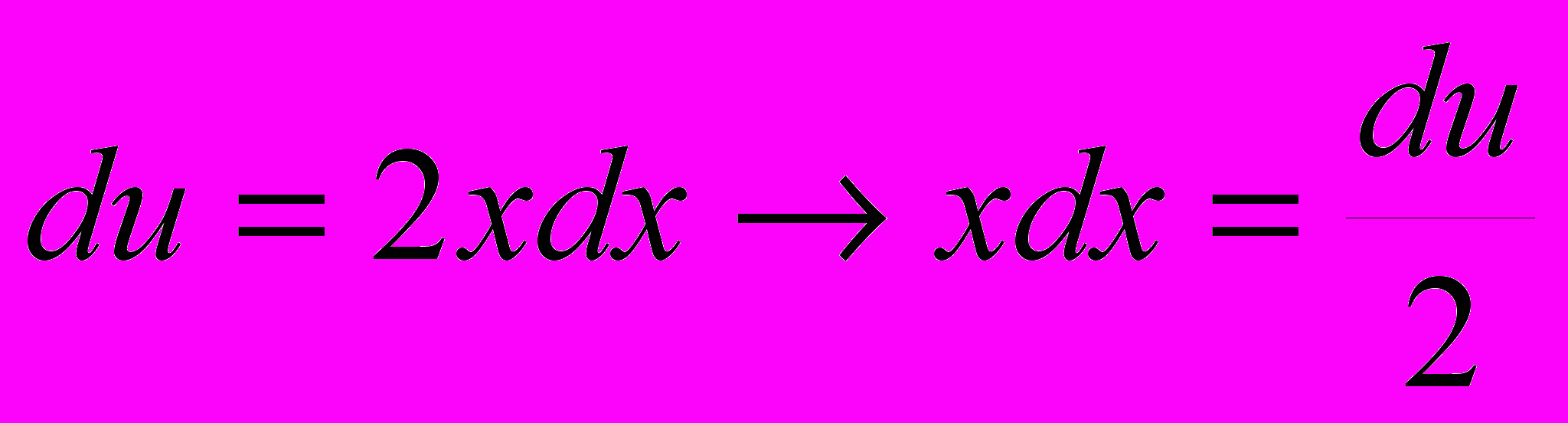 и , по доказанному,
и , по доказанному, 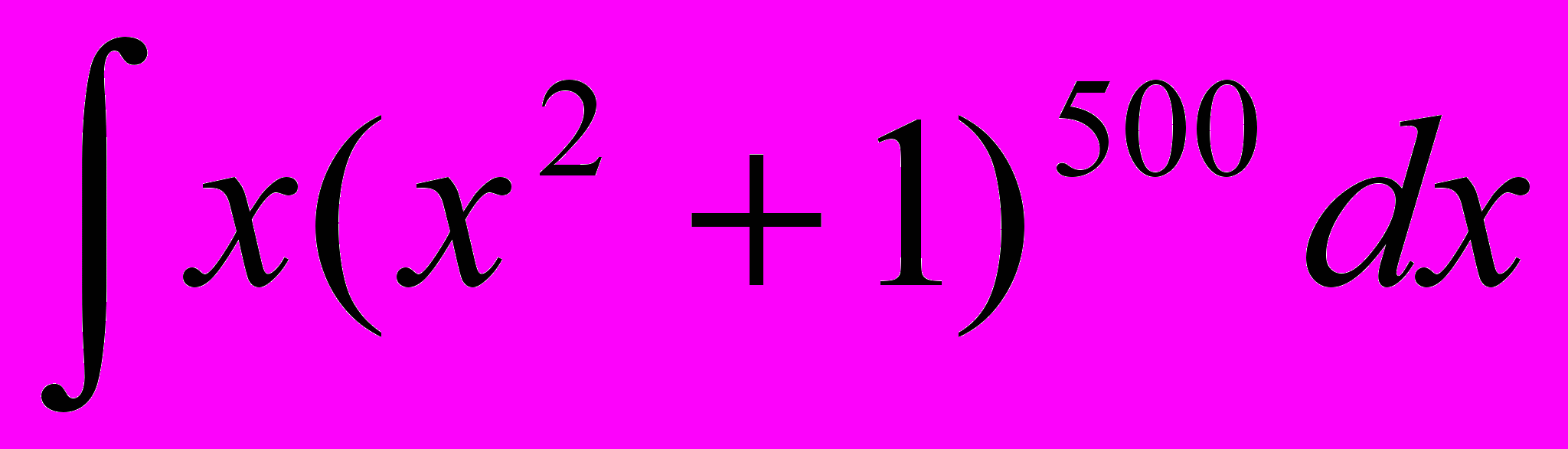 =
=
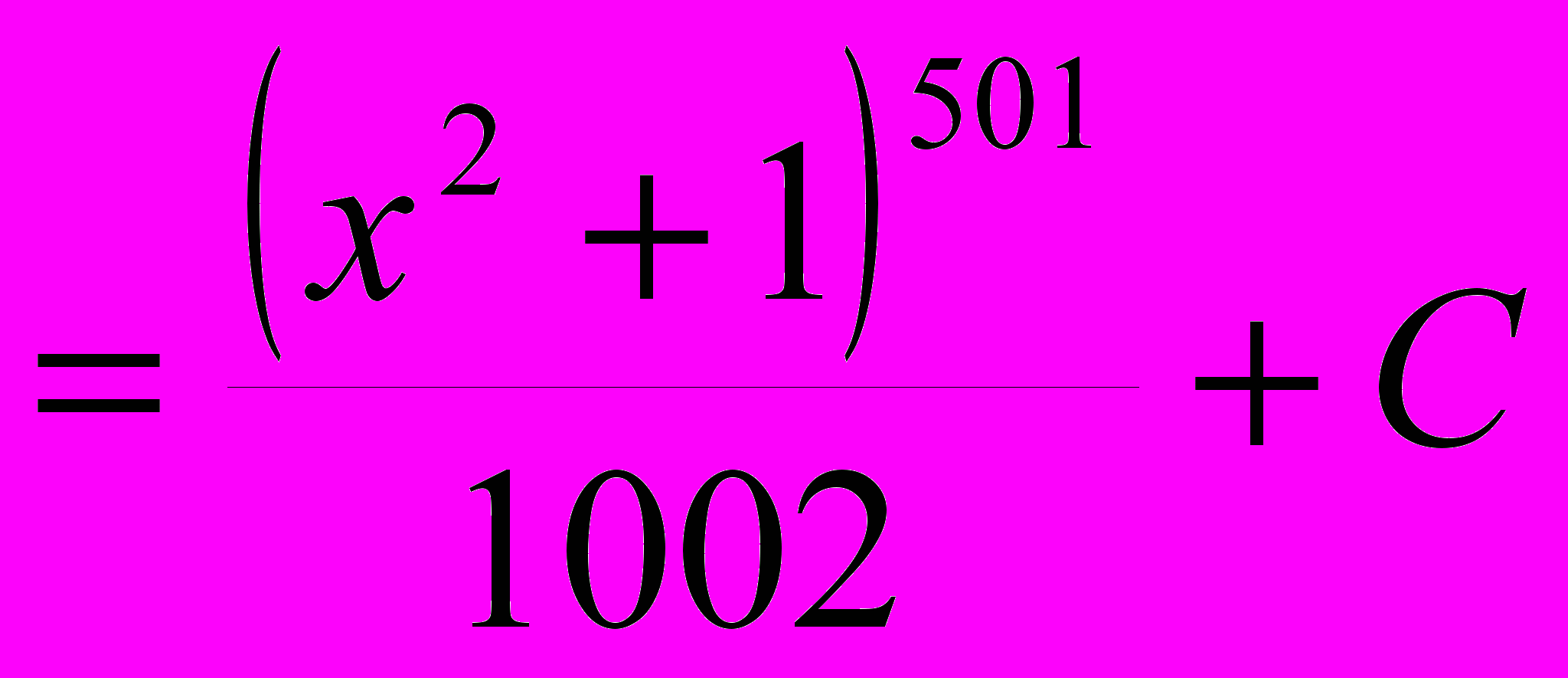 .
.Б. Интегрирование по частям.
ТЕОРЕМА 3. ( формула интегрирования по частям)
Для любых двух функций
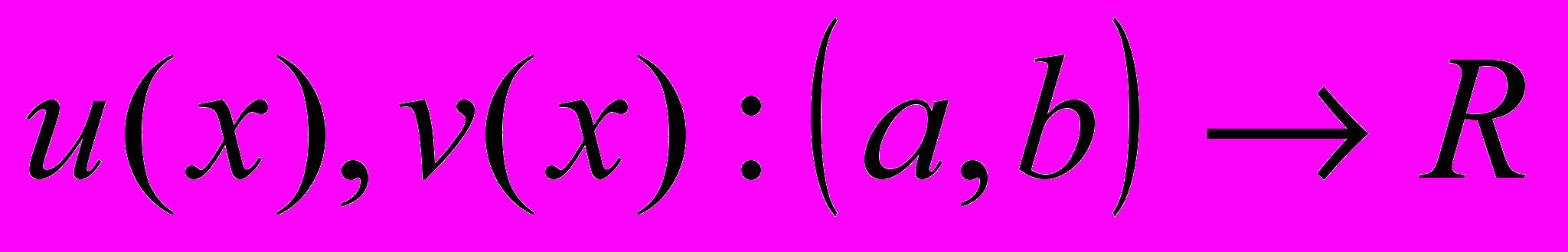 , имеющих непрерывные производные
, имеющих непрерывные производные на
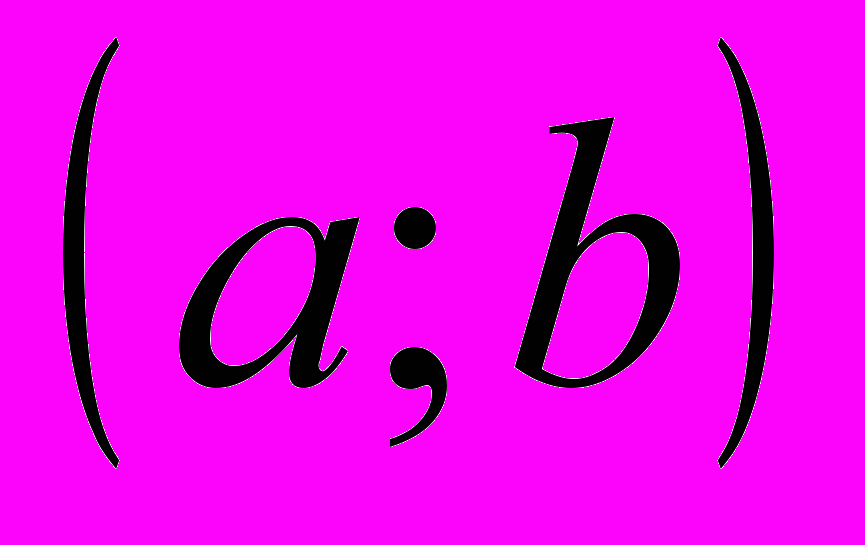 , справедлива формула
, справедлива формула 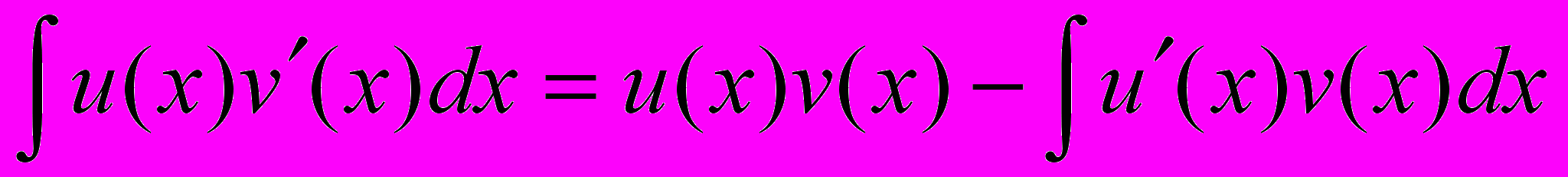 .
.ДОК.
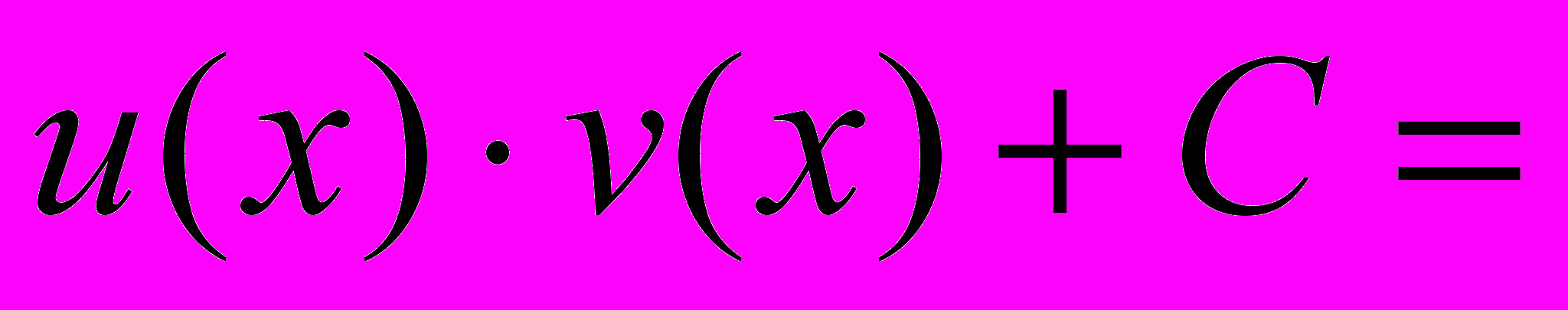
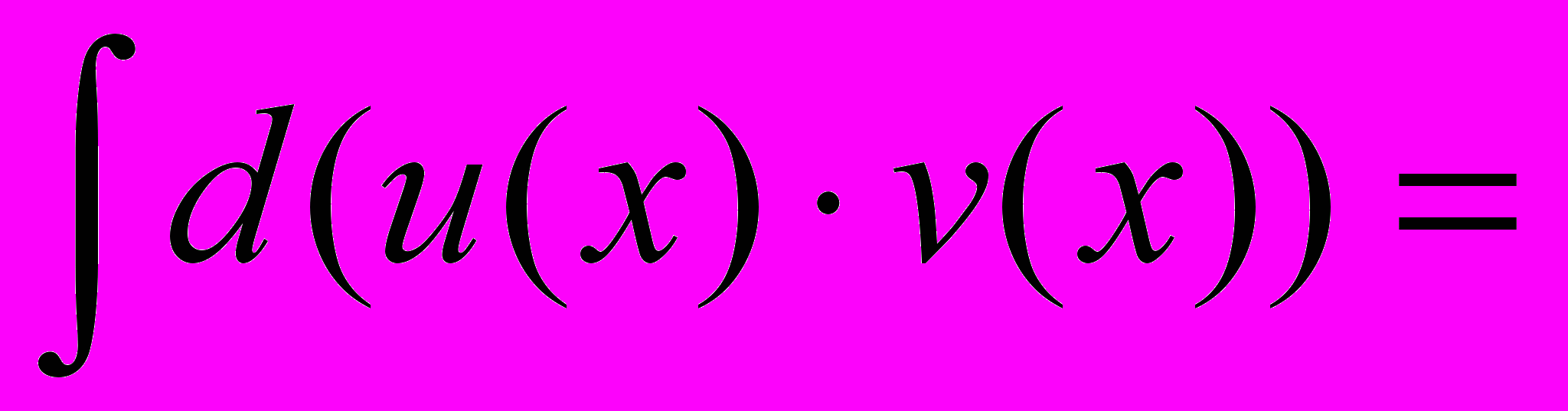
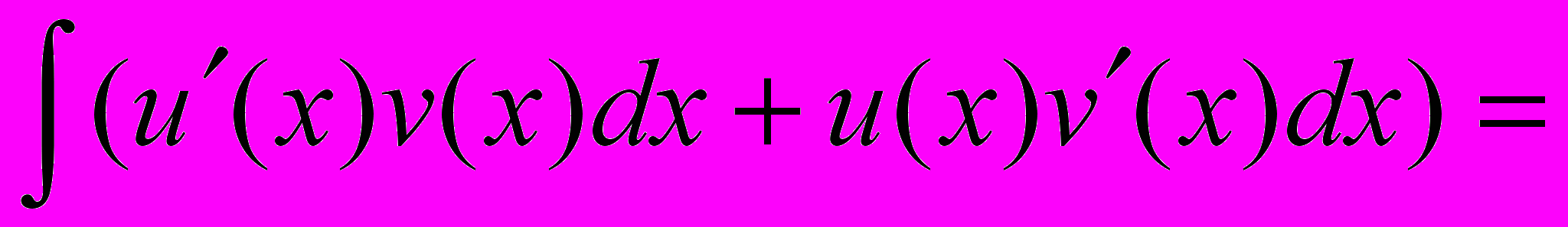
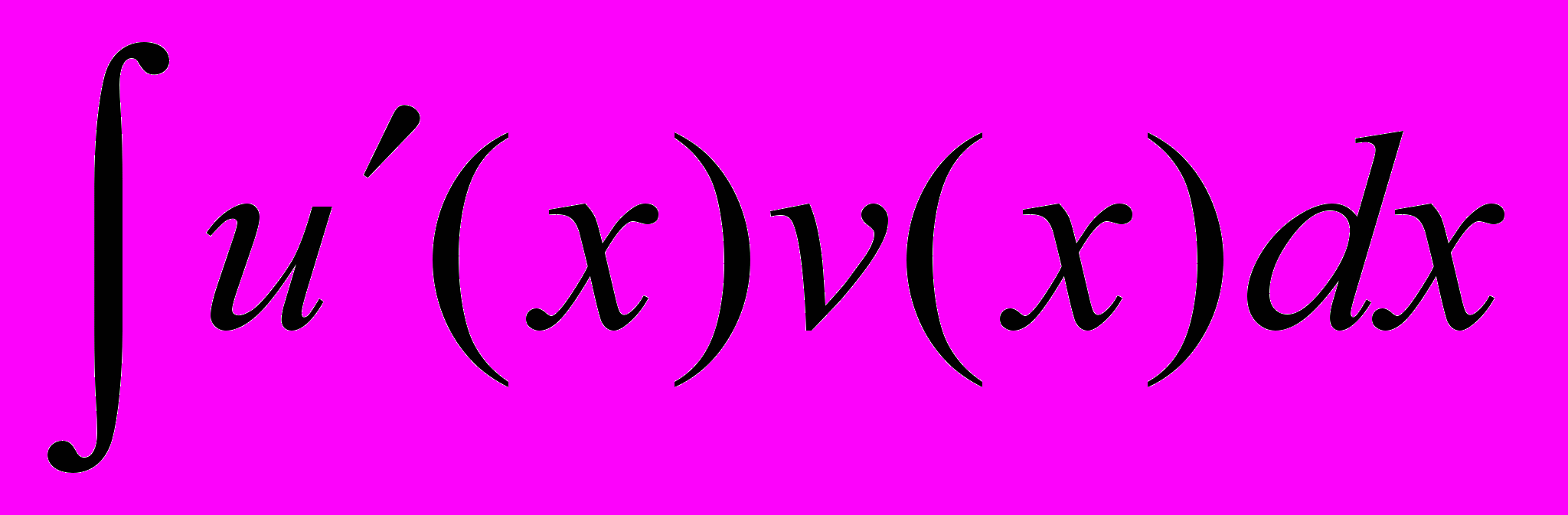 +
+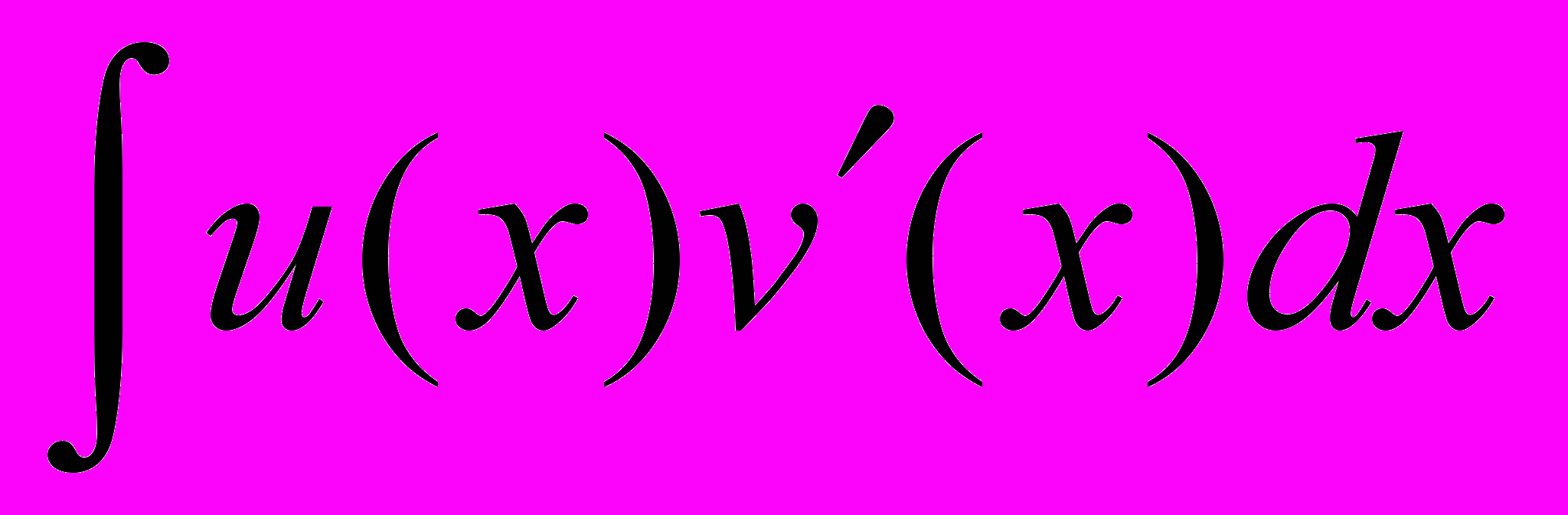 .
.Формулу интегрирования по частям записывают обычно в дифференциальной форме :
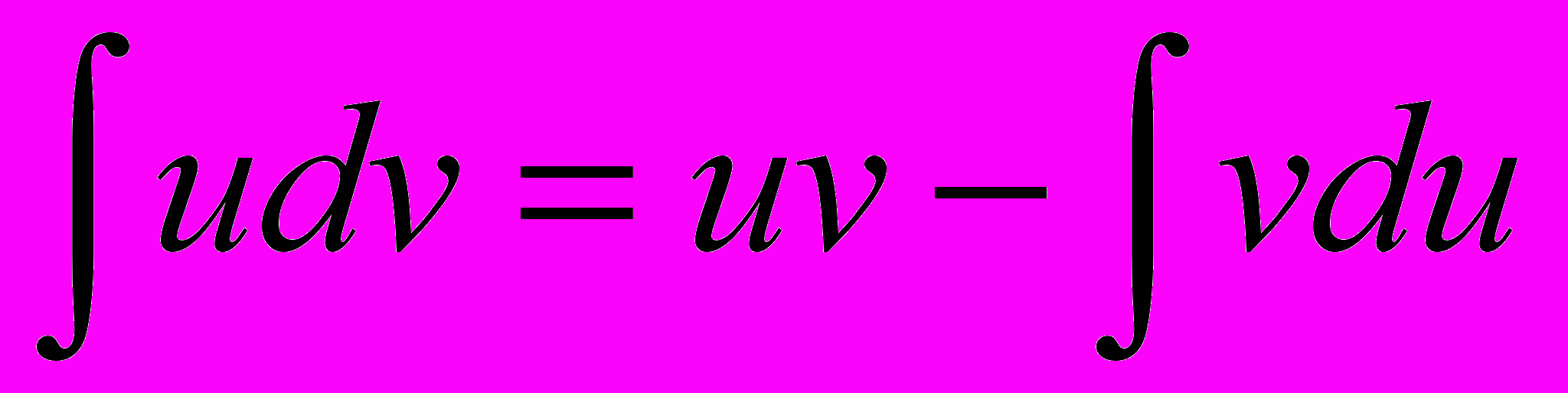
ПРИМЕР. Вычислить интеграл
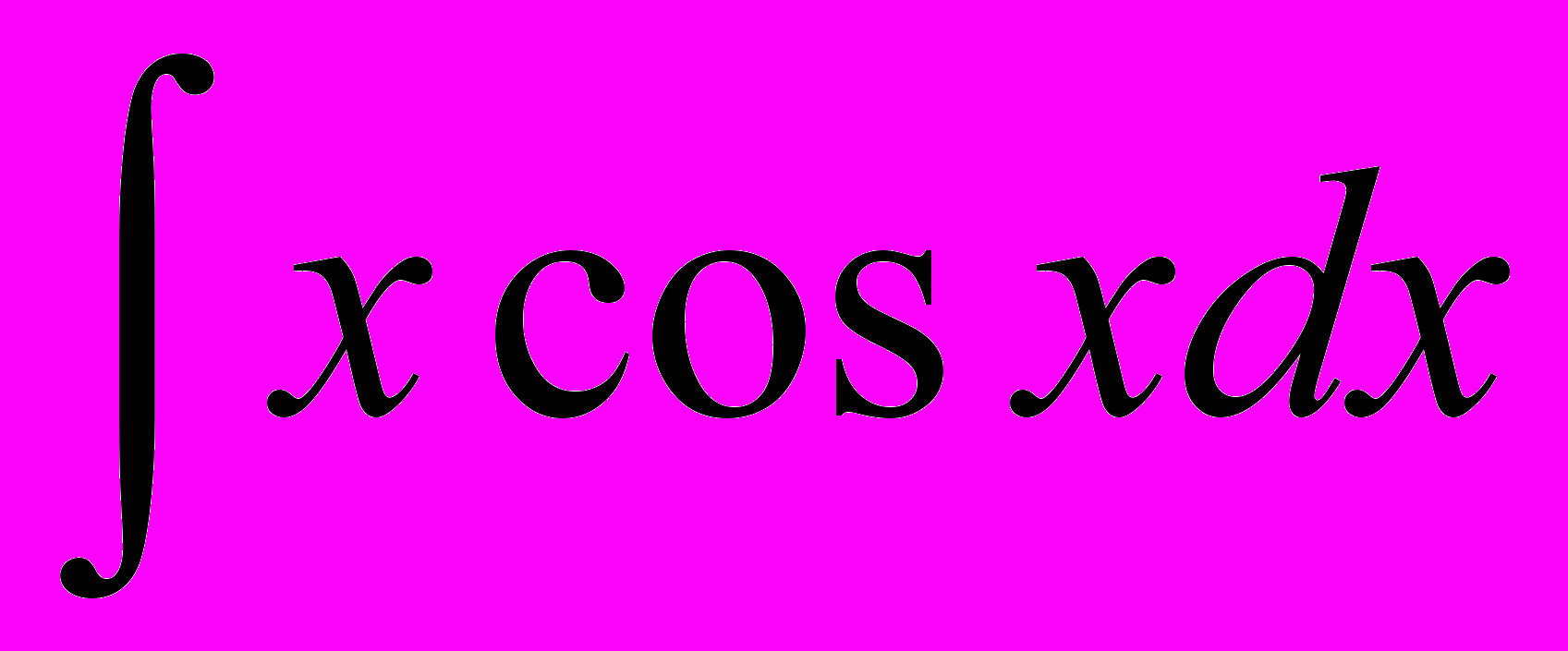 .
.РЕШЕНИЕ.
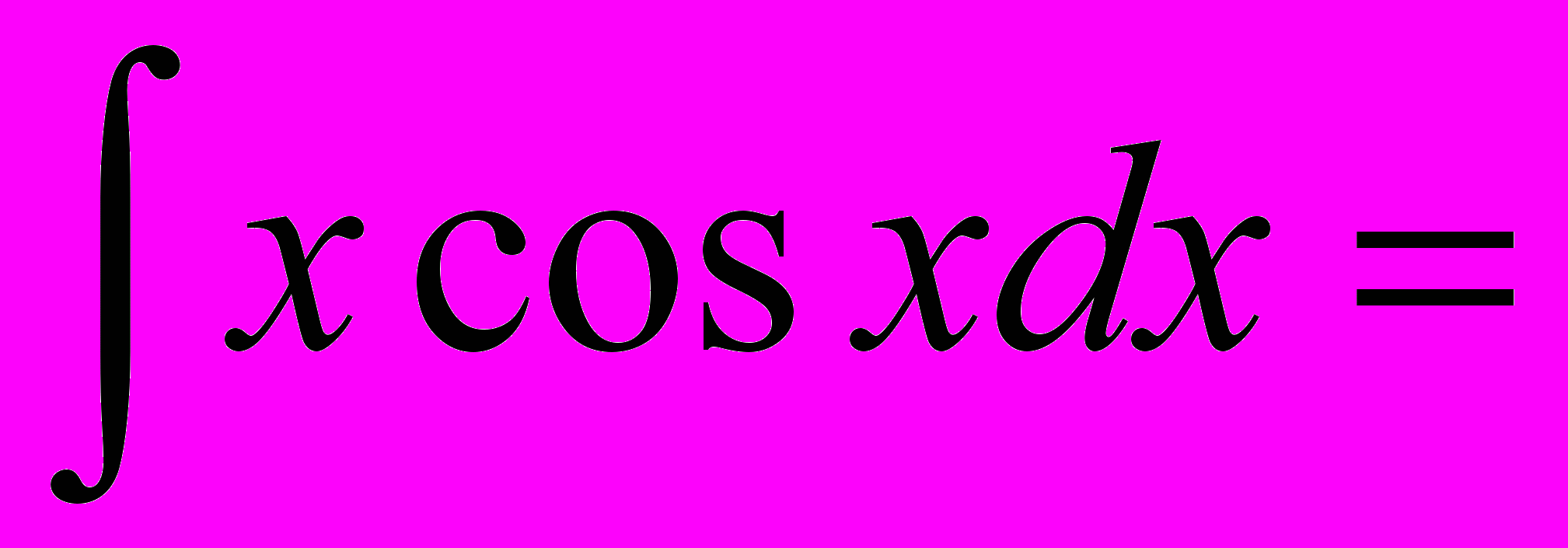
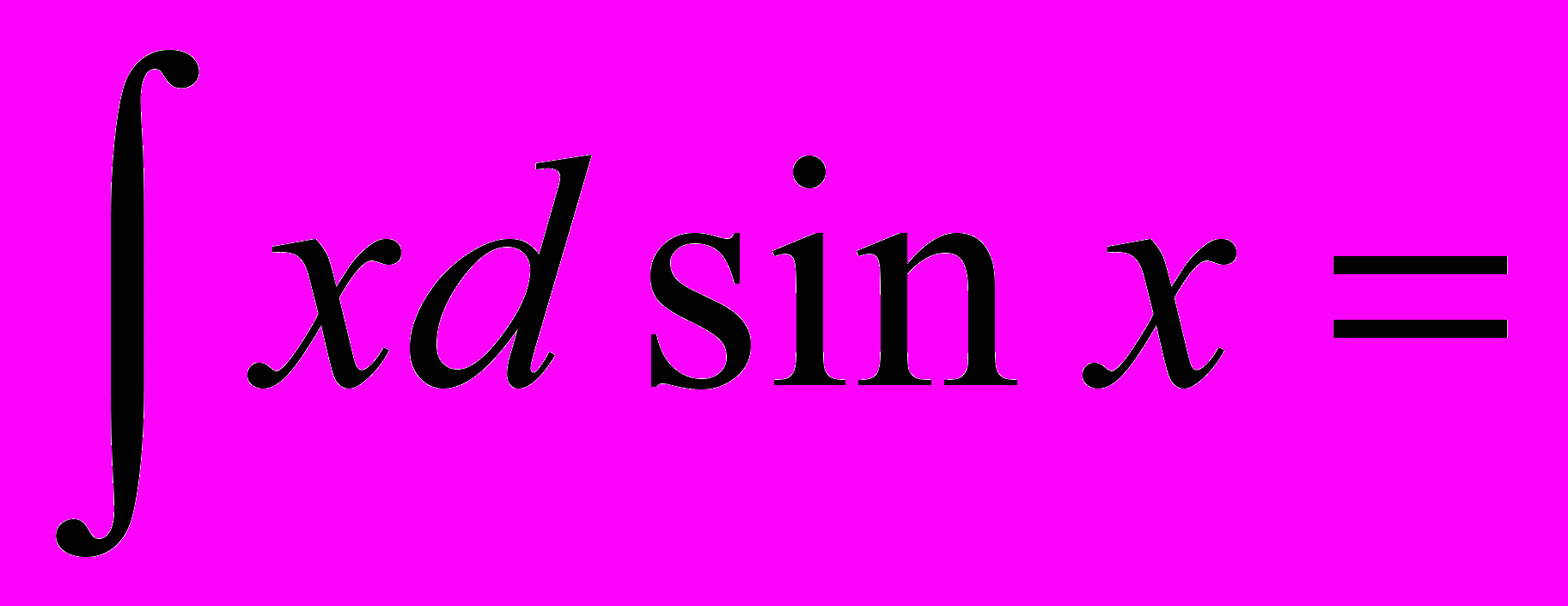
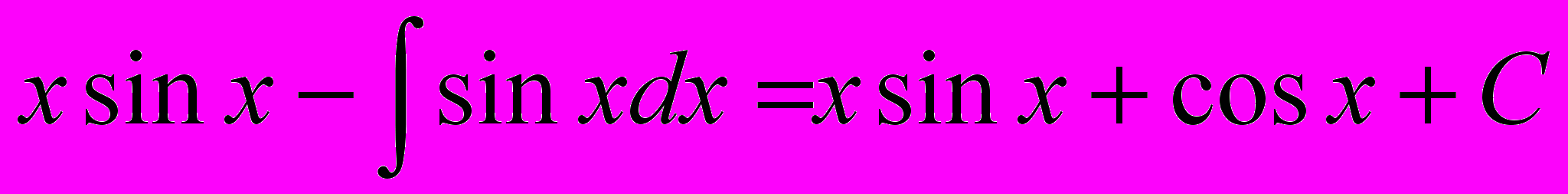 .
.ПРИМЕР. Вычислить интеграл
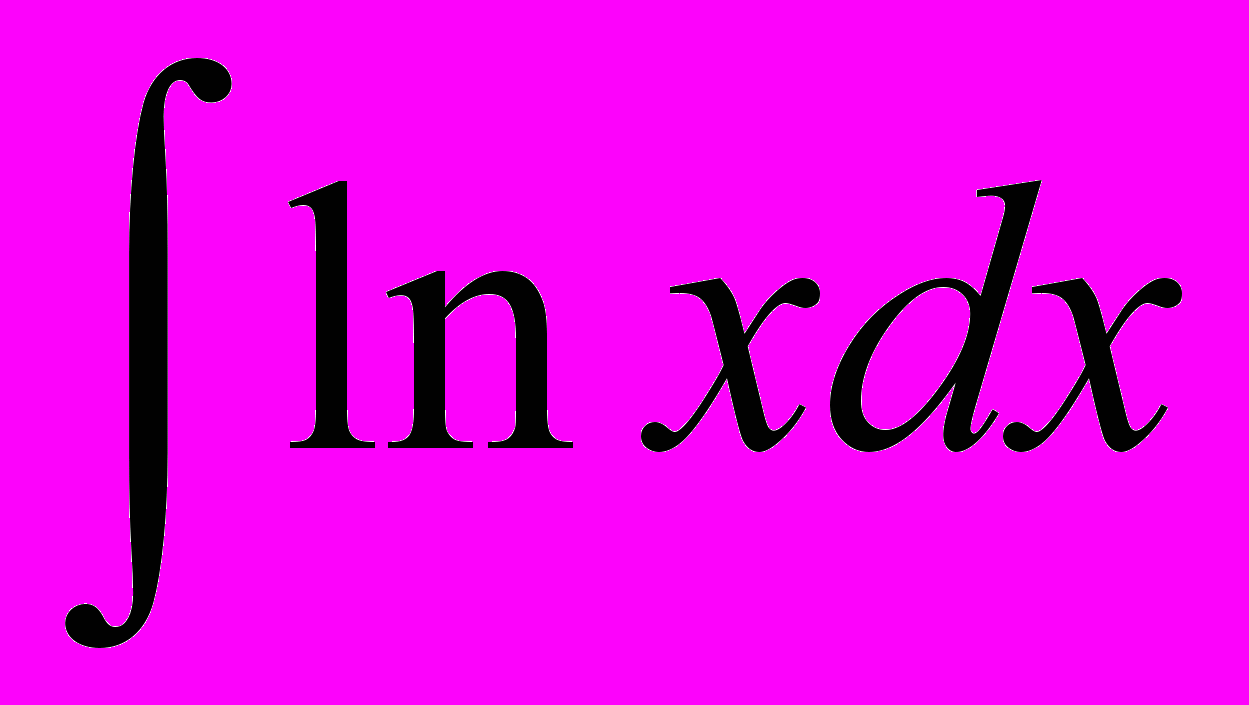 .
.РЕШЕНИЕ.
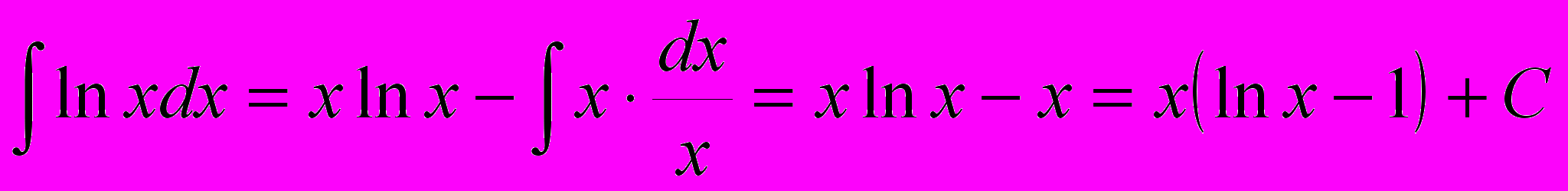 .
.П.3 Таблица первообразных элементарных функций.
Следующая таблица является обращением таблицы производных элементарных функций.
Каждый результат проверяется дифференцированием.
1.
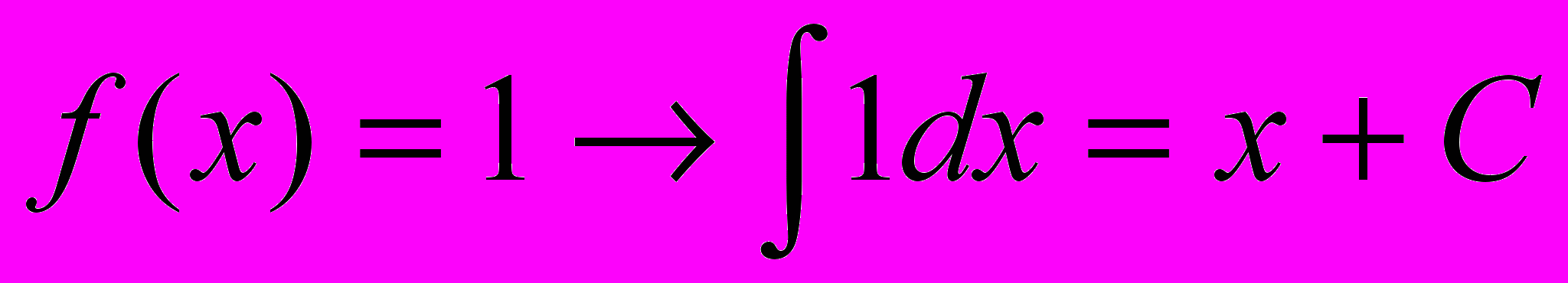 9.
9. 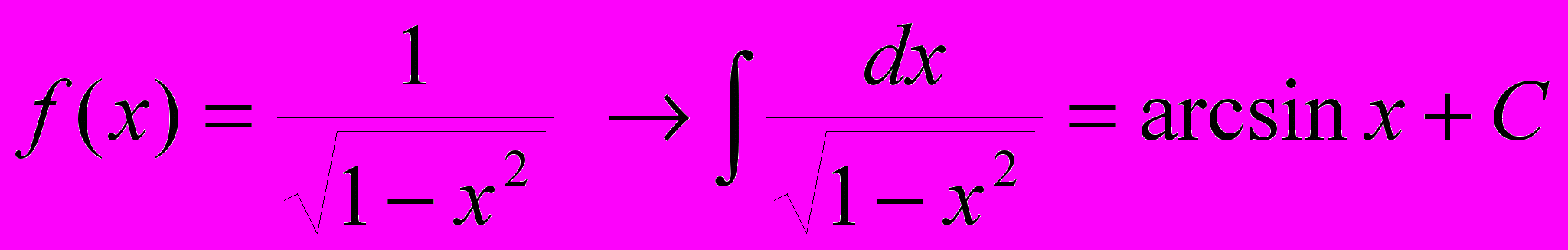
2.
 10.
10. 
3.
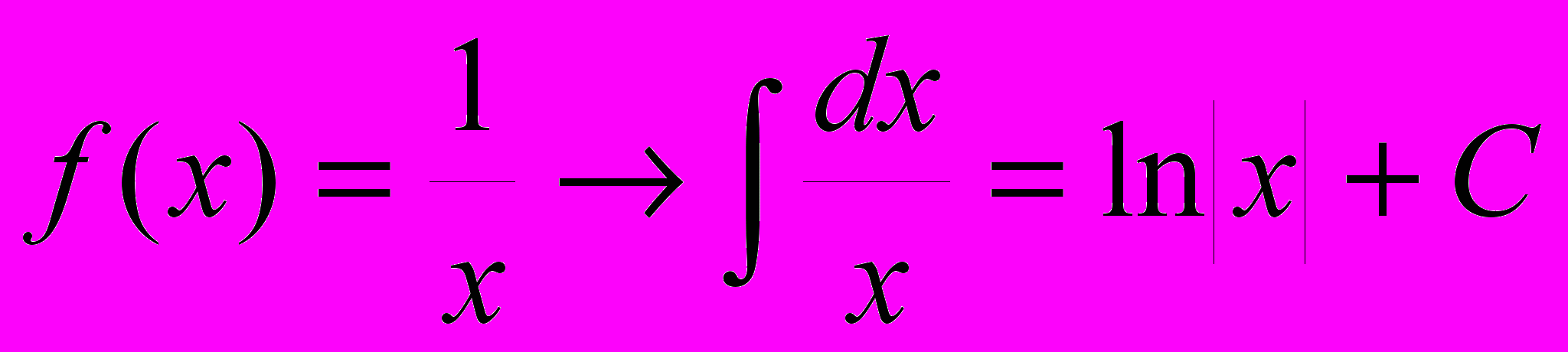 11.
11. 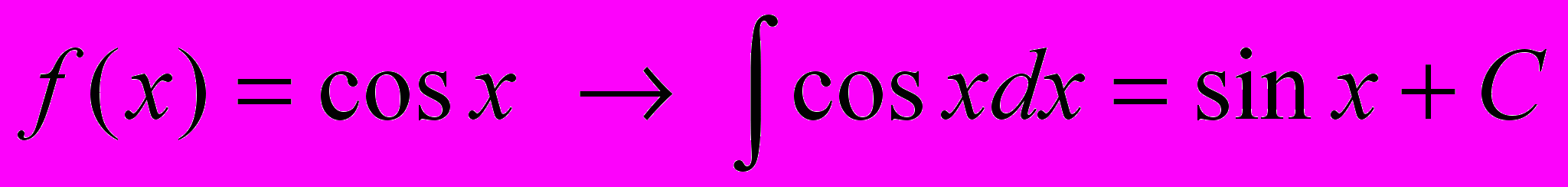
4.
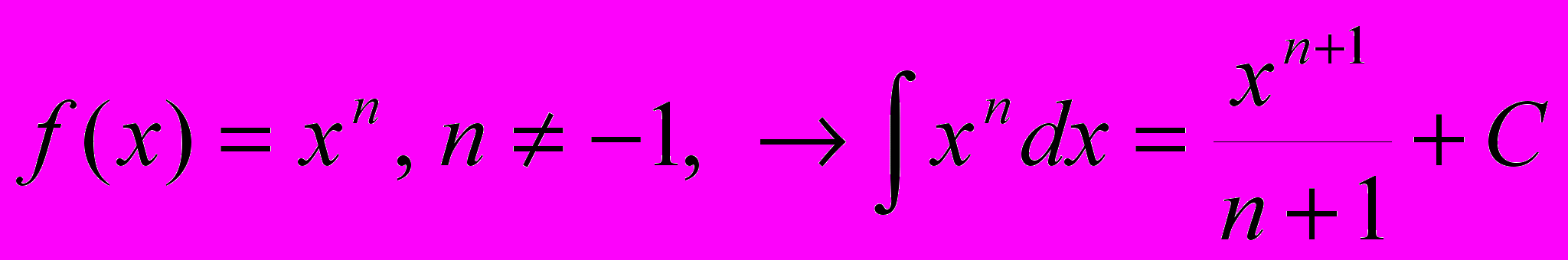 12.
12. 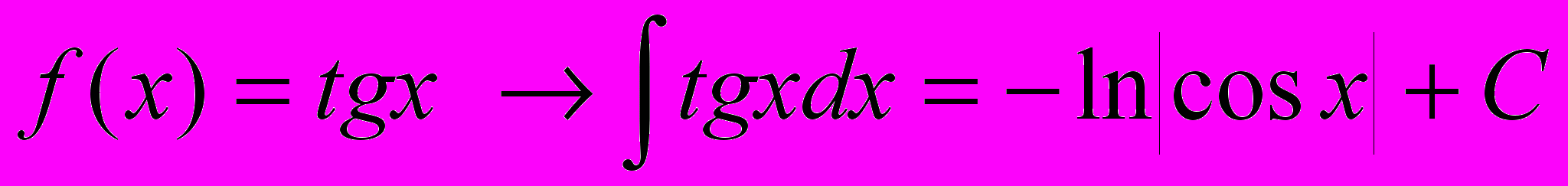
5.
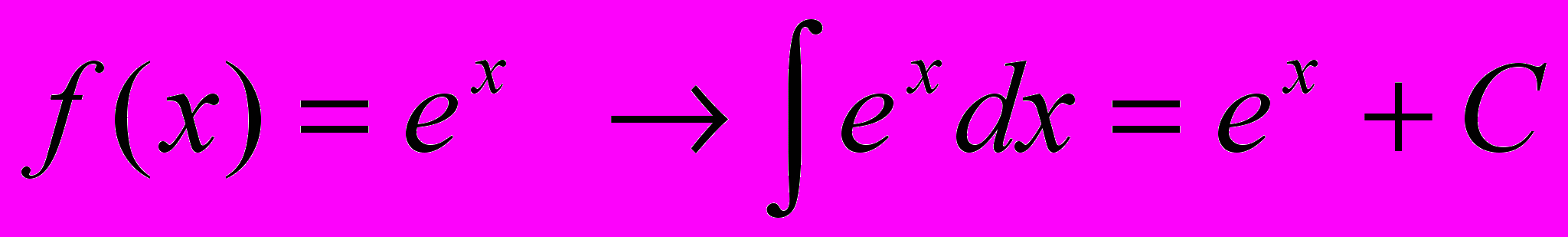 13.
13. 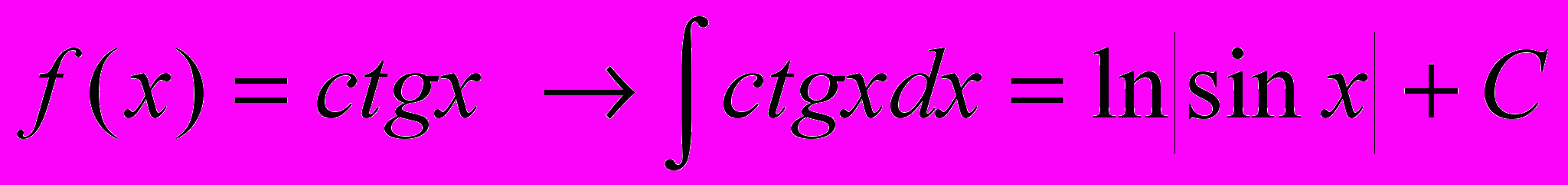
6.
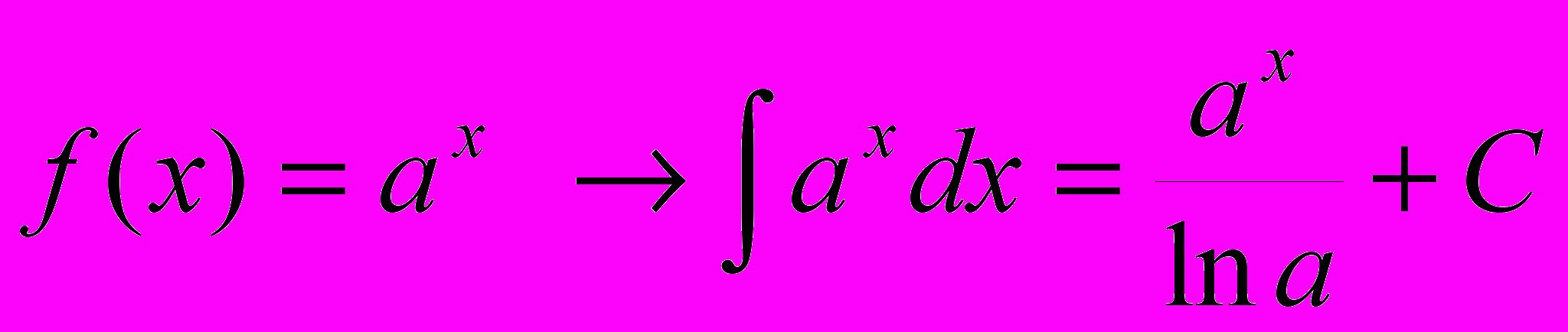 14.
14. 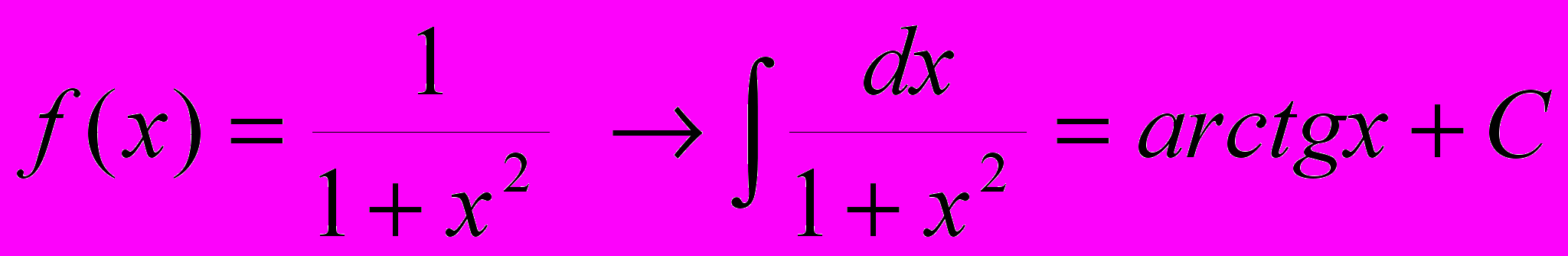
7.
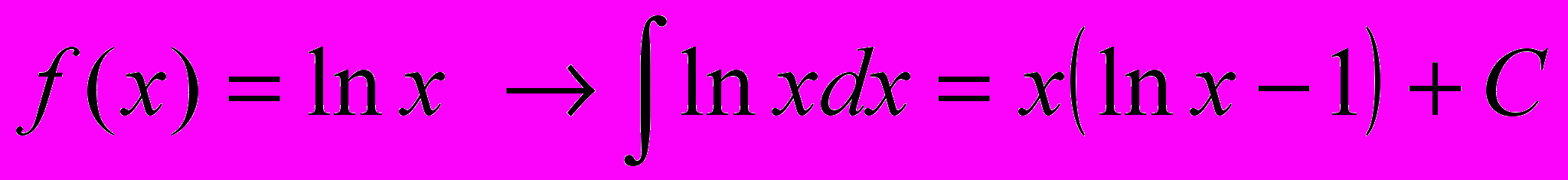 15.
15. 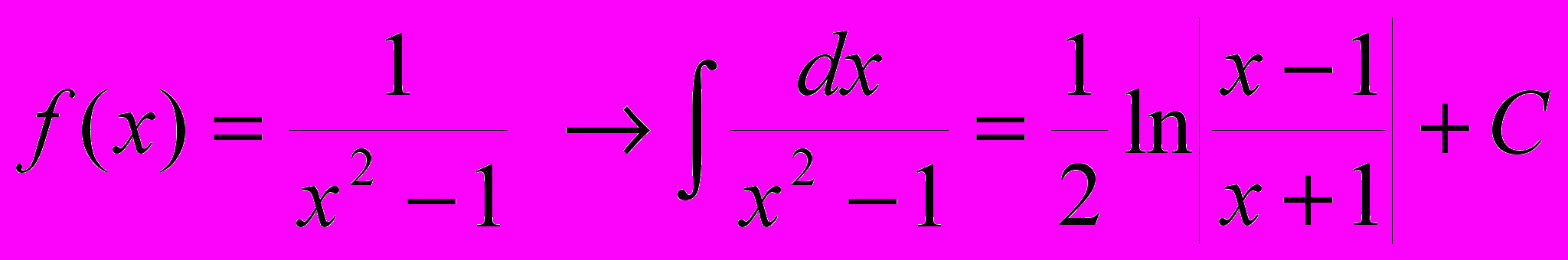
8.
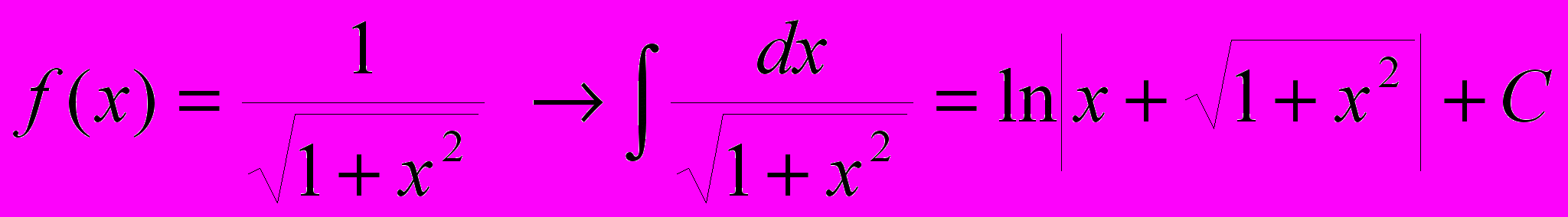 16.
16. 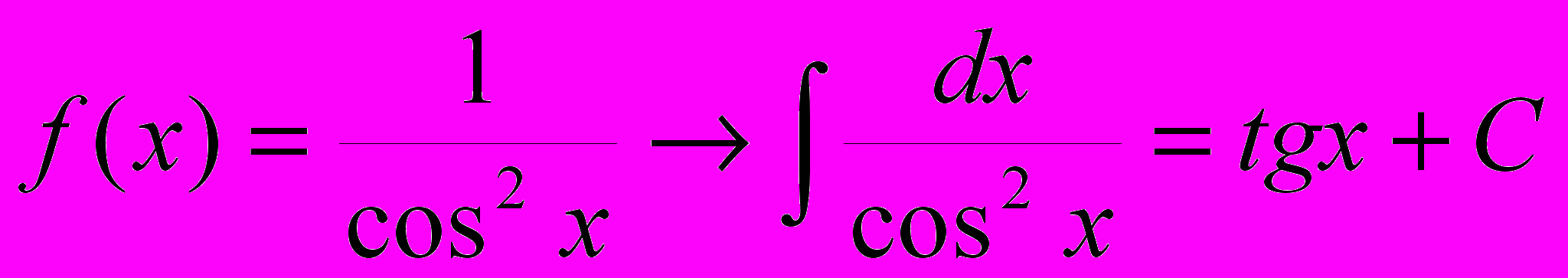
17.
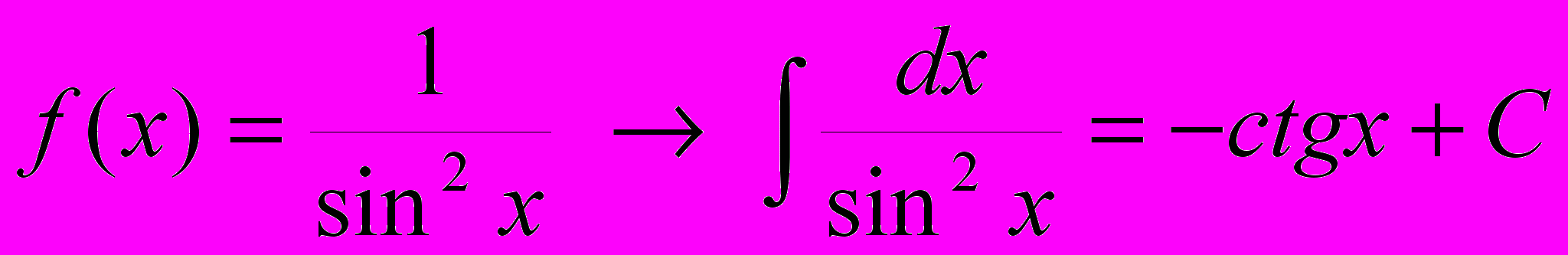 18.
18. 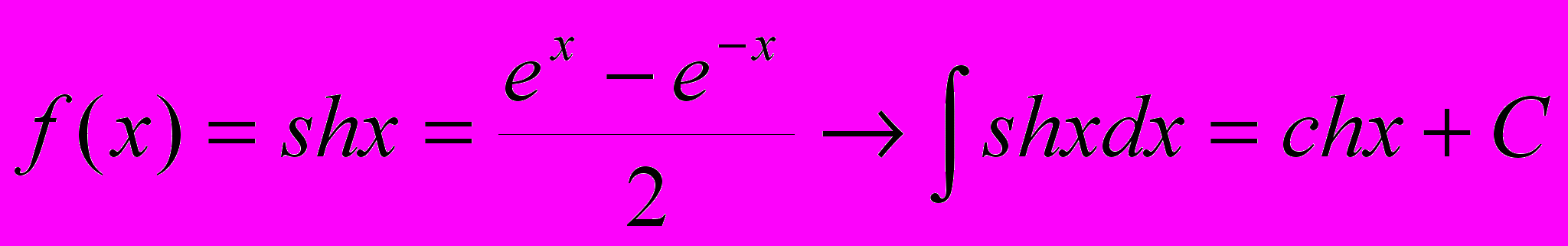
19.
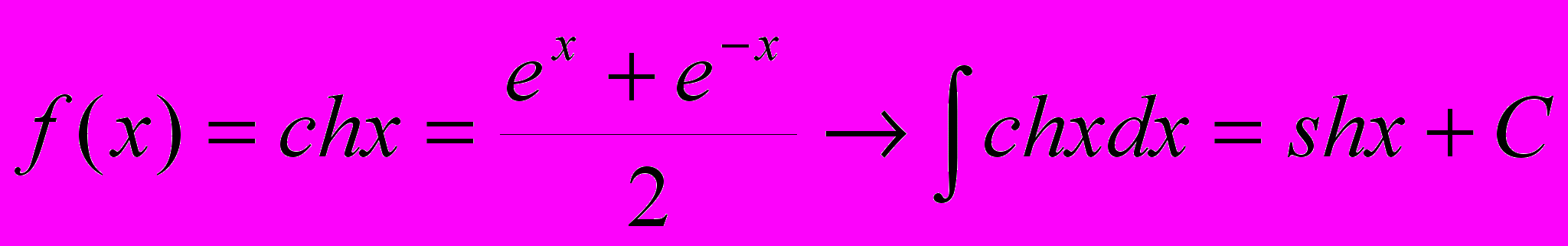 20.
20. 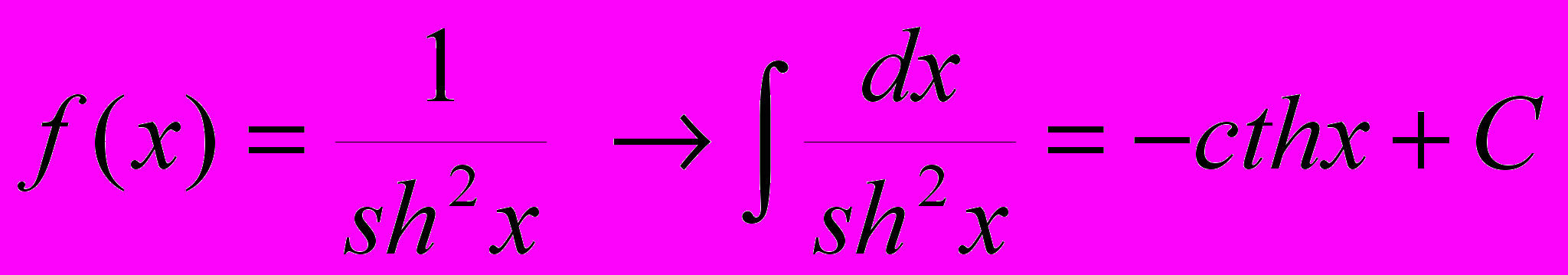
21.
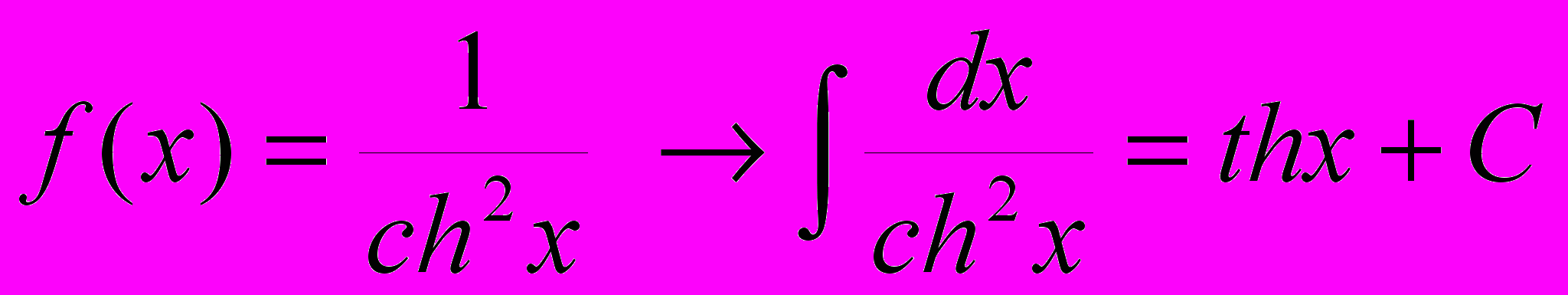 .
.УПРАЖНЕНИЕ.
1. Докажите формулу линейной замены :
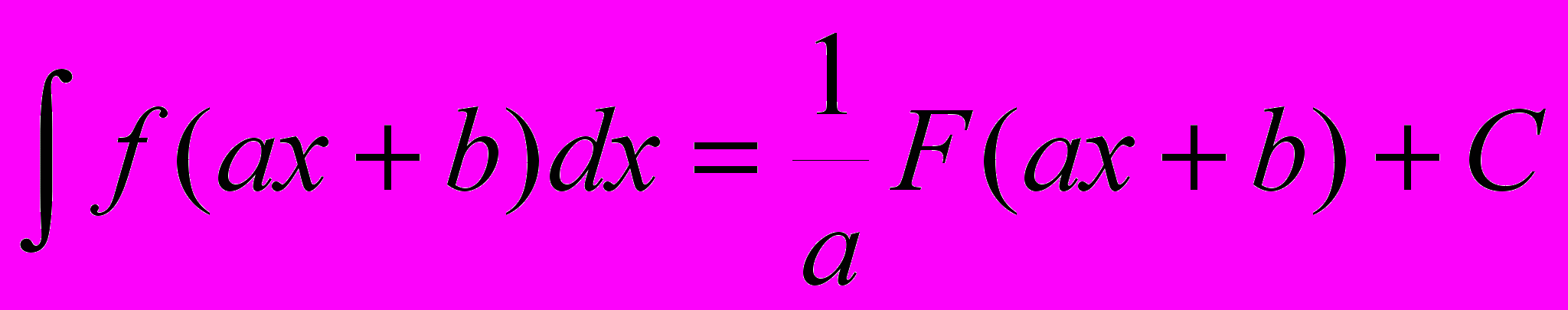
2. Вычислите интеграл
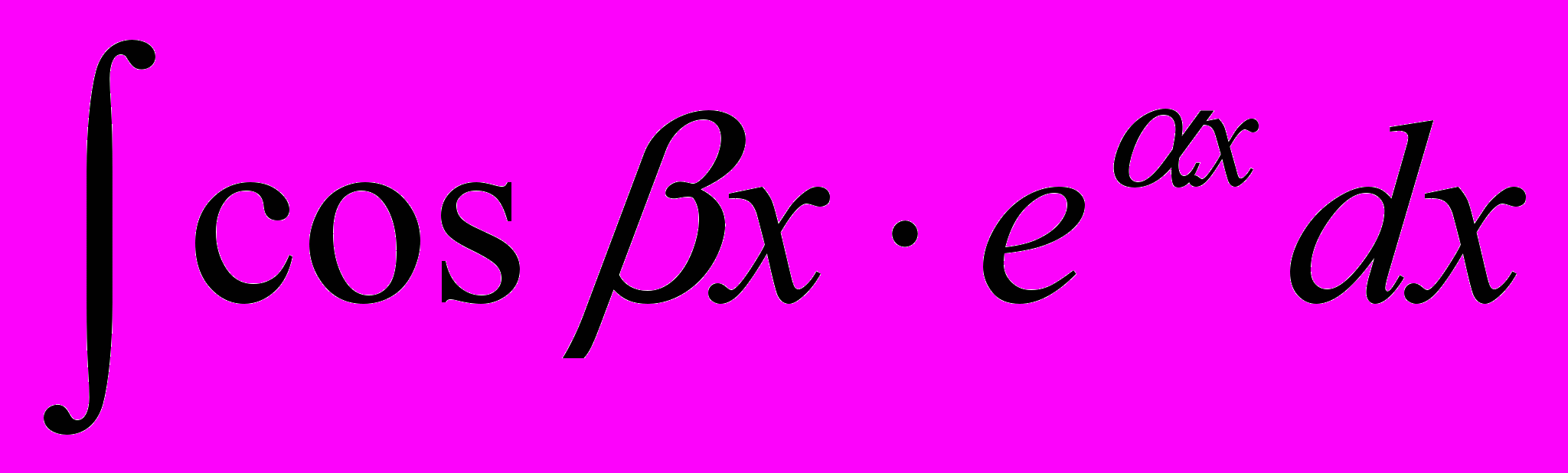 , используя представление
, используя представление 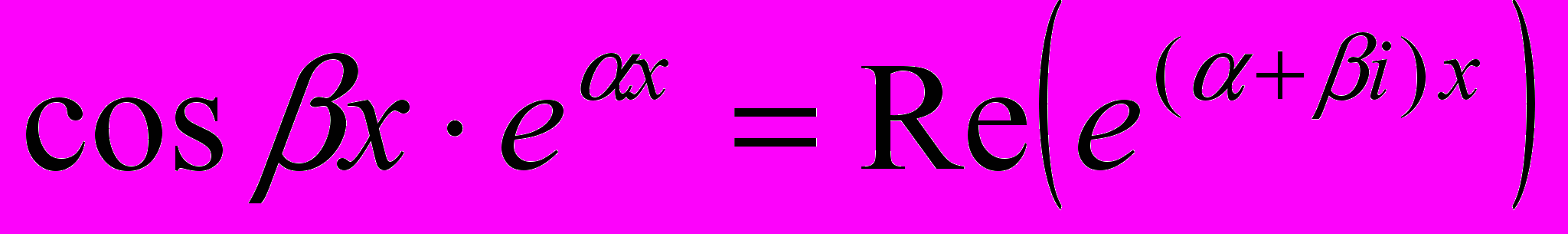 .
.ВОПРОСЫ К ЭКЗАМЕНУ.
1) Понятие неопределенного интеграла. Теорема о структуре множества первообразных.
2) Теорема о замене переменной в неопределенном интеграле. Примеры.
3) Теорема об интегрировании по частям в неопределенном интеграле. Примеры.
4) Таблица неопределенных интегралов.
