Первообразная. Неопределённый интеграл

Вид материала

Документы

Содержание C  – любая постоянная, называемая постоянной интегрирования

Подобный материал:

• Интегральное исчисление неопределённый интеграл § Первообразная функция и неопределённый, 83.07kb.
• Задачи, приводящие к понятию определенного интеграла. Определенный интеграл и его свойства., 79.79kb.
• Правила дифференцирования, исследование функций; ( в 1 сем) основы интегрального исчисления:, 10.67kb.
• Лекция 12. Первообразная и неопределённый интеграл, 41.05kb.
• Урок алгебры и начал анализа в 11 классе. Тема: «Первообразная и интеграл», 73.08kb.
• Курс многочлен с одной переменной и его корни, 32.04kb.
• Домашнее задание №2 Неопределенный интеграл Составили дз №2 Хомутова Л. Ю., Мишина, 22.72kb.
• Лекция 14. Неопределенный интеграл, 26.23kb.
• Неопределенный интеграл, 106.73kb.
• Анализа и теории функций календарныйпла нучебных занятий по дисциплине "Высшая математика", 54.18kb.

Первообразная. Неопределённый интеграл

 

Первообразная. Неопределённый интеграл.

Постоянная интегрирования.

 

 

Первообразная. Непрерывная функция  F ( x ) называется  первообразной для функции  f ( x ) на промежутке  X ,  если для каждого   

 

F’ ( x ) = f ( x ).

                 

П р и м е р . Функция  F ( x ) = x ³ является первообразной для функции

                        f ( x ) = 3x ²  на интервале  ( так как

 

                                               F’ ( x ) = ( x ³ )’  = 3x ² =  f ( x )

 

                       для всех  x ( .

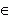                       Легко проверить, что функция x ³ + 13 имеет ту же производную

                       3x ², поэтому x ³ + 13 также является первообразной для функции

                       3x ²  для всех   x 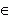( . Ясно, что вместо 13 можно взять

                       любую постоянную.

 

Таким образом, задача нахождения первообразной имеет бесчисленное множество решений. Этот факт нашёл отражение в определении неопределённого интеграла.

 

Неопределённый интеграл функции  f ( x ) на промежутке  X есть множество всех её первообразных. Это записывается в виде:



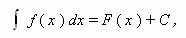
где  C  – любая постоянная, называемая постоянной интегрирования.

 

Основные свойства неопределённого интеграла

Если функция  f ( x ) имеет первообразную на промежутке  X, и  k – число, то



Короче: постоянную можно выносить за знак интеграла.

Если функции  f ( x )  и  g ( x ) имеют первообразные на промежутке  X , то



Короче: интеграл суммы равен сумме интегралов.

Если функция  f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:



 

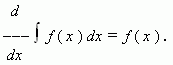
Короче: производная от интеграла равна подынтегральной функции.

 

Если  функция  f ( x )  непрерывна на промежутке  X  и дифференцируема во внутренних точках этого промежутка, то:



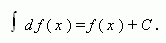
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.