Лекция 26. Неопределённый интеграл или свойства первообразных Вматематике как и в жизни нередко действию можно сопоставить обратное действие. По отношению к дифференцированию таким обратным действием является интегрирование
| Вид материала | Лекция |
- Задачи, приводящие к понятию определенного интеграла. Определенный интеграл и его свойства., 79.79kb.
- Интегральное исчисление неопределённый интеграл § Первообразная функция и неопределённый, 83.07kb.
- Вопросы для вступительных экзаменов по магистратуре специальности, 92.59kb.
- Лекция 14. Неопределенный интеграл, 26.23kb.
- Лекция 12. Первообразная и неопределённый интеграл, 41.05kb.
- Социология, 164.17kb.
- Анализа и теории функций календарныйпла нучебных занятий по дисциплине "Высшая математика", 54.18kb.
- Домашнее задание №2 Неопределенный интеграл Составили дз №2 Хомутова Л. Ю., Мишина, 22.72kb.
- Самооценка знаний и умений «атом», 39.57kb.
- Психология как наука о душе ведет свое начало с глубокой древности. Что есть душа?, 176.12kb.
Интегральное исчисление
Лекция 26. Неопределённый интеграл или свойства первообразных
В математике как и в жизни нередко действию можно сопоставить обратное действие. По отношению к дифференцированию таким обратным действием является интегрирование.
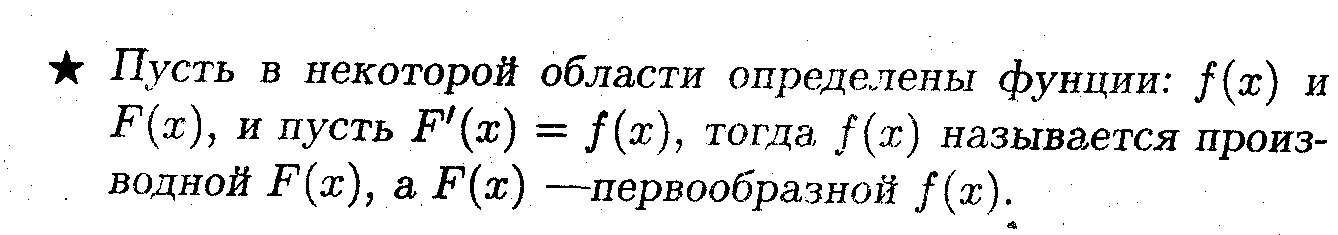
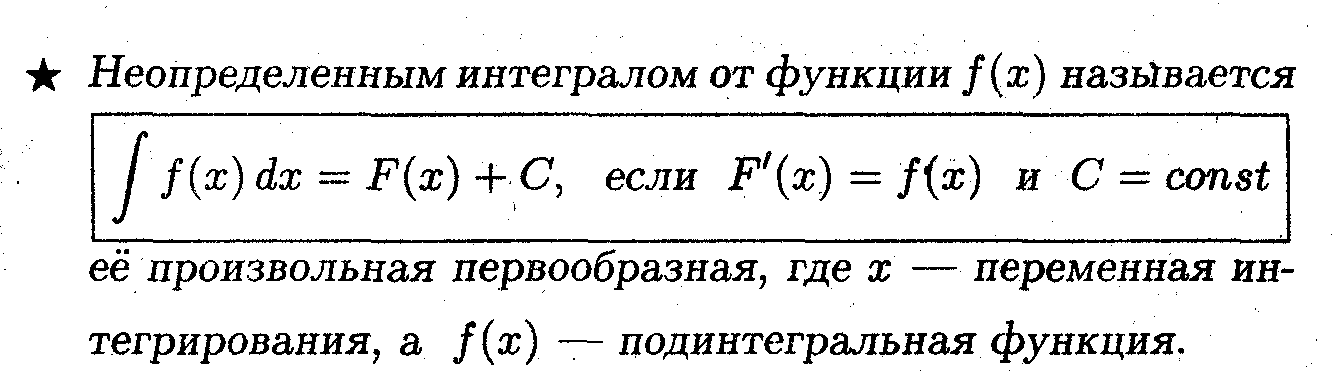
Свойства неопределенного интеграла.
Задача 2
Чему равен дифференциал неопределённого интеграла?
- d ∫ f(x) dx = d(F(x) + С) = dF(x) + dC = F'(x) dx = f(x) dx
1. Дифференциал неопределённого интеграла равен подынтегральному выражению
d ∫ f{x) dx = f(x) dx.
Задача 3
Чему равен неопределённый интеграл дифференциала?
- ∫ dF(x)= ∫ f(x) dx=F(x)+C
2. Неопределённый интеграл дифференциала функции равен самой функции с точностью до произвольной постоянной
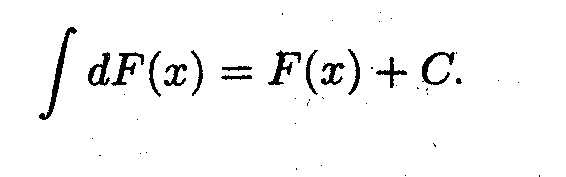
Задача 4
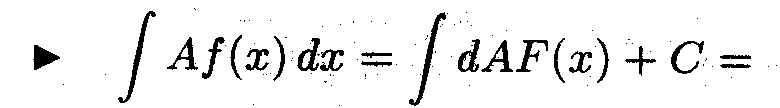
• Поскольку С произвольная постоянная, то после каждого равенства она может переопределяться, что здесь и в дальнейшем неоднократно используется.
3. Постоянная выносится из под знака интеграла
Задача 5
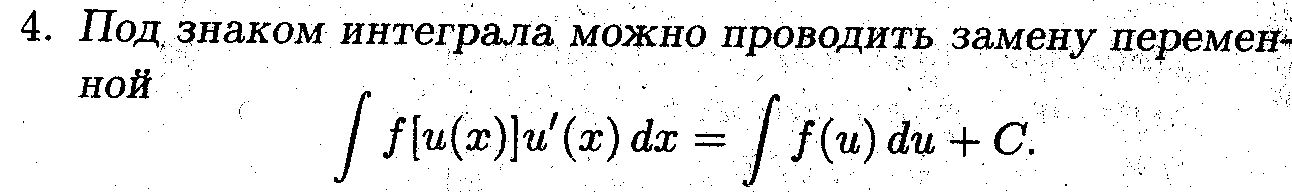
5. Интеграл суммы равен сумме интегралов с точностью до произвольной постоянной (показать самостоятельно)
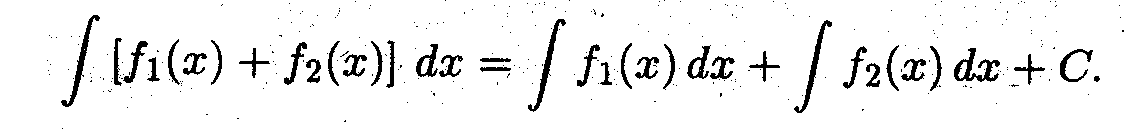
Задача 6
Получить таблицу первообразных, исходя из таблицы производных.
Лекция 27. Определённый интеграл и его свойства
Определённый интеграл отличается от неопределённого тем, что это либо число, либо первообразная с определённой постоянной.
Механический смысл определённого интеграла
Задача 1
На графике ускорения отобразить скорость, а на графике скорости отобразить путь, пройденный телом при равноускоренном движении от t = 0 до момента t, если в начальный момент времени скорость и путь равны нулю.
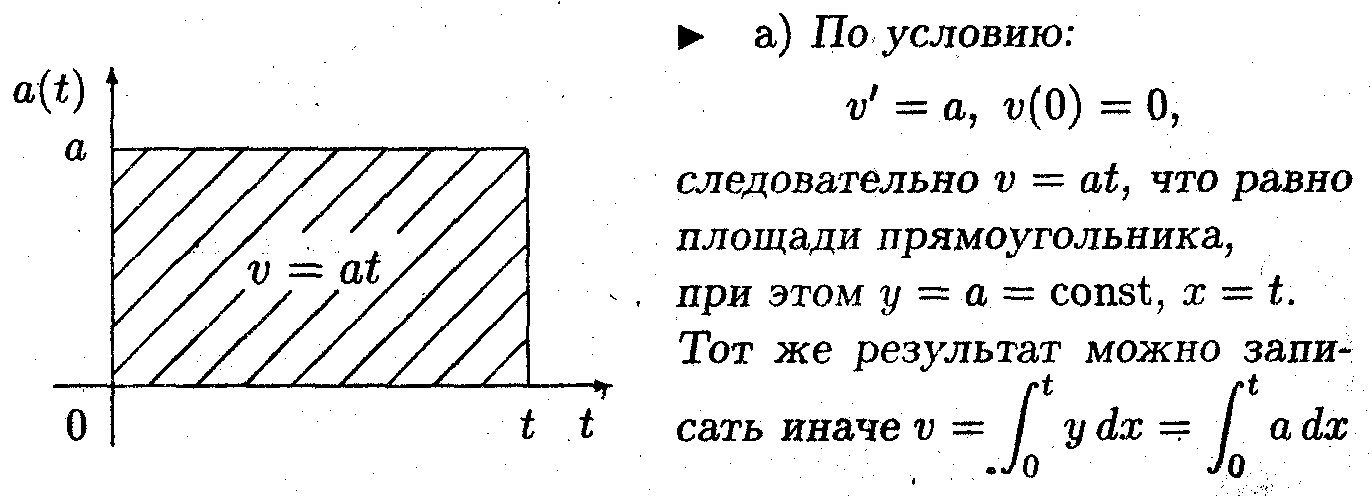
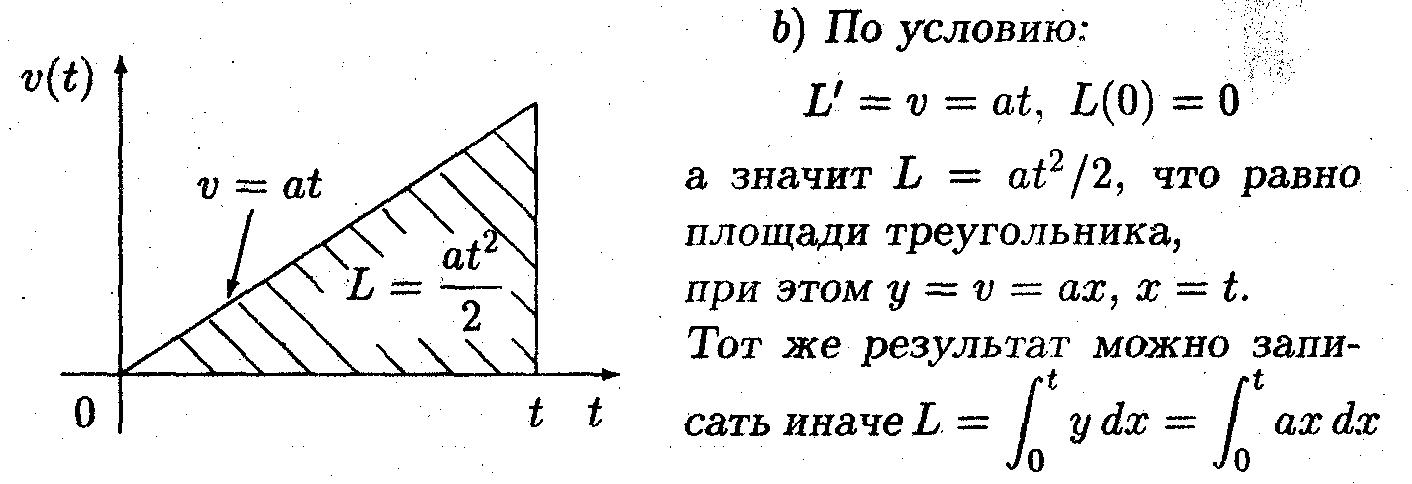
Геометрический смысл определённого интеграла
Определённый интеграл равен площади криволинейной трапеции.
Задача 2
Представить определённый интеграл как предел некоторой суммы.
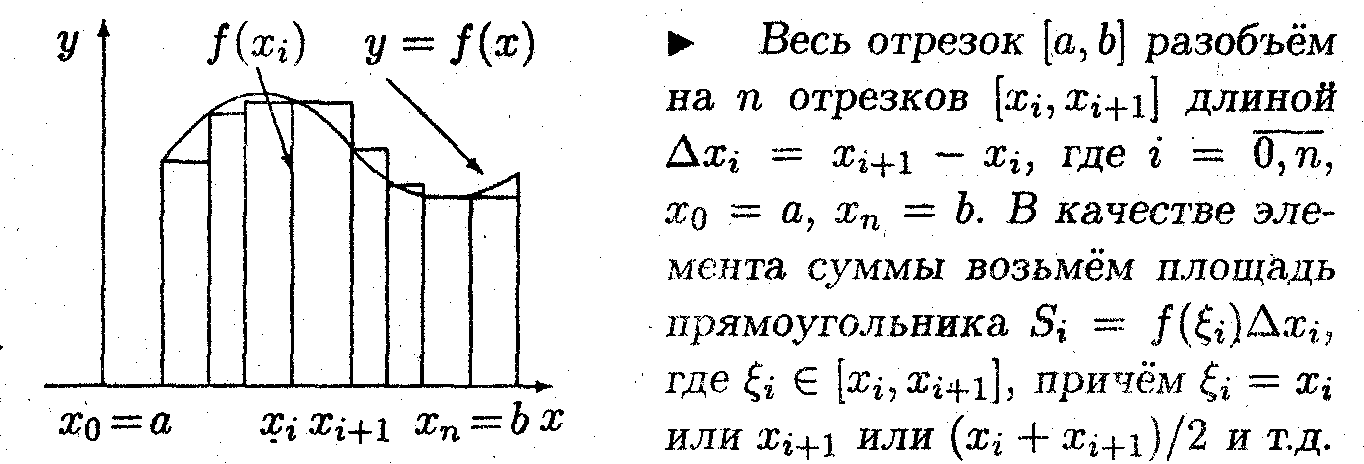
Тогда сумма площадей прямоугольников для каждого ξi имеет вид
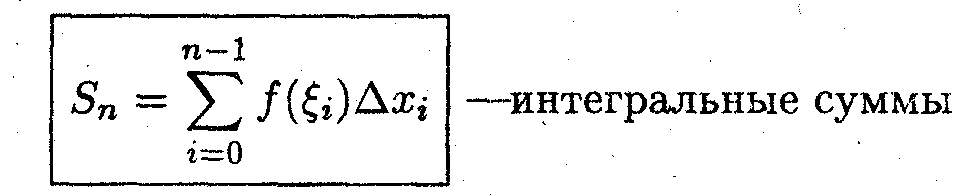
Интуитивно ясно, что при n —> ∞ все интегральные суммы стремятся к площади криволинейной трапеции
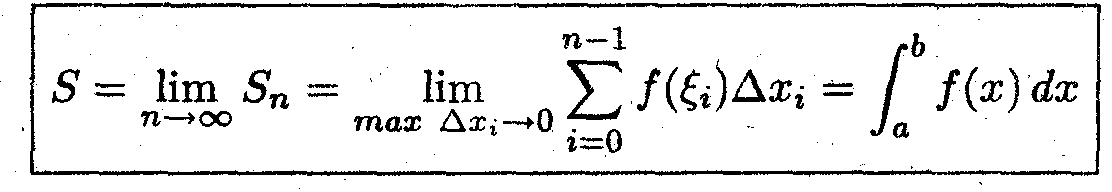
Определённым интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при стремлении максимального частичного отрезка разбиения к нулю.
Числа а и b носят название, соответственно, нижнего и верхнего пределов интегрирования.
Формула Ньютона - Лейбница
Задача 3
Пусть функция f(x) определена, непрерывна и имеет первообразную F(x) на отрезке [a,b]. Показать, что тогда определённый интеграл находится по формуле:
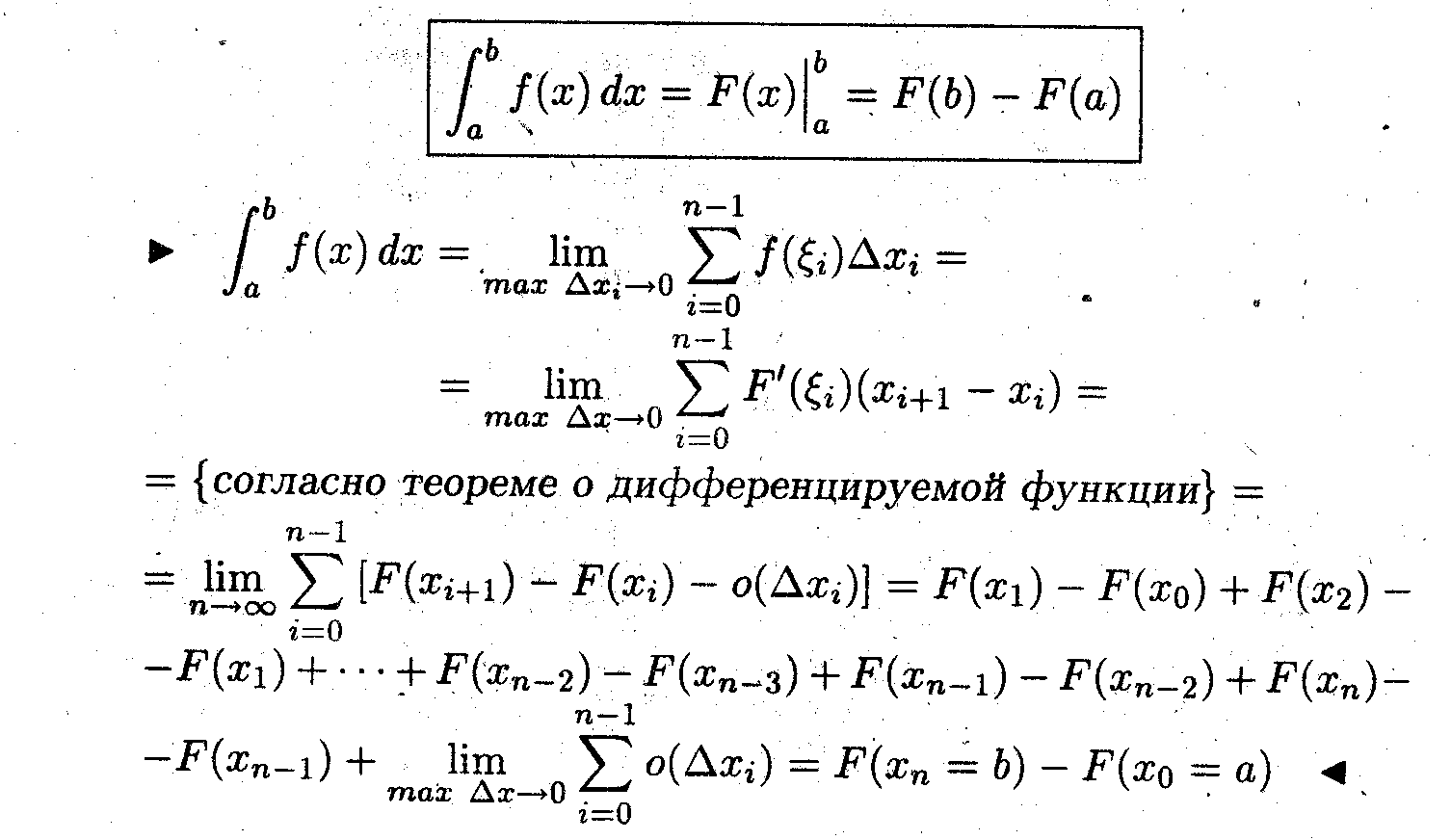
Свойства определённого интеграла
Задача 4
Дать краткое обоснование каждому из приведённых ниже свойств.
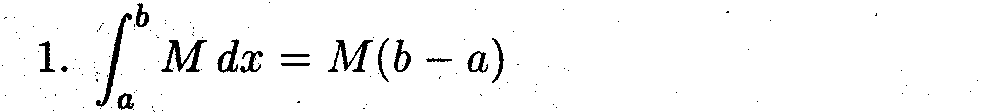
• Это простейший пример формулы Ньютона-Лейбница.
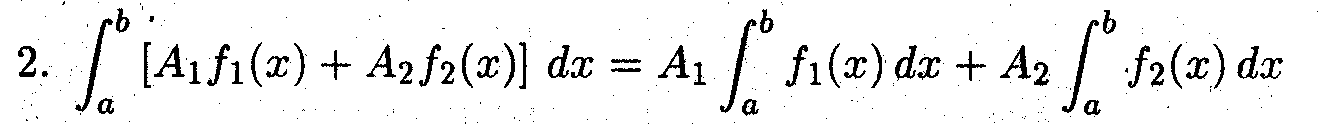
• Используется, что предел суммы равен сумме пределов.
• Используется свойство аддитивности сумм.
• Можно сослаться на формулу Ньютона-Лейбница.
• Следует из аналогичного неравенства для интегральных сумм.
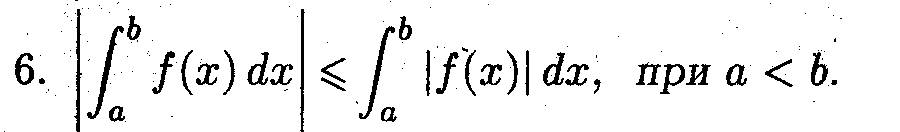
• Неравенство очевидно, если иметь ввиду, что определённый интеграл на отрезке, где функция отрицательна — отрицателен.
Лекция 28. Замена переменной и интегрирование по частям в определённом интеграле
Сегодня вам предоставляется возможность познакомиться с двумя самыми популярными методами интегрирования.
Задача 1
Пусть функция f(x) имеет первообразную F(x)
Показать, что
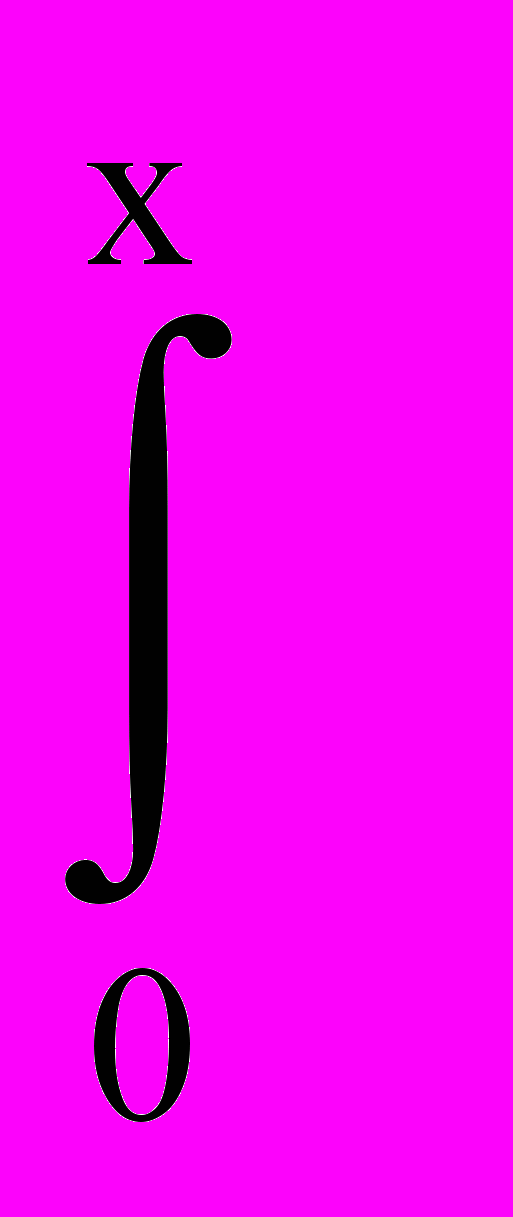f(u)du также первообразная f(x).- Вычислим производную от интеграла с переменным верхним пределом:
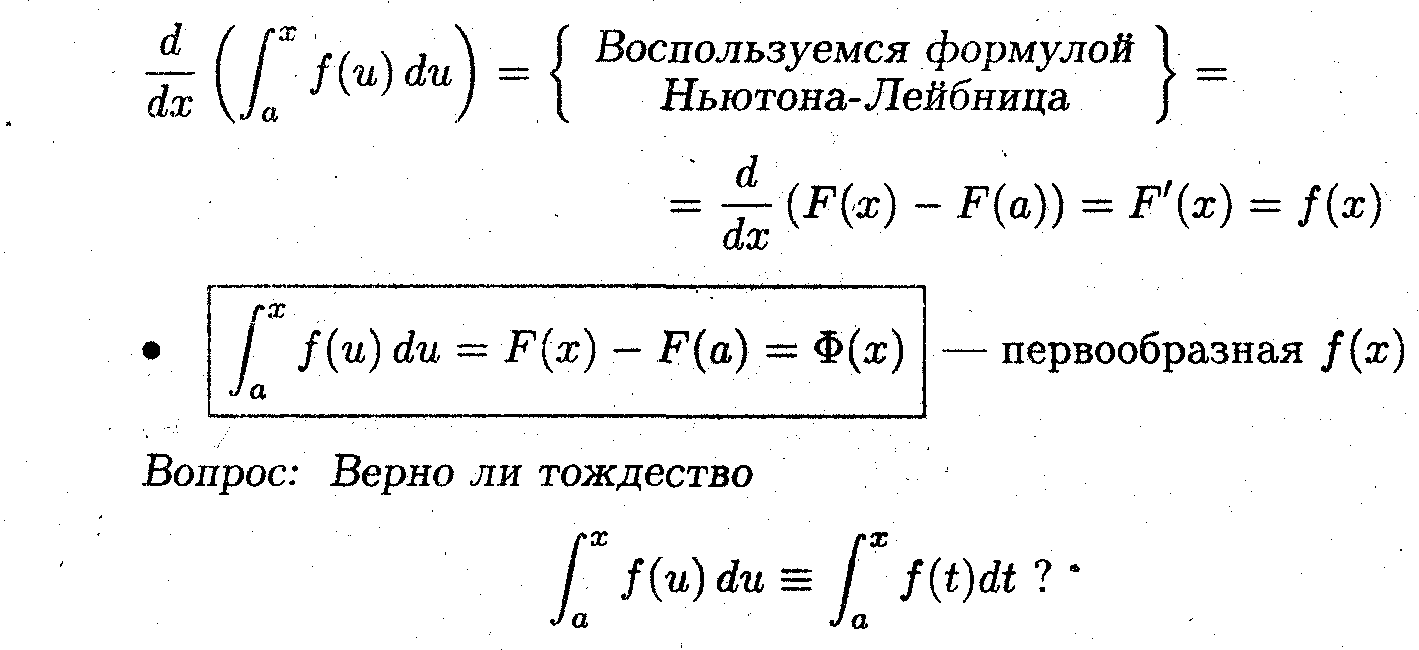
Ответ: Да! Переобозначение переменной интегрирования — это не замена переменной интегрирования.
• Не всякий определённый интеграл с переменным верхним пределом может быть выражен в виде комбинации элементарных функций. В качестве примера таких интегралов, которые получили название специальных функций, приведём
Задача 2 (теорема о среднем)
Пусть функция f(x) непрерывна на отрезке [а,b].
Показать, что в этом случае найдется такая точка ξ
(a,b) ,что выполняется 
- Будем исходить из формулы Ньютона-Лейбница
Вопрос: Каков геометрический смысл теоремы о среднем?
Ответ: Всегда можно подобрать такую высоту прямоугольника, чтобы его площадь равнялась площади криволинейной трапеции с тем же основанием.
Задача 3
Обосновать неравенство
- Неравенство является очевидным следствием Задачи 2.
Задача 4 (о замене переменной)
Пусть f [u(х)] непрерывна, а u(х) дифференцируема, на [a,b], причём u(a) = с, u(b) = d
Показать, что:
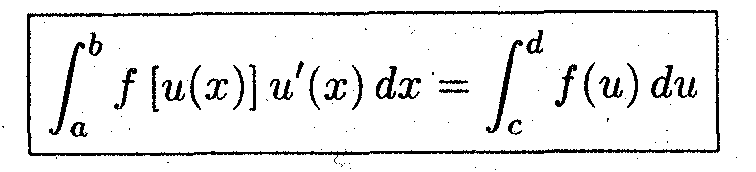
• Пределы интегрирования изменяются!
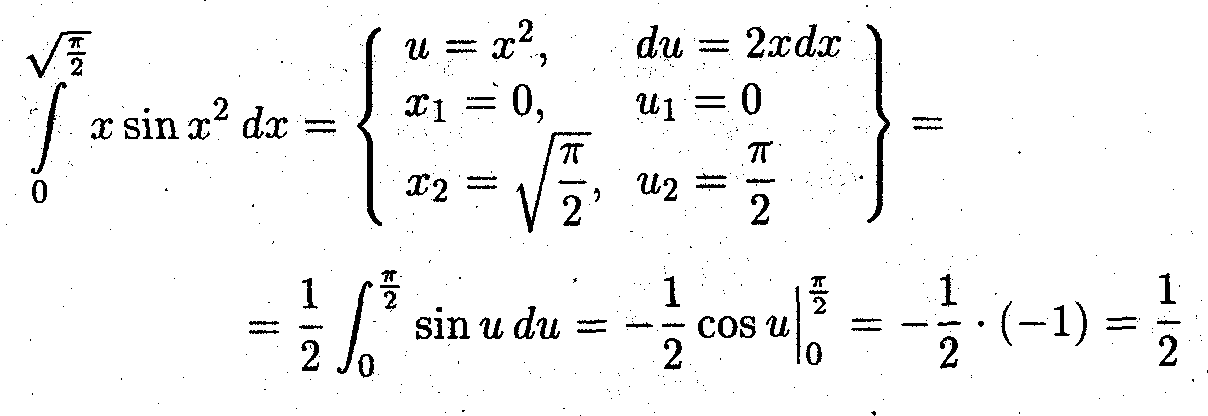
Задача 5 (об интегрировании по частям)
Выполнить перенос производной под знаком интеграла
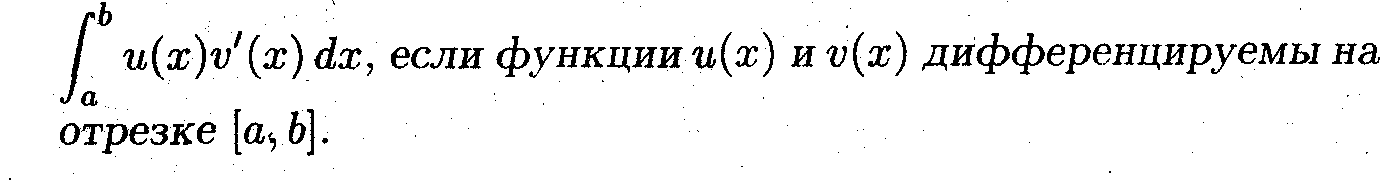
Вопрос: Какое выражение связывает uv' и u'v?
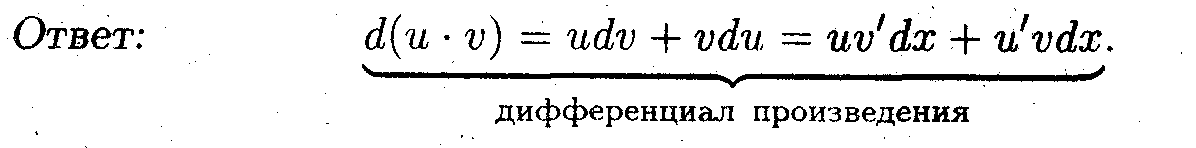
Теперь проинтегрируем это равенство
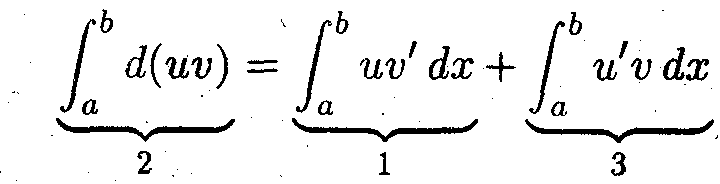
и окончательно получим:
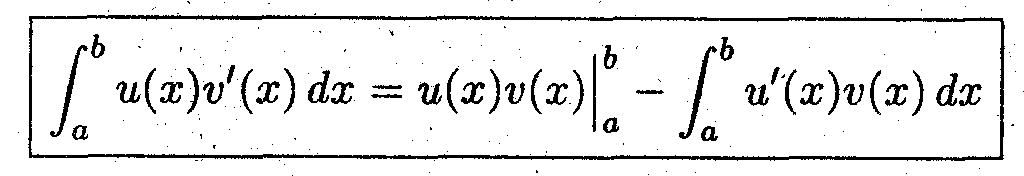
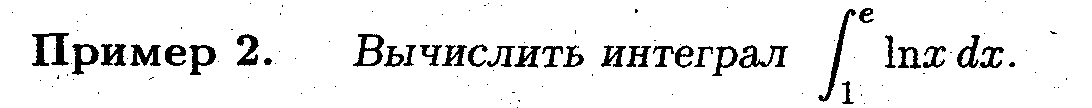
Задача 6
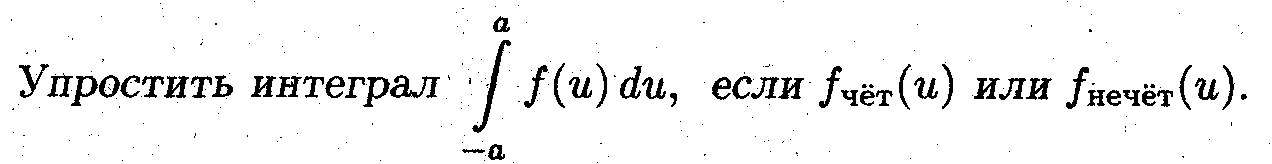
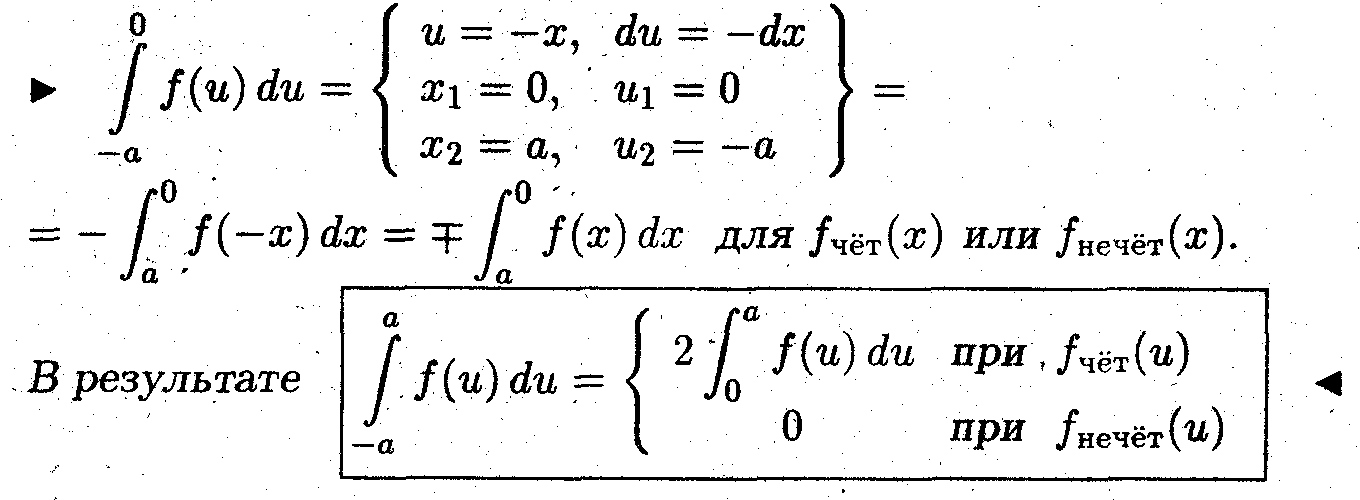
Лекция 29. Методы интегрирования
Всякое обратное действие сложнее прямого. Это в полной мере относится к такому действию как интегрирование. Прежде чем воспользоваться таблицей интегралов необходимо заданный интеграл преобразовать к табличному.
Метод замены переменной интегрирования
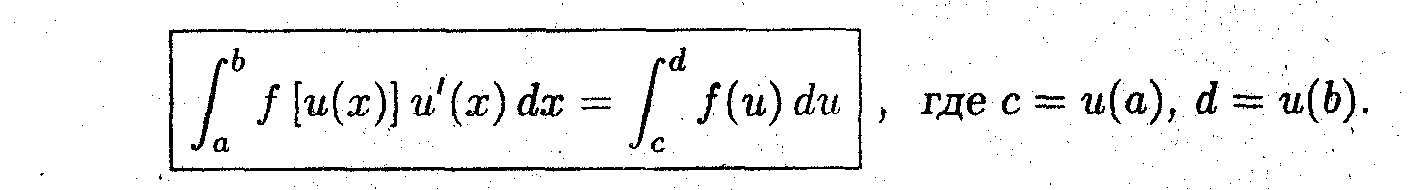
Это наиболее часто используемый метод. Он применяется, когда подинтегральная функция является сложной функцией.
Метод интегрирования по частям
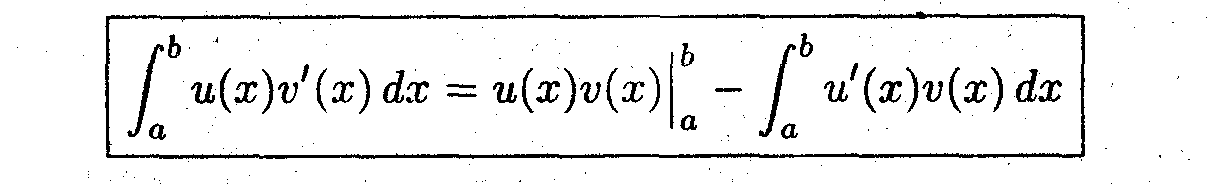
Этот метод применяется тогда, когда подинтегральная функция содержит:
1. Какую-либо обратную функцию: ln x, arcsinx, arccos x и т.д.
2. Произведение степенной функции на экспоненту или тригонометрическую функцию: xsinx, х2ехр х и т.д.
3. Произведение экспоненты на тригонометрическую функцию.
> Для вычисления интеграла от рациональной дроби необходимо:
а) привести эту дробь к правильной дроби, т.е.
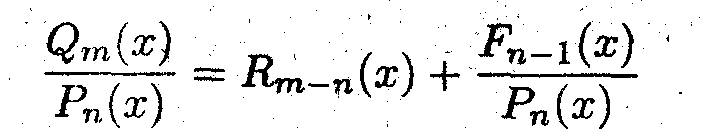
б) преобразовать знаменатель к произведению простейших многочленов, т.е.
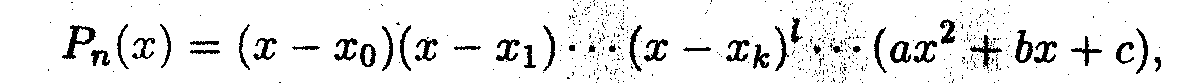
где x
- корень кратности l.в) записать правильную дробь в виде суммы простейших дробей т.е. /
где А, В,...., С, D, К,..., W, Z - неопределённые коэффициенты.
г) приводя сумму простейших дробей к общему знаменателю, получаем систему линейных алгебраических уравнений. Решая её, находим неопределённые коэффициенты.
д) окончательный ответ получится после вычисления интегралов от многочлена и простейших дробей
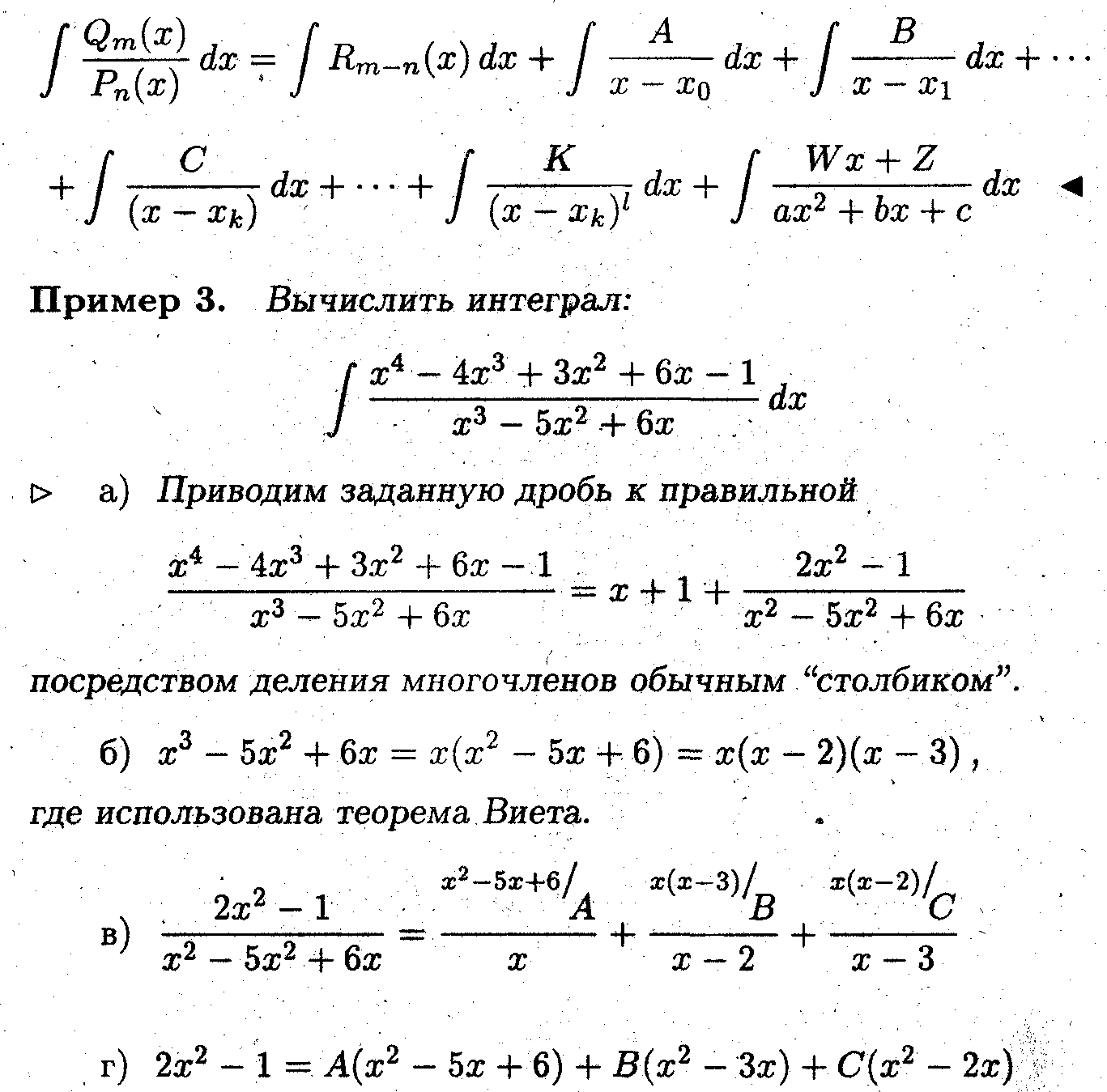
Многочлены равны, если все коэффициенты в них при соответствующих степенях между собой равны.
Лекция 30. Интегрирование иррациональных и тригонометрических выражений
В этой лекции будет продолжено изучение методов интегрального исчисления.
Дополнение к таблице интегралов
Пример 1. Показать, что
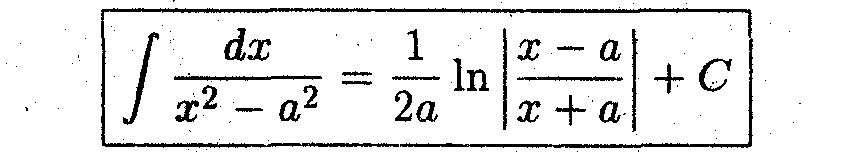
- Воспользуемся методом неопределённых коэффициентов.
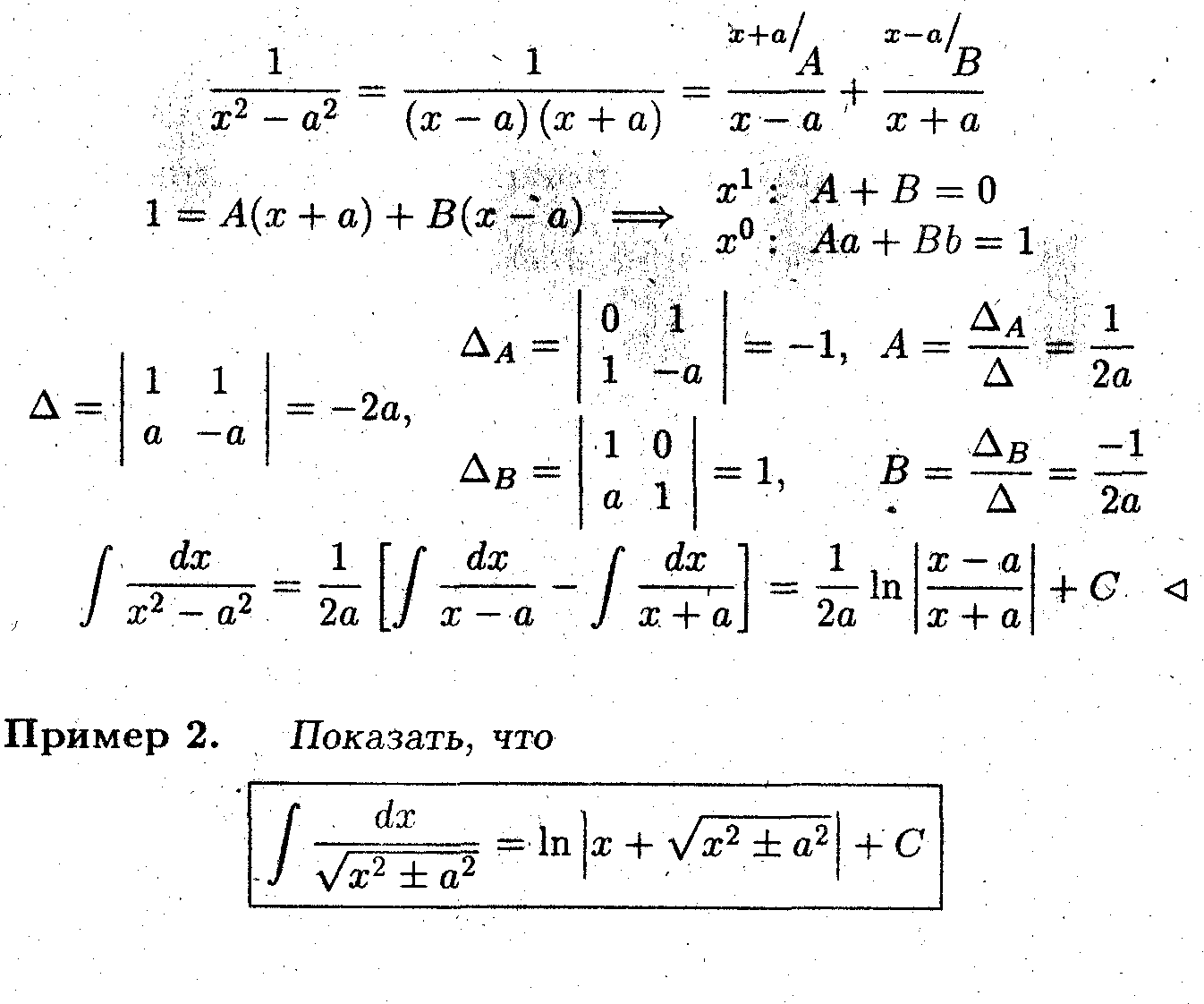
- Чтобы убедиться в правильности первообразной, достаточно вычислить её производную (F'(x) = f(x)). Но прежде ответьте на вопрос.
Вопрос: Как связана производная модуля функции с производной этой функции?
Интегрирование иррациональных выражений
1. Сведение к табличным интегралам.
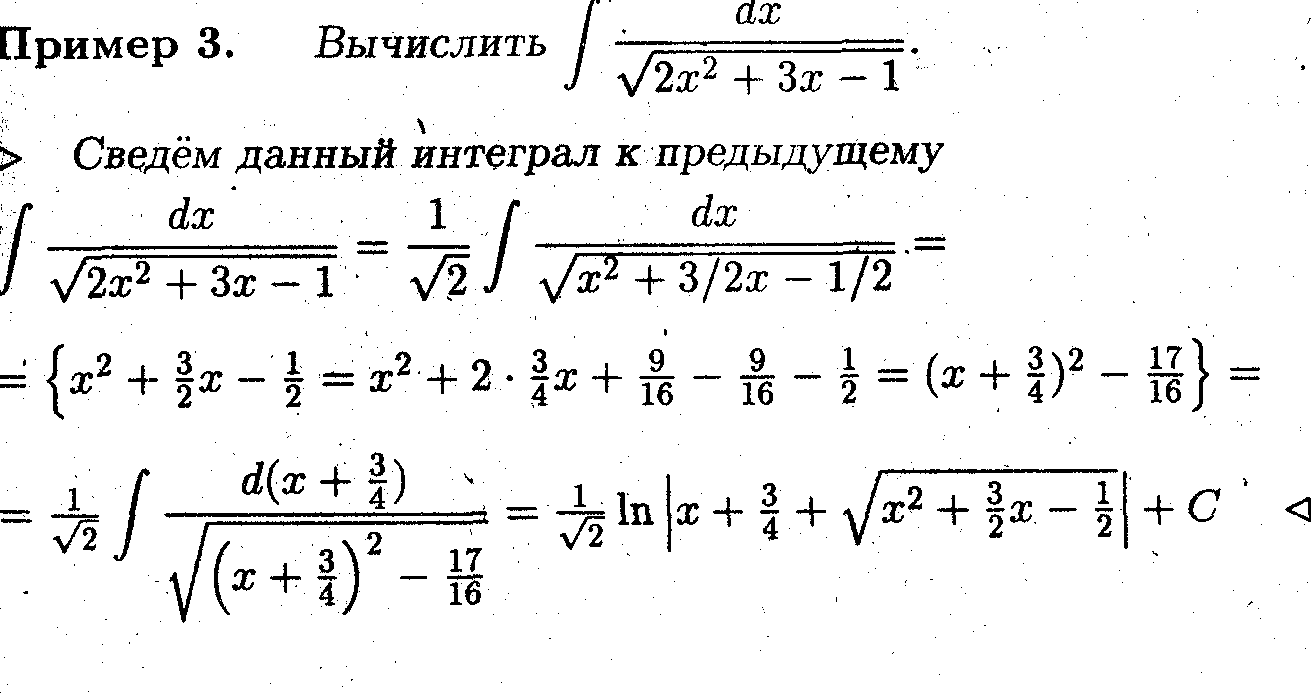
2. Замена переменных, приводящая к избавлению от иррациональности под знаком интеграла.
Вопрос: Как избавиться от иррациональности в интеграле
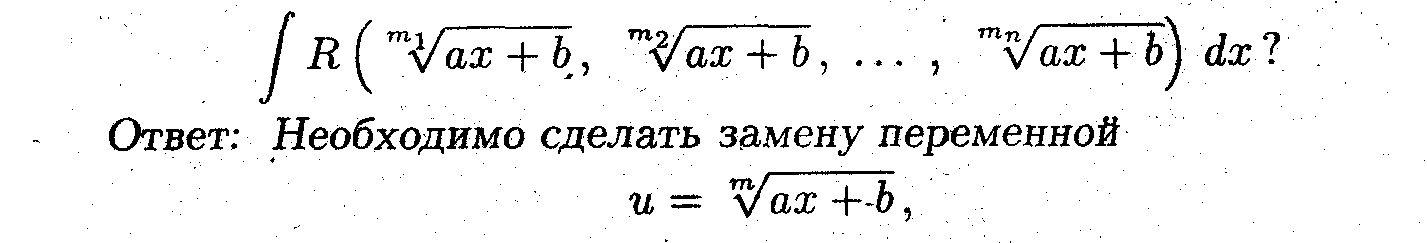
где m - наименьшее общее кратное.
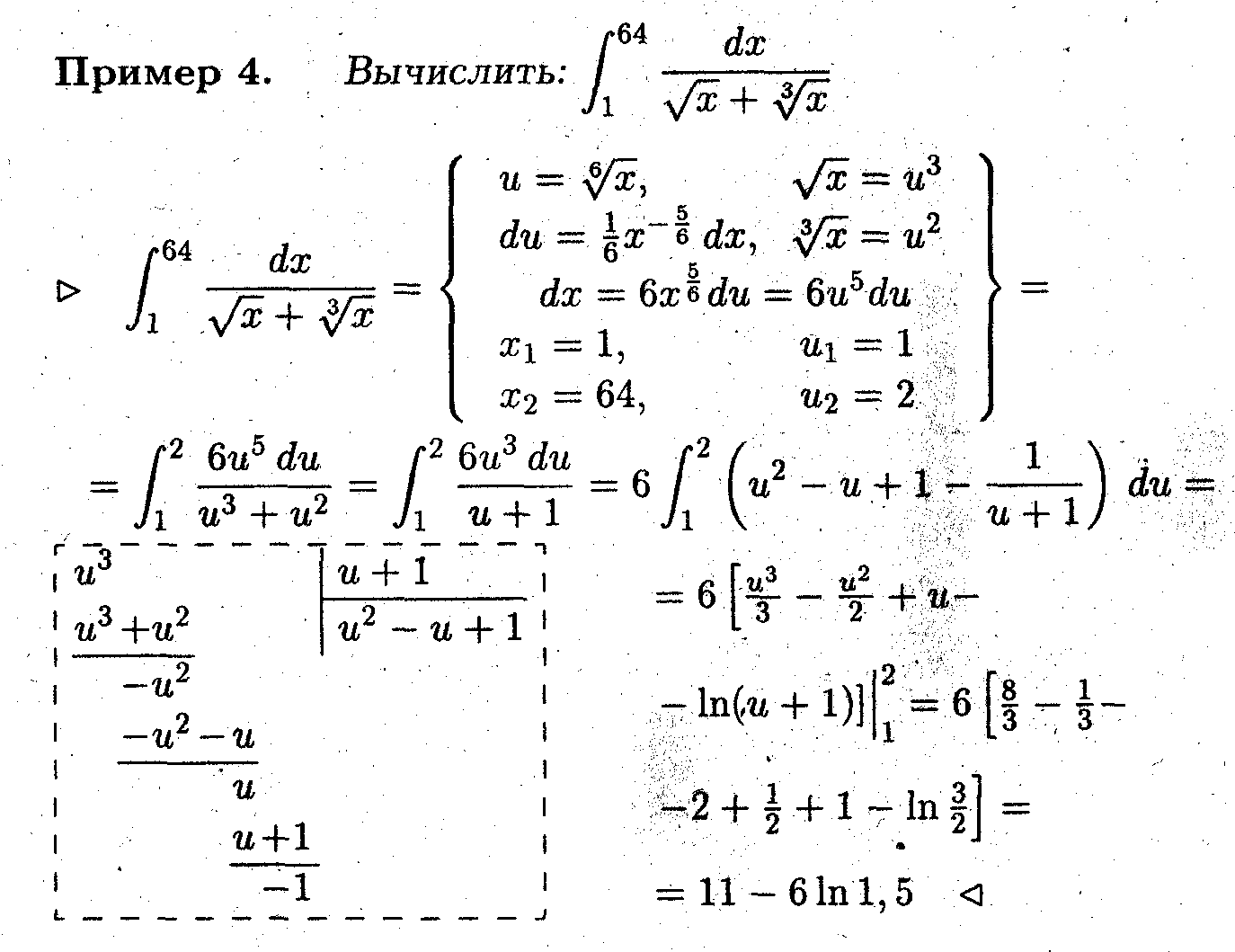
Интегрирование тригонометрических выражений
1. ∫ R(sinx,cosx) dx
Вычисление интеграла такого типа проводится при помощи универсальной тригонометрической подстановки: u = tg (x/2).
задача 1
Выразить sin x, cos x и dx через универсальную тригонометрическую подстановку.
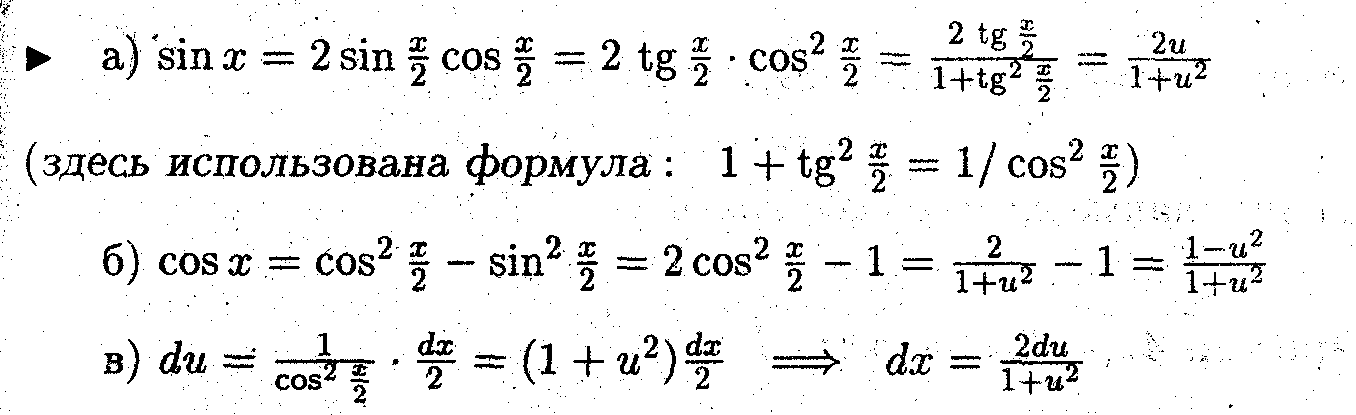
Таким образом универсальная тригонометрическая подстановка означает следующую замену переменной в интеграле:
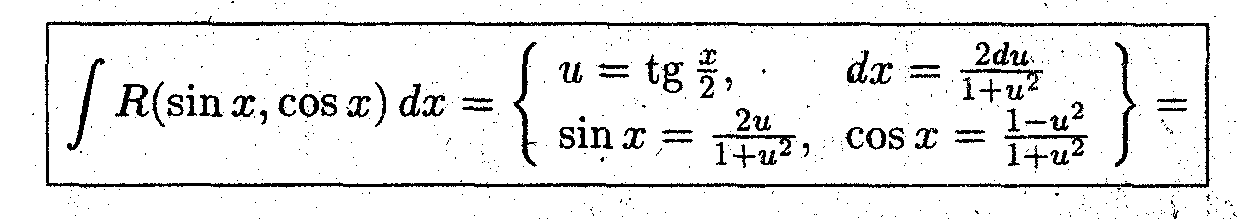
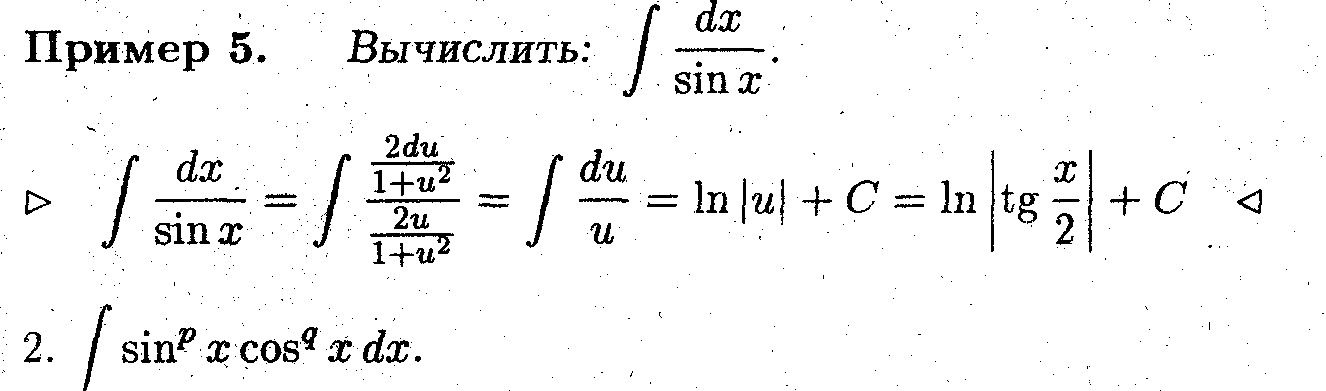
Вычисление интегралов такого типа осуществляется более простыми подстановками по сравнению с универсальной тригонометрической подстановкой:
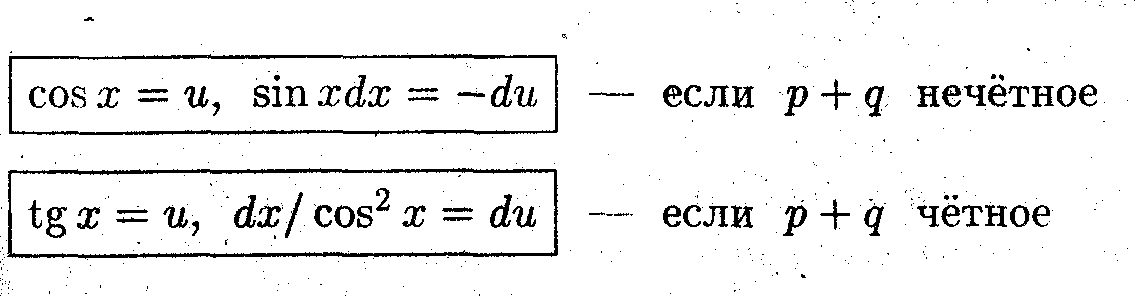
Лекция 31. Геометрические приложения определенных интегралов
Определение определённого интеграла как предела интегральных сумм позволяет получить различные формулы для нахождения длин, площадей и объёмов геометрических объектов.
задача1
Найти площадь криволинейной трапеции, ограниченной линиями:
у =f1(x), у = f2(x), x = а, x= b.
задача 2
Найти площадь криволинейного сектора, ограниченного линиями:
= (φ), φ= a, φ= β.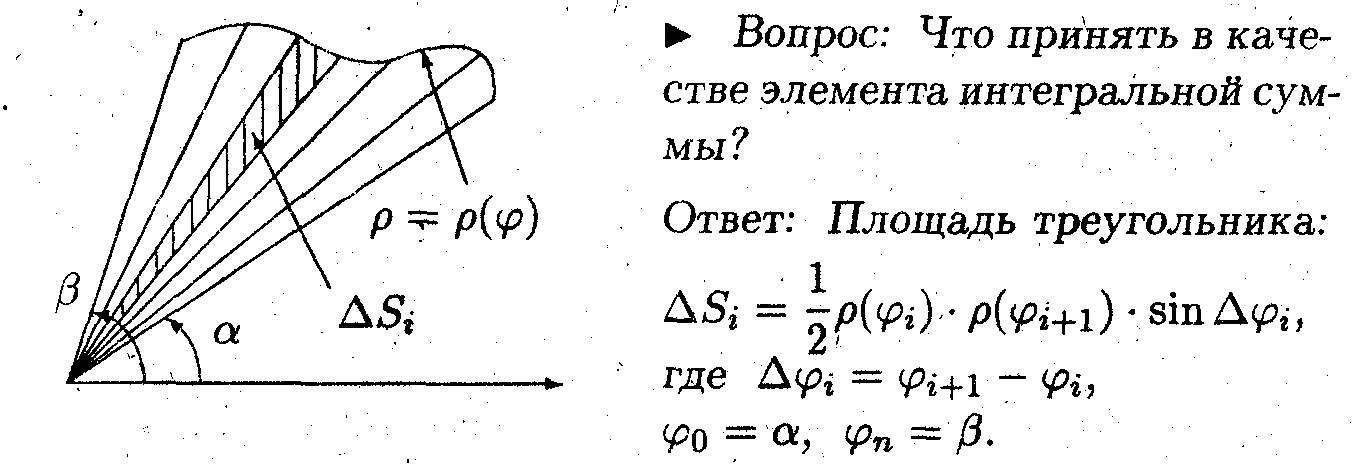
Вопрос: Чему равна эквивалентная площади треугольника?
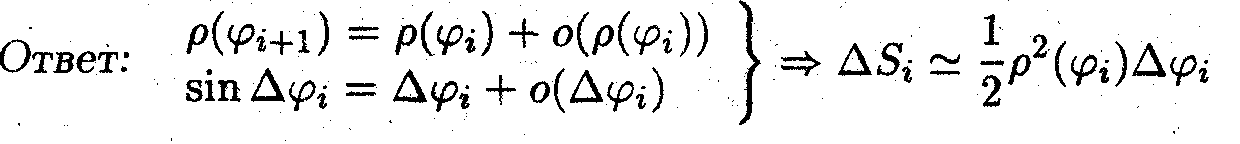
Действуя также как в Задаче 1, получим
Вопрос: Укажите пределы интегрирования для половинки заштрихованного лепестка.
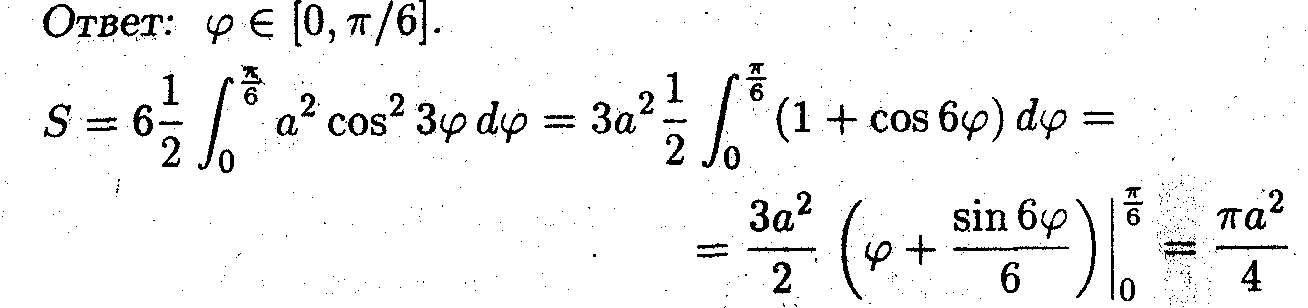
задача 3
В результате
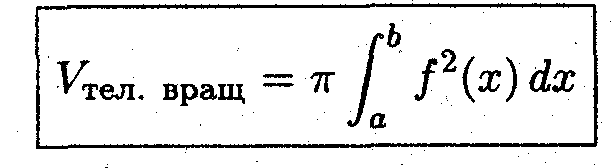
Пример 2. Найти объём шара радиуса R.
- Вопрос: Вращением какой кривой описывается шар?
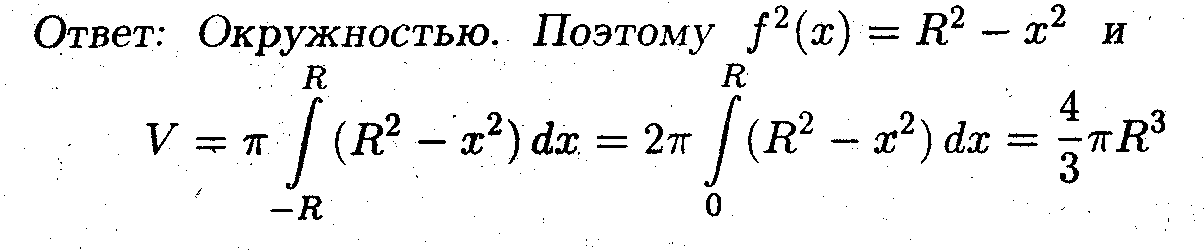
задача 4
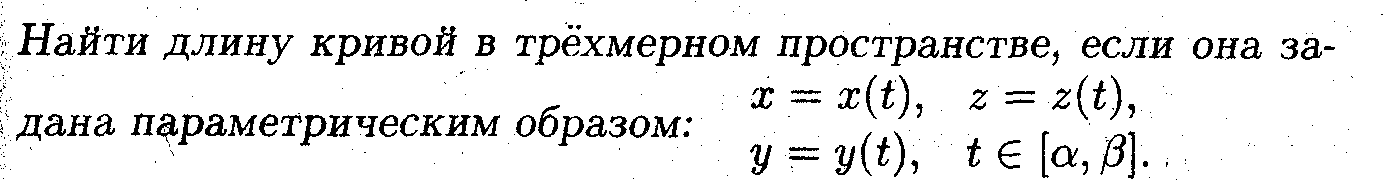
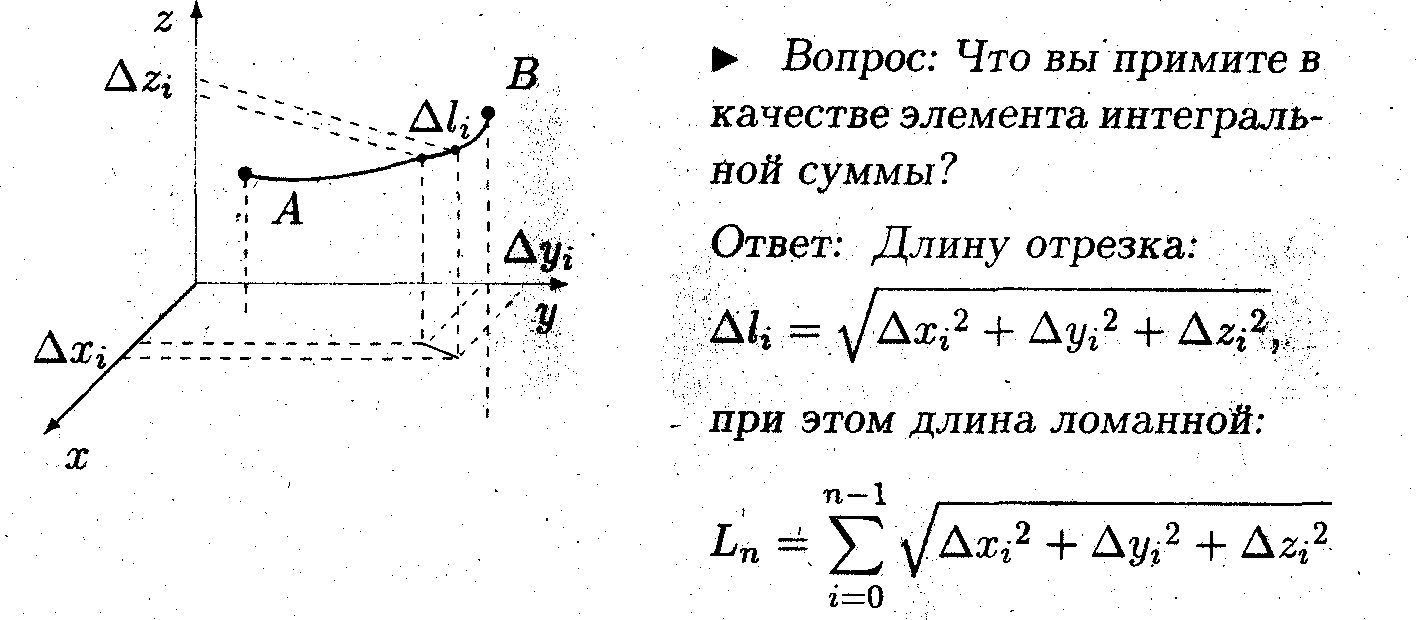
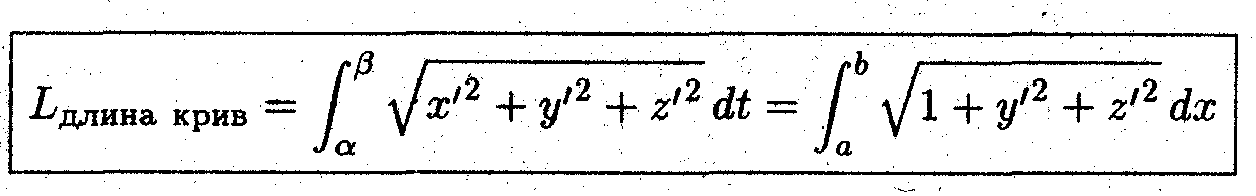
Пример 3. Найти длину окружности радиуса R.
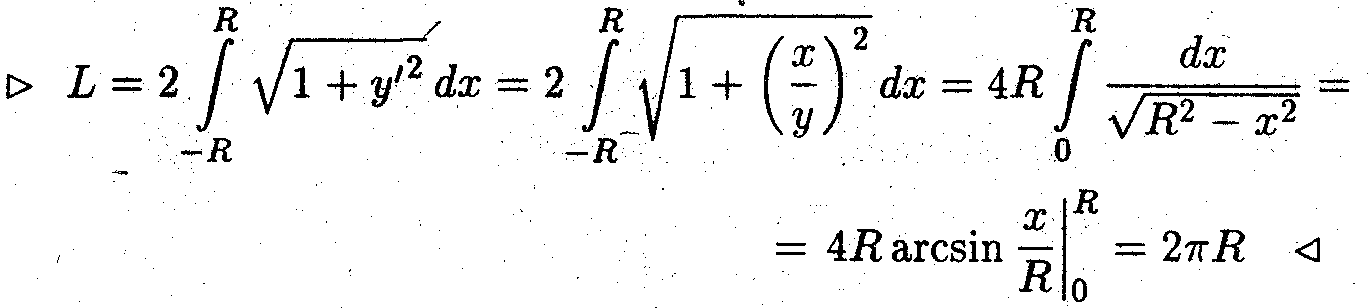
• Здесь у′ = х/у находится из уравнения x ² + у ²= R как производная неявной функции.
задача 5
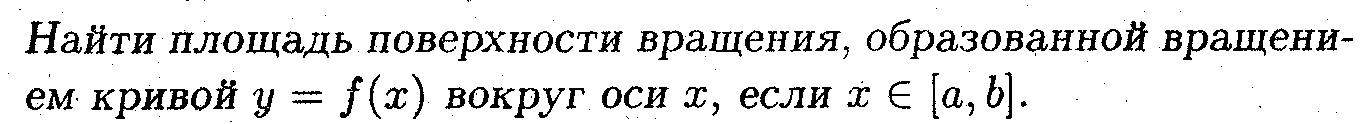
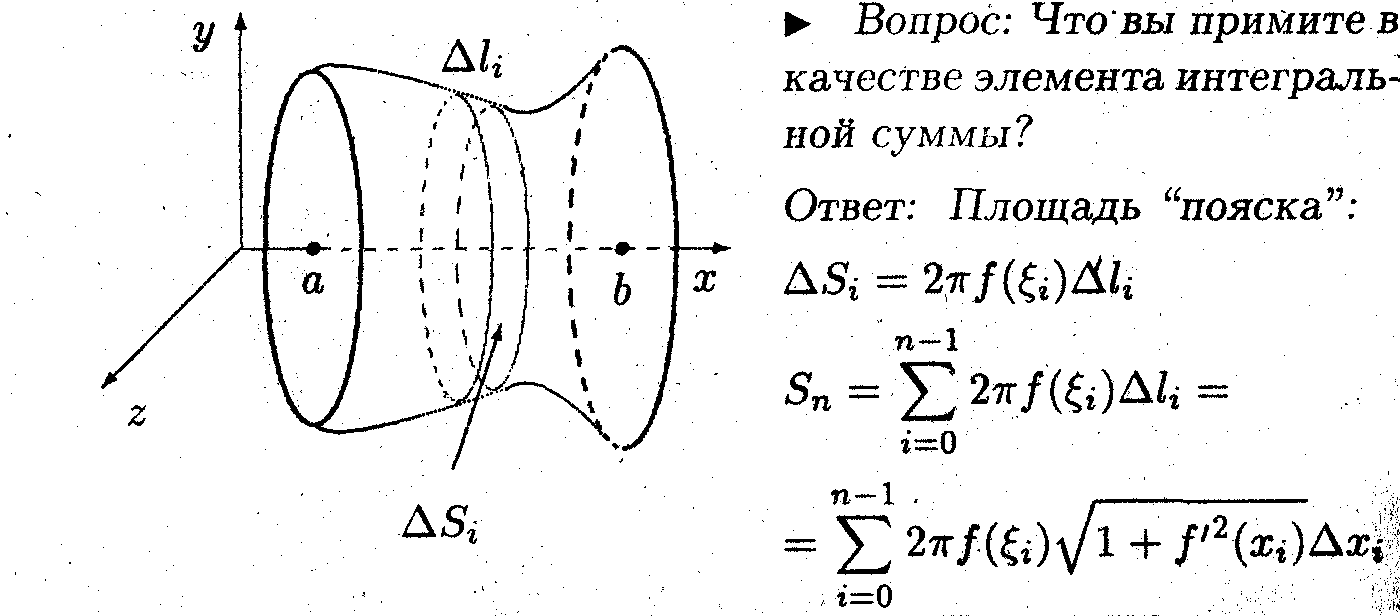
Пример 4. Найти площадь боковой поверхности конуса вращения радиуса R, если длина образующей равна l:
Вопрос: К чему стремится площадь боковой поверхности конуса вращения, если его высота стремится к нулю?
Ответ: К площади круга. <
Лекция 32. Несобственные интегралы
До сих пор мы занимались вычислением интегралов. В данной лекции речь пойдёт о таких интегралах, которые прежде чем вычислять, необходимо исследовать на сходимость.
⋆ Интеграл называется несобственным, если его подинтегральная функция не ограничена на отрезке интегрирования, либо неограничена сама область интегрирования.
⋆ Несобственный интеграл существует (сходится), если существует предел этого интеграла в точке разрыва подинтегральной функции или в бесконечно удалённой точке. В противном случае говорят, что несобственный интеграл не существует (расходится).
Несобственный интеграл с неограниченным пределом интегрирования
Это интеграл следующего вида:
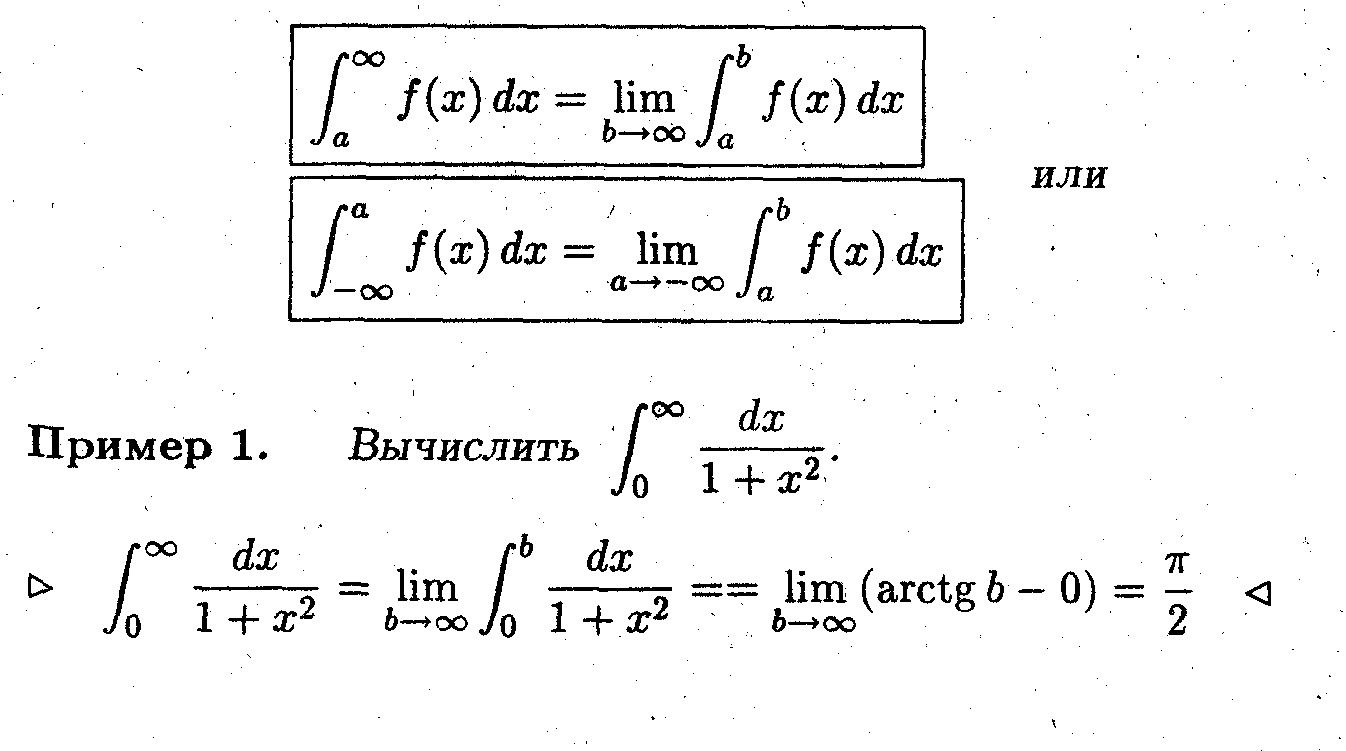
Несобственный интеграл от неограниченной функции
Это интеграл следущего вида:
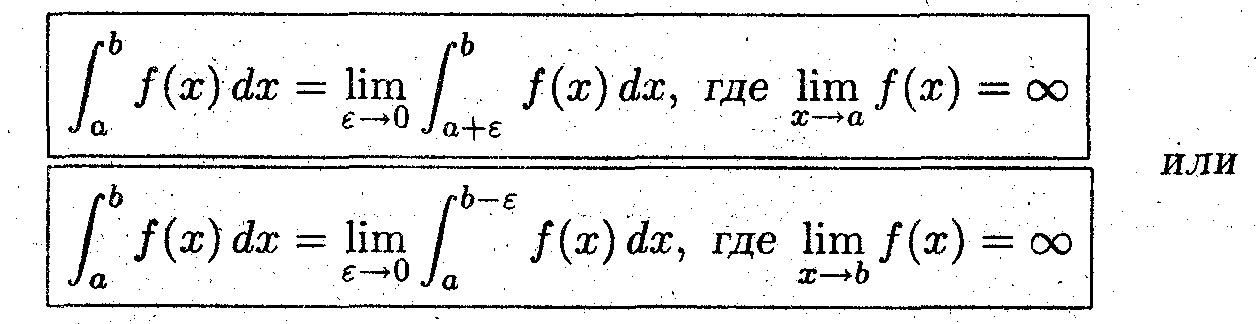
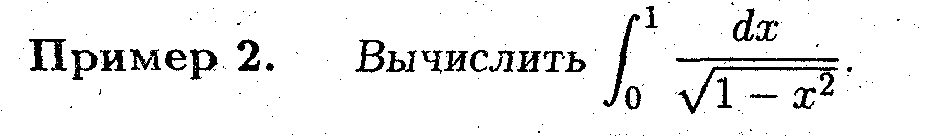
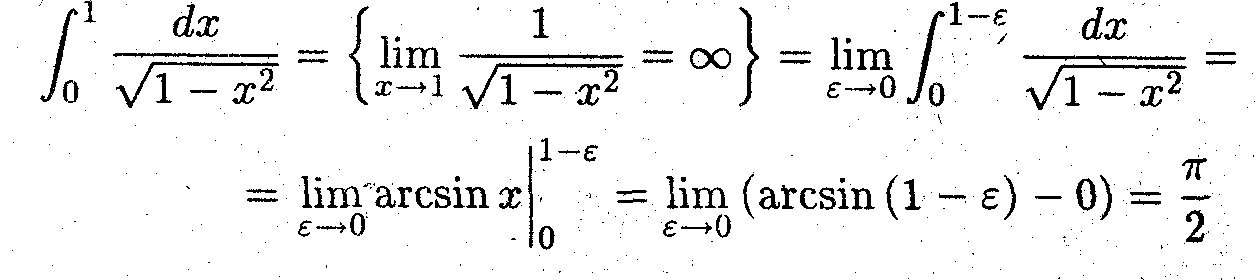
Признаки сходимости несобственных интегралов
задача 1 (признак сравнения)
Пусть выполняется неравенство 0 < g(х) ≤ f(x), где х
[а, ∞ ]. Показать, что если несобственный интеграл сходится от большей функции f{x), то он сходится и от меньшей функции g(x), а если он расходится от меньшей функции, то он расходится и от большей функции.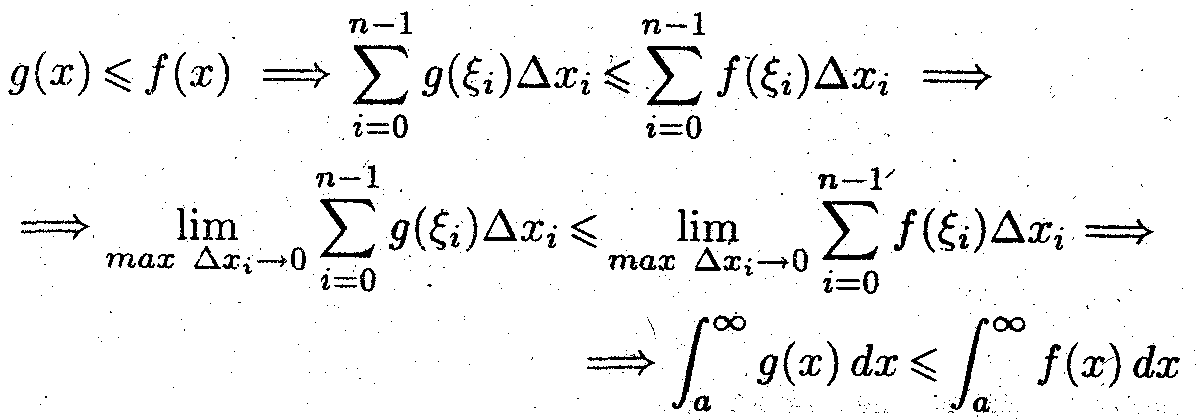
задача 2 (предельный признак сравнения)
Пусть функции f(x) и g{х) с точностью до постоянного множителя эквивалентны в точке их разрыва или в бесконечно удалённой точке.
Показать, что в этом случае несобственные интегралы от этих функций сходятся или расходятся одновременно.
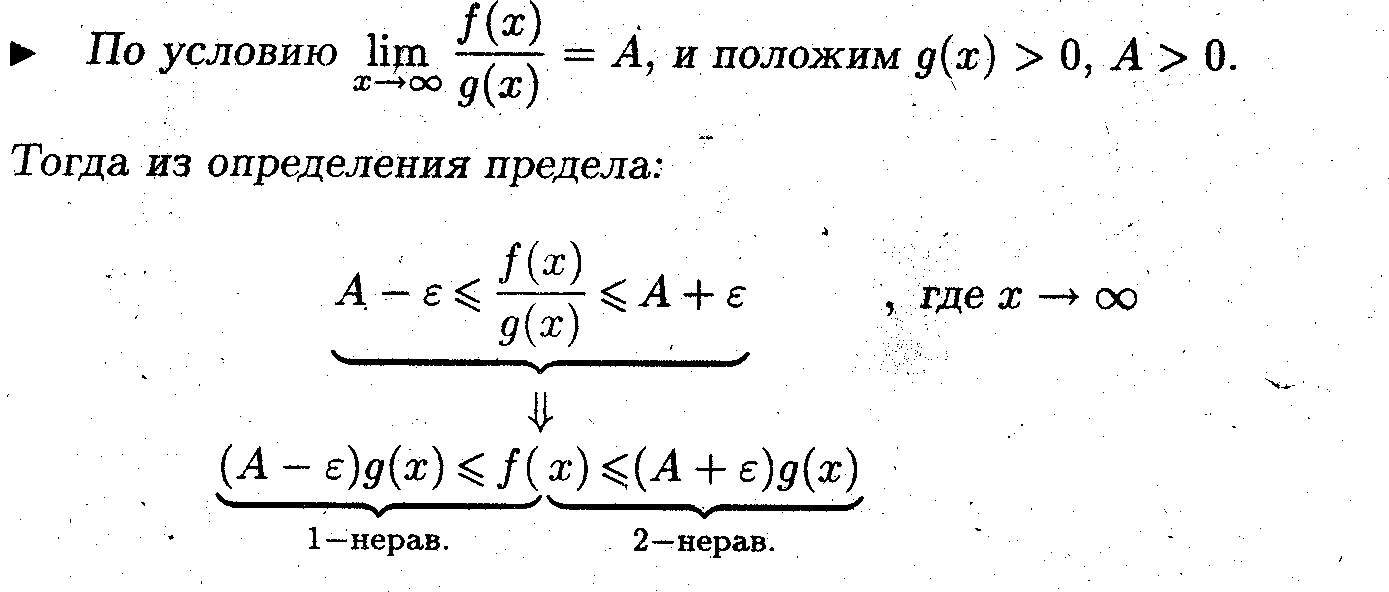
Применим теперь признак сравнения к каждому из неравенств:
из 1 неравенства => если сходится интеграл от f(x), то сходится интеграл от g(х);
из 2 неравенства => если сходится интеграл от g(х), то сходится интеграл от f(x).
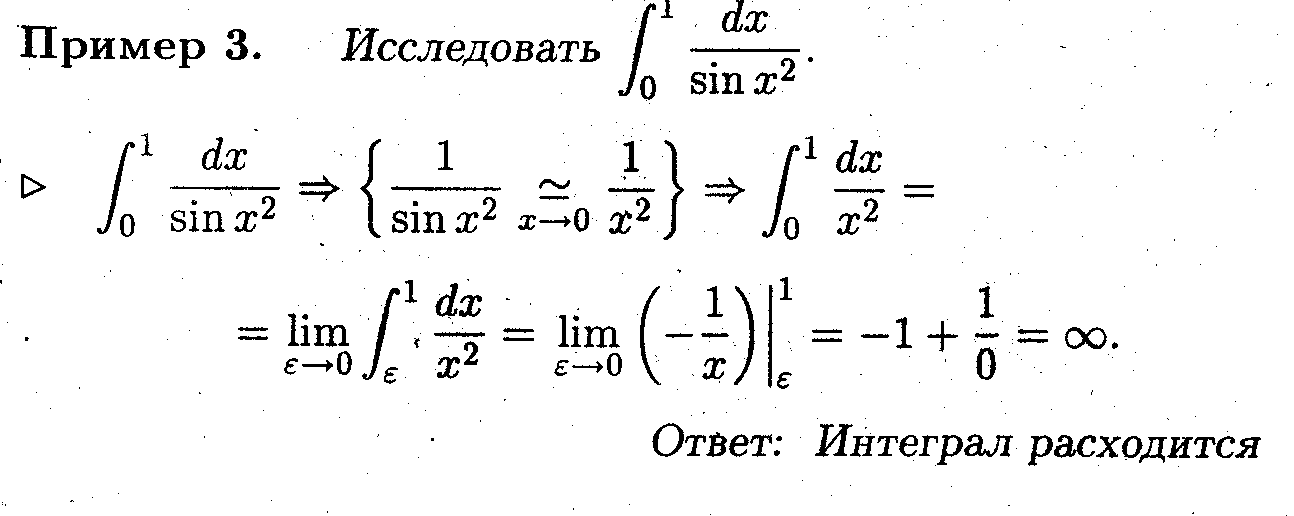
задача 3 (частный предельный признак сходимости для интеграла с неограниченным пределом)
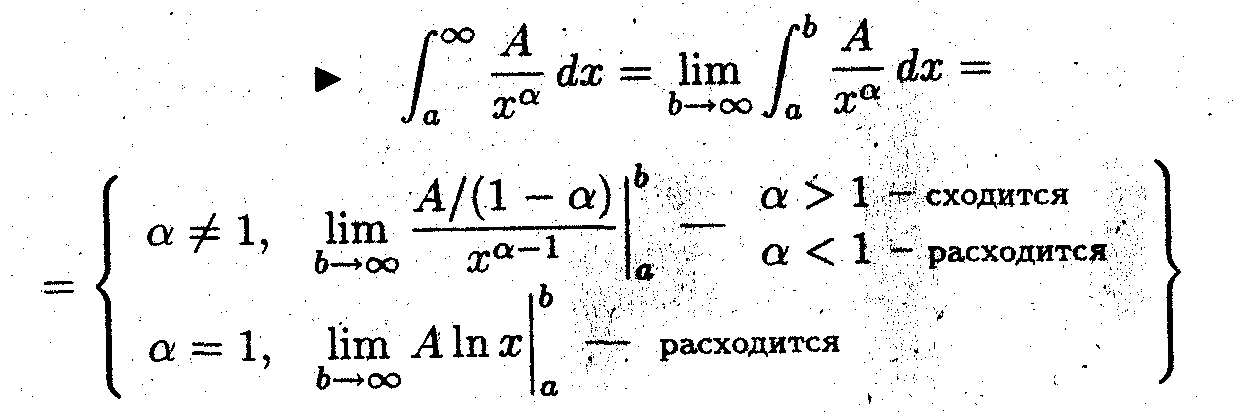
задача 4 (частный предельный признак сходимости для интеграла от неограниченной функции)
- Поскольку
= 2, то согласно Задаче 3 интеграл с неограниченным пределом интегрирования сходится. Но в точке х = 3, принадлежащей отрезку интегрирования, неограниченна подинтегральная функция, и в результате, согласно Задаче 4, интеграл расходится.
Лекция 33. О других методах интегрального исчисления
Изученные нами методы интегрирования позволяют вычислять достаточно простые итегралы. Существуют и другие более изощрённые методы интегрирования. Некоторым из них, например, методу перевала, посвящены монографии. В данной лекции мы лишь коснёмся двух таких методов интегрального исчисления, а именно, метода вычисления итегра-лов с помощью введения параметра и метода приближённого интегрирования.
Вычисление интегралов, зависящих от параметра
⋆Пусть подинтегральная функция является функцией двух переменных f(x, a), каждая из которых задана на соответствующем множестве х
X, a Z, тогда интеграл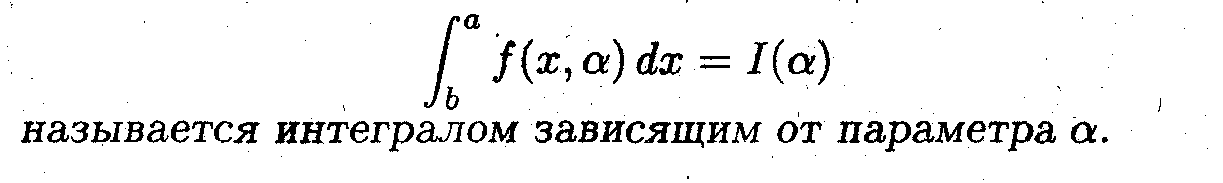
Свойство:
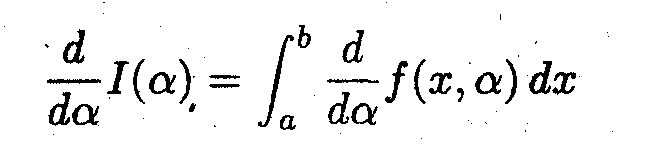
Свойство выполняется, если интеграл
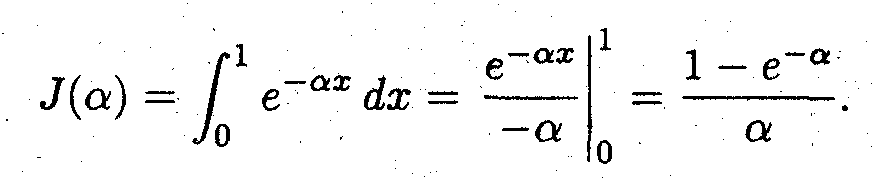
Очевидно, что
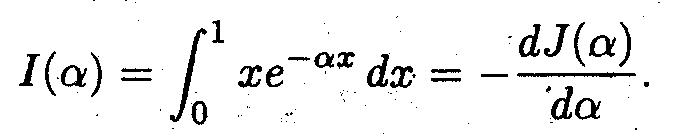
Отсюда следует
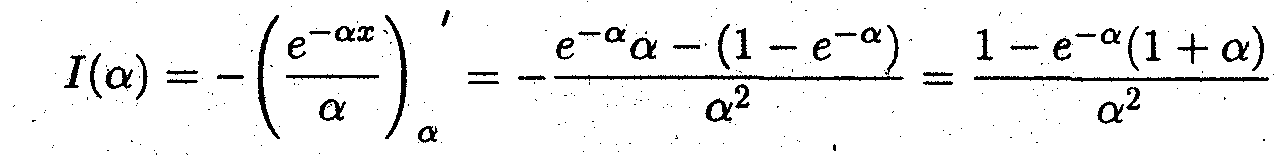
задача 1
- Заданный несобственный интеграл сходится, поскольку подинтегральная функция убывает как х-1 и осциллирует.
• Для осциллирующей подинтегральной функции интеграл сходится и при а=1.
Введём два вспомогательных интеграла
Не трудно убедится, что
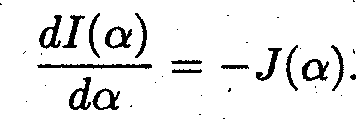
Действительно
Согласно формуле Эйлера (Лекция14)
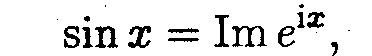
и соответственно
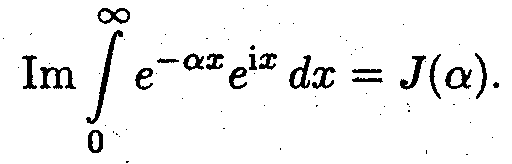
Поскольку
то один из вспомогательных интегралов равен
Теперь подсчитаем второй интеграл
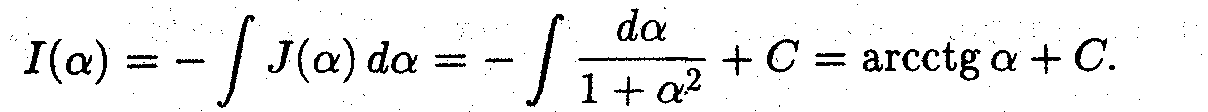
Очевидно
В результате искомый интеграл равен
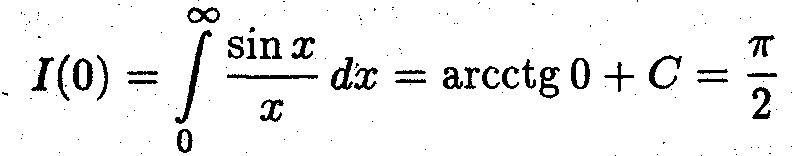
задача 2
- Вопрос: Сходится ли заданный интеграл?
Ответ: Да, заданный несобственный интеграл безусловно сходится, поскольку подинтегральная функция убывает быстрее чем х-1.
Введём два вспомогательных итеграла
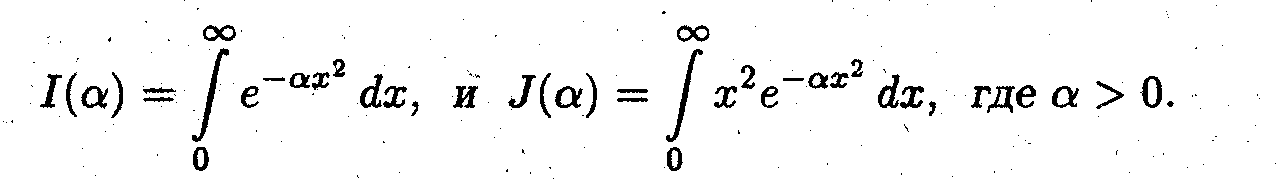
Первый из них простой заменой переменной сводится к интегралу Пуассона
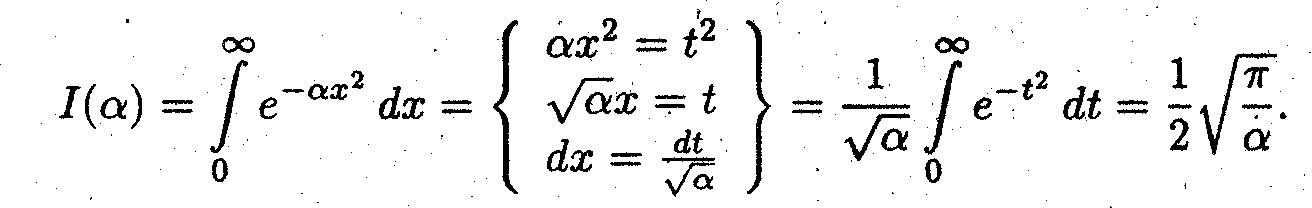
Очевидно, что
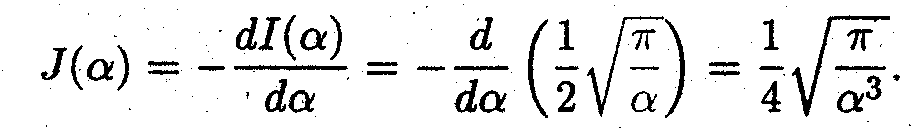
В результате
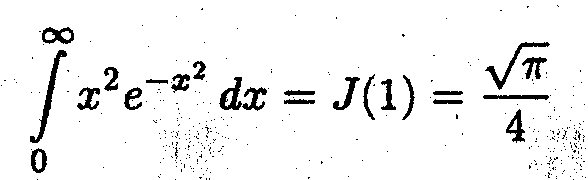
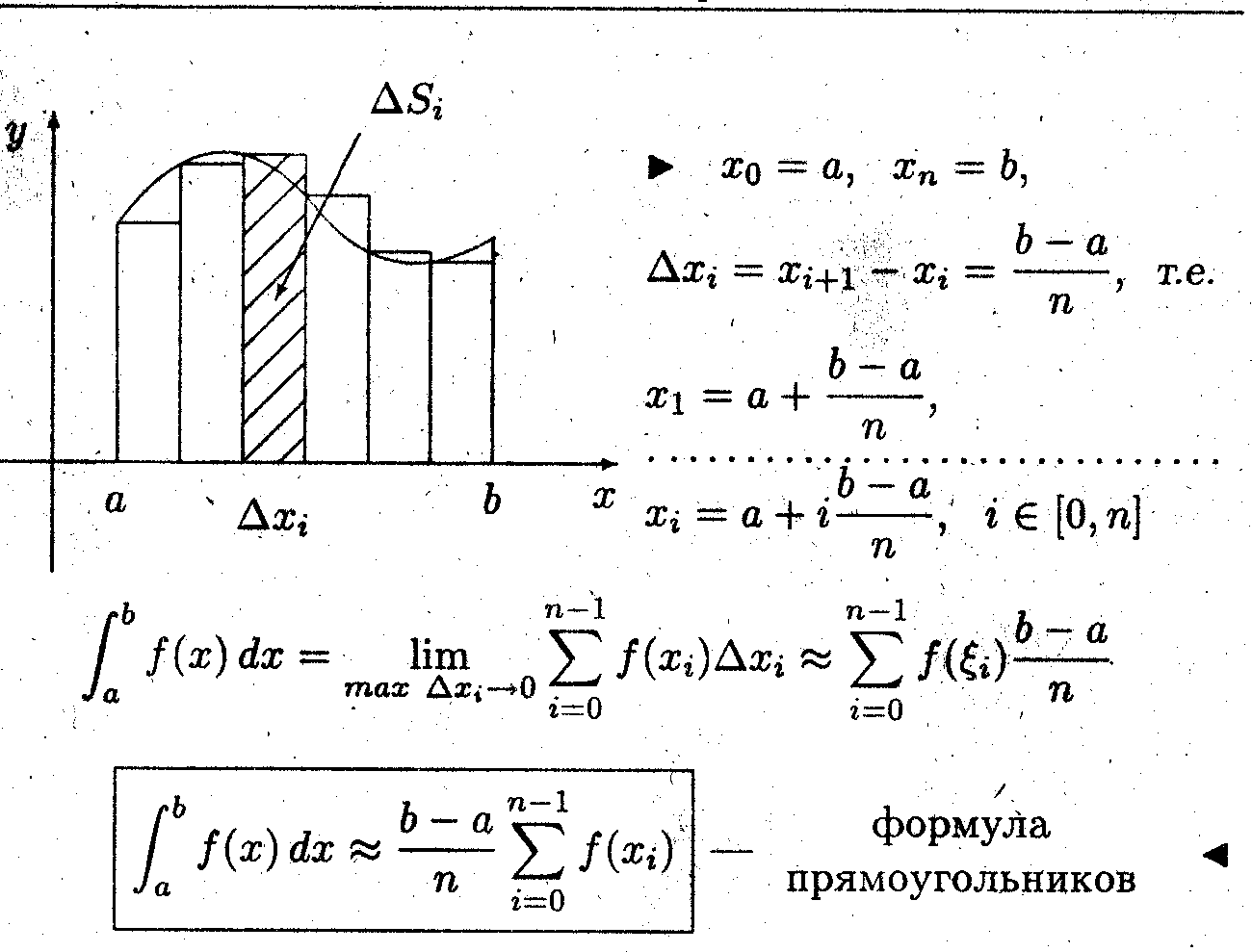
Приближённое вычисление интегралов
Ниже мы получим два простейших численных алгоритма вычисления интегралов.
задача 3 (формула прямоугольников)
Выразить интегральную сумму в виде суммы площадей прямоугольников с равными основаниями.
задача 4 (формула трапеций)
Выразить интегральную сумму в виде суммы площадей трапеций с равными основаниями.
