Развитие линии уравнений в учебнике алгебры н. А. Шапошникова1 И. С. Солосина, Ю. Агеева

Вид материала

Учебник

Подобный материал:

• Методика изучения уравнений в курсе алгебры 7-9 классов Примерное содержание, 12.53kb.
• Некоммутативная геометрия, 36.84kb.
• Программа несущую двойную функцию по решению квадратных уравнений, 49.47kb.
• Урока алгебры и информатики «система счисления. Решение задач с помощью квадратных, 98.53kb.
• Урок по теме «История развития общества, становление науки. Теорема Виета», 124.39kb.
• Тема: «теория матриц» Основная задача линейной алгебры, 28.88kb.
• К и. н. Агеева от; к и. н. Голубев А. В. (отв ред.), 4554.15kb.
• Приближенные методы решения уравнений, 78.01kb.
• Учитель математики и информатики моу сош №3 г. Ак-Довурака Саая, 282.99kb.
• Александровича Агеева «Кузнечик», 28.52kb.

РАЗВИТИЕ ЛИНИИ УРАВНЕНИЙ В УЧЕБНИКЕ АЛГЕБРЫ Н.А. ШАПОШНИКОВА¹


И.С. Солосина, Ю. Агеева


Как известно, во второй половине 19 века педагоги-математики интенсивно разрабатывали учебники по алгебре. Созданием учебников занимались не только ученые, но и рядовые педагоги: директор Московского учительского института А.Ф. Малинин, проф. Московского университета А. Ю. Давидов, А.П. Киселев, Н. А. Шапошников и др. Остановимся подробнее на учебнике Н.А. Шапошникова «Алгебра. Курс старших классов гимназий и реальных училищ. Ч. 2».

Сначала несколько слов об авторе. Николай Александрович Шапошников (1851-1920) окончил в (1868 г.) гимназию с золотой медалью, а затем Московский университет (в 1874 г.) и защитил диссертацию на степень магистра чистой математики (в 1880 г.). Николаю Александровичу очень повезло, ведь он учился в гимназии, где преподавал известный педагог Малинин Александр Федорович. В Московском университете, куда после окончания гимназии поступил Н.А. Шапошников «работали известные профессора: математики и механики А. Ю. Давидов (1823 - 1885), Ф. А. Слудский (1841 - 1897),

В.Я. Цингер (1836 – 1907), Ф.Е. Орлов (1843 - 1892), Н.В. Бугаев; астрономии Ф.А. Бредихин (1831 - 1904); физики А.Г. Столетов (1839 - 1896)». [4, с. 87]

Педагогическая деятельность Н.А.Шапошникова была связана с преподаванием математики в гимназии, на Высших женских курсах и в Московском высшем техническом училище [4, 5]. Его перу принадлежат учебники по алгебре, арифметике, тригонометрии, математическому анализу. Первый опыт написания учебника алгебры Н.А.Шапошников предпринял весьма молодым человеком. В 1876 г. вышла первая часть его книга «Курс алгебры и собрание алгебраических задач», а через год – вторая часть. В 1881 г. появляется первая часть «Сборника алгебраических задач с текстом общих объяснений и разнообразными практическими указаниями», написанного Н.А.Шапошниковым в соавторстве с Н.К. Вальцовым.

В 1880 г. Николай Александрович выпускает «Курс прямолинейной тригонометрии и собрание тригонометрических задач», который был одобрен Комитетом Министерства народного просвещения. Спустя 10 лет выходит в свет его 3-е издание, немного измененное, удостоенное высшей награды – премии Петра Великого. [4]

«В 1881 выходит «Арифметика целых чисел», а через 5 лет «Основания общей арифметики и алгебры». В 1888 г. выходит «Краткое руководство арифметики, объединенной с методикой и систематическим сборником типических задач для гимназии»: ч. 1 – Арифметика целых чисел, ч. 2 – Арифметика дробных чисел, ч. 3 – Общие способы решения арифметических задач…В 1892 г. выходят «Дополнения элементарного курса математики и введения в высший математический анализ». [4, c. 89]

После выхода на пенсию Николай Александрович все свое время посвящает доработке своих книг, написанию статей, «в которых подвергает критике неудовлетворительное состояние математического образования и намечает пути реформы образования». [4, с. 90]

«В 1904 г. он выпускает «Новый курс алгебраической прямолинейной тригонометрии», построенный на векторной основе и комплексных чисел, причем автор в конце предисловия к книге пишет, что книга является учебным руководством для более или менее отдаленного будущего». [4, с. 90]

В период с 1904 – 1911 гг. Николай Александрович выпускает книги «Основной курс математического анализа» и «Основы дифференциального и интегрального исчисления с приложением к геометрии», в 1909 г. – «Основания арифметики и алгебры», в 1911 г. – «Руководство арифметики для преподавателей и учащихся старшего возраста».

В 1890 г. выходят отдельным изданием учебник алгебры (точнее – его первая часть, предназначенная для III и IV класса гимназий) и вторая часть сборника задач. Сборник задач был составлен настолько удачно, что вскоре был одобрен Министерством просвещения и удостоен премии Петра Великого. Всего вышло 24 издания этой популярной книги. Что касается самого учебника алгебры, то он не имел такого распространения как задачник. И, тем не менее, переиздавался неоднократно.

Рассмотрим вторую часть его последнего, 11 издания, предназначенного для старших классов гимназий и реальных училищ. Это издание вышло в 1918г. Общее представление о книге можно получить из оглавления:

- Иррациональные числа. Действия с ними.

- Иррациональные выражения. Действия с ними.

- Степени и корни с дробными показателями.

- Мнимые количества.

- Уравнения второй степени.

- Иррациональные уравнения.

- Уравнения высших степеней.

- Системы уравнений высших степеней.

- Неравенства.

- Неопределенные уравнения.

- Разностная прогрессия.

- Кратная прогрессия.

- Общая теория логарифмов.

- Теория десятичных логарифмов.

- Теория соединений.

- Бином Ньютона.

- Теория непрерывных дробей.

- Способ неопределенных коэффициентов.

- Решение неравенств второй степени.

- Наибольшее и наименьшее значения трехчлена.

- Общие теоремы о рядах.

- Распространение формулы бинома Ньютона.

- Пределы некоторых показательных выражений.

- Разложение показательной функции и логарифма.

Как видно из содержания распределение материала на классы отсутствует, что тогда являлось привычным делом для школьных учебников. По сравнению с современной программой по математике в книгу вошли вопросы, которые не изучается в современной школе. Например, «мнимые количества», «общие теоремы о рядах» и др. Среди вопросов, которые сегодня изучаются: линейные уравнения с одной переменной, рациональные, дробно – рациональные, квадратные, уравнения с двумя переменными, уравнения, содержащие переменную под знаком модуля, показательные, логарифмические, иррациональные уравнения. В этом учебнике Н.А. Шапошникова линия уравнений представлена следующим образом: уравнения второй степени, иррациональные уравнения, уравнения высших степеней, неопределенные уравнения.

Несомненный интерес вызывает изложение материала, посвященное уравнениям второй степени. Квадратным уравнениям посвящен отдельный параграф (§ 23).

В нем дается следующее определение квадратного уравнения: «Уравнением второй степени или квадратным уравнением называется всякое уравнение, которое посредством преобразования его в другие, совместные с ним, приводится к виду .

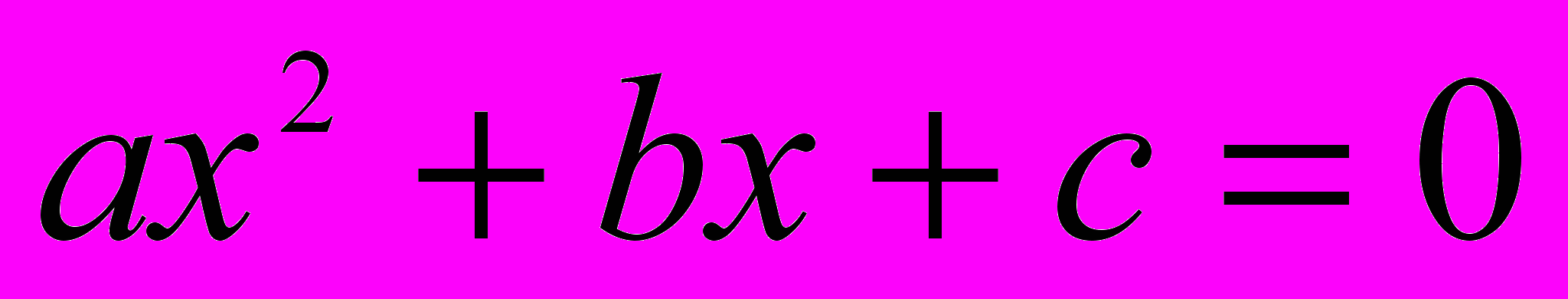Уравнение 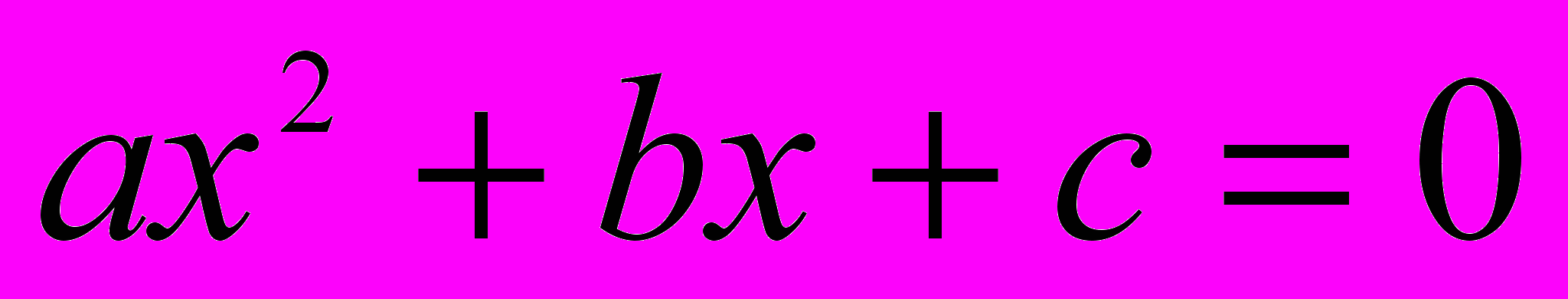называется общим видом квадратного уравнения». [6, с.27] Далее говорится о том, что если бы коэффициент a был отрицательным, то умножив обе части уравнения на -1, его можно сделать положительным; a, b, c – являются коэффициентами уравнения, причем a и c – «крайние», b – «средний», c – «известный член уравнения» ( в современных действующих учебниках c – «свободный член»). Также вводится определение приведенного квадратного уравнения, когда «коэффициент первого члена есть 1».

В § 24 «Решение неполных уравнений» рассматривается способ решения данных уравнений. Приводится 2 вида уравнений: 1) 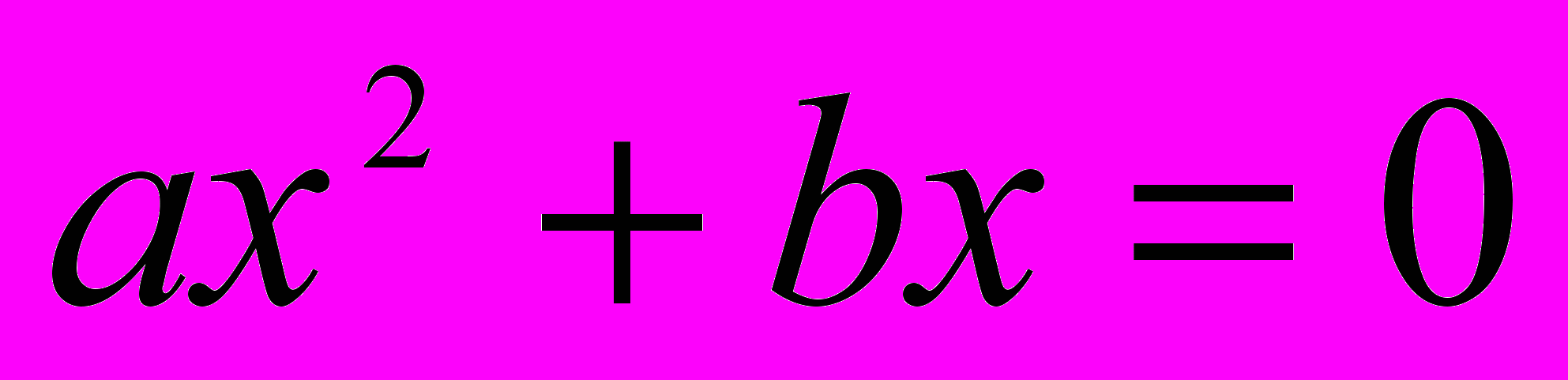и 2) 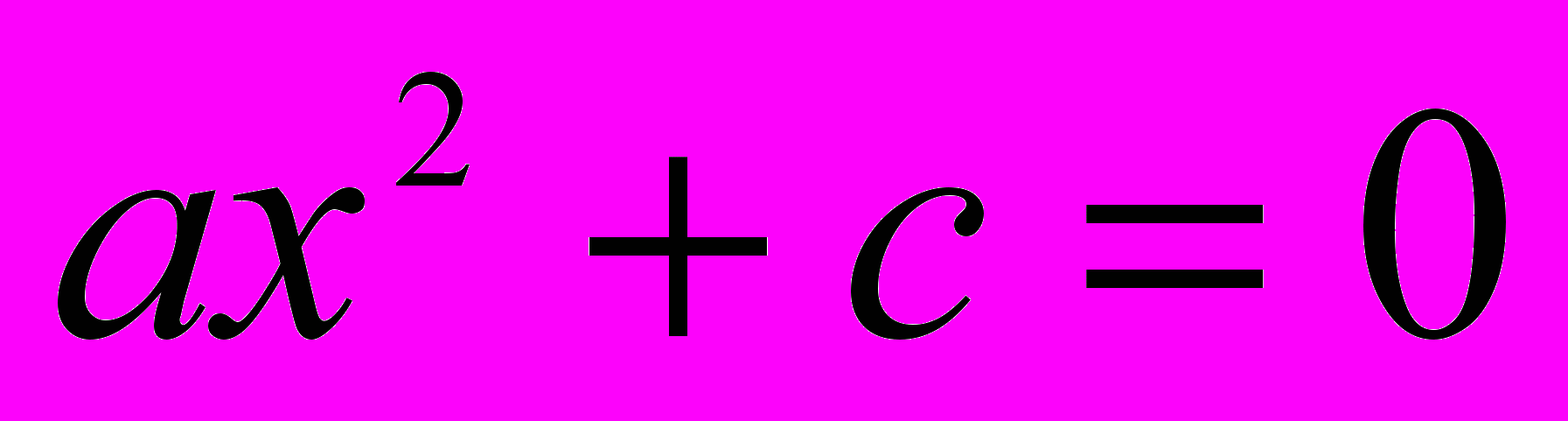. Первое уравнение решается таким же способом, как и в современных учебниках (вынесением х за скобку, а затем рассматривается случай, когда произведение равно нулю: когда хотя бы один из множителей равен нулю). Для второго уравнения рассматриваются 2 случая: когда с – положительное, и когда с – отрицательное. Данные случаи рассматриваются на конкретных примерах. При решении задачи, когда с - положительное, в результате получаются мнимые корни. В наше время для учеников 8 классов обычно говорят, что уравнение не имеет действительных корней.

В § 25 «Решение полного уравнения» автор выводит формулу, по которой можно найти решение уравнения через коэффициенты. В учебнике рассмотрено несколько способов: первый – синтетический, второй – аналитический.

Синтетический

«Дано уравнение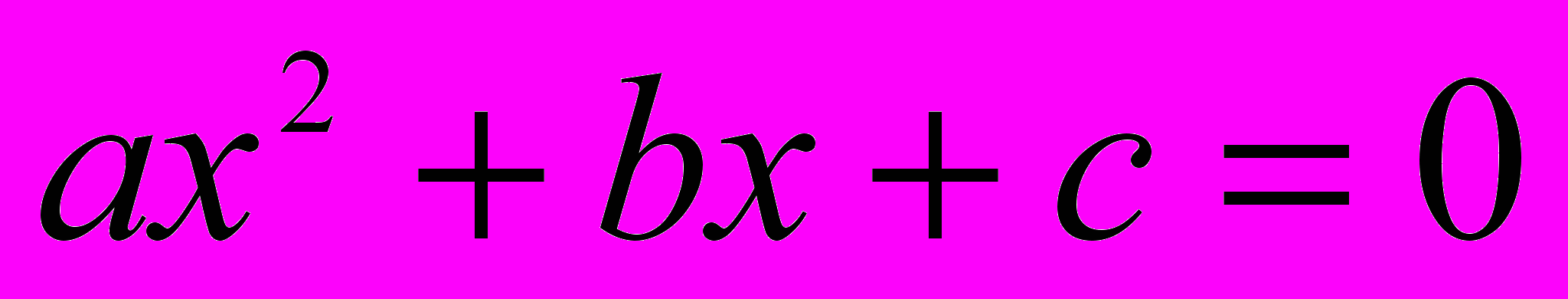. Множим обе части его на 4а; получится 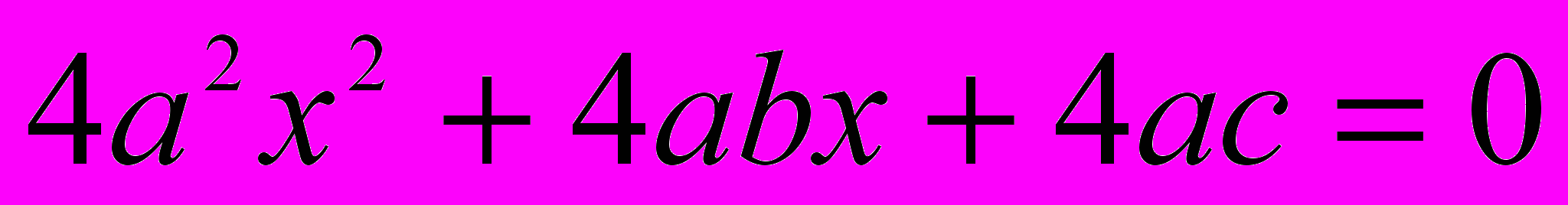. Перенесем 4ас во вторую часть; выйдет 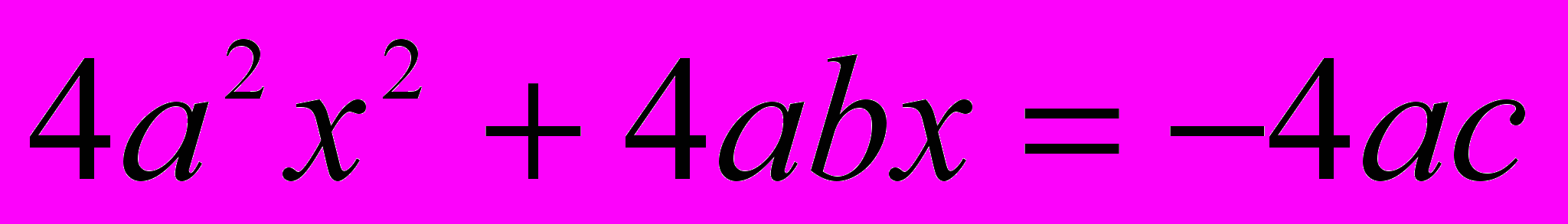. Замечаем, что член 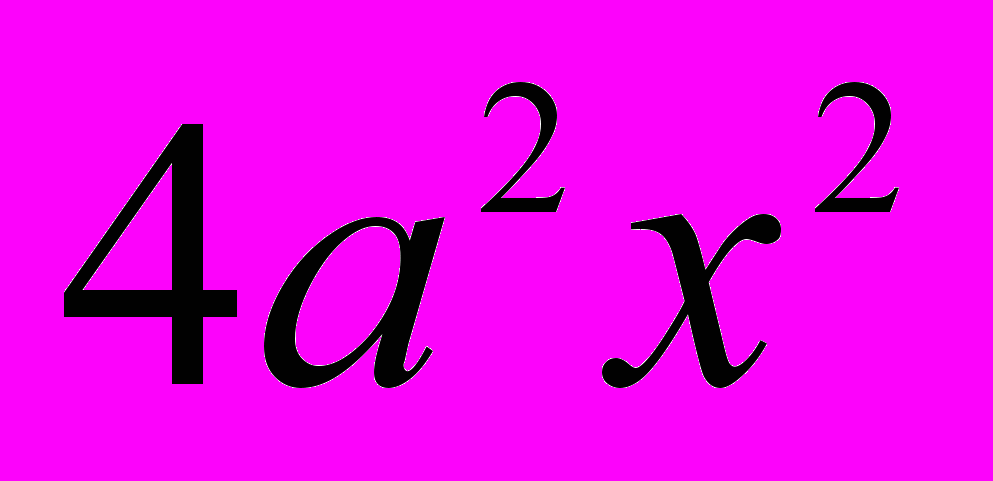есть квадрат от 2ах, а член 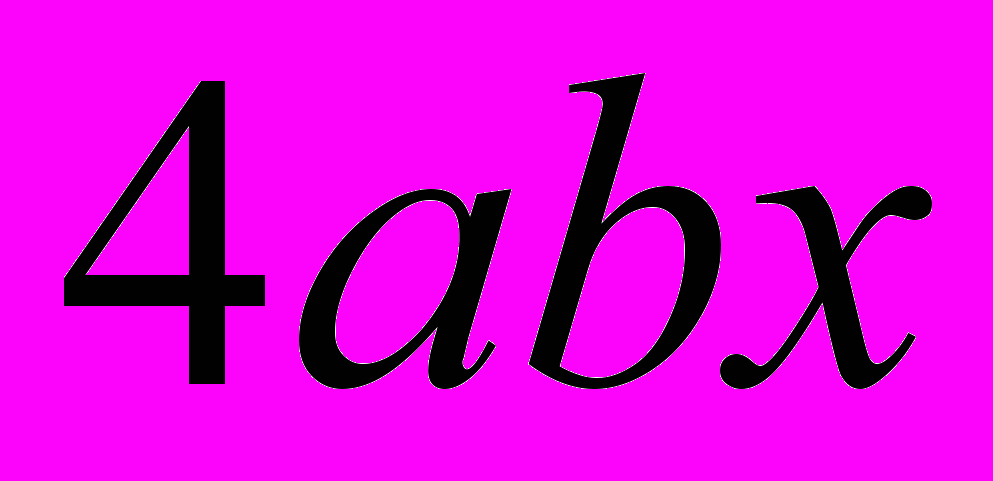есть удвоенное произведение от 2ах на b. Поэтому, если к обеим частям прибавить по 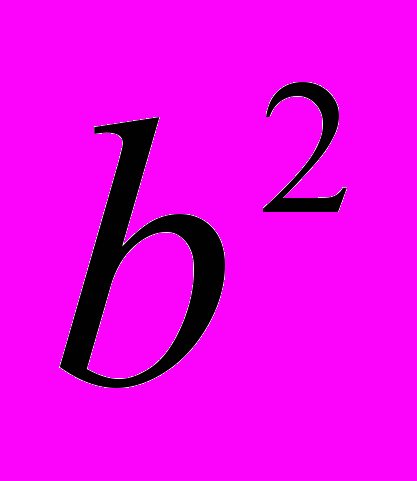, то в первой части составится полный квадрат двучлена, именно получится 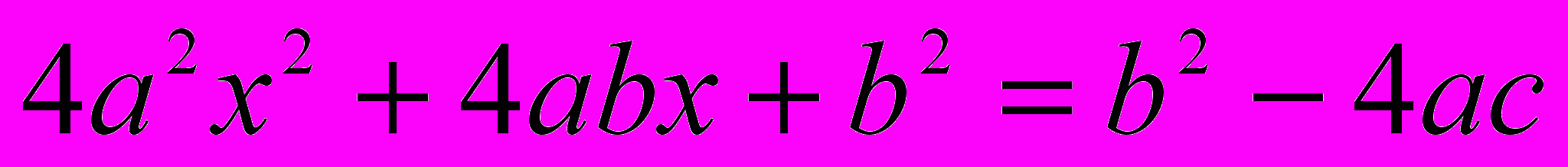, или, выписывая первую часть в явной форме квадрата .

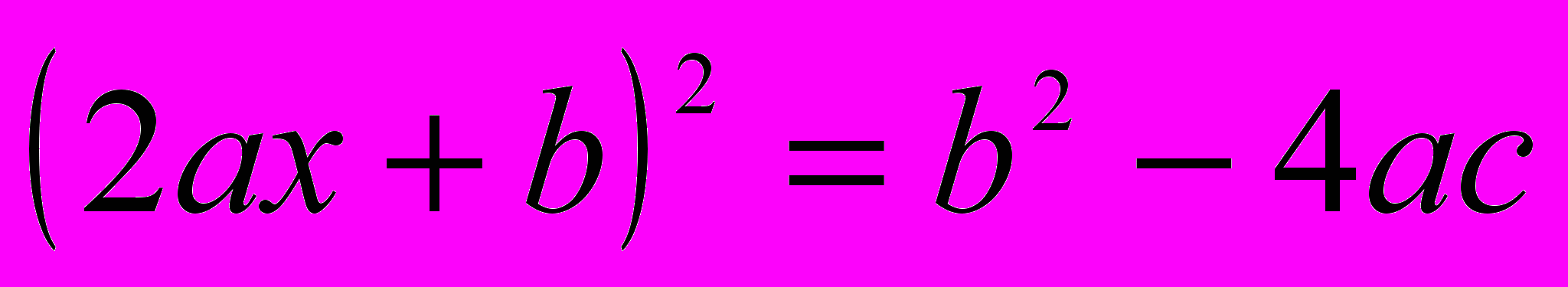Извлечем из обеих частей квадратный корень, при чем во второй части полученной формулы поставим двойной знак; выйдет 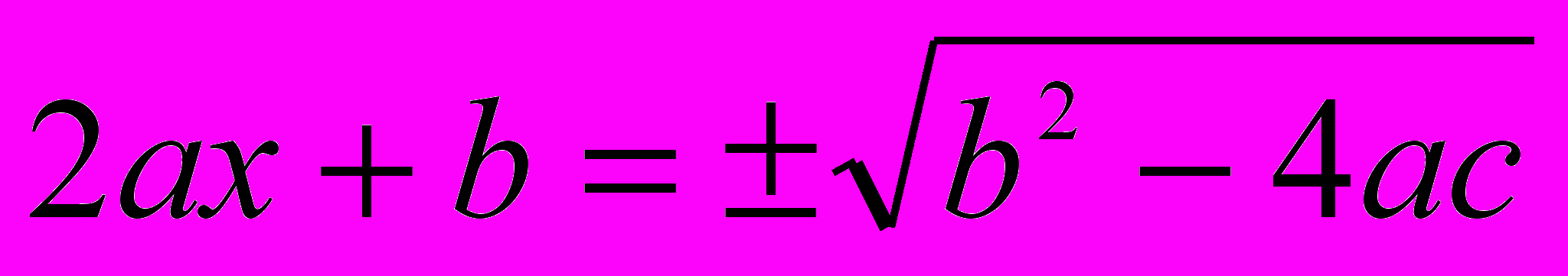. Эта формула соединяет в себе два отдельных уравнения первой степени.

В обоих уравнениях переносим b во вторую часть и затем делим обе части на 2а. Получится формула 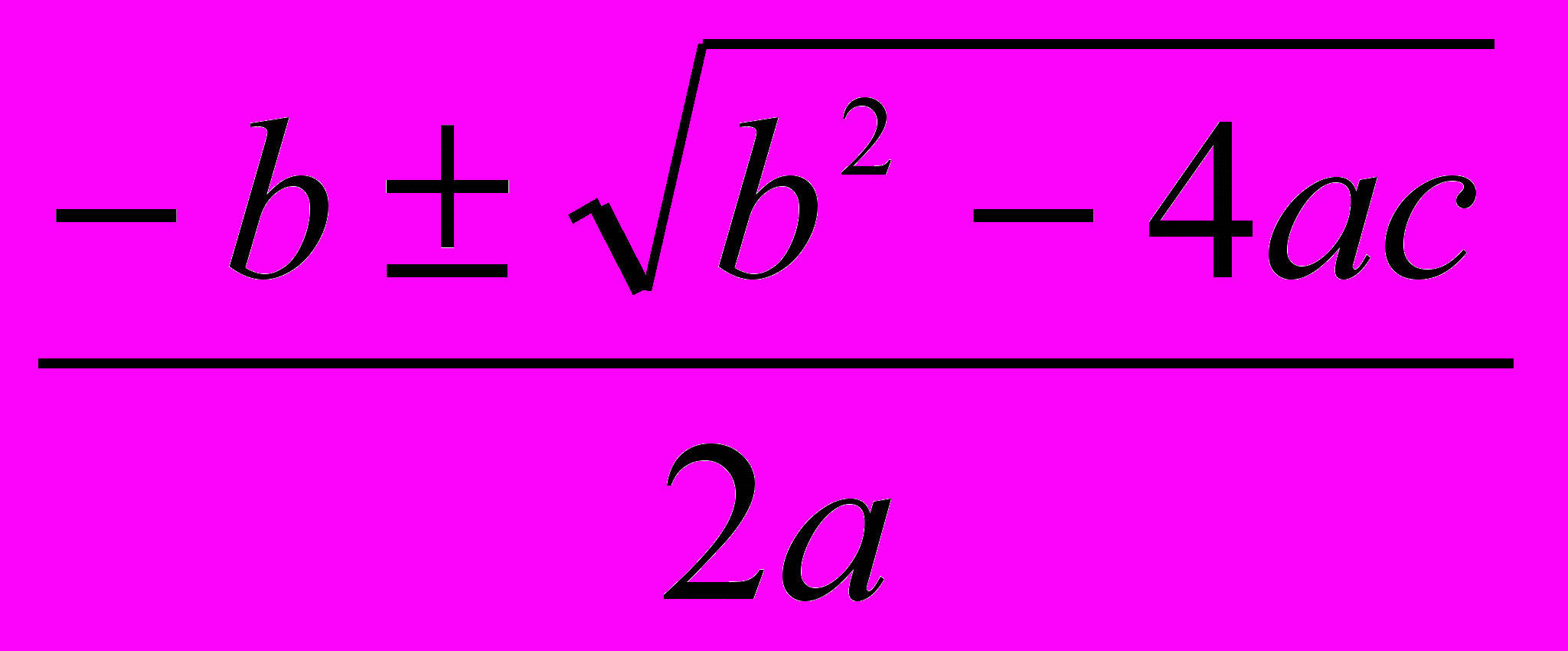, которая определяет два корня данного уравнения, именно первый корень получается тогда, когда радикал возьмем с плюсом, а второй тогда, когда радикалу припишем минус».[6, с. 29]

Аналитический

«Дано уравнение 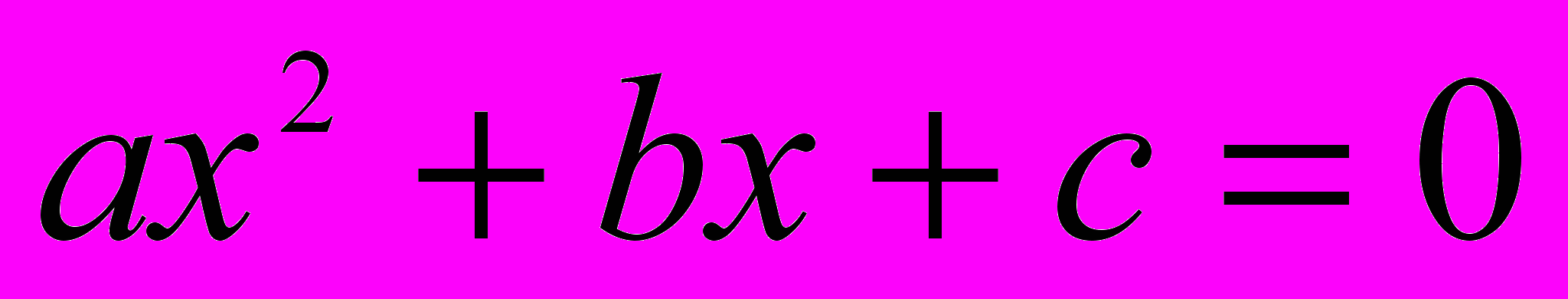. Положим, что 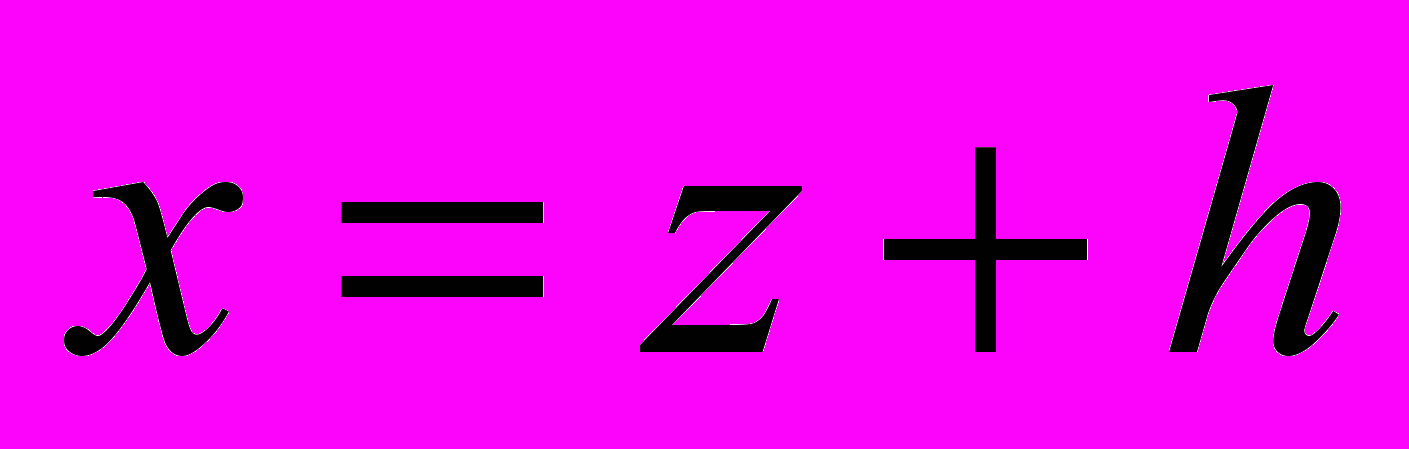, где z есть новое неизвестное, заменяющее собою х, а h есть неопределенное количество, которое мы выберем так, чтобы упростить уравнение. Подставив вместо х его новое выражение, получим уравнение в виде 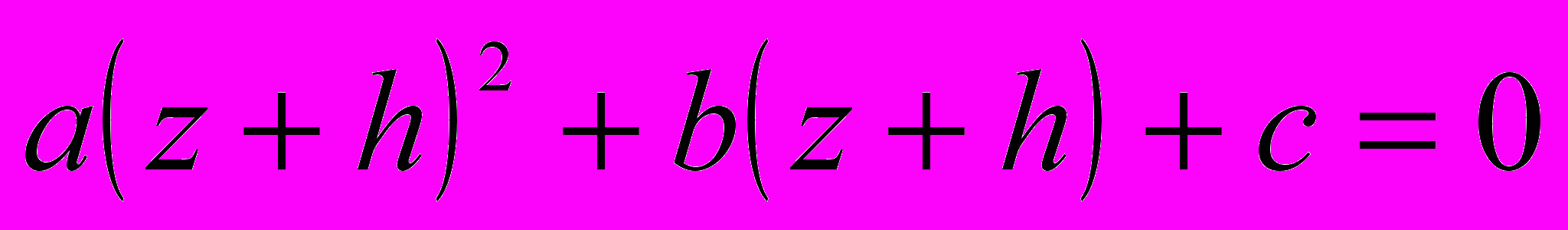, или, раскрыв скобки и разложив по степеням неизвестного, .

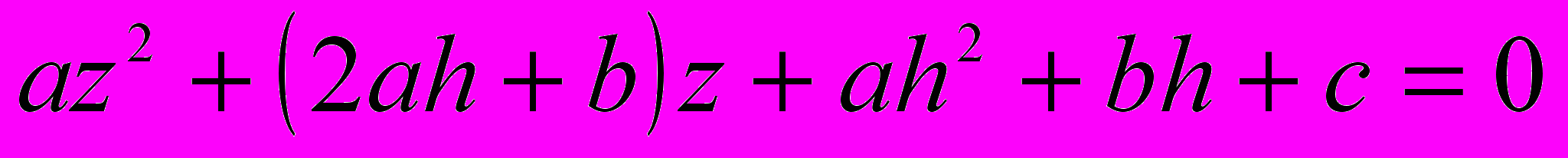Выберем теперь h так, чтобы уничтожить член с первой степенью z. Для этого примем 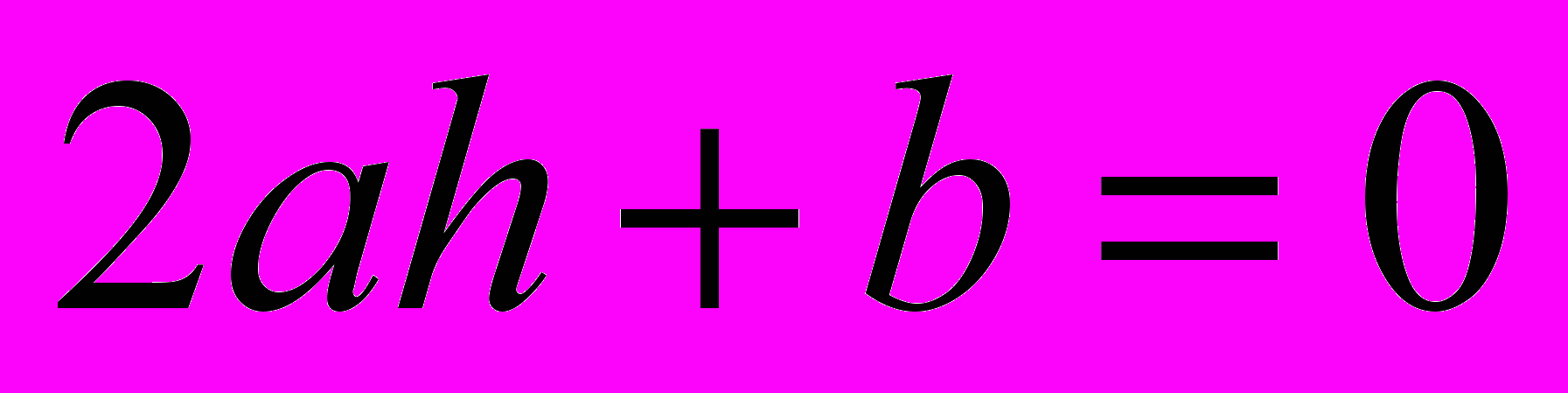, откуда 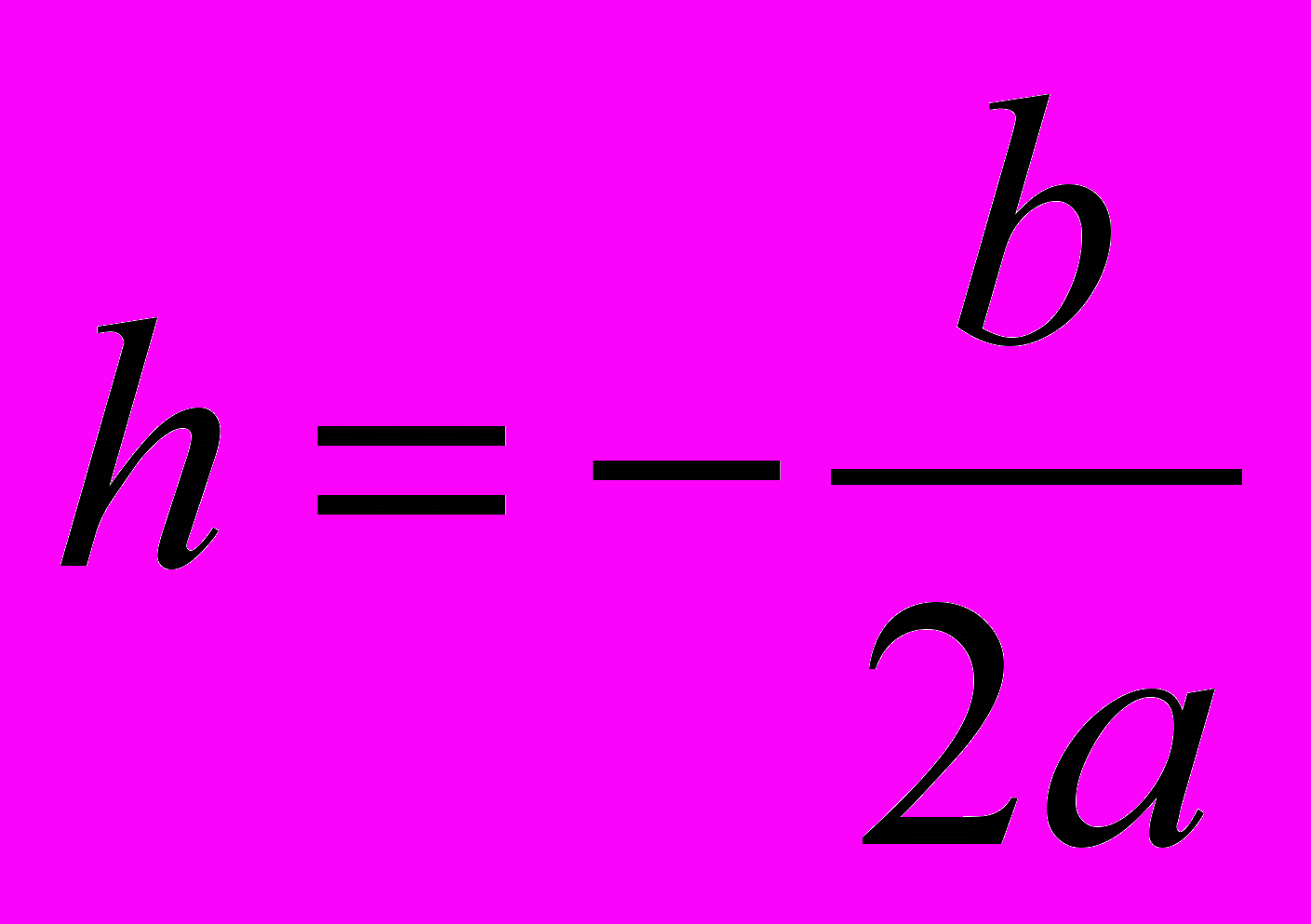. Подставив найденное значение h, мы получим упрощенное уравнение 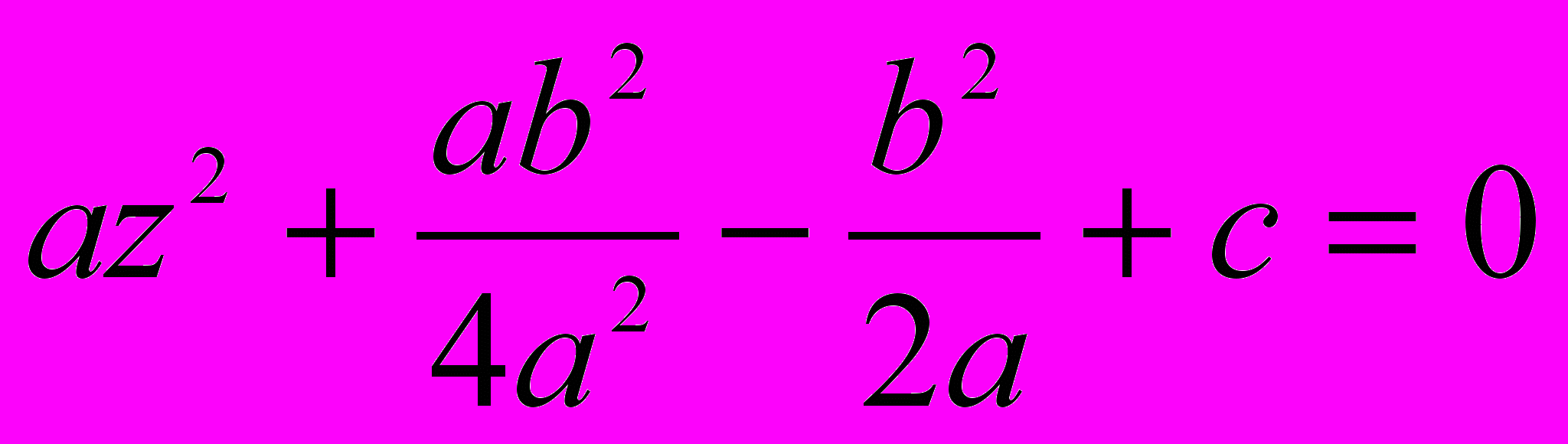, или сделав приведение, 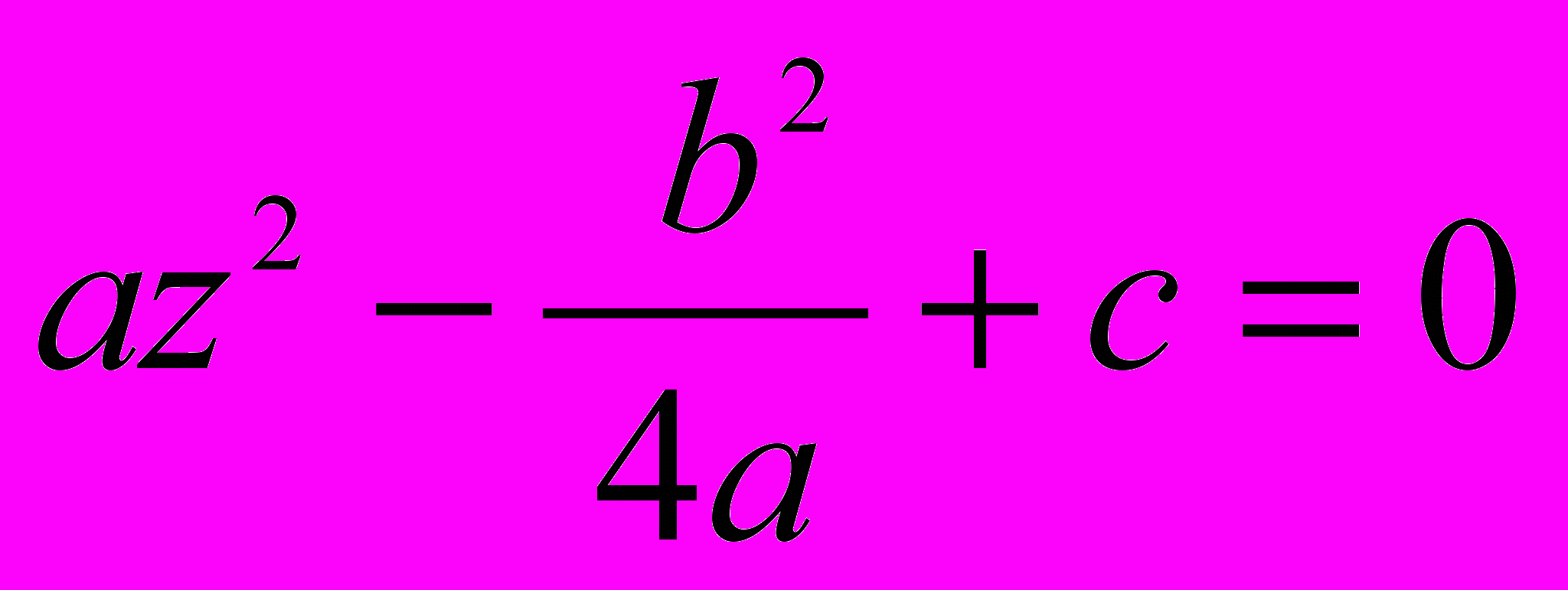. Новое уравнение относительно z есть также квадратное, но неполное, и его решение нам известно. Решая, находим .

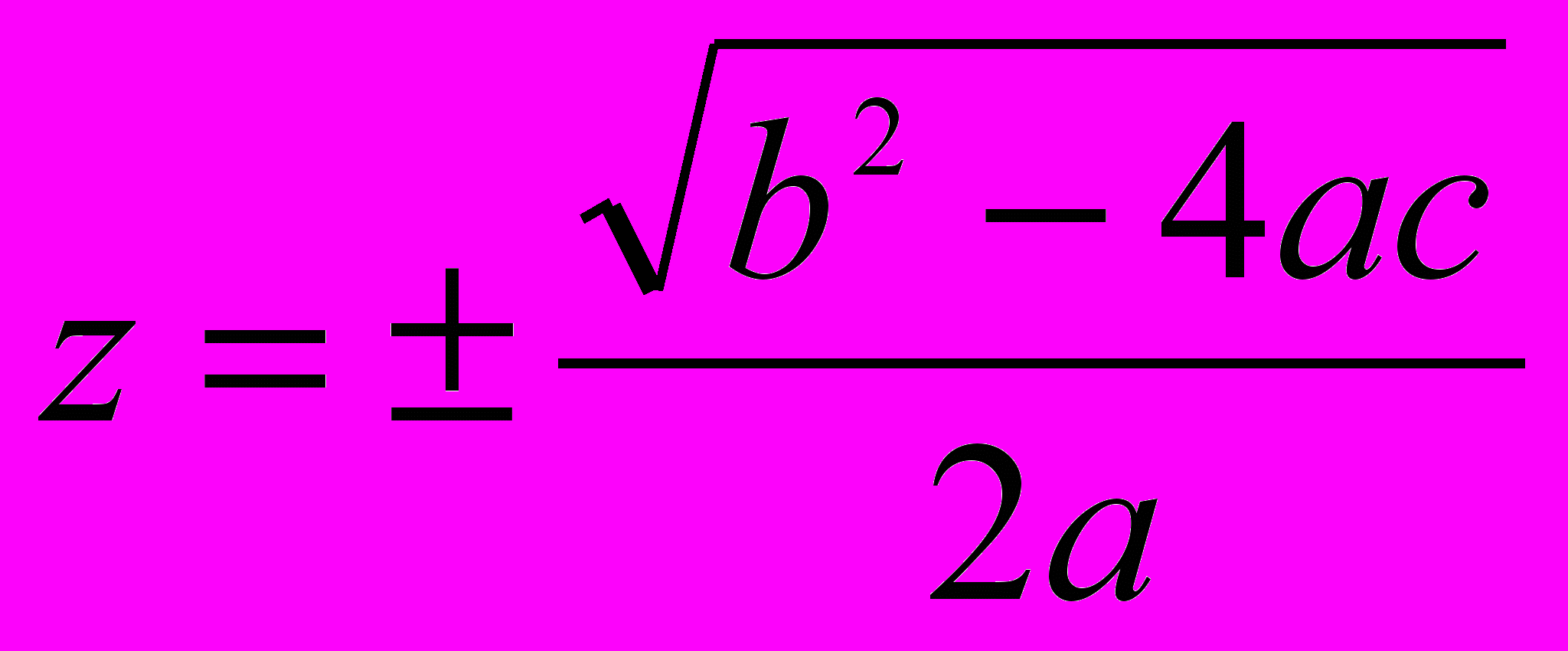Найдя h и z порознь, мы складываем их и находим формулу для первоначального неизвестного 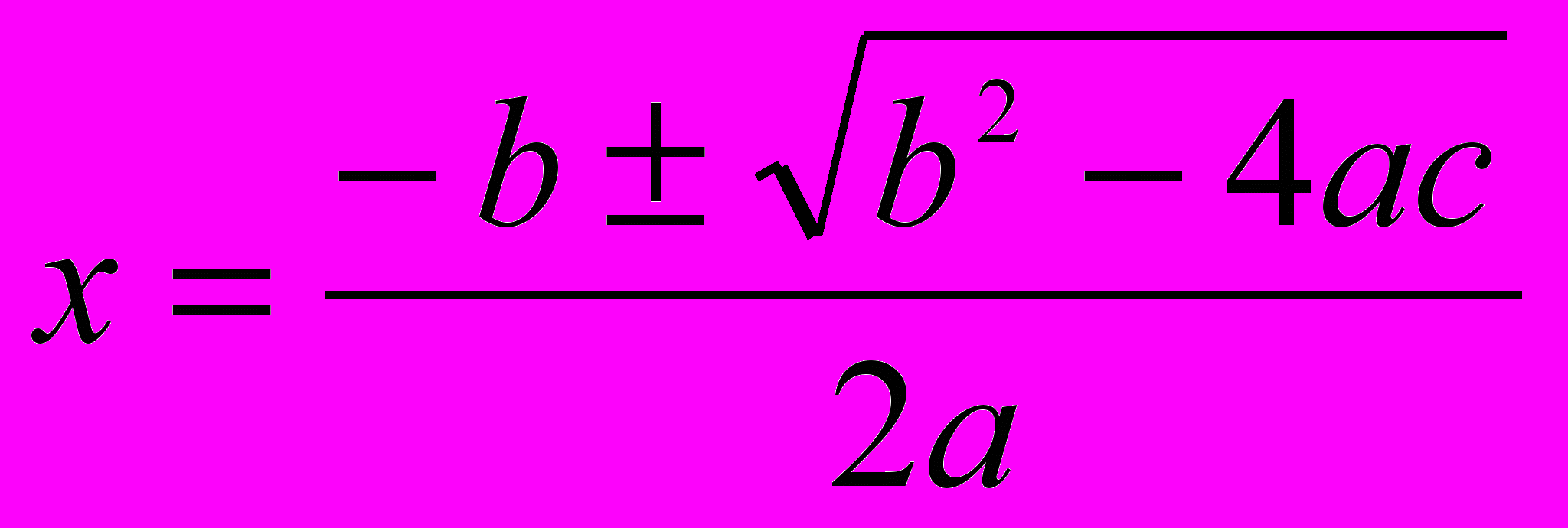такую же, какая была найдена первым способом.

Полученная формула дает возможность найти два корня всякого квадратного уравнения, как скоро оно приведено к виду 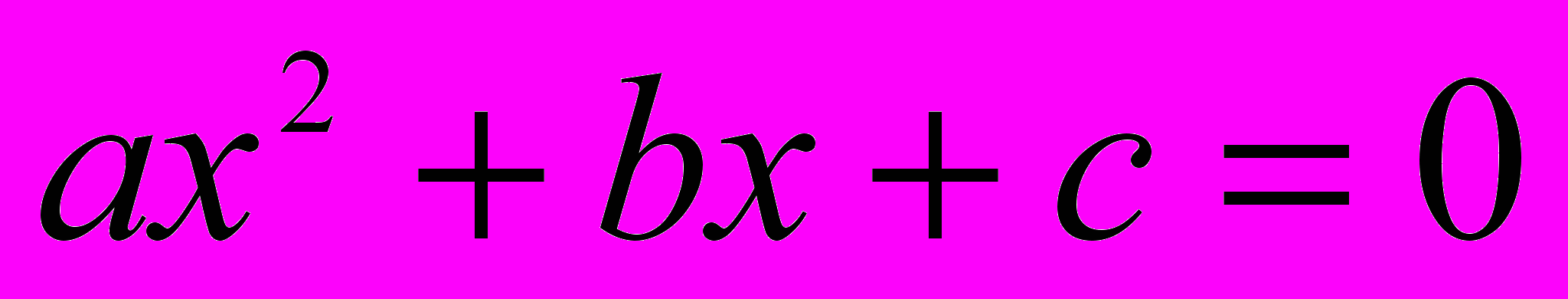. Для отыскания корней нужно только подставить в формулу на место букв a, b и c соответствующие коэффициенты решаемого уравнения и затем упростить полученное выражение.

Чтобы запомнить состав формулы, выражаем её словами так: Корень квадратного уравнения равен среднему коэффициенту, взятому с противоположным знаком, плюс или минус квадратный корень из разности между квадратом среднего коэффициента и учетверенным произведением крайних коэффициентов, все деленное на удвоенный первый коэффициент».[6, с. 30]

При рассмотрении способов решения термин «дискриминант» не вводится. В этом параграфе рассматриваются случаи, когда 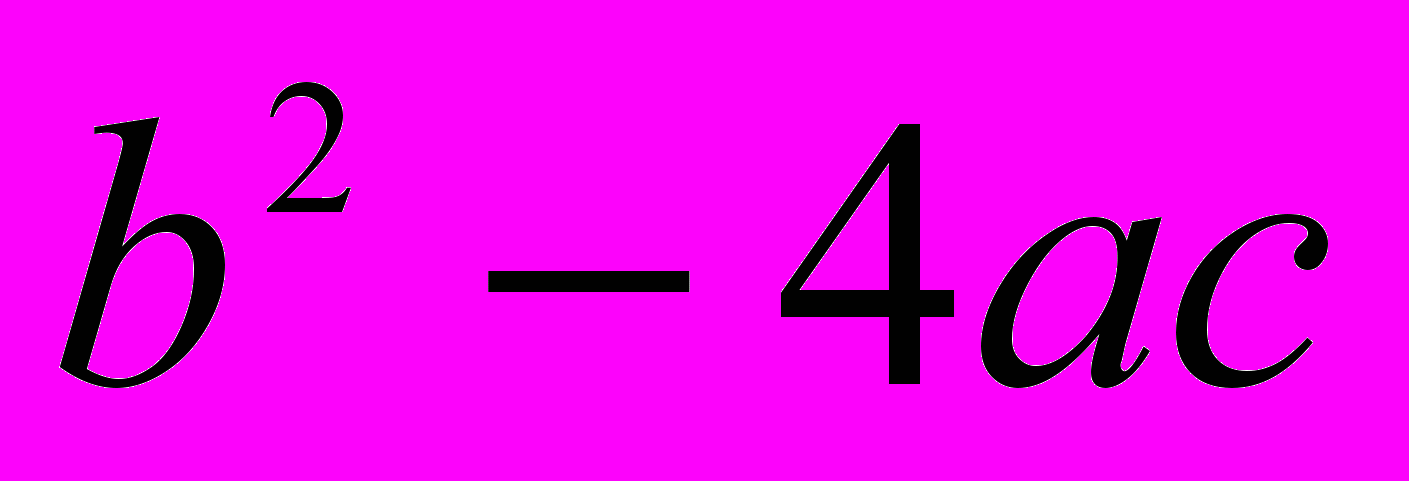>0 (<0, =0).

§ 26 «Сокращенные формулы» знакомит учащихся с уравнениями, в которых коэффициент b является четным, т.е. с формулой для нахождения корней с помощью D/4.

В § 27 «Соотношение между коэффициентами и корнями» формулируются и доказываются прямая и обратная теорема Виета.

Определение трехчлена второй степени вводится в § 29 «Форма первой части квадратного уравнения»: «Первая часть квадратного уравнения, рассматриваемая как выражение относительно х, называется трехчленом второй степени. Выражение 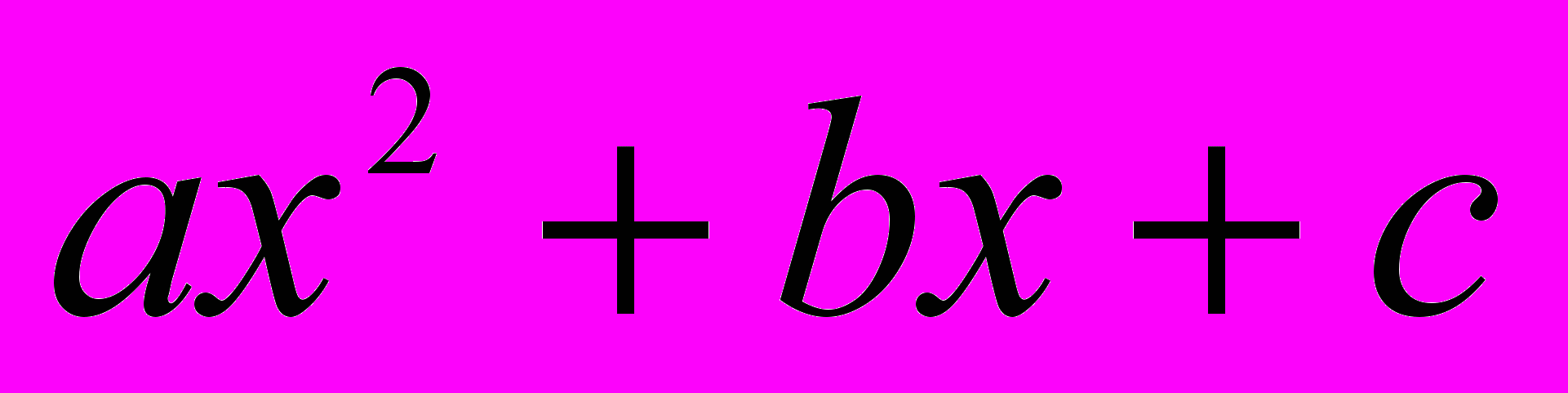называется трехчленом общего вида, а выражение 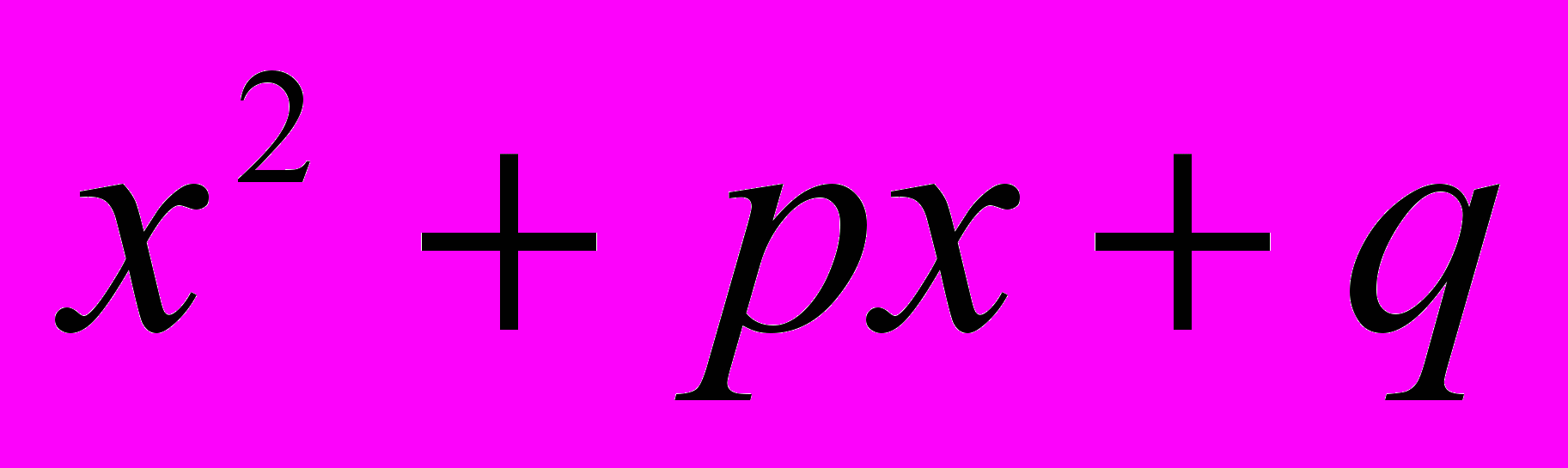- трехчленом приведенного вида, количества a, b и c или p и q называются коэффициентами трехчлена». [6, с. 35]

В § 30 «Разложение первой части квадратного уравнения на множители» приводится известное утверждение:

«Трехчлен общего вида равен произведению разностей между его главной буквой и корнями, умноженными на его первый коэффициент.

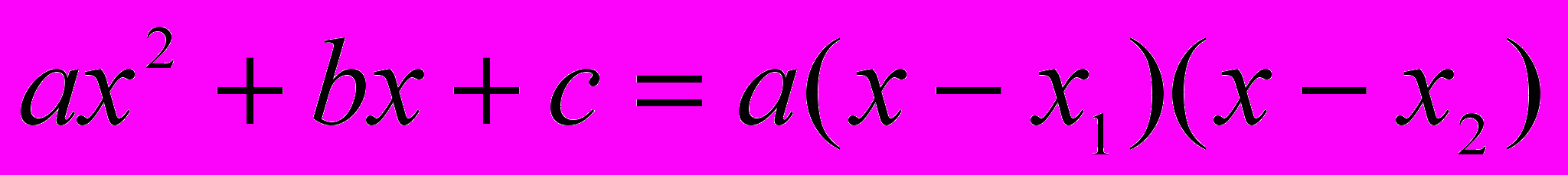». [6, с. 37]

В § 31 «Исследование квадратного уравнения» автор, все-таки, обращает наше внимание на то, что «…квадратное уравнение всегда имеет 2 корня, которые бывают или действительными и различными, или действительными равными, или мнимыми». [6, с. 37] «Для исследования корней всегда обращаем главное внимание на значение выражения 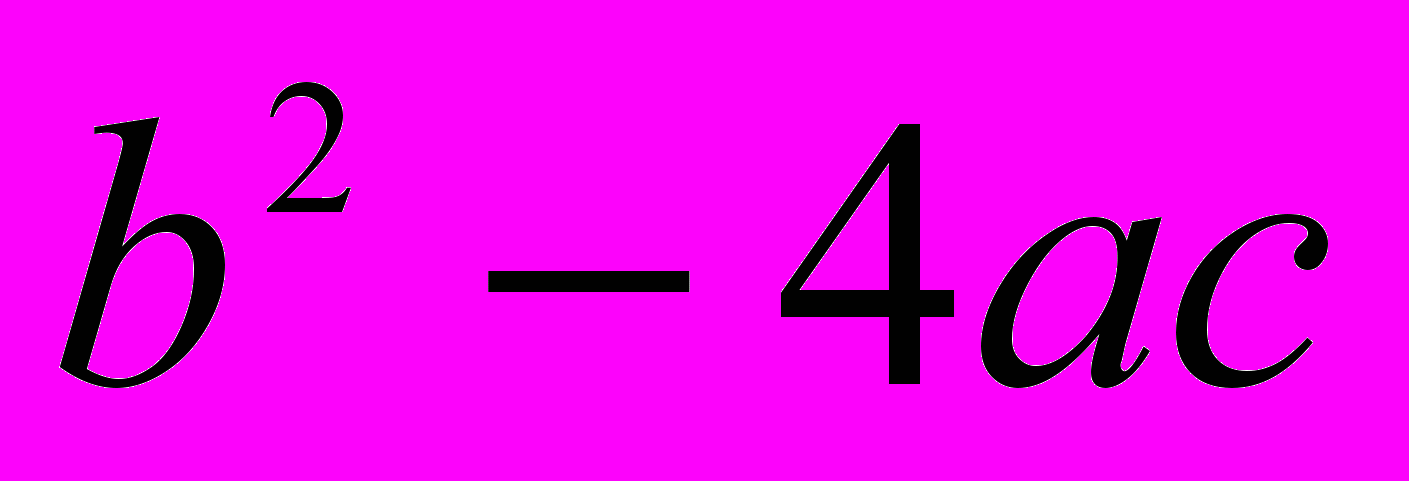. Это выражение называется определителем квадратного уравнения » [6, с. 38], т.е., вместо привычного названия «дискриминант» здесь употребляется термин «определитель».

В учебнике представлен только теоретический материал. После изучения материала приводятся примеры, но упражнения на закрепление изученного отсутствуют. И это понятно, поскольку существовал задачник, составленный этим же автором.

Таким образом, в отличие от современных изданий в исследуемом учебнике предложены сразу два способа доказательства формулы вычисления корней квадратного уравнения. Весьма полезным представляется выделение в самостоятельный параграф материала, касающегося решения неполного квадратного уравнения. Помимо того, введение в рассмотрение комплексных чисел позволило Н.А.Шапошникову высказаться о количестве корней квадратного уравнения точнее, чем это принято в современных учебниках алгебры. В заключение приведем мнение И.К. Андронова об этом учебнике алгебры: «Эта часть построена по весьма четкой системе, в ней нет лишнего и в то же время включен весь материал, необходимый для подготовки к изучению высшей математики». [4, с. 89].


Библиографический список

1. Алгебра: Учеб. Для 7 кл. сред. шк./ Ю.Н. Макарычев и др./ Под ред. С.А. Теляковского. М.: Просвещение, 1989. 240с.
   
2. Алгебра: Учеб. Для 8 кл. сред. шк./ Ю.Н. Макарычев и др./ Под ред. С.А. Теляковского. М.: Просвещение, 1989. 239с.
   
3. Алгебра: Учеб. Для 9 кл. сред. шк./ Ю.Н. Макарычев и др./ Под ред. С.А. Теляковского. М.: Просвещение, 1990. 272с.
   
4. Андронов И. К. Полвека развития школьного математического образования в СССР / И.К.Андронов. М.: Просвещение, 1967. 180с.
   
5. Колягин Ю.М. Русская школа и математическое образование: Наша гордость наша боль / Ю.М. Колягин. М.: Просвещение, 2001. 318 с.
   
6. Шапошников Н.А. Алгебра: Учебник: в 2 ч. Ч. 2: Курсы ст. кл., гимназий и реал. училищ. – М.; П.: Т-во печатного и издат. дела, 1918. – 176 с.