Рабочая программа учебной дисциплины «Математика» Специальность «Прикладная информатика (351400)»
| Вид материала | Рабочая программа |
- Программа по курсу "Математика. Алгебра и геометрия" для специальности 080801 (351400), 143.45kb.
- Программа дисциплины ф дифференциальные уравнения для студентов специальности 010501, 101.63kb.
- Программа дисциплины дс. 08 «Информационная безопасность» для студентов специальности, 149.66kb.
- Рабочая программа по дисциплине «логика» для специальности 351400 Прикладная информатика, 292.77kb.
- Рабочая программа по дисциплине «теория алгоритмов и сложности» для специальности 351400, 390.46kb.
- Рабочая программа по курсу «Мировые информационные ресурсы» 351400 «Прикладная информатика, 315.91kb.
- Рабочая программа дисциплины для магистрантов направления «Прикладная математика, 128.62kb.
- Программа дисциплины ф. 8 Общая физика Разделы «Механика», «Колебания и волны», «Молекулярная, 113.79kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 107.65kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 129.5kb.
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ»
Кафедра высшей математики
«УТВЕРЖДАЮ»
зав. кафедрой,
д. техн. наук, профессор
__________________________ Г. В. Савинов
РАБОЧАЯ ПРОГРАММА
учебной дисциплины
«Математика»
Специальность «Прикладная информатика (351400) »
Рассмотрена на заседании кафедры,
протокол №_____17___________
от «_4___» _октября___ 2006 г.
Санкт-Петербург
2006 г.
Утверждена Научно-методическим советом университета
Рабочая программа учебной дисциплины «Математика». Специальность «Прикладная информатика». ― СПб.: Изд-во СПбГУЭФ, 2006. ― 18 с.
Рабочая программа составлена в соответствии с учебным планом специальности «Прикладная информатика», предназначена для студентов II курса дневной формы обучения.
Программа содержит тематику лекций и практических занятий, вопросы для самоконтроля, список обязательной и дополнительной литературы.
Авторы-разработчики программы:
канд. физ.-мат. наук, доцент В. Г. Дмитриев,
канд. физ.-мат. наук, доцент В. С. Итенберг,
доктор техн. наук, проф. Г. В. Савинов
Рецензент:
канд. эконом. наук, доцент Г. Н. Парфенов
Издательство СПбГУЭФ 2006
СТРУКТУРА ДИСЦИПЛИНЫ
| N темы | Наименование раздела и темы | Количество часов | ||||
| Лекции | Практ. зан. | Контр. раб | Самост. раб. | Итого часов | ||
| | РАЗДЕЛ 1. АЛГЕБРА И ГЕОМЕТРИЯ | 42 | 38 | 4 | 84 | 168 |
| 1. | Аналитическая геометрия | 20 | 18 | 2 | 40 | 80 |
| 1.1. | Геометрические векторы | 4 | 4 | | 8 | 8 |
| 1.2. | Метод координат | 10 | 6 | | 18 | 34 |
| 1.3. | Кривые второго порядка | 4 | 6 | | 10 | 20 |
| 1.4. | Поверхности второго порядка | 2 | 2 | | 4 | 4 |
| 2. | Основные алгебраические структуры | 6 | 6 | | 12 | 24 |
| 2.1. | Группы, кольца, поля | 2 | 2 | | 4 | 8 |
| 2.2. | Комплексные числа | 4 | 4 | | | |
| 3. | Линейные векторные пространства | 16 | 14 | 2 | 32 | 64 |
| 3.1. | Линейное векторное пространство 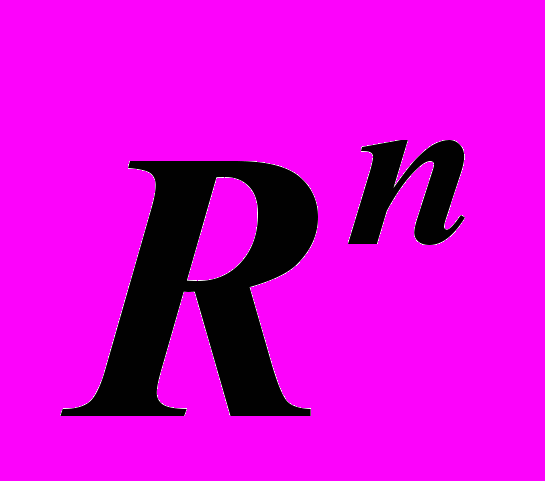 | 4 | 4 | | 8 | 16 |
| 3.2. | Линейные отображения и матрицы | 8 | 6 | | 16 | 32 |
| 3.3 | Системы линейных уравнений | 4 | 4 | | 8 | 16 |
| | РАЗДЕЛ 2. МАТЕМАТИЧЕСКИЙ АНАЛИЗ | 86 | 74 | 12 | 176 | 352 |
| 4. | Введение в математический анализ | 10 | 10 | | 20 | 40 |
| 4.1. | Последовательности | 4 | 4 | | 8 | 16 |
| 4.2. | Элементы топологии пространства 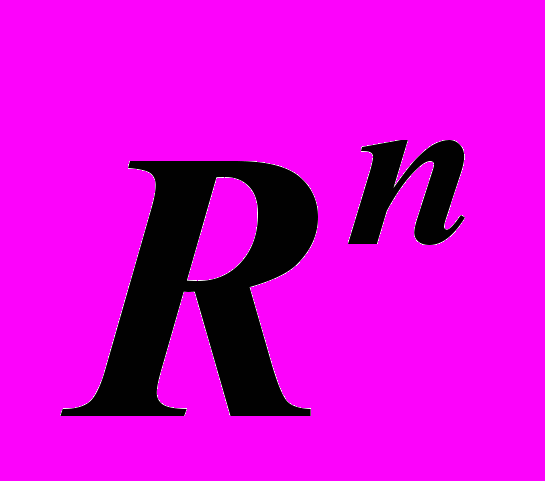 | 2 | 2 | | 4 | 8 |
| 4.3. | Предел и непрерывность функций | 4 | 4 | | 8 | 16 |
| 5. | Дифференциальное исчисление функции одной переменной | 14 | 12 | 2 | 28 | 56 |
| 5.1. | Дифференцирование функции одной переменной | 4 | 4 | | 8 | 16 |
| 5.2. | Свойства дифференцируемых функций | 6 | 2 | | 8 | 16 |
| 5.3. | Монотонность, экстремумы и выпуклость функции одной переменной | 4 | 8 | | 12 | 24 |
| 6 | Интегральное исчисление функции одной переменной | 8 | 6 | 2 | 16 | 32 |
| 6.1. | Неопределенный интеграл | 4 | 2 | | 8 | 16 |
| 6.2. | Определенный интеграл | 4 | 4 | | 8 | 16 |
| 7 | Дифференцирование функций нескольких переменных | 10 | 8 | 2 | 20 | 40 |
| 7.1. | Частные производные | 4 | 4 | | 8 | 16 |
| 7.2. | Дифференцируемые отображения | 2 | 2 | | 4 | 8 |
| 7.3. | Экстремумы и выпуклость функции нескольких переменных | 4 | 2 | | 8 | 16 |
| 8 | Кратные, криволинейные и поверхностные интегралы | 8 | 6 | 2 | 16 | 32 |
| 8.1. | Кратные интегралы | 4 | 4 | | 8 | 16 |
| 8.2. | Криволинейные и поверхностные интегралы | 4 | 2 | | 8 | 16 |
| 9 | Числовые и функциональные ряды | 12 | 10 | 2 | 24 | 48 |
| 9.1. | Числовые ряды | 4 | 4 | | 8 | 16 |
| 9.2. | Степенные ряды | 4 | 4 | | 8 | 16 |
| 9.3. | Элементы гармонического анализа | 4 | 2 | | 8 | 16 |
| 10 | Элементы векторного анализа и теории поля | 6 | 6 | | 12 | 24 |
| 10.1. | Векторные функции | 2 | 2 | | 4 | 8 |
| 10.2. | Дивергенция и ротор векторного поля | 4 | 4 | | 8 | 16 |
| 11 | Элементы теории дифференциальных уравнений | 10 | 8 | 2 | 20 | 40 |
| 11.1 | Обыкновенные дифференциальные уравнения | 6 | 4 | | 12 | 24 |
| 11.2. | Системы линейных дифференциальных уравнений с постоянными коэффициентами | 4 | 4 | | 8 | 16 |
| 12 | Элементы теории численных методов | 8 | 8 | | 16 | 32 |
| 12.1. | Численные методы в алгебре и анализе | 4 | 4 | | 8 | 16 |
| 12.2. | Численные методы решения дифференциальных уравнений | 4 | 4 | | 8 | 16 |
| | РАЗДЕЛ 3.ЭЛЕМЕНТЫ ДИСКРЕТНОЙ МАТЕМАТИКИ | 14 | 14 | | 28 | 56 |
| 13 | Элементы комбинаторики | 4 | 4 | | 8 | 16 |
| 14 | Алгебра логики | 6 | 6 | | 12 | 24 |
| 15 | Элементы теории графов | 4 | 4 | | 8 | 16 |
| | РАЗДЕЛ 4. ЭЛЕМЕНТЫ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ | 8 | 8 | | 16 | 32 |
| 16 | Нечеткие множества и нечеткие отношения | 8 | 8 | | 16 | 32 |
| | ИТОГО | 150 | 134 | 16 | 300 | 600 |
Дисциплина "Математика " изучается на I и II курсах в течение 3-х семестров, каждый семестр завершается экзаменом.
Целью курса является:
- ознакомить студента с важнейшими математическими понятиями и утверждениями;
- научить студента постановке математической модели стандартной задачи и анализу полученных знаний;
- привить студенту определенную грамотность, достаточную для самостоятельной работы с экономико-математической литературой;
В результате изучения дисциплины студент должен овладеть:
а) фундаментальными математическими понятиями;
б) классическими методами решения основных математических задач, к которым могут приводить те или иные экономические проблемы;
в) навыками самостоятельной работы с математической литературой.
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
РАЗДЕЛ 1. АЛГЕБРА И ГЕОМЕТРИЯ
ТЕМА 1. Аналитическая геометрия
- 1.1. Геометрические векторы
Геометрические векторы, линейные операции, линейно зависимые и линейно независимые системы векторов, базисы, координаты вектора, скалярное произведение, ортонормированные базисы.
Определители второго и третьего порядков. Векторное и смешанное произведение. Понятие об определителях
 -го порядка.
-го порядка.1.2. Метод координат
Прямоугольные координаты на плоскости и в пространстве. Расстояние между точками, деление отрезка в заданном отношении. Понятие об уравнении линий и поверхностей. Различные формы уравнения прямой на плоскости. Основные задачи на прямую линию на плоскости. Уравнения плоскости. Уравнения прямой в пространстве. Основные задачи на плоскость и прямую в пространстве.
1.3. Кривые второго порядка
Окружность, эллипс, гипербола, парабола. Определения, основные свойства. Полярные координаты на плоскости. Полярные уравнения кривых второго порядка. Исследование общего уравнения второго порядка.
1.4. Поверхности второго порядка
Уравнения сферы, эллипсоида, параболоидов и гиперболоидов. Сферические и цилиндрические координаты в пространстве.
ТЕМА 2. Элементы теории алгебраических структур
- 2.1. Основные алгебраические структуры.
Элементы теории множеств. Понятие о бинарных операциях и бинарных отношениях. Определение группы. Абелевы группы. Примеры групп. Подгруппы. Классы смежности и факторгруппы. Примеры. Определения и основные свойства колец, полей, алгебр.
2.2. Комплексные числа
Определение комплексных чисел. Действия с комплексными числами. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа. Алгебраическая и тригонометрическая формы комплексного числа. Показательная форма комплексного числа. Формула Эйлера. Корни из комплексных чисел.
ТЕМА 3. Линейные векторные пространства
- 3.1. Линейное векторное пространство
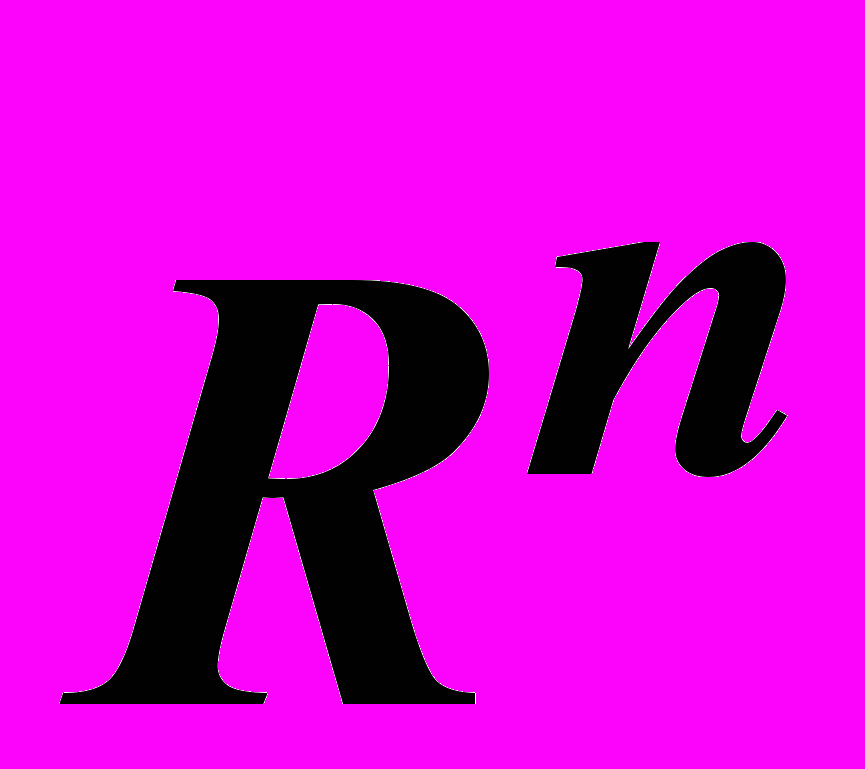
Определение и свойства линейных операций над
 -мерными векторами, векторное пространство
-мерными векторами, векторное пространство 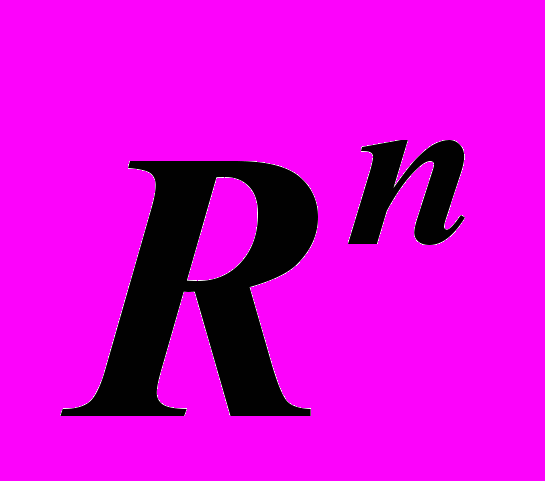 . Линейно зависимые и линейно независимые системы векторов. Скалярное умножение, неравенство Коши, норма (длина)
. Линейно зависимые и линейно независимые системы векторов. Скалярное умножение, неравенство Коши, норма (длина)  -мерного вектора. Ортогональность, угол между векторами. Базисы, координаты вектора относительно базиса, размерность. Ортогональные и ортонормированные базисы, процедура ортогонализации. Подпространства и линейные оболочки. Ранг системы векторов.
-мерного вектора. Ортогональность, угол между векторами. Базисы, координаты вектора относительно базиса, размерность. Ортогональные и ортонормированные базисы, процедура ортогонализации. Подпространства и линейные оболочки. Ранг системы векторов. 3.2. Линейные отображения и матрицы
Линейные отображения (преобразования, операторы). Матрицы, связь матриц с линейными отображениями. Алгебра линейных отображений и алгебра матриц. Транспонирование матрицы и его свойства. Ранг линейного отображения и ранги матриц. Обратимые линейные отображения. Обратная матрица. Преобразование координат вектора и элементов матрицы при переходе к новому базису.
3.3. Системы линейных уравнений
Исследование систем линейных уравнений. Теоремы Кронекера-Капелли, Крамера, Фредгольма. Методы решения систем линейных уравнений. Собственные векторы и собственные числа матрицы. Квадратичные и билинейные формы. Критерий Сильвестра положительной определенности квадратичной формы.
РАЗДЕЛ 2. . МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ТЕМА 4. Ведение в математический анализ
- 4.1. Последовательности
Определение и примеры числовой последовательности. Пределы числовой последовательности. Свойства сходящихся числовых последовательностей. Поведение монотонных и ограниченных числовых последовательностей. Число
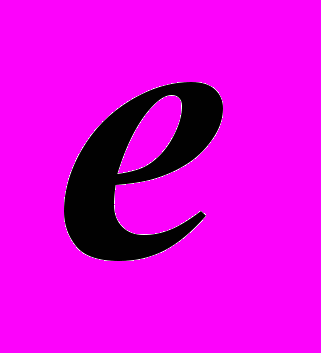 . Векторные последовательности. Сходимость векторных последовательностей.
. Векторные последовательности. Сходимость векторных последовательностей. 4.2. Элементы топологии пространства 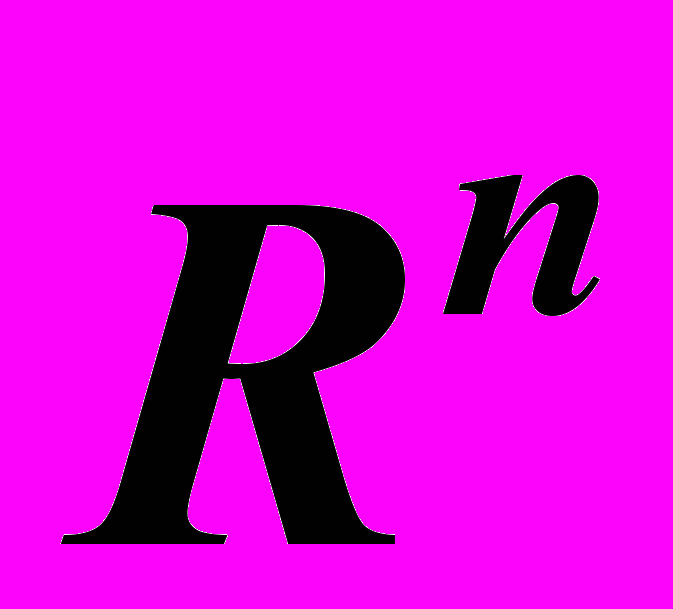
Открытые шары в пространстве
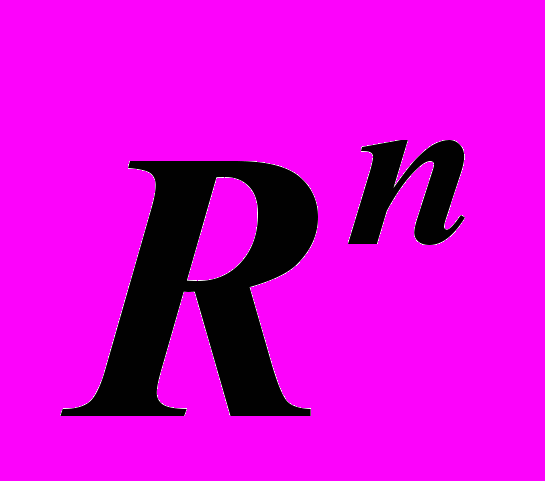 . Классификация точек множества. Открытые и замкнутые множества, их свойства. Граница множества. Компактные множества. Выпуклые множества. Линейно связные множества.
. Классификация точек множества. Открытые и замкнутые множества, их свойства. Граница множества. Компактные множества. Выпуклые множества. Линейно связные множества.4.3. Предел и непрерывность функций
Определение пределов функции. Свойства пределов. Односторонние пределы. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых. Непрерывность функции в точке. Свойства непрерывных функций. Примеры непрерывных функций. Односторонняя непрерывность. Понятие о точках разрыва и их классификации. Замечательные пределы. Свойства функций, непрерывных на компактном множестве.
ТЕМА 5. Дифференциальное исчисление функции одной переменной
5.1. Дифференцирование функции одной переменной
Определение производной функции в точке. Связь между непрерывностью и существованием конечной производной в точке. Односторонние производные. Дифференциал функции в точке, его связь с производной в точке. Производная функция. Дифференцирование алгебраических операций. Производная сложной и обратной функции. Дифференцирование функций, заданных параметрически. Производные и дифференциалы высших порядков.
5.2. Свойства дифференцируемых функций
Теоремы Ферма, Ролля, Лагранжа, Коши, Лопиталя. Теорема Тейлора. Разложение основных элементарных функций по формуле Тейлора. Применение формулы Тейлора для приближенных вычислений, оценка ошибки.
5.3. Монотонность, экстремумы и выпуклость функции одной переменной
Признаки монотонности функции одной переменной. Определение и признаки локальных экстремумов функции одной переменной. Задача оптимизации функции, дифференцируемой на замкнутом промежутке. Определение и признаки выпуклости функции одной переменной. Точки перегиба графика функции. Асимптоты графика функции одной переменной. Исследование функции одной переменной и построение графика.
ТЕМА 6. Интегральное исчисление функции одной переменной
6.1. Неопределенный интеграл
Первообразная и неопределенный интеграл. Линейные свойства операции неопределенного интегрирования, замена переменной и интегрирование по частям в неопределенном интеграле. Таблица неопределенных интегралов. Основные классы интегрируемых функций.
6.2. Определенный интеграл
Определение определенного интеграла и его свойства. Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Применения определенного интеграла. Несобственные интегралы, признаки сходимости несобственных интегралов.
ТЕМА 7. Дифференцирование функций нескольких переменных
7.1. Частные производные
Определение частных производных первого порядка. Первый дифференциал (полная производная) функции нескольких переменных. Дифференцируемые функции нескольких переменных, условие дифференцируемости. Сложная функция нескольких переменных. Производная вдоль вектора и по направлению. Градиент и его свойства. Частные производные и дифференциалы высших порядков. Формула Тейлора для функции нескольких переменных (без доказательства).
7.2. Дифференцируемые отображения
Отображения множеств из пространства
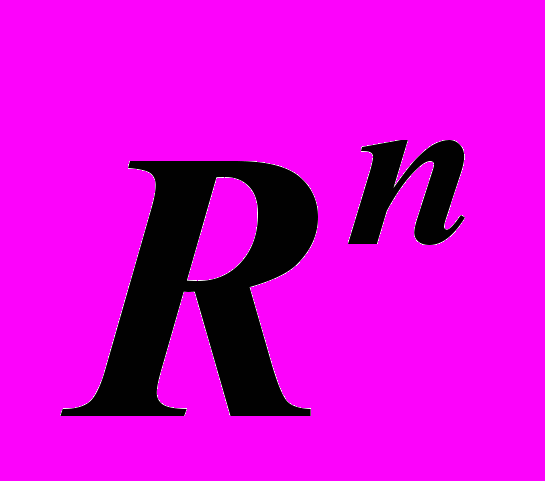 в пространство
в пространство 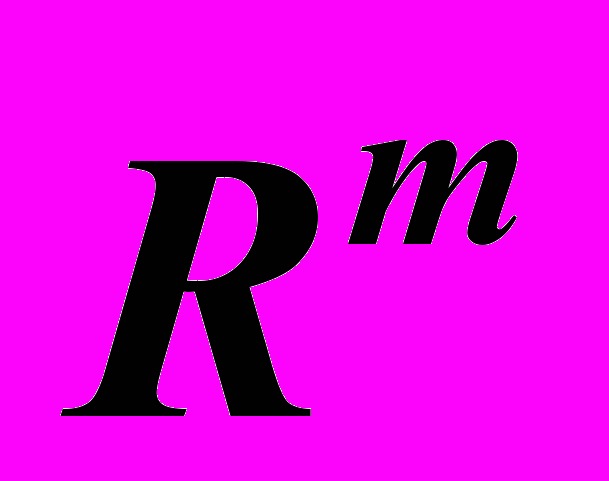 . Непрерывные и дифференцируемые отображения. Якобиан отображения. Условие независимости системы функций. Неявные функции. Теорема существования (без доказательства). Дифференцирование неявной функции. Теорема об обратной функции (без доказательства). нескольких переменных (без доказательства).
. Непрерывные и дифференцируемые отображения. Якобиан отображения. Условие независимости системы функций. Неявные функции. Теорема существования (без доказательства). Дифференцирование неявной функции. Теорема об обратной функции (без доказательства). нескольких переменных (без доказательства). 7.3. Экстремумы и выпуклость функции нескольких переменных
Определение локальных экстремумы функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Условный экстремум. Метод множителей Лагранжа. Определение и признаки выпуклости функции нескольких переменных. Неравенство Иенсена.
ТЕМА 8. Кратные, криволинейные и поверхностные интегралы
8.1. Кратные интегралы
Повторные интегралы. Изменение порядка интегрирования в повторных интегралах. Двойной и тройной интегралы, определения и свойства. Сведение кратного интеграла к повторному. Понятие
 -кратного интеграла. Замена переменных в кратных интегралах.).
-кратного интеграла. Замена переменных в кратных интегралах.). 8.2. Криволинейные и поверхностные интегралы
Понятие кривой. Гладкие и кусочно гладкие кривые. Длина кривой. Криволинейные интегралы. Их свойства и вычисление. Понятие поверхности. Касательная плоскость и нормаль к поверхности. Площадь поверхности. Поверхностные интегралы Их свойства и вычисление
ТЕМА 9. Числовые и функциональные ряды
9.1. Числовые ряды
Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами. Ряды с неотрицательными членами. Признаки сходимости. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимости. Признак Лейбница. Свойства абсолютно сходящихся рядов
9.2. Степенные ряды
Понятие о функциональных рядах. Область сходимости. Равномерная сходимость. Признак Вейерштрасса. Свойства равномерно сходящихся рядов. Степенные ряды. Теорема Абеля. Круг сходимости. Ряды Тейлора и Маклорена. Разложение функций в степенные ряды. Приложение рядов.
9.3. Элементы гармонического анализа
Метрические пространства. Нормированные пространства. Бесконечномерные евклидовы пространства. Полнота пространства. Банаховы и гильбертовы пространства. Ортогональные и ортонормированные системы. Процесс ортогонализации. Ряды Фурье по ортогональным системам. Минимальное свойство частных сумм рядов Фурье. Неравенство Бесселя. Равенство Парсеваля-Стеклова. Полнота и замкнутость системы. Тригонометрические ряды Фурье.
ТЕМА 10. Элементы векторного анализа и теории поля
10.1. Векторные функции
Определение и примеры векторных функций. Непрерывность, дифференцируемость и интегрирование векторных функций. Понятие о скалярном и векторном полях. Циркуляция векторного поля вдоль кривой. Поток поля через поверхность.
10.2. Дивергенция и ротор векторного поля
Формула Гаусса-Остроградского. Дивергенция векторного поля, ее физический смысл. Формула Стокса (без вывода). Ротор векторного поля, его физический смысл. Потенциальное поле, его свойства. Условие потенциальности. Нахождение потенциала. Соленоидальное поле, его свойства. Условие соленоидальности. Векторный потенциал.
ТЕМА 11. Элементы теории дифференциальных уравнений
11.1. Обыкновенные дифференциальные уравнения
Определение дифференциального уравнения. Порядок уравнения. Решения дифференциального уравнения. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши. Основные классы уравнений, интегрируемых в квадратурах. Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах для дифференциальных уравнений. Уравнения, допускающие понижение порядка. Линейные дифференциальные уравнения. Общее решение. Фундаментальная система решений. Метод Лагранжа вариации постоянных. Линейные дифференциальные уравнения с постоянными коэффициентами. Уравнения с правой частью специального вида
11.2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
Нормальная система дифференциальных уравнений. Векторная запись нормальной системы. Задача Коши для нормальной системы дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Системы линейных дифференциальных уравнений с постоянными коэффициентами. Понятие о качественной теории дифференциальных уравнений, фазовое пространство (плоскость), фазовая траектория и скорость.
ТЕМА 12. Элементы теории численных методов
12.1. Численные методы в алгебре и анализе
Понятие о численных методах, применение ЭВМ для решения задач. Решение нелинейных уравнений методом Ньютона и методом простых итераций. Сходимость, оценка погрешности. Интерполяционные многочлены Лагранжа и Ньютона, численное дифференцирование и интегрирование. Оценка погрешности. Градиентные методы решения гладких экстремальных задач.
12.2. Численные методы решения дифференциальных уравнений
Численные методы решения задач для обыкновенных дифференциальных уравнений. Решение задачи Коши: методы Эйлера и Рунге-Кутта. Оценка погрешности.
РАЗДЕЛ 3. ЭЛЕМЕНТЫ ДИСКРЕТНОЙ МАТЕМАТИКИ
ТЕМА 13. Элементы комбинаторики
Отношение эквивалентности и частичного порядка. Упорядоченные и неупорядоченные множества. Правило суммы. Формула включений и исключений. Правило произведения. Размещения, перестановки, сочетания. Размещения и сочетания с повторениями. Перестановки с повторениями. Бином Ньютона.
ТЕМА 14. Алгебра логики
Алгебра высказываний. Предикаты. Кванторы существования и всеобщности. Понятие логического следствия. Прямая, обратная и противоположная теоремы. Необходимое и достаточное условия. Метод доказательства от противного. Метод математической индукции.
Булевы алгебры. Булевы функции. Элементарные булевы функции. Совершенные нормальные формы. Полиномы Жегалкина.
ТЕМА 15. Элементы теории графов
Основные понятия теории графов. Матричное представление графов. Числовые характеристики графов. Обходы графов. Эйлеровы и гамильтоновы циклы в графах.
РАЗДЕЛ 4 ЭЛЕМЕНТЫ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
ТЕМА 16. Нечеткие множества и нечеткие отношения
Определение и свойства нечетких множеств и нечетких отношений. Операции над нечеткими множествами. Понятие о нечетких алгоритмах и теории неопределенности.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
РАЗДЕЛ 1. АЛГЕБРА И ГЕОМЕТРИЯ
ТЕМА 1. Аналитическая геометрия
- 1.1. Геометрические векторы
Геометрические векторы, линейные операции, базисы, координаты вектора, скалярное произведение, решение геометрических задач с помощью векторов.
Определители второго и третьего порядков. Векторное и смешанное произведение. Вычисление площадей и объемов. Вычисление определителей
 -го порядка.
-го порядка.1.2. Метод координат
Расстояние между точками, деление отрезка в заданном отношении. Задачи на составление уравнений линий на плоскости. Основные задачи на прямую линию на плоскости. Основные задачи на плоскость и прямую в пространстве.
1.3. Кривые второго порядка
Канонические уравнения окружности, эллипса, гиперболы, параболы. Вычисление основных характеристик. Определение кривых по их геометрическим свойствам. Полярные координаты на плоскости. Приведение общего уравнения второго порядка к каноническому виду.
1.4. Поверхности второго порядка
Исследование поверхностей второго порядка методом сечений. Сферические и цилиндрические координаты в пространстве.
Контрольная работа 1. Геометрические векторы, прямая на плоскости и прямая и плоскость в пространстве. Кривые второго порядка.
ТЕМА 2. Элементы теории алгебраических структур
- 2.1. Основные алгебраические структуры.
Теоретико-множественные операции и их свойства. Примеры групп: группа перестановок, группы преобразования плоскости.
2.2. Комплексные числа
Действия с комплексными числами в различных формах. Формула Эйлера. Корни из комплексных чисел.
ТЕМА 3. Линейные векторные пространства
- 3.1. Линейное векторное пространство
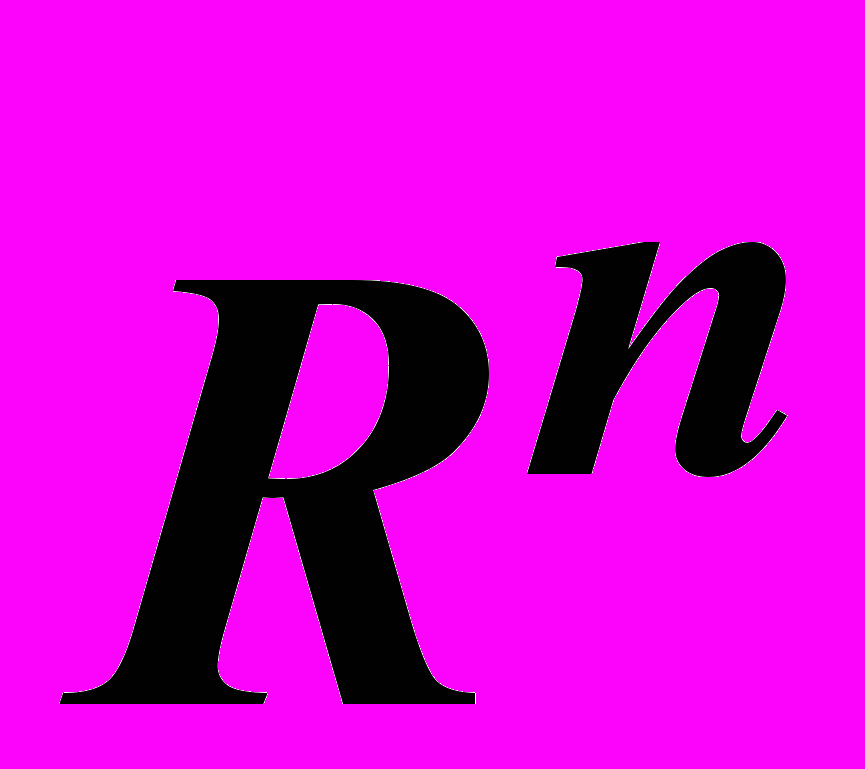
Действия с
 -мерными векторами. Линейно зависимые и линейно независимые системы векторов. Скалярное умножение, ортогональность, угол между векторами. Базисы, координаты вектора относительно базиса. Ортогональные и ортонормированные базисы, процедура ортогонализации. Вычисление ранга системы векторов.
-мерными векторами. Линейно зависимые и линейно независимые системы векторов. Скалярное умножение, ортогональность, угол между векторами. Базисы, координаты вектора относительно базиса. Ортогональные и ортонормированные базисы, процедура ортогонализации. Вычисление ранга системы векторов. 3.2. Линейные отображения и матрицы
Примеры линейных отображений. Матрицы, построение матриц линейных отображений. Действия с матрицами. Вычисление ранга матрицы. Методы вычисления обратной матрицы. Решение матричных уравнений.
3.3. Системы линейных уравнений
Методы решения систем линейных уравнений. Вычисление собственных векторов и собственных чисел матрицы.
Контрольная работа 2. Комплексные числа. Действия с матрицами, решения систем линейных уравнений.
РАЗДЕЛ 2. . МАТЕМАТИЧЕСКИЙ АНАЛИЗ
ТЕМА 4. Ведение в математический анализ
- 4.1. Последовательности
Примеры числовых последовательностей. Вычисление пределов числовых последовательностей.
4.2. Элементы топологии пространства 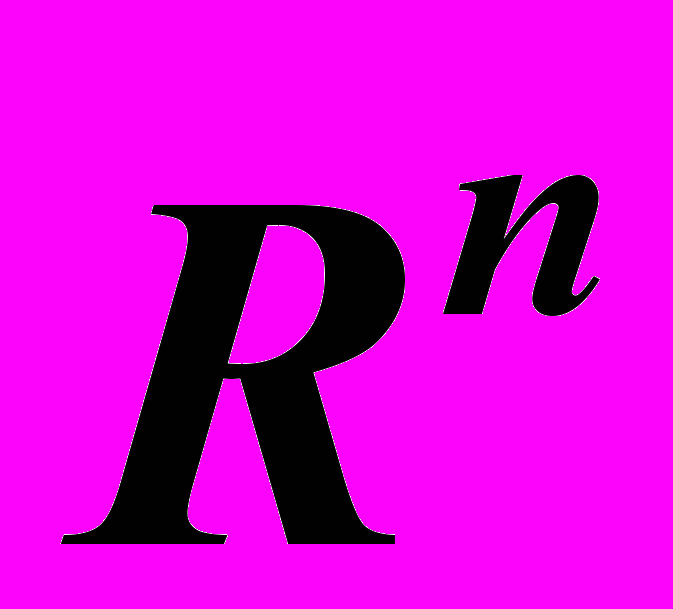
Классификация точек множества. Примеры открытых, замкнутых и компактных множеств.
4.3. Предел и непрерывность функций
Доказательство пределов с помощью определений. Примеры бесконечно малых и бесконечно больших функций. Эквивалентные бесконечно малые. Вычисление пределов. Примеры непрерывных функций.
ТЕМА 5. Дифференциальное исчисление функции одной переменной
5.1. Дифференцирование функции одной переменной
Вычисление производных с помощью определения. Таблица производных. Техника дифференцирования. Дифференцирование функций, заданных параметрически. Производные и дифференциалы высших порядков.
5.2. Свойства дифференцируемых функций
Разложение элементарных функций по формулам Тейлора и Мак-Лорена. Применение формулы Тейлора для приближенных вычислений, оценка ошибки.
5.3. Монотонность, экстремумы и выпуклость функции одной переменной
Вычисление промежутков монотонности и локальных экстремумов функции одной переменной. Задача оптимизации функции на замкнутом промежутке. Вычисление промежутков выпуклости и точек перегиба функции одной переменной. Асимптоты графика функции одной переменной. Исследование функции одной переменной и построение графика.
Контрольная работа 3. Вычисление пределов, производных, исследование функции и построение графика.
ТЕМА 6. Интегральное исчисление функции одной переменной
6.1. Неопределенный интеграл
Таблица неопределенных интегралов. Замена переменной и интегрирование по частям в неопределенном интеграле. Вычисление неопределенных интегралов. Основные классы интегрируемых функций.
6.2. Определенный интеграл
Формула Ньютона-Лейбница. Замена переменной и интегрирование по частям в определенном интеграле. Применения определенного интеграла. Несобственные интегралы, признаки сходимости несобственных интегралов.
Контрольная работа 4. Неопределенные и определенные интегралы.
ТЕМА 7. Дифференцирование функций нескольких переменных
7.1. Частные производные
Вычисление частных производных первого порядка. Сложная функция нескольких переменных. Производная вдоль вектора и по направлению. Градиент и его свойства. Частные производные и дифференциалы высших порядков.
7.2. Дифференцируемые отображения
Примеры отображений. Якобиан отображения. Неявные функции. Дифференцирование неявной функции.
7.3. Экстремумы и выпуклость функции нескольких переменных
Вычисление локальных экстремумы функций нескольких переменных. Условный экстремум. Метод множителей Лагранжа.
Контрольная работа 5. Частные производные, производная по направлению и градиент, локальные экстремумы функции нескольких переменных.
ТЕМА 8. Кратные, криволинейные и поверхностные интегралы
8.1. Кратные интегралы
Повторные интегралы. Изменение порядка интегрирования в повторных интегралах. вычисление двойных и тройных интегралов.
8.2. Криволинейные и поверхностные интегралы
Криволинейные и поверхностные интегралы и их применение. Вычисление длины кривой, площади поверхности.
Контрольная работа 6. Кратные, криволинейные и поверхностные интегралы.
ТЕМА 9. Числовые и функциональные ряды
9.1. Числовые ряды
Ряды с неотрицательными членами. Признаки сходимости. Знакопеременные ряды, ряды с комплексными членами. Абсолютная и условная сходимости. Признак Лейбница. Исследование сходимости числовых рядов.
9.2. Степенные ряды
Исследование сходимости степенных рядов. Разложение функций в степенные ряды. Приложение рядов.
9.3. Элементы гармонического анализа
Разложение функций в тригонометрические ряды Фурье.
Контрольная работа 7. Числовые, степенные и тригонометрические ряды.
ТЕМА 10. Элементы векторного анализа и теории поля
10.1. Векторные функции
Примеры скалярного и векторного поля. Вычисление циркуляции и потока векторного поля.
10.2. Дивергенция и ротор векторного поля
Вычисление дивергенции и ротора векторного поля. Исследование векторных полей.
ТЕМА 11. Элементы теории дифференциальных уравнений
11.1. Обыкновенные дифференциальные уравнения
Решение дифференциальных уравнений первого порядка. Уравнения с разделяющимися переменными, линейные и однородные уравнения. Дифференциальные уравнения второго порядка, допускающие понижение порядка. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Уравнения с правой частью специального вида
11.2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
Решение систем линейных дифференциальных уравнений с постоянными коэффициентами.
Контрольная работа 8. Дифференциальные уравнения.
ТЕМА 12. Элементы численных методов
12.1. Численные методы в алгебре и анализе
Решение нелинейных уравнений методом Ньютона и методом простых итераций. Интерполяционные многочлены Лагранжа и Ньютона.
12.2. Численные методы решения дифференциальных уравнений
Приближенные методы решения дифференциальных уравнений Эйлера и Рунге-Кутта. Оценка погрешности.
РАЗДЕЛ 3. ЭЛЕМЕНТЫ ДИСКРЕТНОЙ МАТЕМАТИКИ
ТЕМА 13. Элементы комбинаторики
Размещения, перестановки, сочетания. Размещения и сочетания с повторениями. Перестановки с повторениями. Бином Ньютона.
ТЕМА 14. Алгебра логики
Булевы алгебры. Булевы функции. Элементарные булевы функции. Совершенные нормальные формы.
ТЕМА 15. Элементы теории графов
Основные понятия теории графов. Матричное представление графов.
РАЗДЕЛ 4 ЭЛЕМЕНТЫ ТЕОРИИ НЕЧЕТКИХ МНОЖЕСТВ
ТЕМА 16. Нечеткие множества и нечеткие отношения
Примеры и свойства нечетких множеств и нечетких отношений. Операции над нечеткими множествами.
ЛИТЕРАТУРА
Разделы 1 - 4
- Бугров Я.С. , Никольский С.М. Элементы линейной алгебры и аналитической геометрии. –М . : Наука , 1980 , 1984.
- Бугров Я.С. , Никольский С.М. Дифференциальное и интегральное исчисление. –М. :Наука ,1980.
- Бугров Я.С. Никольский С.М. Высшая математика: Задачник. -М.: Наука , 1982.
- Бугров Я.С. Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. ФКП. –М.: Наука , 1981.
- Ведина О.И., Десницкая В.Н., Варфоломеева Г.Б., Тарасюк А.Ф. Математика. Математический анализ для экономистов. –М.: Филинь, 2000
- Воеводин В.В. Линейная алгебра. М., Наука, 1980.
- Высшая математика для экономистов/Под ред. Кремера Н.Ш., - М.: ЮНИТИ, 1998.
- Гаштольд Л.П., Лицкевич И.К., Матвеев В.М., Шапошникова Т.О. Линейная алгебра. Темы: «Ранг матрицы», « Системы m линейных уравнений с n неизвестными», «Собственные числа и собственные векторы матрицы», «Квадратичные формы»: Методические указания. -Изд-во СпбГУЭФ, 1997
- Гаштольд Л.П., Лицкевич И.К., Матвеев В.Н., Шапошникова Т.О. Линейная алгебра». Темы: «Матрицы», «Определители», «Системы лине6йных уравнений»:Методические указания. – СПб.: Изд-во СПбГУЭФ, 1994
- Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах: Уч. пособие. Ч.1,2.-1980
- Ежов И.И., Скороход А.В., и др. Элементы комбинаторики. –М.: Наука, 1977
- Идельсон А.В., Блюмкина И.А. Аналитическая геометрия. Линейная алгебра. –М.: ИНФРАМ, 2000
- Карасев А.И., Аксютина З.М., Савельева Т.И. Курс высшей математики для экономических вузов. -М.: Высшая математика, 1982
- Кропотов А.И. Элементы линейной алгебры: Уч. пособие.-Л.: ЛФЭИ, 1977
- Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики: Учебник.-М., Гос.Изд.физ-мат.литература,1983
- Кузнецов Л.А. Сборник задач по высшей математике (типовые расчеты). –М.: Высшая школа, 1983
- Математика в экономике: учебно-методическое пособие. Под ред. Н.Ш Кремера. – М.: Финстатинформ, 1999.
- Михайлов А.Б., Плоткин А.И., Рисс Е.А., Яшина Е.Ю. Математический язык в задачах. – СПб: Изд-во ГПУ им. Герцена, 2000
- Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М. Методы оптимизации. –М.: Наука, 1978
