Региональный методический конкурс образовательных учреждений Костромской области Методическая разработка по предмету «Математика» Раздел «Многогранники»

Вид материала

Конкурс

Содержание Основные требования к знаниям и умениям по данной теме Учащийся должен уметь Замечания (обрати внимание). Классификация двугранных углов по величине. Выучи. Определение многогранника. Призма. Виды призм. Рассмотри рисунок. Виды призм. Наклонная призма. Свойства прямой призмы Правильная призма. Задача (разбери решение, запиши в тетрадь). Задача (воспользуйся планом решения и реши задачу). ТЕОРЕМА (выучи) Виды параллелепипедов. Прямоугольный параллелепипед. Обрати внимание Реши самостоятельно и сверь ответ Правильные многогранники. Прочитай, это интересно Практические задания ( выполни ) ... Полное содержание

Подобный материал:

• Елена Леонидовна Шиман Предмет: литература, 165.42kb.
• Методическая разработка на тему, 461.38kb.
• Областной методический конкурс педагогов образовательных учреждений Костромской области, 1076.51kb.
• Администрация костромской области постановление от 27 июня 2011 г. N 238-а об уполномоченном, 26.81kb.
• Методическая разработка урока с использованием компьютера. Предмет Литература Класс, 157.33kb.
• Конкурс Уровень Результат 2008 нпо «Образование» Конкурс образовательных учреждений, 71.62kb.
• Протокол заседания экспертной комиссии регионального методического конкурса педагогов, 1617.32kb.
• Администрация костромской области постановление от 26 апреля 2010 г. N 133-а об областной, 1531.03kb.
• Конкурс педагогического мастерства 2009 Номинация «Методическая разработка», 316.09kb.
• Баранова Ольга Анатольевна, учитель истории моу сош №2 города Неи Костромской области, 81.84kb.

Департамент образования и науки Костромской области

ГОУ СПО «Костромской автодорожный колледж»

Региональный методический конкурс образовательных учреждений

Костромской области


Методическая разработка по предмету « Математика »

Раздел « Многогранники »


Преподаватель математики:

Смирнова И.В.


Кострома 2009г


Содержание.


1. Пояснительная записка стр. 3

2. Двугранный угол стр. 4

а) Линейный угол двугранного угла

б) Классификация двугранных углов.

3. Определение многогранника стр. 4

4.Призма. Свойства призмы стр. 5

5. Виды призм и их свойства стр.6

6. Параллелепипеды и их виды стр.7

7. Свойства прямоугольного стр.8

параллелепипеда

8.Элементы симметрии стр.9

параллелепипеда

9.Правильные многогранники стр. 10

10. Виды правильных многогранников стр. 11

11. Дополнительный материал по

теме «Правильные многогранники» стр. 11 – 14

12. Практические задания стр. 15 – 16

13. Пирамида ее виды и свойства стр.16 – 18

14. Дополнительный материал по стр. 18

теме: «Правильная пирамида»

15. Задачи. Усеченная пирамида стр. 19 – 21

16. Контрольные вопросы стр. 21

17. Приложение стр. 23-27


Пояснительная записка.


Опорные конспекты по теме: «Многогранники» составлены в соответствие с тематикой и содержанием, охватывающим требования учебника «Геометрия» А. В. Погорелова. Основные задачи методической разработки:

1. В лаконичной форме дать учащемуся все основные определения, свойства, алгоритмы, которые встречаются в данной теме.
   
2. Проиллюстрировать основные определения рисунками, не обремененными техническими трудностями, а лишь разъясняющими суть определения.
   
3. Расположить материал так, чтобы поиск нужной информации был достаточно прост.
   

Для решения последней задачи в материале выделено, что необходимо выучить, на что особо обратить внимание, приведены примеры задач с решениями, рисунками, ответами, для самоконтроля предложены вопросы.

Методическое пособие рекомендуется для учащихся не достаточно хорошо освоивших данную тему, а так же для учащихся пропустивших урок по какой – либо причине.

Опорные конспекты составлены в рамках экспериментальной работы по теме: «Индивидуализация учебно-воспитательного процесса в условиях модернизации образования».

Основные требования к знаниям и умениям по данной теме:

Учащийся должен знать: определение двугранного угла, линейного угла, многогранника, призмы и ее свойства, виды призм, определение параллелепипеда, его виды и свойства, определение правильного многогранника, виды правильных многогранников, определение пирамиды, основные элементы пирамиды (основание, боковые ребра, боковые грани, вершина, высота), определение правильной пирамиды, определение апофемы, определение усеченной пирамиды.

Учащийся должен уметь: изображать многогранники на рисунке, решать типовые задачи, используя теоретические знания по теме, правильно использовать термины.


Правила пользования методическим пособием для учащихся:

1. Внимательно прочитай опорные конспекты.
   
2. Выучи определения, встречающиеся в данной теме.
   
3. Рассмотри рисунки и изучи пояснения к ним.
   
4. Разбери предложенную к теме задачу и запиши ее решение в тетрадь.
   
5. Обрати особое внимание на свойства.
   
6. Постарайся решить самостоятельно предложенные задачи, сверь ответ.
   
7. Проконтролируй свои знания – ответь на контрольные вопросы.
   

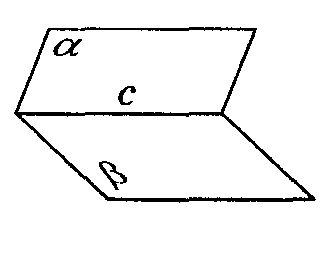
Двугранный угол.

Выучи. Двугранным углом называется фигура, образованная двумя полуплоскостями (гранями двугранного угла) с общей ограничивающей их прямой (ребром двугранного угла).

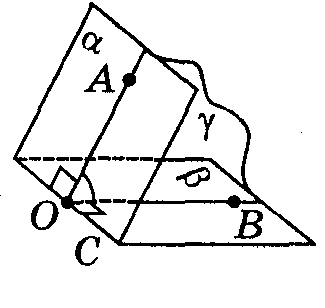
Линейным углом двугранного угла называется угол между полупрямыми, по которым плоскость, перпендикулярная ребру двугранного угла, пересекает его грани.

Мерой двугранного угла называется мера соответствующего ему линейного угла.

Замечания (обрати внимание).



1.Линейный угол двугранного угла - это угол с вершиной на ребре двугранного угла, образованного двумя лучами, лежащими в гранях двугранного угла и перпендикулярными его ребру.

2.Мера двугранного угла не зависит от выбора линейного угла.



Классификация двугранных углов по величине.







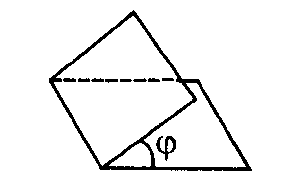
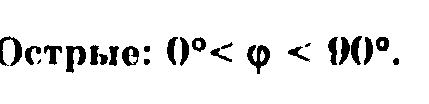
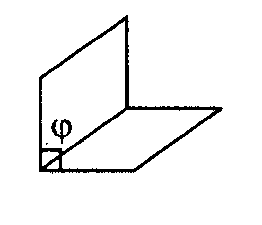
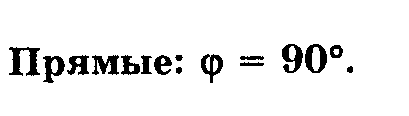
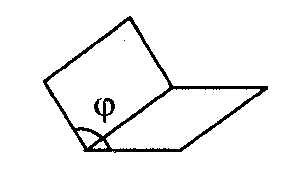
Задача (реши сверь ответ).

На одной грани двугранного угла выбраны две точки, удаленные от второй грани на 16 и 12 см. Первая точка удалена от ребра угла на 24см.Найди расстояние от второй точки до ребра угла.

Ответ: 18см.

Выучи.

Определение многогранника.

Многогранником называется тело, поверхность которого состоит из конечного числа плоских многоугольников.

Плоские многоугольники называются гранями многогранника.

Ребрами многогранника называются стороны его граней.

Вершинами – вершины граней.

Многогранник называется выпуклым, если он расположен по одну сторону ( лежит в одном полупространстве) относительно плоскости каждой его грани.




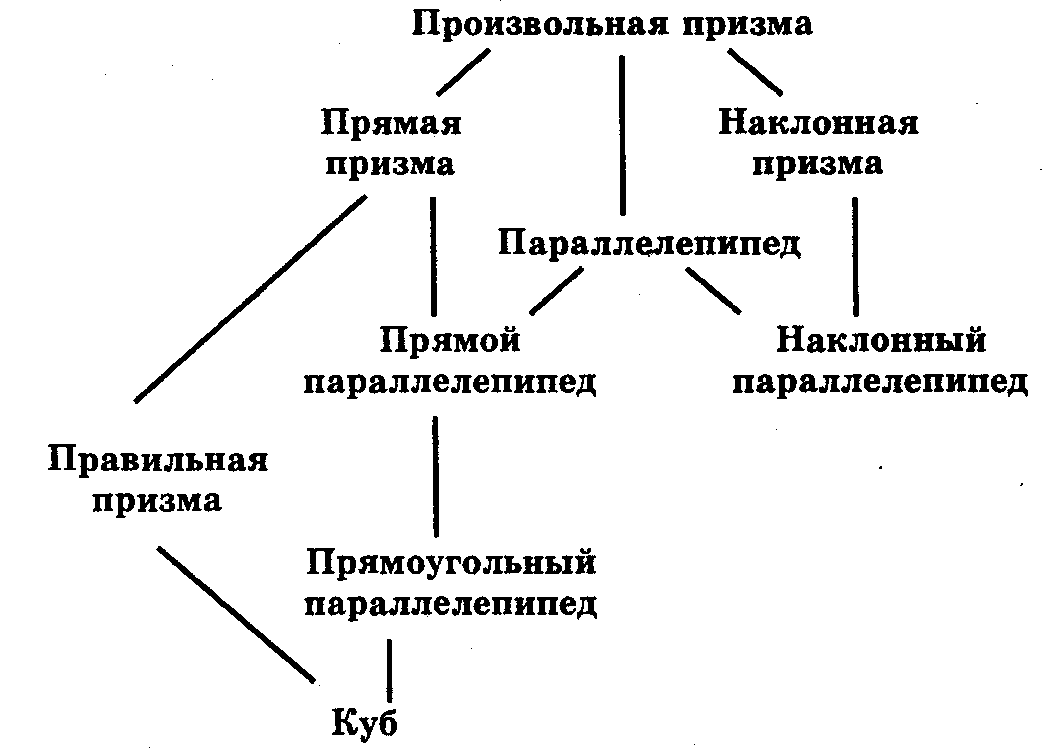
Призма. Виды призм.

Выучи.

Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников



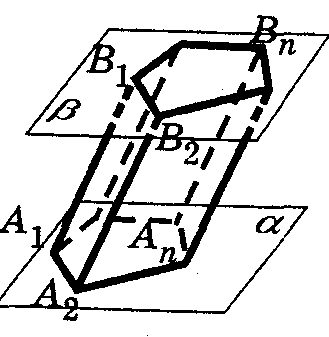
Многоугольники называются основаниями призмы, а отрезки, соединяющие вершины, - боковыми ребрами призмы.

А₁А₂…А_n и В₁В₂…В_n – основания призмы.

А₁А₂В₂В₁, А₂А₃В₃В₂, …., А_nА₁В₁В_n – боковые грани призмы,

А₁В₁, А₂В₂, …, А_nВ_n –боковые ребра призмы.

Обрати внимание: призма обозначается последовательным названием ее оснований:

А₁А₂…А_nВ₁В₂…В_n.

Высотой призмы называется перпендикуляр, проведенный из какой – либо точки плоскости одного основания к плоскости другого основания (или расстояние между плоскостями оснований призмы)

Диагональю призмы называется отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

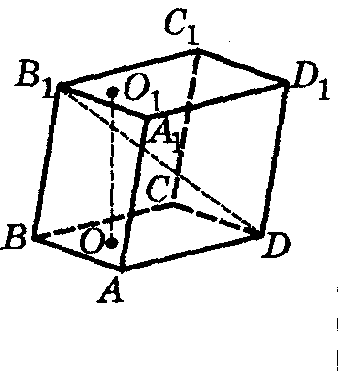
Рассмотри рисунок.

ОО₁ – высота призмы

В₁D – диагональ призмы.



Запомни.

Свойства призмы.

1. Основания призмы – равные многоугольники, лежащие в параллельных плоскостях.
   
2. Боковые ребра призмы параллельны и равны.
   
3. Боковые грани призмы – параллелограммы
   

Запомни.

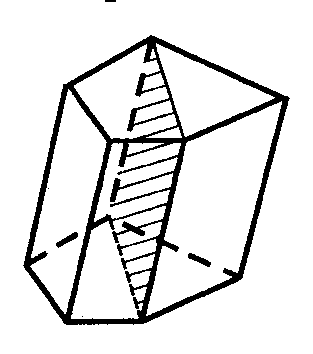
Определение диагонального сечения призмы

Диагональным сечением призмы называется сечение призмы плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.



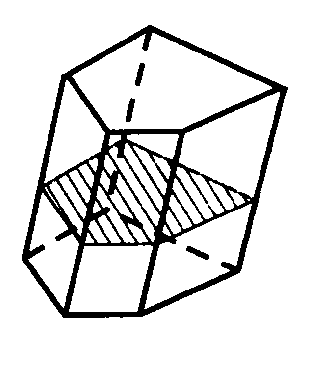
- Сечением призмы плоскостью, параллельной основаниям, является многоугольником,

равным многоугольникам оснований.

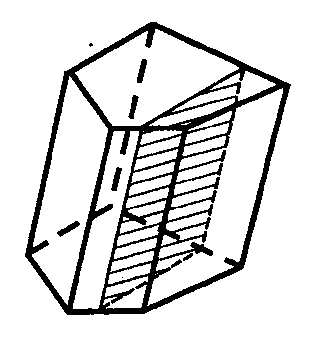
- Сечением призмы плоскостью, параллельной боковым ребрам, является параллелограммом.



Виды призм.

Прямая призма.

Выучи.

Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.

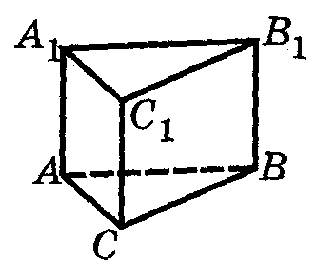АВСА₁В₁С₁ – прямая призма.

Наклонная призма.

Выучи.

Призма называется наклонной, если ее боковые ребра не перпендикулярны основаниям.

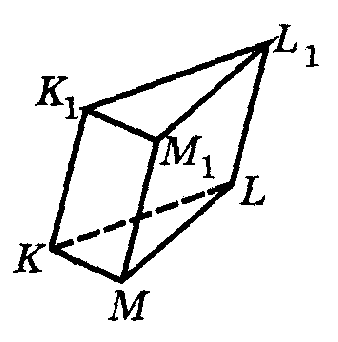КLMК₁L₁M₁ – наклонная призма.

Обрати внимание и используй при решении задач.

Свойства прямой призмы:

Основания прямой призмы – равные многоугольники, лежащие в параллельных плоскостях.

Боковые ребра прямой призмы параллельны, равны и перпендикулярны плоскостям оснований (являются высотами). Высота прямой призмы равна длине бокового ребра.

Правильная призма.

Правильной призмой называется прямая призма, основания которой – правильные многоугольники.



Задача (разбери решение, запиши в тетрадь).

В прямой треугольной призме стороны основания равны 10 см, 17 см и 21 см, а высота призмы 18 см.

Найди площадь сечения, проведенного через боковое ребро и меньшую высоту основания.

Задача (воспользуйся планом решения и реши задачу).

Плоскость, проходящая через сторону основания правильной треугольной призмы и середину противолежащего ребра, образует с основанием угол 45⁰. сторона основания л. Найдите боковую поверхность призмы.

План решения.

1. Построй линейный угол двугранного угла между сечением АВМ и основанием призмы АВС.
   
2. Из прямоугольного треугольника МСН определи угол МСН
   
3. Треугольник АВМ – равнобедренный (докажи).
   
4. Найди СН.
   
5. Найди МС.
   
6. Вычисли периметр основания.
   
7. Вычисли боковую поверхность призмы.
   

S_{бок. пов}.= 3* √3 l²

Параллелепипед.

Выучи.

Параллелепипедом называется призма, основание которой – параллелограмм

Обрати внимание: так как параллелепипед является призмой, то все свойства призмы справедливы и для параллелепипеда.



Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.

АВСД и А₁В₁С₁Д₁, АА₁В₁В и ДД₁С₁С, АА₁Д₁Д и ВВ₁С₁С – противолежащие грани.

Грани параллелепипеда, имеющие общее ребро, называются смежными.



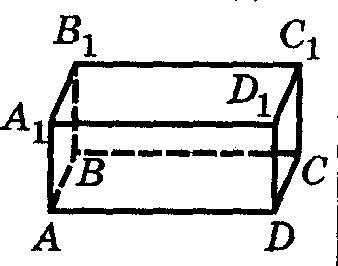
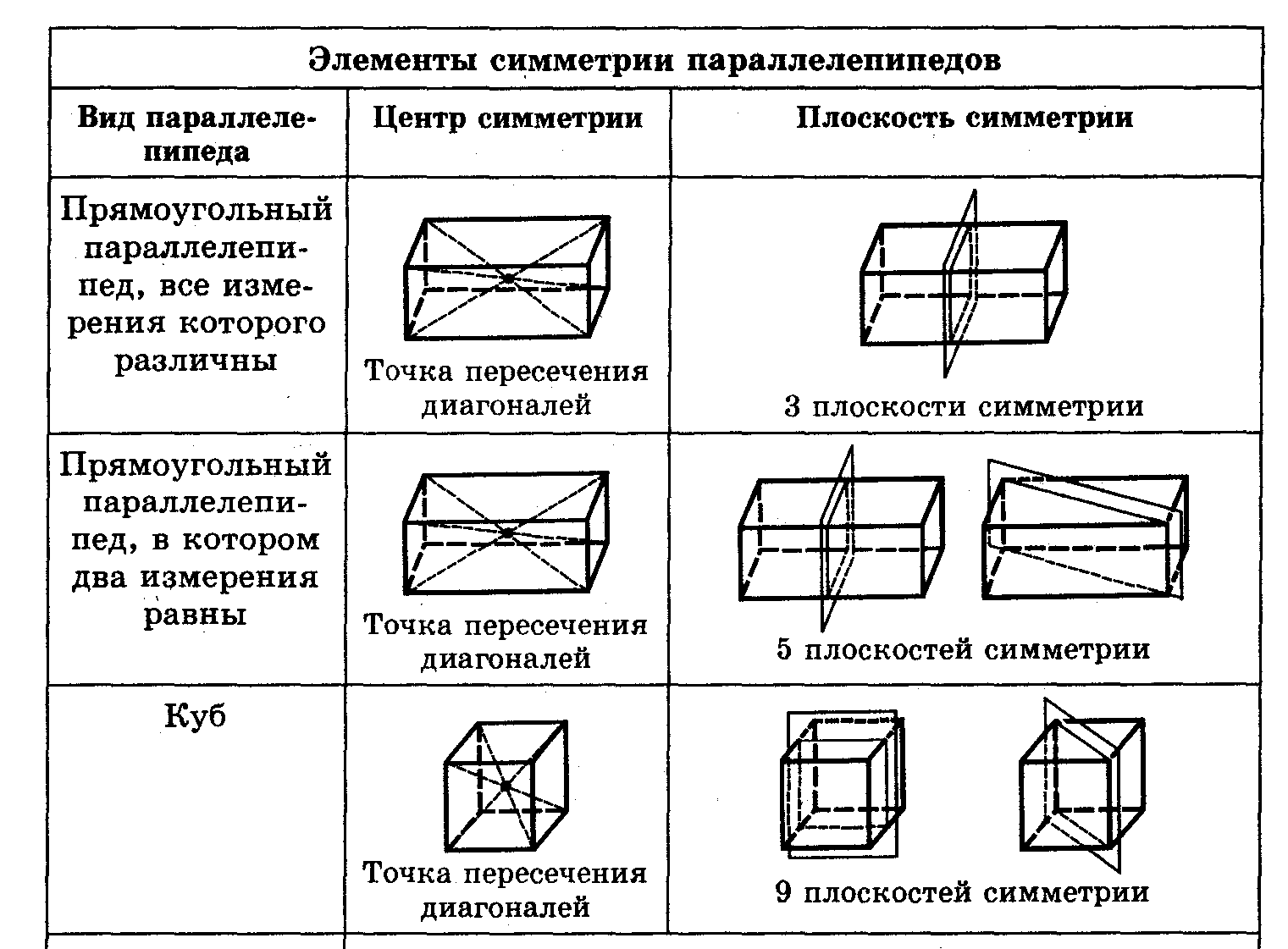
ТЕОРЕМА (выучи) Противолежащие грани параллелепипеда параллельны и равны.

ТЕОРЕМА (выучи) Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.



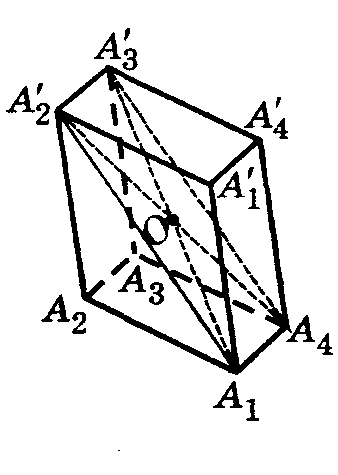
Точка пересечения диагоналей параллелепипеда является центром его симметрии.

Виды параллелепипедов. Прямоугольный параллелепипед.

Выучи.

Параллелепипед называется прямым, если его боковые ребра перпендикулярны плоскостям оснований.

Обрати внимание: прямой параллелепипед является прямой призмой, основание которой – параллелограмм.


Свойства прямоугольного параллелепипеда:

1. Основания прямого параллелепипеда – равные параллелограммы, лежащие в параллельных плоскостях.
   
2. Боковые ребра прямого параллелепипеда параллельны, равны и перпендикулярны плоскостям оснований. Высота прямого параллелепипеда равна длине бокового ребра.
   
3. Противолежащие боковые прямого параллелепипеда – равные прямоугольники. Плоскости боковых граней перпендикулярны плоскостям оснований.
   
4. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.
   

Прямоугольный параллелепипед ( выучи)

Прямоугольным параллелепипедом называется прямой параллелепипед, основанием которого является прямоугольник.




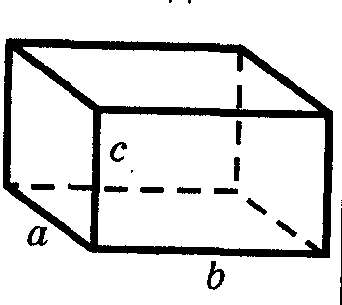
Запомни:

длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями).

Теорема (выучи):

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:





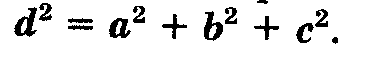
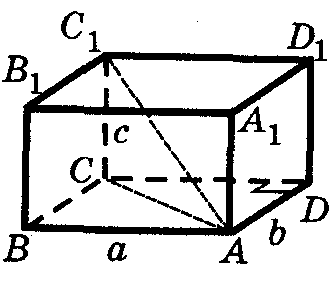
Свойства прямоугольного параллелепипеда:

1. Противолежащие грани прямоугольного параллелепипеда (в том числе основания) — равные прямоугольники.

2. Боковые ребра прямоугольного параллелепипеда параллельных, равны и перпендикулярны плоскостям оснований.

3. Все двугранные углы прямоугольного параллелепипеда — прямые.

4. Диагонали прямоугольного параллелепипеда равны и точкой пересечения делятся пополам.

5. Диагональные сечения прямоугольного параллелепипеда — прямоугольники.

Определение куба ( выучи ):


Кубом называется прямоугольный параллелепипед, все ребра которого равны.




Свойства куба:

1. Все грани куба равные квадраты.

2. Из каждой вершины куба исходят три взаимно перпендикулярных равных ребра.

З. Все двугранные углы куба — прямые.

4. Диагонали куба с ребром а равны а√3 и точкой пересечения делятся пополам.

5. Диагональное сечение куба с ребром а — прямоугольник со сторонами а и а√2



Виды призм





Задача( разбери готовое решение):





Реши самостоятельно и сверь ответ:

1. Найдите сторону основания и высоту правильной четырехугольной призмы, если ее боковая поверхность равна 8 см², а полная поверхность равна 40 см² Ответ: 4см; 0,5 см.

2. В прямом параллелепипеде с высотой √15 м стороны основания АВСD равны 2 м и 4 м, диагональ АС равна 5 м Найдите площадь диагонального сечения параллелепипеда, проходящего через вершины В и D.

Ответ: S = 15 м².

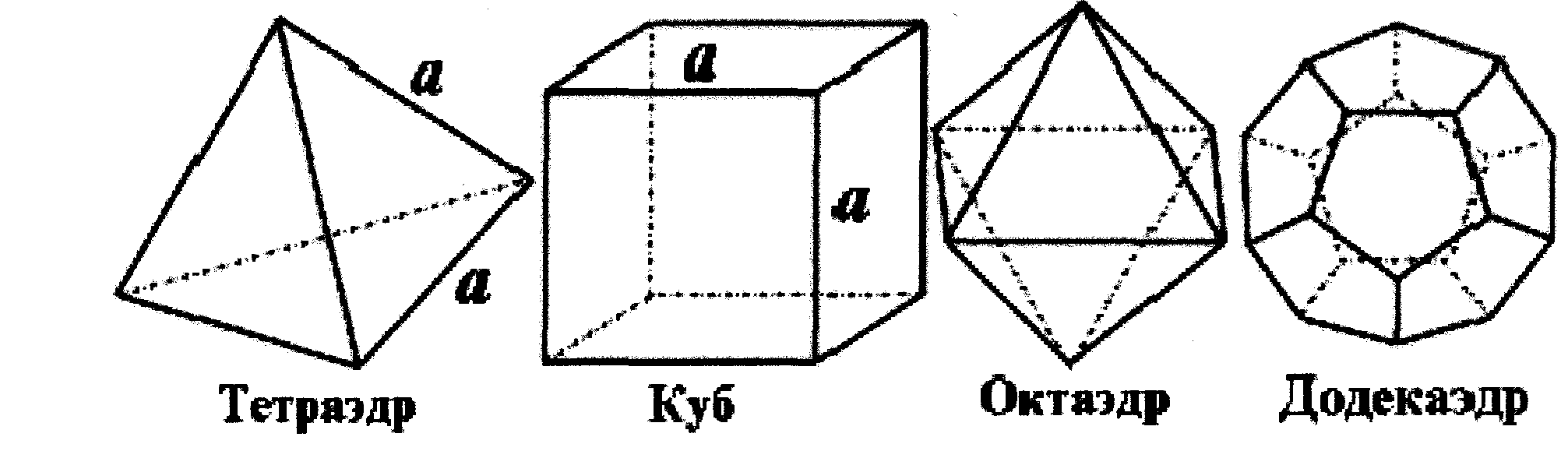
Правильные многогранники.

Определение (выучи):

Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

Свойства правильных многогранников

1.Все ребра правильного многогранника равны.

2.Все двугранные углы правильного многогранника, содержащие грани с общим ребром, равны.




Икосаэдр

Теорема Эйлера. Число вершин – число ребер + число граней = 2






Прочитай, это интересно

Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона (427-347 до н. э.) "Тимаус". Поэтому правильные многогранники также называются платановыми телами (хотя известны они были задолго до Платона). Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя "земными" элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с "неземным" элементом - небом (додекаэдр). Знаменитый математик и астроном Кеплер построил модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер.

Имеется несколько эквивалентных определений правильных многогранников. Одно из них звучит так: многогранник называется правильным, если существуют три концентрические сферы, одна из которых касается всех граней многогранника, другая касается всех его ребер и третья содержит все его вершины (определение А). Это определение напоминает одно из возможных определений правильного многоугольника: многоугольник называется правильным, если он вписан в некоторую окружность и описан около другой окружности, причем эти окружности концентричны.

Другое определение: правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные углы попарно равны (определение В).

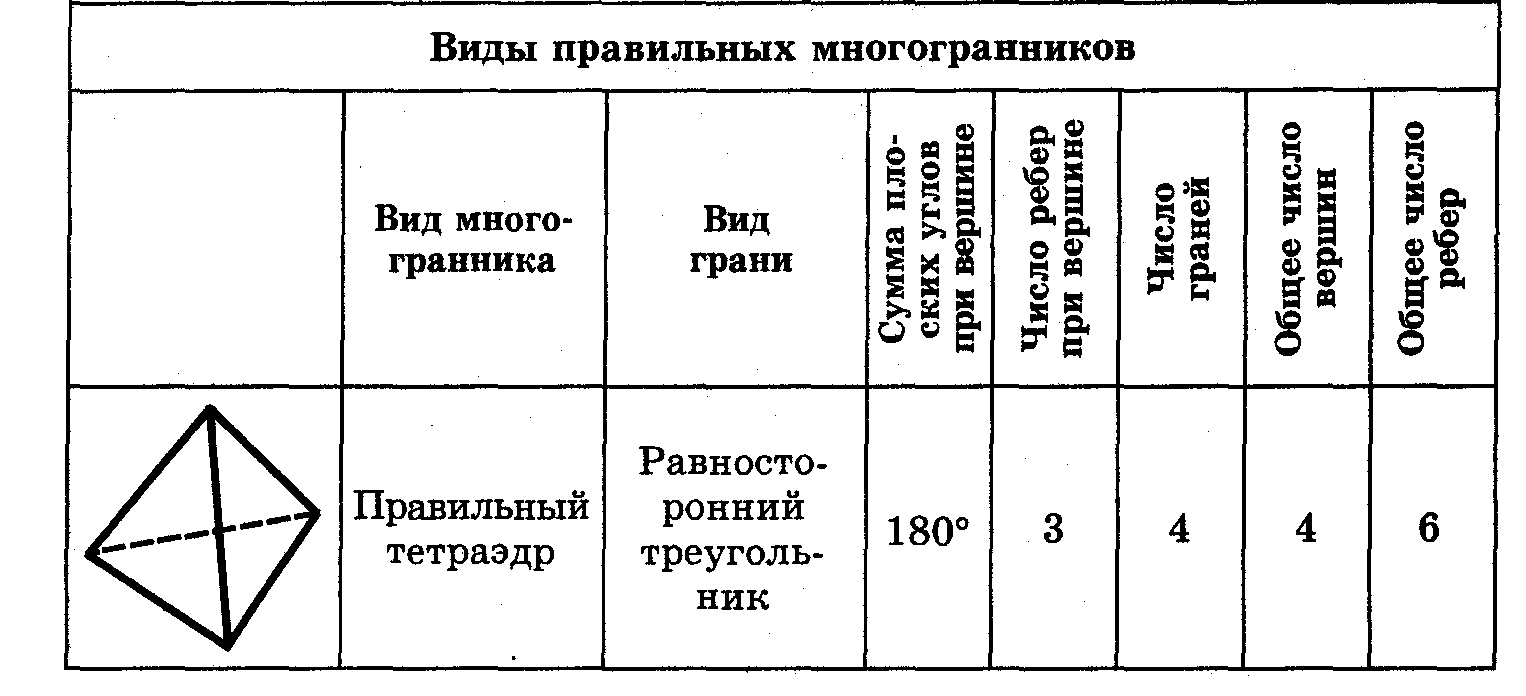
Следует обратить внимание на замечательное обстоятельство. Если правильные многоугольники существуют с любым числом сторон n≥3, то правильных многогранников (с точностью до подобия) всего пять и число граней у них равно 4, 6, 8, 12 или 20.

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.




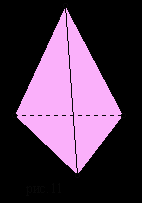
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.



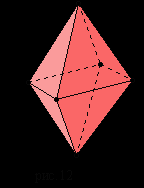
Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 270°.




Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равнв 270°.



Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.



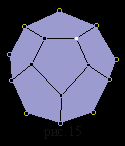
Других видов правильных многогранников, кроме перечисленных пяти, нет. Докажем это.

Обозначим через p число сторон у грани правильного многогранника. Так как двугранные углы равны, то все пространственные углы в правильном многограннике также равны. Поэтому в каждой вершине правильного многогранника сходится одно и тоже число граней, которое мы обозначим через q .

Используя правильность граней и равенство двугранных углов, древние греки легко получили, что для правильных многогранников пары целых чисел ( p , q ) могут быть лишь такими (3, 3), (4, 3), (3, 4), (3, 5), (5, 3). Однако благодаря теореме Эйлера можно получить те же пять пар чисел не только для правильных многоугольников, но и вообще для произвольных выпуклых многогранников, у которых каждая грань имеет одинаковое число p сторон и в каждой вершине сходится одинаковое число q граней.

Действительно, так как каждое ребро принадлежит ровно двум граням, а каждая грань имеет ровно p ребер, то p · Г равно удвоенному числу ребер в многограннике: p · Г = 2Р. Поскольку каждое ребро имеет ровно два конца, а в каждой вершине сходится ровно q ребер, то q · В = 2Р. Итак,

Г = 2Р/ p и В = 2Р/ q (4)

Подставим отношение (4) в формулу Эйлера:

2P/ q + 2P/ p = P + 2 (5)

Найдем Р из (5):

P = 2 pq /(2 · ( p + q ) - pq ) (6)

Знаменатель дроби в (6) равен 4 - ( p - 2)( q - 2). а так как знаменатель положителен, то ( p - 2)( q - 2)<4. С другой стороны, как число p сторон у грани, так и число q граней, сходящихся в вершине, не меньше 3. Поэтому уравнение (5) при условии p ≥3, q ≥3 имеет пять и только пять целочисленных решений (p , q ): (3, 3), (3, 4), (4, 3), (3, 5), (5, 3).

Отсюда следует, что комбинаторно различных многогранников, у которых все грани одноименные многоугольники и в каждой вершине сходится одинаковое число граней, не более пяти.

Вернемся теперь к правильным многогранникам. Соответствующая правильному многограннику пара чисел (p , q ) называется его символом Шлефли. У правильного многогранника может быть один из пяти символов Шлефли. Теперь покажем, что для каждого из символов Шлефли существует правильный многогранник.

Легко убедиться, что символу Шлефли (3, 3) соответствует правильный тетраэдр, а символу (4, 3) - куб. К многограннику с символом Шлефли (3, 4) - октаэдру - легко прийти от куба. Нужно взять центры квадратных граней куба - их шесть. На каждой тройке центров граней, прилегающих к каждой из 8 вершин куба, построим по правильному треугольнику. Легко проверить, что все двугранные углы между гранями равны. Этот многогранник правильный. Он имеет восемь граней и называется октаэдром.

Несколько сложнее убедиться в существование правильного многогранника, соответствующего символу (3, 5), т. е. многогранника с треугольными гранями, сходящимися по пять в каждой вершине. Возьмем три равных золотых прямоугольника, т.е. прямоугольника с соотношением сторон (√5+1)/2. Расположим их во взаимно перпендикулярных плоскостях, как показано на рисунке 17. Пусть стороны золотых прямоугольников для определенности равны √5 + 1 и 2. Возьмем произвольную вершину А₁ одного из прямоугольников. Существуют в точности пять вершин этих прямоугольников, а именно вершины В₁, А₂, В₃, D₃, D₂ находящиеся от А₁ на одинаковом расстоянии 2. По теореме Пифагора можно установить, что треугольники А₁В₁А₂, А₁А₂В₃, А₁В₃D₃, А₁D₃D₂, А₁D₂В₁ правильные. Кроме того, любые два смежных треугольника образуют равные двугранные углы. Точно такие правильные треугольники появляются во всех 12 вершинах прямоугольников, по пять в каждой. Таким образом, существует правильный многогранник, соответствующий символу (3, 5). Этот многогранник называется икосаэдром, что в переводе с греческого означает двадцатигранник. У икосаэдра 12 вершин.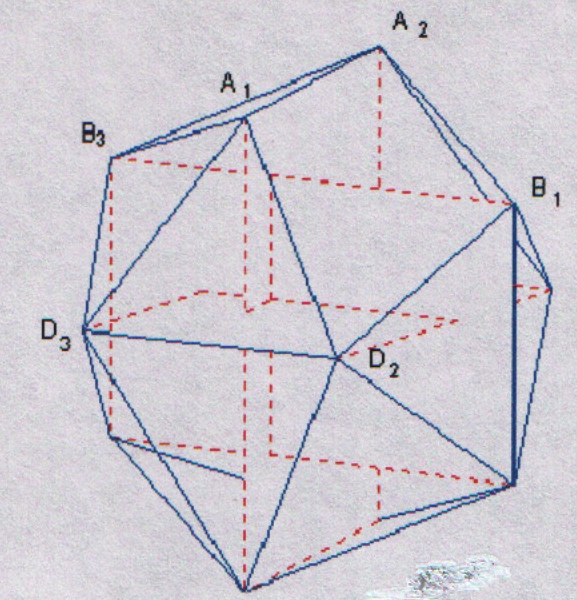



Чтобы построить правильный многогранник с символом (5, 3), возьмем в качестве вершин этого многогранника центры всех двадцати треугольных граней икосаэдра. Центры пяти треугольников, сходящихся в той или иной вершине икосаэдра, образуют вершины плоского правильного пятиугольника. Всего таких пятиугольников столько же, сколько вершин у икосаэдра - двенадцать. Эти правильные пятиугольники, сходящиеся по три в каждой вершине (в центре треугольной грани икосаэдра), образуют двенадцатигранник – додекаэдр. Все двугранные углы у этого додекаэдра равны. Поэтому этот многогранник является правильным.

Два правильных многогранника - октаэдр и додекаэдр - строились при помощи других многогранников - куба и икосаэдра. Причем каждая вершина, скажем, октаэдра соответствовала некоторой вершине куба. То же самое можно сказать и о паре многогранников икосаэдр - додекаэдр.

Два многогранника называются дуальными, если между множеством граней одного из них и множеством вершин другого существует взаимно однозначное соответствие, причем такое, что если две грани первого из них смежные ребру, то соответствующие этим граням вершины второго многогранника соединяются с ребром. Следует отметить, что у пары дуальных многогранников число вершин одного равно числу граней другого, а ребер у них поровну.

Дуальные многогранники состоят лишь из пяти- и шестиугольников, причем в каждой вершине сходятся по три грани. Такие многогранники называются фуллеренами. Изучение фуллеренов очень важно для приложений в химии, медицине, архитектуре. Теорема Грюнбаума в переводе на язык фуллеренов означает, что во всяком фуллерене имеется в точности двенадцать пятиугольников, а шестиугольников может быть какое угодно число, не меньше двух.

Чрезвычайно важная задача - как перечислить всевозможные структуры фуллеренов с наперед заданным числом n шестиугольников и сколько их в зависимости от n - остается актуальной и по сей день.

Практические задания ( выполни )

Задание №1.

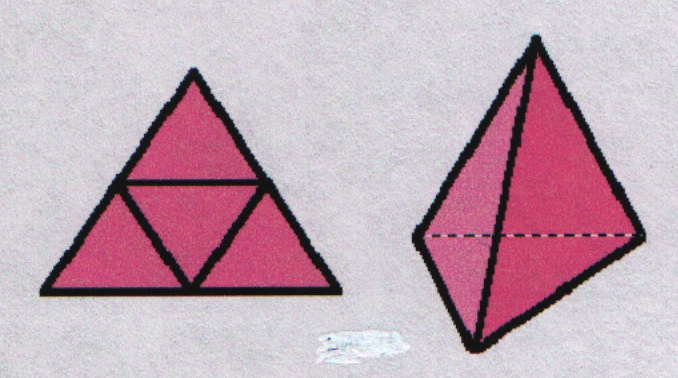
На рисунке изображена развертка правильного тетраэдра. Перерисуйте её на плотный лист бумаги в большом масштабе, вырежьте развертку и склейте из неё тетраэдр.




Задание №2.

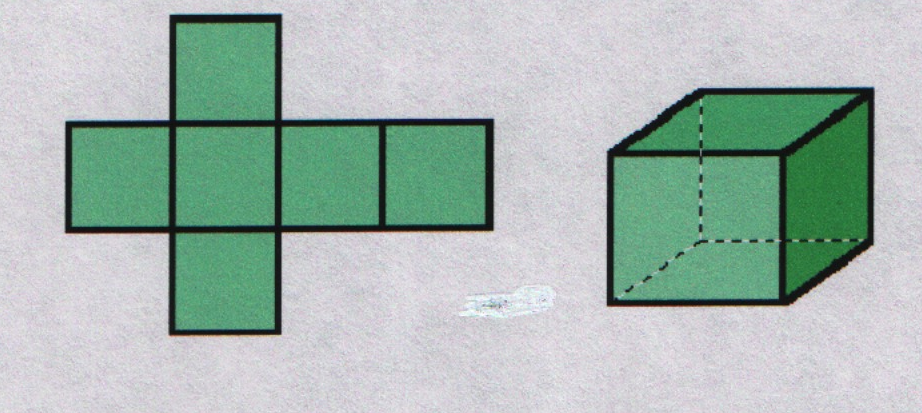
На рисунке изображена развертка куба. Перерисуйте её на плотный лист бумаги в большом масштабе, вырежьте развертку и склейте из неё куб.




Задание №3.

На рисунке изображен развертка правильного октаэдра. Перерисуйте её на плотный лист бумаги в большом масштабе, вырежьте развертку и склейте из неё октаэдр.




Задание №4.

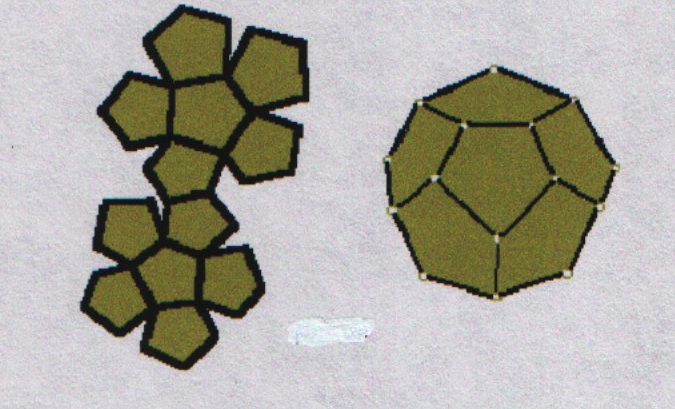
На рисунке изображена развертка правильного додекаэдра. Перерисуйте её на плотный лист бумаги в большом масштабе, вырежьте развертку и склейте из неё додекаэдр.




Задание №5.

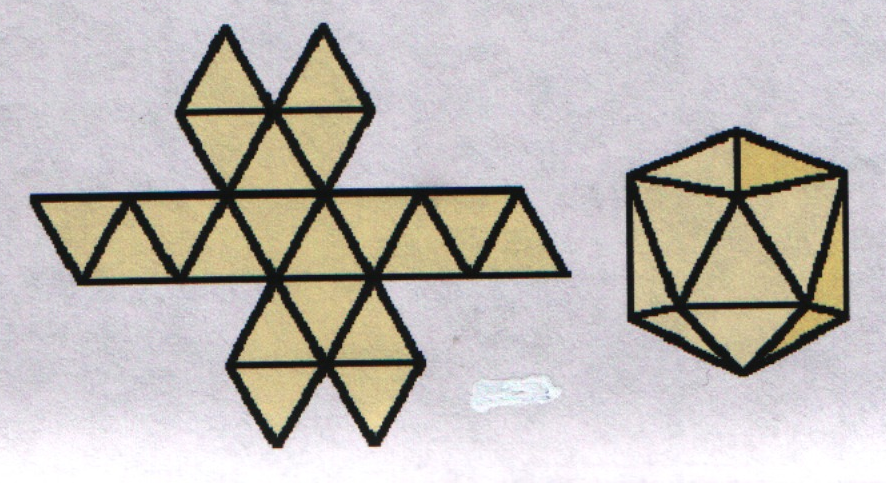
На рисунке изображена развертка правильного икосаэдра. Перерисуйте её на плотный лист бумаги в большом масштабе, вырежьте развертку и склейте из неё икосаэдр.




Пирамида. Правильная пирамида. Усеченная пирамида.


Слово «пирамида» в геометрию ввели греки,

которые, как полагают, заимствовали его у

египтян, создавших самые знаменитые

пирамиды в мире. Другая теория выводит этот ЭТО ИНТЕРЕСНО

термин из греческого слова «пирос»

(рожь) – считают, что греки выпекали хлебцы,

имевшие форму пирамиды.


Выучи:

Пирамида – это многогранник, одна из граней которого – произвольный многоугольник, а остальные грани – треугольники с общей вершиной.

- многоугольник называется основанием пирамиды;

- треугольники называются боковыми граням,

- ребра пирамиды, не принадлежащие основанию, называются ее боковыми ребрами,

- общая вершина всех боковых граней называется вершиной пирамиды,

-объединение боковых граней пирамиды называется ее боковой поверхностью.

- перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называется

высотой пирамиды.


Рассмотри рисунок:




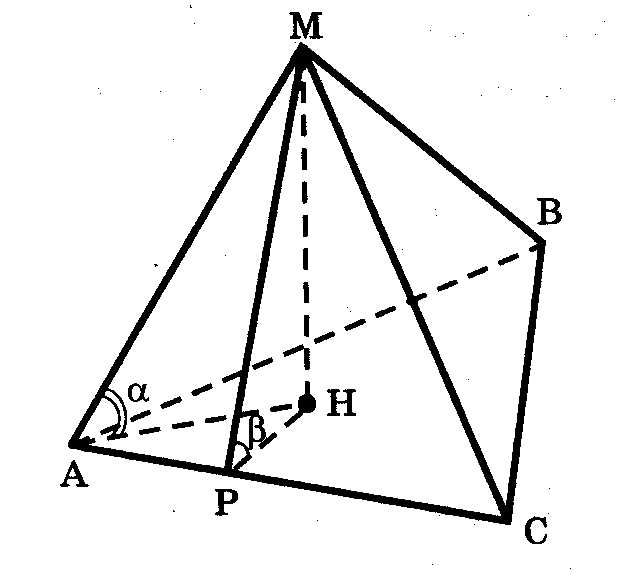
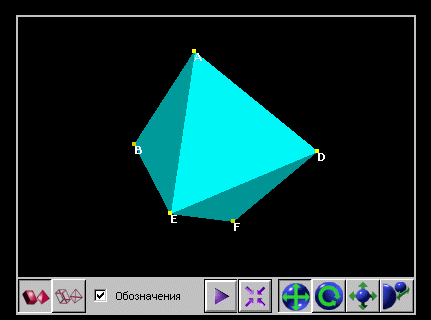
МАВС – треугольная пирамида, треугольник АВС – основание, точка М – вершина,

МА, МВ, МС – боковые ребра пирамиды, МАВ, МАС, МВС – боковые грани пирамиды,

МН – высота.

Использование знаний в стандартной ситуации.

Задача (разбери и запомни): Основанием четырехугольной пирамиды является параллелограмм со сторонами 20 см и 36 см. площадь основания равна 360 см². Н – точка пересечения диагоналей, СН – высота, равная 12 см. Вычислить площадь боковой поверхности пирамиды.




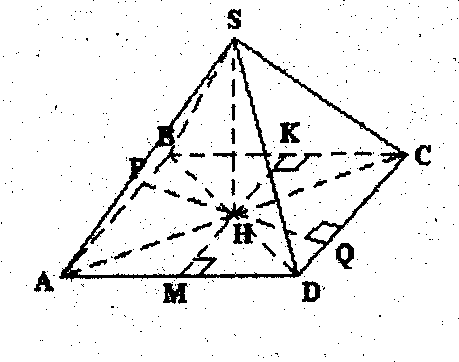
Дано: SАВСД – пирамида,

АВСД – параллелограмм,

АВ = 20 см, АД= 36 см,

S_АВСД= 360 см²,

Н – середина диагоналей АС и ВД,

SН – высота, SН= 12см.

Найти: S_бок.

Решение: S_АВСД = АД*КМ

360 = 36*х , х = 10

S_АВСД = РQ*СД

РQ = 18см

SQ = (9²+12²)^1/2 = 15см.

SМ = (12²+5²)^1/2 = 13,

SМ перпендикулярна АД,

SQ перпендикулярна СД

S_АSД = S_SВС = 0,5 АД*SМ = 0,5*36*13 = 234 см².

S_АВS = S_СДS = 0,5*СД*SQ = 0,5*20*15 =150 см²,

S_бок = 2*234 + 2*150 = 768см²

Ответ: 768см².


Задача






Использование знаний в стандартной ситуации. Реши задачу самостоятельно и сверь ответ:

Основание пирамиды - прямоугольник со сторонами 6см и 8 см. Каждое боковое ребро пирамиды равно 13 см. Вычислить высоту пирамиды. Ответ:12см.

Правильная пирамида.

Прочитай, это интересно.

Одним из примеров правильной пирамиды являются египетские пирамиды.

Первую пирамиду долго строили и перестраивали, всё это заняло 29 лет. Получилась шести ступенчатая пирамида. Издали она выглядит как шесть поставленных друг на друга масштаб. Ступенчатая форма пирамиды означала лестницу с шестью ступеньками, ведущую к площадке наверху (седьмой ступеньки). И это число – семь – совпадает с количеством планет, известных древним египтянам. Так же оно символизирует семь стадий, которые, по мнению древних, преодолевает душа в потустороннем мире.



Выучи:

Пирамида называется правильной, если ее основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.


Выучи:

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой этой пирамиды. Все апофемы равны друг другу.

Обрати внимание на рисунок:




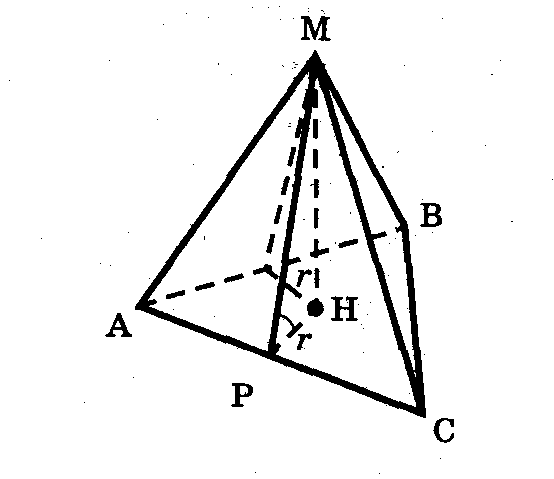
МР – апофема пирамиды, или, что то же самое, высота боковой грани. (МР перпендикулярна АС).

Обрати внимание и используй при решении задач.

Некоторые свойства правильной пирамиды:

- все боковые ребра равны между собой;

-все боковые грани – равные равнобедренные треугольники;

- все двугранные углы при основании равны;

- все плоские углы при вершине равны;

- все плоские углы при основании равны;

- апофемы боковых граней одинаковы по длине.

Реши задачу, используя план решения.

Задача: Апофема правильной четырехугольной пирамиды 6см, высота пирамиды равна 32см. Найти сторону основания пирамиды.

План решения:

1. Запиши данные решения задачи.
   
2. Сделай рисунок.
   
3. Запиши, что нужно найти, используя буквенные обозначения.
   
4. На рисунке сделай дополнительные построения: соедини основание высоты пирамиды и основание апофемы.
   
5. Рассмотри получившийся прямоугольный треугольник.
   
6. Вырази из прямоугольного треугольника по теореме Пифагора неизвестный катет.
   
7. Подставь в полученную формулу цифровые значения и вычисли.
   
8. Найди сторону основания пирамиды.
   
9. Запиши ответ.
   

Реши задачу и сверь ответ:

Задача: В правильной четырехугольной пирамиде апофема равна 4см, а боковое ребро – 5см. Найди: а) сторону основания пирамиды;

б) высоту пирамиды.

Ответ: а) 6см; б) 4см.

Усеченная пирамида.

Выучи.

Усеченная пирамида – часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию.


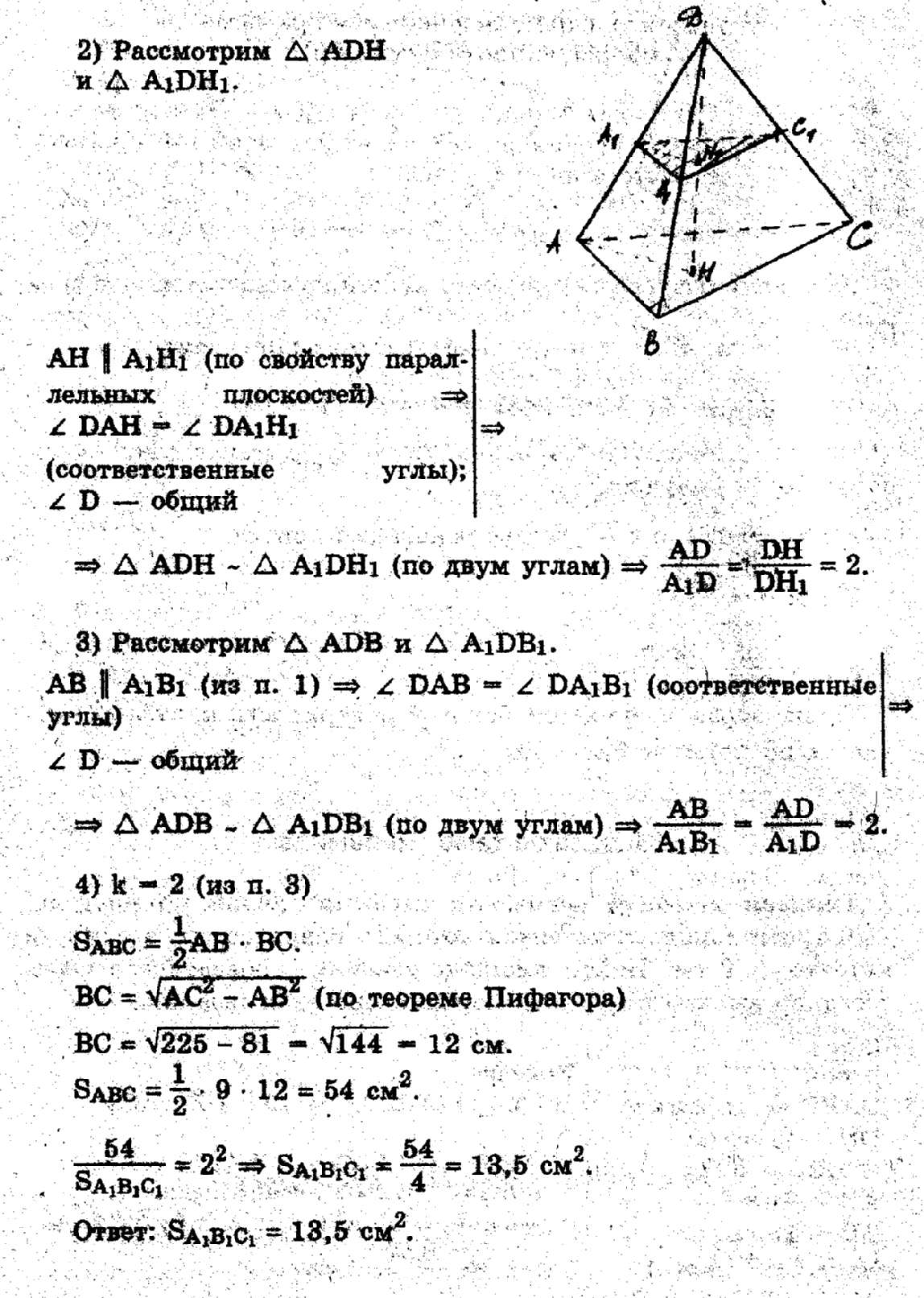
Рассмотри рисунок:





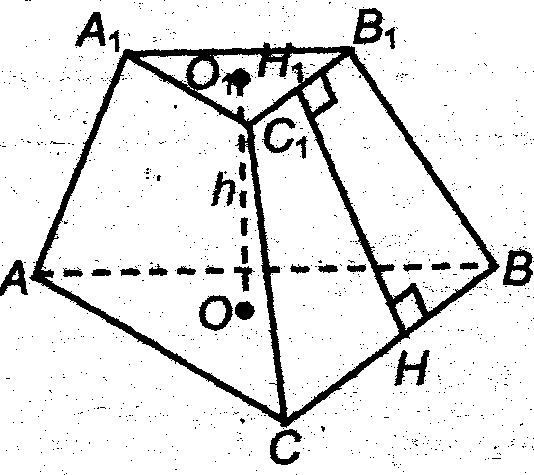
АВСА₁В₁С₁ – усеченная пирамида

АВС – нижнее основание усеченной пирамиды;

А₁В₁С₁ – верхнее основание усеченной пирамиды;

ОО₁ – высота усеченной пирамиды;

АСС₁А₁, ВСС₁В₁, АВВ₁А₁ – боковые грани усеченной пирамиды.

НН₁ – высота боковой грани усеченной пирамиды.

Запомни: основания правильной усеченной пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции.

Обрати внимание на свойства усеченной пирамиды и используй при решении задач:

- боковые ребра и высота пирамиды разделяются на пропорциональные отрезки;

- в сечении получится многоугольник, подобный многоугольнику, лежащему в основании;

- площади сечения и основания будут относиться между собой, как квадраты их расстояний от вершины пирамиды.






Проверь себя. Ответь на контрольные вопросы.

1) Что такое двугранный угол (грань угла, ребро угла)?

2) Что такое линейный угол двугранного угла?

3) Что такое многогранник?

4) Что такое призма (основания призмы, боковые грани, ребра)?

5) Что такое высота призмы, диагональ призмы?

6) Что представляет собой диагональное сечение?

7) Перечислите виды призм и их свойства.

8) Что такое параллелепипед?

9) Назовите виды параллелепипедов. Опишите их свойства.

10) Сколько плоскостей симметрии у прямоугольного параллелепипеда?

11)Что такое пирамида (основание пирамиды, боковые грани, ребра, высота)?

12) Какая пирамида называется правильной?

13) Что такое апофема правильной пирамиды?

14) Объясните, что такое усеченная пирамида.

Реши типовые задачи:

1)Основание пирамиды – квадрат, ее высота проходит через одну из вершин основания. Найти боковую поверхность пирамиды, если сторона основания равна 20дм, а высота 21дм.

Ответ: 10 м².

2) У четырехугольной усеченной пирамиды стороны одного основания равны 6, 7, 8, 9 см, а меньшая сторона другого основания равна 5 см. Найдите остальные стороны этого основания.

Ответ: 35/6см, 20/3см, 15/2см.

3) Высота пирамиды равна 16м. Площадь основания равна 512м². На каком расстоянии от основания находится сечение, параллельное ему, если площадь сечения 50м²?

Ответ: 11м.