Рабочая программа дисциплины «Методы решения оптимизационных задач в бизнесе» Рекомендуется для направления подготовки
| Вид материала | Рабочая программа |
- 1 Общая характеристика оптимизационных задач и методов их решения, 47.12kb.
- Рабочая программа дисциплины «Анализ хозяйственной деятельности» Рекомендуется для, 209.54kb.
- Рабочая программа дисциплины «Анализ хозяйственной деятельности» Рекомендуется для, 215.14kb.
- Рабочая программа дисциплины «психология коммерции» Рекомендуется для направления подготовки, 172.25kb.
- Рабочая программа дисциплины «управление персоналом» Рекомендуется для направления, 170.45kb.
- Рабочая программа дисциплины «основы управления персоналом» Рекомендуется для направления, 292.56kb.
- Рабочая программа дисциплины «методы регионоведческих исследований» Рекомендуется для, 138.47kb.
- Рабочая программа дисциплины «теория и методы экономического прогнозирования» Рекомендуется, 410.81kb.
- Рабочая программа дисциплины «современные методы внутрифирменного планирования» Рекомендуется, 209.17kb.
- Рабочая программа дисциплины «высокоуровневые методы информатики и программирования», 171.28kb.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
«Методы решения оптимизационных задач в бизнесе»
Рекомендуется для направления подготовки
0230700 Прикладная информатика
Квалификация выпускника - бакалавр
Санкт-Петербург
2011 год
1. Цели и задачи дисциплины:
Учебная дисциплина «Методы решения оптимизационных задач в бизнесе» направлена на:
- Развитие системного взгляда и системного мышления на основе анализа подходов к математическому моделированию, построения и сравнительного анализа разных типов моделей;
- Ознакомление с математическими свойствами моделей и методов оптимизации, используемых в решении экономических и управленческих задач.
2. Место дисциплины в структуре ООП:
Цикл профессиональный, включается в вариативную часть блока «Математический и естественно-научный» ООП.
. Дисциплина опирается на предшествующие ей дисциплины: «Теория систем и системный анализ», «Экономическая теория», «Менеджмент».
Она является предшествующей для дисциплин «Системы поддержки принятия решений», «Математические методы в экономике».
3. Требования к результатам освоения дисциплины:
Процесс изучения дисциплины направлен на формирование следующих профессиональных компетенций:
способен при решении профессиональных задач анализировать социально-экономические проблемы и процессы с применением методов системного анализа и математического моделирования (ПК-2);
способен осуществлять и обосновывать выбор проектных решений по видам обеспечения информационных систем (ПК-5); с
пособен проводить обследование организаций, выявлять информационные потребности пользователей, формировать требования к информационной системе, участвовать в реинжиниринге прикладных и информационных процессов (ПК-8);
способен применять методы анализа прикладной области на концептуальном, логическом, математическом и алгоритмическом уровнях (ПК-17);
В результате изучения дисциплины студент должен:
Знать: основные принципы и математические методы анализа и оптимизации управленческих решений.
Уметь: выбирать рациональные варианты действий в практических задачах принятия решений с использованием экономико-математических моделей.
Владеть: методами построения и анализа эффективных решений и соответствующими возможностями информационных технологий.
4. Объем дисциплины и виды учебной работы
Общая трудоемкость дисциплины составляет 3 зачетных единиц.
| Вид учебной работы | Всего часов |
| Аудиторные занятия (всего) | 54 |
| В том числе: | - |
| Лекции | 22 |
| Практические занятия (ПЗ) | 32 |
| Семинары (С) | |
| Лабораторные работы (ЛР) | |
| Самостоятельная работа (всего) | 54 |
| В том числе: | - |
| Расчетно-графическая работа | 18 |
| Реферат | 18 |
| Мультимедийная презентация | 18 |
| Вид промежуточной аттестации (экзамен) | |
| Общая трудоемкость час зач. ед. | 108 |
| 4 |
5. Содержание дисциплины
5.1. Содержание разделов дисциплины
Раздел I. Введение. Математические модели и оптимизация в экономике. Математические модели в экономике. Примеры: модели поведения потребителя и планирования производства в фирме. Принятие экономических решений.
Основные представления о статической задаче оптимизации. Инструментальные переменные и параметры математической модели. Допустимое множество. Критерий выбора решения и целевая функция. Линии уровня целевой функции.
Формулировка детерминированной статической задачи оптимизации. Неопределенность в параметрах и ее влияние на решение. Глобальный экстремум и локальные экстремумы. Экстремумы во внутренних и граничных точках допустимого множества. Причины отсутствия оптимального решения.
Раздел II. Линейное программирование
Формулировка задачи линейного программирования (ЛП). Примеры задач ЛП. Стандартная (нормальная) и каноническая формы представления задачи ЛП и сведение к ним. Свойства допустимого множества и оптимального решения в задаче ЛП. Основные представления о методах решения задач ЛП, основанных на направленном переборе вершин (симплекс-метод и др.).
Двойственные задачи линейного программирования. Взаимность двойственности. Теоремы двойственности. Интерпретация двойственных переменных. Анализ чувствительности оптимального решения к параметрам задачи линейного программирования. Некоторые специальные задачи линейного программирования (транспортная, производственно-транспортная и т.д.).
Раздел III. Нелинейное программирование
Общая задача нелинейного программирования (НЛП). Задача НЛП и классическая задача условной оптимизации. Функция Лагранжа для задачи НЛП. Седловая точка функции Лагранжа. Достаточное условие оптимальности в общей задаче НЛП. Условия Куна-Таккера. Выпуклые задачи оптимизации. Основные понятия геометрии многомерного линейного пространства. Выпуклые множества. Примеры выпуклых множеств. Выпуклые и вогнутые функции. Строгая выпуклость. Условия выпуклости и вогнутости функций. Свойства выпуклых функций. Теоремы о локальном максимуме в выпуклом случае.
Формулировка выпуклой задачи НЛП. Теорема Куна-Таккера. Экономическая интерпретация множителей Лагранжа. Зависимость решения от параметров.
Задача выбора решений в условиях неопределенности. Критерии выбора решений в условиях неопределенности (принцип гарантированного результата, критерий Гурвица, критерий Байеса-Лапласа, критерий Сэвиджа). Применение принципа гарантированного результата в задачах экономического планирования. Множество допустимых гарантирующих программ. Наилучшая гарантирующая программа.
Принятие решение при случайных параметрах. Вероятностная информация о параметрах. Принятие решений на основе математического ожидания. Случайность и риск. Учет склонности к риску.
5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми
(последующими) дисциплинами
| № п/п | Наименование обеспечиваемых (последующих) дисциплин | № № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин | |||
| 1 | 2 | 3 | 4 | ||
| 1. | Математические методы в экономике | + | + | + | + |
| 2. | Системы поддержки принятия решений | + | | + | + |
5.3. Разделы дисциплин и виды занятий
| № п/п | Наименование раздела дисциплины | Лекц. | Практ. зан. | Лаб. зан. | Семин. | СРС | Все-го |
| 1. | Введение. Математические модели и оптимизация в экономике | 3 | 4 | | | 12 | 19 |
| 2. | Линейное программирование | 6 | 8 | | | 13 | 27 |
| 3. | Нелинейное программирование | 13 | 20 | | | 29 | 62 |
| Итого: | | 22 | 32 | | | 54 | 108 |
6. Лабораторный практикум – не предусмотрено
7. Практические занятия (семинары)
| № п/п | № раздела дисциплины | Тематика практических занятий (семинаров) | Трудо-емкость (час.) |
| 1. | 1. | Статическая задача оптимизации | 2 |
| 2. | 1. | Графическая интерпретация | 1 |
| 2. | 2. | Задача линейного программирования. Каноническая форма | 2 |
| | 2. | Основные методы решений | 2 |
| | 2. | Теоремы двойственности | 2 |
| 3. | 3. | Функция Лагранжа | 2 |
| 4. | 3. | Условия Куна-Таккера | 2 |
| | 3. | Условия выпуклости и вогнутости функций. Экономическая интерпретация множителей Лагранжа. Зависимость решения от параметров | 3 |
| 5. | 3. | Критерии выбора решений в условиях неопределенности | 3 |
| 6 | 3 | Принятие решение при случайных параметрах. | 3 |
8. Примерная тематика курсовых проектов (работ) – не предусмотрено
9. Учебно-методическое и информационное обеспечение дисциплины:
а) основная литература
- Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М.: Высшая школа, 2001.
- Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента. СПб.: Лань, 2000.
б) дополнительная литература
- Интрилигатор М. Математические методы оптимизации и экономическая теория. М.: Изд. Айрис-Пресс, 2002.
- Чернов В.П. Введение в линейное программирование. СПб: Наука, 2002
- Чернов В.П. Математические модели и методы в экономике и менеджменте: Учебное пособие. СПб: СПбГУЭФ, 2010
- Чернов В.П. Сборник практических заданий по дисциплине «Математические методы и модели исследования операций» к разделу «Математическое программирование». СПб: СПбГУЭФ, 2010.
- Иванилов Ю.П., Лотов А.В. Математические модели в экономике. М.: Наука, 1979.
- Лотов А.В. Введение в экономико-математическое моделирование. М.: Издательство «Наука», 1984.
- Хазанова Л.Э. Математические методы в экономике. Учебное пособие. М.: Изд. БЕК, 2002.
- Васильев Ф.П. Методы оптимизации. М.: Издательство «Факториал», 2001.
- Токарев В.В., Соколов А.В. Методы оптимальных решений (ридер).
- Ларичев О.И. Теория и методы принятия решений. М.: Логос, 2000.
в) программное обеспечение
ОС Windows XP, Windows 7, ППП Statgraphics V3.1 или ППП Statgraphics V5.0
г) базы данных, информационно-справочные и поисковые системы
www.gov.ru,
www.gks.ru
10. Материально-техническое обеспечение дисциплины:
Специально оборудованные кабинеты и аудитории: компьютерные классы, аудитории, оборудованные мультимедийными средствами обучения.
11. Методические рекомендации по организации изучения дисциплины:
В основу разработки балльно-рейтинговой системы положены принципы, в соответствии с которыми формирование рейтинга студента осуществляется постоянно в процессе его обучения в университете. Настоящая система оценки успеваемости студентов основана на использовании совокупности контрольных точек, оптимально расположенных на всём временном интервале изучения дисциплины. При этом предполагается разделение всего курса на ряд самостоятельных блоков и модулей и проведение по ним промежуточного контроля.
Контроль знаний студентов включает формы текущего и итогового контроля. Текущий контроль осуществляется в виде работ, выполненных с использованием вычислительной техники. Итоговый контроль осуществляется в виде экзамена.
| Самостоятельная работа студентов | Количество баллов | |
| Зачётный минимум | Зачётный максимум | |
| Расчетно-графическая работа | 15 | 34 |
| Реферат | 15 | 33 |
| Мультимедийная презентация | 15 | 33 |
| | 55 | 100 |
Максимальное число баллов, которое можно получить за работу в семестре, равно 100. Максимальное число баллов, которое можно получить на экзамене, также равно 100. Итоговая оценка (в баллах) вычисляется по формуле
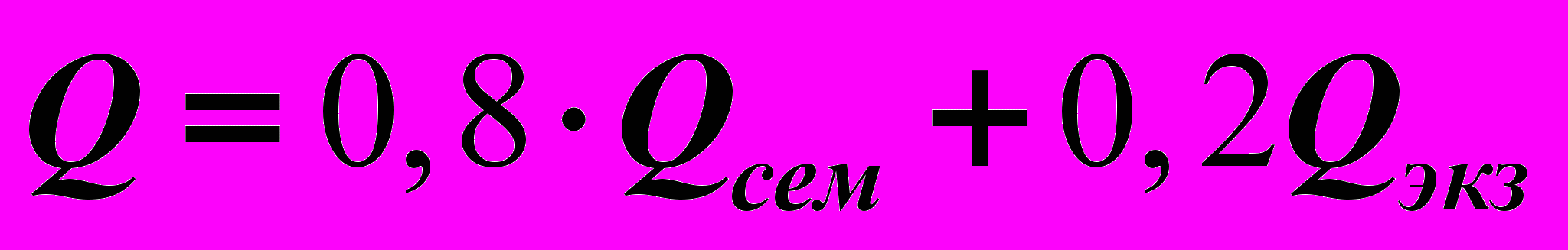, где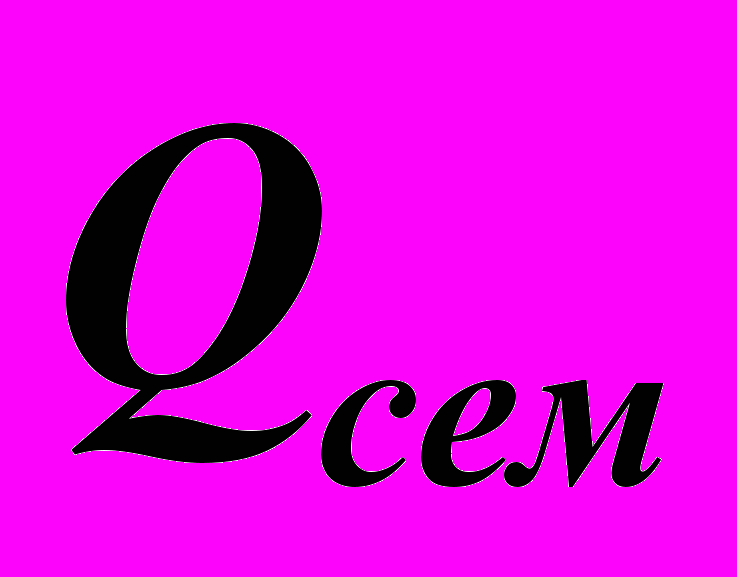 
– баллы, полученные за работу в семестре, а 
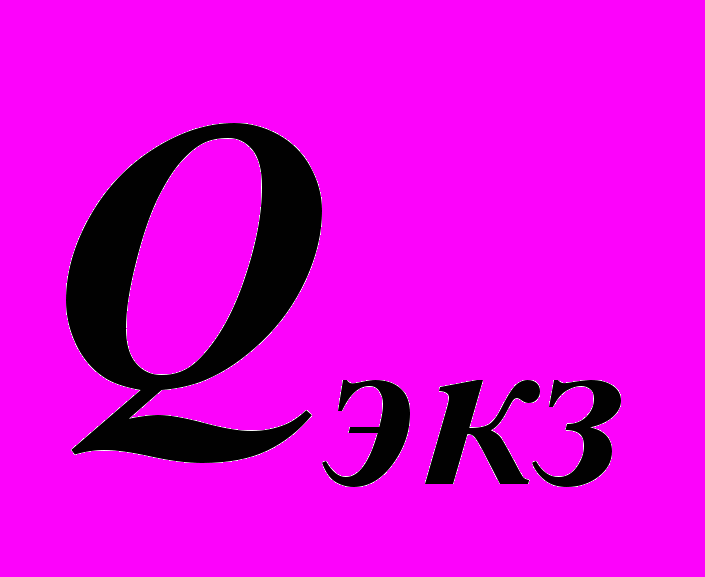– за экзамен в устной форме. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:| Итоговое количество баллов | оценка |
| до 55  | неудовлетворительно |
| от 55 до 70 | удовлетворительно |
| от 70 до 85 | хорошо |
| от 85 | отлично |
Разработчики:
___СПбГУЭФ ____ д.э.н., профессор В.П. Чернов____
(место работы) (занимаемая должность) (инициалы, фамилия)
Эксперты:
СПбЭМИ РАН Директор, проф.Л.А. Руховец
(место работы) (занимаемая должность) (инициалы, фамилия)