Плоскости, касательные к поверхностям. Пересечение поверхностей

Вид материала

Лекция

Содержание Пересечение поверхностей 28. Построение линии пересечения многогранных поверхностей 28.1 Первый тип задач - обе поверхности имеют вырожденный вид 28.2 Второй тип задач - одна из поверхностей имеет вырожденный вид.

Подобный материал:

• Темы лекций по начертательной геометрии для студентов очной формы обучения 1 курс, 26.7kb.
• Лекция №9 26. пересечение плоскости и поверхности, определение натуры сечения, 151.71kb.
• 3 Виды поверхностеЙ и их проекции, 84.24kb.
• Моделирование и динамическая стабилизация нановыглаживания прецизионных поверхностей, 151.88kb.
• Конспект урока Тема : Параллельность в пространстве, 55.65kb.
• 12. ломаные и кривые линии (плоские и пространственные). Винтовая линия, 91.72kb.
• Основы многомасштабного представления информации, 1916.63kb.
• 9 + 1 б/пл, 109.75kb.
• Глонасс, 248.4kb.
• Замощение плоскости в пространстве, 274.38kb.

ЛЕКЦИЯ №10

27. ПЛОСКОСТИ, КАСАТЕЛЬНЫЕ К ПОВЕРХНОСТЯМ.

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ.

28. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ.

Е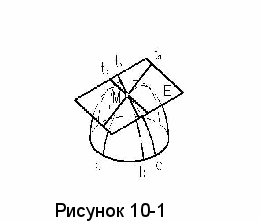сли через произвольную точку М кривой поверхности Б (рисунок 10-1) провести произвольные линии α,b и c, принадлежащие этой поверхности, а затем к этим кривым в точке М построить касательные прямые tα, tb и tc, то все касательные прямые будут лежать в одной плоскости Е, называемой касательной плоскостью к поверхности.

Следовательно, касательная плоскость является геометрическим местом всех касательных, проведенных к данной кривой поверхности и проходящих через одну ее точку.

Д
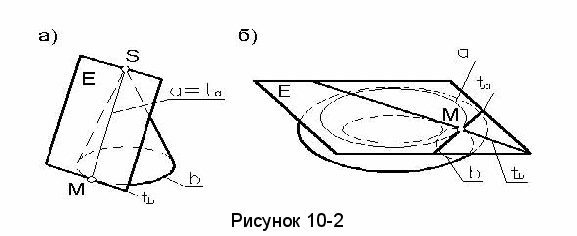
ля построения касательной плоскости к поверхности в ее точке М достаточно через эту точку провести на поверхности только две кривые линии α и b, и к ним построить касательные прямые tα и tb (рисунок 10-2).

Две эти касательные прямые и определяют касательную плоскость Е. Вполне естественно, что в качестве таких кривых линий поверхности выбирают ее графически простые линии. Например, для линейчатых поверхностей одной из этих кривых может служить ее прямолинейная образующая, (она будет совпадать со своей касательной), а для поверхности вращения – ее параллель (окружность). В зависимости от вида поверхности касательная плоскость может касаться ее в одной точке (рисунок 10-1 – сфера), по прямой линии (рисунок 10-2а – конус), по кривой линии (рисунок 10-2б – тор).

В 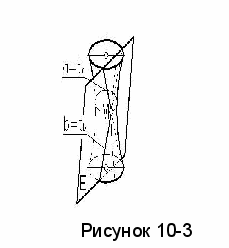приведенных примерах поверхность располагается по одну сторону от касательной плоскости и не пересекается последней. Однако касательная плоскость может и пересекать поверхность. Так, плоскость Е, касательная к однополостному гиперболоиду, пересекает его по двум образующим α и b, которые при этом являются и касательными tα и tb, определяющими касательную плоскость Е (рисунок 10-3).

Рассмотрим примеры построения касательной плоскости к различным поверхностям.

Пример 1. Построить плоскость Е, касательную к поверхности вращения в ее точке М (рисунок 10-4).

В 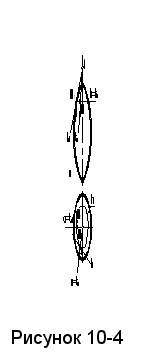качестве двух кривых линий поверхности, касательные к которым определят искомую плоскость Е, выберем параллель h и меридиан α, проходящие через точку М.

Параллель h является окружностью, расположенной горизонтально, и построение касательной th к ней не составляет труда. Для построения касательной tα к меридиану α предварительно преобразуем чертеж, повернув меридиан вокруг оси поверхности вращения до фронтального положения α1. При этом точка М займет положение М1. Теперь построим касательную tα к фронтальному меридиану α1 в его точке М1 и, произведя обратное вращение, получим искомую касательную к меридиану α.

Касательная к поверхности вращения плоскость Е определяется двумя пересекающимися прямыми th и tα.

Пример 2. Построить плоскость Е, касательную к поверхности конуса в его точке М (рисунок 10-5).

Т
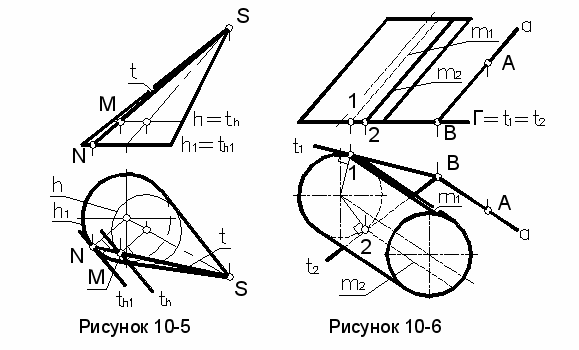
ак как конус – поверхность линейчатая, то, проведя через точку М образующую t (являющуюся в то же время и касательной), получим одну из прямых, определяющих искомую плоскость Е. Второй прямой будет касательная th к окружности на поверхности конуса h в ее точке М.

Отметим, что касательная th параллельна касательной t1, проведенной в точке N к окружности основания конуса. Поэтому искомую касательную плоскость Е можно задать образующей t и касательной t1, не строя вспомогательной окружности h, проходящей через точку М.

Пример 3. Построить касательную к цилиндрической поверхности плоскость Е, проходящую через точку А, расположенную вне поверхности цилиндра (рисунок 10-6).

Поскольку искомая касательная плоскость должна содержать в себе образующую цилиндрической поверхности, то в качестве первой прямой, определяющей касательную плоскость, можно провести через данную точку А прямую α параллельную образующей цилиндра.

Если теперь провести через точку В (точку пересечения прямой α с плоскостью Г) касательные к окружности основания цилиндра прямые t1 и t2, то прямая α и касательные t1 и t2 определят две касательные плоскости Е(αхt1) и К(αхt2). Эти плоскости касаются поверхности цилиндра с разных сторон по его образующим т1 и т2.

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ

Линия пересечения двух поверхностей, называемая линией перехода, это такая линия, все точки которой одновременно принадлежат обеим поверхностям.

В общем случае она представляет собой пространственную кривую или ломаную линию (при пересечении многогранных поверхностей), которая может распадаться на две или более частей. В отдельных случаях эти части могут быть плоскими кривыми или многоугольниками.

28. ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ МНОГОГРАННЫХ ПОВЕРХНОСТЕЙ

Для построения линии пересечения таких поверхностей (ломаной линии) необходимо найти точки пересечения ребер одного многогранника с гранями второго, а затем наоборот - ребер второго с гранями первого, т.е. нужно многократно решить задачу на пересечение прямой с плоскостью. Полученные точки будут являться вершинами ломаной линии.

Следует помнить, что точки линии пересечения всегда будут находиться в пределах площади наложения проекций поверхностей.

Полученные точки соединяем между собой, учитывая при этом, что соединять можно только те точки, которые лежат в одной грани первого многогранника и, одновременно, в одной грани второго многогранника.

При соединении вершин ломаной линией необходимо сразу же решать вопрос видимости отрезков этой ломаной линии. Видимыми будут те отрезки, которые одновременно принадлежат видимым граням обоих многогранников.

Линию пересечения можно построить также путем многократного решения задачи на пересечение двух плоскостей, т.е. строить линию пересечения граней одного многогранника с гранями другого и наоборот. Этот способ требует большего количества построений, поэтому на практике используется реже.

Все задачи на пересечение двух поверхностей можно условно разделить на три типа:

1. Обе поверхности имеют вырожденный вид;

2. Одна из двух поверхностей имеет вырожденный вид;

3. Ни одна из поверхностей не имеет вырожденного вида.
   

28.1 Первый тип задач - обе поверхности имеют вырожденный вид

П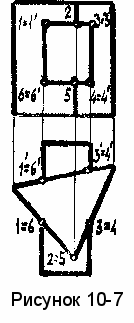ример 1. Построить линию пересечения призмы с параллелепипедом (рисунок 10-7).

В данном случае линия пересечения распадается на две пространственные кривые.

Так как каждая из поверхностей имеет вырожденный вид, то линия пересечения на видах уже есть. На виде спереди она совпадает с вырожденным видом параллелепипеда 1-2-3-4-5-6, а на виде сверху с вырожденным видом призмы 1-2-3-4-5-6 и 1-2-4-6.

28.2 Второй тип задач - одна из поверхностей имеет вырожденный вид.

П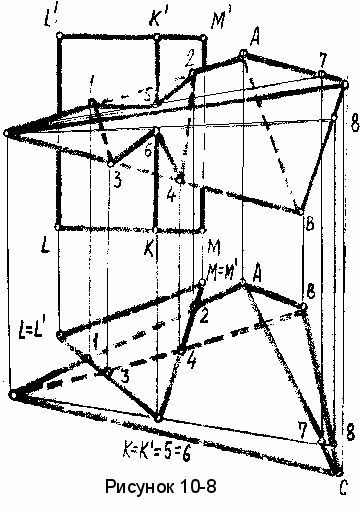ример 2. Построить линию пересечения прямой треугольной призмы с треугольной пирамидой. (рисунок 10-8).

Поскольку боковая поверхность призмы на виде сверху вырождается в линию (треугольник), то точки 1,2,3 и 4 здесь будут точками пересечения ребер АS и BS пирамиды с гранями призмы LL'K'K и КК'М'М, а точки 5 и 6- точки пересечения ближнего ребра призмы КК' с гранями пирамиды ACS и BCS.

Остальные ребра призмы и пирамиды точек пересечения с гранями не имеют. Зная положение точек линии пересечения на виде сверху, способом принадлежности находим их на виде спереди. Для нахождения на виде спереди точек 5 и 6, проводим на гранях АСS и ВСS пирамиды вспомогательные прямые S7 и S8 проходящие через точки 5 и 6, а затем, на основании свойства принадлежности. Находим их.

Полученные вершины линии пересечения соединяем отрезками прямых. При этом соединяем точки, принадлежащие как одной грани призмы, так и одной грани пирамиды.

Видимым будет участок линии пересечения только в том случае, если он находится одновременно в видимой грани призмы и видимой грани пирамиды. Во всех остальных случаях участки линии пересечения будут невидимы.