Geum.ru

Моу сош №2 г. Кирсанова Тамбовской области

Вид материалаДокументы

Содержание


Цели урока.
Подобный материал:

МОУ СОШ №2 г.Кирсанова Тамбовской области


Геометрический проект на тему








Учитель математики:

И.А. Глушкова


2007 г

Главная проблема проекта:


«Что означает понятие “подобные треугольники”?»


Учебный предмет – геометрия.


Участники – 8 класс.


Аннотация


Проект подготовлен учителем математики муниципального общеобразовательного учреждения средней общеобразовательной школы №2 города Кирсанова Тамбовской области Глушковой Ириной Альбертовной с применением проектной технологии. Реализуется в рамках программы по геометрии 8 класса по теме «Признаки подобия треугольников». Проект включает в себя информационную и исследовательскую часть. Аналитическая работа с информацией систематизирует знания о подобных фигурах. Самостоятельные исследования учащихся, а также приобретённые практические знания, умения и навыки учат видеть важность данного теоретического материала при применении его на практике. Дидактические задания (Приложение 5) помогут проконтролировать степень усвоения учебного материала.


Основополагающий вопрос: «Как и где можно применять признаки подобия треугольников в жизни?»


Гипотеза: «Если человек знает признаки подобия треугольников, возникнет ли необходимость их применять в жизни?»


Дидактические цели:
  1. формирование компетентности в сфере познавательной деятельности;
  2. усвоение навыков самостоятельной и коллективной работы;
  3. приобретение навыков самостоятельной работы с большим объёмом информации;
  4. развитие интереса учащихся к геометрии как к предмету;
  5. формирование критического мышления.


Методические задачи:
  1. изучить признаки подобия треугольников;
  2. оценить важность предмета «геометрия»;
  3. развивать умение применять теоретический материал при решении практических задач;
  4. формировать умения определять признаки подобия треугольников при решении геометрических задач;
  5. закрепить полученные теоретические знания на практике;
  6. развить интерес к науке и технике через поиск примеров применения данной темы в жизни;
  7. расширить математический кругозор и изучить новые подходы к решению задач;
  8. приобрести навыки исследовательской работы.



Темы самостоятельных исследований учащихся:
  1. Из истории возникновения подобия треугольников (Сообщение).
  2. Недоступные высоты (Презентация).
  3. Как определить ширину оврага или водоёма (Презентация).



Этапы проведения проекта:
  1. Мозговой штурм (формирование тем исследований учащихся).
  2. Формирование групп для проведения исследований, выдвижение гипотез, обсуждение путей решения проблем.
  3. Выбор творческого названия проекта.
  4. Обсуждение плана теоретической и практической работы учащихся в группе.
  5. Обсуждение с учащимися возможных источников информации.
  6. Самостоятельная работа групп.
  7. Подготовка учащимися презентаций и докладов по отчёту о проделанной работе.
  8. Представление исследовательских работ.



План урока с использованием проектной технологии
на уроке геометрии

по теме







«Сделать учебную работу насколько возможно интересной для ребёнка и не превратить эту работу в забаву – это одна из труднейших и важнейших задач дидактики»

К. Д. Ушинский


Цели урока.

Обучающие: закрепить знание определения подобных фигур, формулировки признаков подобных треугольников; уметь решать задачи прикладного характера с применением признаков подобия треугольников.


Воспитательные: формировать отношение к образованию как к важному и необходимому; развивать навыки самоконтроля.


Развивающие: развивать творческое мышление, умение анализировать, умение учебно-познавательной деятельности (работа с книгой); развивать волевую и любознательную личность и умение преодолевать трудности при решении задач; вызвать интерес к предмету.


Ход урока.

  1. Организационный момент.

Сообщается тема урока, цели урока, мотивация деятельности учащихся.

  1. Актуализация опорных знаний:
    1. Проверка домашнего задания по карточкам (Приложение 1) – 4 ученика.
    2. Фронтальный опрос
      • Дайте определение подобных треугольников
      • Сформулируйте признаки подобных треугольников
    3. Задачи по готовым чертежам (Приложение 2).



  1. Работа в классе с учениками


Решая различные задачи по теме «Признаки подобия треугольников» мы не задумывались, где и как можно применить полученные знания в жизни. Сегодня у нас необычный урок, мы с вами познакомимся с проектными работами групп учащихся, которые нас постараются убедить, что ранее полученные знания нужны в жизни, а предмет геометрия – наука, которая тесно связана с жизненными ситуациями.
  1. Сообщение о развитии практической геометрии в древней Руси (Приложение 3).
  2. Презентация «Недоступные высоты».
  3. Презентация «Как измерить ширину водоёма».



  1. Самостоятельная работа в парах.


Работа по карточкам (Приложение 4).

  1. Вывод.

Без знаний геометрии не обойтись!


Скажи мне – и я забуду.

Покажи мне – и я запомню.

Вовлеки меня – и я научусь.

Китайская пословица.

В процессе реализации проекта учащиеся:
  • Изучили тему признаки подобия треугольников
  • Овладели навыками работы с большим объёмом информации
  • Провели теоретические и практические исследования
  • Оценили знания геометрии в жизни
  • Реализовали творческие возможности, работая над заданиями
  • Представили результаты своей деятельности в различных формах



Использованные источники информации:

  1. Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 7–9: Учебник для общеобразовательных учреждений. – М., Просвещение, 2003.
  2. В.Г. Прочухаев. Измерения в курсе математики средней школы. – М., Просвещение, 1965.
  3. Я.И. Перельман. Занимательная геометрия. – М., Государственное издательство физико-математической литературы, 1958.
  4. Ф.В. Корнев. Практические занятия по геометрии. – Барнаул, Алтайское книжное издательство, 1959.
  5. Г.И. Глейзер. История математики в школе. – М., Просвещение, 1964.
  6. М.М. Лиман. Практические занятия по геометрии для восьмилетней школы. – М., Учпедгиз, 1962.


Приложение 1.

Карточка 1


Продолжение боковых сторон АВ и СD трапеции ABCD пересекается в точке Е. Доказать, что треугольник AED подобен треугольнику ВЕС.


Карточка 2


Диагонали трапеции АВСD пересекаются в точке Е. Докажите подобие треугольников ВСЕ и DAE.


Карточка 3


В трапеции АВСD с диагональю АС углы АВС и АСD равны. Найдите диагональ АС, если основания ВС = 12, АD = 27.


Карточка 4


Отрезки АВ и СD пересекаются в точке О, так, что АО : ОВ = 2 : 3, угол АСО равен углу ВDO, периметр треугольника ВОD = 21. Найдите периметр треугольника АСО.


Приложение 2

Рисунок 1




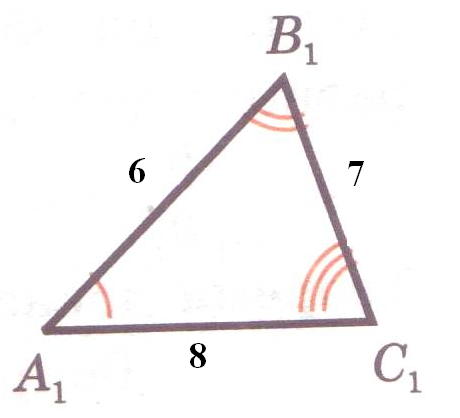
Т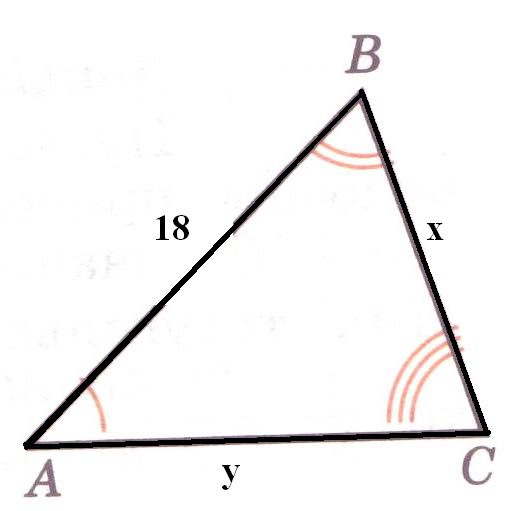реугольник АВС подобен треугольнику А1В1С1. Найти х, у.


Рисунок 2




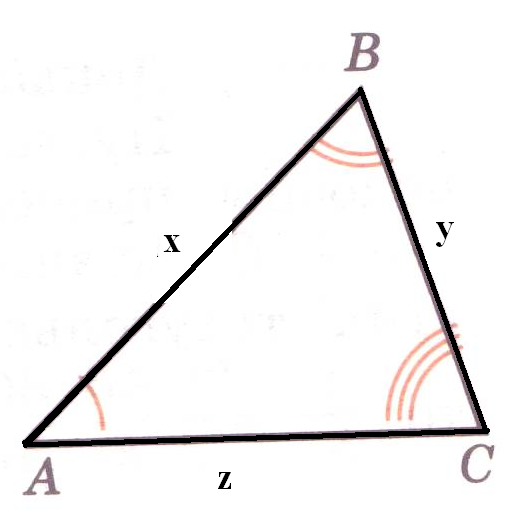
Треугольник АВС подобен треугольнику А1В1С1. Найти х, у, z, если дано АВ : А1В1 = 2.


Рисунок 3




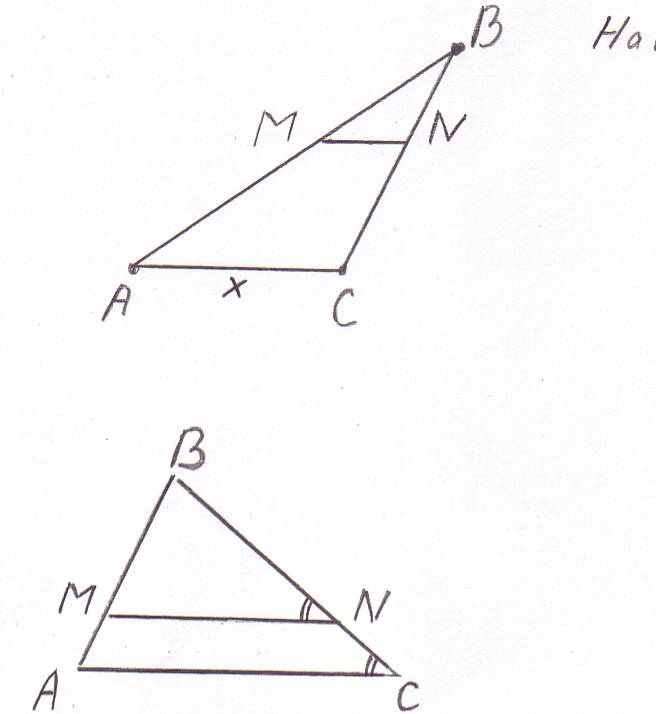
Найти х, если MN || AC, MN = 6, BC = 12, CN = 4.


Рисунок 4





Найдите пары подобных треугольников и докажите их подобие. Запишите равенство отношений соответствующих сторон.


Приложение 3

О развитии практической геометрии в древней Руси.


Уже в XVI в. нужды землемерия, строительства и военного дела при­вели к созданию рукописных руко­водств геометрического содержания. Первое дошедшее до нас сочинение этого рода носит название «О земном верстании, как земля верстать». Оно является частью «Книги сошного пись­ма», написанной, как полагают, при Иване IV в 1556 г. Сохранившаяся копия относится к 1629 г.

П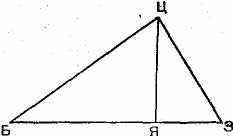ри разборе Оружейной Палаты в Москве в 1775 г. была обнаружена инструкция «Устав ратных, пушечных и "других дел, касающихся до военной науки», изданная в 1607 и 1621 годах и содержащая некоторые геометрические сведения, которые сво­дятся к определенным приемам решения задач на нахождение расстояний. Вот один пример.

Для измерения расстояния от точки Я до точки Б (см. рис.) рекомендуется вбить в точке Я жезл примерно в рост человека. К верхнему концу жезла Ц прилагается вершина прямого угла угольника так, чтобы один из катетов (или его продолжение) проходил через точку Б. Отмечается точка 3 пересечения дру­гого катета (или его продолжения) с землей. Тогда расстоя­ние БЯ относится к длине жезла ЦЯ так, как длина жезла к расстоянию ЯЗ. Для удобства расчетов и измерений жезл был разделен на 1000 равных частей.


Приложение 4

Задача 1.


Стороны треугольника 15 см , 35 см, 30 см. Большая сторона подобного ему треугольника 7 см. Чему равна меньшая сторона этого треугольника?


Указания к задаче:

- Построй два треугольника MNP и  M1N1P1. Угол M = углу M1, угол N = углу N1,         угол P = углу P1

- Составь отношения сходственных сторон (сходственные стороны лежат против равных углов)
- Найди коэффициент подобия k
- Ответь на вопрос задачи 





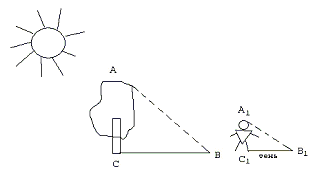
Задача 2.


Длина тени дерева 21 м. В это же время суток тень человека ростом 1,8 м составляет 2,7 м. Какова высота дерева?


З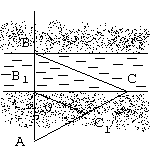адача 3. № 583 учебника


На рисунке показано, как можно определить ширину BB1 реки, рассматривая два подобных треугольника ABC и A1B1C1. Определите BB1, если AC = 100 м, AC1 = 32 м, AB1 = 34 м.

Приложение 5

Дидактические задания.





1. Определяя расстояние АВ (точка А недоступна), построили на местности направления с помощью вех (столбиков). ВС  АВ и ВD  AC. Как вычислить АВ?


2. Построить треугольник, подобный данному, но имеющий в два раза большую площадь.


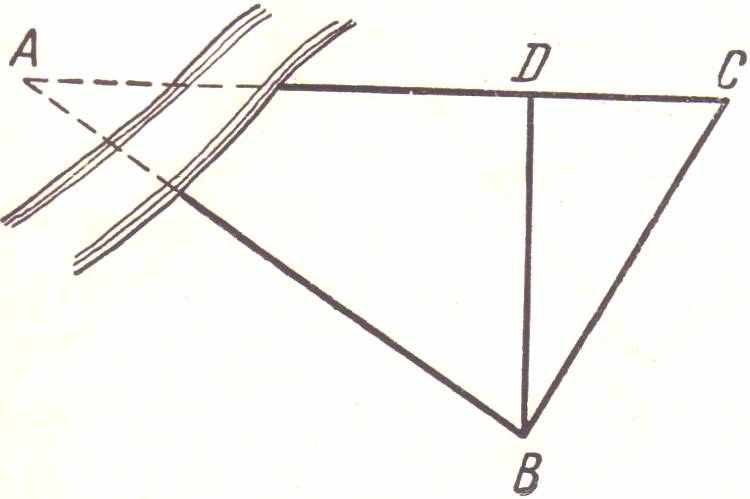
3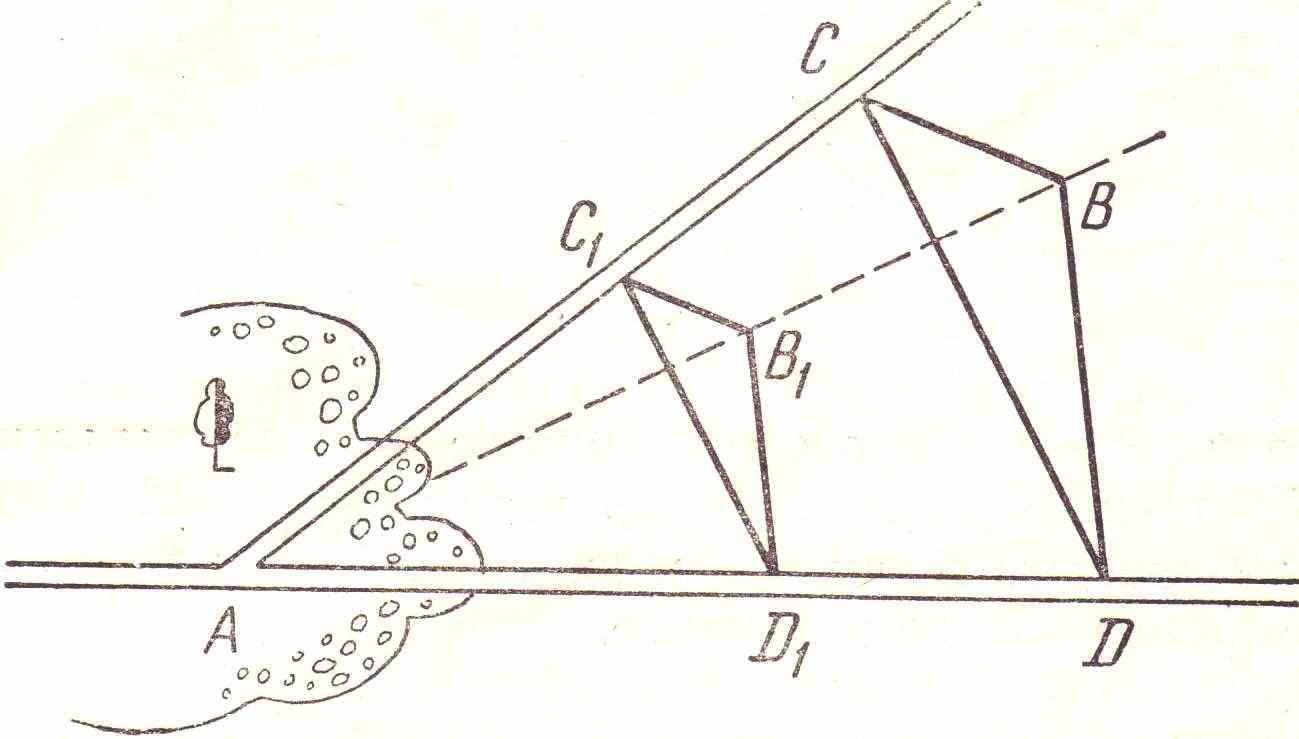. Из пункта В к месту пересечения двух дорог АС и АD требуется провести узкоколейную дорогу. Как на местности наметить трассу дороги ВА, если место А окружено лесом?

Указание. Используй любой признак подобия треугольников (см. рис.).


4. Определить расстояние до недоступной точки путём построения подобных треугольников.


5. По тени определить высоту предмета, к основанию которого нельзя подойти.


6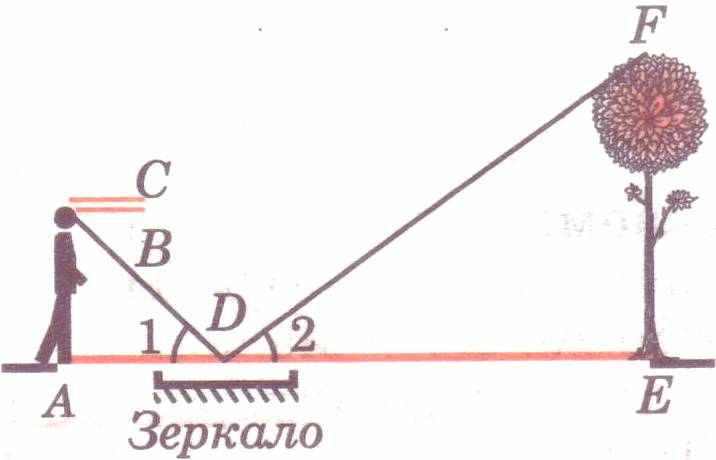. №581 учебника. Для определения высоты дерева можно использовать зеркало так, как показано на рисунке. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека (точку В). Определите высоту дерева, если АС = 165 см, ВС = 12 см, АD = 120 см, DE = 4,8 м, 1 = 2.


7. №582 учебника. Для определения расстояния от точки А до недоступной точки В на местности выбрали точку С и измерили отрезок АС, углы ВАС и АСВ. Затем построили на бумаге треугольник А1В1С1, подобный треугольнику АВС. Найдите АВ, если АС = 42 м, А1С1 = 6,3 см, А1В1 = 7,2 см.