Geum.ru

Курс научный руководитель Перваков Алексей Преподаватель Пиявский С. А

Вид материалаПояснительная записка

Содержание


Экран оценки творческого уровня работы
Кластерный анализ
Анализ и интерпретация его результатов
Подобный материал:


ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУВПО «Самарский государственный архитектурно-строительный университет»

Факультет информационных систем и технологий

Кафедра прикладной математики и вычислительной техники


ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ


по дисциплине

ТЕХНОЛОГИЯ ПРОФЕССИОНАЛЬНОЙ ДЕЯТЕЛЬНОСТИ


на тему


«Кластерный анализ матрицы ассоциативных связей»


1 СЕМЕСТР 1 КУРС


Научный руководитель Перваков Алексей

Преподаватель Пиявский С.А.

Методический руководитель Пиявский С.А.
Выполнил:

студент ГИП-109 Жирнов С.А.




подпись дата















Оценка преподавателя _______________


Оценка комиссии по результатам защиты_______________


2010 г.

УДК 004.023+519.237.8


Расшифровка:

Информационные технологии. Компьютерные технологии. Теория вычислительных машин и систем

Эвристические методы

Кластеризация

Ключевые слова

Графово-эвристические методы, кластеризация, информационные технологии.


Аннотация:


Для кластеризации матрицы ассоциативных связей мне потребовалось сделать ее. Для этого я опросил свою группу на тему их интересов и создал таблицу в Exel. Для кластеризации я проанализировал разщные методы кластеризации и выбрал метод **** изучив его, была написана программа на Visual Basic. Успешно выделив кластер я взял программу шефа что бы так же выделить кластер и сравнить результаты.


Экран оценки творческого уровня работы





Кластерный анализ— задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.

Опросив свою группу по интересам и составив таблицу ассоциативных связей, мне нужно было разбить их на кластеры.

Для этого я выбрал метод кластеризации “K-средних (K-means)”- наиболее популярный метод кластеризации. Алгоритм представляет собой модификацию EM-алгоритма для разделения смеси гауссиан. Он разбивает множество элементов векторного пространства на заранее известное число кластеров k. Действие алгоритма таково, что он стремится минимизировать среднеквадратичное отклонение на точках каждого кластера.


Программа была написана на Visual Basic, но к сожалению мне не удалось доработать ее самостоятельно и поэтому сейчас она не работает, однако я взял программу своего шефа который так же писал курсовую работу по схожей тематике, но использовал другой метод кластеризации .

Им написана программа, реализующая графово-эвристический методов кластеризации. Для работы программы требуется xls файл в котором содержится сам словарь лексем, а также таблица коэффициентов ассоциативности между всеми возможными парами лексем словаря.

В моем случае лексемы это ученики группы ГИП-109, а коэффициенты ассоциативности совпадение их интересов.

Кластерный анализ (англ. Data clustering) — задача разбиения заданной выборки объектов (ситуаций) на подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались. Задача кластеризации относится к статистической обработке, а также к широкому классу задач обучения без учителя. Кластерный анализ — это многомерная статистическая процедура, выполняющая сбор данных, содержащих информацию о выборке объектов, и затем упорядочивающая объекты в сравнительно однородные группы (кластеры)(Q-кластеризация, или Q-техника, собственно кластерный анализ). Кластер — группа элементов, характеризуемых общим свойством, главная цель кластерного анализа — нахождение групп схожих объектов в выборке (примечание 1). Спектр применений кластерного анализа очень широк: его используют в археологии, медицине, психологии, химии, биологии, государственном управлении, филологии, антропологии, маркетинге, социологии и других дисциплинах. «Тематика исследований варьирует от анализа морфологии мумифицированных грызунов в Новой Гвинее до изучения результатов голосования сенаторов США, от анализа поведенческих функций замороженных тараканов при их размораживании до исследования географического распределения некоторых видов лишая в Саскачеване» (примечание 1). Однако универсальность применения привела к появлению большого количества несовместимых терминов, методов и подходов, затрудняющих однозначное использование и непротиворечивую интерпретацию кластерного анализа.


Задачи и условия

Кластерный анализ выполняет следующие основные задачи:
  • Разработка типологии или классификации.
  • Исследование полезных концептуальных схем группирования объектов.
  • Порождение гипотез на основе исследования данных.
  • Проверка гипотез или исследования для определения, действительно ли типы (группы), выделенные тем или иным способом, присутствуют в имеющихся данных (примечание 1).



Независимо от предмета изучения применение кластерного анализа предполагает следующие этапы: — Отбор выборки для кластеризации. — Определение множества переменных, по которым будут оцениваться объекты в выборке. — Вычисление значений той или иной меры сходства между объектами. — Применение метода кластерного анализа для создания групп сходных объектов. — Проверка достоверности результатов кластерного решения (примечание 1).


Кластерный анализ предъявляет следующие требования к данным: во-первых, показатели не должны коррелировать между собой; во-вторых, показатели должны быть безразмерными; в-третьих, их распределение должно быть близко к нормальному; в-четвёртых, показатели должны отвечать требованию «устойчивости», под которой понимается отсутствие влияния на их значения случайных факторов; в-пятых, выборка должна быть однородна, не содержать «выбросов» (примечание 2). Если кластерному анализу предшествует факторный анализ, то выборка не нуждается в «ремонте» — изложенные требования выполняются автоматически самой процедурой факторного моделирования (есть ещё одно достоинство — z-стандартизация без негативных последствий для выборки; если её проводить непосредственно для кластерного анализа, она может повлечь за собой уменьшение чёткости разделения групп). В противном случае выборку нужно корректировать.

Анализ и интерпретация его результатов


При анализе результатов социологических исследований рекомендуется осуществлять анализ методами иерархического агломеративного семейства, а именно методом Уорда, при котором внутри кластеров оптимизируется минимальная дисперсия, в итоге создаются кластеры приблизительно равных размеров. Метод Уорда наиболее удачен для анализа социологических данных. В качестве меры различия лучше квадратичное евклидово расстояние, которое способствует увеличению контрастности кластеров (примечание 1). Главным итогом иерархического кластерного анализа является дендрограмма или «сосульчатая диаграмма». При её интерпретации исследователи сталкиваются с проблемой того же рода, что и толкование результатов факторного анализа — отсутствием однозначных критериев выделения кластеров. В качестве главных рекомендуется использовать два способа — визуальный анализ дендрограммы и сравнение результатов кластеризации, выполненной различными методами (примечание 1; примечание 2). Визуальный анализ дендрограммы предполагает «обрезание» дерева на оптимальном уровне сходства элементов выборки. «Виноградную ветвь» (терминология Олдендерфера М. С. и Блэшфилда Р. К.) целесообразно «обрезать» на отметке 5 шкалы Rescaled Distance Cluster Combine, таким образом будет достигнут 80 % уровень сходства. Если выделение кластеров по этой метке затруднено (на ней происходит слияние нескольких мелких кластеров в один крупный), то можно выбрать другую метку. Такая методика предлагается Олдендерфером и Блэшфилдом (примечание 1).


Теперь возникает вопрос устойчивости принятого кластерного решения. По сути, проверка устойчивости кластеризации сводится к проверке её достоверности. Здесь существует эмпирическое правило — устойчивая типология сохраняется при изменении методов кластеризации. Результаты иерархического кластерного анализа можно проверять итеративным кластерным анализом по методу k-средних. Если сравниваемые классификации групп респондентов имеют долю совпадений более 70 % (более 2/3 совпадений), то кластерное решение принимается.


Проверить адекватность решения, не прибегая к помощи другого вида анализа, нельзя. По крайней мере, в теоретическом плане эта проблема не решена. В классической работе Олдендерфера и Блэшфилда «Кластерный анализ» подробно рассматриваются и в итоге отвергаются дополнительные пять методов проверки устойчивости: 1) кофенетическая корреляция — не рекомендуется и ограниченна в использовании; 2) тесты значимости (дисперсионный анализ) — всегда дают значимый результат; 3) методика повторных (случайных) выборок, что, тем не менее, не доказывает обоснованность решения; 4) тесты значимости для внешних признаков пригодны только для повторных измерений; 5) методы Монте-Карло очень сложны и доступны только опытным математикам (примечание 1).

Имеется список учеников группы ГИП-109, степень близости их интересов, отражает параметр названный коэффициент ассоциативности (К-А). Если имеется таблица коэффициентов ассоциативности между всеми учениками, тогда можно легко произвести кластеризацию, приняв за основной параметр кластеризации К-А.

Программа была написана на Visual Basic, но к сожалению мне не удалось доработать ее самостоятельно и поэтому сейчас она не работает, однако я взял программу своего шефа который так же писал курсовую работу по схожей тематике, но использовал другой метод кластеризации .

Им разработана программа реализации одного из графово-эвристических методов кластеризации: Алгоритм выделения связанных компонент.

Суть метода заключается в том, что строится полный граф из N элементов. Каждое ребро этого графа имеет параметр P(j, j), где i и j номера элементов связанных данным ребром. Вводится параметр R. И в графе удаляются все ребра для которых выполняется условие P(i,j)>R. Соединенными остаются только наиболее близкие объекты. Суть метода заключается в том чтобы подобрать такой параметр R принадлежащий [Pmin(i,j);Pmax(i,j)], при котором граф начинает распадаться на несколько связанных компонент. Эти компоненты и будут являться кластерами.

В таком случае если за элемент графа принять фамилию ученика. А за параметр P(i ,j) взять коэффициент ассоциативности между i-той и j-той фамилии. А также поменять знак неравенства в выражение P(i,j)>R на < так как нам надо удалять ребра имеющие наименьший К-А.



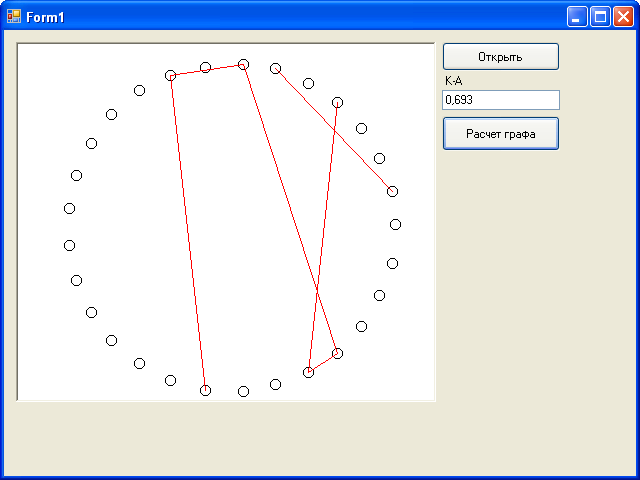
Получили 2 кластера:

Кузьмин Евгений

Полищук Антон

Саярова Алёна

Жирнов Станислав

Корчагин Павел

Ханов Михаил


Соловьёва Дарья

Янюшкина Анна


Теоретически это 2 группы людей у которых должны быть схожи интересы.

Библиографический список.
  1. Кластеризация – Википедия [Электронный ресурс] // Режим доступа: ссылка скрыта.
  2. Что такое кластеризация // Режим доступа: www.biometrica.tomsk.ru/cluster_2.htm.
  3. Кулачев А.П. – Методы и средства комплексного анализа данных. 1999г - 120 с.
  4. Загоруйко Н.Г.- Прикладные методы анализа данных и знаний. 2006г - 45 с.