Geum.ru

Интегрирование по частям

Вид материалаЗадача

Содержание


Интегрирование рациональных функций
Всякую неправильную дробь можно представить в виде суммы многочлена и правильной дроби, разделив числитель на знаменатель
Подобный материал:
Интегрирование по частям

Третий общий прием интегрирования называется интегрированием по частям. Этот метод следует из формулы дифференцирования произведения двух функций.

Пусть функции u(x) и v(x) дифференцируемы по x, тогда:

.

Интегрируя обе части последнего равенства, получаем: 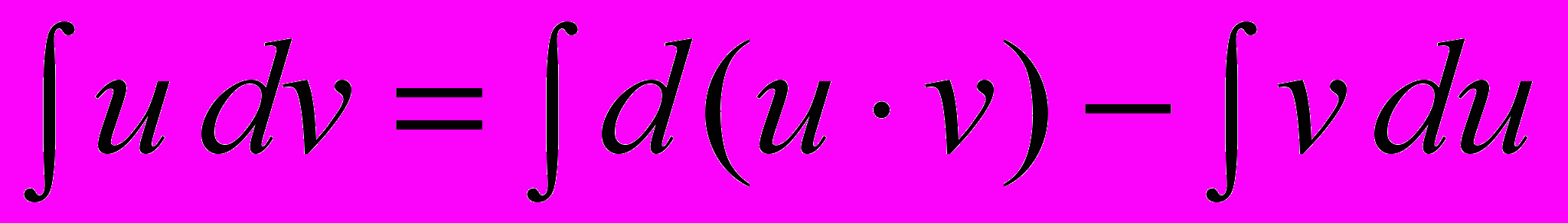, или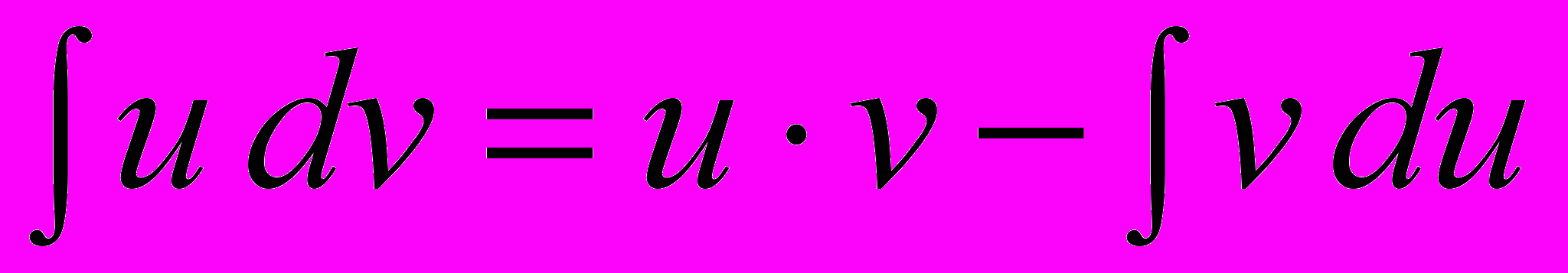

.

Это и есть формула интегрирования по частям.

При интегрировании по частям вычисление данного интеграла сводится к вычислению двух более простых интегралов:

1. 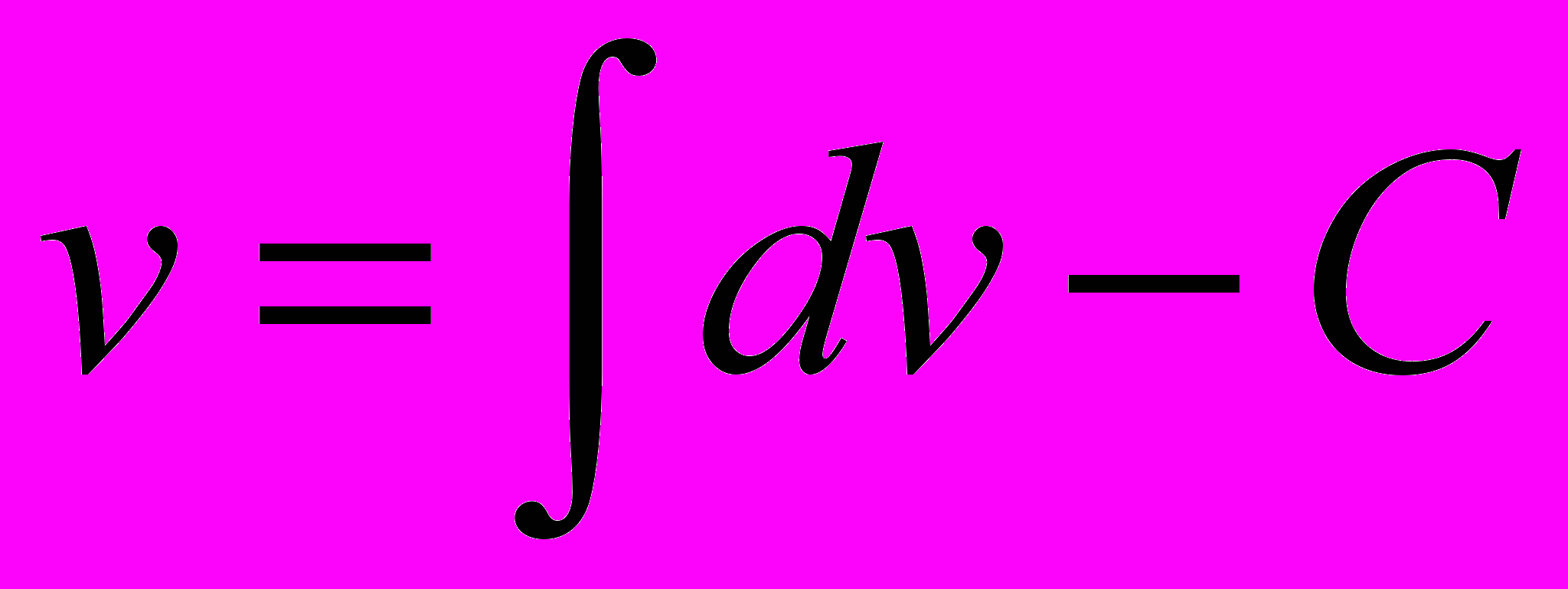; 2. .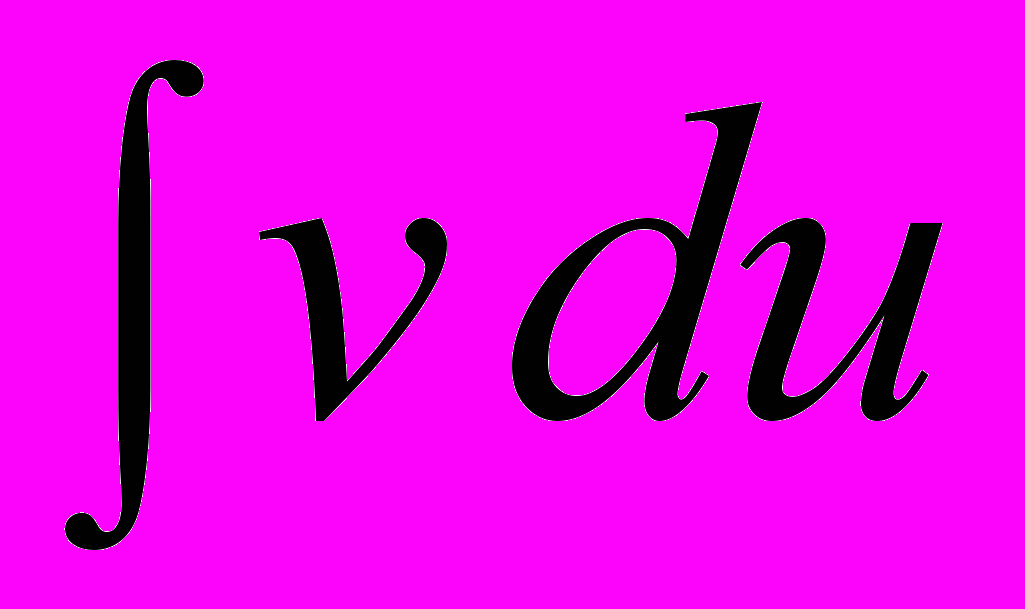

Задача интегрирования по частям сводится к удачному разбиению подынтегрального выражения, так, чтобы указанные два интеграла можно было легко вычислить.

Можно рекомендовать правило для вычисления по частям некоторых типов интегралов (ниже Р(х) – многочлен, а - число):

1. 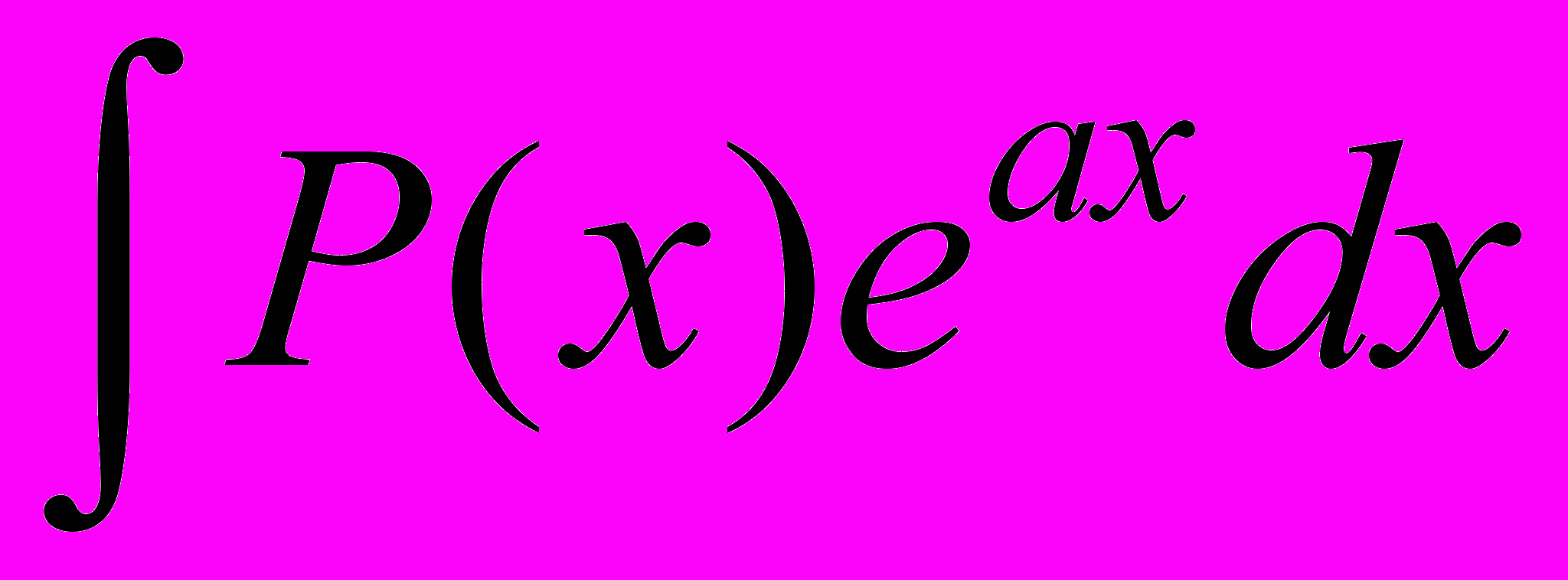, (k  1) тогда ;

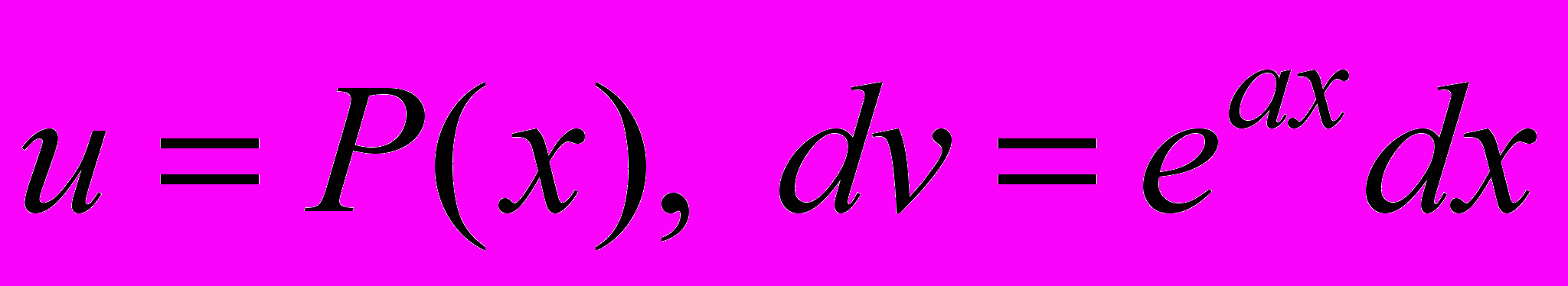2. 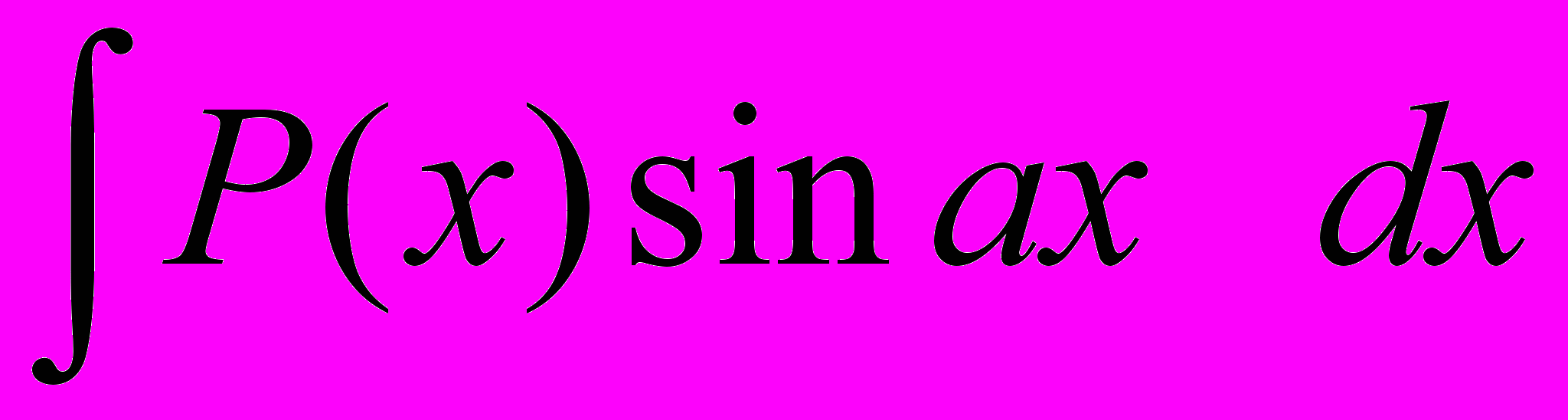, (k  1) тогда ;

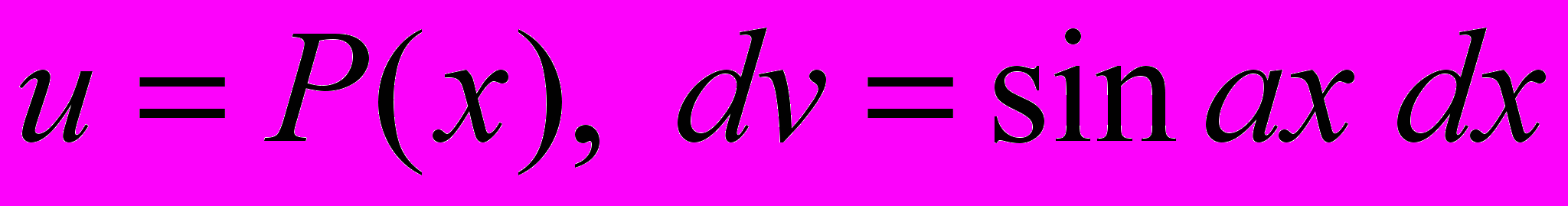3. 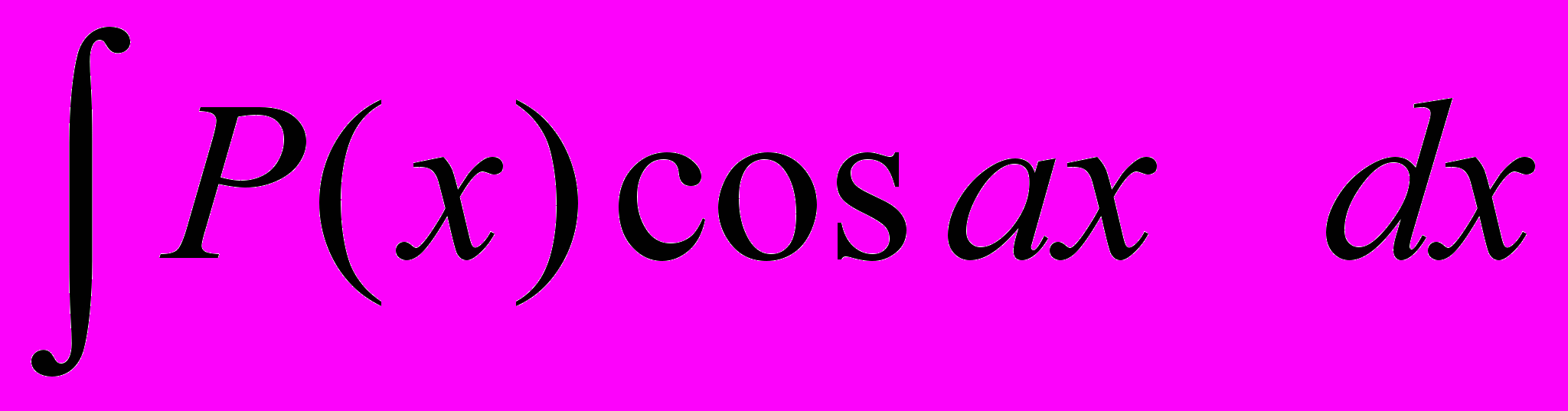, (k  1) тогда ;

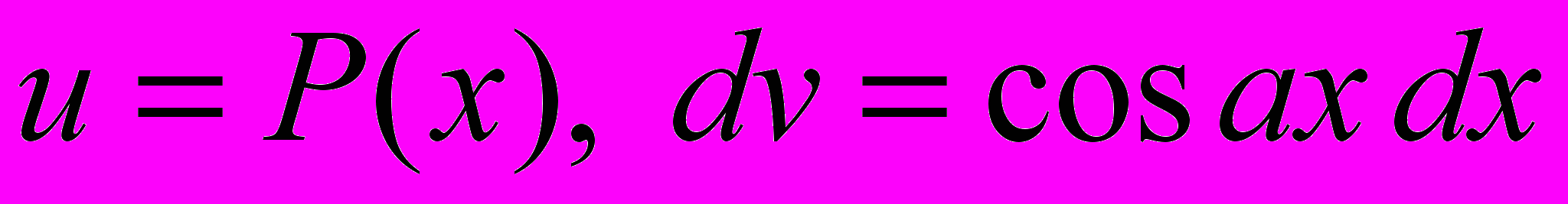4. 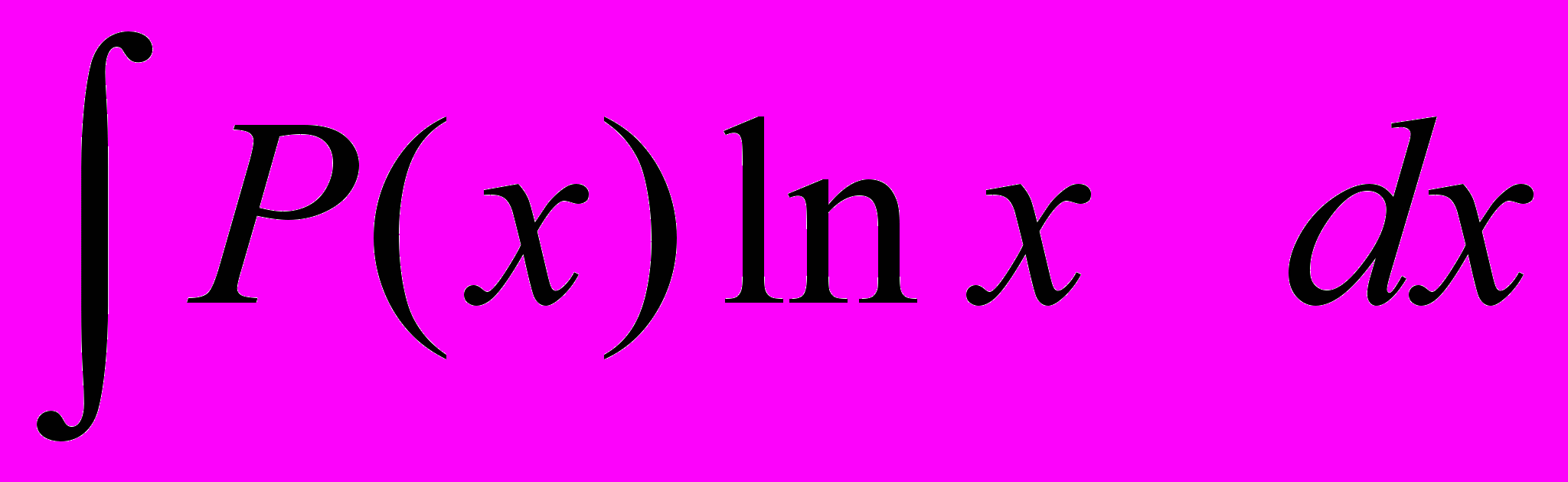, (k  0) тогда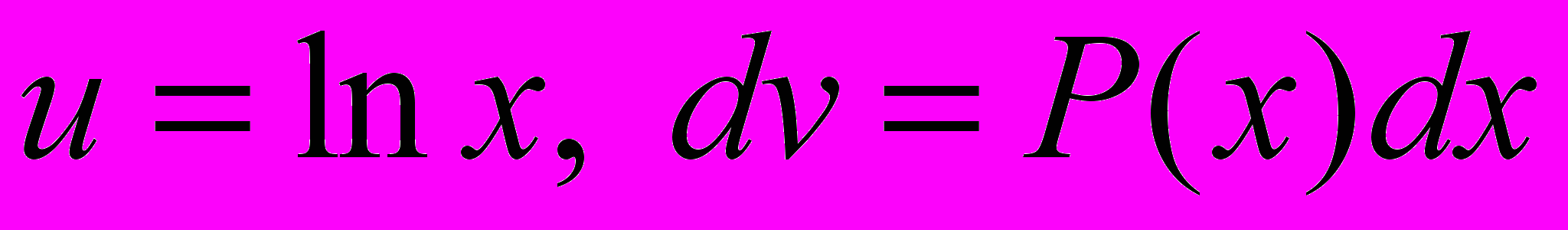

(или сводится к типу 1 заменой t=lnx);

5. 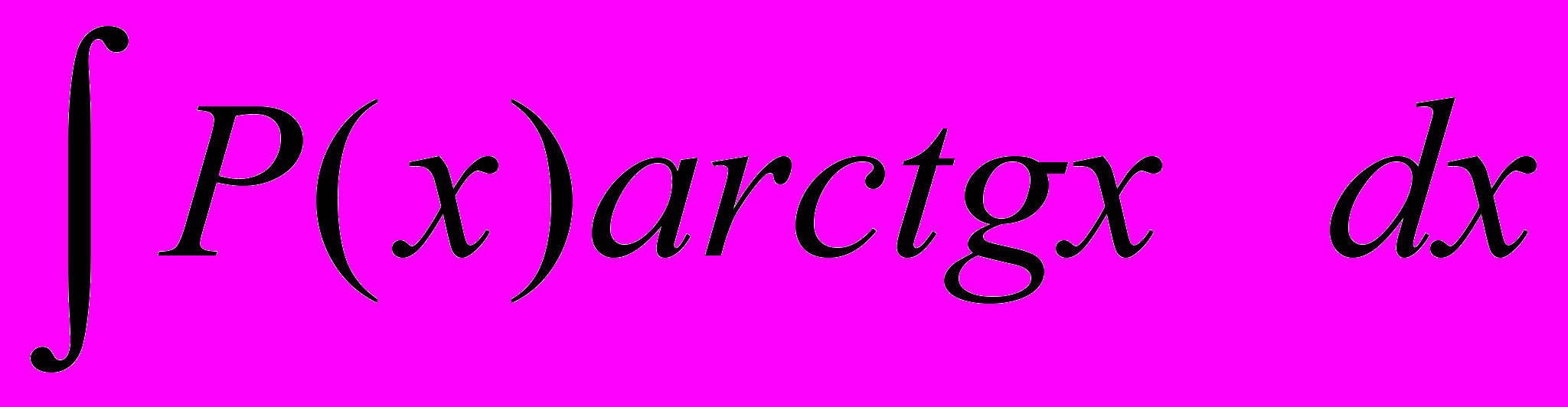, (k  0) тогда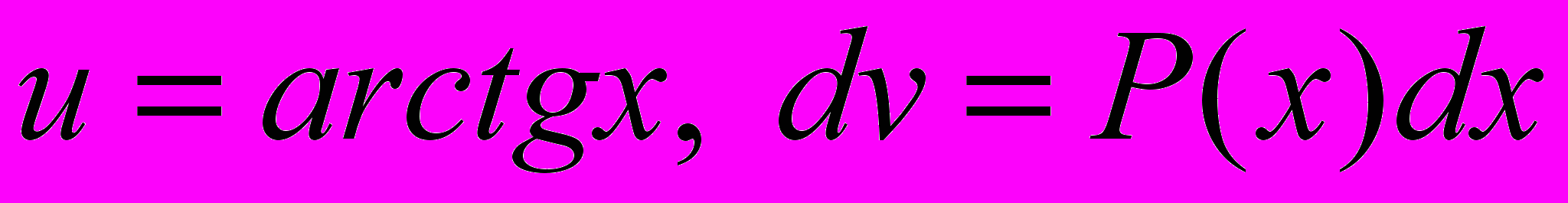

(то же для arcsinx, arccosx).

Замечание. Если выбрано неподходящее разбиение, то 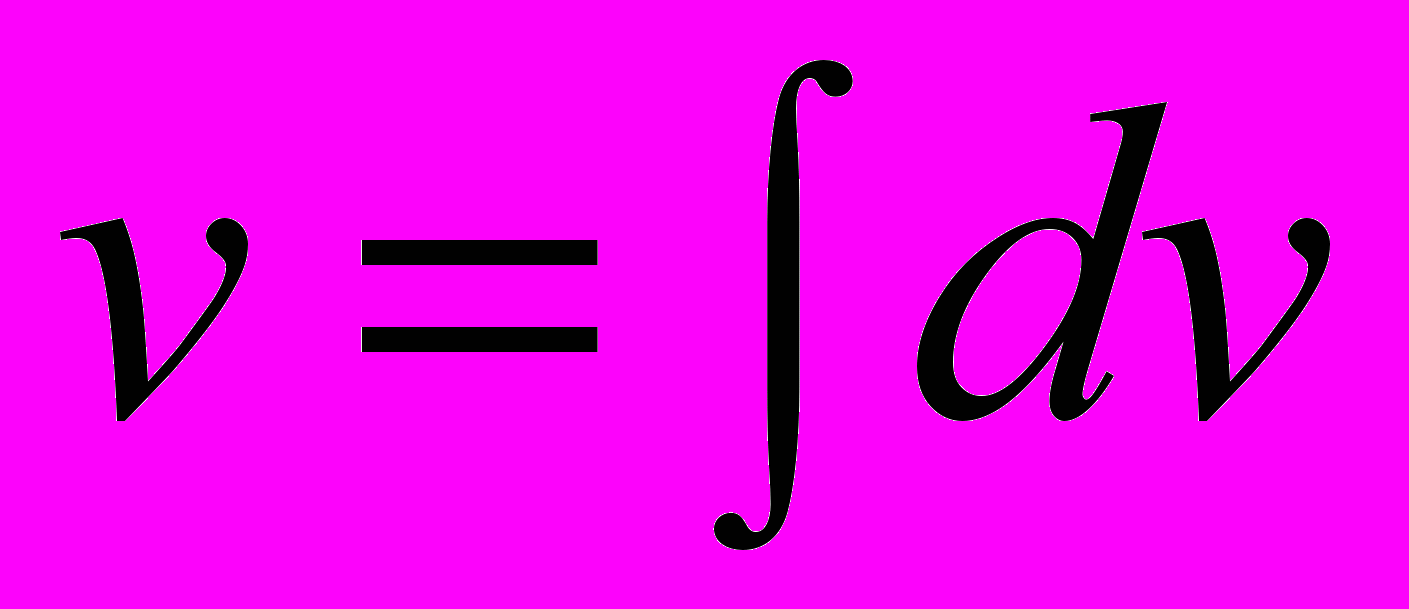или 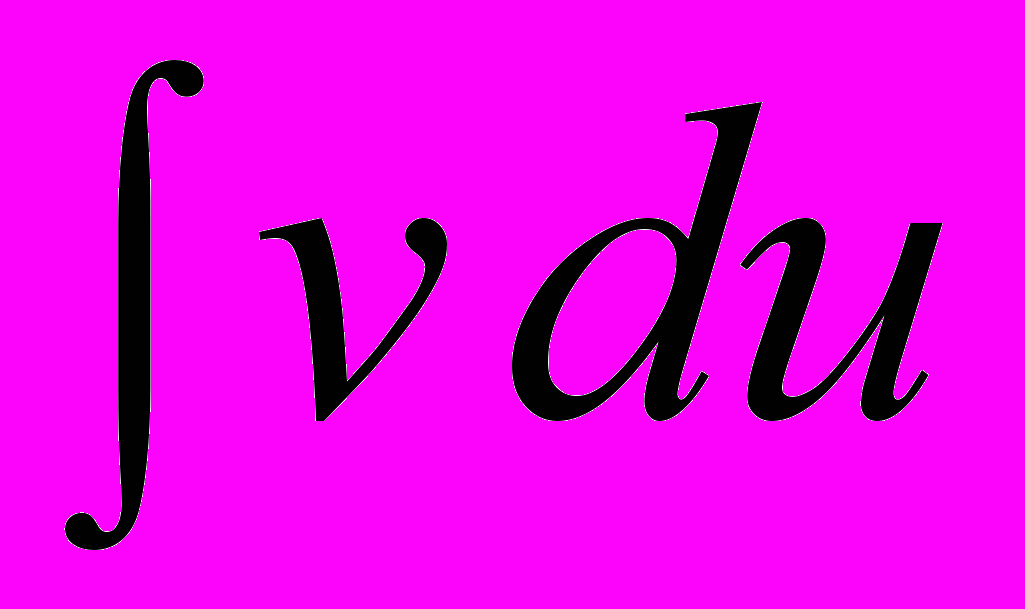оказывается проинтегрировать сложно или вообще невозможно. Поэтому если подынтегральное выражение возможно упростить с помощью какой-либо замены, следует это сделать, прежде чем применять метод интегрирования по частям.


Пример 1. Вычислить

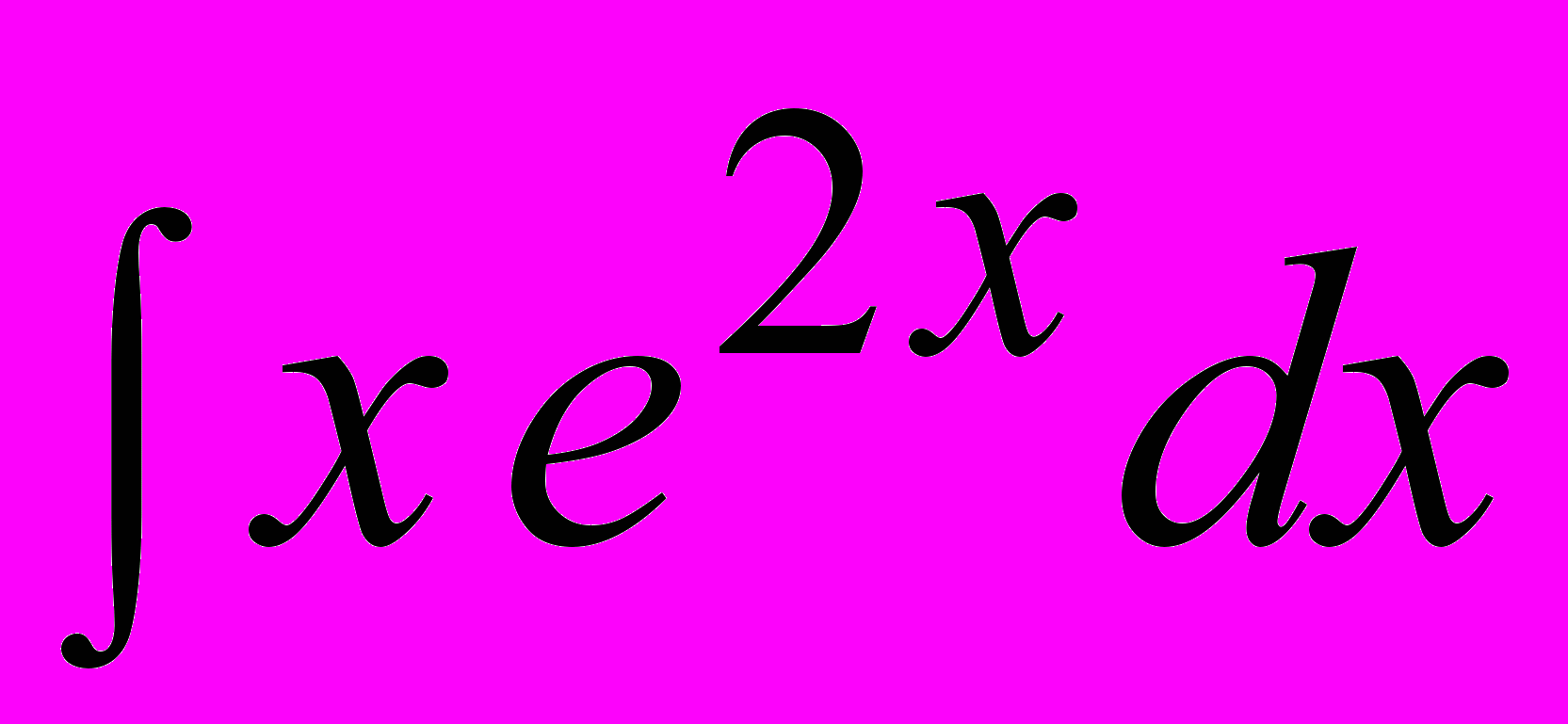
Примем

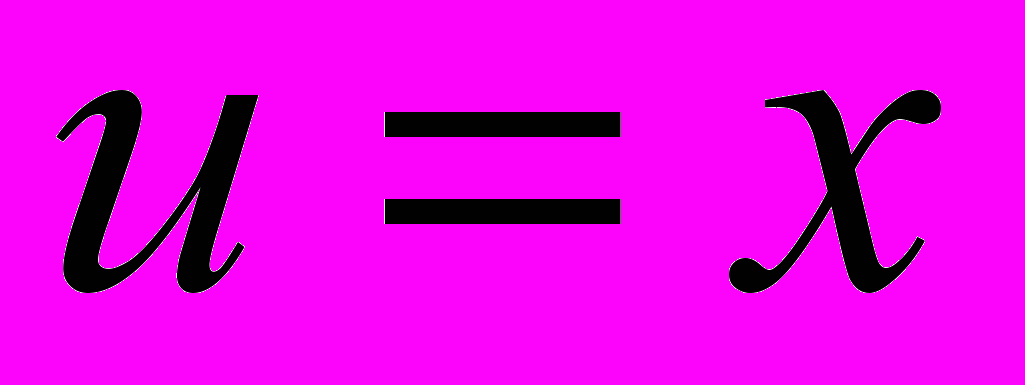
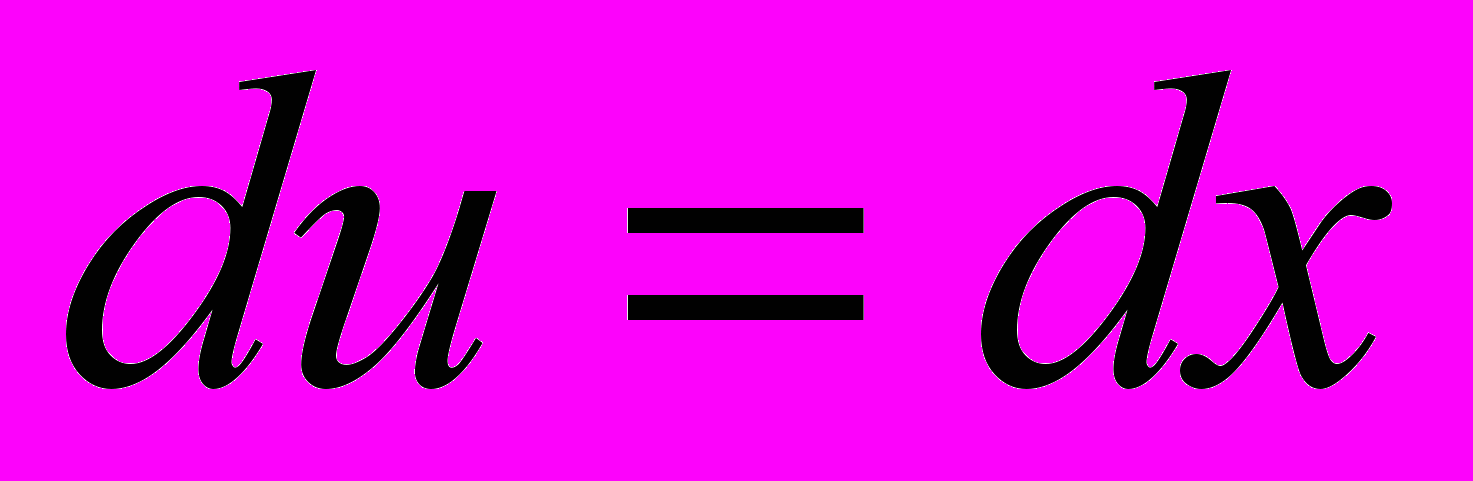
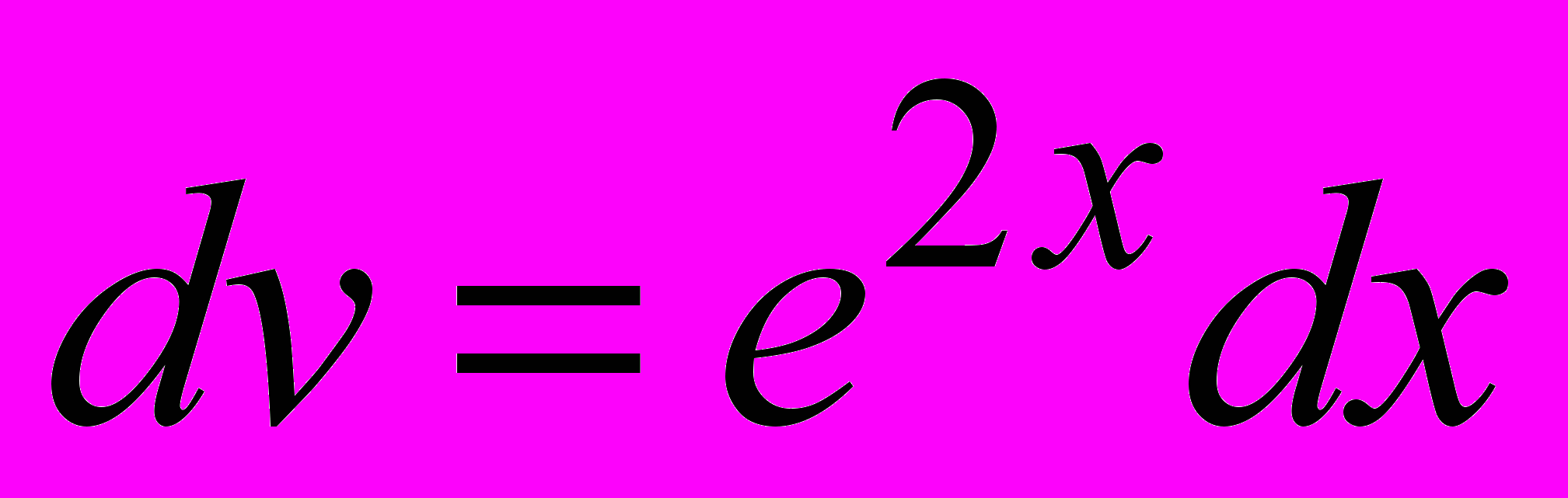
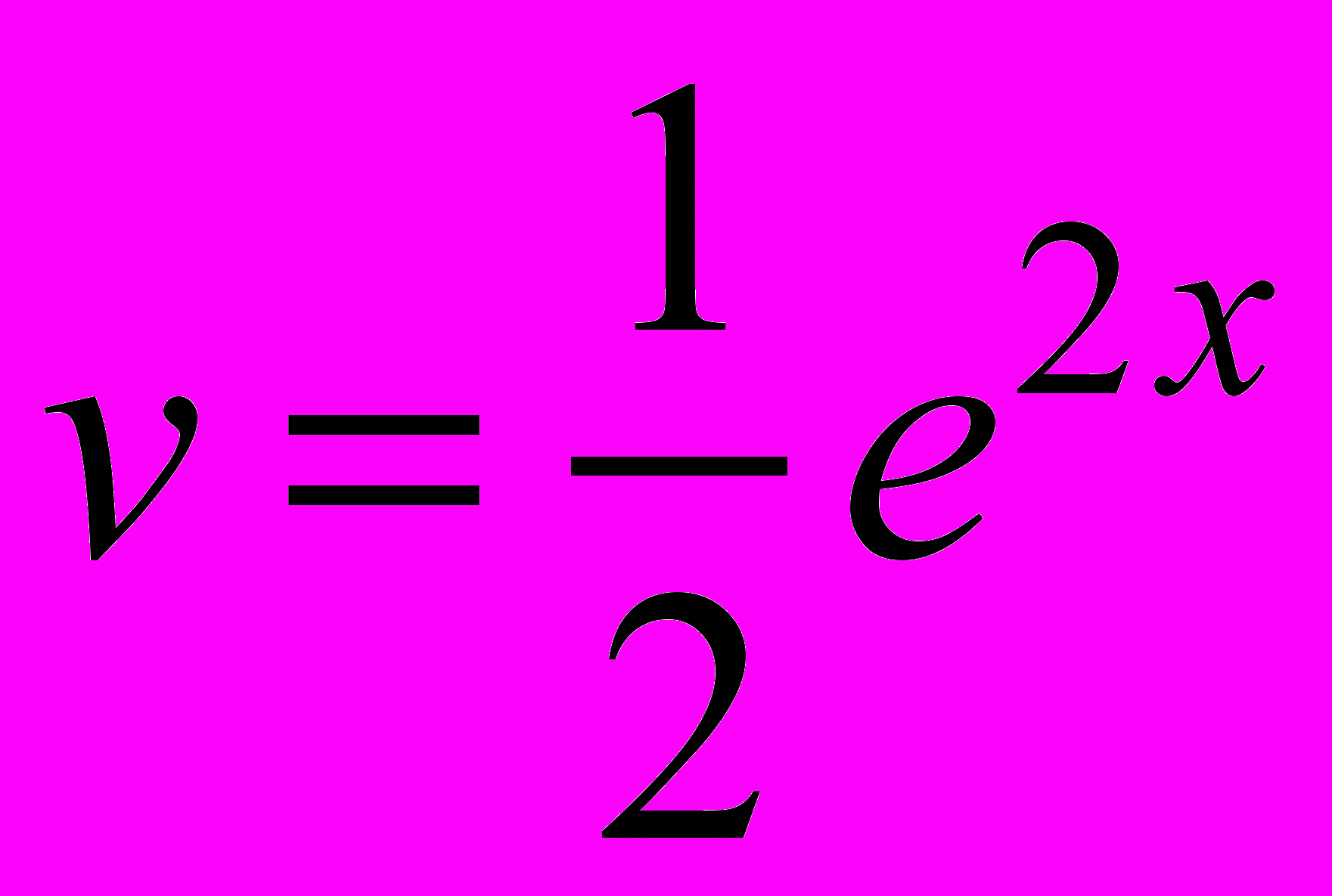(не пишем +С, т.к. требуется лишь одна первообразная функция v).

Подставляя в формулу интегрирования по частям, имеем:

.

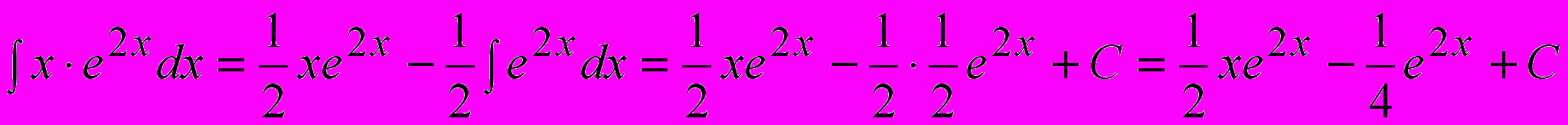Пример 2. 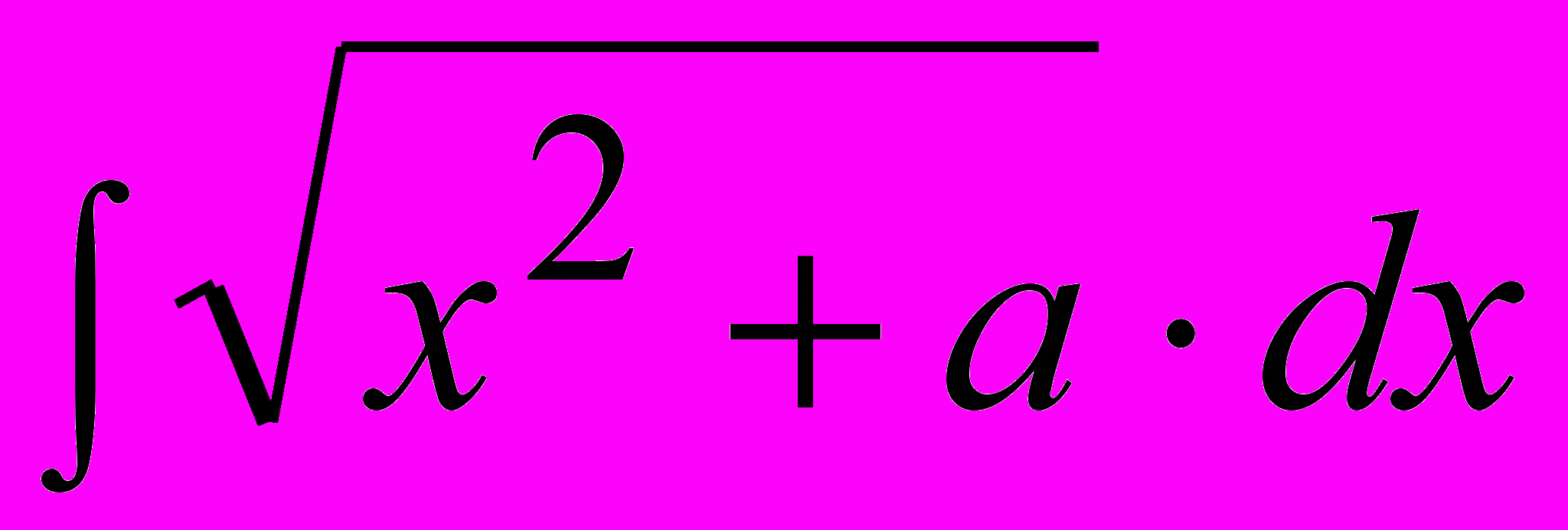(15-й интеграл из таблицы)

Примем



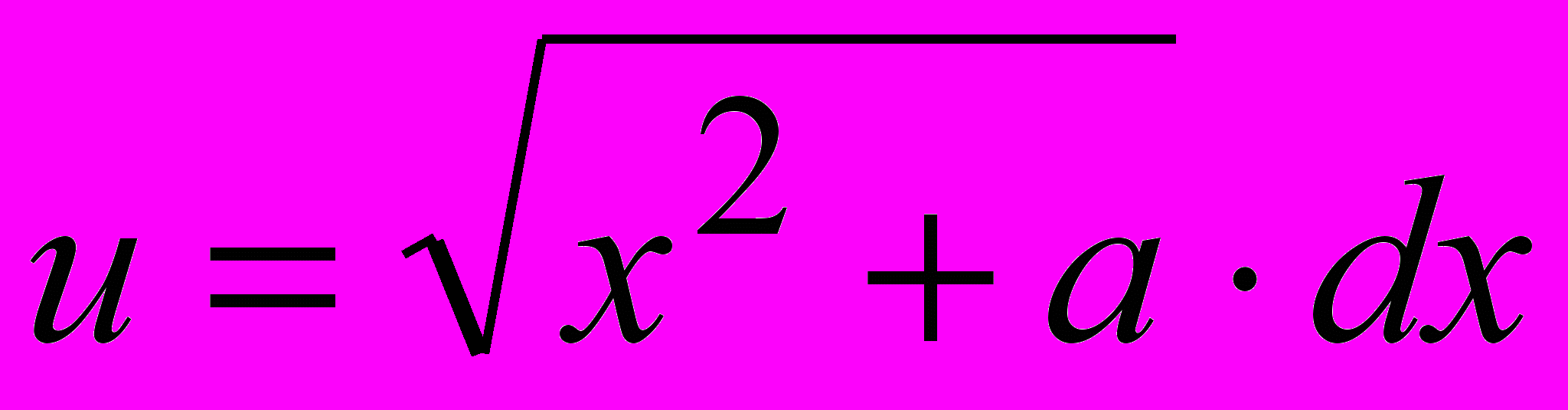
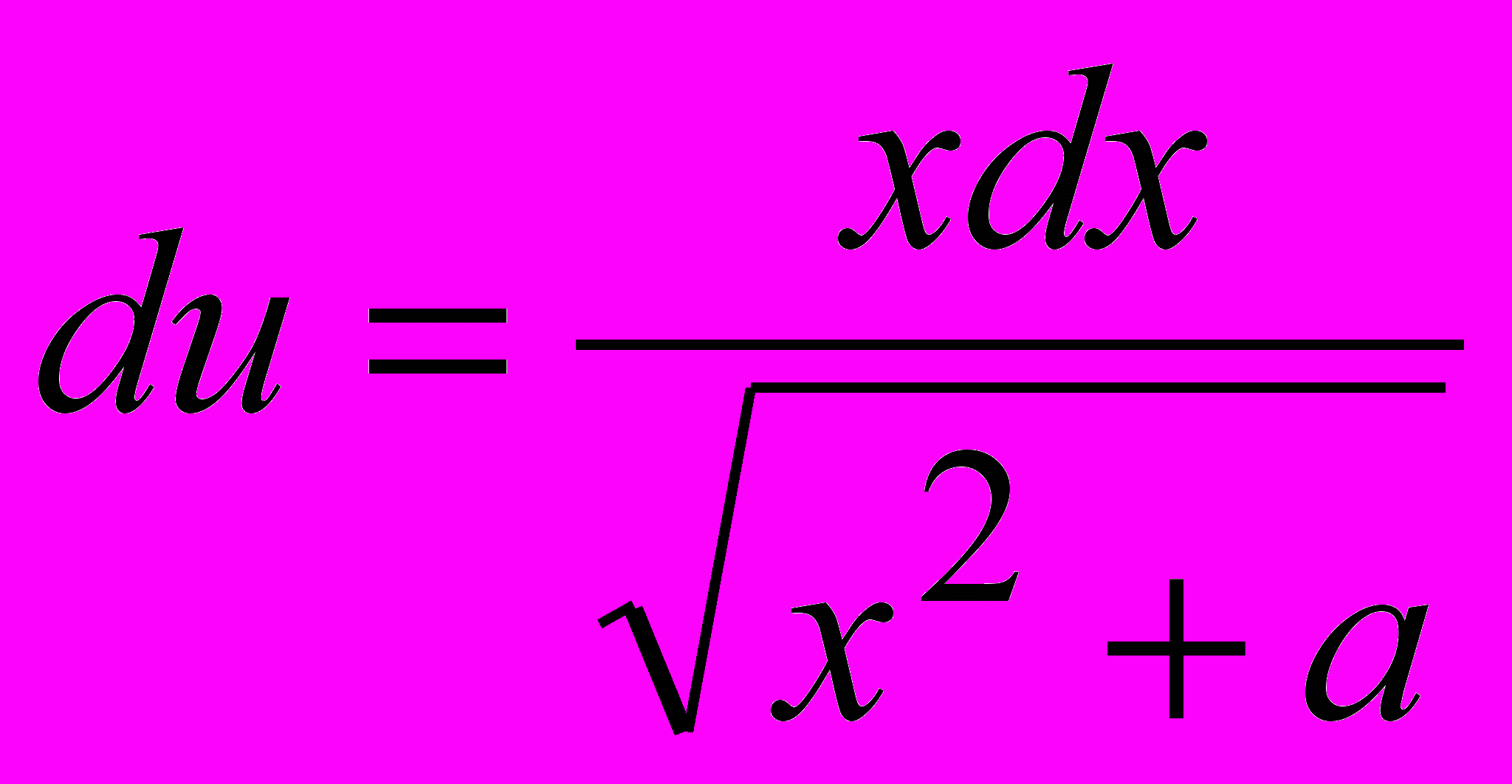
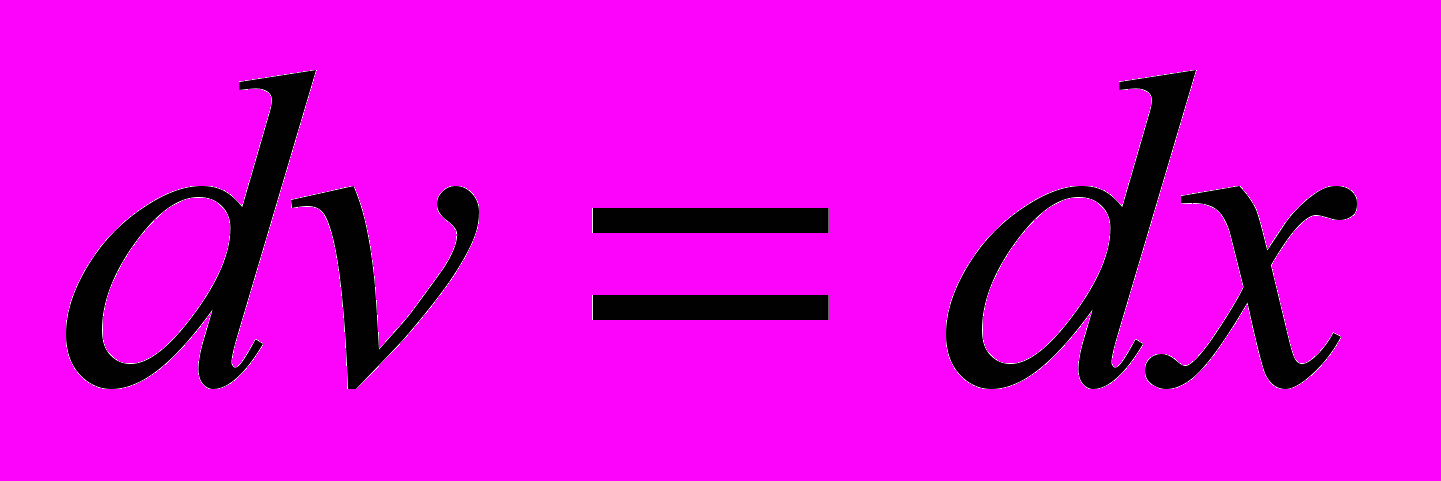
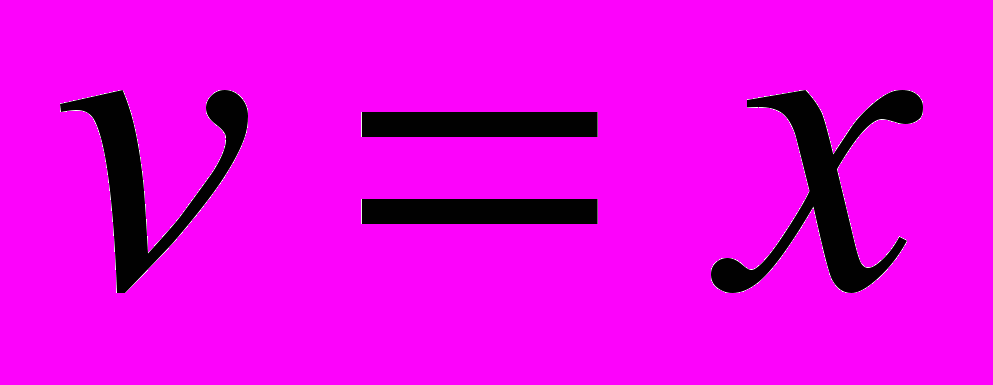
Тогда



.

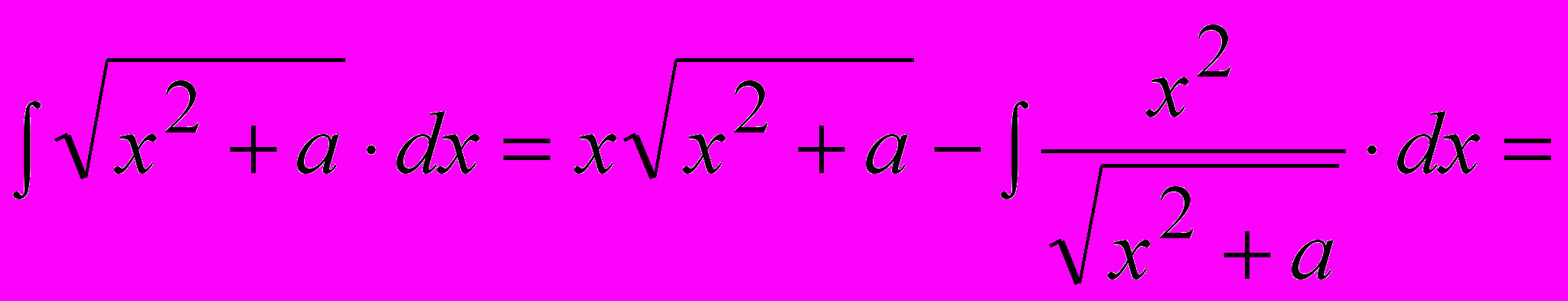
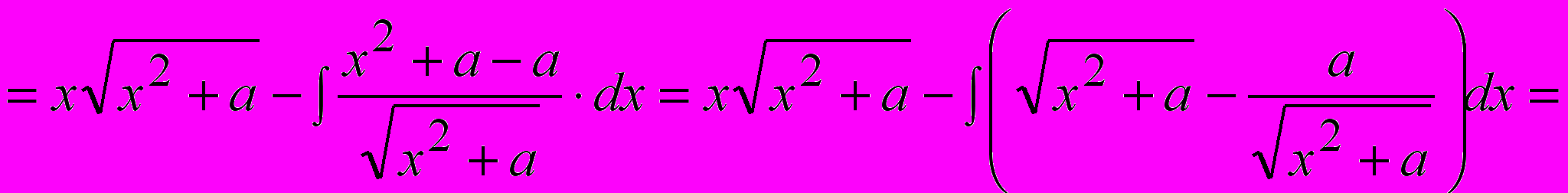
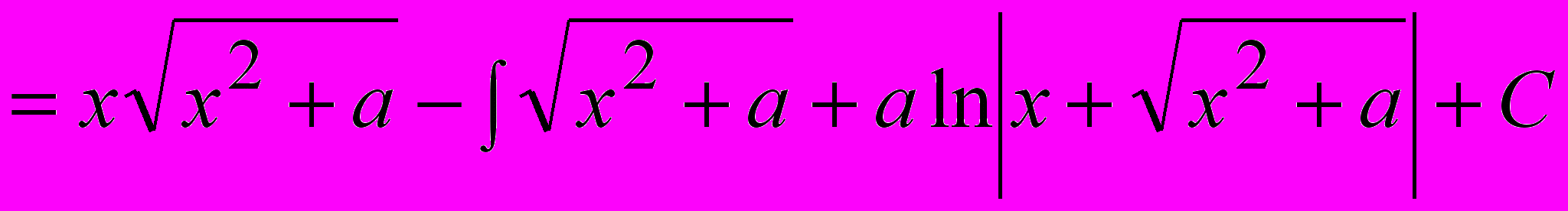В правой части полученного равенства фигурирует искомый интеграл (такие интегралы называются возвратными). Переносим его в левую часть равенства:

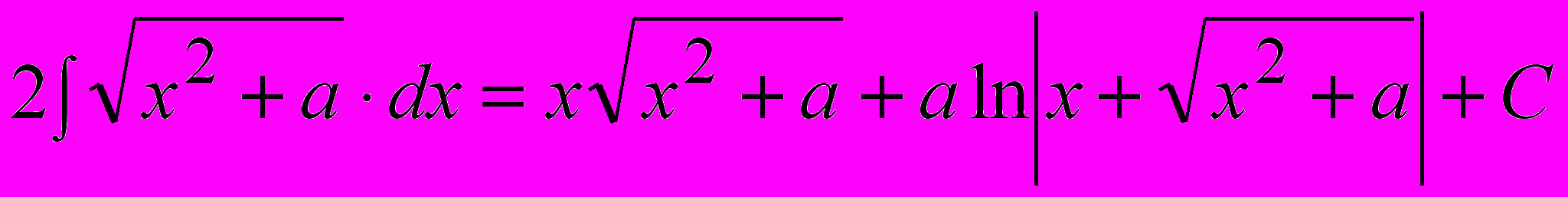, откуда:

.


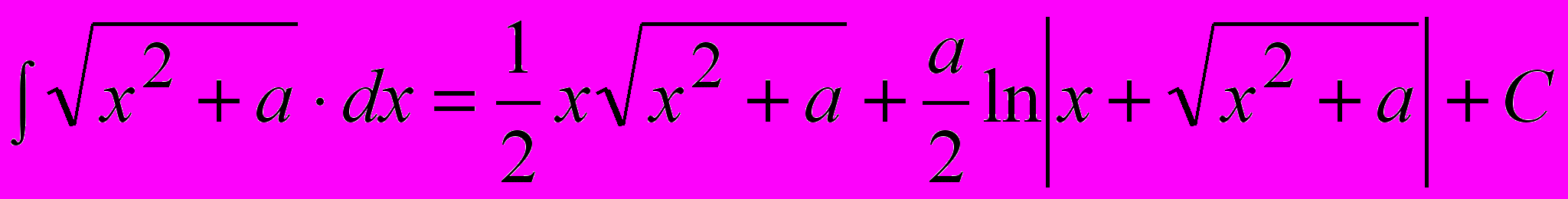Замечание. Также возвратными являются интегралы вида 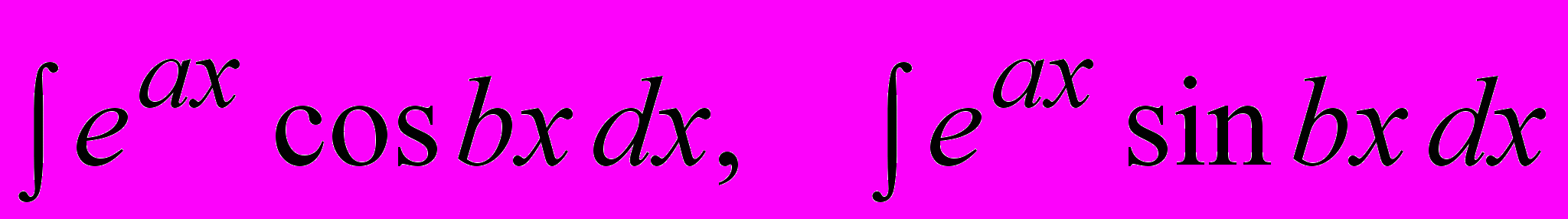. Двукратным последовательным интегрированием по частям они сводятся к первоначальным независимо от разбиения.


Интегрирование выражений, содержащих квадратный трехчлен

Для вычисления неопределенных интегралов вида

,

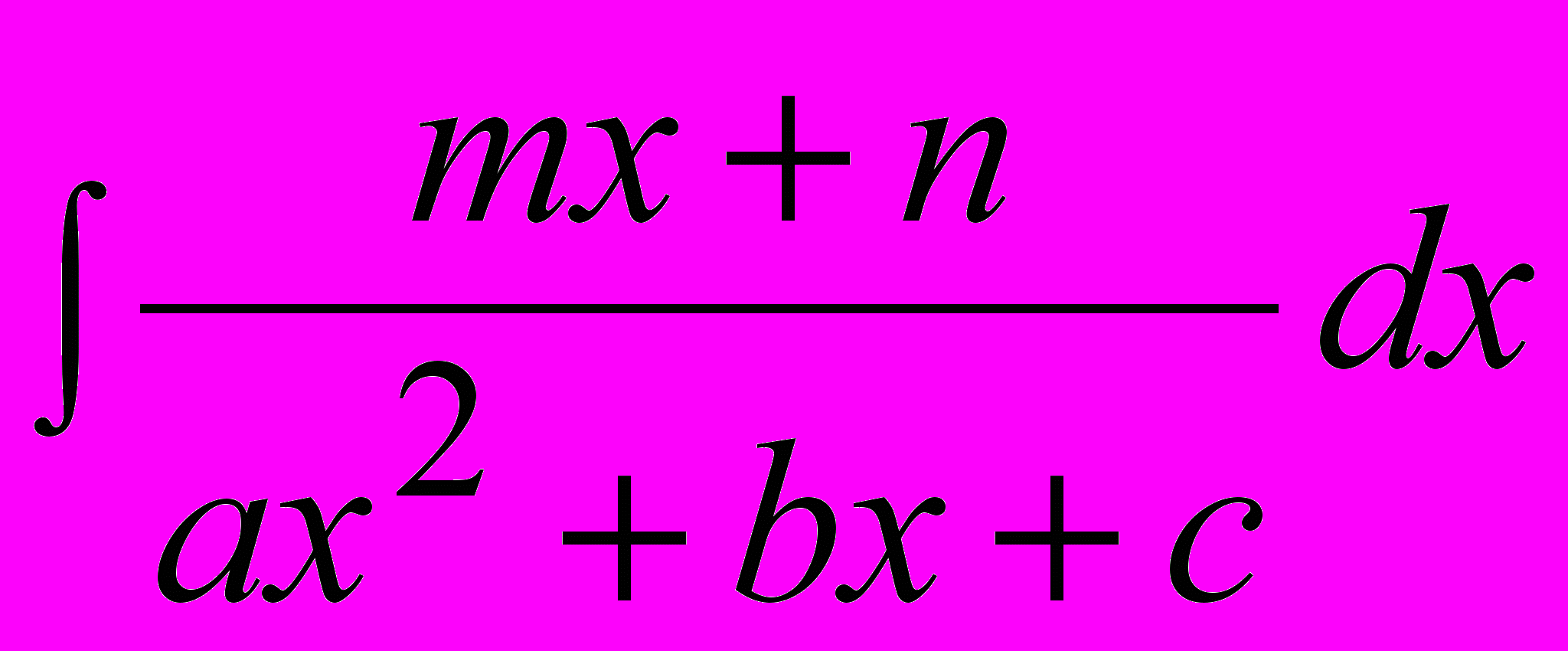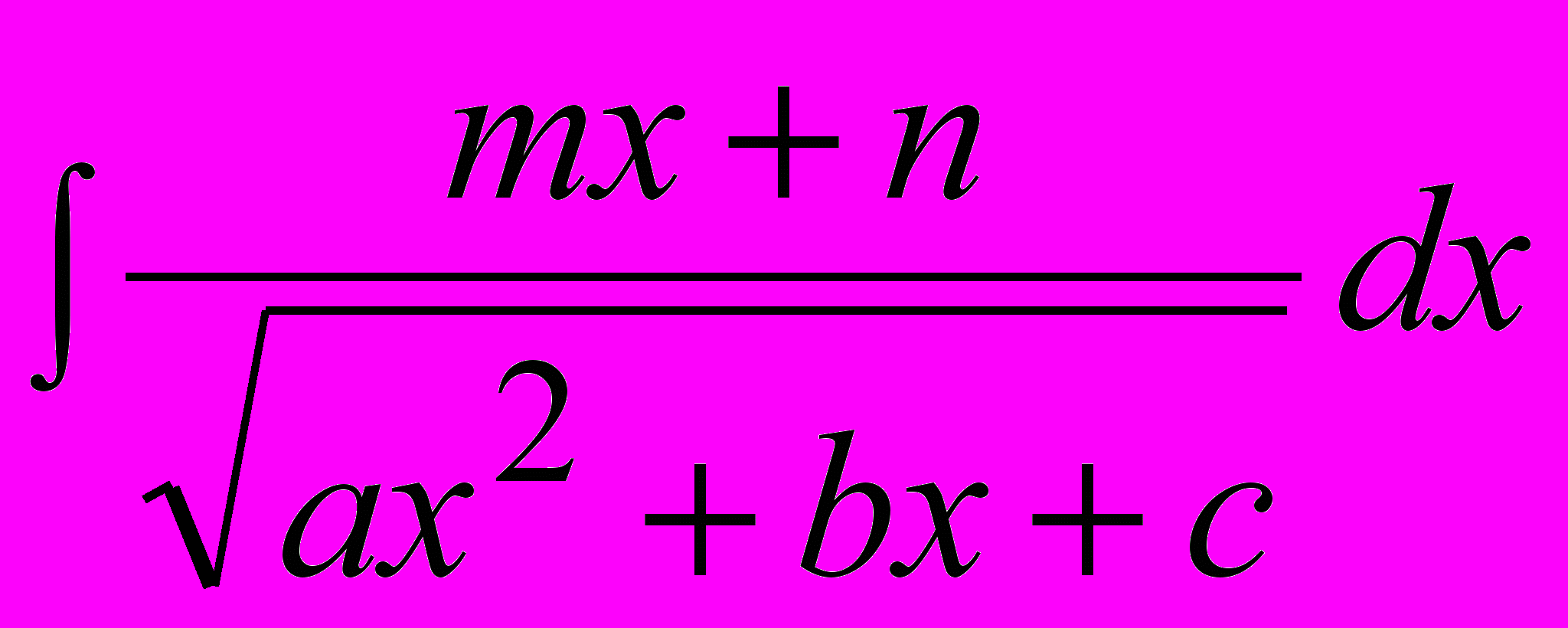
необходимо выполнить следующие действия:

1) выделить из квадратного трехчлена ax2 + bx + c полный квадрат:

;

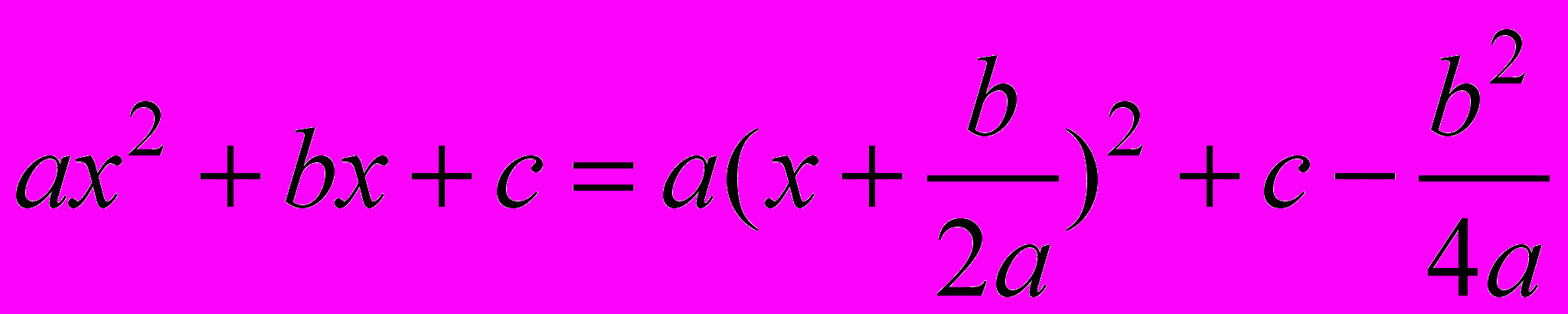2) выполнить в интеграле подстановку .

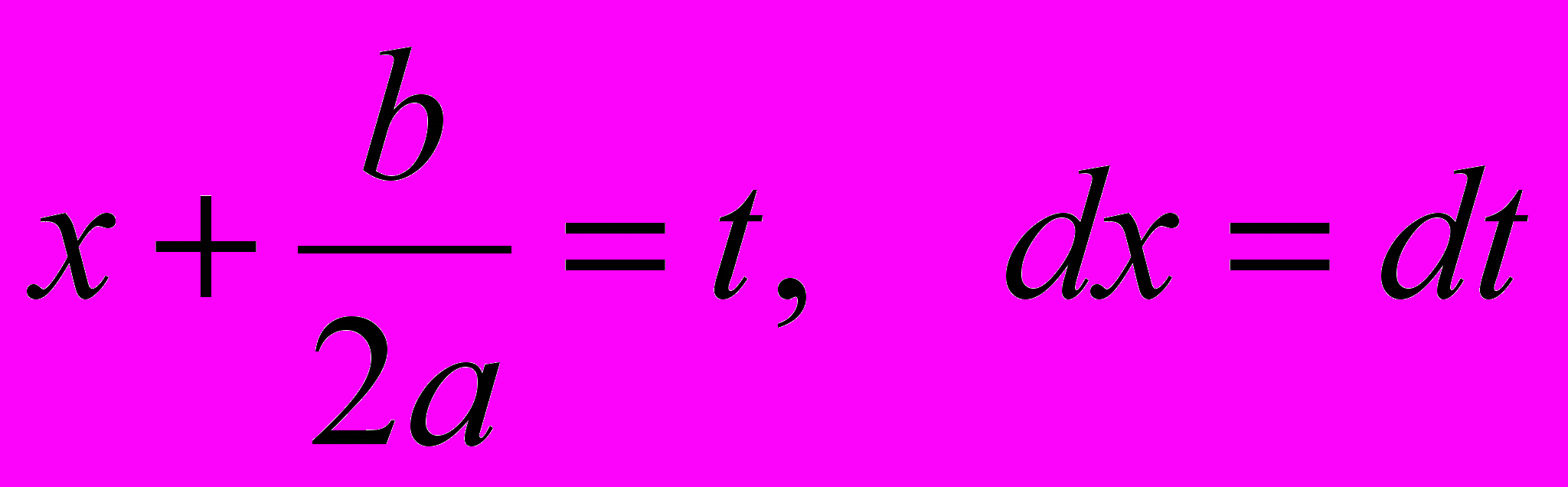3) получившийся интеграл представить в виде суммы двух интегралов, один из которых является табличным, а другой – вычисляется способом внесения переменной t под знак дифференциала: .

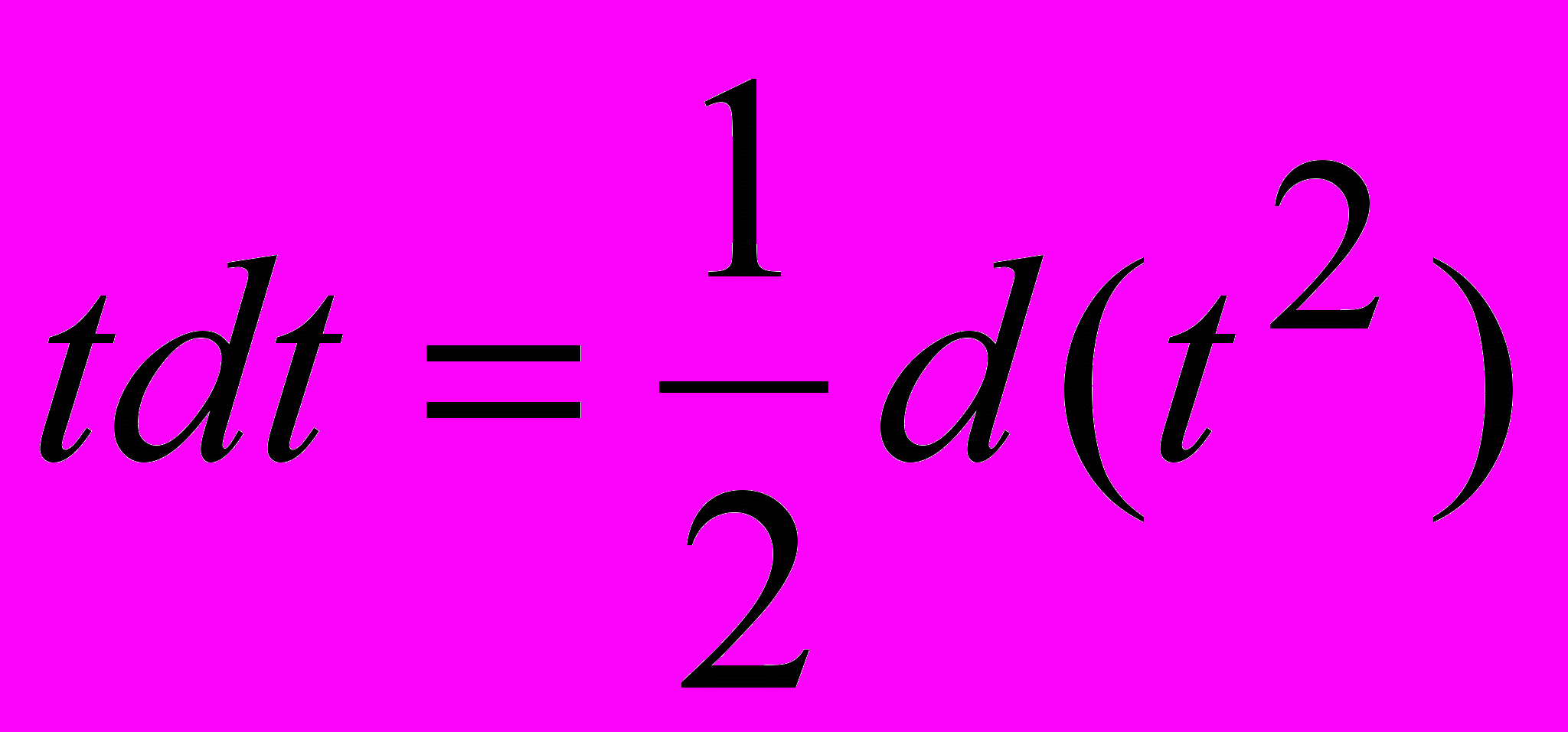Пример 1.





.


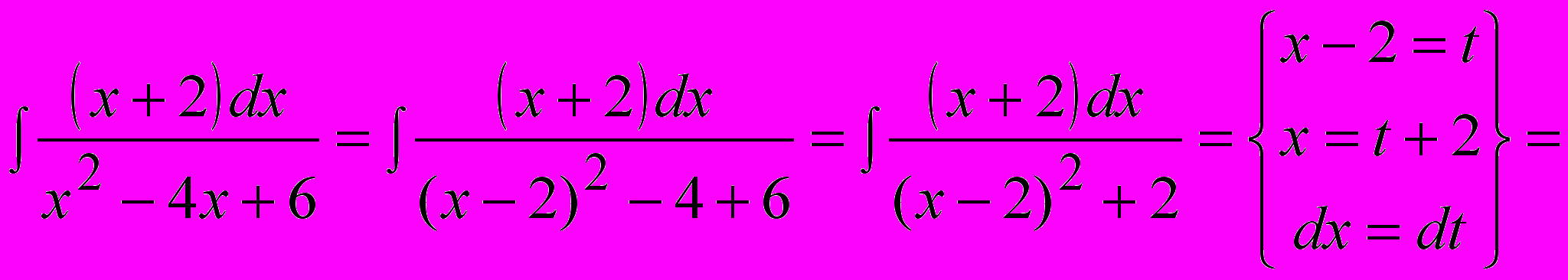
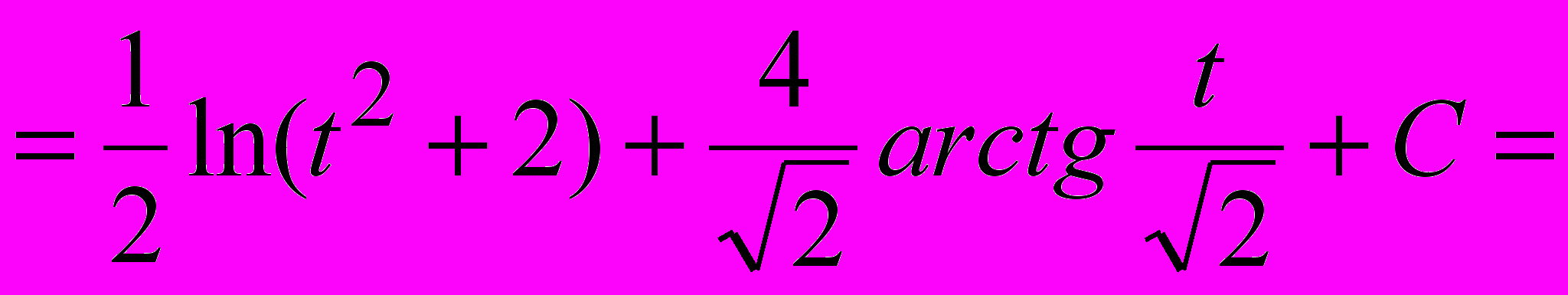
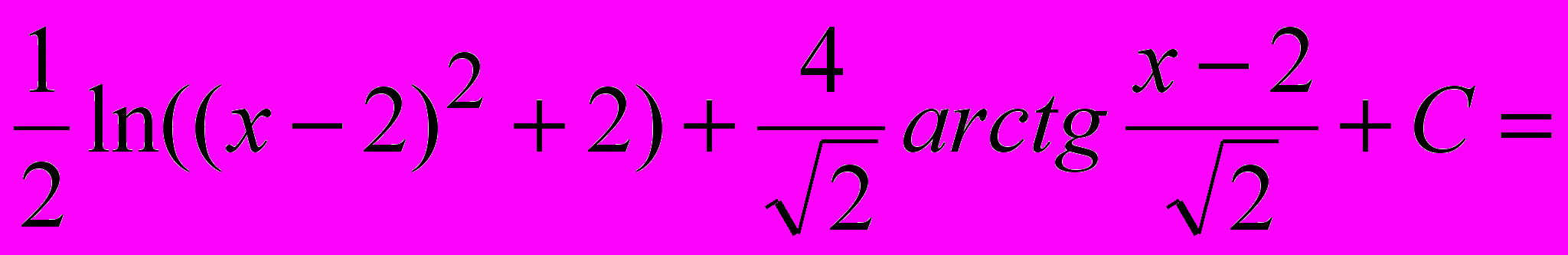
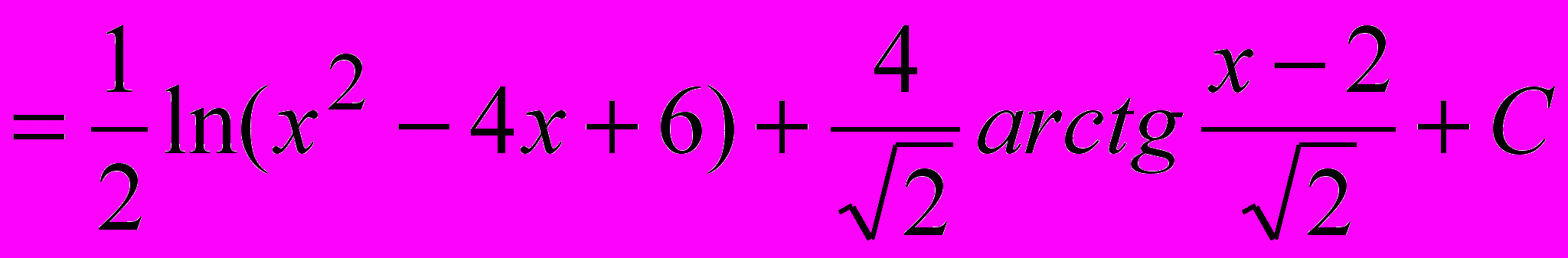Пример 2.



.


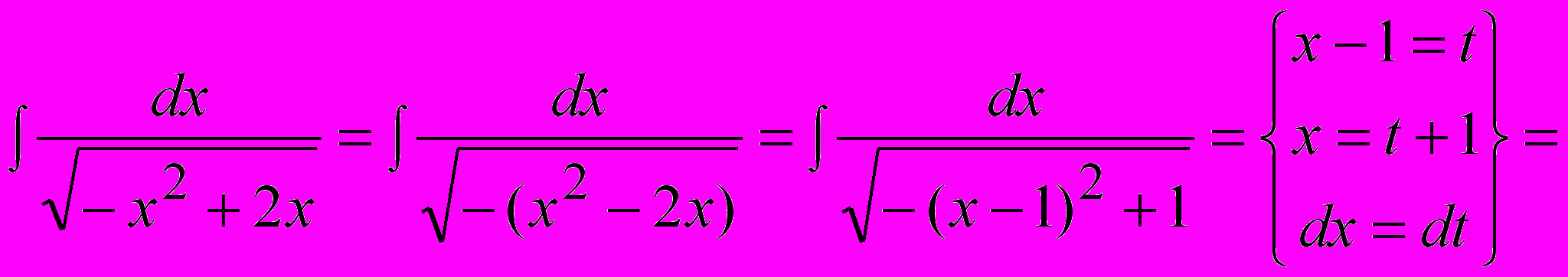
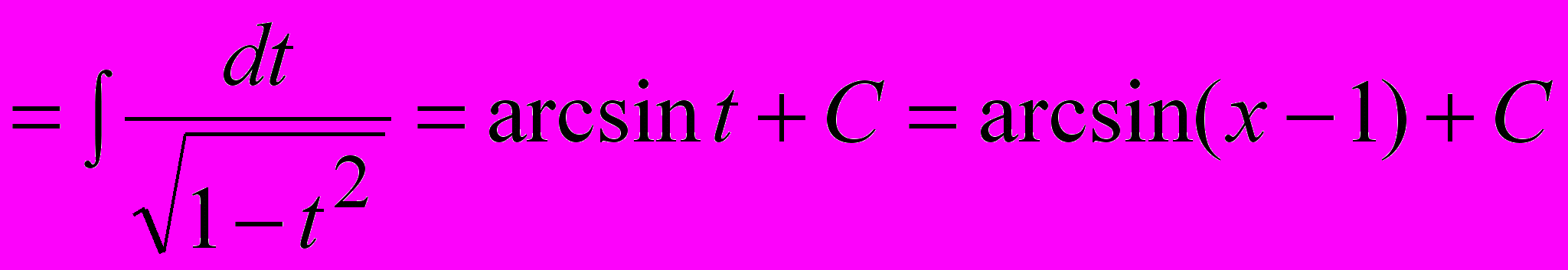Интегрирование рациональных функций


Рациональной функцией называется такая функция, которую можно представить в виде отношения двух многочленов:



Если m, то дробь называется правильной, в противном случае – неправильной.

Заметим, что всякая постоянная величина может рассматриваться как многочлен нулевой степени: С=Сх0, таким образом, многочлены являются также рациональными функциями.

Задача интегрирования многочленов не представляет трудностей, поэтому рассмотрим интегрирование алгебраических дробей (т.е. рациональных функций со степенью знаменателя больше нуля).


Всякую неправильную дробь можно представить в виде суммы многочлена и правильной дроби, разделив числитель на знаменатель:

.

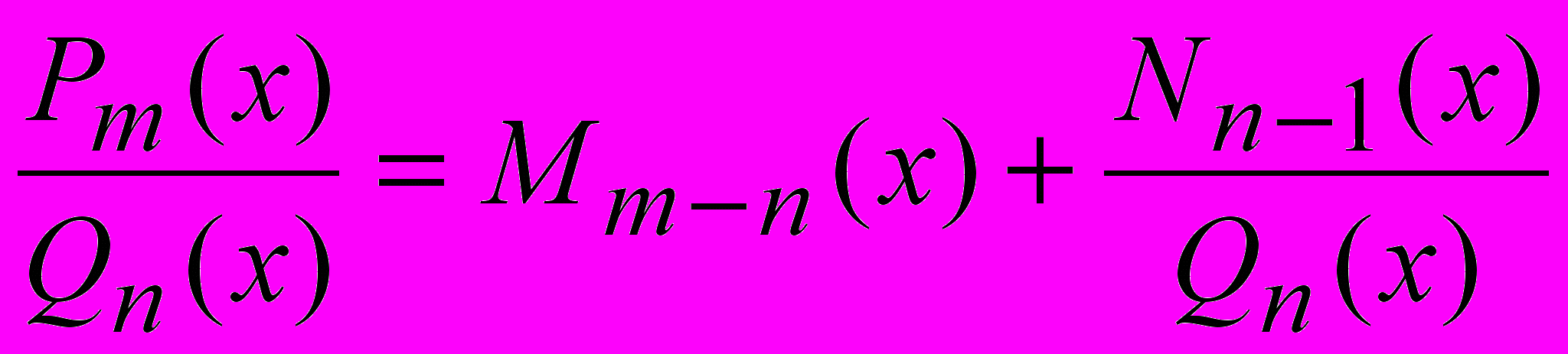  • Правильные рациональные дроби вида:

I. ;

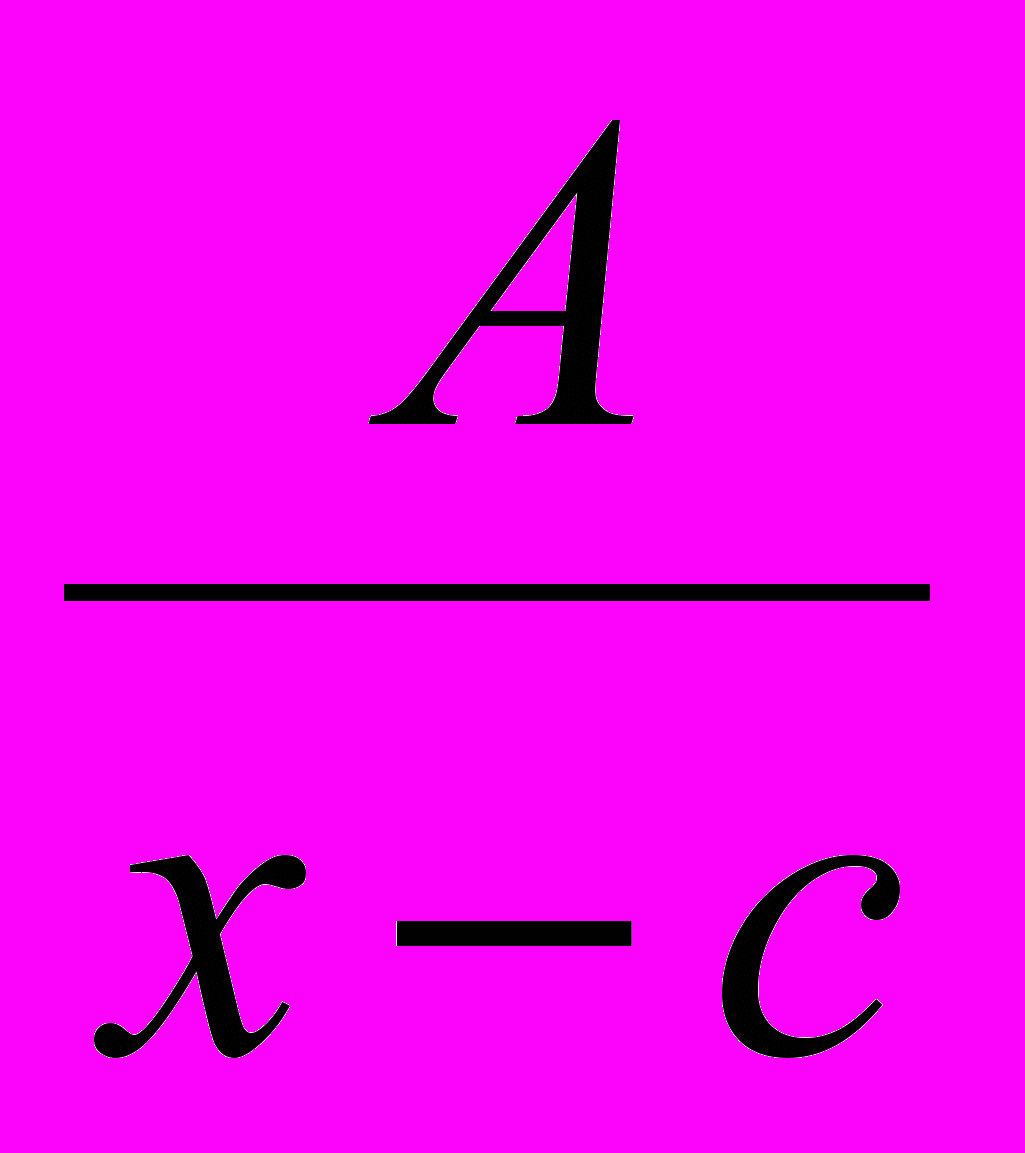II. ;

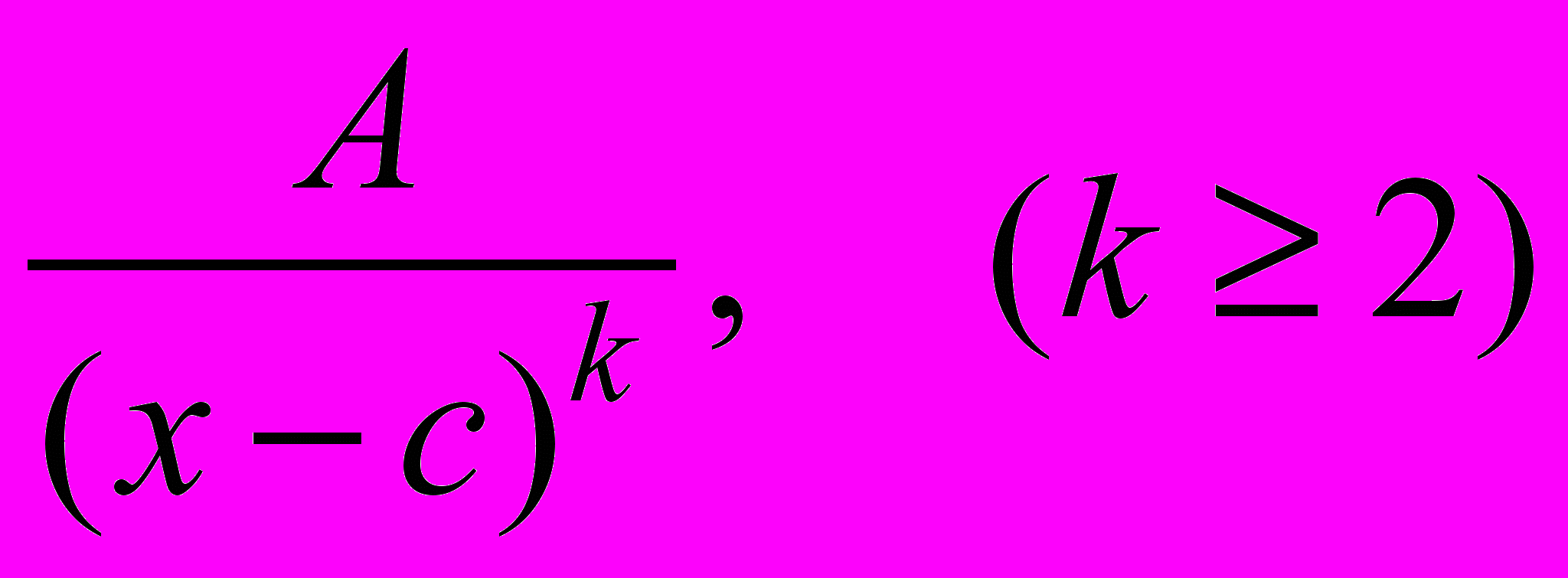III. ;

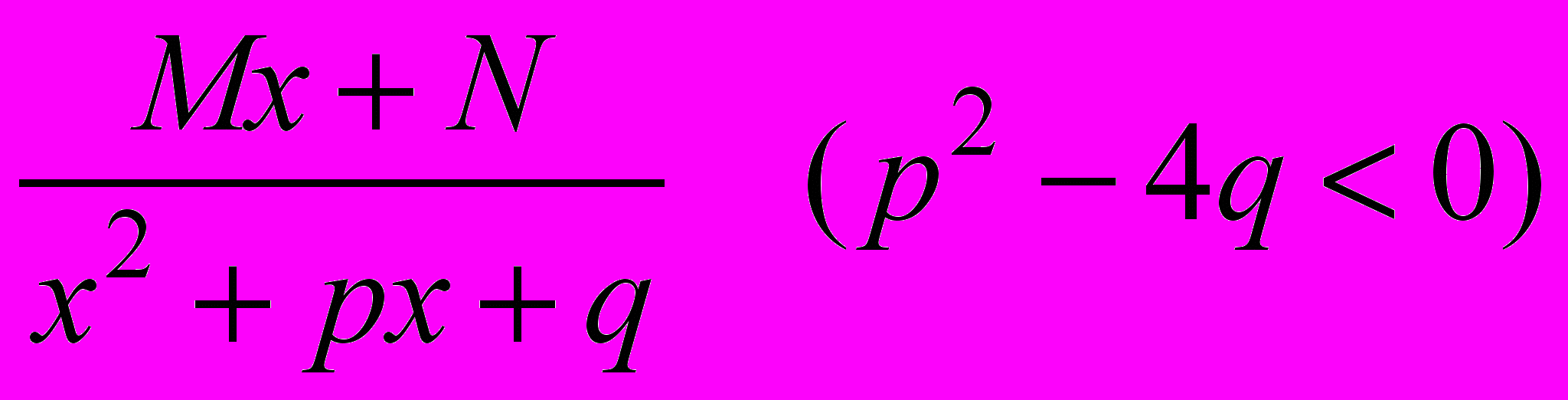IV. ;

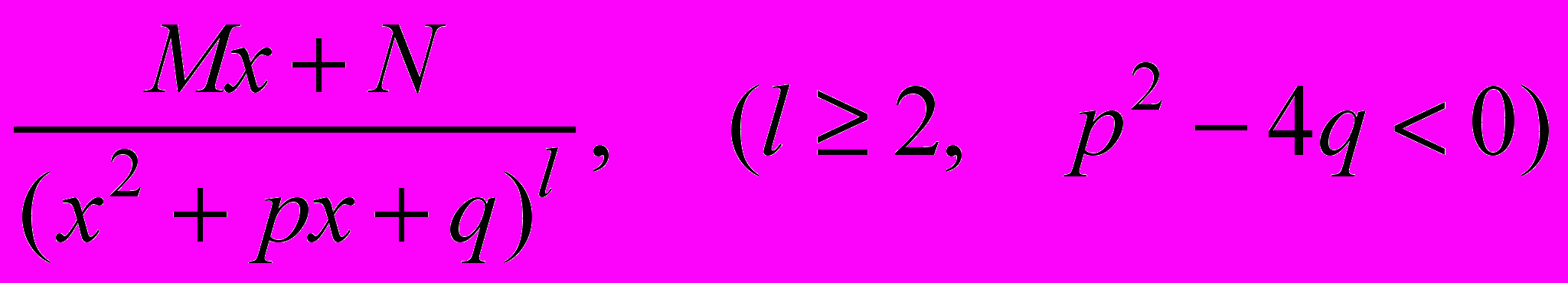где A,c,M,N,p,q – действительные числа, называются простейшими рациональными дробями I, II, III, IV типов.

Теорема. Всякую правильную рациональную дробь 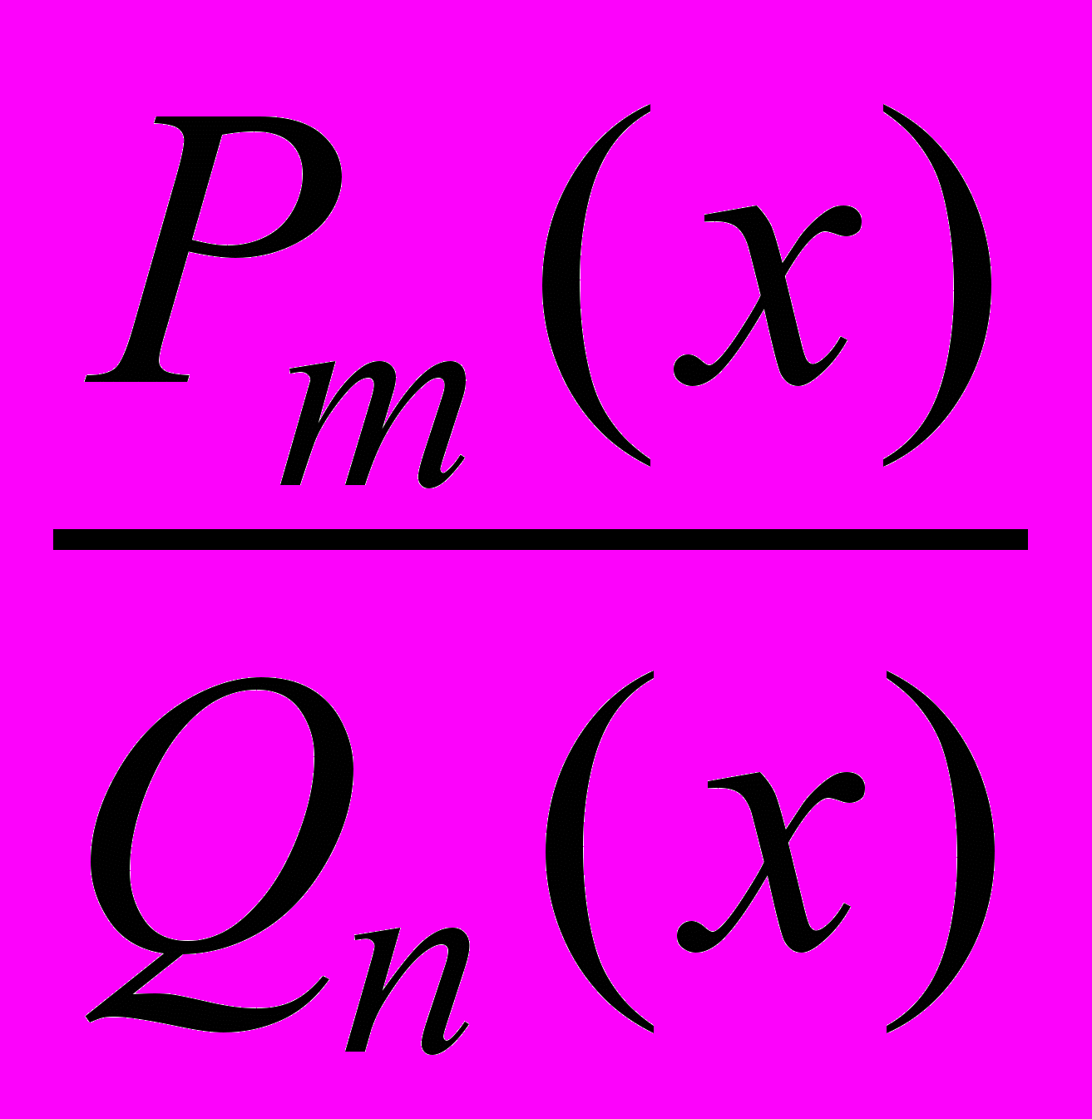, знаменатель которой разложен на множители

,

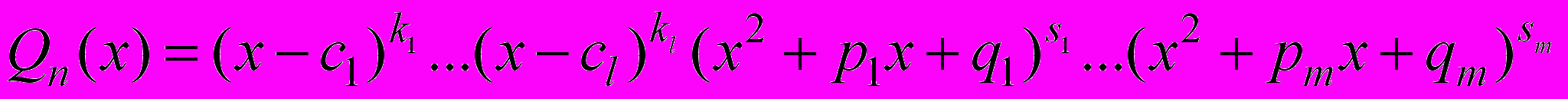можно представить единственным образом в виде суммы простейших дробей:

(*)



.

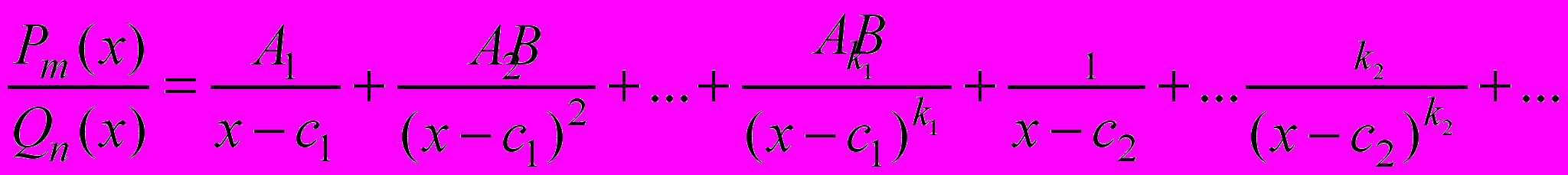
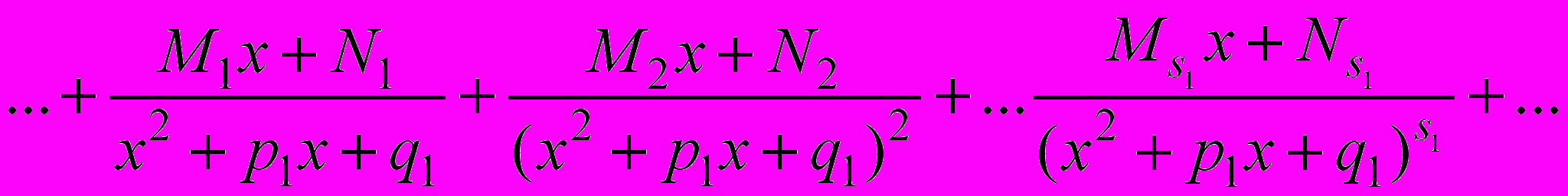
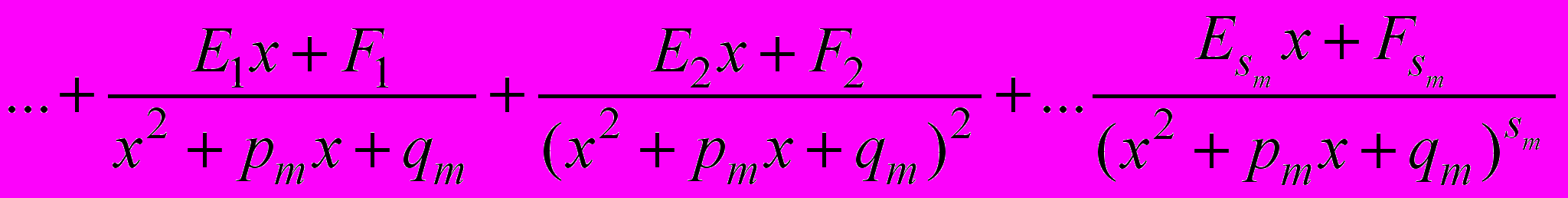где Ai,Bi,…,Mi,Ni,…,Ei,Fi – некоторые действительные коэффициенты.

Для нахождения неопределенных коэффициентов Ai,Bi,…,Mi,Ni,…,Ei,Fi можно применить метод сравнения коэффициентов:
  • В правой части равенства (*) приводят дроби к общему знаменателю Qn(x), в результате получают тождество 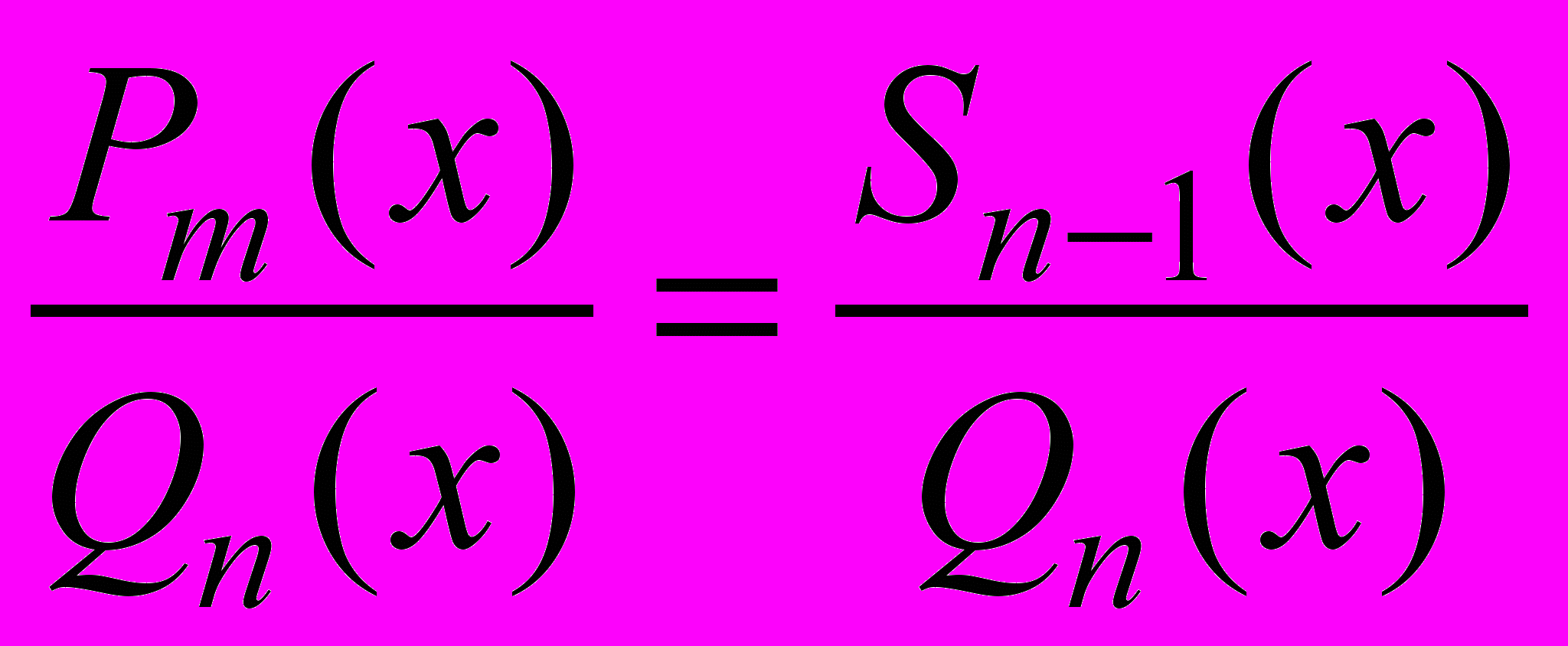, где Sn-1(x) – многочлен с неопределенными коэффициентами.
  • Так как в полученном равенстве знаменатели равны, то равны и числители: .
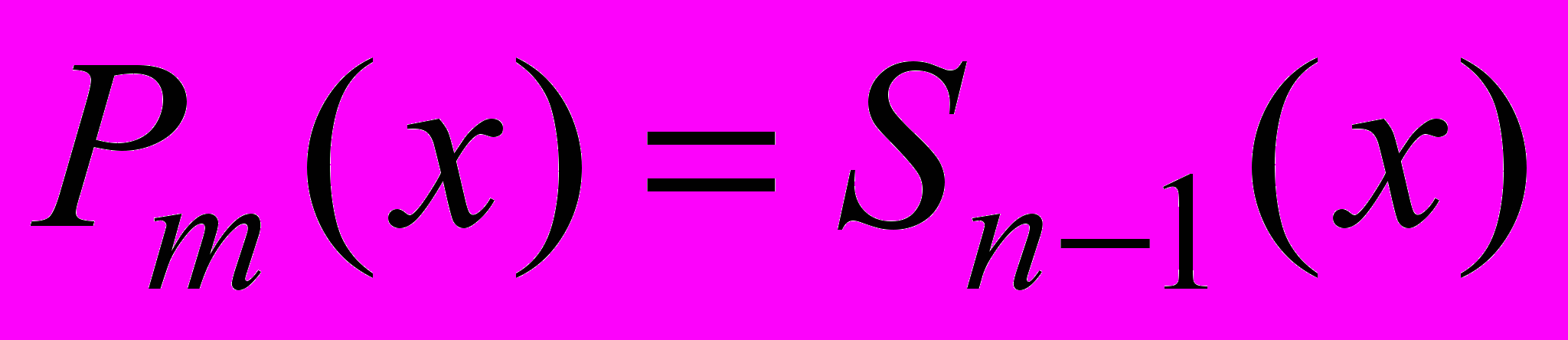  • По теореме о равенстве многочленов приравнивают коэффициенты в обеих частях последнего тождества, получив систему n линейных уравнений, из которой и определяют искомые коэффициенты Ai,Bi,…,Mi,Ni,…,Ei,Fi.

Также для нахождения неопределенных коэффициентов можно применять метод отдельных значений аргумента: в равенстве 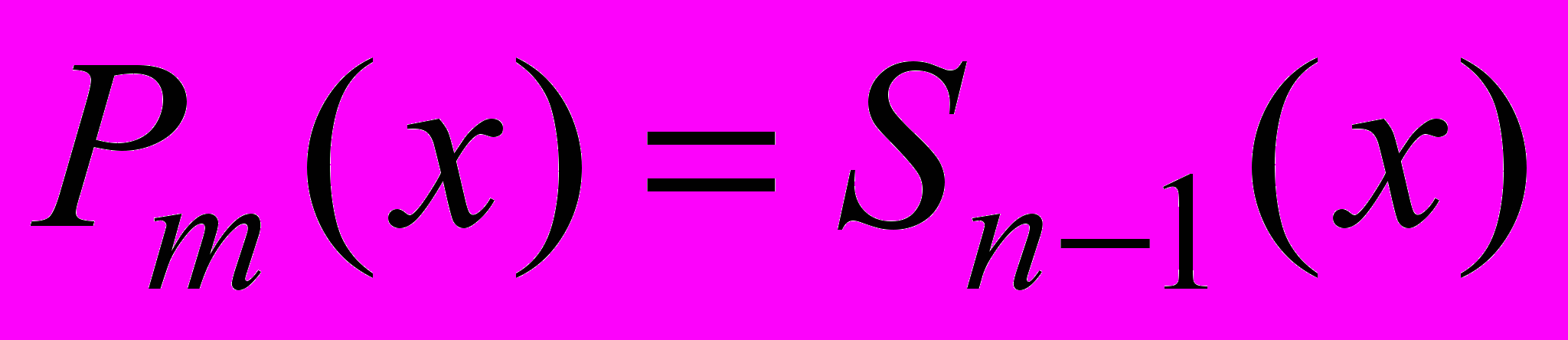аргументу х придают конкретные значения, что превращает это равенство в линейное уравнение относительно искомых коэффициентов. Обычно при этом полагают вместо x значения корней многочлена Qn(x).

Пример 1.

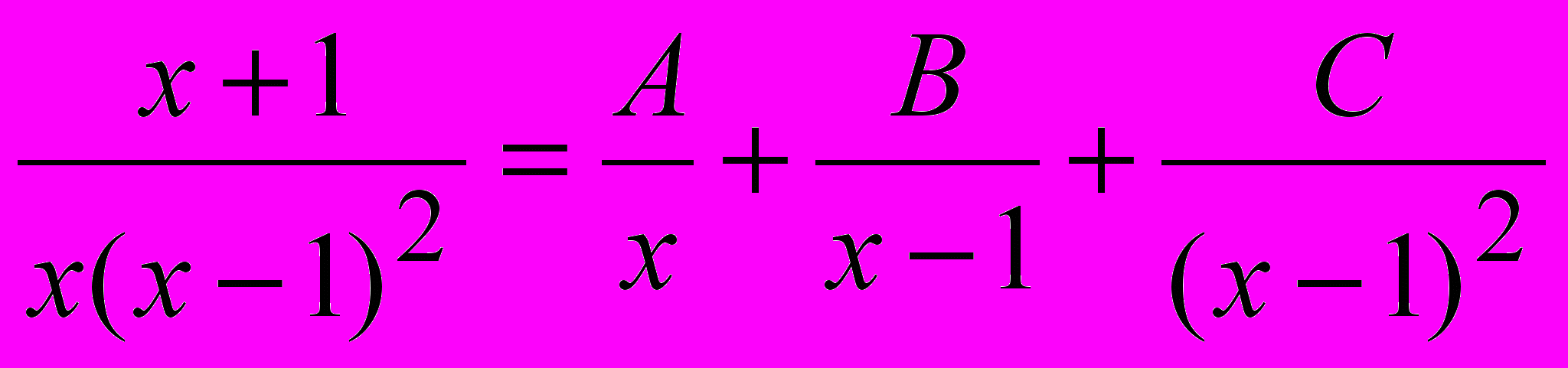
Приравнивая числители, получаем: х+1=А(х-1)2+Вх(х-1)+Сх.

Положим х=0, получим А=1; при подстановке х=1 получим С=2.

Для нахождения В возьмем любое значение, например, х=-1, получим 0=4+2В-2, откуда В=-1. Таким образом, разложение имеет вид: .

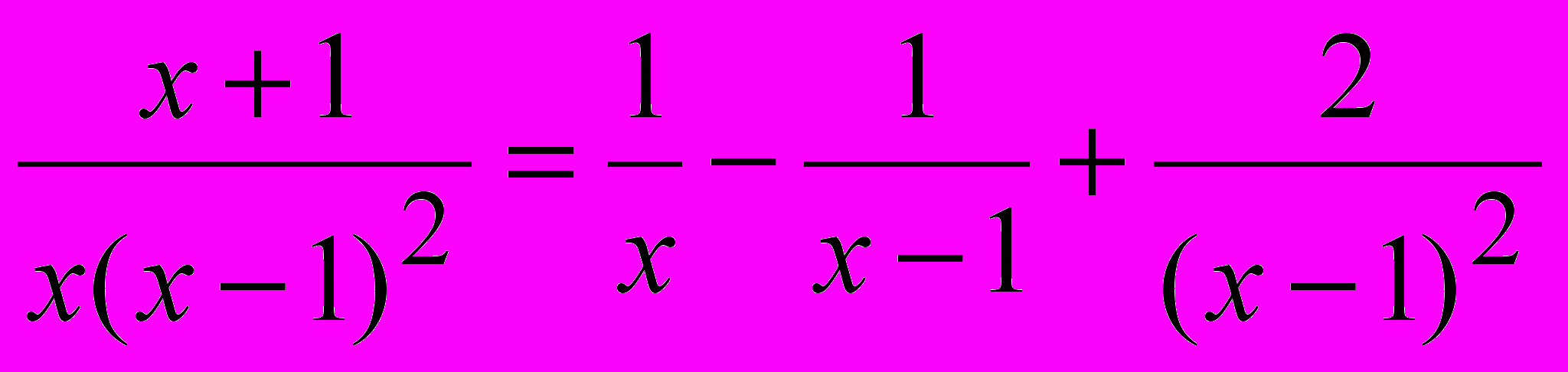Пример 2.



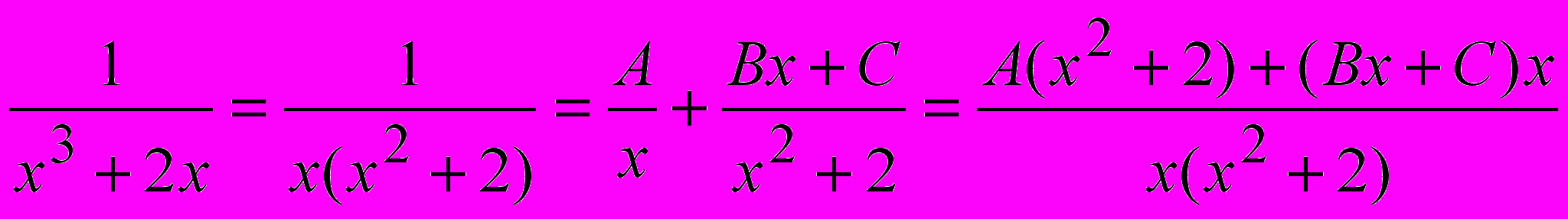
Приравнивая числители и приводя подобные слагаемые в правой части, получаем: 1=х2(А+В)+Сх+2А. Отсюда получаем систему уравнений:



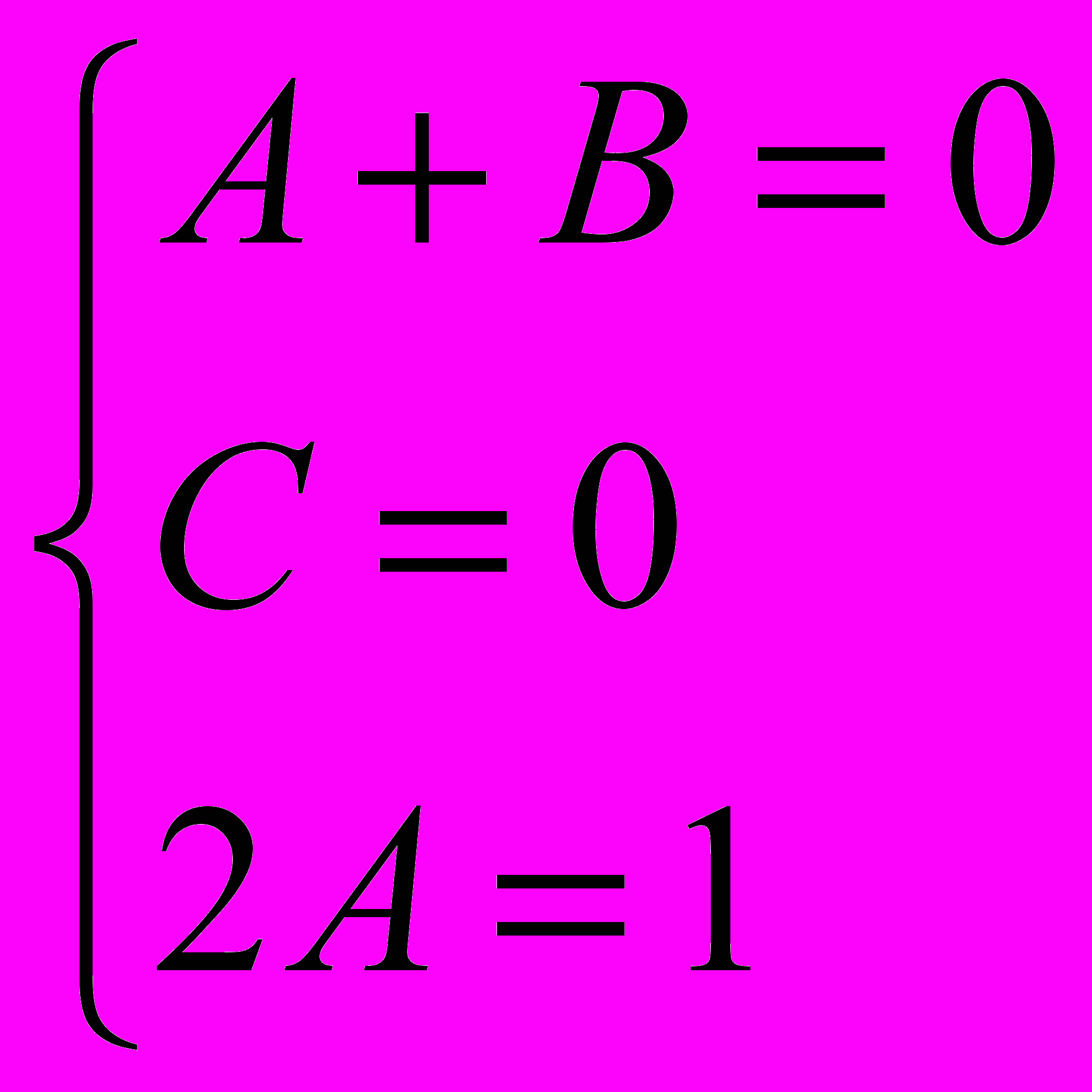
Следовательно, А=1/2, В=-1,2, С=0, и искомое разложение имеет вид: .


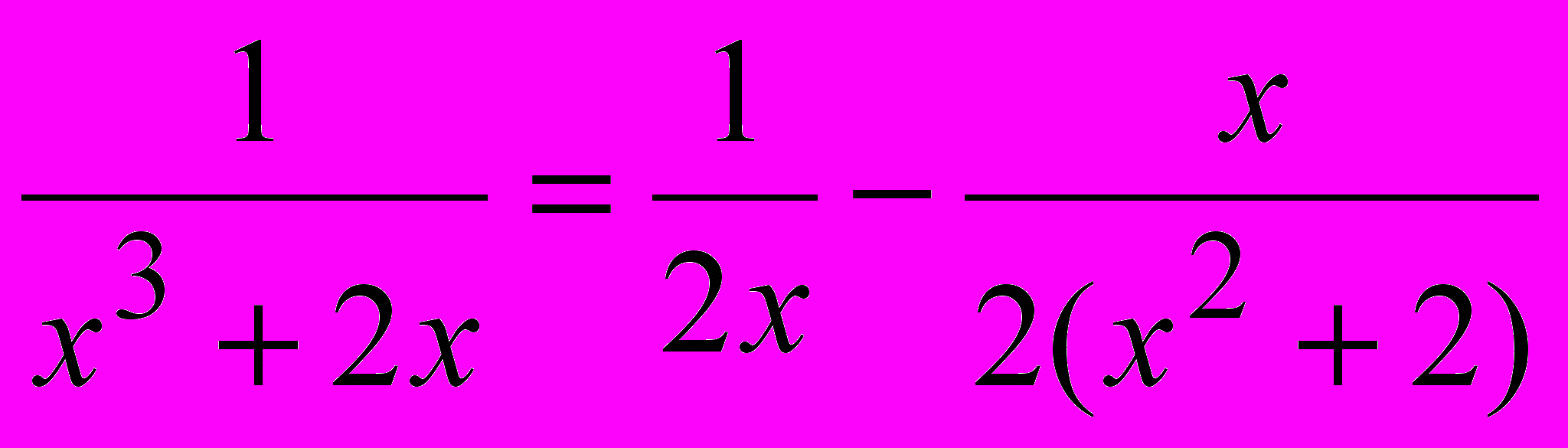Таким образом, для того, чтобы проинтегрировать правильную алгебраическую дробь, следует разложить ее на элементарные дроби и проинтегрировать каждое слагаемое.

I. ;

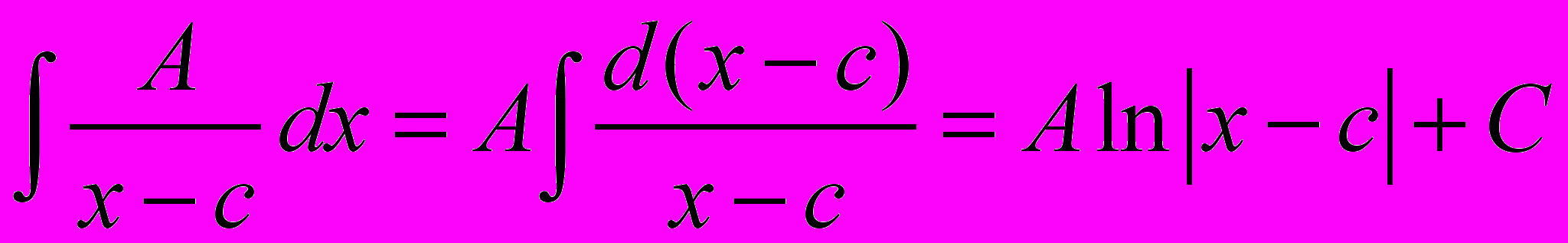II. ;

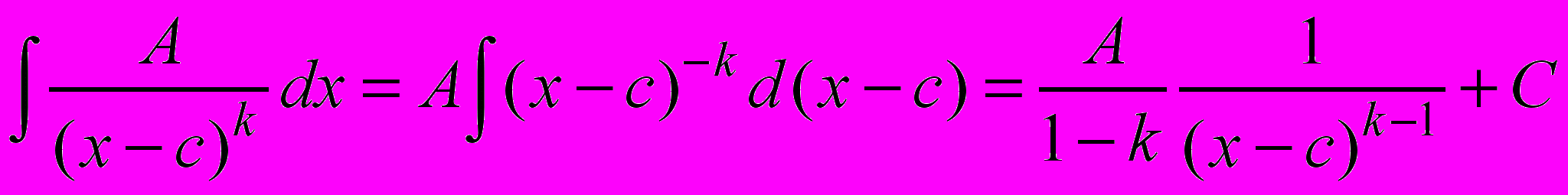III.





;

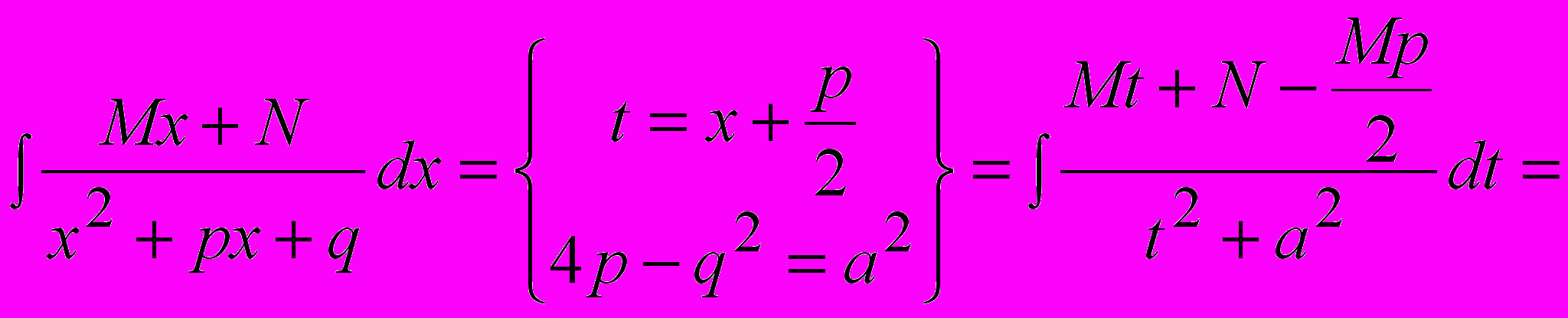
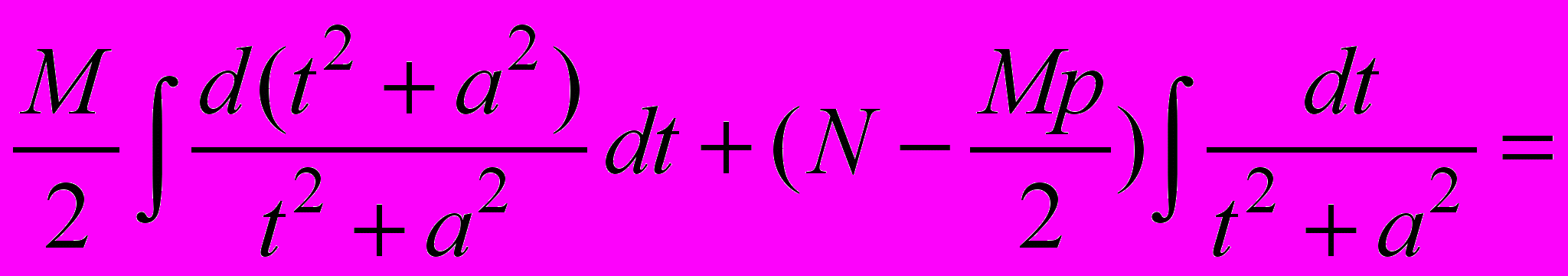
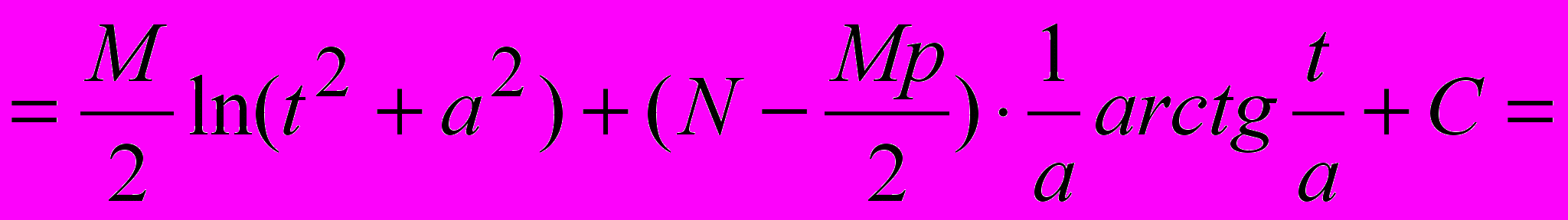
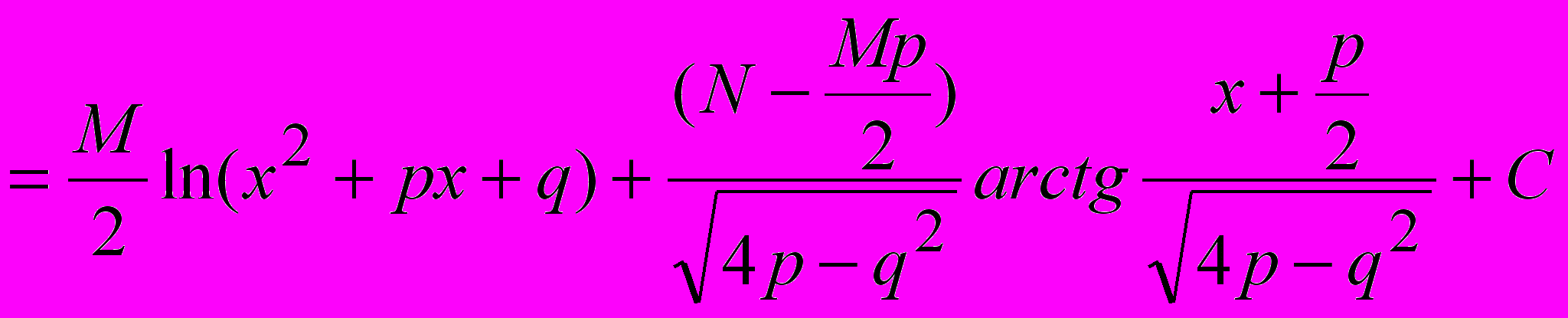IV.



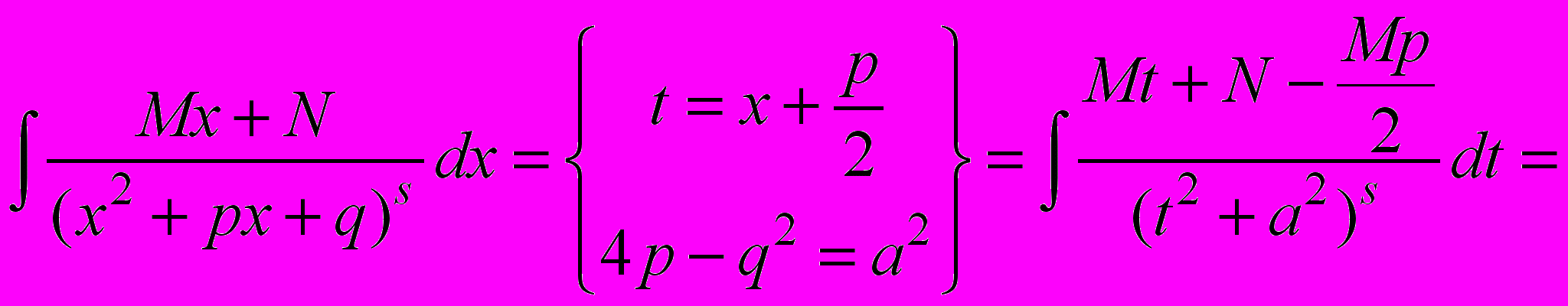
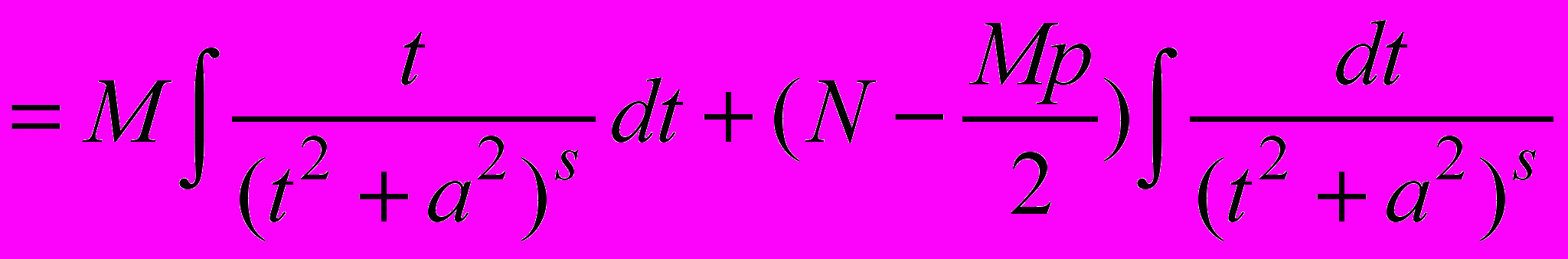
Первый интеграл в сумме вычисляется просто:



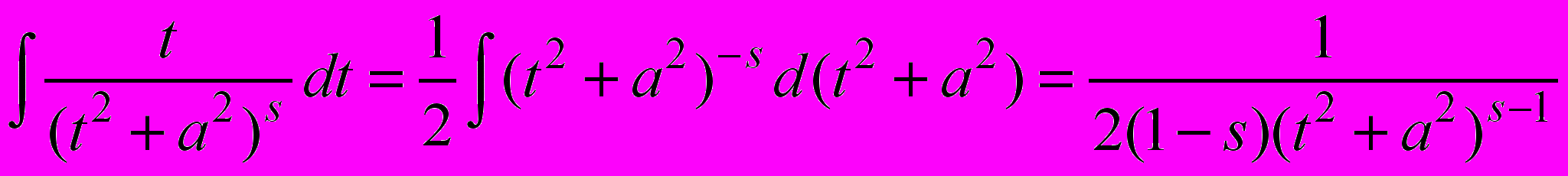
Вычислить второй интеграл позволяет рекуррентная формула. Которую мы запишем без вывода:

.

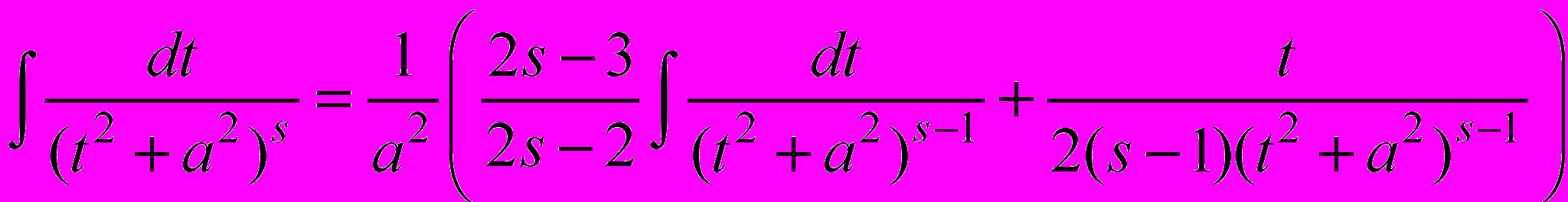В частности,

.


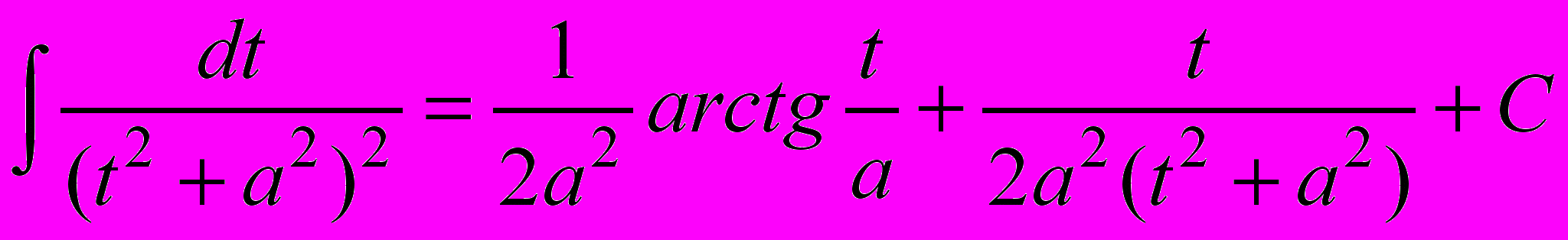Итак, сформулируем общее правило интегрирования рациональных дробей:

1. Если дробь неправильная, то представить ее в виде суммы многочлена и правильной дроби, разделив числитель на знаменатель.

2. Правильную дробь разложить на простейшие рациональные дроби при помощи метода неопределенных коэффициентов.

3. Проинтегрировать полученное разложение.






>