Geum.ru

Доклад на II международной научной конференции «Математика. Образование. Культура» 1-3 ноября 2005 г., Россия, г. Тольятти, тгу

Вид материалаДоклад
Подобный материал:
Доклад на II Международной научной конференции

«Математика. Образование. Культура»

1-3 ноября 2005 г., Россия, г.Тольятти, ТГУ


ОБУЧЕНИЕ ГЕОМЕТРИИ ШКОЛЬНИКОВ С НИЗКИМ СОДЕРЖАТЕЛЬНО-ОПЕРАЦИОННЫМ КОМПОНЕНТОМ


Кильдяева Л.Г.


МОУ «Кульминская средняя общеобразовательная школа»

Россия, 431702, Республика Мордовия, с.Кульмино, ул. Советская, 30

Тел.(83437)26-1-36, факс (83437)26-1-36, e-mail: kulmsh@rambler.ru


In article, written by L.G.KILDYAEVA is spoken about division schoolboy depending on structures of the personalities: her (its) motivations, will and profound-operating component. System of the burn-in exercises is described in article for schoolboy with high motivation or will and low profound-operating component. These exercises promote the assimilation new notion and theorems and achievement schoolboy level obligatory result education.


Существуют несколько десятков критериев, по которым школьники могут быть объединены в группы для осуществления дифференцированного обучения: уровень успеваемости, уровень познавательной самостоятельности, степень действенности интереса к учению (Е.С.Рабунский); обучаемость, учебные умения, обученности, познавательные интересы (И.Унт); успеваемость по предмету, уровень усвоения знаний и умений по предмету (Р.А.Утеева); структура личности (Г.И.Саранцев).

Основаниями образования групп при последнем подходе служат уровни сформированности мотивационного, операционно-действенного и волевого компонентов личности. Состояние личности ученика можно характеризовать объектом <МiСjВk>, где i=1,2; j=1,2,3; k=1,2.

М1- учебная мотивация школьника низкая.

М2- учебная мотивация школьника высокая.

С1- ученик часто неправильно применяет теоремы, допускает существенные неточности при формулировании теорем и определений. Ему трудно выделить главное в учебно-познавательной деятельности и составить план предстоящей работы. Редко прибегает к самоконтролю.

С2- ученик правильно применяет теоремы, не допускает существенных неточностей при формулировании теорем и определений, в изложении допускает небольшие пробелы. Выделяет основное в предстоящей учебно-познавательной деятельности и на этой основе ставит цель. Стремится учесть эту цель при самоконтроле, но не всегда учитывает специфику изучаемого материала.

С3- ученик чётко формулирует определения понятий и теорем, не испытывает затруднений в доказательстве теорем и решении задач. Чётко выделяет главное в учебно-познавательной деятельности и в соответствии с этим ставит её цель и последовательно раскрывает её в задачах. С учётом целей и задач составляет полный план работы. Осуществляет самоконтроль в соответствии с целями и задачами работы.

В1-школьник слабо проявляет волевые усилия по преодолению познавательных затруднений; на занятиях по математике часто расслабляется, не стремится довести решение задачи до конца, отказывается от выполнения при первых же затруднениях, не проявляет систематичности в самостоятельной работе.

В2- школьник характеризуется тем, что проявляет волевые усилия во всех видах учебно-познавательной деятельности; на занятиях по математике работает напряжённо; стремится довести решение задачи до конца, даже если сталкивается с затруднениями.

Остановимся подробнее на группах школьников, имеющих низкий

уровень содержательно-операционного компонента, т.е. характеризующихся объектами: <М1С1В1>, <М1С1В2>, <М2С1В1>, <М2С1В2> . Несмотря на то, что школьники <М2С1В1>, <М2С2В2> имеют высокую учебную мотивацию, а <М1С1В2>, <М2С1В2> прилагают волевые усилия в учебной работе, такие учащиеся из-за низкого содержательно-операционного компонента едва достигают уровня обязательных результатов, часто не справляются с решением даже простейших геометрических задач. Ситуация осложняется ещё учебными условиями, в которых оказываются учащиеся: 1) в учебниках геометрии очень мало заданий на отработку теории; 2) в обучении этап первичного применения знаний минуется очень быстро и слишком поспешный переход к решению со всем классом более сложных задач не позволяет учащимся в полной мере осознать теорию, закрепить первичный навык, а при решении сложных задач в лучшем случае такие школьники бессознательно переписывают решение с доски, и если его мысль не имеет опоры достаточно длительное время, то они просто отключаются от работы.

Школьникам с низким уровнем содержательно-операционного компонента необходимо предлагать больше тренировочных упражнений на отработку изучаемой теории. Они должны полноценно пройти все этапы работы с новым для них понятием или теоремой. Остановимся подробнее на изучении школьных теорем и напомним этапы работы с теоремой: 1) мотивация изучения теоремы, 2) ознакомление с теоремой, 3) усвоение содержания теоремы, 4) запоминание формулировки теоремы, 5) ознакомление со способом доказательства, 6) доказательство теоремы, 7) применение теоремы, 8) установление связей теоремы с теоремами, изученными ранее.

Рассмотрим систему задач и тренировочных упражнений, которую можно предложить школьникам при изучении теоремы о площади параллелограмма.

1 и 2 этапы работы с теоремой объединяем и предлагаем учащимся такие практические задачи.

Задача 1. Имеется проволочный каркас прямоугольной формы размером 4 дм х 2 дм, которому изменили форму до параллелограмма с высотой 1 дм и основанием 4 дм. Изменилась ли площадь фигуры, ограниченной каркасом? Вычислите площадь получившегося параллелограмма.

Задача 2.Паркетный пол сложен из десяти плиток размерами 4дм х 2дм. Изменится ли количество плиток и как, если они будут иметь форму параллелограммов со сторонами 4дм х 2дм и высотой 1дм.

Учащиеся обсуждают решения этих задач, затем учитель задаёт им вопрос: «Как можно вычислить площадь параллелограмма?»

Учащиеся выдвигают гипотезу: чтобы найти площадь параллелограмма нужно основание умножить на высоту, проведённую к этому основанию.

На 3 и 4 этапах решаем задачи на распознавание ситуаций, удовлетворяющих теореме.


1.Верно ли найдена площадь параллелограммов на следующих рисунках:




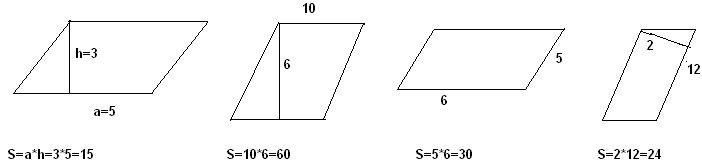
2.Найдите площади параллелограммов, изображённых на рисунках:





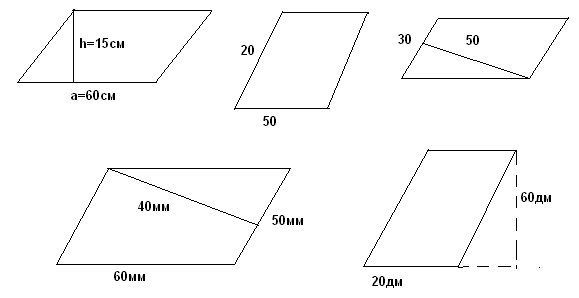
На 5 и 6 этапах знакомимся со способом доказательства и доказательством теоремы о площади параллелограмма, согласно учебнику.

7 этап можно разделить на 2 подэтапа:

а). Первоначальное закрепление теоремы.

б). Непосредственное применение теоремы.

Первоначальное закрепление можно организовать при выполнении таких практических заданий:

1.Предложить школьникам модели параллелограммов различной формы (эти модели учащиеся могут подготовить сами при изучении темы определение параллелограмма и его свойства), площади которых надо вычислить.

2.Нарисуйте в тетрадях параллелограммы, выполните необходимые измерения и вычислите площади фигур двумя способами.

Когда учащиеся усвоят теорему, запомнят её формулировку можно перейти к решению задач на применение, используя упражнения учебника геометрии.

8 этап. Установление связей можно осуществить при обобщении изученного материала предложив учащимся: 1) составить «родословную» доказательства теоремы; 2) сгруппировать теоремы по приёмам доказательства; 3) придумать схемы, связывающие теоремы изучаемой главы. Например, такие:

S прямоугольника→S параллелограмма→ S треугольника→ S трапеции

или такие:



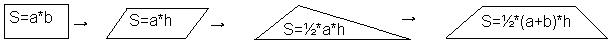
Такое поэтапное ознакомление с новым фактом позволяет школьникам с низким содержательно-операционным компонентом усвоить содержание теоремы, запомнить её формулировку и при необходимости применить теорему к решению задач в стандартных и несколько изменённых ситуациях.