Рабочая программа для аспирантов по специальности Экономическая теория

Вид материала

Рабочая программа

Содержание Далее определим издержки фирмы на производство 2400 игрушек издержки MC 3 ед. продукции в месяц, продаваемые по цене 70 240 ден. ед. Следовательно, экономическая прибыль фирмы, проводящей ценовую дискриминацию, составит 56 МС известна, она равна 20 Q в функцию спроса определяем Р 5. Рынки ресурсов 450 тыс. руб. фирме целесообразно приобрести станок, так как 493,3 > 450,0. 60 тыс. руб., есть альтернатива: окончить годичный курс обучения стоимостью 30 N второй сомножитель несущественен. Так, если работник предполагает работать 40 60 тыс. руб.) и платы за обучение 30

Подобный материал:

• Рабочая программа по дисциплине «система государственного управления», 182.78kb.
• Рабочая программа по дисциплине экономическая теория I для студентов специальности, 329.19kb.
• Рабочая программа Подготовки аспирантов Научная специальность 08. 00. 01 Экономическая, 129.91kb.
• Рабочая программа Подготовки аспирантов Научная специальность 08. 00. 01 Экономическая, 126.16kb.
• Рабочая программа Подготовки аспирантов Научная специальность 08. 00. 01 Экономическая, 165.24kb.
• Учебная программа для специальности: 1-31 03 06 Экономическая кибернетика (код специальности), 177.23kb.
• Учебная программа для специальности: 1-31 03 06 Экономическая кибернетика (код специальности), 187.17kb.
• Программа курса «Экономическая теория» для поступающих в аспирантуру по специальности, 349.1kb.
• Программа учебной дисциплины «Экономическая теория» для специальности 050501. 18 Профессиональное, 497.85kb.
• Программа спецкурса " Стратегия устойчивого развития национальной экономики " для специальности, 50.04kb.

Далее определим издержки фирмы на производство 2400 игрушек

ТС₂₄₀₀ = АТС₂₄₀₀  2400

АТС₂₄₀₀ = АVC₂₄₀₀ + AFC₂₄₀₀

AFC₂₄₀₀ = =

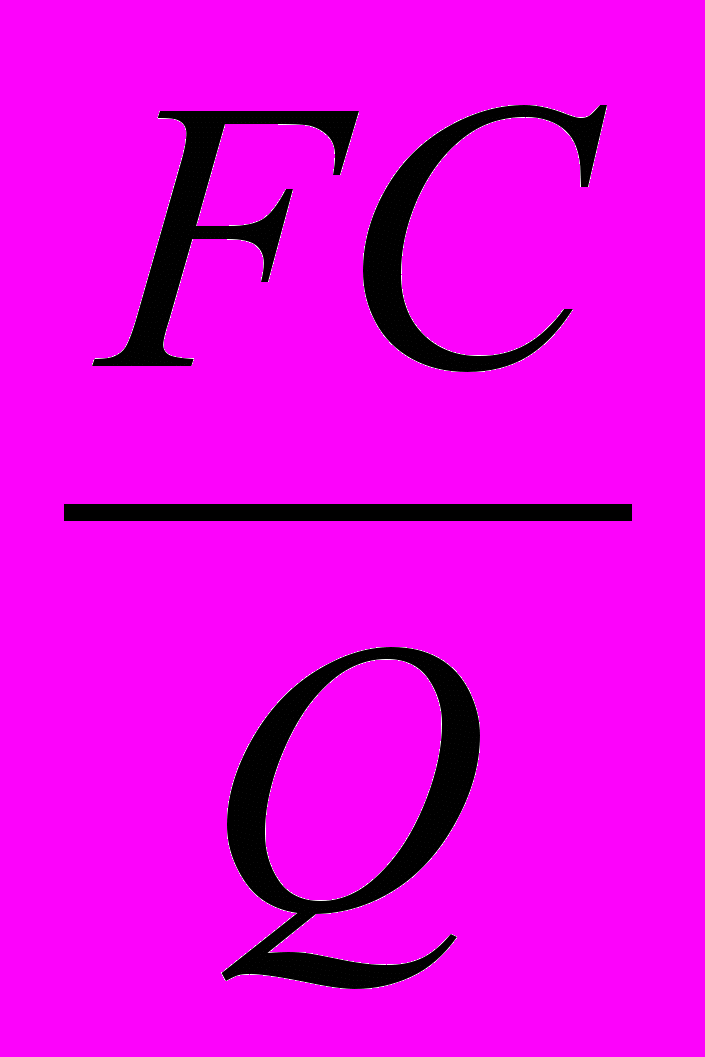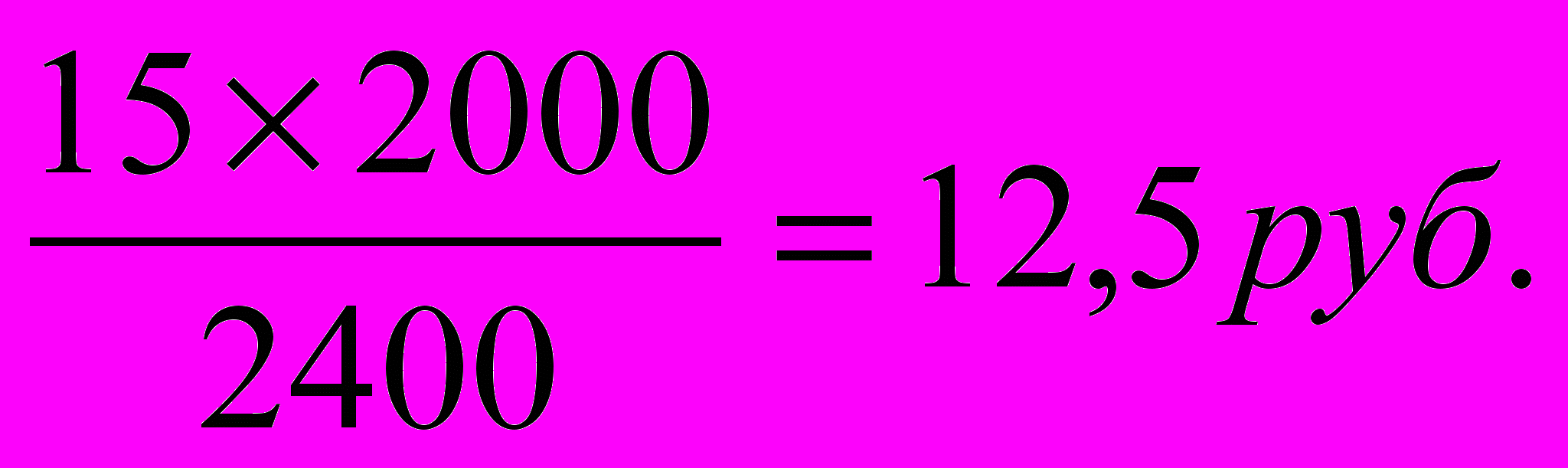
Известно, что АVC₂₀₀₀ = AVC₂₄₀₀, поэтому AVC₂₄₀₀ = 40 – 15 = 25 руб. Следовательно, АТС₂₄₀₀ = 25 + 12,5 = 37,5 руб., а ТС₂₄₀₀ = 37,5  2400 = 90 000 руб.

Отсюда следует, что

П₂₄₀₀ = ТR₂₄₀₀ – TC₂₄₀₀ = 114 000 – 90 000 = 24 000 руб.

Таким образом, при продаже 2000 игрушек на внутреннем рынке и 400 – на внешнем, фирма получит дополнительно 4000 (24 000 – 20 000) руб. прибыли, поэтому ей целесообразно расширить производство.


Задача 6. Используя графики, необходимо ответить на следующие вопросы:

а) в какой точке появляется убывающая отдача?

б) какие кривые и куда сдвинутся, если:

• повысится налог на имущество фирмы;
  
• повысятся тарифы на электроэнергию;
  
• повысится номинальная заработная плата рабочих.
  

в) чему равны VC производства 20 ед. изделий

г) если при выпуске 10 изделий АFC составят 12,5 руб., то каковы AVC при выпуске 25 изделий?

(Ответ: а) в точке А (при Q = 8 ед.); б) 1) АТС сдвинется вверх; 2-3) все три кривые сдвинутся вверх; в) VC = 160 руб.; г) АVC при выпуске 25 изделий равны 15 руб.

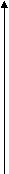
издержки MC

D АТС

30

C АVC

20


B

8 A

·

0 Q

8 20 25 28


3. Фирма в условиях совершенной конкуренции

Задача 1. В краткосрочном периоде фирма-конкурент, максимизирующая прибыль, прекратит производство, если окажется, что:

а) цена меньше минимальных АТС; б) общий доход меньше общих издержек; в) цена меньше минимальных АVC; г) общий доход меньше VC.

Правильный ответ -в


Задача 2. Фирма на рынке совершенной конкуренции получает максимальную прибыль если…….

МС = Р; AVC = MC; ATC = MC; ATC = P; AFC = P; MC < MR; MR > MC.

Правильный ответ - 1


Задача 3. Функция общих издержек фирмы имеет вид ТС = 35Q + Q² . Реализуя продукцию на совершенно конкурентном рынке по цене 155 рублей, она получит прибыль, равную:

3600 рублей; 3750 рублей; 3550 рублей; 3500 рублей.

Правильный ответ - 3600


Задача 4. Кривая предложения конкурентной фирмы в краткосрочном периоде – это:

4. а) линия цены товара; б) часть кривой АТС, лежащей выше АТС_min; в) часть кривой МС, лежащей выше АVC_min; г) часть кривой АVC, лежащей выше АVC_min.
   

Правильный ответ - в


4. Поведение фирмы на рынках несовершенной конкуренции


Задача 1. Объем спроса, цена на товар, общие издержки фирмы-монополиста в течение месяца и предельные издержки первой единицы продукции представлены в табл.

Таблица 1




Объем спроса (D), шт. 1 2 3 4 5

Цена (Р), ден. ед. 84 76 70 68 64

Общие издержки (ТС), ден. ед. 80 120 176 240 400

Предельные издержки (МС), ден. ед. 60 … … … …


Необходимо определить:

а) объем производства и цену, максимизирующие прибыль. Какова величина максимальной прибыли?;

б) как изменится валовой доход фирмы, в случае проведения ею совершенной ценовой дискриминации по сравнению с ситуацией отсутствия ценовой дискриминации?;

в) как изменится выпуск фирмы при проведении ею совершенной ценовой дискриминации?


Решение задачи:

а) определение цены и объема производства, при которых прибыль монополиста максимальна, осуществляем на основе условия равновесия фирмы-монополиста: МС = MR < P. Информация об этих величинах представлена в табл. 2.


Таблица 2




Q, шт. 1 2 3 4 5

Р, ден. ед. 84 76 70 66 62

ТС, ден. ед. 80 120 176 240 400

МС (ТС/Q), ден. ед. 60 40 56 64 160

АТС (ТС / Q), ден. ед. 80 60 58,7 60 80

TR (P × Q), ден. ед. 84 152 210 264 310

MR (TR/Q), ден. ед. 84 68 58 54 46

Прибыль экономическ. (+)

или убыток ( - ), ден. ед + 4 + 32 + 34 + 24 - 90


Объем производства, при котором прибыль максимальна, составит 3 ед. продукции в месяц, продаваемые по цене 70 ден. ед. Максимальная прибыль при этом составит 34 ден. ед. ( ТR ₃ – TC ₃ = 210 – 176 );

б) в случае проведения ценовой дискриминации общий доход фирмы увеличится по сравнению с ее отсутствием, так как при ценовой дискриминации будут покупатели, желающие приобрести первую ед. продукции по цене 84 ден. ед., вторую ед. по цене 76 ден. ед. и третью ед. покупатель купит по цене 70 ден. ед.. Общий доход при этом составит: TR ₁ = 84 + 76 + 70 = 230 ден. ед.

При отсутствии ценовой дискриминации все три единицы продукции фирма продает по цене, максимизирующей прибыль, 70 ден. ед. Общий доход фирмы при этом составит TR ₂ = 70 × 3 = 210 ден. ед.

Различие в общем доходе фирмы в случае проведения ценовой дискриминации и при отсутствии дискриминации составляет:

TR = TR ₁ – TR ₂ = 230 – 210 = 20 ден. ед.;

в) объем выпуска фирмы при проведении ценовой дискриминации также увеличится. Если при проведении ценовой дискриминации фирма понижает цену, то по этой цене продается только дополнительная единица продукции, а не вся предшествующая продукция вместе с дополнительной единицей. В этом случае цена и предельный доход для любой проданной дополнительной единицы равны. И пока для дополнительно продаваемых единиц продукции будет соблюдаться условие Р = MR > MC фирма, имея цель получить максимум прибыли, будет наращивать выпуск.

Поэтому рассматриваемая фирма, проводя ценовую дискриминацию, сочтет необходимым произвести и продать четвертую единицу продукции, так как при этом Р = MR > MC или 66 > 64. Дополнительный доход от продажи четвертой единицы продукции составит 66 ден. ед., а общий доход фирмы от продажи четырех единиц при проведении ценовой дискриминации составит:

TR = 84 + 76 + 70 + 66 = 296 = ден. ед.


В то же время общие издержки для четырех единиц продукции равны 240 ден. ед. Следовательно, экономическая прибыль фирмы, проводящей ценовую дискриминацию, составит 56 ден. ед., тогда как при отсутствии ценовой дискриминации экономическая прибыль фирмы составила бы лишь 34 ден. ед.


Задача 2. Функция общих затрат фирмы-монополиста ТС = 30 + 20Q.

Функция спроса на продукцию монополиста на двух рынках: Р₁ = 40 – 2Q₁; Р₂ = 80 – 10Q₂.

Необходимо определить:

а) равновесные объемы продаж и цены на каждом из двух рынков, прибыль монополии;

б) максимальную прибыль, если ценовая дискриминация не проводится.


Решение задачи:


а) Условием, обеспечивающим максимум прибыли монополиста, проводящего ценовую дискриминацию 3-ей степени, является равенство предельного дохода на каждом рынке предельным затратам на суммарный выпуск продукции:

MR₁ (Q₁) = MR₂ (Q₂) = MC (Q₁ + Q₂)


Исходя из этого условия, определяем функции предельных доходов на каждом рынке и величину предельных издержек.

=



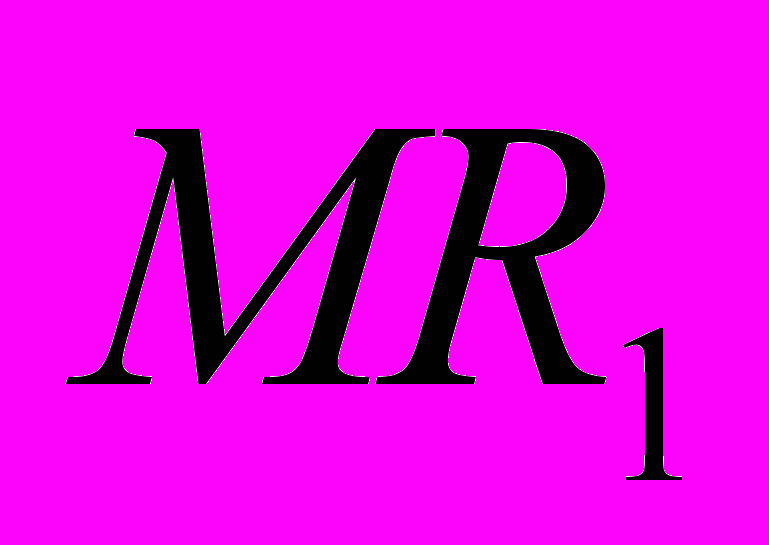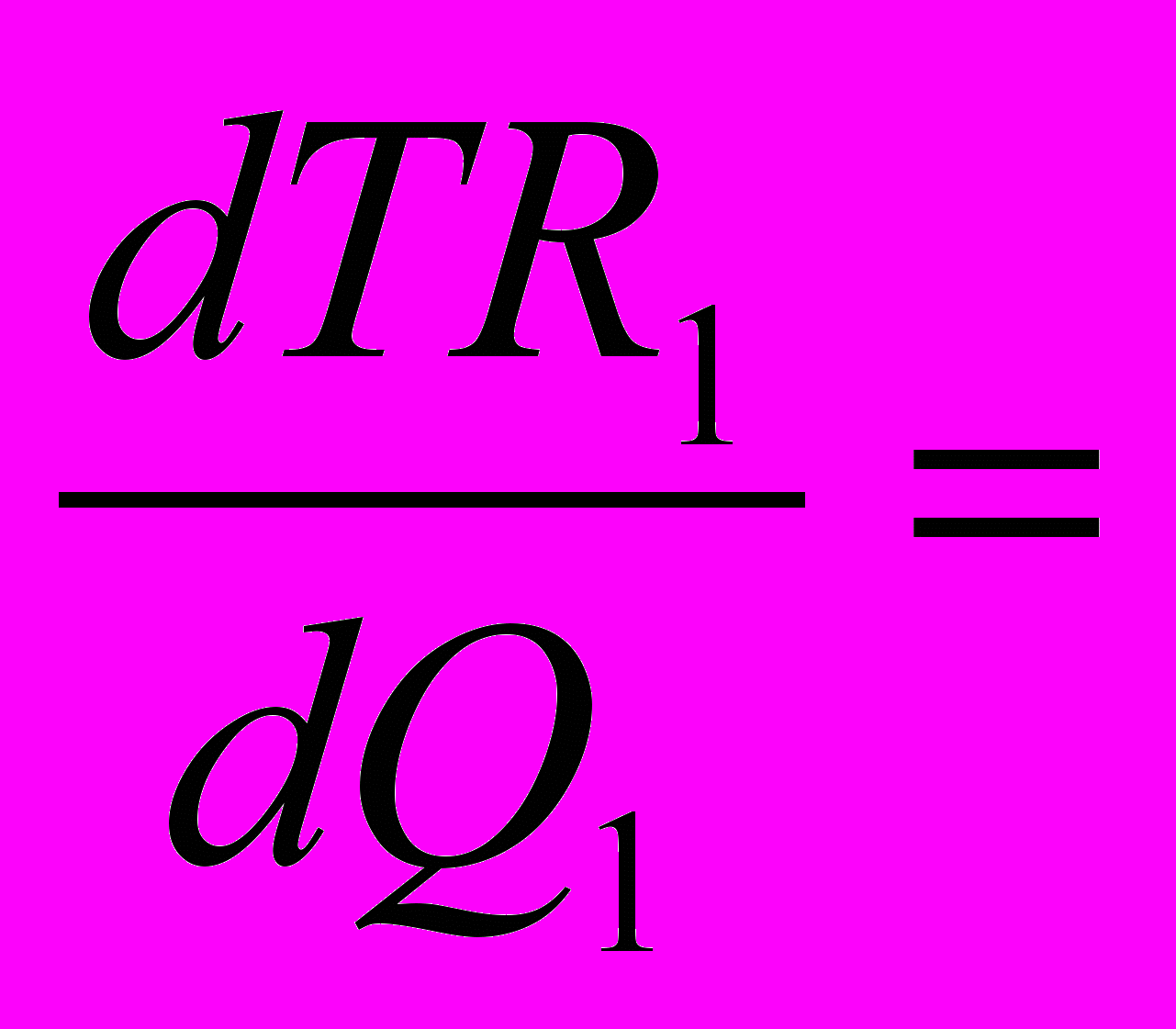
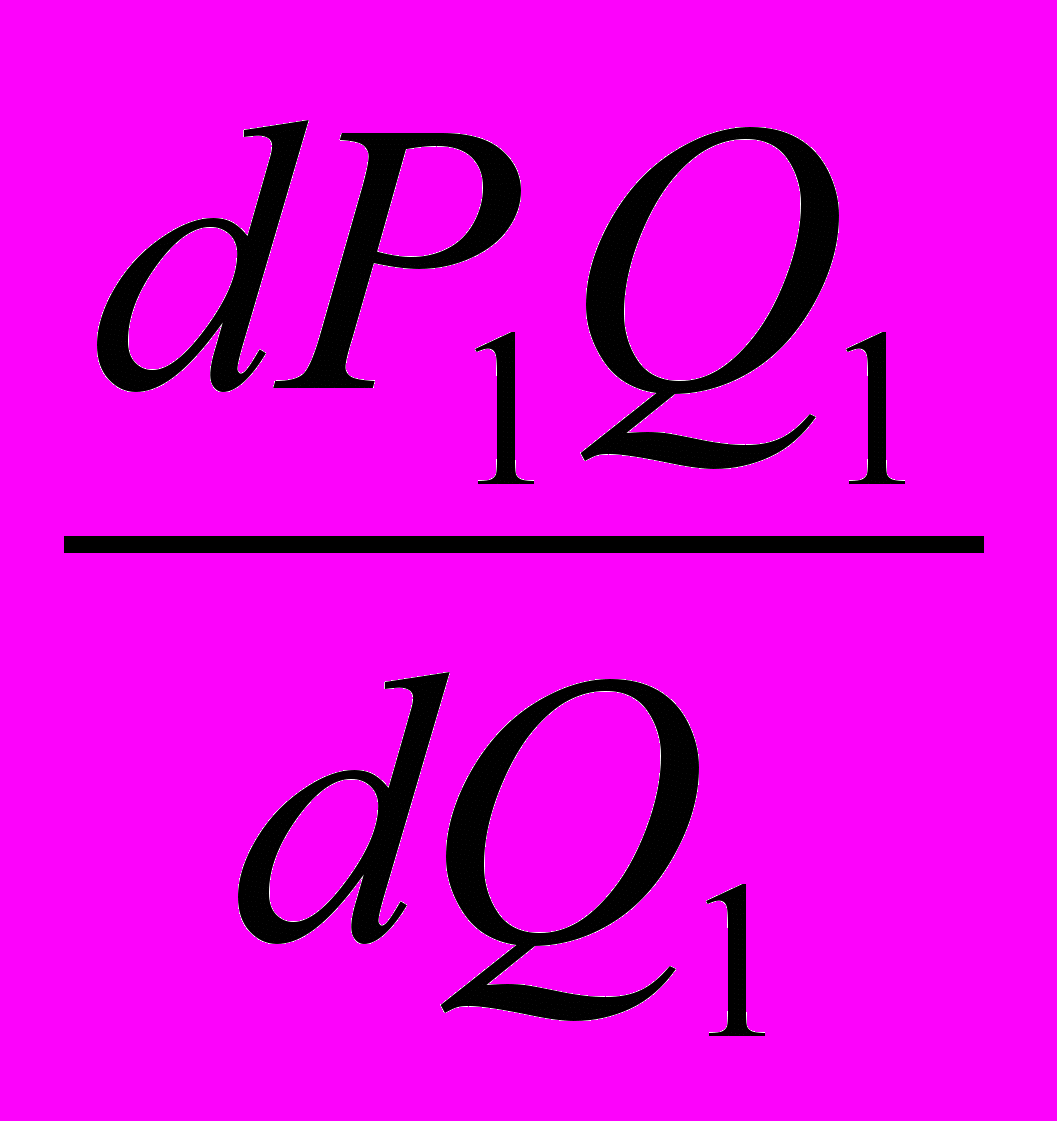
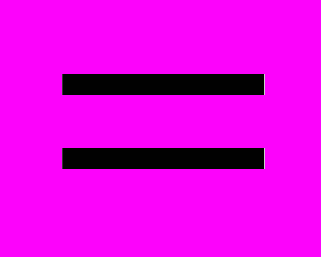
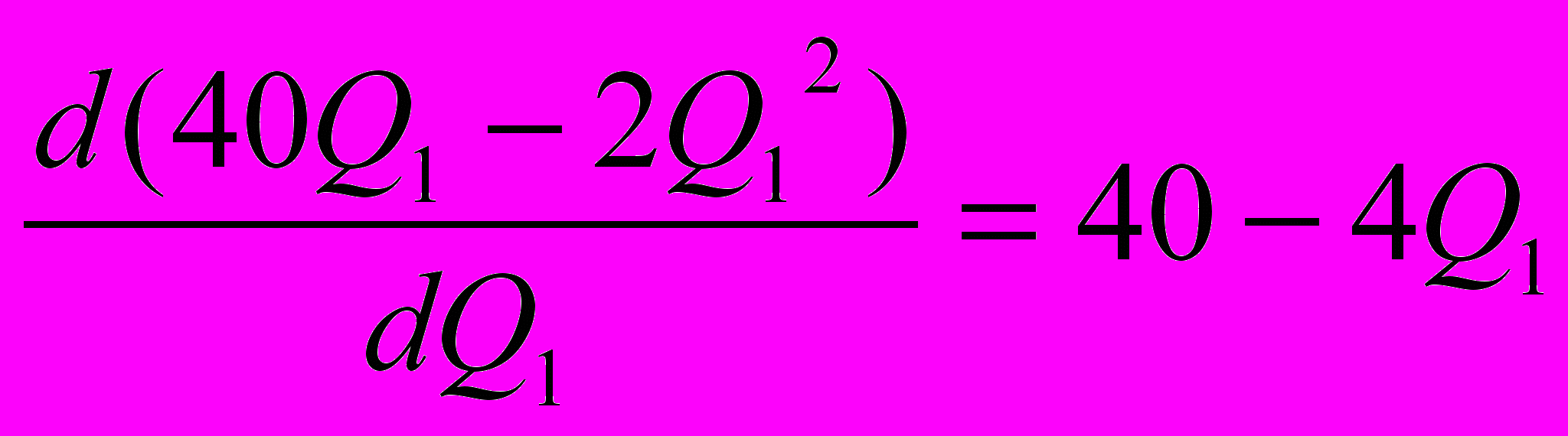
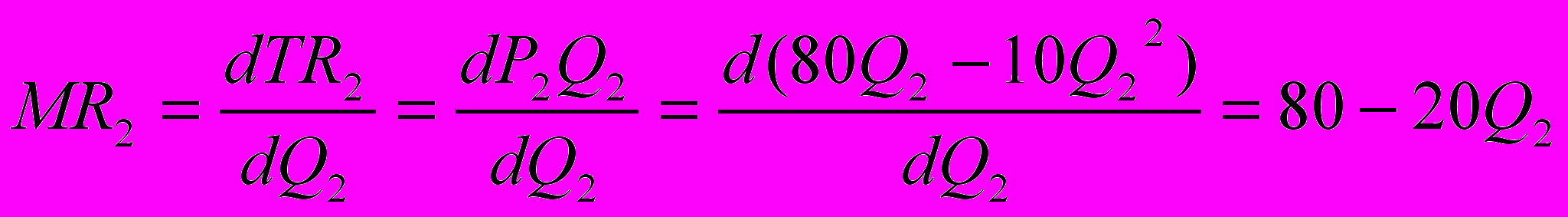
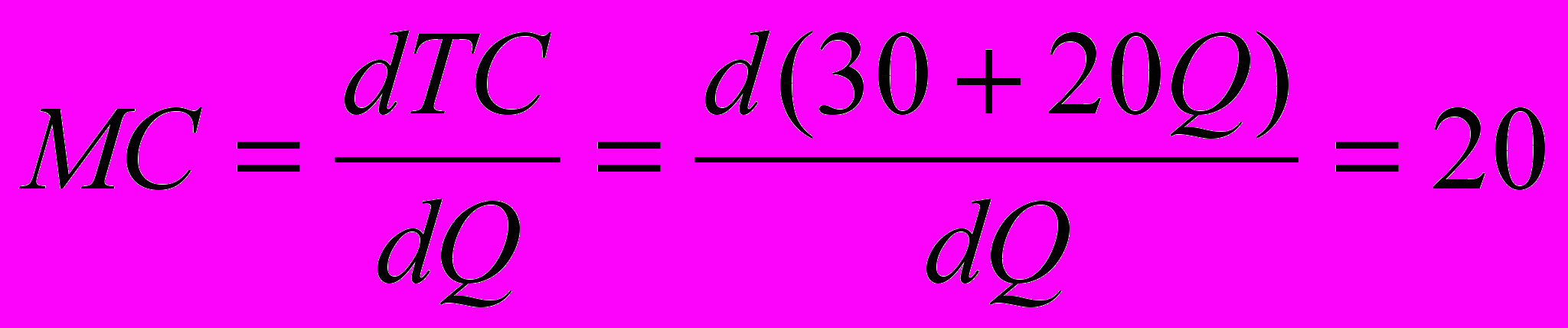ден. ед.


Далее, приравняв предельные доходы на каждом рынке к предельным издержкам на весь выпуск, определяем объем продаж на каждом рынке.


MR₁ = MC; 40 – 4Q₁ = 20; Q₁ = 5 ед. продукции

MR₂ = MC; 80 – 20Q₂ = 20; Q₂ = 3 ед. продукции


Подставляя значения Q₁ и Q₂ в функции спроса, находим цены, устанавливаемые монополией на каждом рынке.

Р₁ = 40 – 2Q₁ P₁ = 30 ден. ед

Р₂ = 80 – 10Q₂ P₂ = 50 ден. ед.


Прибыль монополии (П) определяем как разницу между TR и TC


П =TR – TC = (30  5 + 50  3) – (30 + 20  8) = 110 ден. ед.


б) максимальную прибыль, получаемую монополией без проведения ценовой дискриминации, определяем исходя из того, что монополист в этом случае определяет цену и объем продаж при условии равенства предельного дохода и предельных издержек.

Величина МС известна, она равна 20 ден. ед. Поэтому необходимо определить функцию MR монополии, для чего вначале определим функцию суммарного спроса на продукцию монополии на обоих рынках:

Если Q₁ = 20 – Р₁/2 , а Q₂ = 8 – P₂/10, то функция суммарного спроса составит: Q = 28 – (P/2 + Р/10) или Q = 28 – (3/5)Р,

отсюда Р = 140/3 – (5/3)Q, а TR = Р  Q = (140/3)Q – (5/3)Q² , и MR = 140/3 – (10/3)Q,

Приравняв MR и МС , определяем объем продаж монополией:

20 = 140/3 – 10/3Q, откуда Q = 8 ед. продукции.

Подставив Q в функцию спроса определяем Р, при которой прибыль монополии максимальна: 8 = 28 – (3/5)Р, Р = 20 ден. ед.

Прибыль монополии (П) без проведения ценовой дискриминации определяем как разницу между TR и TC: П = Р  Q – (30 + 20Q) = 20  8 – (30 + 20  8) = - 30 ден.ед.

Таким образом, при отсутствии ценовой дискриминации монополист получит убыток, равный 30 ден. ед.


5. Рынки ресурсов


Задача 1. Предположим, что фирма намерена купить новый станок, использовать его в течение трех лет и получить в течение этого срока чистый доход 600 тыс. руб., который при этом распределяется по годам следующим образом: в первый год 150 тыс. руб., во второй год – 250 тыс. руб. и в третий – 200 тыс. руб. Ставка ссудного процента равна 10 %.

Необходимо определить: целесообразно ли фирме при вышеуказанных условиях приобретать станок по текущей цене его покупки: а) 510 тыс. руб.; б) 450 тыс. руб.; в) 493,3 тыс. руб.?


Решение


Дисконтированная стоимость ожидаемого чистого дохода от использования станка равна:


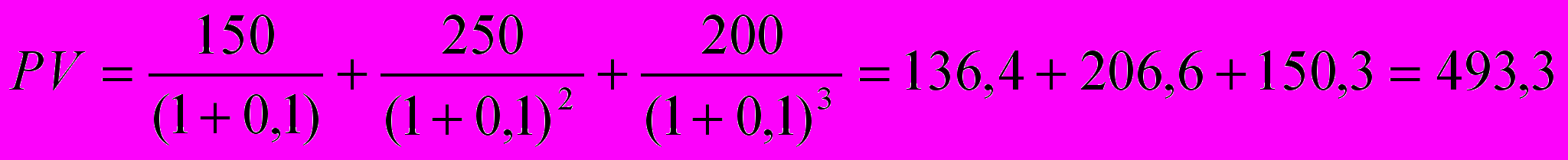тыс. руб.

а) дисконтированная стоимость станка, равная 493,3 тыс. руб. – это максимальная цена, которую фирма могла бы заплатить. Cледовательно, при текущей цене станка 510 тыс. руб. ей не следует его покупать. Доказательство следующее: доход фирмы через три года использования станка складывается из суммы ожидаемого чистого дохода и процента с чистого дохода, полученного после первого и второго года. Он составит: 600,0 + 31,5 + 25,0 = 656,5 тыс. руб. Если бы фирма вложила 510 тыс. руб. в банк под 10 % годовых, то через три года имела бы альтернативный доход, равный: 510  (1,1)³ = 678,8 тыс. руб. Нецелесообразность покупки станка по цене 510 тыс. руб. подтверждает и расчет чистой дисконтированной стоимости:


NPV = PV – I = 493,3 – 510,0 = - 16,7 тыс. руб., т.е. чистая дисконтированная стоимость отрицательна;


б) при цене покупки 450 тыс. руб. фирме целесообразно приобрести станок, так как 493,3 > 450,0. Доход от его использования 656,5 тыс. руб. будет больше альтернативного дохода от вложения 450 тыс. руб. в банк под 10 % годовых, который равен: 450  (1,1)³ = 598,9 тыс. руб. Этот вывод подтверждается и положительной величиной чистой дисконтированной стоимости: NPV = 493,3 – 450 = + 43,3 тыс. руб.;


в) при цене покупки 493,3 тыс. руб. фирме будет безразлично приобретать или не приобретать станок, так как доход от его использования 656,5 тыс. руб. равен альтернативному доходу от вложения 493,3 тыс. руб. в банк под 10 % годовых. Чистая дисконтированная стоимость в этом случае равна нулю (NPV = 493,3 – 493,3 = 0).


Задача 2. У работника, являющегося младшим бухгалтером и имеющим годовую заработную плату 60 тыс. руб., есть альтернатива: окончить годичный курс обучения стоимостью 30 тыс. руб. и занять должность старшего бухгалтера.

Необходимо определить: насколько минимально выше должна быть заработная плата старшего бухгалтера, чтобы обучение было целесообразным, если работник считает приемлемой для себя норму отдачи от вложений 15 % годовых?


Решение


Для ответа на вопрос задачи необходимо иметь в виду, что вложения в образование эффективны если выгоды, получаемые работником при этом, по меньшей мере равны затратам.

Получаемые работником выгоды представляют собою дисконтированные выгоды (или приведенную к текущему моменту ценность выгод). Если обозначим через Х тыс. руб. размер повышения заработной платы работника после окончания курсов, то дисконтированные выгоды равны:

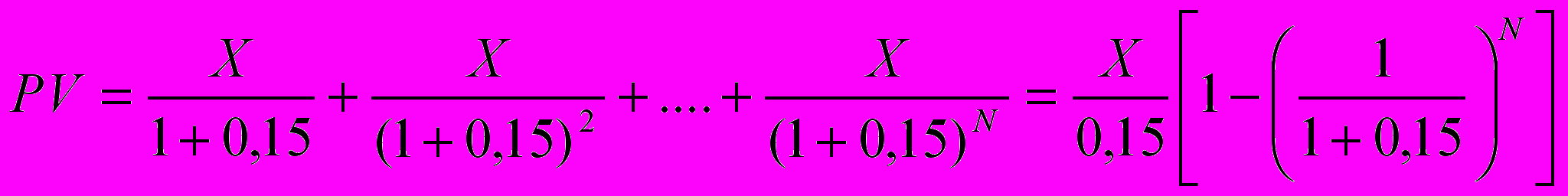, где

N – число лет будущей работы в должности старшего бухгалтера

При достаточно большом N второй сомножитель несущественен. Так, если работник предполагает работать 40 лет, то он равен 0,0037.

Поэтому PV = X / 0,15.

Затраты на образование состоят из суммы упущенных заработков ( 60 тыс. руб.) и платы за обучение 30 тыс. руб., т.е. всего 90 тыс. руб.

Приравняв дисконтированную выгоду к затратам на образование, определим минимально необходимое повышение зарплаты после окончания работником курсов.

Х / 0,15 = 90 000; Х = 13500 руб.