Geum.ru

Рабочая программа для аспирантов по специальности Экономическая теория

Вид материалаРабочая программа

Содержание


Тема 2. Производственная функция и условие равновесия производителя
Подобный материал:
1   2   3   4   5

Решив уравнение, определим, что Рd = 3 д.е. Подставив значение цены Рd в функцию спроса или предложения, наедем, что Qd = 22,5 ед., т.е. объем продажи газа возрастет на 12,5%.



Задача 2. Спрос и предложение на рынке некоего товара описываются следующими уравнениями: QD = 9 – P , QS = - 0,5 + 1,5Р.

Необходимо определить:

а) если государство вводит налог (t) – 1 руб. с каждого кг проданных товаров, то какую часть налога платит продавец и какую – покупатель?

б) если государство выплачивает дотацию (h) – по 1 руб. на каждый кг проданных товаров, то кто получает большую долю выделенных средств, продавец или покупатель?


Решение задачи


a) Без вмешательства государства функции спроса и предложения имеют вид

QD = 9 – P, QS = - 0,5 + 1,5 P.

Приравняв правые части уравнений , определяем равновесную цену РE = 3,8 руб./кг. При введении налога t = 1 руб./кг, выплачиваемого продавцом, получаем новую функцию предложения

QtS = - 0,5 + 1,5(P – t) = - 0,5 + 1,5(P – 1) = - 2 + 1,5P.

Новая равновесная цена РЕt определяется из условия равенства спроса и предложения QD = QtS, откуда последовательно получаем:

9 – РEt = -2 + 1,5РEt ; PEt = 11/2,5 = 4,48 руб./кг.

Реальное увеличение цены, уплачиваемой покупателем,

Р = РEt – РE = 4, 48 – 3,8 = 0,68 руб./кг.

Взнос покупателя (Р / t) 100% = (0,68 / 1) 100% = 68%, взнос продавца – 32%, т.е. взнос покупателя в 2,2 раза больше взноса продавца.


б) Дотация, получаемая продавцом, снижает цену на величину дотации, так что

Рh = Р – h, откуда Р = Рh + h.

Новая функция предложения имеет вид:

QhS = - 0,5 + 1,5 (P + h) = - 0,5 + 1,5 (P + 1) = 1 + 1,5P.

Новая равновесная цена РEh определяется из условия равенства спроса и предложения QD = QhS, откуда последовательно получаем:

9 – РEh = 1 + 1,5 РEh ; РEh = 8 / 2,5 = 3, 2 руб. / кг.

Реальное снижение цены, получаемое покупателем

Р = РЕ - РEh = 3,8 – 3,2 = 0,6 руб. / кг.

Покупатель получает (Р / h) 100% = (0,6 / 1) 100% = 60% дотации, продавец – 40 %, т.е. покупатель получает в 1,5 раза больше, чем продавец.


Задача 3. Функции спроса и предложения на продукт описываются следующими уравнениями: QD = 9 – P ; QS = - 0,5 + 1,5P.

После увеличения расходов на рекламу спрос возрос на 50%. Необходимо определить:

а) доход, получаемый продавцом в условиях рыночного равновесия до и после увеличения спроса;

б) максимальный доход, который может получить продавец до и после увеличения спроса;

в) каким должен быть налог, чтобы продавец получил максимальный доход до и после увеличения спроса.


Решение задачи:

В условиях свободной конкуренции на рынке продавец продает равновесный объем товара QE = QD = QS по равновесной цене РE = РD = РS, получая доход R = QE · PE.

а) До увеличения спроса РЕ = 3,8 руб./кг, QЕ = 5,2 кг и продавец получает доход

RЕ = 5,2 · 3,8 = 19,76 руб.

При увеличении спроса на 50% значения всех объемов увеличатся в 1,5 раза, и новая функция спроса будет иметь вид

Q1D = 1,5 · (9 – P)

Новая равновесная цена Р1 определяется из условия равенства спроса и предложения: Q1D = QS и после подстановки объемов спроса и предложения получаем уравнение

1,5 ·(9 – Р1) = - 0,5 + 1,5 Р1.

Решая уравнение получаем Р1 = 4,67 руб/кг.

Q1 = 1,5 · (9 – 4,67) = 6,5кг.

Значит, доход, получаемый продавцом, после повышения спроса составит

R1 = 6,5 · 4,67 = 30,33 руб.

б) Доход будет максимальным при такой цене Рmax , при которой коэффициент ценовой эластичности спроса равен – 1. Для функции спроса QD = 9 – P, при Р < 9 имеем

ЕpD= - Р/(9 – Р)

и для цены Рmax получаем уравнение Рmax/ (9 – Рmax), решая которое определяем Р = 4,5 руб./кг.

Максимальный доход равен произведению цены Рmax на объем спроса при этой цене. До увеличения спроса его объем при Рmax равен 4,5 кг (9 – 4,5), а после увеличения спроса – 6,75 кг [1,5 ·(9 – 4,5)]. Таким образом, до увеличения спроса максимальный доход равен 4,5 · 4,5 = 20,25 руб. а после увеличения спроса – 4,5 · 6,75 = 30,375 руб.

в) До увеличения спроса продавец получал доход RЕ = 19,76 руб., продавая товар по равновесной цене РЕ = 3,8 руб./кг, и при данном спросе мог бы получать максимальный доход, равный 20,25 руб., продавая товар по цене Рmax = 4,5 руб./кг.

Чтобы цена Рmax = 4,5 руб./кг была ценой продажи, она должна быть равновесной. При неизменном спросе координаты равновесной точки могут изменяться смещением кривой предложения при введении налога t. Новая кривая предложения определяется уравнением

QtS= - 0,5 + 1,5 · (P – t)

При Р = Рmax из условия равновесия QtS = QD получаем

9 – 4,5 = - 0,5 + 1,5 · (4,5 – t)

Решая уравнение определяем t = 1,17 руб./кг.

Аналогично после изменения спроса и введения налога новая кривая спроса определяется уравнением

QD = 1,5 ·(9 – P),

а кривая предложения QtS = - 0,5 + 1,5 · (P – t).

Исходя из условия равновесия QD = QtS, получаем

1,5 · (9 – 4,5) = - 0,5 + 1,5 · (4,5 – t),

откуда t = - 0,33 руб./кг. Отрицательная величина налога означает дотацию.


Задача 4. Функция предложения имеет вид QрS = - 0,5 + 1,5 P. Необходимо определить формулу коэффициента точечной эластичности предложения и значения коэффициента дуговой эластичности предложения при изменениях цены: а) от 1 руб. до 3 руб.; б) от 3 руб. до 5 руб.; в) от 5 руб. до 8 руб.; г) от 8 руб. до 10 руб.


Решение задачи:


В функции предложения QS = - 0,5 + 1,5 P, цена Р  1/3.

Коэффициент точечной эластичности для этой функции согласно формуле ЕрS = (dQS/dP) · P/Q имеет вид:


ЕрS = 1,5 Р/ (1,5Р – 0,5) = 1 + 1 / (3Р – 1)

Коэффициенты дуговой эластичности предложения для этой функции согласно формуле (Q2 – Q1)/(Q2 + Q1)  (P2 + P1)/(P2 – P1) принимают значения:


ЕS(1,3) = (4 – 1)/(4 + 1) · (3 + 1)/(3 – 1) = 1,2,

ES(3,5) = (7 – 4)/(7 + 4) · (5 + 3)/(5 – 3) = 1,091,

ES(5,8) = (11,5 – 7)/(11,5 + 7) · (8 + 5)/(8 – 5) = 1,054,

ES(8,10) = (14,5 – 11,5)/(14,5 + 11,5) · (10 + 8)/(10 – 8) = 1,04.


Задача 5. На рыбном рынке установились равновесные значения цены РЕ = 30 руб./кг и объема QЕ = 500 кг. Коэффициент эластичности спроса на рыбу равен 0,1, а коэффициент эластичности предложения равен 0,2.

Необходимо определить линейные функции спроса и предложения на рыбу.


Решение задачи

Допустим, что линейные функции спроса и предложения на рыбу имеют вид:

QD = а – в ·Р, в  0; QS = c + d ·P, d > 0

Для определения четырех неизвестных параметров в этих функциях а, в, с, d выразим заданные равновесные значения цены и объема продаж и коэффициенты эластичности через эти параметры.

Из условия QD = QS = QE, P = PE получаем QE = а – в · РE и а – в · РE = с + d · PE, откуда определяем PE = (а –с) / (в + d).

Для коэффициента эластичности спроса получаем

ЕpD = - (dQ / dP)  PE /QE = - в·РE /QE.

Аналогично для коэффициента эластичности предложения

ЕpS = dQ / dP  PE /QE = d · PE /QE.

Полученные четыре уравнения образуют систему для определения четырех неизвестных:




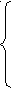
QЕ = а – в · РЕ

РE = (а – с)/ (в + d)

ЕpD = - в · РE / QE

EpS = d · PE / QE


После подстановки исходных данных система имеет следующий вид:


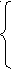500 = а – в · 30

30 = (а – с) / (в + d)

- 0,1 = - в · 30/ 500

0,2 = d · 30/ 500


Решая систему уравнений, определяем неизвестные:

d = 0,2 · 500/30 = 10/3 = 3,33;

в = 0,1 · 500/30 = 5/3 = 1,67;

а = 500 + 5/3 · 30 = 550;

с = а - 30 · (в + d) = 550 – 30 · (5/3 + 10/3) = 400.

Таким образом, функции спроса и предложения на рыбу имеют следующий вид: QD = 550 – 1,67 · Р; QS = 400 + 3,33 · P.

Функция предложения определена при любых положительных значениях цены, а функция спроса принимает отрицательные значения при Р > 550/1,67 = 330, поэтому при Р > 330 придадим величине спроса (QD) нулевое значение. Окончательно функции спроса и предложения записываются в виде:

QD = max {550 – 1,67 · P,0};

QS = 400 + 3,33 · P.


Задача 6. Функция полезности потребителя описывается формулой ТU = ХУ/ 2 , где Х – объем потребления бананов, У – объем потребления пепси-колы. Цена 1 кг бананов 15 руб., 1 л пепси-колы стоит 10 руб. Летом потребитель тратил на покупку этих товаров 120 руб. в неделю. Зимой цена бананов поднялась до 20 руб. за 1 кг, цена пепси-колы осталась без изменения. Необходимо определить:

а) Объем оптимального потребления бананов и пепси-колы летом;

б) Величину расходов, необходимую зимой для достижения того же уровня полезности, что и летом;

в) Количественное значение эффекта дохода и эффекта замены.


Решение

В ситуации равновесия (оптимального потребления) соблюдается условие:

МUx / Muy = Px / Py,

поэтому необходимо определить предельные полезности Х и У.

МUx = (ТU)x =У / 2, а Мuy = (ТU)y =X / 2.

Исходя из этого условие равновесия выглядит так:

У / Х = 15 / 10, или У / Х = 3 / 2

При оптимальном потреблении потребитель ограничен своим бюджетом:

Рх  Х + Ру  У = I,

или после подстановки имеющихся данных:

15  Х + 10  У =120

Таким образом, мы имеем возможность составить систему уравнений:

У / Х = 3 / 2

15 Х + 10У = 120.

Решив эту систему уравнений, определим, что Х = 4; У = 6.

Общая полезность потребления 4 кг бананов и 6 л пепси-колы составляет 12 единиц полезности (ТU = ХУ / 2 = (4  6) / 2 = 12 единиц полезности).

Для достижения оптимального уровня общей полезности должно соблюдаться условие:

МUх / MUу = Pх / Pу , или У / Х = 20 / 10, или после сокращения У / Х = 2.

Таким образом, есть возможность составить систему уравнений:

ХУ / 2 = 12

У / Х = 2

Решив эту систему уравнений, определим, что Х = 3,5; У = 7

Расходы на покупку 3,5 кг бананов и 7 л пепси-колы составляют 140 руб.

Эффект замены составит – 0,5 кг бананов и 1 л пепси-колы. Если бы покупатель тратил зимой на покупки 120 руб., то его оптимальный набор составил бы 3 кг бананов и 6 л пепси-колы. Следовательно, эффект дохода составляет 0,5 кг бананов и 1 л пепси-колы.


Тема 2. Производственная функция и условие равновесия производителя


Задача 1. Производство в фирме описывается функцией Q = 108Х + 9Х 2 – Х 3,

где Q – количество производимой продукции;

Х – количество переменного ресурса, используемого в производстве.

Необходимо определить:

а) уравнения для предельного продукта МР и среднего продукта АР;

б) если при производстве используются 4 единицы переменного ресурса, то какова величина предельного продукта?

в) при каком количестве использования переменного ресурса у фирмы будет максимальный выпуск? Чему он равен?

г) значение переменного ресурса, при котором начинается убывание предельной отдачи от дополнительного привлечения переменного ресурса? Какому выпуску продукции это соответствует?

д) при каком количестве использования переменного ресурса предельный продукт и средний продукт равны между собой?


Решение


а) Исходя из того, что МРх = dТРх / dХ , функция предельного продукта переменного ресурса Х описывается уравнением

МРх = 108 + 18Х – 3Х 2

Так как АРх = ТРх / Х, то функция среднего продукта переменного ресурса Х описывается уравнением

АРх = 108 + 9Х – Х 2

б) Поскольку МРх = 108 + 18X – 3X 2, то

МРХ = 4 = 108 + 18 · 4 – 3 · 4 2 = 132


в) Так как ТР максимален, когда МР = 0, то количество использования переменного ресурса фирмой, при котором будет максимальный выпуск, определяется из уравнения:

108 + 18Х – 3Х 2 = 0

Решив уравнение, находим Х = 9,7

Максимальный выпуск при затратах переменного ресурса Х = 9,7 определяется из выражения

ТРх = 108 · 9,7 + 9 · 9,7 2 – 9,7 3 = 981 ед.


г) Функция МРх = 108 + 18Х – 3Х 2 достигает максимального значения, когда dMPх/dX = 0. Отсюда следует, что предельный продукт достигает максимального значения при затратах переменного фактора Х, определяемых из следующего уравнения:

18 – 6Х = 0.

Решив уравнение, определяем Х = 3 ед. переменного фактора. При затратах Х > 3 начинает действовать убывающая отдача и уменьшаться предельный продукт. При затратах переменного фактора Х в количестве 3 ед.

ТРх = 378 ед. продукции.

д) Предельный продукт и средний продукт переменного фактора равны между собой, когда средний продукт достигает максимального значения. Функция АРх = 108 + 9Х – Х 2 достигает максимального значения, когда dAPх/ dX = 0. Отсюда следует, что средний продукт достигает максимального значения при затратах переменного фактора Х, определяемых из уравнения:

9 – 2Х = 0.

Решив уравнение, определяем Х = 4,5 ед. переменного фактора. При таких затратах переменного фактора МРх = АРх = 128,25 ед. продукции.


Задача 2. Производственная функция Р = L0,8K 0,2. Издержки производителя равны 30 д. ед. Цена труда – 4 д. ед., капитала – 5 д. ед.Необходимо определить равновесный расход ресурсов.


Решение

Расход ресурсов будет равновесным при соблюдении двух условий:

МRTSKL = MPL / MPK = PL / PK и

РL · L + PK · K = C

Эти два условия при имеющейся информации позволяют составить систему из двух уравнений с двумя неизвестными ( K и L ), решение которой и позволяет определить равновесный расход ресурсов.

МRTSKL = 0,8L- 0,2 K0,2 / 0,2L0,8K - 0,8 = 4K / L

4К/ L = PL/PK = 4/5

PL · L + PK · K = 30

4L + 5K = 30




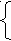
4K / L = 4/5

4L + 5K = 30

Решив систему уравнений, определяем равновесный расход L = 6, К = 1,2.


Задача 3. Технология, по которой работает фирма, описывается производственной функцией Q = L0,6 K 0,4. Цена труда – 8 д. ед., а цена капитала – 16 д. ед.

Необходимо определить: среднюю производительность труда (АРL) при нахождении фирмы в равновесном состоянии.


Решение


Из условия равновесия фирмы МРL / МРK = РL / РK следует:

0,6К / 0,4L = 8 / 16

Из последнего уравнения определяем К / L = 1 / 3.

Тогда АРL = ТРL/L = L0,6 K0,4 / L = (K / L)0,4 = (1 / 3)0,4 = 0,644


Задача 4. Владелец фирмы выплатил наемному работнику 40 тыс. руб. Плата процентов за кредит составляет 10 тыс. руб. Первоначальная стоимость основного капитала была 100 тыс. руб., а сейчас составляет 80 тыс. руб. Норма амортизации – 20 %, затраты на сырье, отопление, освещение, ремонт и т.д. – 40 тыс. руб. Выручка от продажи продукции фирмы составила 160 тыс. руб.

Владелец фирмы имеет возможность устроиться на работу в магазин и получать за работу 30 тыс. руб. Его жена работает в этой же фирме, а за такую же работу в другом месте могла бы получать 10 тыс. руб. Владелец фирмы должен вернуть банку ссуду 50 тыс. руб., взятую под основной капитал. От вложений своего капитала в другое предприятие он мог бы получать 10% дохода.

Необходимо определить:

а) бухгалтерские издержки;

б) экономические издержки;

в) бухгалтерскую прибыль;

г) экономическую прибыль;

д) следует ли владельцу фирмы продолжать вести свое дело?

Решение

Определение бухгалтерских и экономических издержек произведено в табл. 1


Таблица 1.




Элементы издержек Бухгалтерские Экономические

издержки издержки




1. Зарплата наемному работнику тыс. руб. 40 40

2. Уплата процентов за кредит тыс. руб. 10 10

3. Амортизационные отчисления тыс. руб. 20 20

4. Затраты на сырье, отопление, освещение

и т.д., тыс. руб. 40 40

5. Неявная зарплата владельца фирмы,

тыс. руб. - 30

6. Неявная зарплата жены владельца фирмы,

тыс. руб. - 10

7. Неявный процент на фактически имеющий-

ся капитал, равный 80 – 50 = 30 тыс. руб. - 3



Итого тыс. руб. 110 153


Бухгалтерская прибыль = 160 – 110 = 50 тыс. руб.

Экономическая прибыль = 160 – 153 = 7 тыс. руб.

Вывод: владельцу фирмы следует продолжать вести свое дело, так как, работая с женой в других фирмах и, вложив имеющийся капитал в другое предприятие, он получит доход, равный 43 (30 + 10 + 3) тыс. руб., а продолжая вести свое дело, получит прибыль, равную 50 тыс. руб.


Задача 5. Фирма, выпускающая игрушки, производит 2000 игрушек в неделю по цене 50 руб. за ед. Производственные мощности позволяют увеличить выпуск до 3000 ед. Общие издержки на единицу (АТС2000) равны 40 руб., в т.ч. постоянные затраты (АFC2000) равны 15 руб.

Необходимо определить: следует ли фирме принимать решение о расширении производства, если ей предлагают производить эти игрушки на экспорт в количестве 400 ед. в неделю по контрактной цене 35 руб. При этом предполагается, что АVC2400 = AVC2000.

Решение


Фирме целесообразно расширять производство, если при увеличении выпуска она получит дополнительную прибыль. Поэтому необходимо выяснить получит ли фирма дополнительную прибыль, если будет продавать дополнительно 400 игрушек при значительно меньшей цене (35 руб. < 50 руб.).

Вначале определим прибыль (П) при продаже фирмой 2000 игрушек на внутреннем рынке: П2000 = ТR2000 – TC2000 = 50  2000 – 40  2000 = 20 000 руб.

При определении прибыли фирмы при увеличении выпуска игрушек на 400 ед., (т.е. П2400) вначале определим выручку фирмы при продаже 2400 игрушек.

ТR2400 = 50  2000 + 35  400 = 114 000 руб.