Рабочая программа учебной дисциплины (модуля) информатика
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины «информатика» очно-заочная, 167.63kb.
- Рабочая программа учебной дисциплины математика и информатика, 188.66kb.
- Рабочая программа учебной дисциплины «теория систем и системный анализ» Направление, 223.11kb.
- Рабочая программа учебной дисциплины «Математика» Специальность «Прикладная информатика, 322.42kb.
- Рабочая программа по учебной дисциплине Экономика наименование учебной дисциплины (полное,, 876.11kb.
- Рабочая программа учебной дисциплины (модуля) Мордовский национальный костюм, 257.38kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 129.5kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 107.65kb.
- Рабочей программы учебной дисциплины автоматизация технологических процессов (наименование, 28.16kb.
- Рабочая программа учебной дисциплины ф тпу 1 21/01 федеральное агентство по образованию, 187.41kb.
ОБРАЗЕЦ 1 ТИТУЛЬНОГО ЛИСТА
Министерство образования и науки Российской Федерации
ГОУВПО «Мордовский государственный университет им. Н.П.Огарёва»
Математический факультет
Кафедра систем автоматизированного проектирования
-
«УТВЕРЖДАЮ»
_____________________
_____________________
«______»__________2011 г.
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ (МОДУЛЯ)
ИНФОРМАТИКА
Направление подготовки
270800(строительство)
Профиль подготовки
1-Промышленное и гражданское строительство
2- Городское строительство и хозяйство
3- Автомобильные дороги и аэродромы
Квалификация (степень) выпускника
Бакалавр
Форма обучения
очная
)
г. Саранск
2011 г.
ОБРАЗЕЦ 2 ТИТУЛЬНОГО ЛИСТА
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОУВПО «Мордовский государственный университет им. Н.П.Огарёва»
____________________________________________________
(Наименование факультета)
_______________________________________________________________
(Наименование кафедры)
-
«УТВЕРЖДАЮ»
_____________________
_____________________
«____»__________201__ г.
РАБОЧАЯ ПРОГРАММА УЧЕБНОЙ ДИСЦИПЛИНЫ
_____________________________________
Наименование дисциплины
для направлений подготовки
___________________________________
____________________________________
Квалификация (степень) выпускника
Бакалавр
Форма обучения
__________________________________
(очная, очно-заочная, заочная, экстернат)
г. Саранск
201__ г.
- Цели и задачи учебной дисциплины:
Целью освоения информатики является знание основных принципов и методов сбора и обработки информации профессионального характера с применением средств математического моделирования, алгоритмической и программной реализации соответствующих задач, умение применять существующее программное обеспечение для решения профессиональных задач, а также интерпретировать полученные результаты, осуществлять их анализ и находить оптимальные решения, систематизировать и обрабатывать результаты научных исследований.
Кроме того, целью курса является умение находить в глобальных сетях информацию профессионального характера и применять существующие программные комплексы в профессиональной и учебной деятельности.
Задачами курса являются:
- овладение важнейшими методами решения научно-технических задач и основными алгоритмами математического моделирования явлений и процессов предметной области;
- формирование устойчивых навыков по применению математического моделирования, алгоритмических конструкций и программного обеспечения при научном анализе ситуаций, возникающих в ходе создания новой техники и новых технологий;
В процессе решения указанных задач необходимо сформировать у студентов следующую целостную систему знаний, умений и навыков:
- знание основных методов сбора, хранения, обработки и передачи информации, ее основных свойств;
- знание основных алгоритмических конструкций;
- знание основ языка программирования высокого уровня;
- знание основных численных методов решения профессиональных задач;
- знание технологии подготовки и обработки информации тестового и смешанного характера;
2)Умения:
- интерпретировать явления профессиональной области при помощи соответствующего теоретического аппарата;
- составлять алгоритмические модели явлений и процессов предметной области на основе стандартных алгоритмических конструкций;
- составлять программы на языке высокого уровня для реализации составленных алгоритмических структур;
- подготовить и оформить текстовую информацию в текстовом редакторе;
- формировать наборы данных и обрабатывать их средствами СУБД;
- использовать электронные таблицы для проведения расчетов и реализации основных численных методов.
Навыки:
- построения и исследования математических моделей явлений предметной области;
– применения типовых алгоритмов исследования явлений предметной области
– использования возможностей современных компьютеров и информационных технологий при аналитическом и численном исследования моделей технических систем.
- Место учебной дисциплины в структуре ООП.
Информатика относится к циклу дисциплин естественно-научного характера (базовая часть). Необходимыми для ее изучения являются знания математики, информатики и физики в объеме стандарта общего образования:
- математика: аналитические уравнения прямой на плоскости, параболы, окружности, свойства геометрических фигур, свойства элементарных функий, аналитические методы решения уравнений;
- информатика: системы счисления, кодирование информации, измерение количества информации, локальные и глобальные сети, аппарвтное обеспечение ЭВМ, виды программного обеспечения;
- физика: основные физические законы.
Кроме самостоятельного значения курс является предшествующей дисциплиной для многих общепрофессиональных дисциплин, использующих компьютерные технологии и математическое моделирование для решения профессиональных задач.
3. Требования к результатам освоения дисциплины
Процесс изучения дисциплины направлен на формирование следующих компетенций:
1) общекультурные компетенции: владеть культурой мышления, способностью к анализу, обобщению, синтезу информации, уметь проводить аналогии с ранее известной информацией, ставить цель и определять способы ее достижения (ОК-1); использовать основные законы естественно-научных дисциплин в профессиональной деятельности;
2) общепрофессиональные компетенции: применение методов математического анализа и моделирования в профессиональной деятельности (ПК-1, ПК-2), владение основными методами, способами и средствами получения, хранения, переработки информации, навыками работы с компьютером как средством управления информацией, способностью работать с информацией в глобальных компьютерных сетях (ПК-5, ПК-6).
В результате изучения дисциплины студент должен:
Знать: основные понятия информатики, современные средства вычислительной техники, основы алгоритмического языка и технологию составления программ (ПК-2,ПК-5,ПК-6);
Уметь: работать на персональном компьютере и пользоваться основными офисными приложениями(ПК-2,ПК-5,ПК-6);
Владеть: методами практического использования современных компьютеров для обработки информации и основами численных методов для решения инженерных задач(ПК-2,ПК-5,ПК-6).
4. Образовательные технологии
В процессе изучения дисциплины предусмотрены традиционные образовательные технологии – лекция, лабораторное занятие, индивидуальное задание с отчетностью. Кроме того, в качестве образовательных технологий могут быть использованы лекции в форме презентации, обучающие и тестирующие программы, электронные учебники.
5.1 Содержание учебной дисциплины Объем дисциплины и виды учебных занятий
Общее содержание дисциплины, включая СРС, составляет 180 часов(5 зачетных ед.)
| Вид учебной работы | Всего часов | Семестры | |
| 1 | 2 | ||
| Аудиторные занятия (всего) | 86 | 51 | 35 |
| В том числе: | - | - | - |
| Лекции | 34 | 17 | 17 |
| Лабораторные работы (ЛР) | | 34 | 18 |
| Самостоятельная работа (всего) | 94 | 39 | 55 |
| Индивидуальное задание (12 заданий) | - | 8- | 4 |
| Вид текущего контроля успеваемости | | Инд/зад. и отчет | Индзад. и отчет |
| Вид промежуточной аттестации (зачет, экзамен) | | зач | экз |
| Подготовка к зачету | 8 | 8 | |
| Подготовка к экзамену | 36 | | 36 |
| Общая трудоемкость 180 час = 5 зачетных единиц | |||
5.2. Содержание разделов учебной дисциплины
| № п/п | Наименование раздела дисциплины | Содержание раздела | Формы текущего контроля успеваемости (по неделям семестра) |
| 1. | Алгоритмы | Виды алгоритмов, их свойства, представление алгоритмов в виде блок-схем, базовые алгоритмы | Инд.задание (2-4 нед. 1 сем) |
| 2. | Язык программирования | Основы языка Pascal: типы данных, структура программы, ввод-вывод и форматирование данных, реализация разветвляющихся алгоритмических конструкций, реализация циклических конструкций, работа с пользовательскими типами данных, подпрограммы, обработка текстов. | Инд.задание (5-9 нед. 1 сем) |
| 3 | Офисные технологии | 1.MICROSOFT WORD: форматирование данных, работа с фрагментами текста, реализация формул, работа с таблицами, вставка графических объектов, работа со списками; 2. MICROSOFT EXCEL: вычисления, стандартные функции, дополнительные надстройки, сортировка и фильтрация данных, построение диаграмм; | Инд.задание |
| 4 | Численные методы | Методы решения нелинейных уранений. Методы решения дифференциальных уравнений. Интерполяция и аппроксимация функций. Линейная и нелинейная оптимизация. | Инд.задание |
5.3 Разделы учебной дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
| № п/п | Наименование обеспе-чиваемых (последую-щих) дисциплин | № № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин | |||
| 1 | 2 | 3 | 4 | ||
| 1. | Строительная механика | + | + | + | + |
| 2. | Технология строительного производства | + | + | + | + |
5.4 Разделы дисциплин и виды занятий
| № п/п | Наименование раздела дисциплины | Лекц. | Лаб. зан. | СРС | Все-го час. |
| 1. | Алгоритмы | 0 | 6 | 20 | 26 |
| 2. | Язык программирования | 14 | 18 | 20 | 42 |
| 3. | Офисные технологии | 10 | 12 | 20 | 42 |
| 4. | Численные методы | 10 | 16 | 34 | 60 |
6. Лабораторный практикум
| № п/п | № раздела дисциплины | Наименование лабораторных работ | Трудо-емкость (час.) |
| 1. | 2 | Программирование алгоритмов разветвляющейся и циклической структуры | 12 |
| 2. | 2 | Работа с пользовательскими типами данных | 6 |
| 3. | 2 | Обработка символьных данных. Графические построения | 4 |
| 4. | 3 | Работа в тестовом редакторе MICROSOFT WORD | 4 |
| 5. | 3 | Работа в MICROSOFT EXCEL | 6 |
| 6. | 3 | Работа в MICROSOFT ACCESS | 6 |
| 7. | 4 | Решение нелинейных уравнений. Вычисление интегралов. Решение систем линейных уравнений. Интерполяция и аппроксимация функций. Решение дифференциальных уравнений | 13 |
8. В качестве примера средств текущего контроля приводятся задания, представленные в приложении 1.
9. Учебно-методическое и информационное обеспечение учебной дисциплины:
а) Основная литература
1. Томилина О.А., Рябухина Е.А., Кузнецов Н.М. Информатика.Учебное пособие/Саранск, изд-во МГУ, 200г. 240с.
2. Вычислительная техника в инженерных и экономических расчетах: Учебник для вузов/Под ред.А.В.Петрова.-:Высш.шк.,1984.320 С.
3.Алексеев В.Е., Баулин А.С., Петрова Г.Б. Вычислительная техника в инженерных и экономических расчетах: Сборник задач и упражнений/Под ред.А.В.Петрова.-М: Высш.школа, 1984. 136 с.
4.Белов В.Ф., Кочугаев П.Н. Лабораторный практикум по курсу "Программирование и применение ЭВМ". Саранск, 1986. 68 с.
5.Электронные вычислительные машины: В кн.: Учебн.пособие для вузов / Под ред.А.Л.Савельева. Кн.3. Алгоритмизация и основы программирования/ Г.И.Светозарова. -М.: Высш.школа, 1987. 128 с.
6. Дьяконов В.П. Справочник по алгоритмам и программам для ПВМ -М.: Наука, 1987.
7. Поляков Д.В., Круглов И.Ю. Программирование в среде Турбо Паскаль - М.: Изд-во МНИ, 1992, 576 с.
8.Фигурнов В.Е. IBM PС для пользователя - М.: Финансы и статистика, 1990, 240 с.
9. Воробьев Г.Н.,Дашкова А.Н. Практикум по вычислительной математике. -.,Высш.шк.1990-208 с.
10. Шуп Т.Е. Прикладные численные методы в физике и технике. - М. Высш. шк.1990, 255 с.
11. Лёвин А. Самоучитель работы на компьютере. - М.: Нолидж, 1998, 624 с.
12. Ковальски С. Exсel 2000. Русская версия.- М.:Бином,2000,448 с.
13. Вемпен Ф. Мicrosoft Office - 97. - М.: Бином, 1997,720 с.
14. Банди Б. Методы оптимизации. М: Радио и связь, 1988-188 с.
15. Томилина О.А., Рябухина О.А., Кузнецов Н.М. Информатика.- Саранск:Изд-во МГУ, 2003 г.,224 с.
16. ЗолотареваС.И. Практикум по ACCESS – М.:Финансы и статистика, 2000 144с.
17. Ковальски С. EXCEL 2000 без проблем. – М.: Бином, 2000. 480 с.
18. Робинсон С. MICROSOFT ACCESS 2000:учебный курс–СПб.:Питер,2000 512с.
19. Хоффбауэр М. ACCESS: сотни полезных советов. / М. Хоффбауэр, К. Шпильман. – К.: BHV, 1997. 400 с.
б) дополнительная литература
1. Уолш Т. Программирование на Бейсике. - М.: Радио и связь, 1987. 336 с.
2. Белов В.Ф. Лабораторный практикум по курсу "Численные методы решения задач строительства на ЭВМ"/ Мордов.ун-т. Саранск, 1986. 24 с.
3. Белов В.Ф. Учебно-исследовательская система автоматизированного проектирования: подсистемы моделирования и оптимизации: Учебн.пособие/ Мордов. ун-т. -Саранск,1988. 84 с.
4. Пинтер Л. FoxPro 2.0. - М: Эдэль, 1994. 364 с.
в) программное обеспечение и Интернет- ресурсы: MICROSOFT OFFICE, Free Pascal, Visual Basic for Application(VBA).
10. Материально-техническое обеспечение дисциплины:
Персональный компьютер с ОС WINOWS XP, оперативная память не менее 1 Гб, процессор не раньше Intel Pentium 4 или аналог, тактовая частота не менее 3 ГГц.
Авторы (разработчики):
| кафедра САПР | | доцент | | Рябухина Е.А. |
| Рецензенты(эксперты) | | | | |
| Кафедра строительных материалов и технологий | | доцент | | Ерофеева А.А. |
| Кафедра строительной механики | | профессор | | Черкасов В.Д. |
Программа одобрена на заседании
(Наименование уполномоченного органа вуза (УМК, НМС, Ученый совет)
от года, протокол № .
.
5. Структура учебной дисциплины (модуля)
| № п/п | Раздел учебной дисциплины | Курс | Семестр | Неделя семестра | Виды учебной работы, в т.ч. СРС и трудоёмкость (в часах) | Формы текущего контроля успеваемости (по неделям семестра) | Форма промежуточной аттестации | ||
| лекции | Лабораторные занятия | СРС | |||||||
| 1. | Алгоритмы | 1 | 1 | 1-3 | | 6 | 20 | отчет | |
| 2. | Язык программирования | 1 | 1 | 1-18 | 14 | 18 | 20 | отчет | зачет |
| 3. | Офисные технологии | 1 | 2 | 1-9 | 10 | 12 | 20 | отчет | |
| 4. | Численные методы | 1 | 2 | 10-18 | 10 | 16 | 34 | отчет | экзамен |
Приложение1.
- Заменить отрицательные элементы под главной диагональю матрицы А(5,5) их квадратами ( матрицу А считать целочисленной).
- Разделить элементы матрицы А(5,5), лежащие в интервале [3;7] на сумму элементов главной диагонали.
- Поменять местами строки с минимальным и максимальным элементами матрицы А(5,5)(матрицу А считать целочисленной).
- Подсчитать количество строк матрицы А(5,5), не содержащих отрицательные элементы ( матрицу А считать целочисленной).
- Определить, является ли матрица А(5,5) симметричной относительно главной диагонали ( матрицу А считать целочисленной).
- В матрице А(5,5) заменить элементы, лежащие в интервале [1;5] на симметричные им относительно главной диагонали( матрицу А считать целочисленной, определить ее таким образом, чтобы два симметричных элемента не относились оба к указанному интервалу).
- Верно ли, что сумма элементов четных строк матрицы А(6,6) в два раза больше суммы элементов нечетных строк (матрицу А считать целочисленной).
- Подсчитать сумму элементов главной и побочной диагоналей матрицы А(6,6) (матрицу А считать целочисленной).
- Верно ли, что минимальный и максимальный элемент матрицы А(5,5) находятся в одном столбце или одной строке. ( матрицу А считать целочисленной).
- Подсчитать количество строк матрицы А(5,5), являющихся арифметической прогрессией ( матрицу А считать целочисленной).
- Поменять местами минимальный и максимальный элементы матрицы А(5,5).
- Заменить в матрице А(5,5) элементы, лежащие в интервале [2;6] на максимальный элемент предшествующей строки (первая строка остается без изменений!).
- Определить максимальный из минимальных элементов каждого столбца матрицы А(5,5)
- В матрице А(5,5) поменять местами строки с максимальной и минимальной суммами элементов.
- Исключить из матрицы А(6,4) строку с минимальным элементом.
- Вставить в матрицу А(5,5) строку, состоящую из нулей, после строки с максимальным элементом.
- Подсчитать количество строк матрицы А(5,5), начинающихся с нуля или заканчивающихся нулем.
- Разделить положительные элементы матрицы А(5,5) на максимальный элемент под ее главной диагональю.
- Верно ли, что максимальный и минимальный элементы матрицы А(5,5) расположены по разные стороны ее главной диагонали.
- Верно ли, что сумма средних арифметических положительных элементов каждой строки матрицы в два раза больше ее максимального элемента.
- Верно ли, что сумма положительных элементов над главной диагональю матрицы А(5,5) равна сумме квадратов отрицательных элементов под ее главной диагональю.
- Вставить в матрицу А(5,5) строку, содержащую первые элементы каждой строки, после строки с номером К.
Вариант 1
- Вывести на печать неотрицательные значения функции
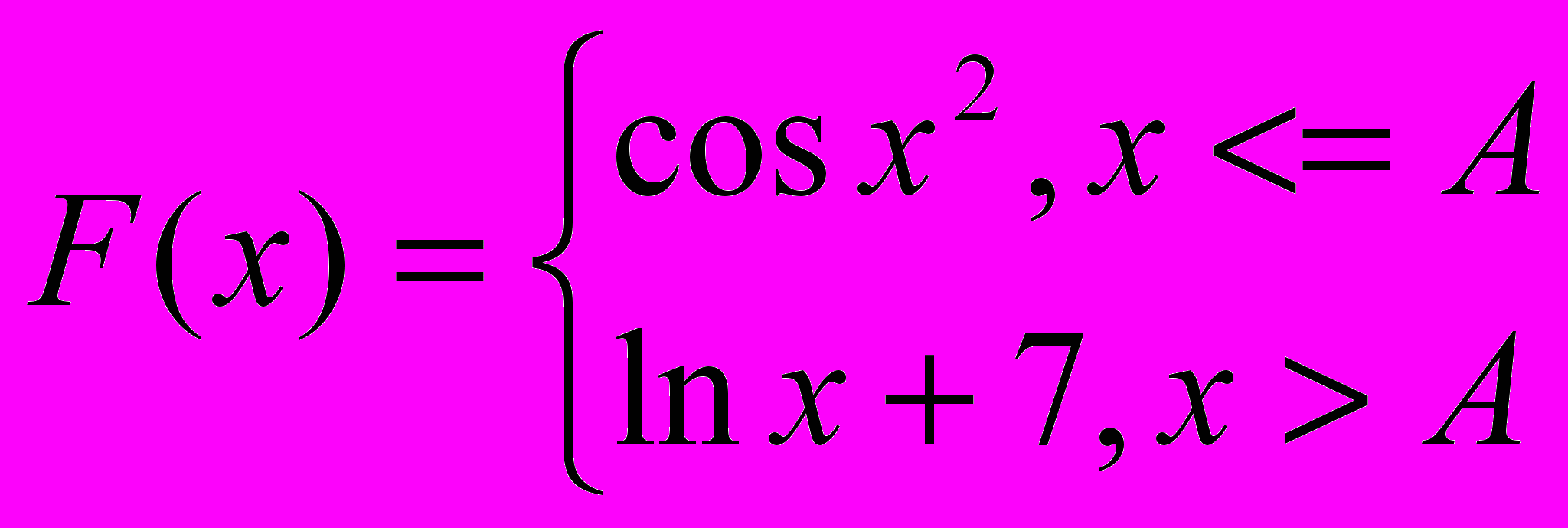 , Х изменяется от 1 до 12 с шагом 0.4 (С помощью всех четырех способов).
, Х изменяется от 1 до 12 с шагом 0.4 (С помощью всех четырех способов).
- Подсчитать сумму значений функции
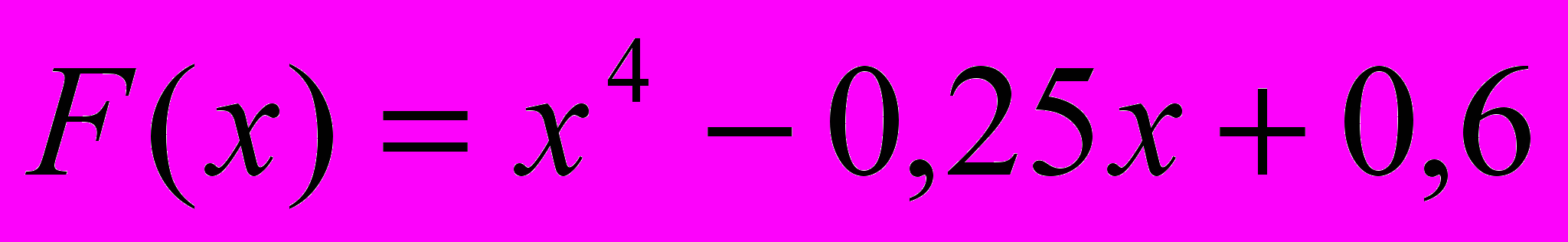 , лежащих в интервале [a;b]. Х изменяется от 10 до 12 с шагом 0.04.
, лежащих в интервале [a;b]. Х изменяется от 10 до 12 с шагом 0.04.
Вариант 2
- Вычислить величину
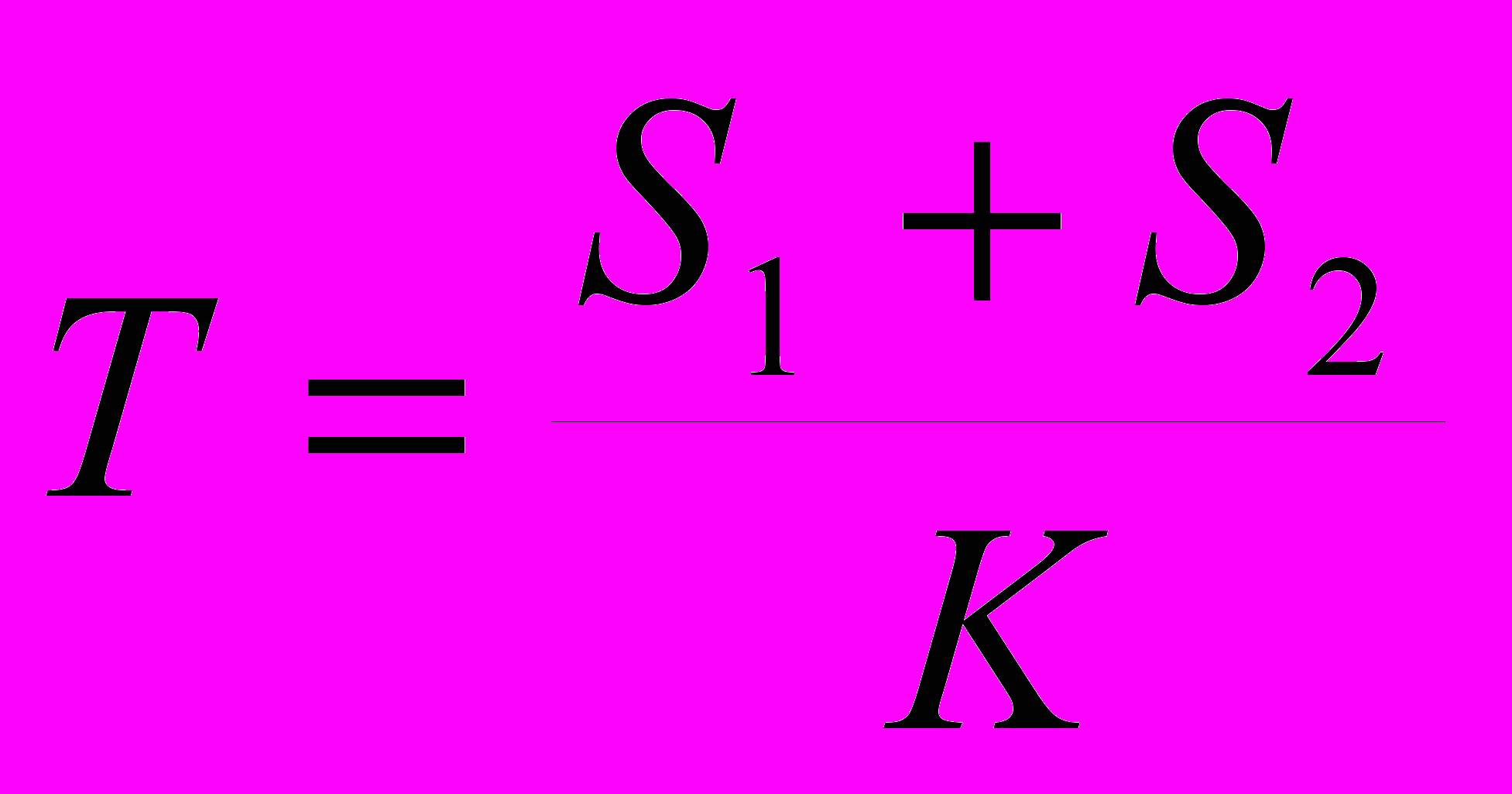 , где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов).
, где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов).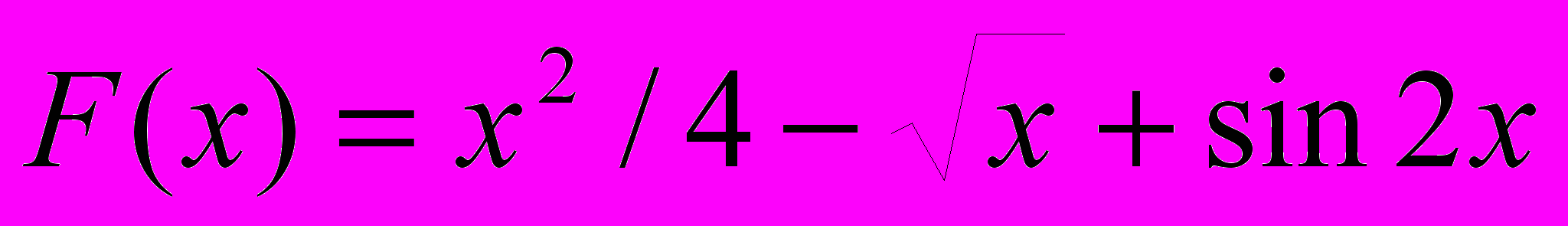
- Вывести на печать значения функции
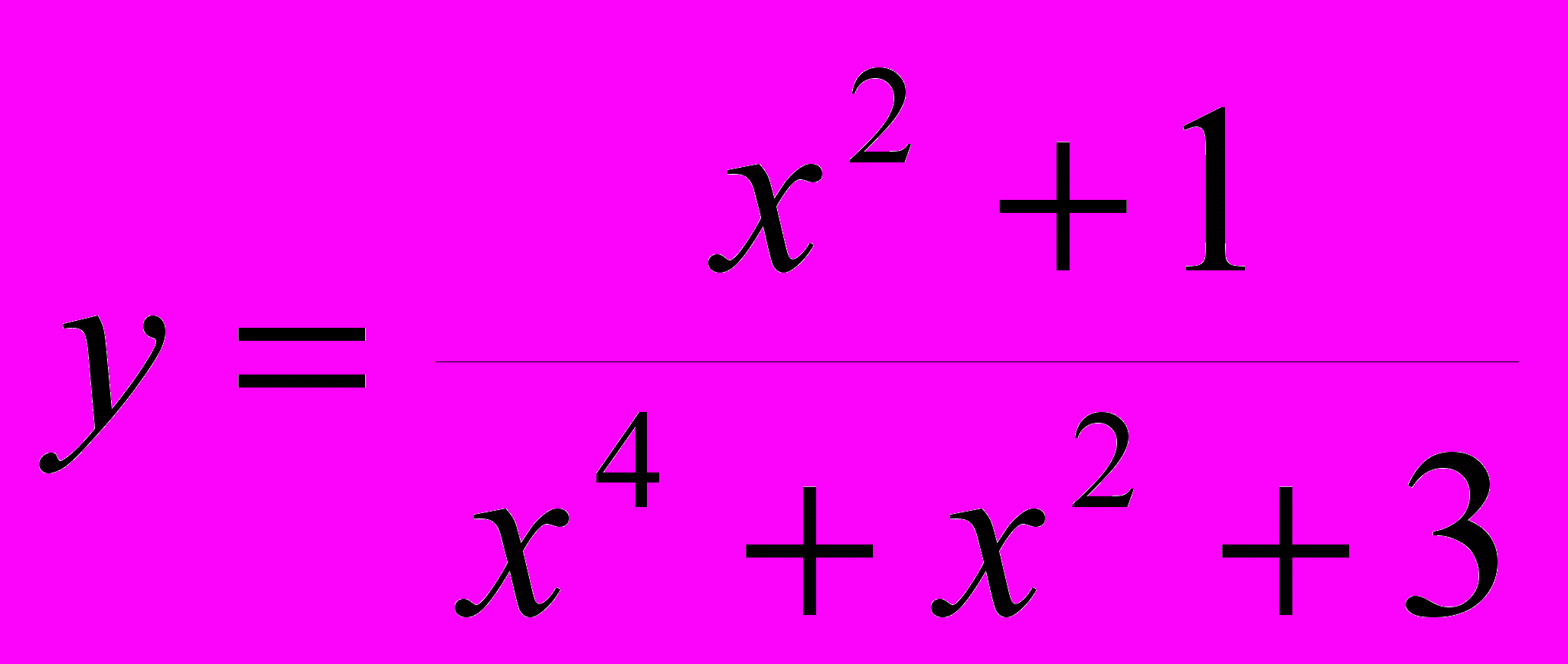 , при x изменяющемся от 0 с шагом 0.5 до y<0.005.
, при x изменяющемся от 0 с шагом 0.5 до y<0.005.
Вариант 3.
- Верно ли, что мах F(X) в 2 раза больше суммы модулей ее отрицательных значений. x изменяется от 1 до 18 с шагом 1 (с помощью всех четырех способов).
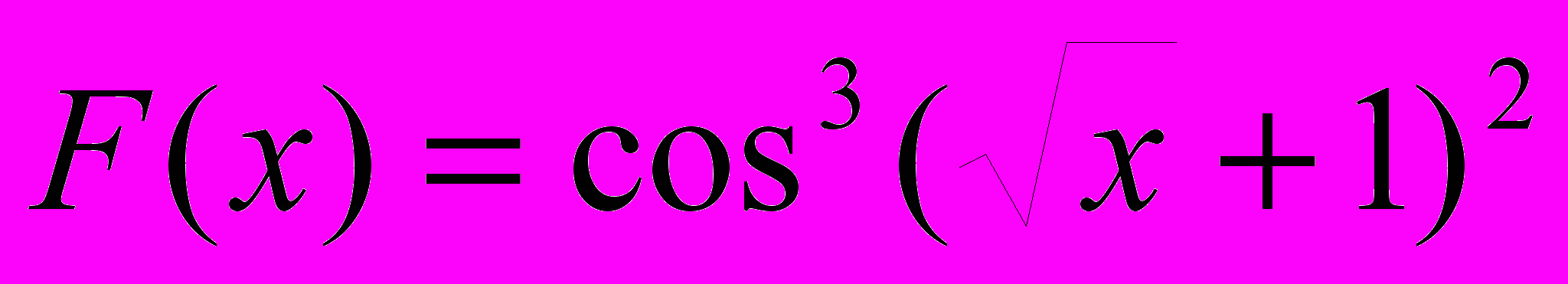
- Вычислить величину
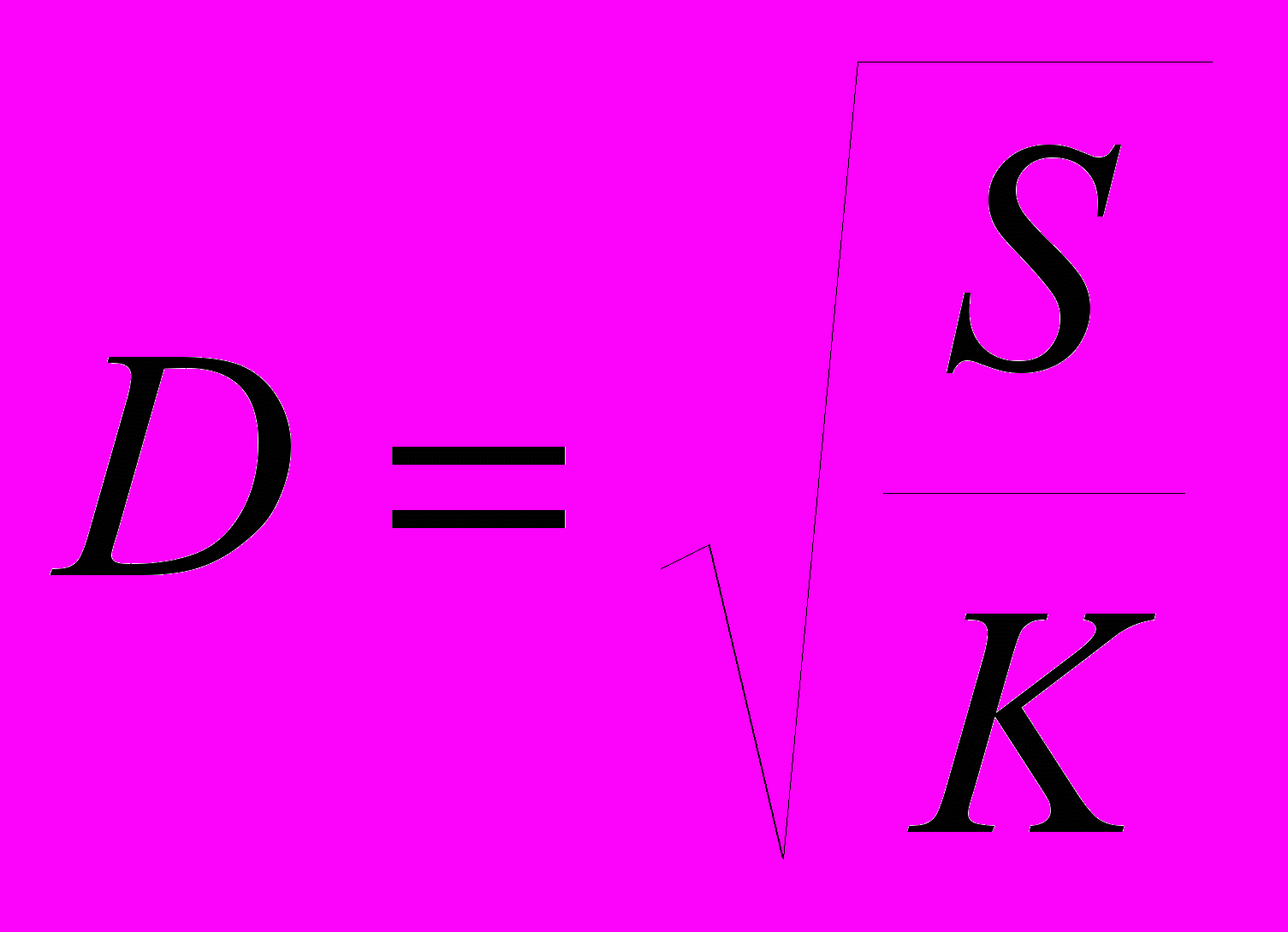 , где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений.
, где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений.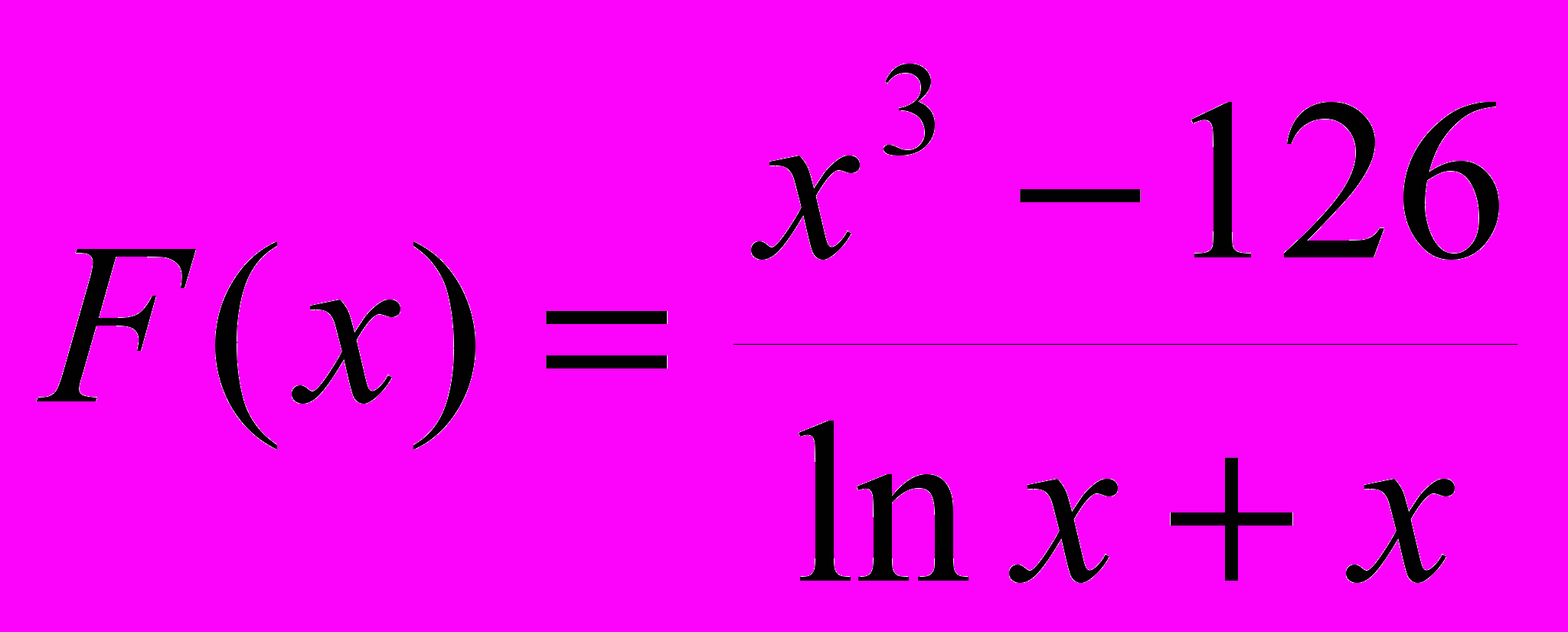 .Х изменяется от 1 до 13 с шагом 0.1
.Х изменяется от 1 до 13 с шагом 0.1
Вариант 4.
- Вывести на печать значений функции F(x), не лежащие в интервале [a,b]. x изменяется от 5 до 16 с шагом 0.2.
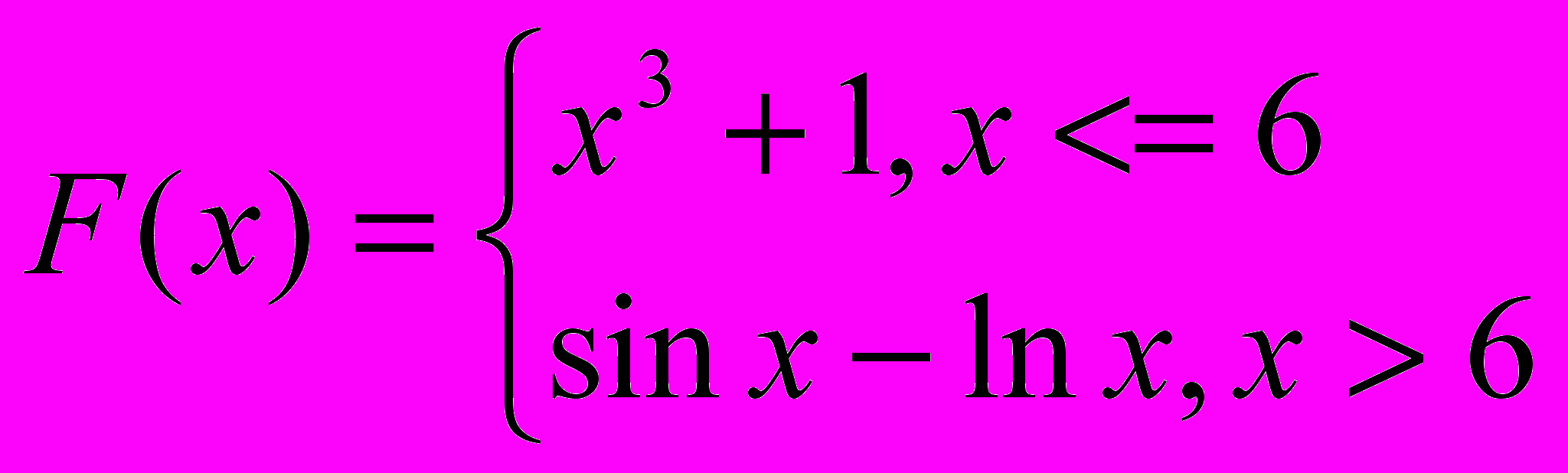
- Верно ли, что среднее арифметическое неотрицательных значений функции F(x) больше некоторого числа P. x изменяется от 4 до 81 с шагом 2.
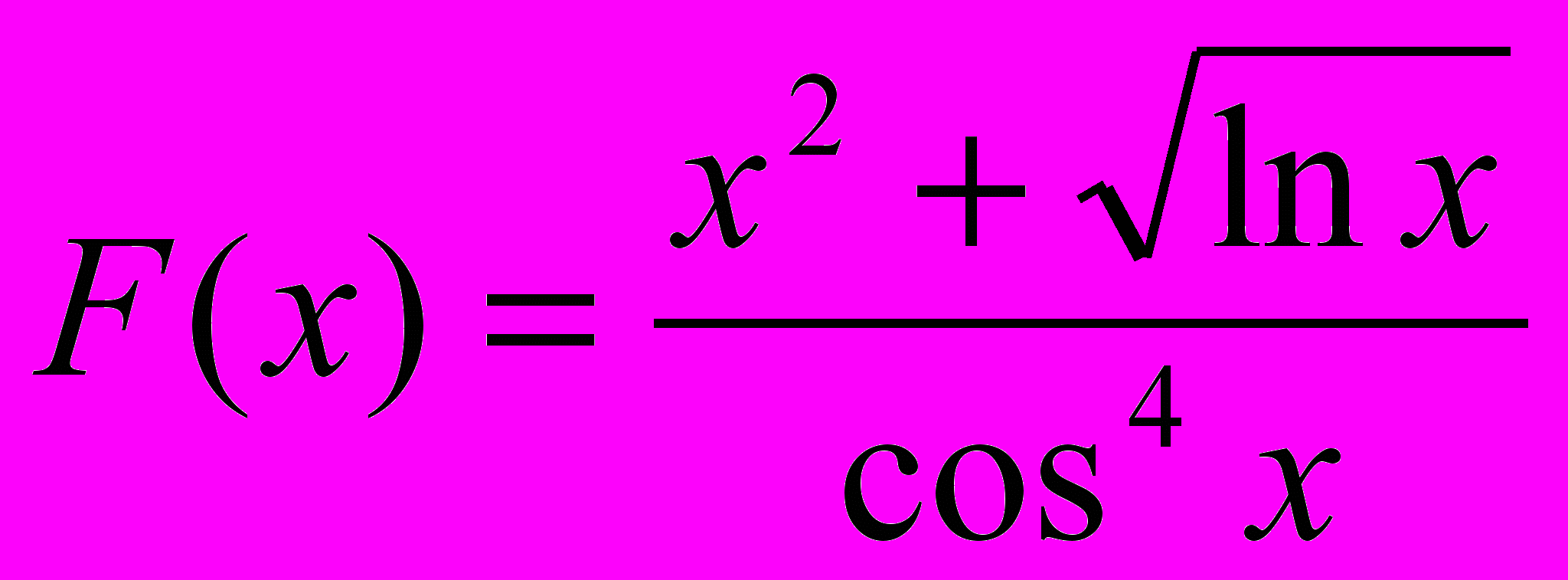
Вариант 5.
- Верно ли, что функция F(x) на интервале изменения x от 6 от 13 с шагом 0.3 принимает только положительные значения.
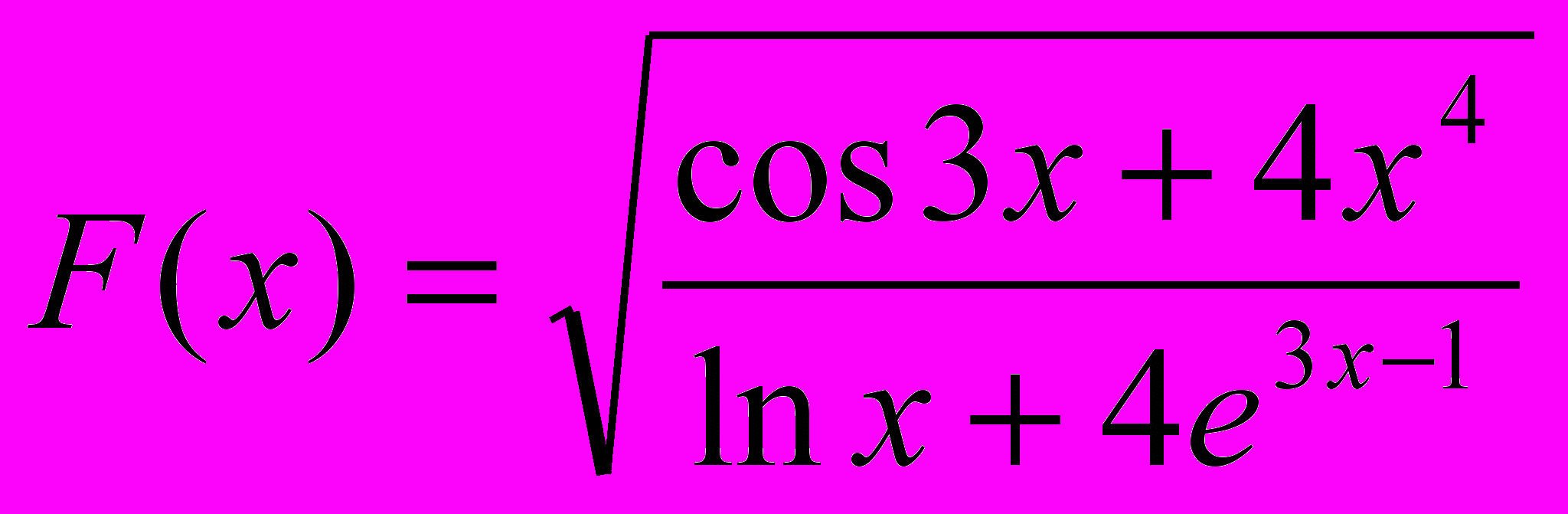
- Подсчитать сумму значений функции
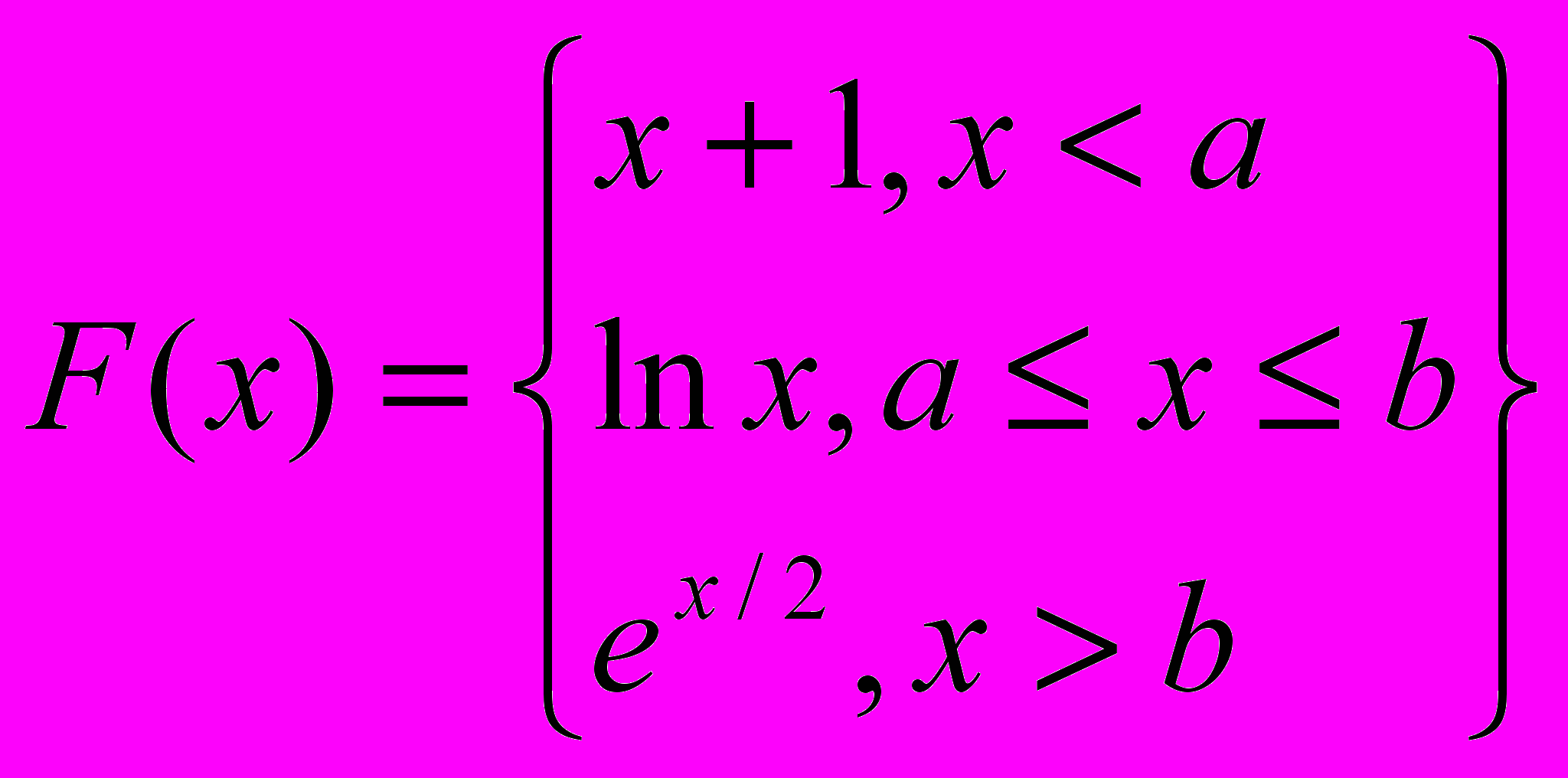 , меньших некоторого числа W. x изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).
, меньших некоторого числа W. x изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).
Вариант 6.
- Верно ли, что сумма положительных значений F(x) в 3 раза больше ее минимального значения ? х изменяется от 1 до 16 с шагом 0.3.
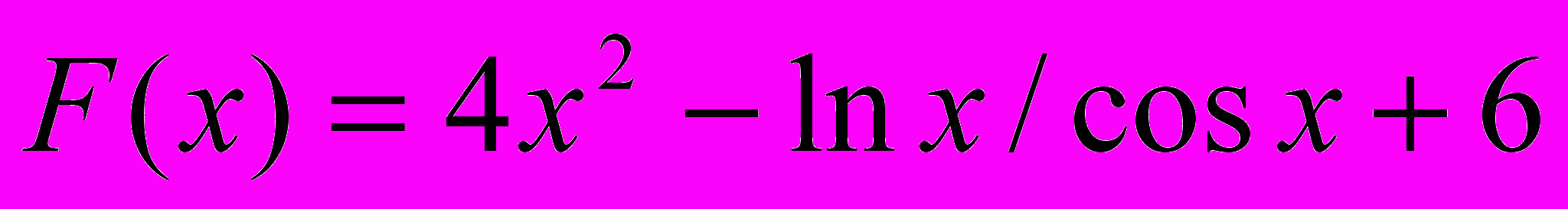
- Вывести на печать значения функции
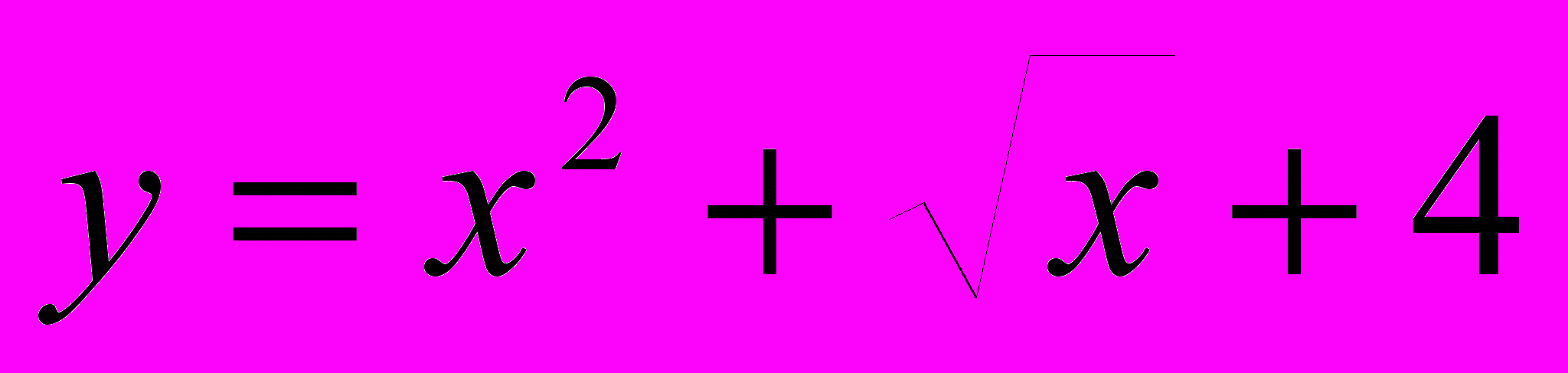 до y> 150. х изменяется от 1 с шагом 0.3.
до y> 150. х изменяется от 1 с шагом 0.3.
Вариант 7.
- Верно ли, что максимум функции F(x) в три раза больше ее минимума. х изменяется от 4 до 13 с шагом 0.1.
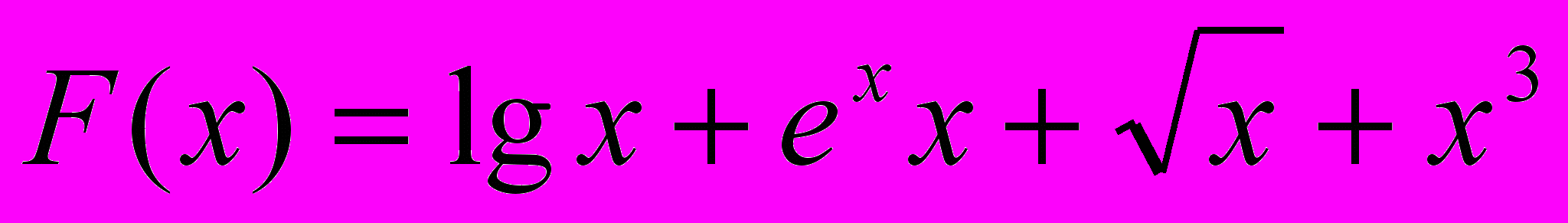
- Вычислить величину
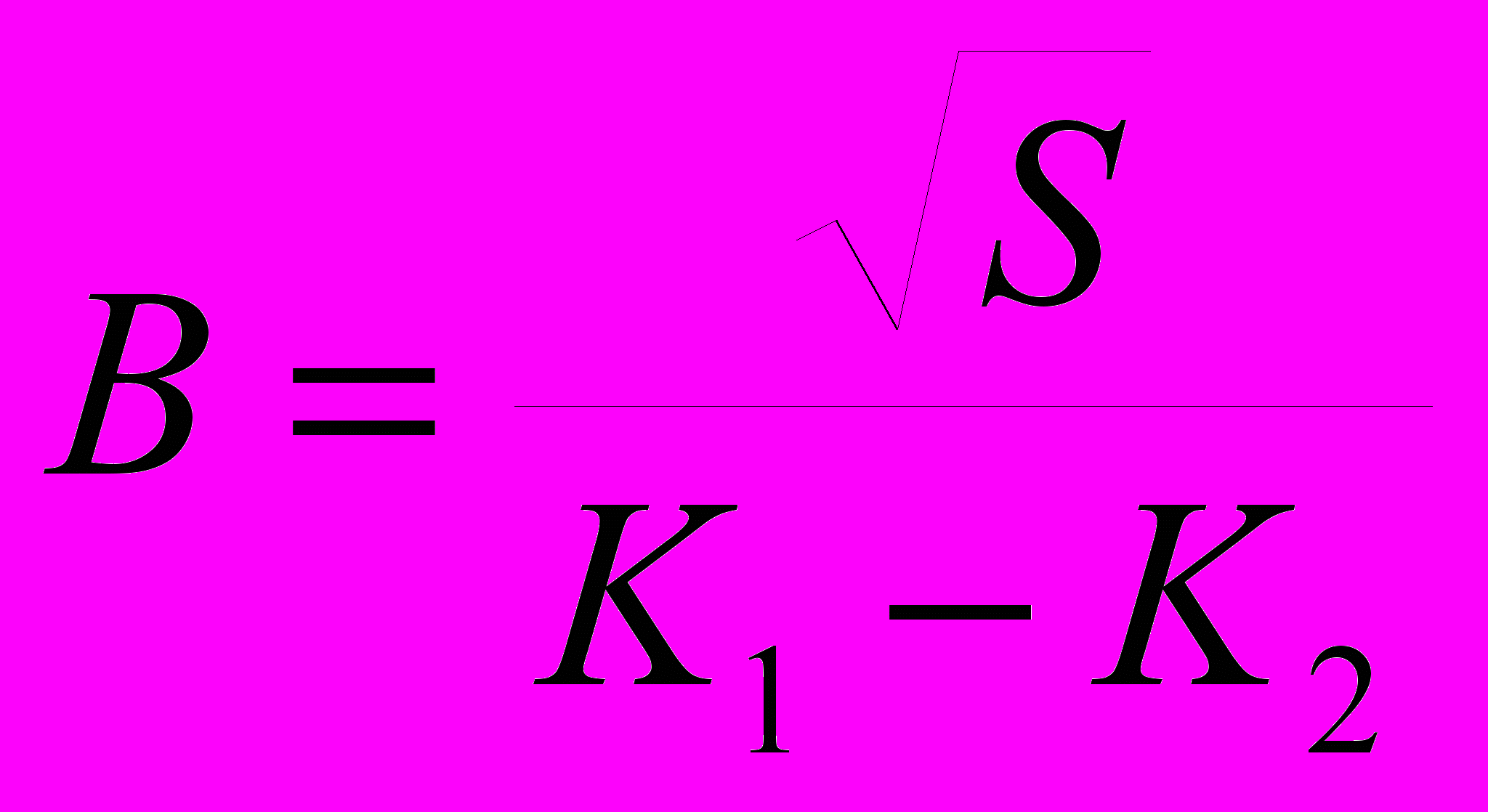 , где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. х изменяется от 5 до 15 с шагом 0.4.
, где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. х изменяется от 5 до 15 с шагом 0.4.

Вариант 8.
- Верно ли, что максимум функции F(x) лежит в интервале [5;12]. Х изменяется от 4 до 18 с шагом 0.5. (с помощью всех четырех способов).
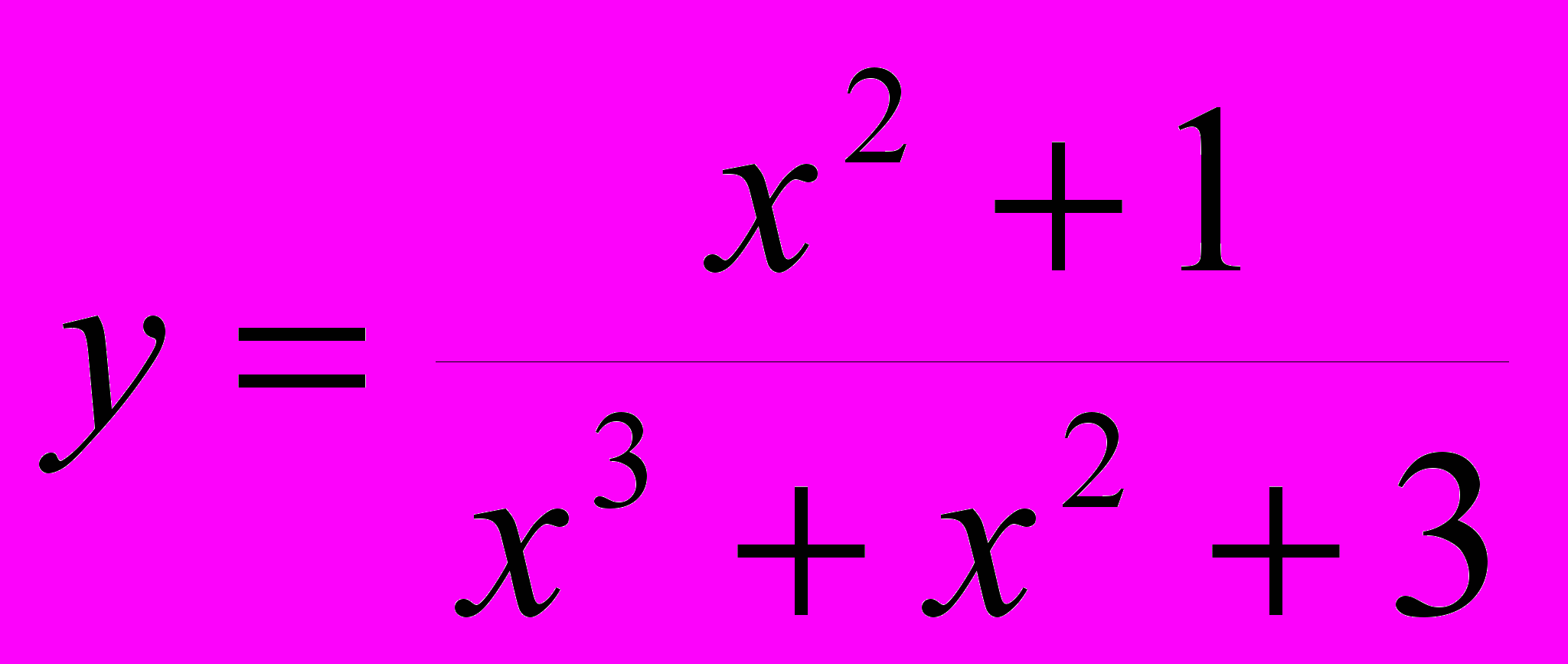 +6х
+6х
- Верно ли, что среднее значение функции
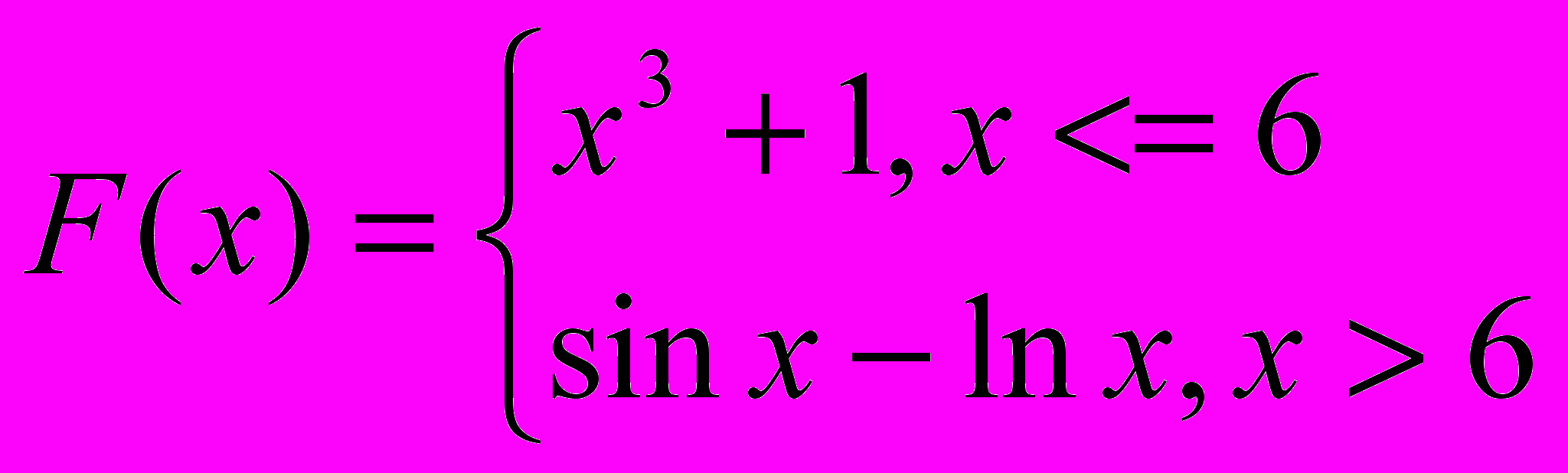 равно полусумме ее максимума и минимума. Х изменяется от 4 до 8 с шагом 0.3.
равно полусумме ее максимума и минимума. Х изменяется от 4 до 8 с шагом 0.3.
Вариант 9.
- Подсчитать количество значений функции F(x), меньших ее среднего значения ровно на 1. Х изменяется от 4 до 15 с шагом 0.2.
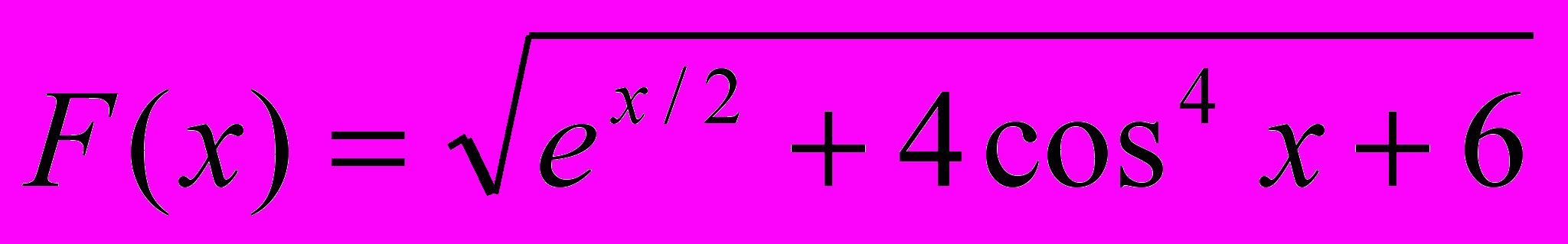
- Верно ли, что функция F(x) на отрезке изменения х от а до b с шагом 0.2 принимает только отрицательные значения.
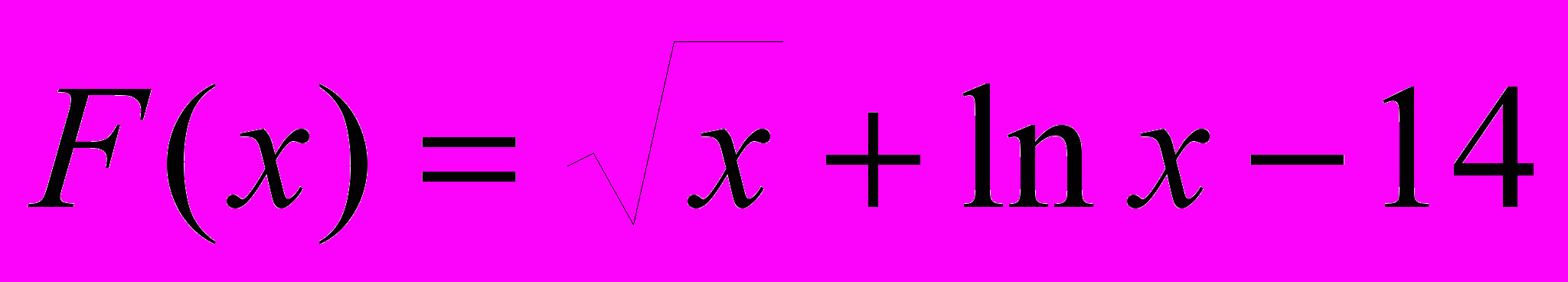
Вариант 10.
- Вычислить величину
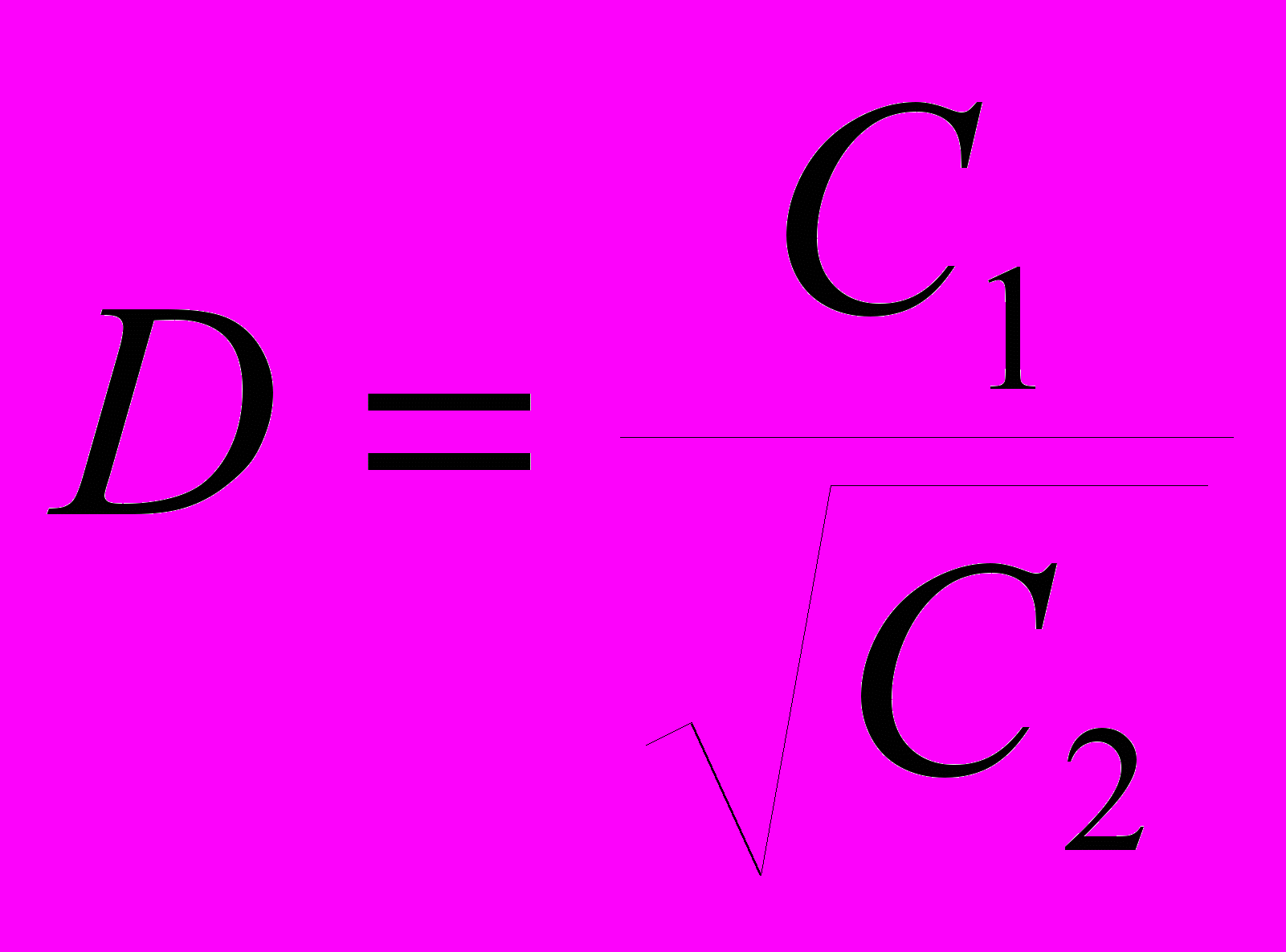 . где С2- среднее арифметическое положительных значений функции, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 5 до 18 с шагом 0.2.
. где С2- среднее арифметическое положительных значений функции, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 5 до 18 с шагом 0.2. 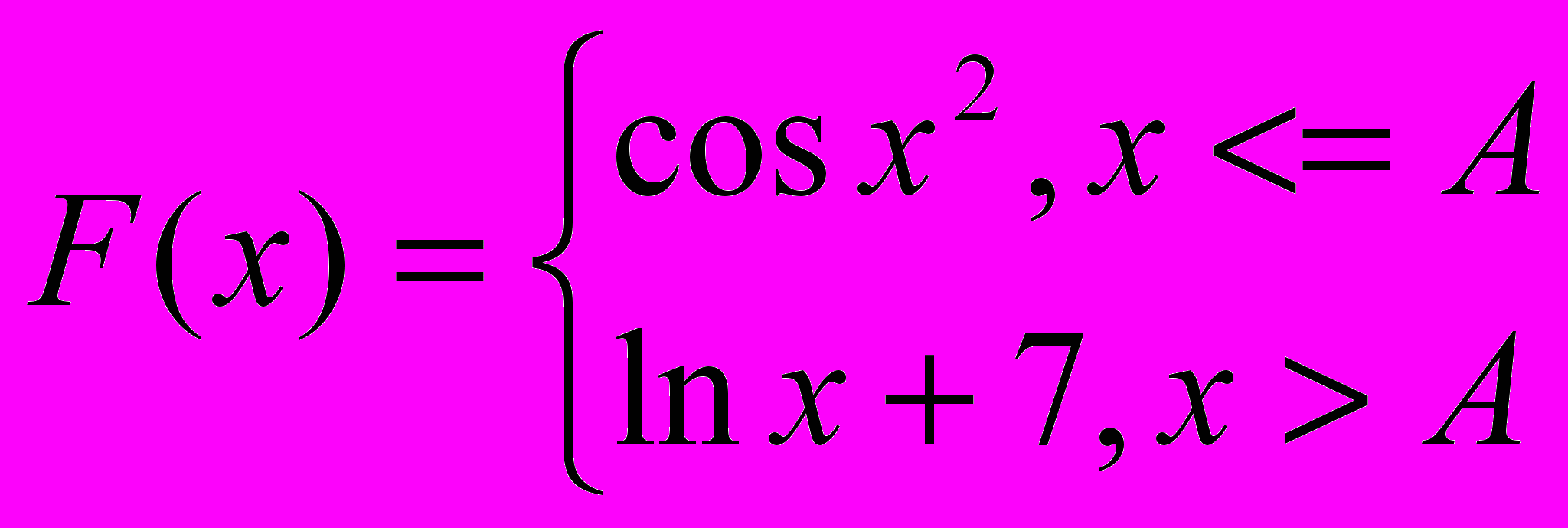
- Вывести на печать значения функции
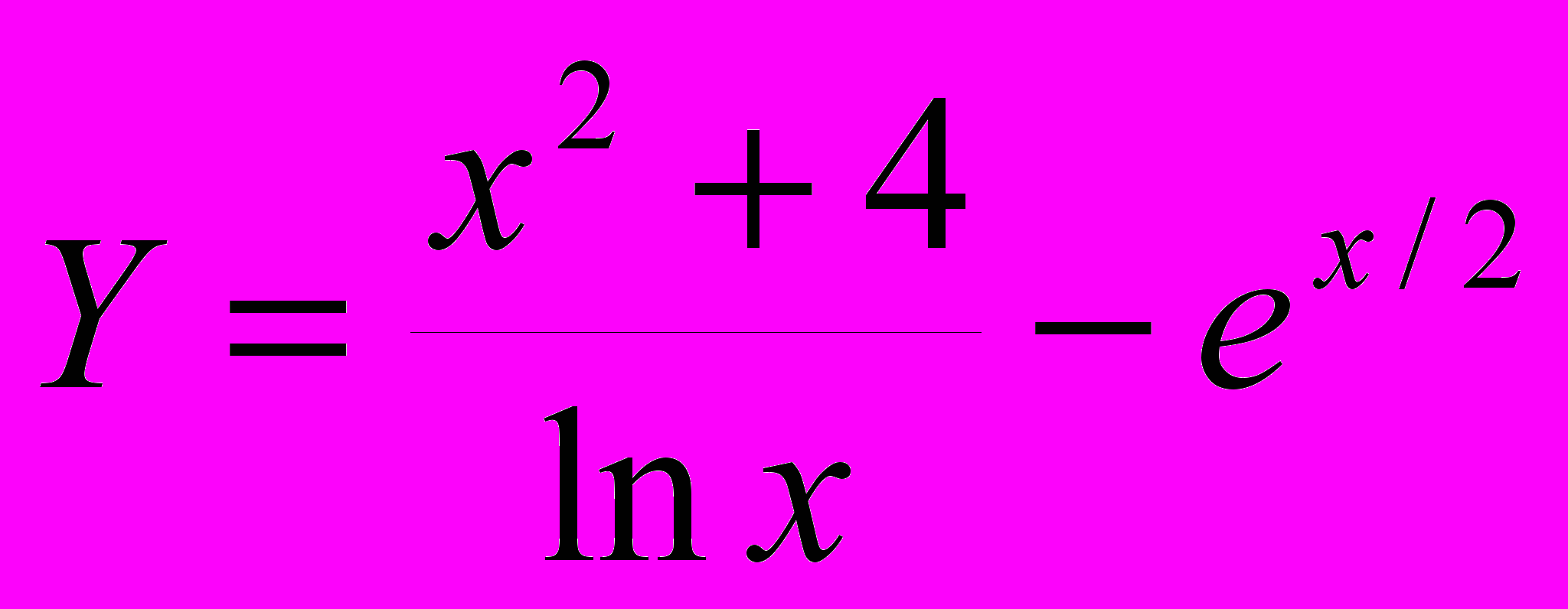 до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.
до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.
Вариант 11.
- Вычислить величину
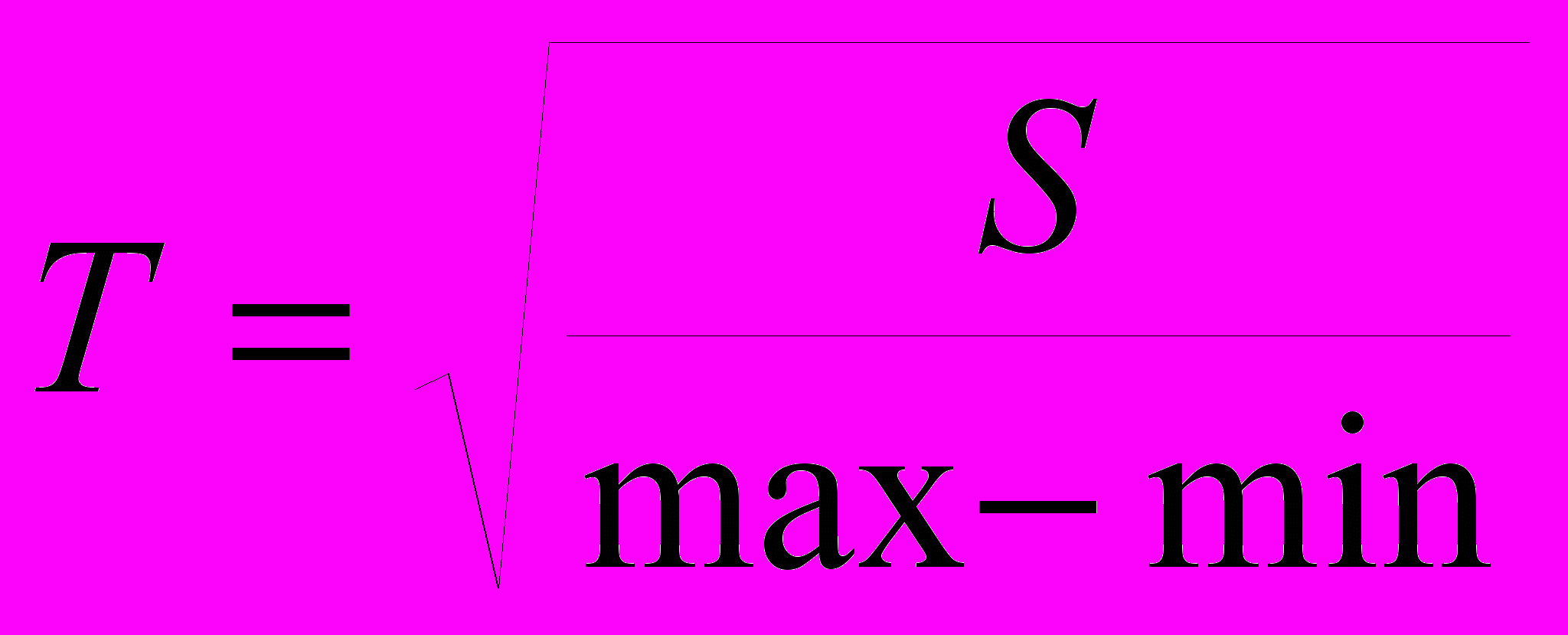 , где S – сумма неотрицательных значений функции F(x), Х изменяется от 4 до 8 с шагом 0.1.
, где S – сумма неотрицательных значений функции F(x), Х изменяется от 4 до 8 с шагом 0.1. 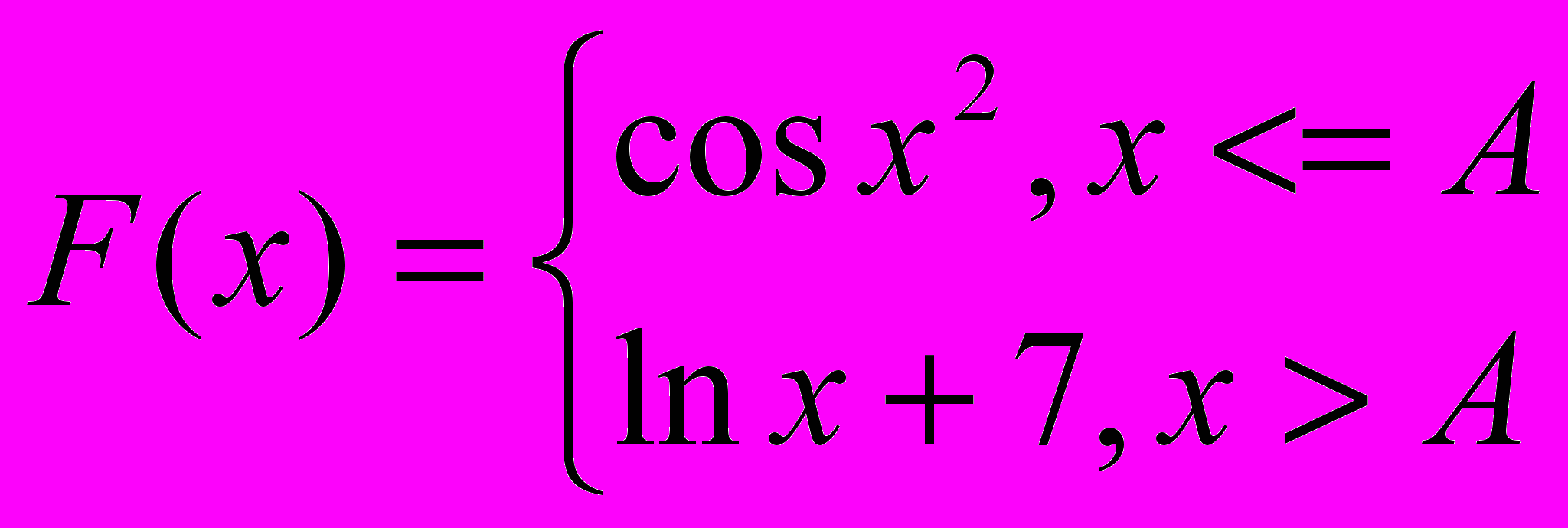
- Верно ли, что количество положительных значений функции F(x) в три раза меньше суммы ее положительных значений. Х изменяется от 30 до 36 с шагом 0.2
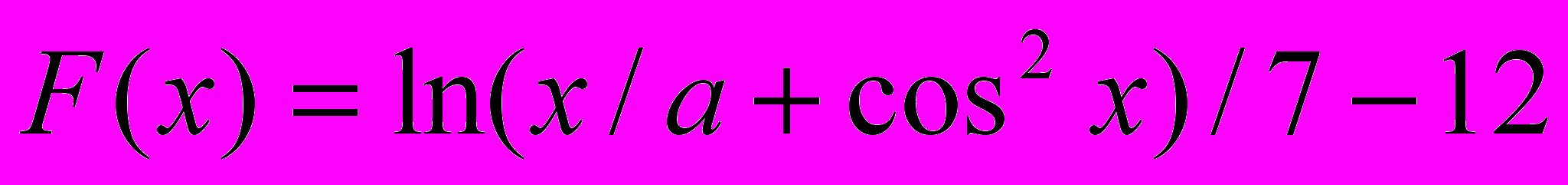
Вариант 12
1. Вывести на печать значения функции
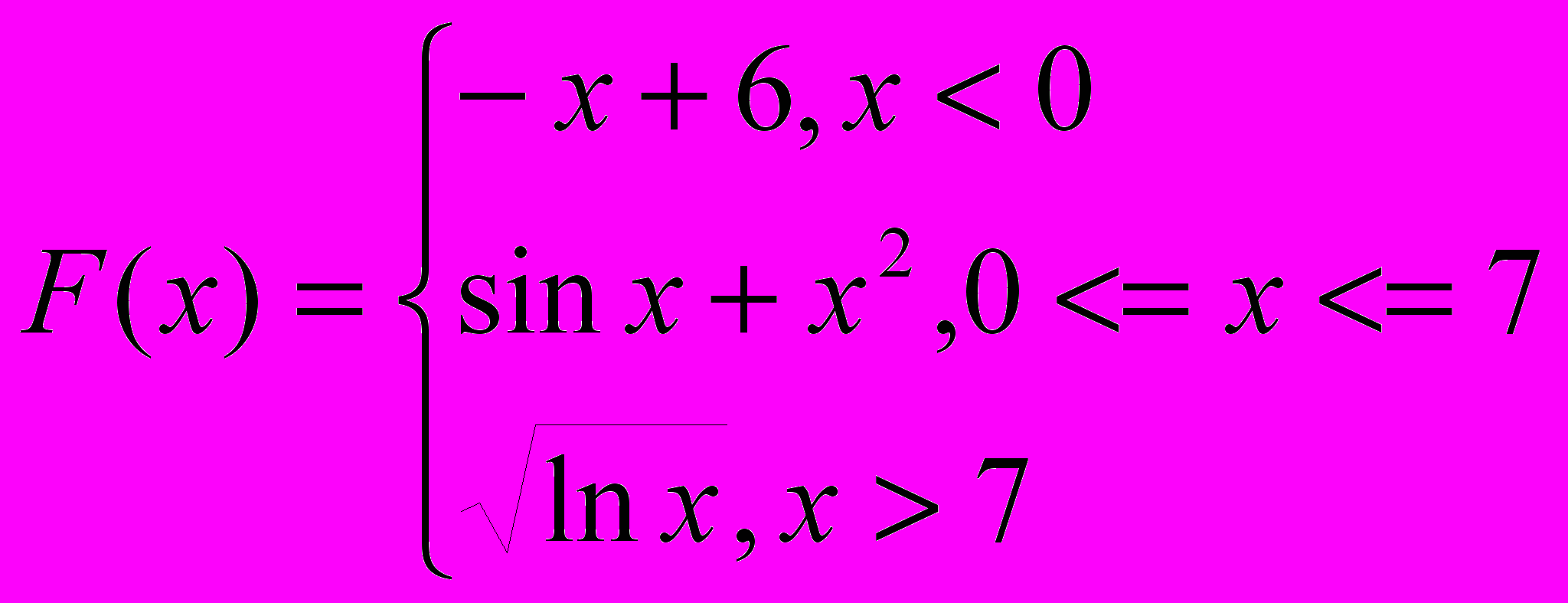 , лежащие в интервале [4;6] . Х изменяется от -5 до 6 с шагом 0.1.
, лежащие в интервале [4;6] . Х изменяется от -5 до 6 с шагом 0.1.2. Подсчитать сумму значений функции F(x), ровно в 2 раза меньших минимума функции. Х изменяется от 5 до 30 с шагом 0.3.
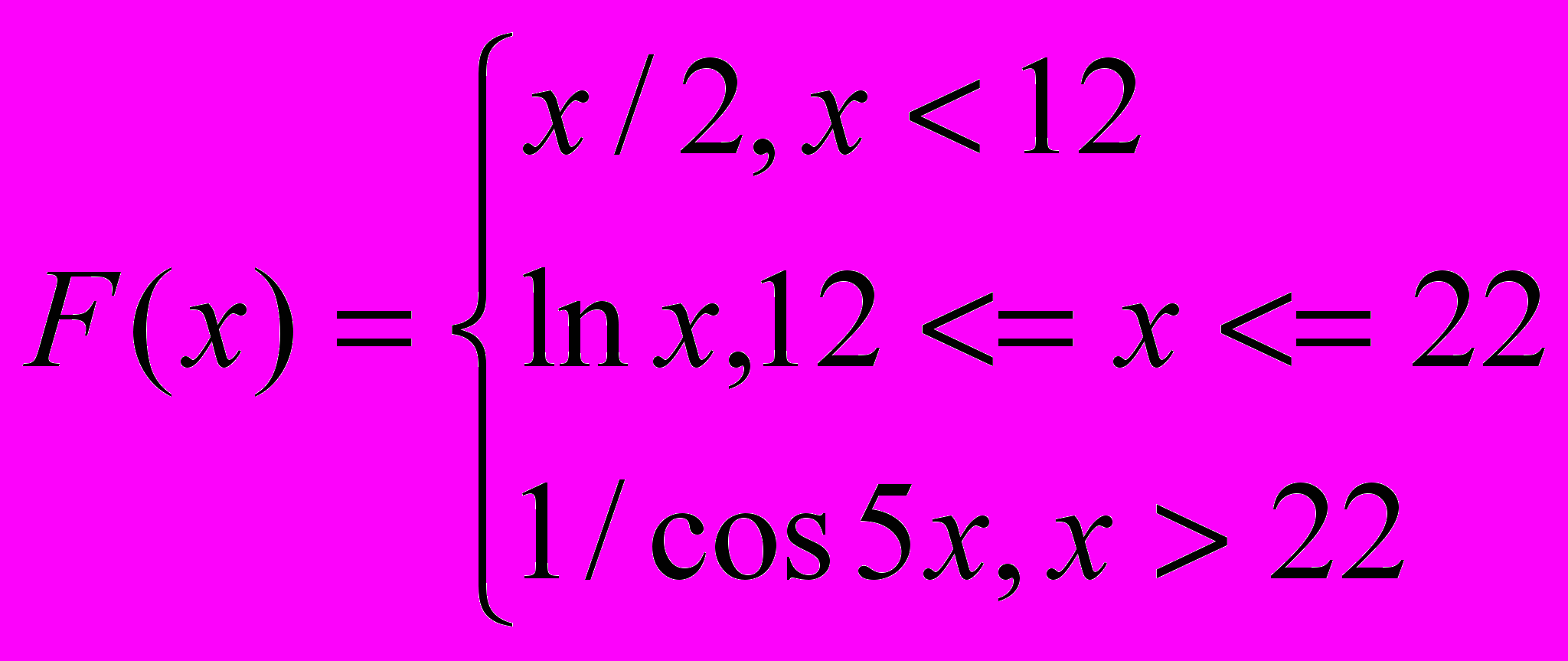
Вариант 13
1. Вывести на печать неотрицательные значения функции
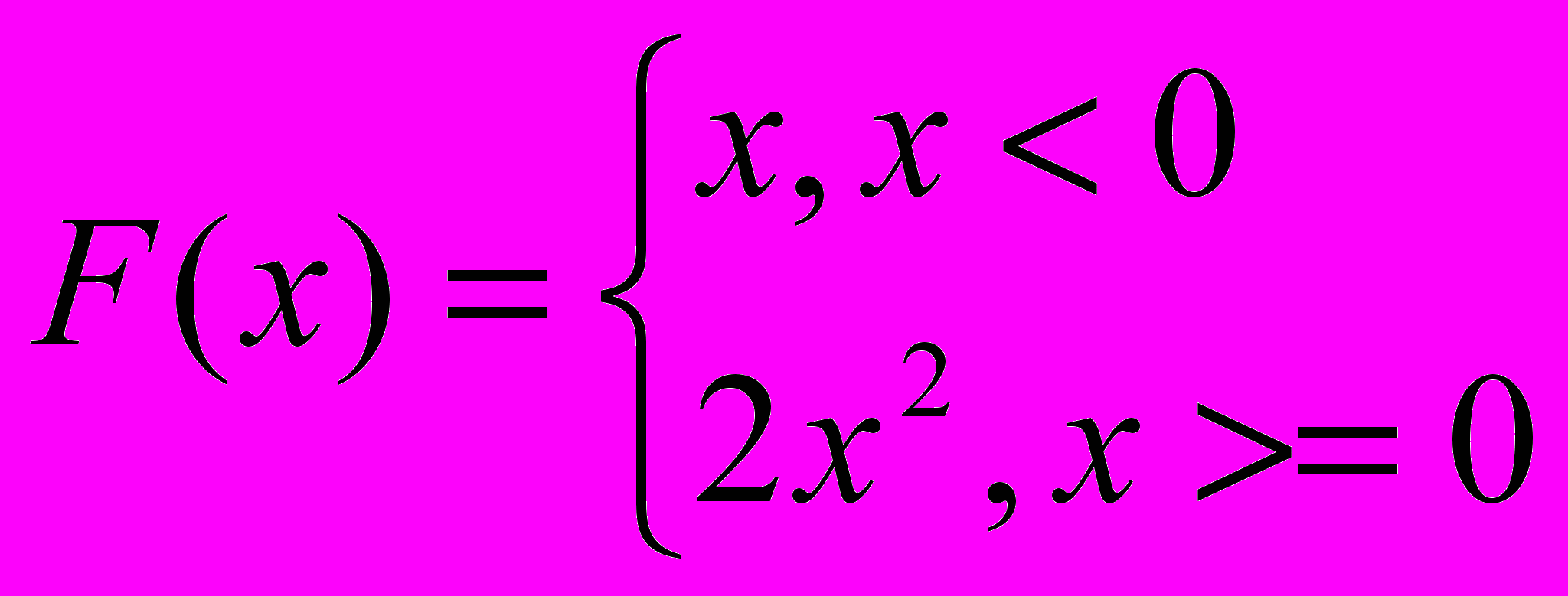 , Х изменяется от 1 до 12 с шагом 0.5 (С помощью всех четырех способов).
, Х изменяется от 1 до 12 с шагом 0.5 (С помощью всех четырех способов).2. Подсчитать сумму значений функции,
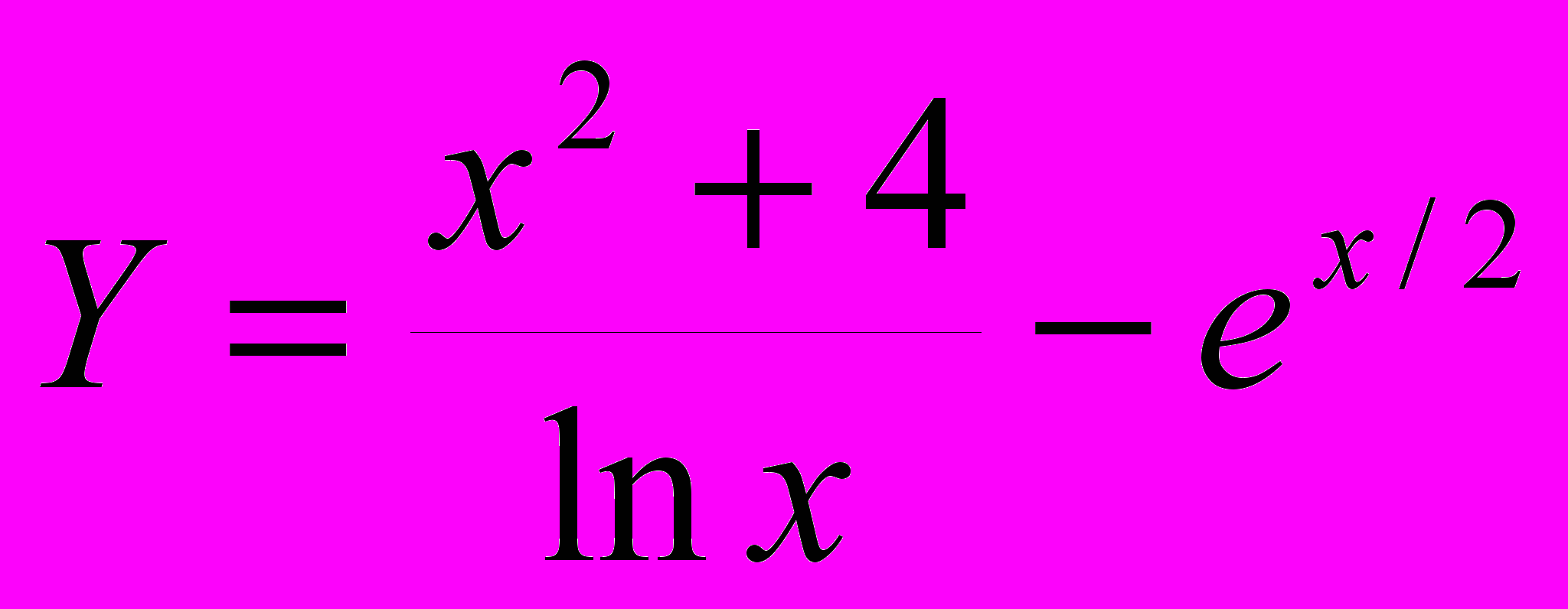 ,лежащих в интервале [a;b].Х изменяется от 3 до 12 с шагом 0.2.
,лежащих в интервале [a;b].Х изменяется от 3 до 12 с шагом 0.2.Вариант 14
1. Вычислить величину
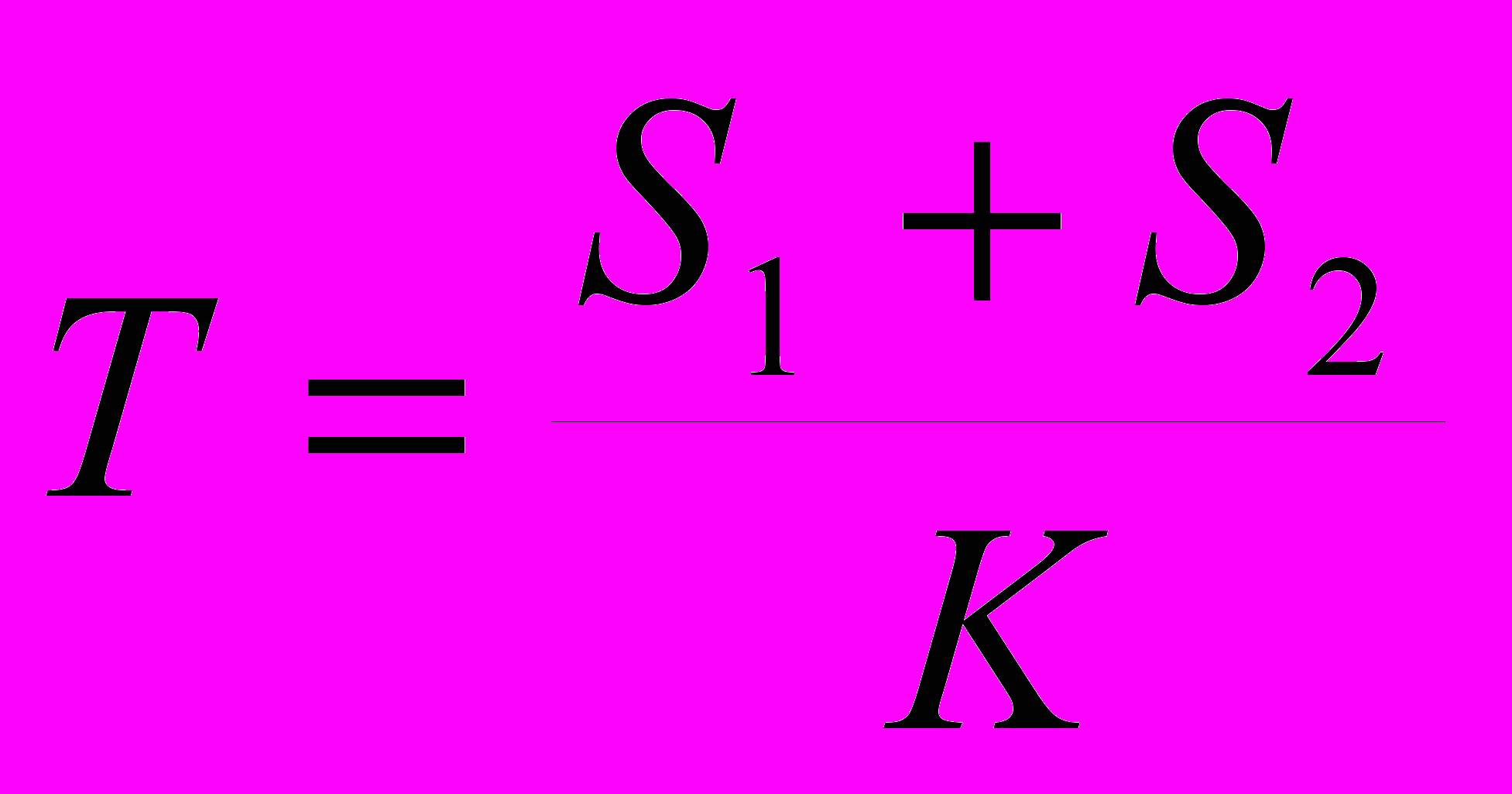 , где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов).
, где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов).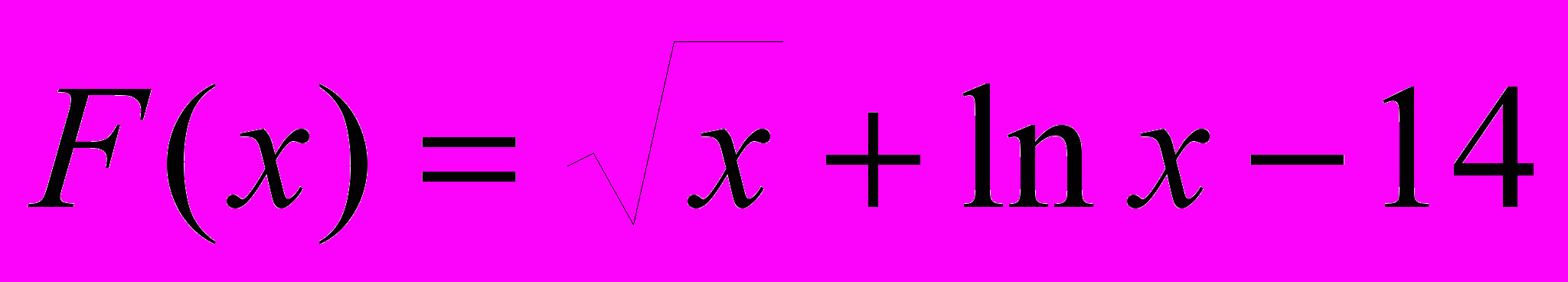 . Х изменяется от 4 до 15 с шагом 0.2.
. Х изменяется от 4 до 15 с шагом 0.2.2. Вывести на печать значения функции
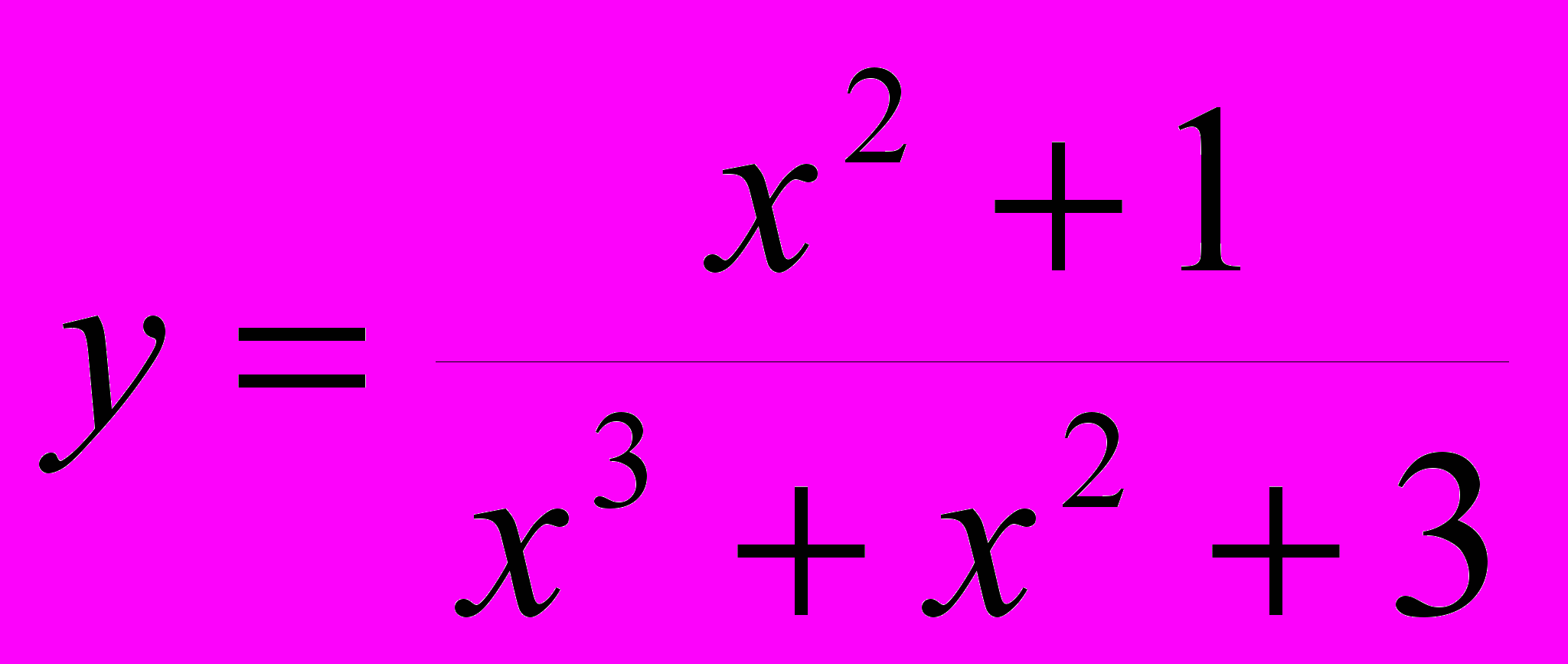 , при x изменяющемся от 5 с шагом 0.5 до y<0.003.
, при x изменяющемся от 5 с шагом 0.5 до y<0.003.Вариант 15.
1. Верно ли, что мах F(X) в 2 раза больше суммы модулей ее отрицательных значений. Х изменяется от 10 до 28 с шагом 1 (с помощью всех четырех способов).
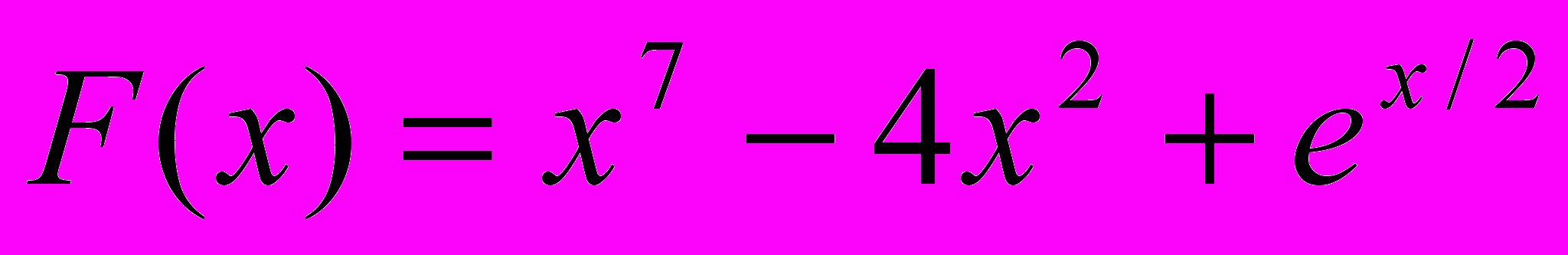
2. Вычислить величину
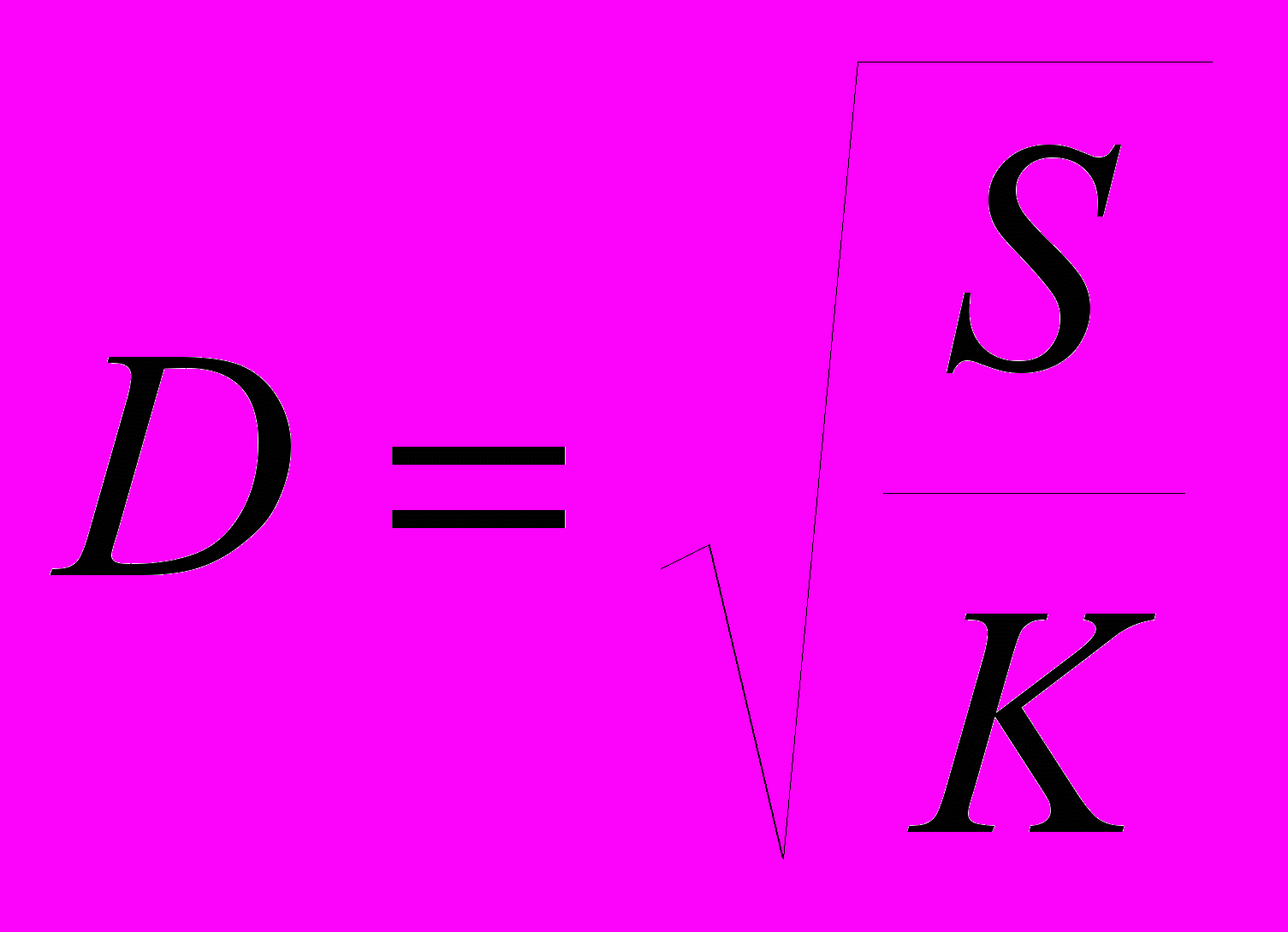 , где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений.
, где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений. 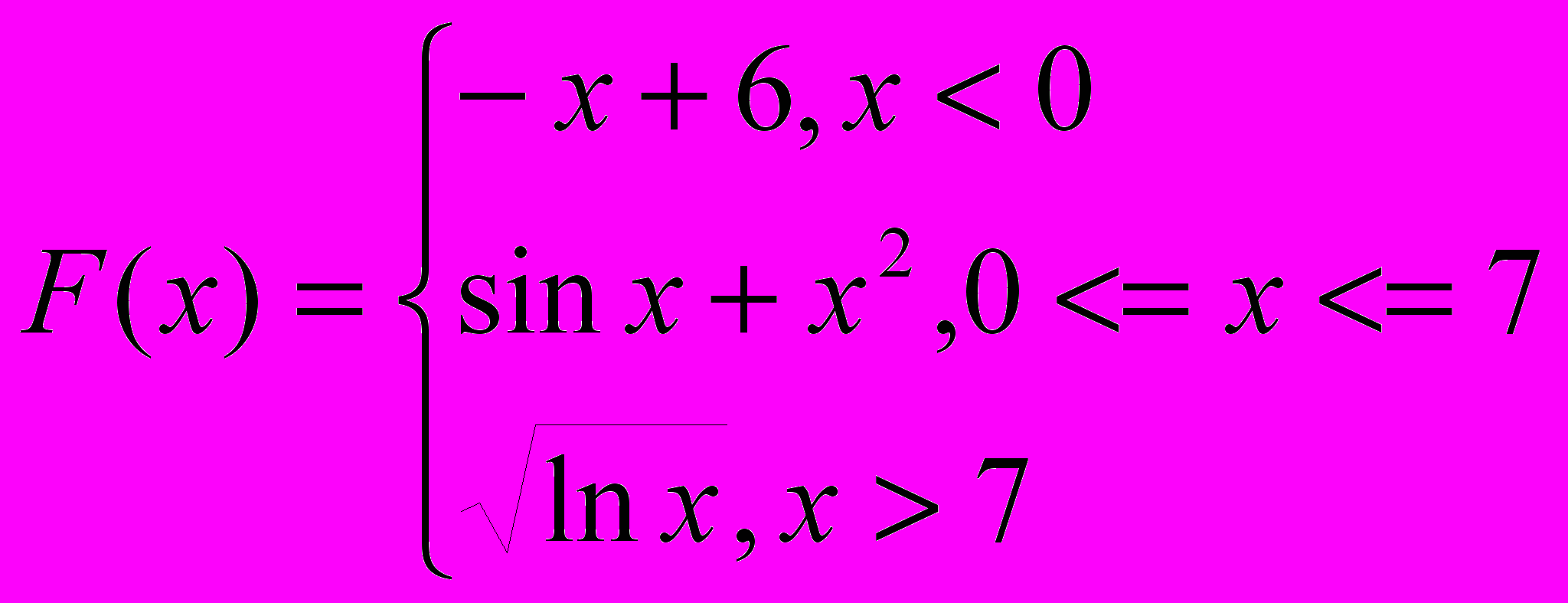
Вариант 16.
1. Вывести на печать значений функции F(x), не лежащие в интервале [a,b]. x изменяется от 5 до 16 с шагом 0.2.
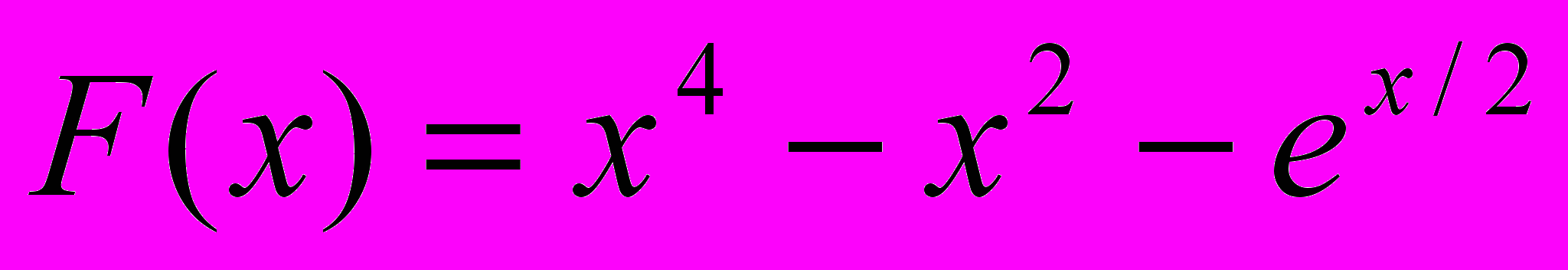
2.Верно ли, что среднее арифметическое неотрицательных значений функции
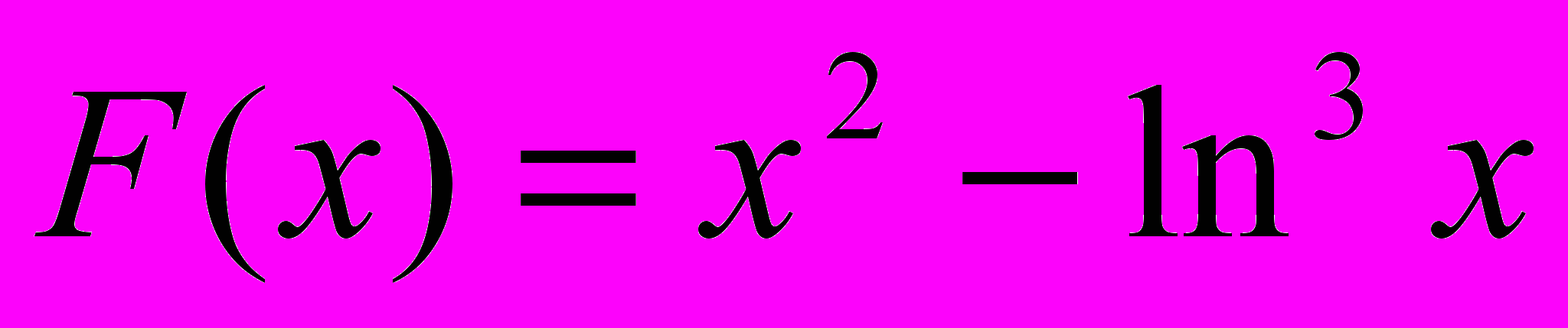 больше некоторого числа P. Х изменяется от 4 до 81 с шагом 2.
больше некоторого числа P. Х изменяется от 4 до 81 с шагом 2.Вариант 17.
1. Верно ли, что функция
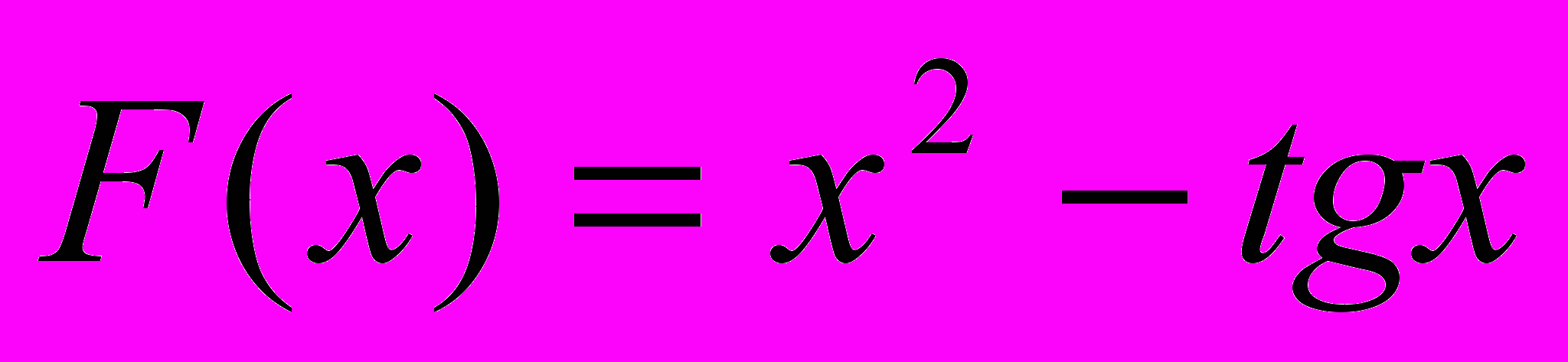 на интервале изменения x от 9 от 15 с шагом 0.3 принимает только значения, большие числа Р.
на интервале изменения x от 9 от 15 с шагом 0.3 принимает только значения, большие числа Р.2. Подсчитать сумму значений функции
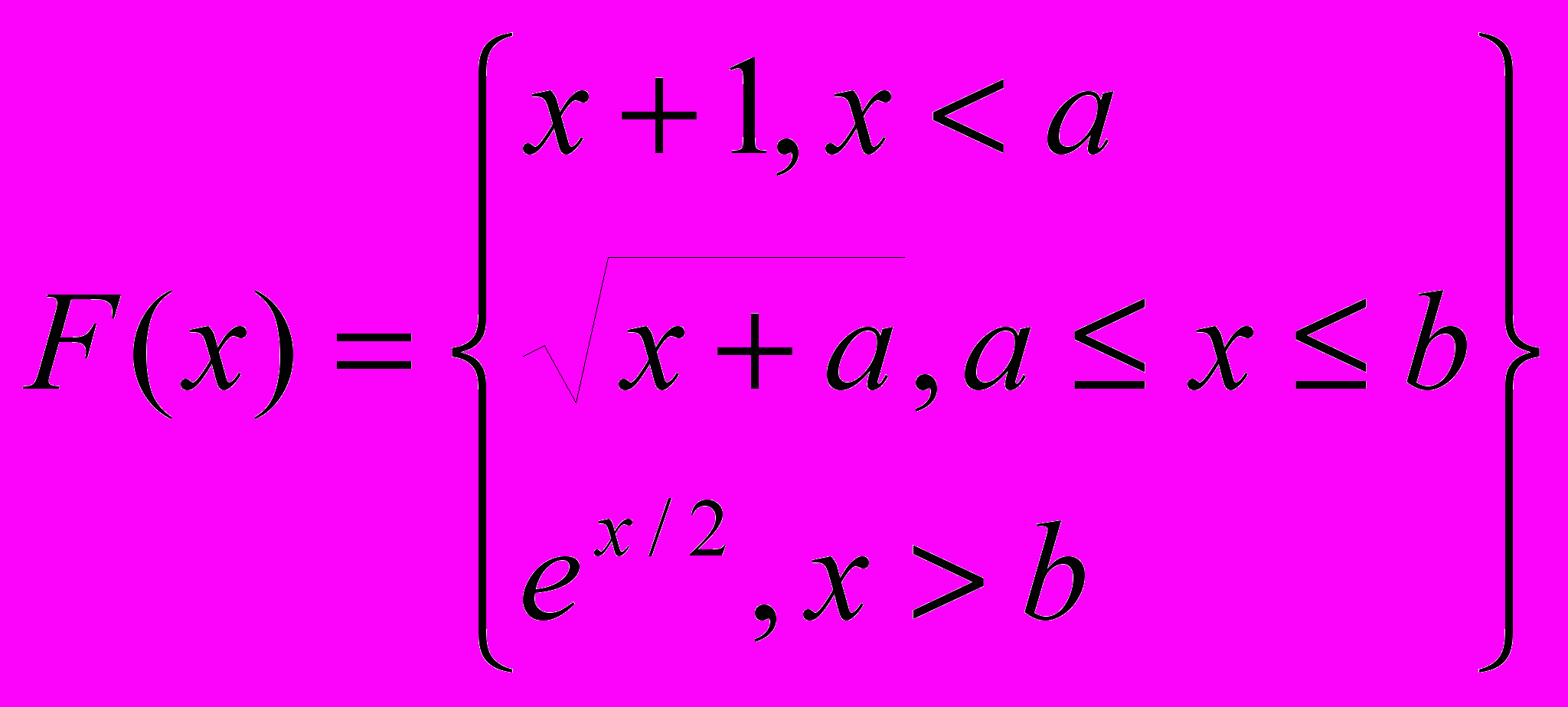 , меньших некоторого числа W. Х изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).
, меньших некоторого числа W. Х изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).Вариант 18.
1. Верно ли, что сумма положительных значений
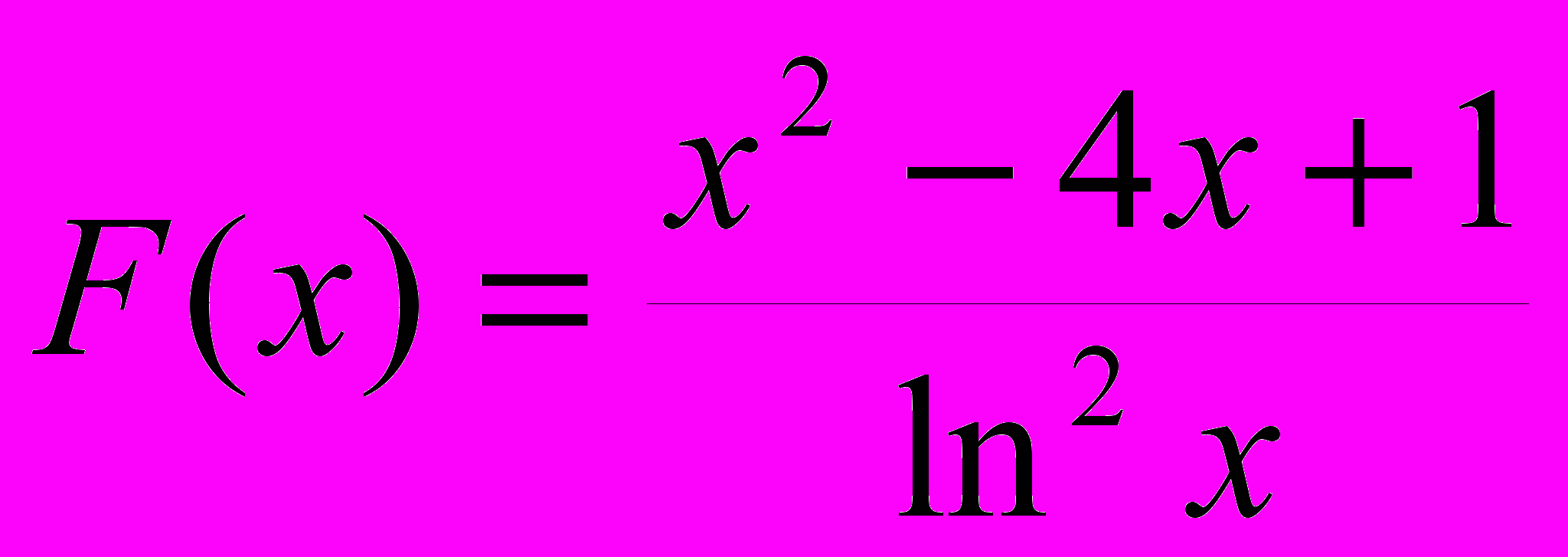 в 3 раза больше ее минимального значения ? Х изменяется от 10 до 29 с шагом 0.55.
в 3 раза больше ее минимального значения ? Х изменяется от 10 до 29 с шагом 0.55.2. Вывести на печать значения функции
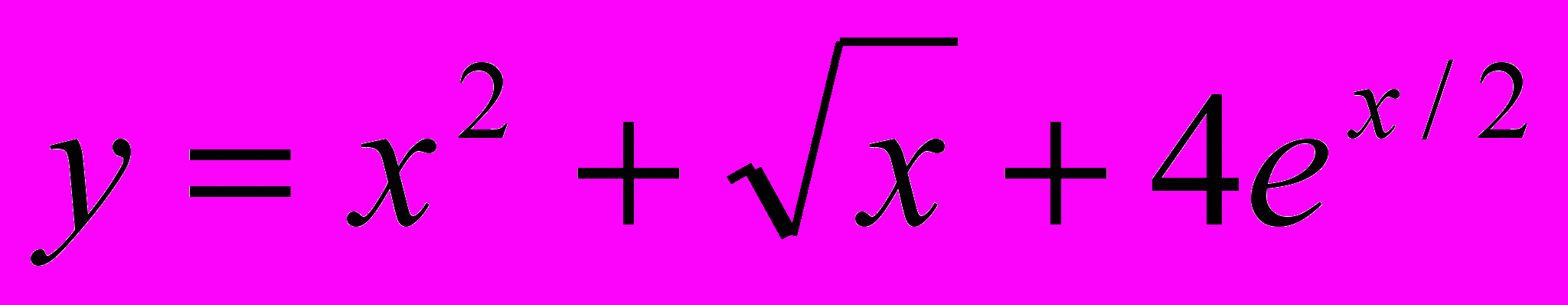 до y> 100. х изменяется от 0 с шагом 0.3.
до y> 100. х изменяется от 0 с шагом 0.3.Вариант 19.
1. Верно ли, что максимум функции F(x) в 5 раз больше ее минимума. Х изменяется от 4 до 13 с шагом 0.1.
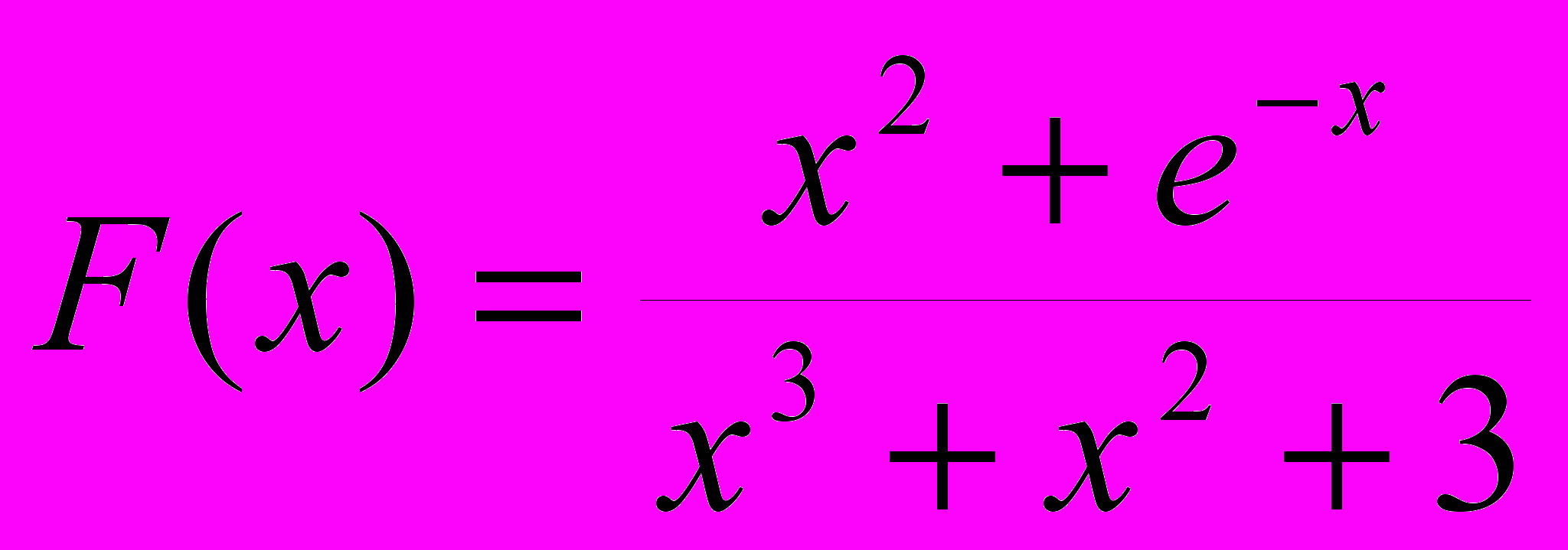
2. Вычислить величину
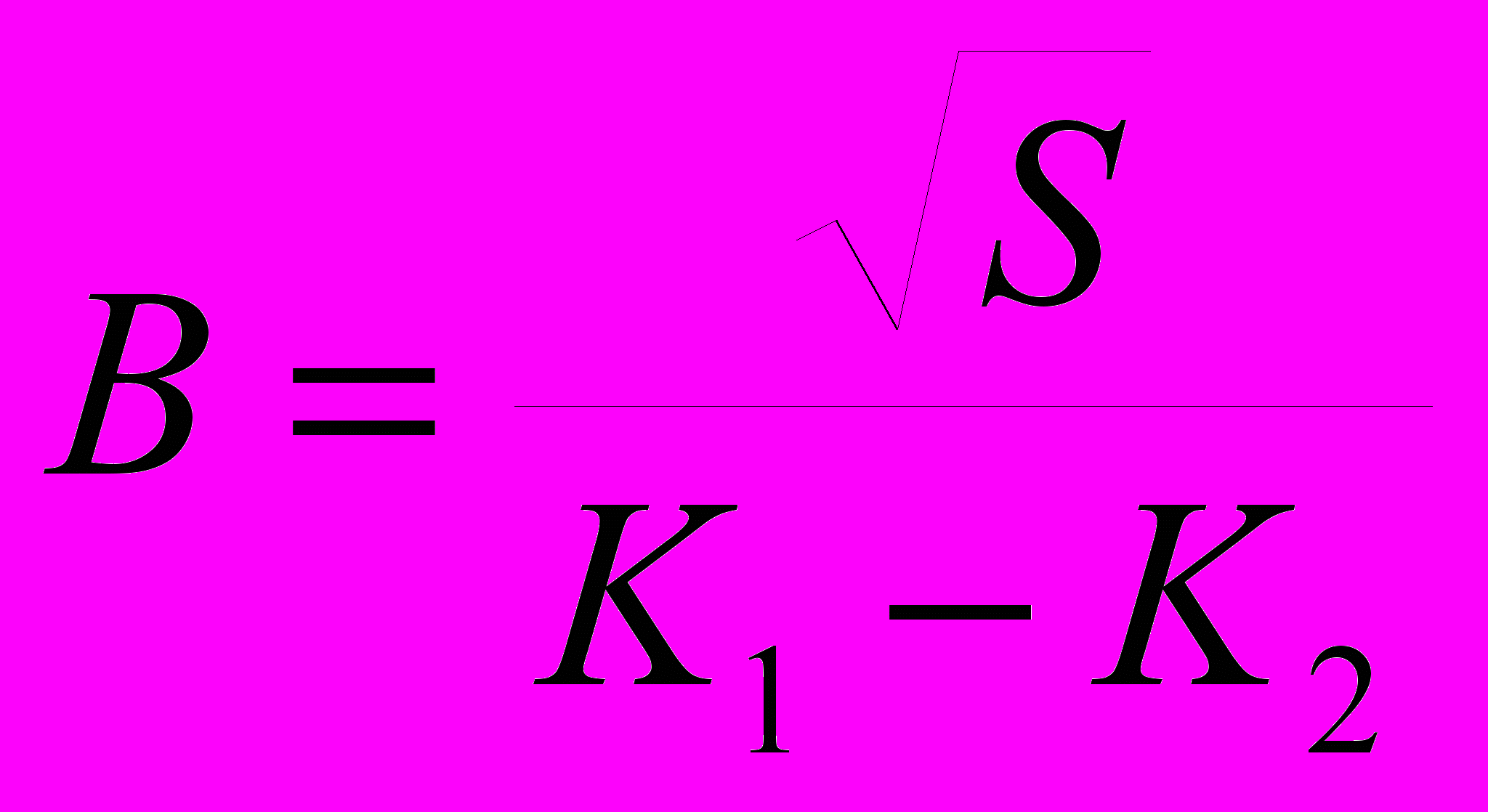 , где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. Х изменяется от 5 до 15 с шагом 0.4.
, где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. Х изменяется от 5 до 15 с шагом 0.4. 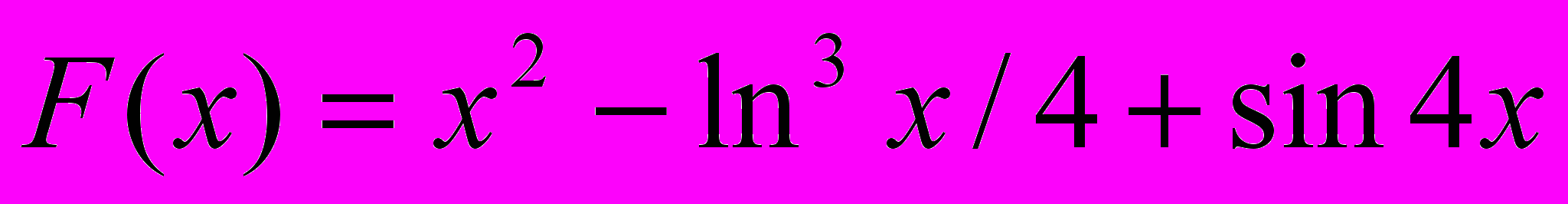
Вариант 20.
1. Верно ли, что максимум функции
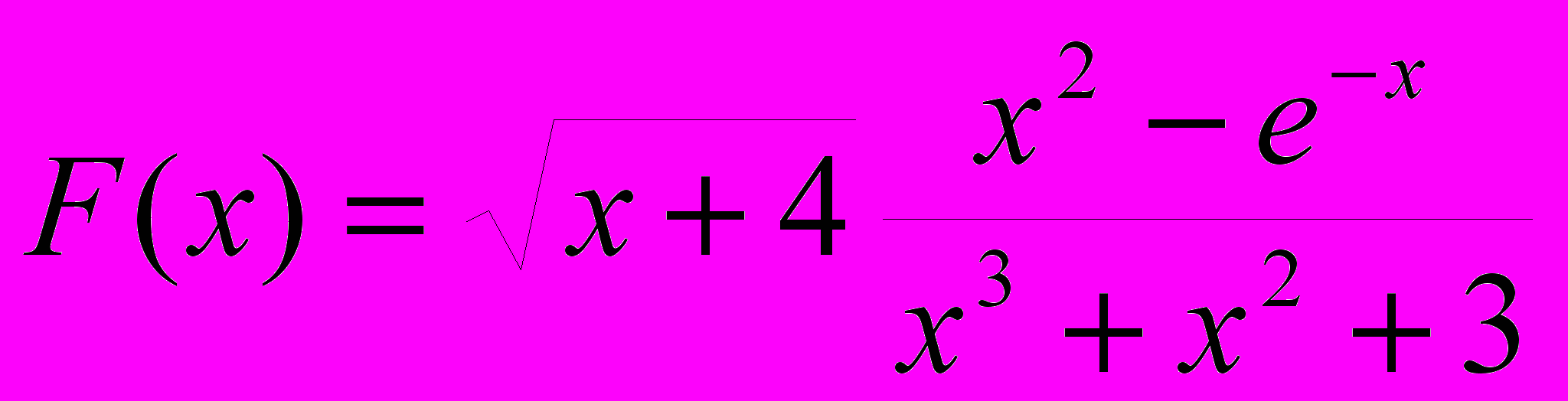 лежит в интервале [15;22]. Х изменяется от 1 до 8 с шагом 0.25. (с помощью всех четырех способов).
лежит в интервале [15;22]. Х изменяется от 1 до 8 с шагом 0.25. (с помощью всех четырех способов).2. Верно ли, что среднее значение функции
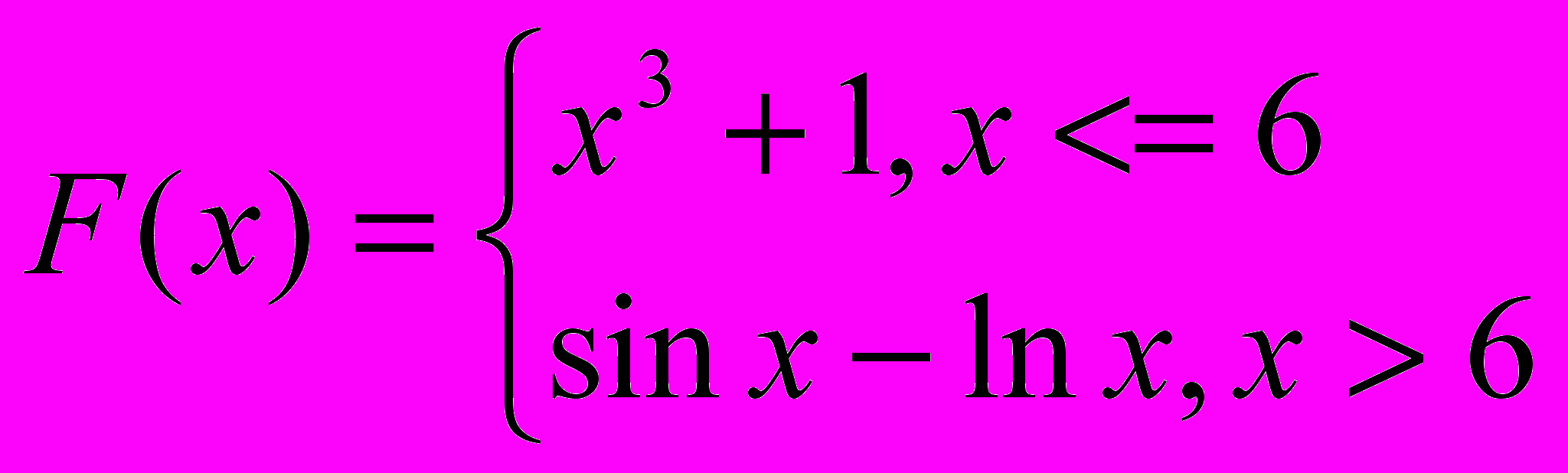 равно полусумме ее максимума и минимума. Х изменяется от 14 до 18 с шагом 0.3.
равно полусумме ее максимума и минимума. Х изменяется от 14 до 18 с шагом 0.3.Вариант 21.
1. Подсчитать количество значений функции
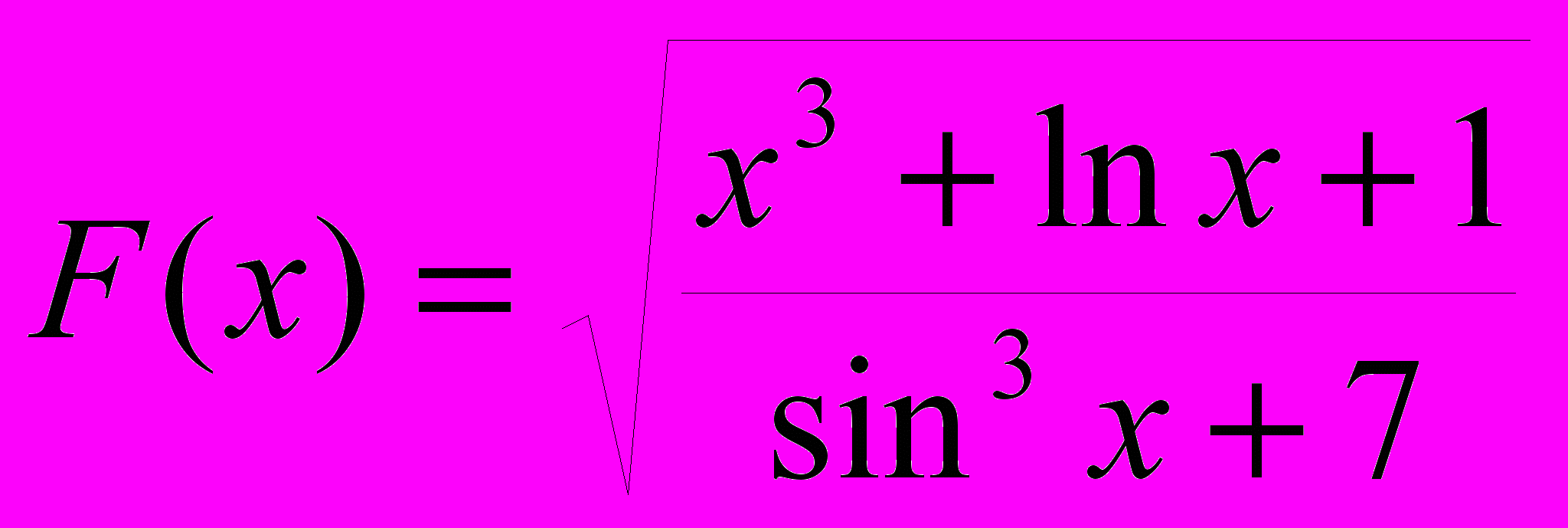 , меньших ее среднего значения ровно в два раза. Х изменяется от 4 до 15 с шагом 0.2.
, меньших ее среднего значения ровно в два раза. Х изменяется от 4 до 15 с шагом 0.2.1. Верно ли, что функция
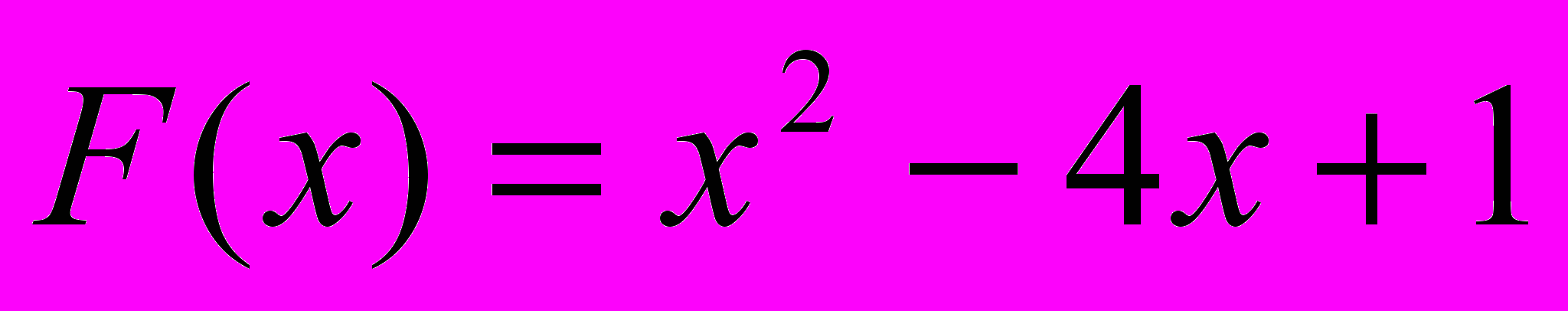 на отрезке изменения х от а до b с шагом 0.2 принимает только отрицательные значения.
на отрезке изменения х от а до b с шагом 0.2 принимает только отрицательные значения. Вариант 22.
1. Вычислить величину
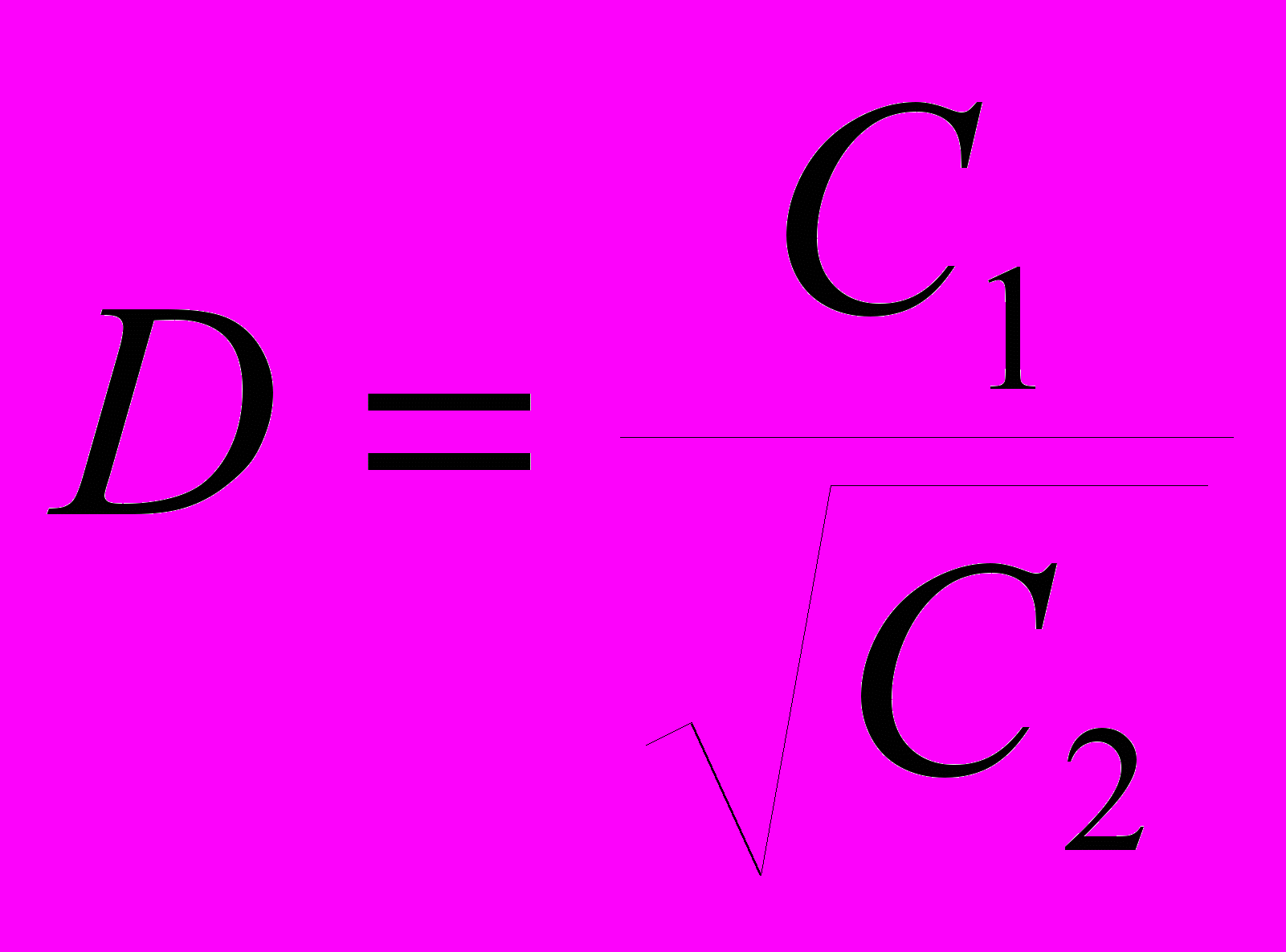 , где С2- среднее арифметическое положительных значений функции, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 6 до 17 с шагом 0.2.
, где С2- среднее арифметическое положительных значений функции, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 6 до 17 с шагом 0.2. 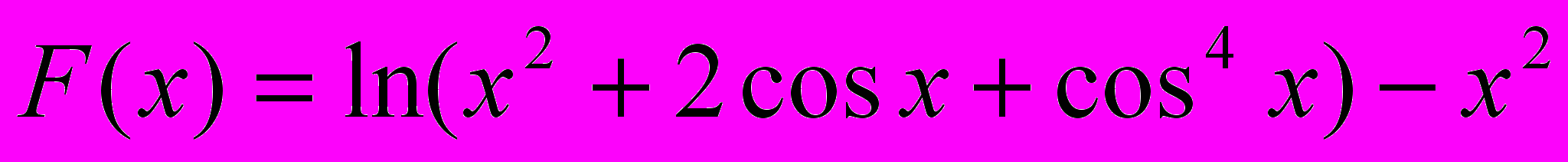
2. Вывести на печать значения функции
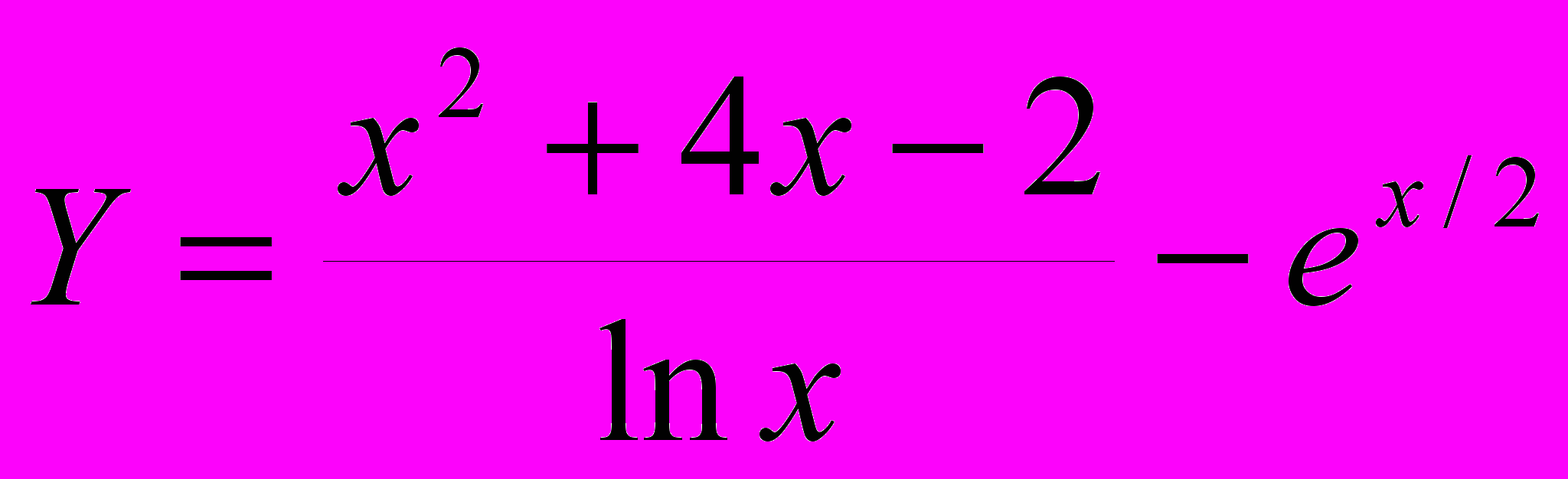 до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.
до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.Вариант 23.
1. Вычислить величину
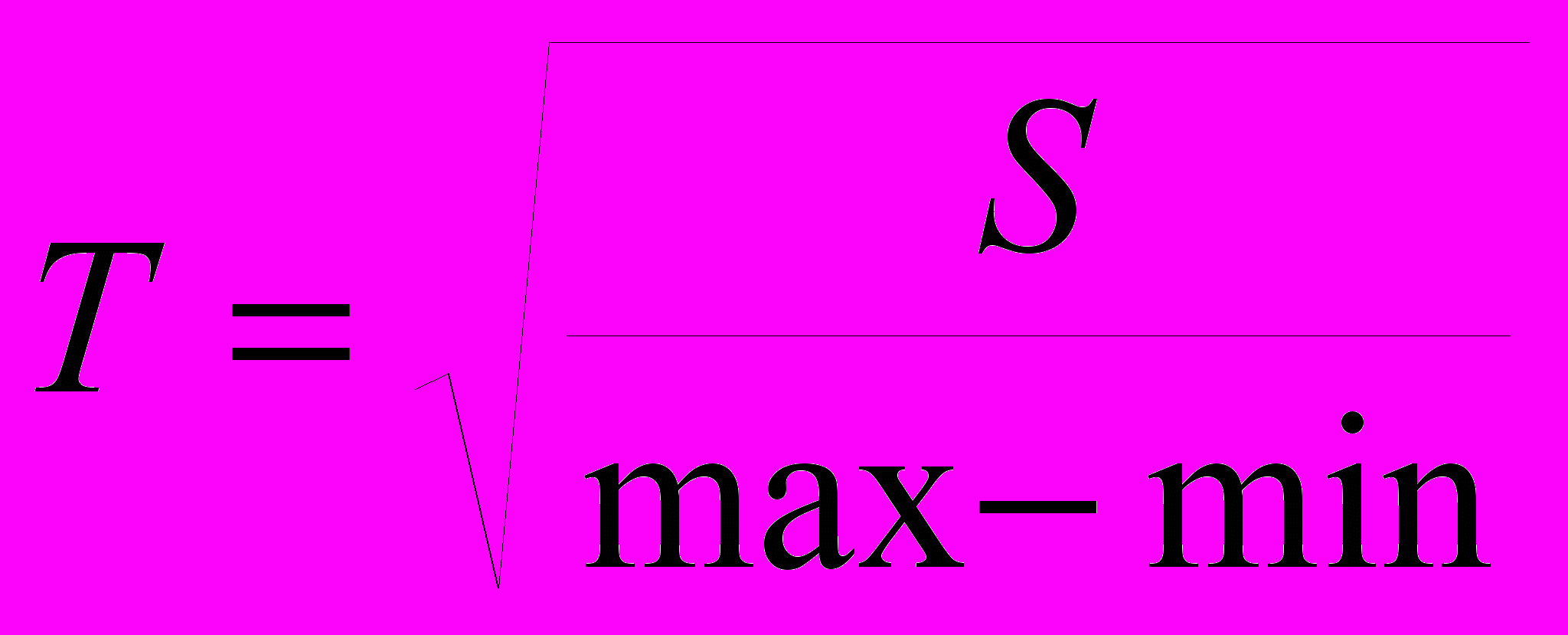 , где S – сумма неотрицательных значений функции
, где S – сумма неотрицательных значений функции 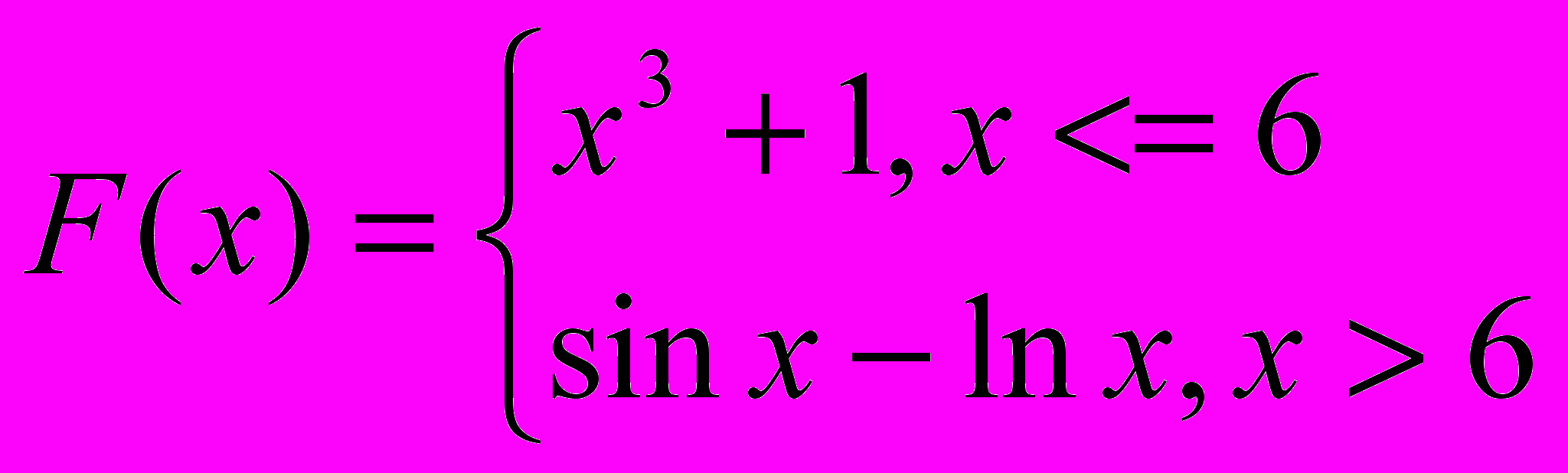 , Х изменяется от 4 до 8 с шагом 0.1.
, Х изменяется от 4 до 8 с шагом 0.1.2. Верно ли, что количество положительных значений функции
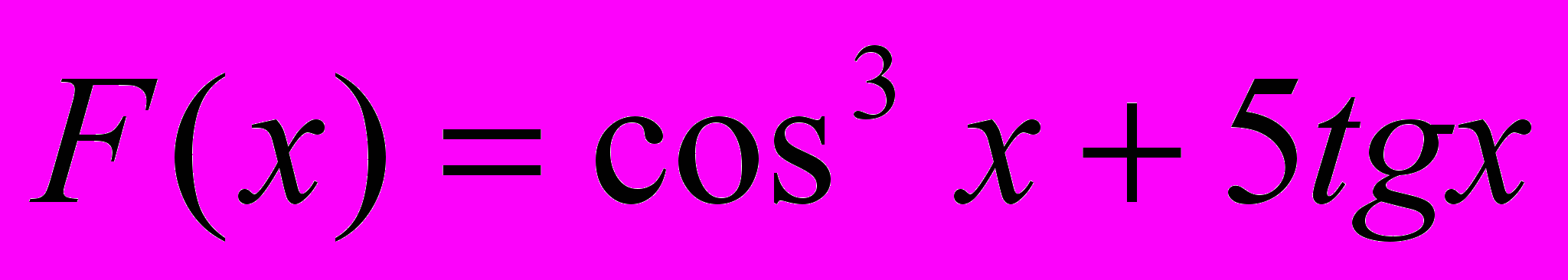 в три раза меньше суммы ее положительных значений. Х изменяется от 30 до 36 с шагом 0.2
в три раза меньше суммы ее положительных значений. Х изменяется от 30 до 36 с шагом 0.2Вариант 24
1. Вывести на печать значения функции
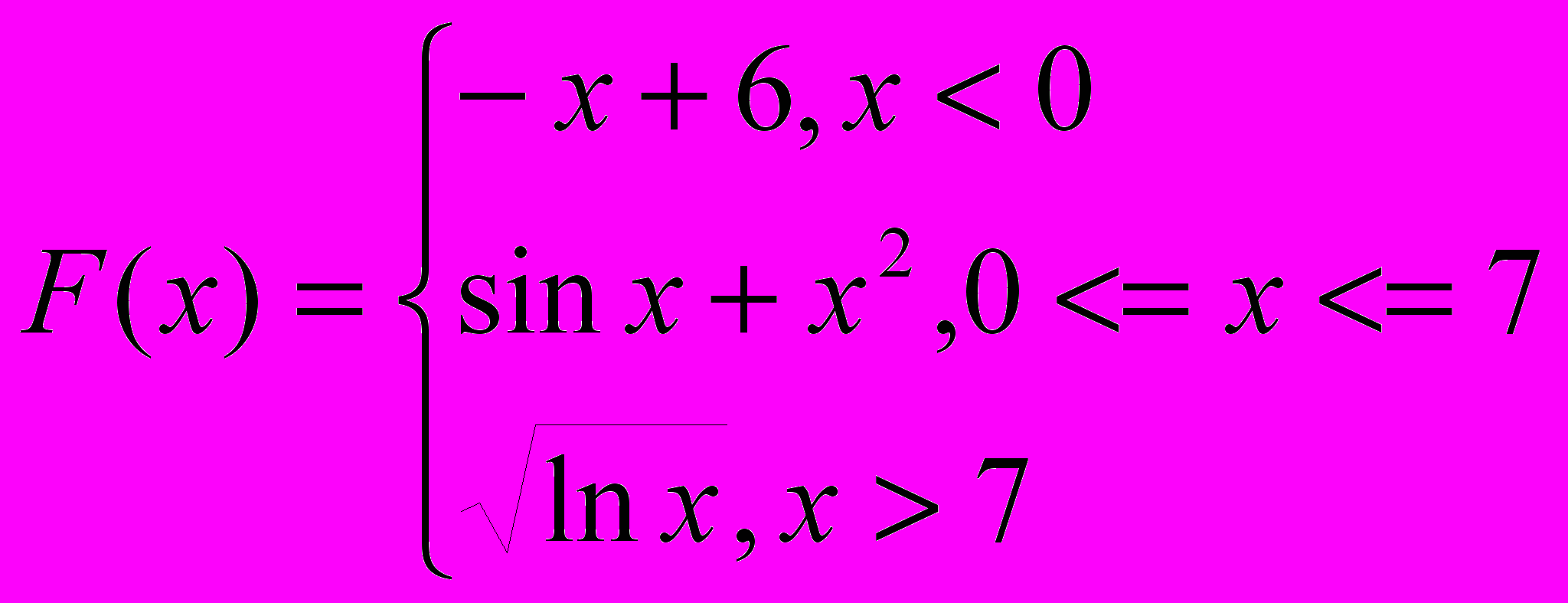 , лежащие в интервале [4;6] . Х изменяется от -5 до 6 с шагом 0.1.
, лежащие в интервале [4;6] . Х изменяется от -5 до 6 с шагом 0.1.2. Подсчитать сумму значений функции F(x), ровно в 2 раза меньших минимума функции. Х изменяется от 5 до 30 с шагом 0.3.
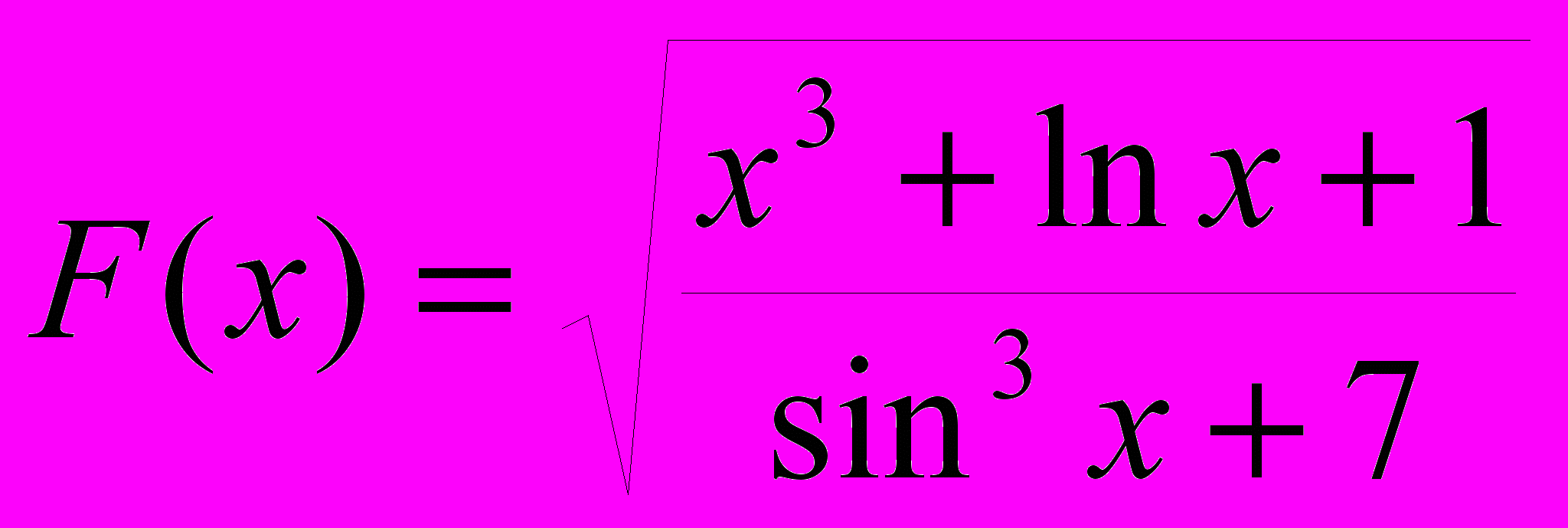
Вариант 25
1. Вывести на печать неотрицательные значения функции F(x), x изменяется от 1 до 12 с шагом 0.4 (С помощью всех четырех способов).
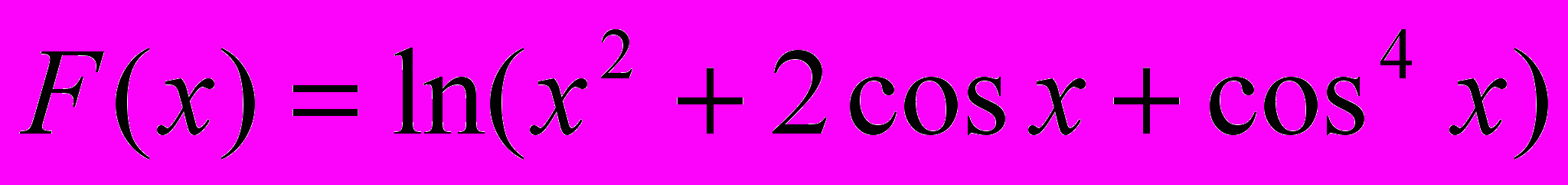
2. Подсчитать сумму значений функции, лежащих в интервале [a;b].
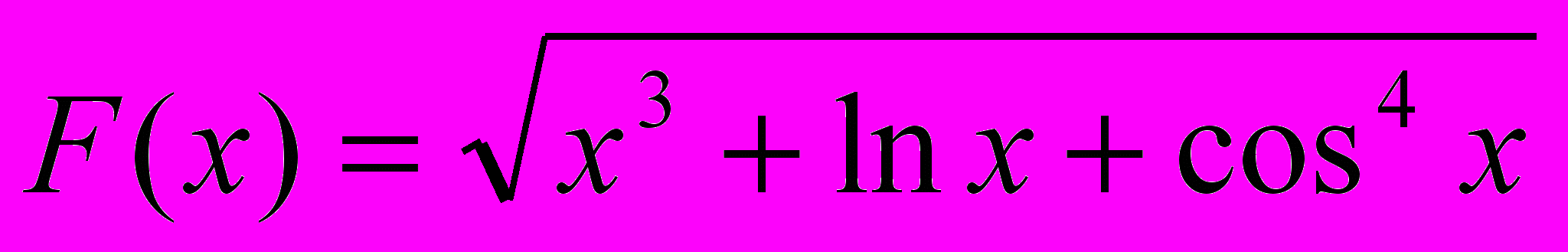
Вариант 26
1. Вычислить величину
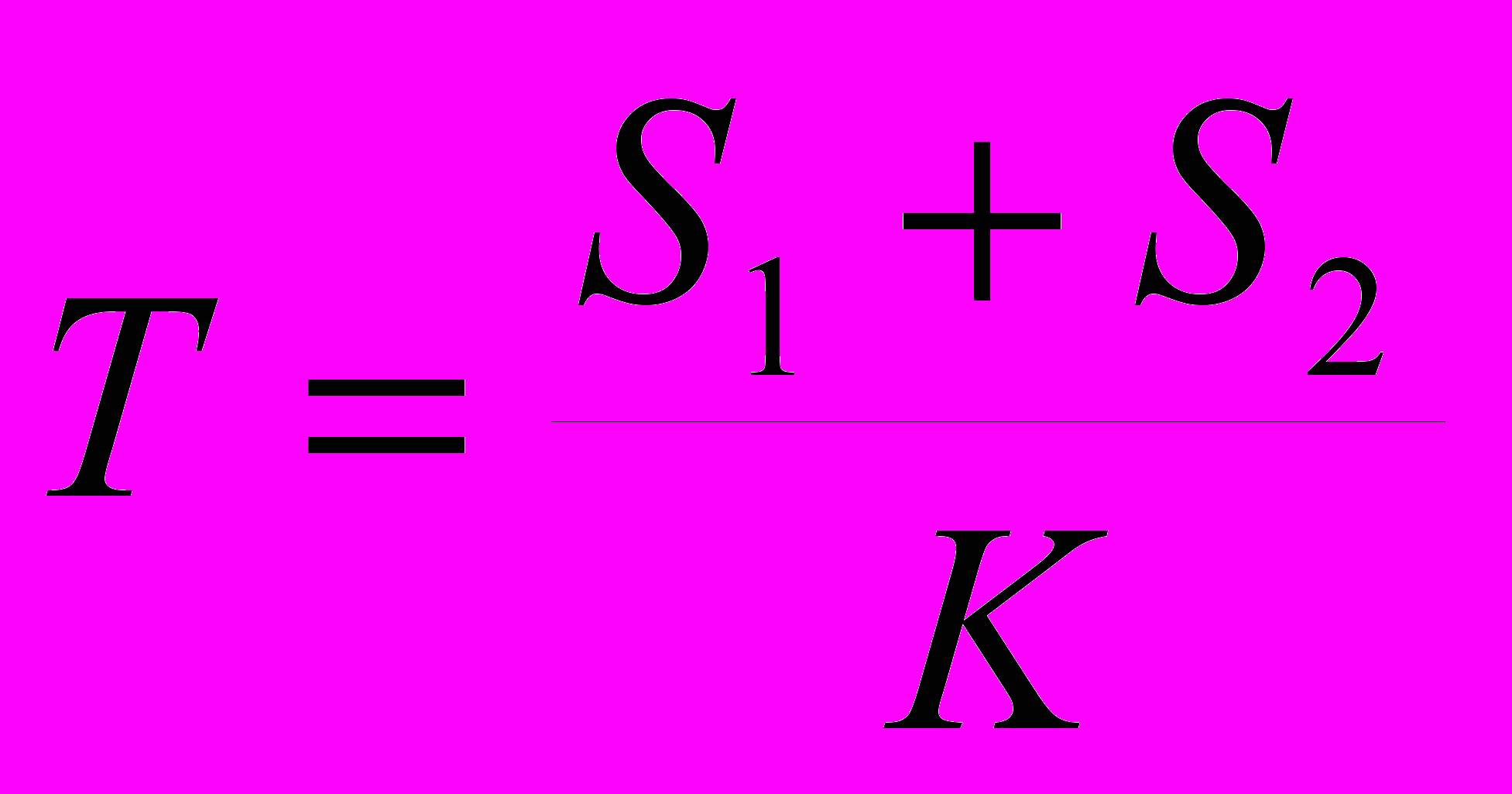 , где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов).
, где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов). 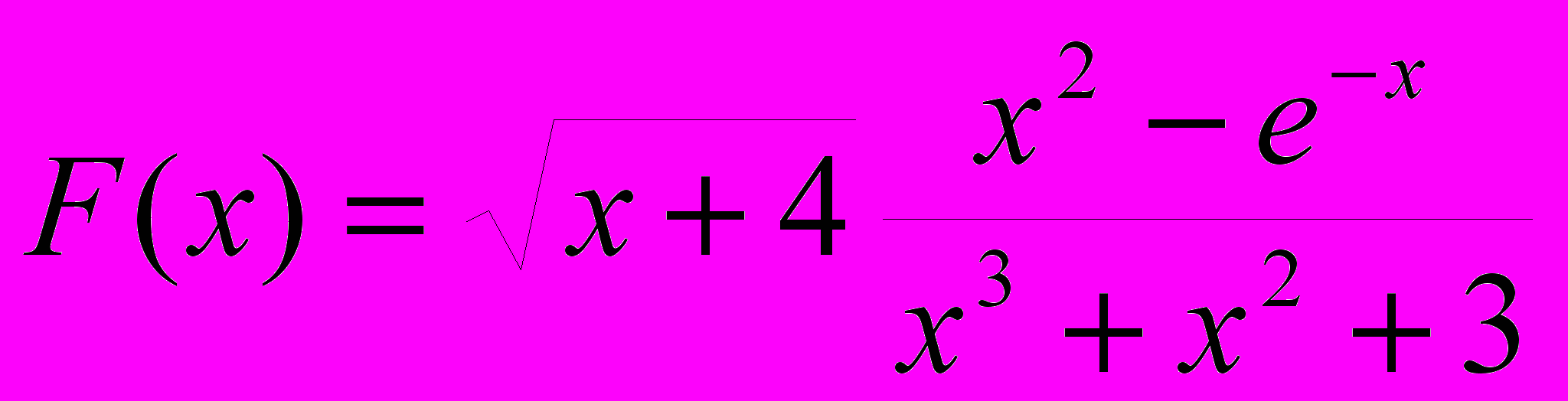
2. Вывести на печать значения функции
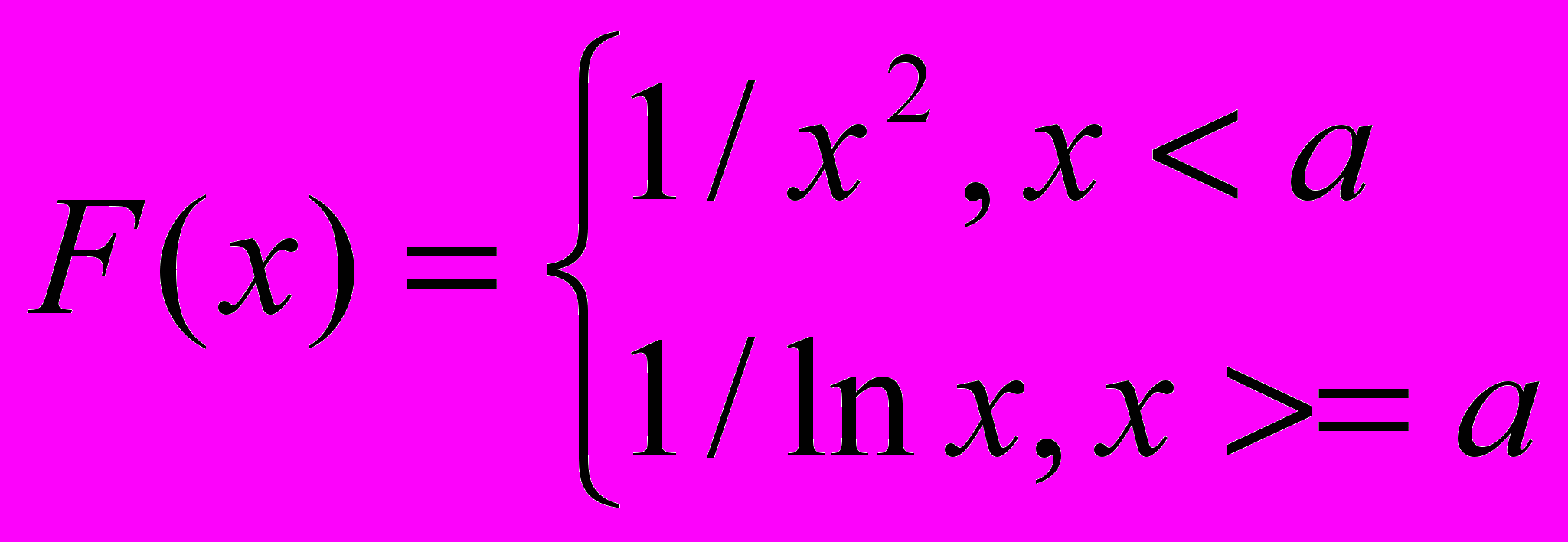 , при x изменяющемся от 1 с шагом 0.5 до y<0.005.
, при x изменяющемся от 1 с шагом 0.5 до y<0.005.Вариант 27.
1. Верно ли, что мах F(X) в 2 раза больше суммы модулей ее отрицательных значений. X изменяется от 1 до 18 с шагом 1 (с помощью всех четырех способов).
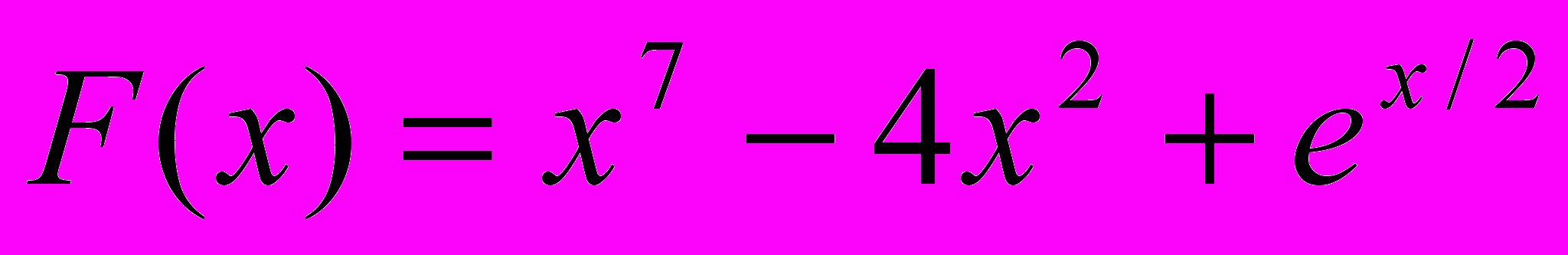
2. Вычислить величину
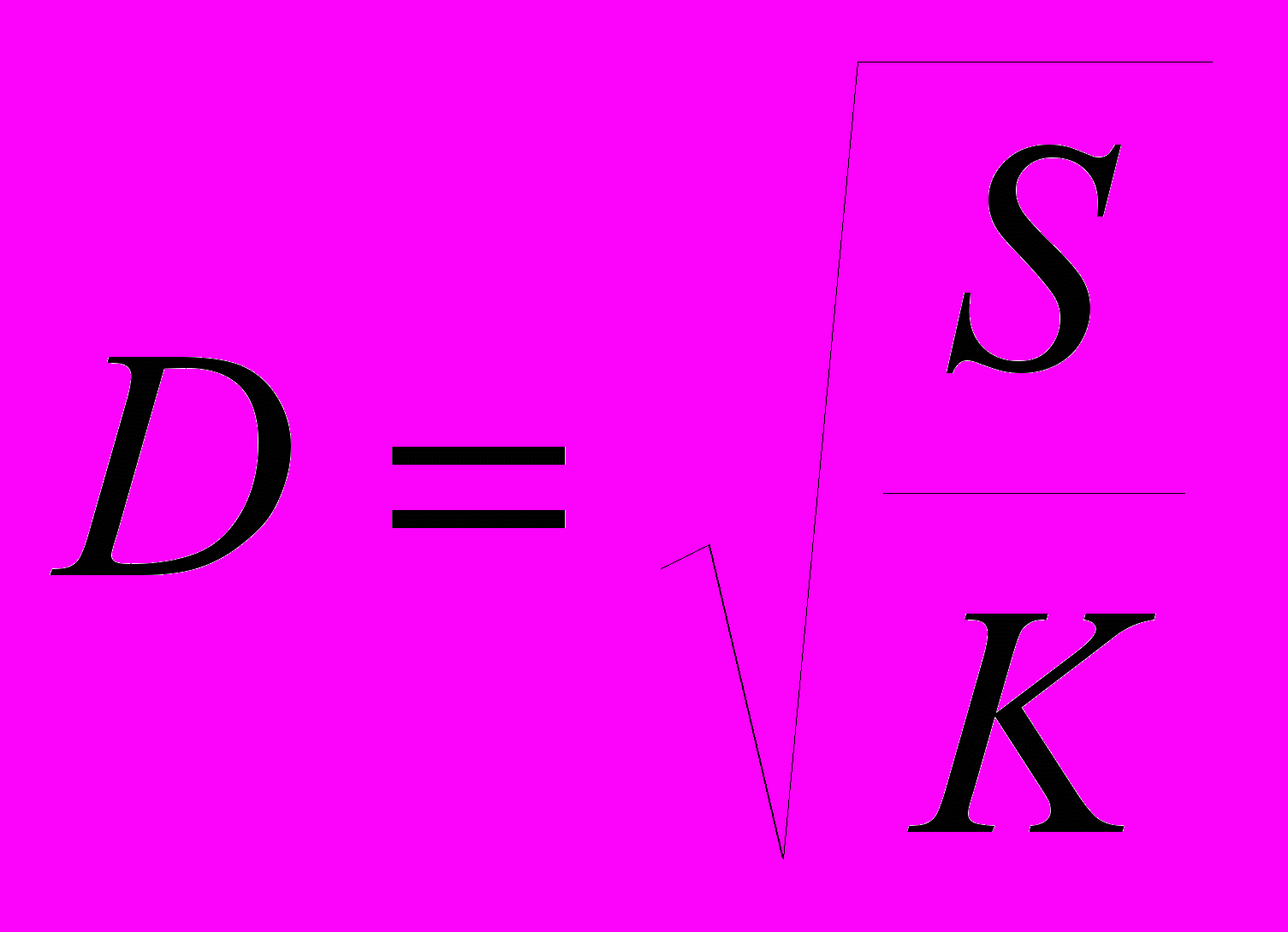 , где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений.
, где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений. 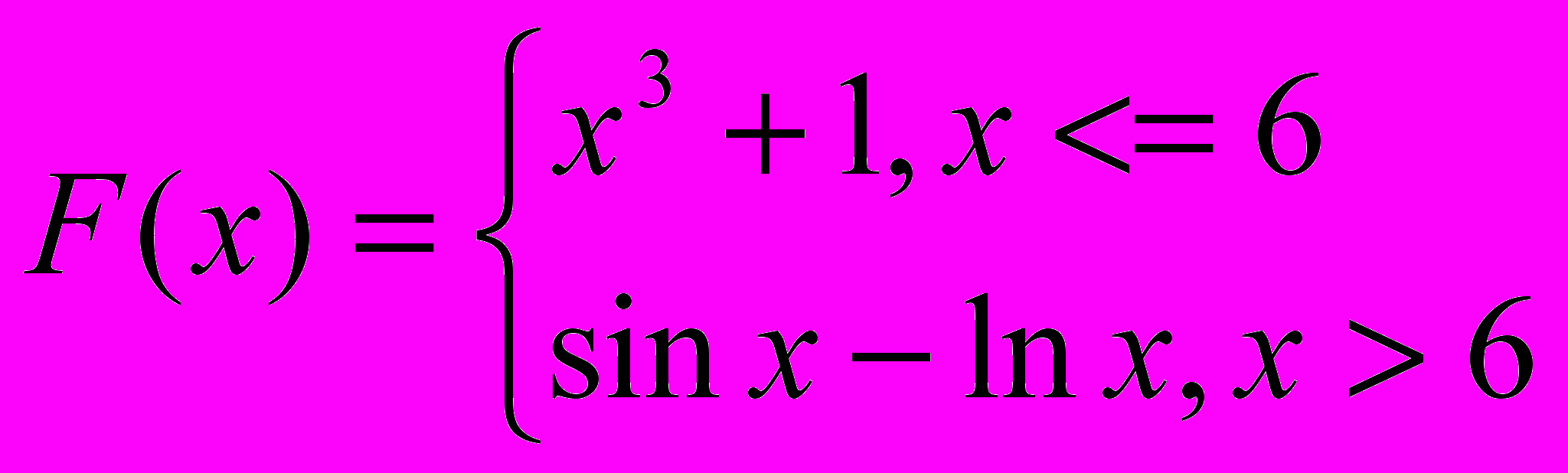
х изменяется от 1 до 8 с шагом 0.2
Вариант 28.
- Вывести на печать значений функции F(x), не лежащие в интервале [a,b]. x изменяется от 5 до 16 с шагом 0.2.
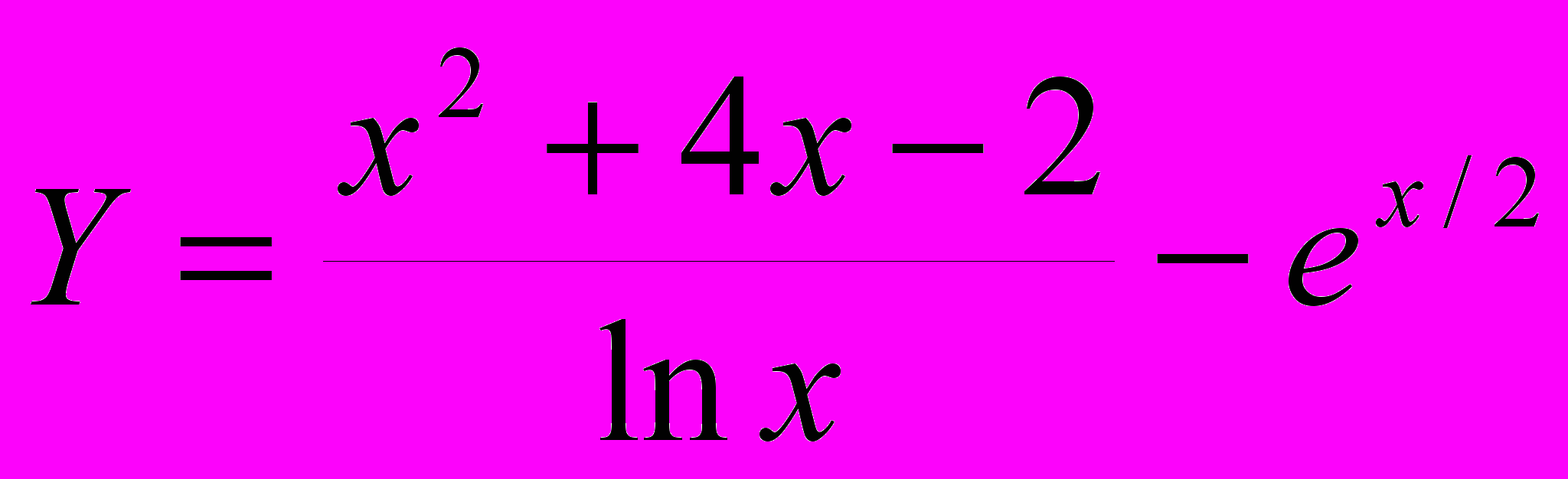
- Верно ли, что среднее арифметическое неотрицательных значений функции F(x) больше некоторого числа P. x изменяется от 4 до 81 с шагом 2.
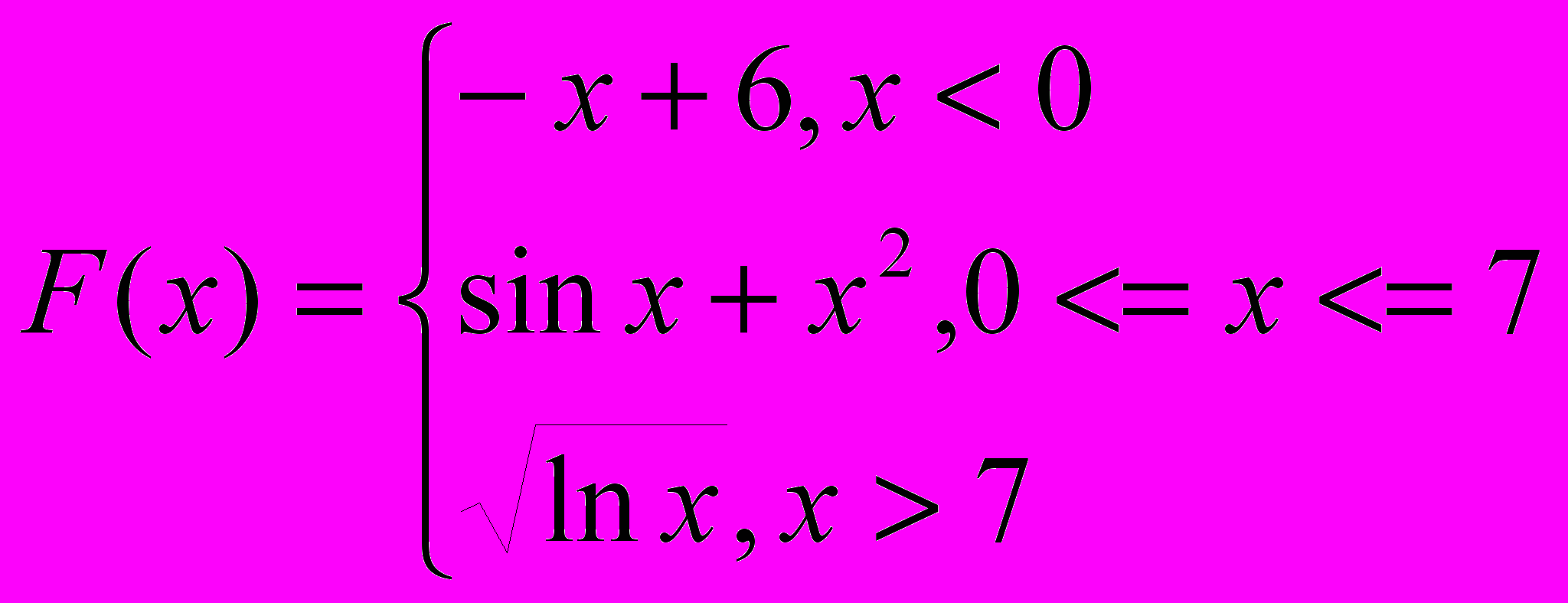
Вариант 29.
1. Верно ли, что функция F(x) на интервале изменения x от 6 от 13 с шагом 0.3 принимает только положительные значения.
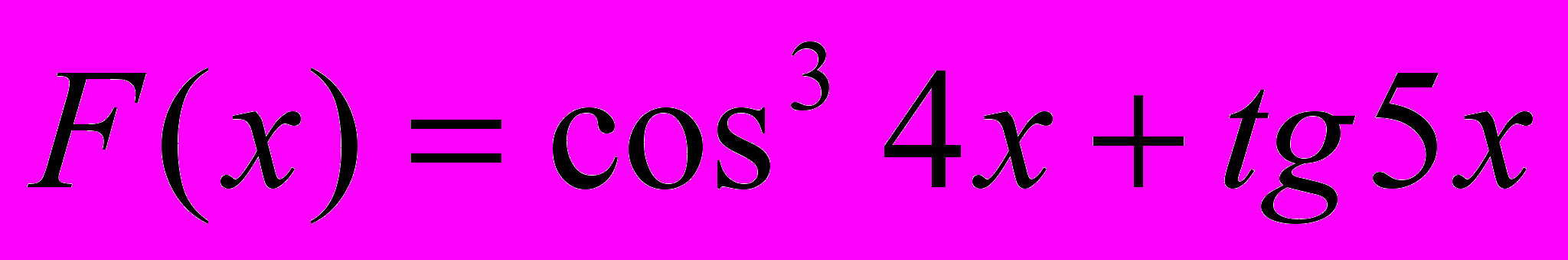
2. Подсчитать сумму значений функции
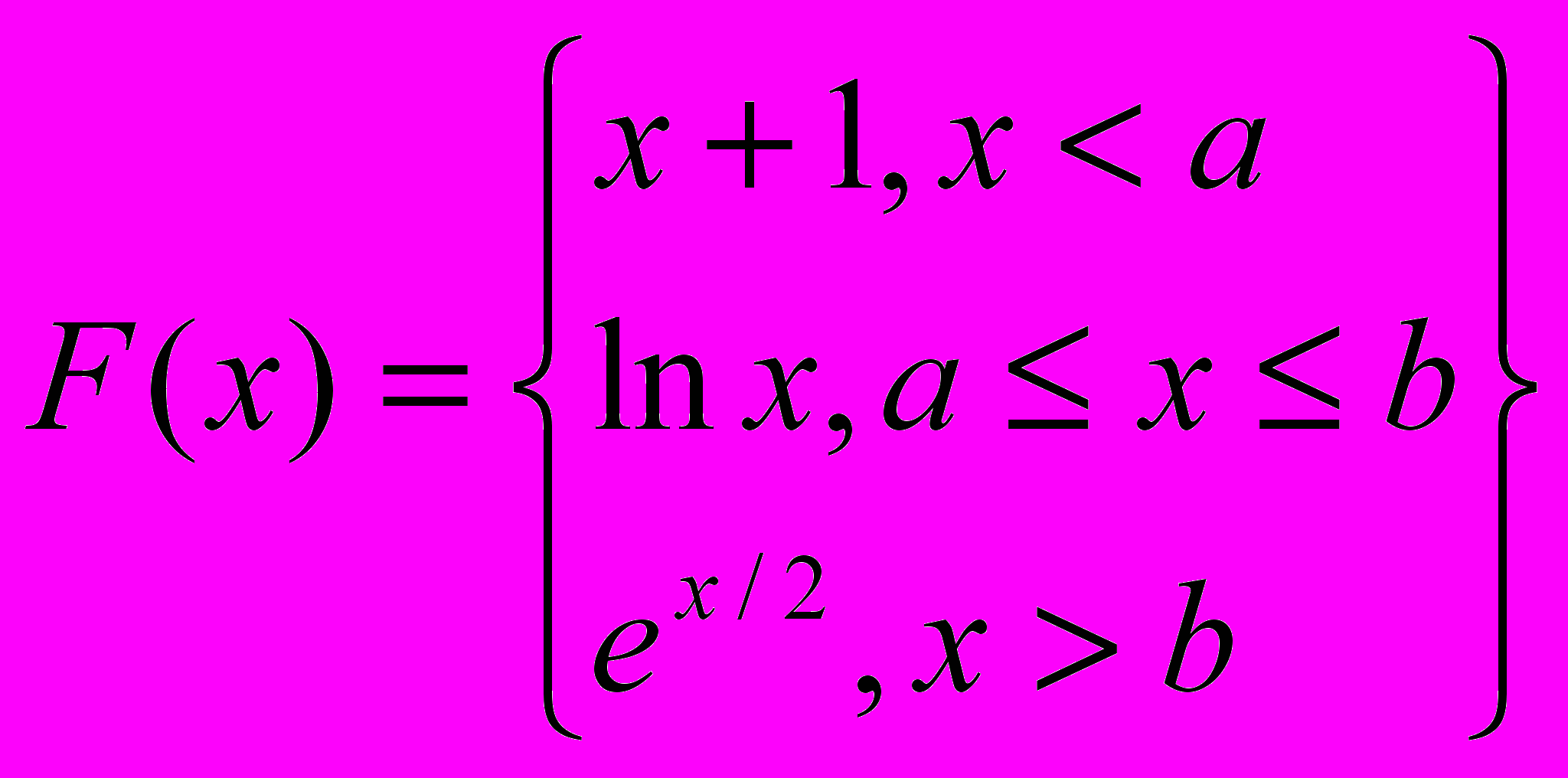 , меньших некоторого числа W. x изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).
, меньших некоторого числа W. x изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).Вариант 30.
1. Верно ли, что сумма положительных значений F(x) в 3 раза больше ее минимального значения ? х изменяется от 1 до 16 с шагом 0.3.
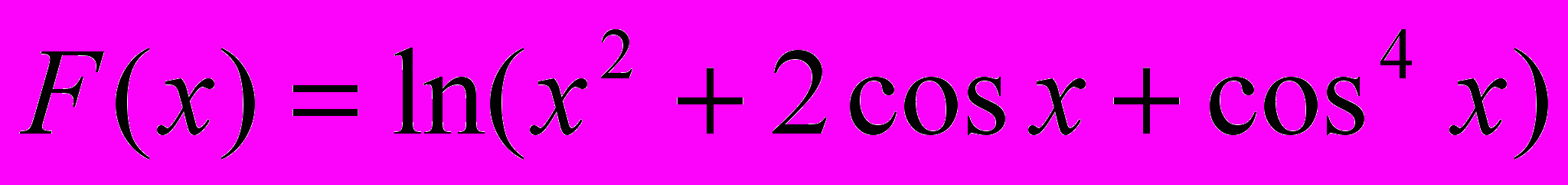 -5
-52. Вывести на печать значения функции
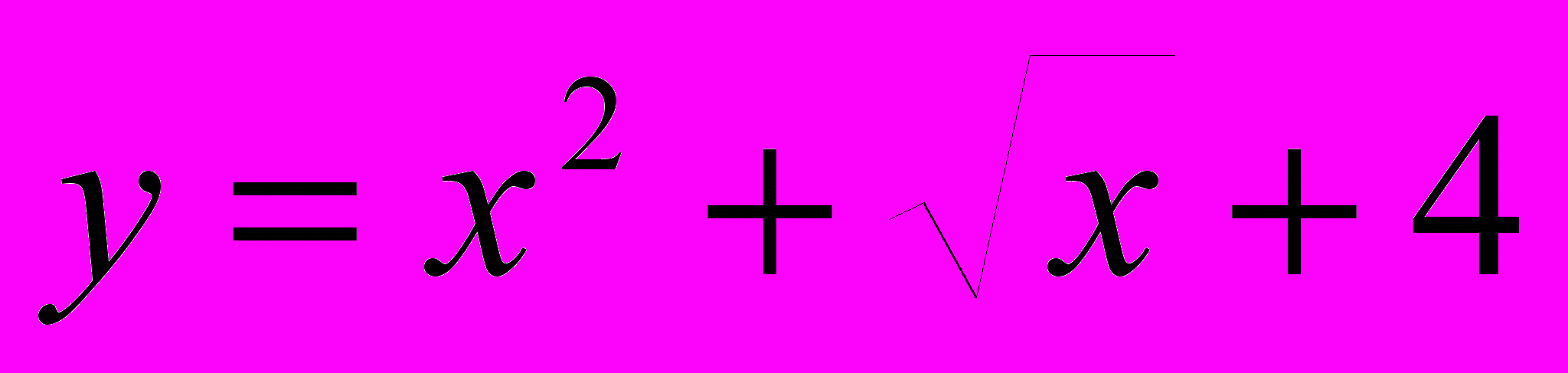 до y> 150. х изменяется от 1 с шагом 0.3.
до y> 150. х изменяется от 1 с шагом 0.3.Вариант 31.
1. Верно ли, что максимум функции F(x) в три раза больше ее минимума. Х изменяется от 4 до 13 с шагом 0.1 .
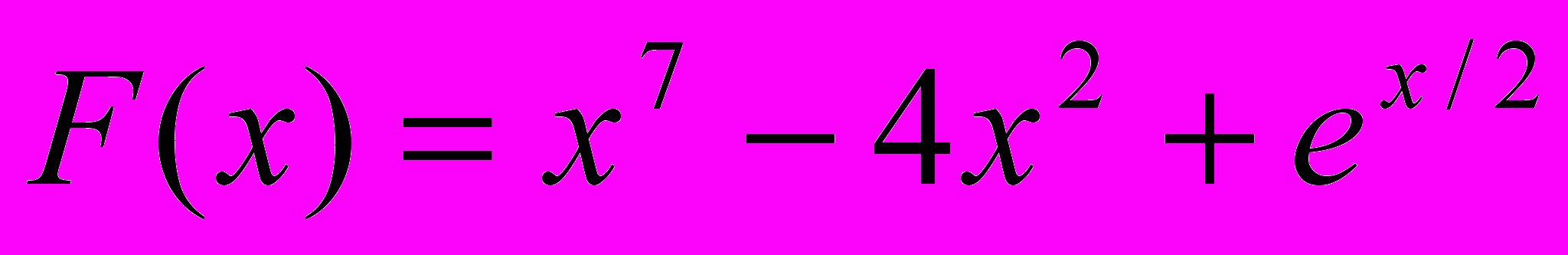
2. Вычислить величину
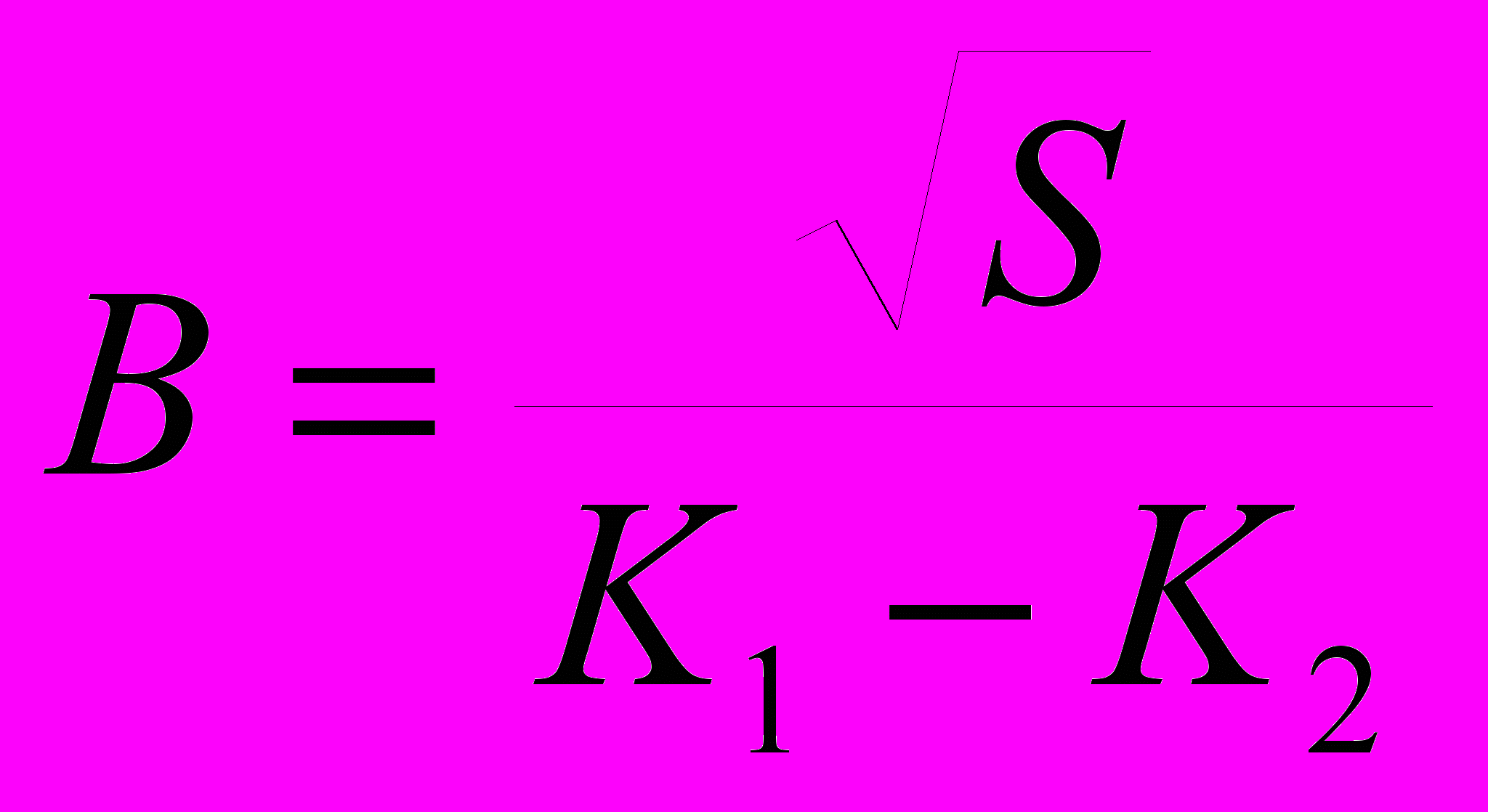 , где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. х изменяется от 5 до 15 с шагом 0.4.
, где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. х изменяется от 5 до 15 с шагом 0.4. 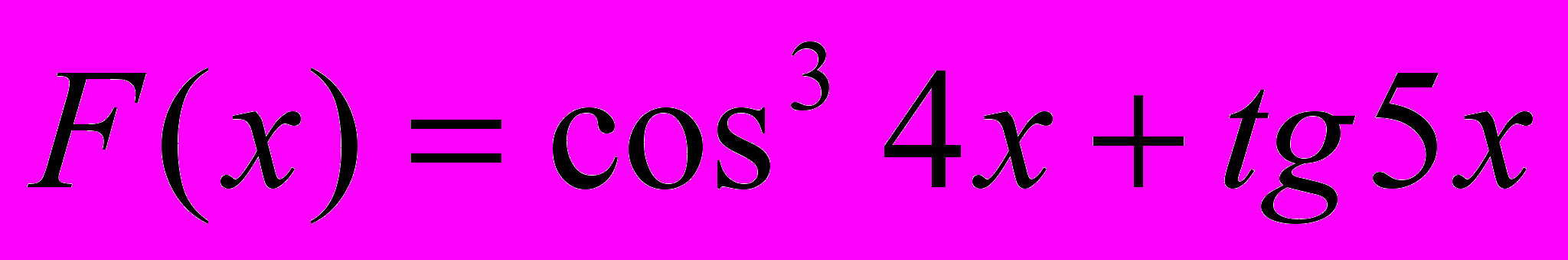
Вариант 32.
1. Верно ли, что максимум функции F(x) лежит в интервале [5;12]. Х изменяется от 4 до 18 с шагом 0.5. (с помощью всех четырех способов).
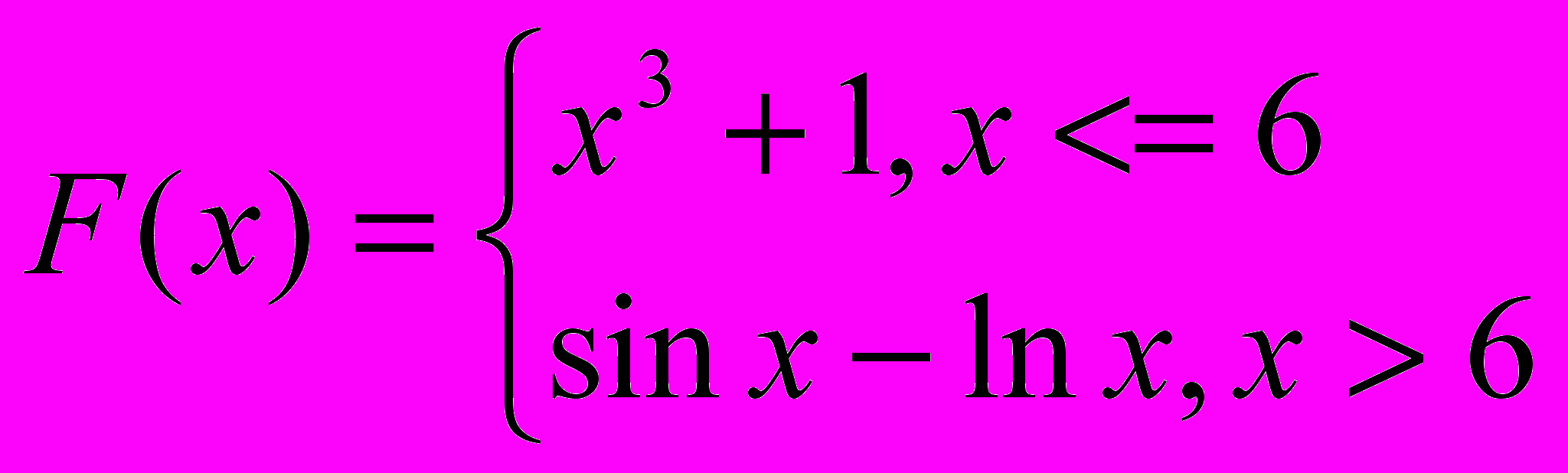
2. Верно ли, что среднее значение функции
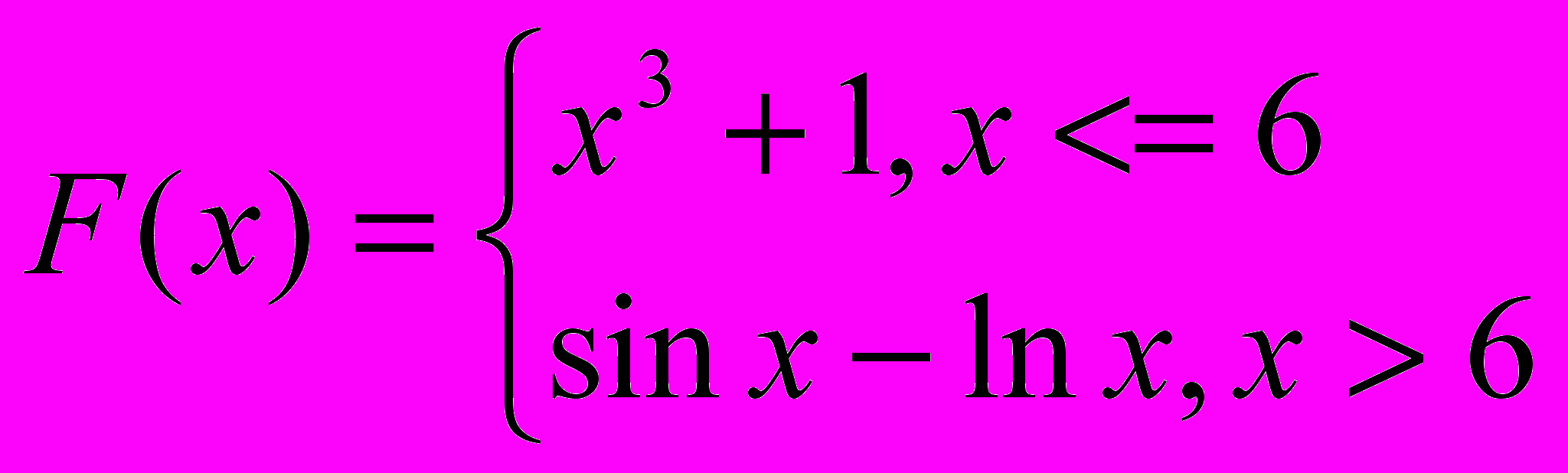 равно полусумме ее максимума и минимума. Х изменяется от 4 дот 8 с шагом 0.3.
равно полусумме ее максимума и минимума. Х изменяется от 4 дот 8 с шагом 0.3.Вариант 33.
1. Подсчитать количество значений функции F(x), меньших ее среднего значения ровно на 1. Х изменяется от 4 до 15 с шагом 0.2.
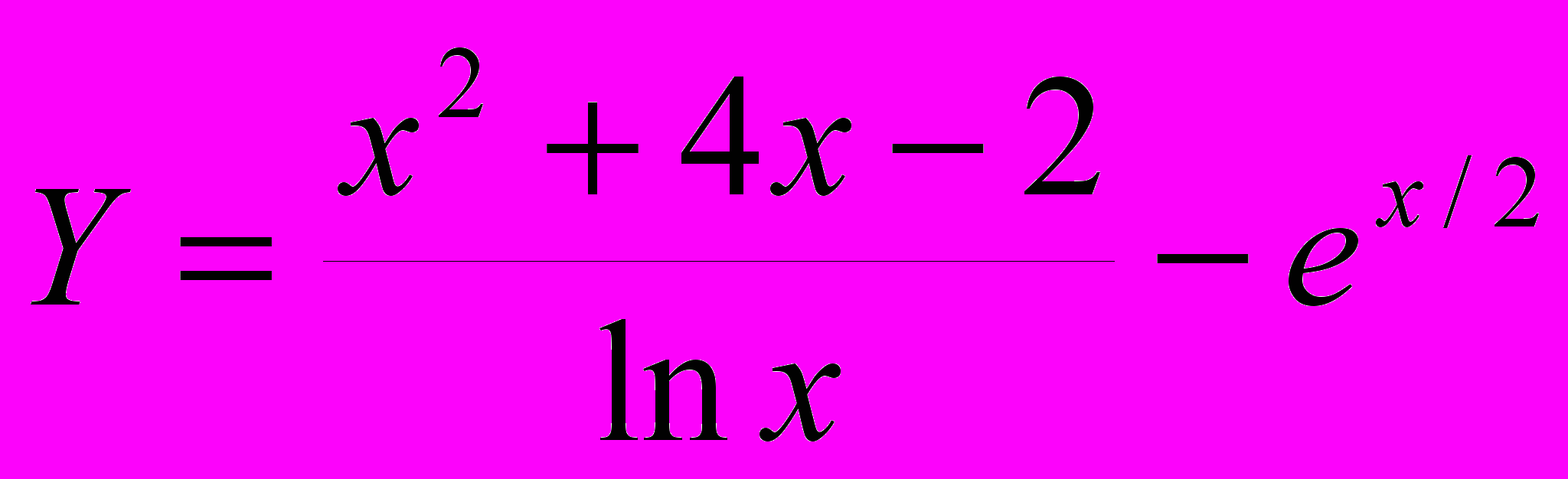
2. Верно ли, что функция F(x) на отрезке изменения х от а до b с шагом 0.2 принимает только отрицательные значения.
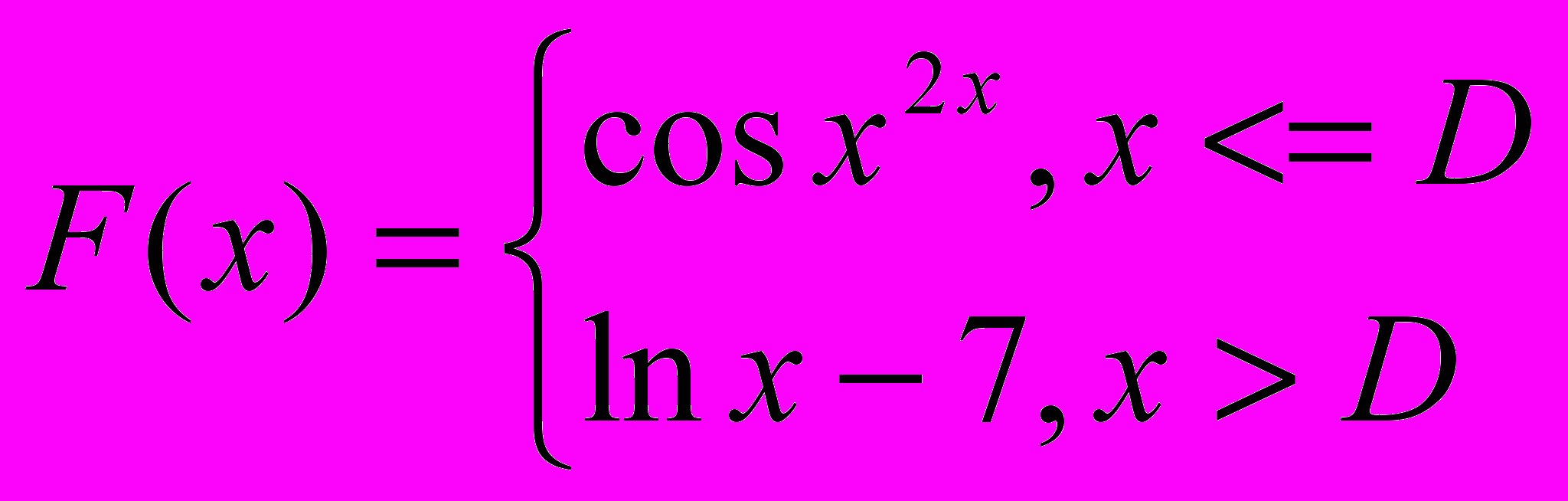
Вариант 34
1. Вычислить величину
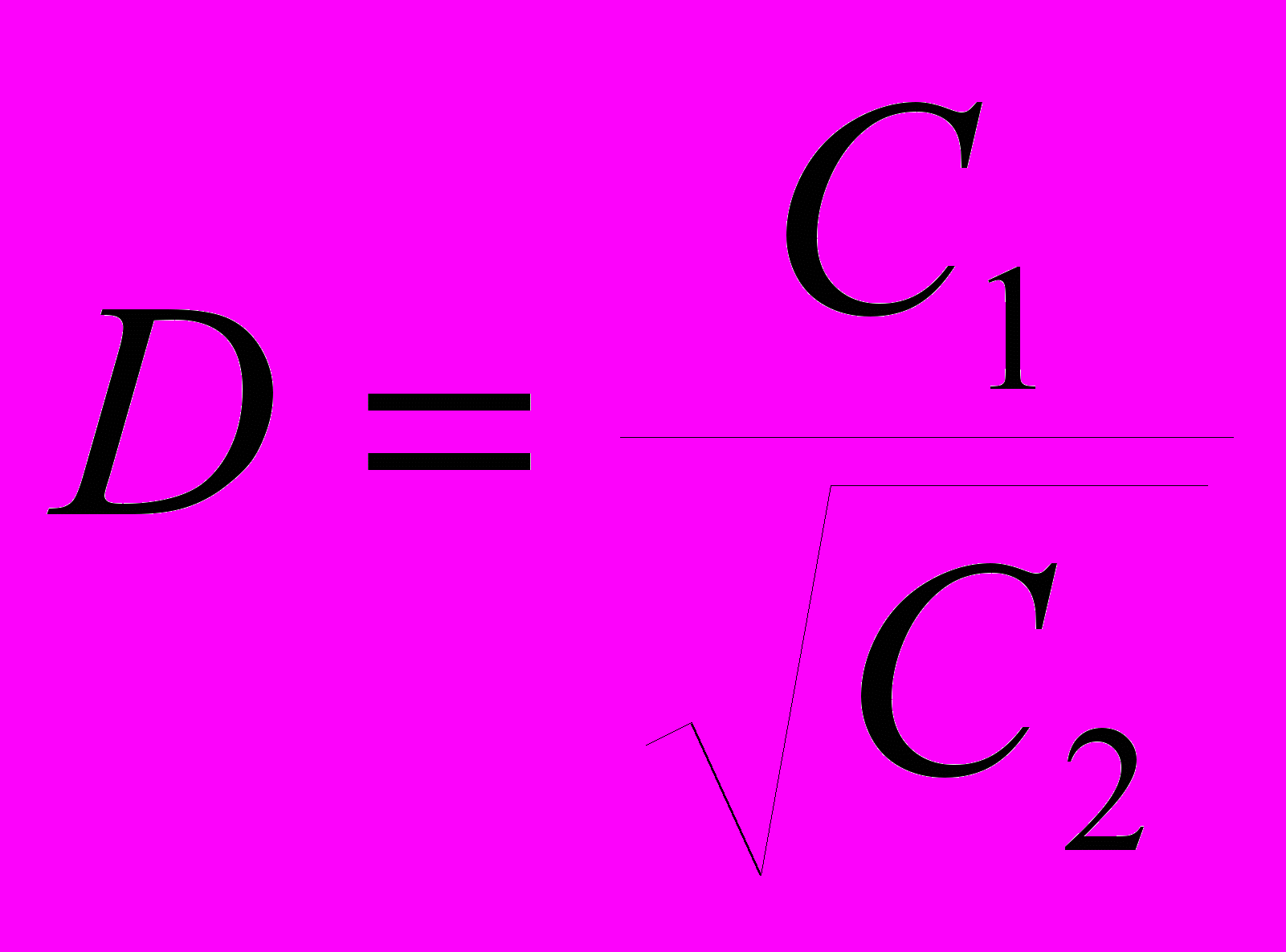 . Где С2- среднее арифметическое значений функции, больших числа D, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 3 до 28 с шагом 0.2.
. Где С2- среднее арифметическое значений функции, больших числа D, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 3 до 28 с шагом 0.2.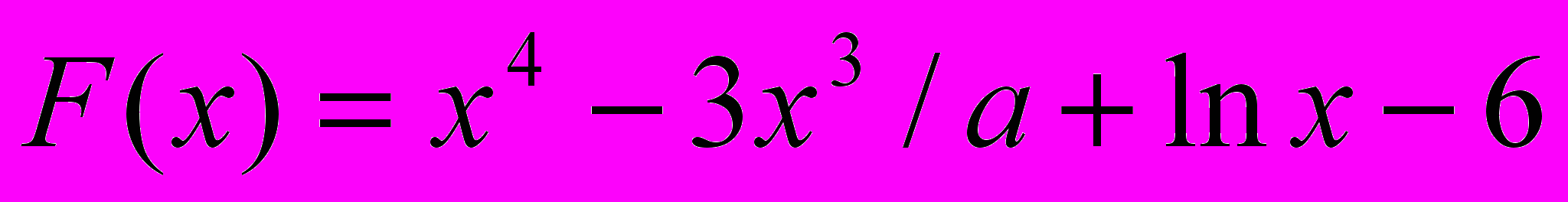
2. Вывести на печать значения функции
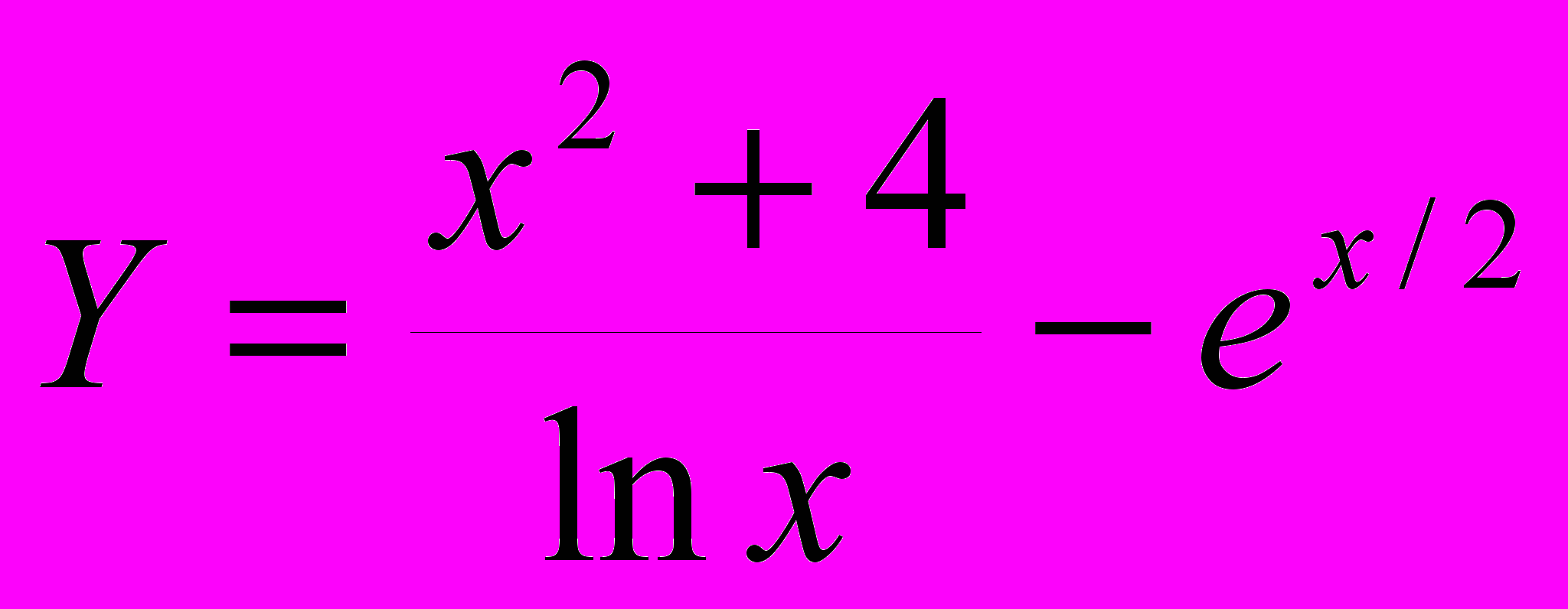 до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.
до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.Вариант 35
1. Вычислить величину
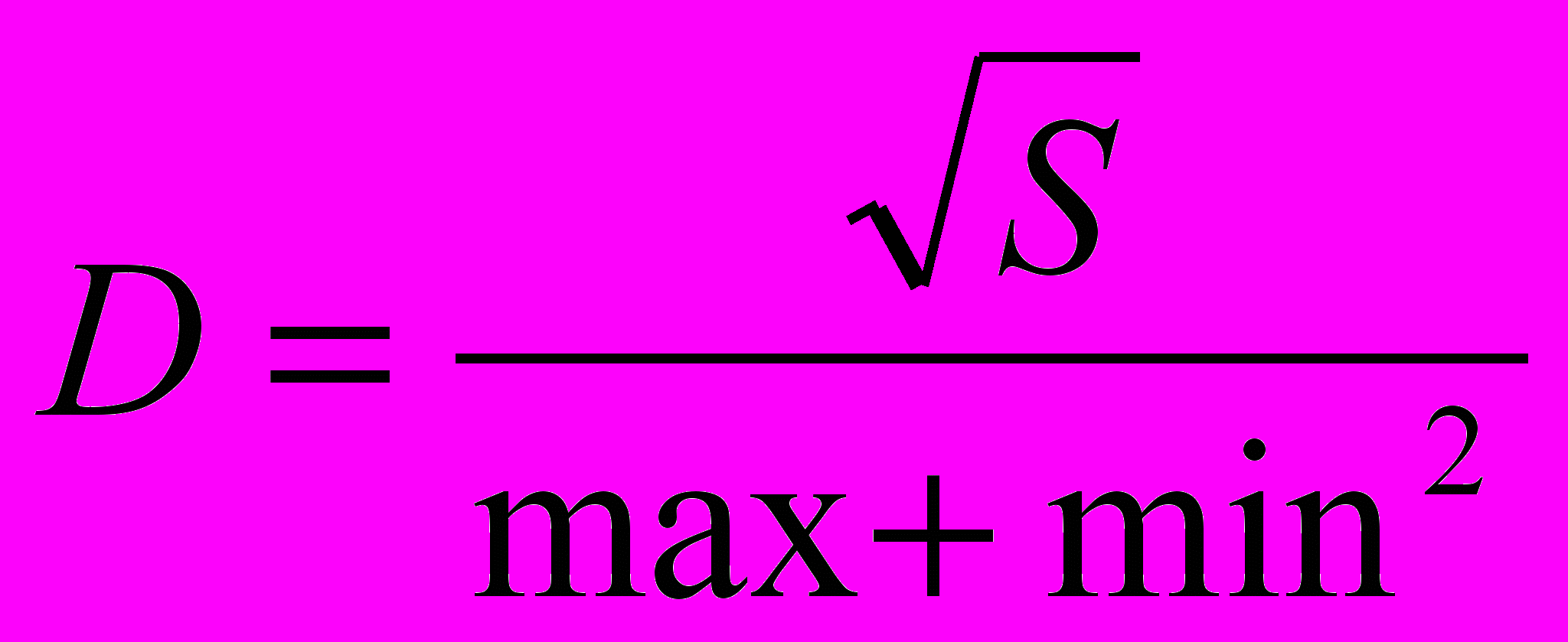 , где S – сумма неотрицательных значений функции F(x), Х изменяется от 4 до 8 с шагом 0.1.
, где S – сумма неотрицательных значений функции F(x), Х изменяется от 4 до 8 с шагом 0.1. 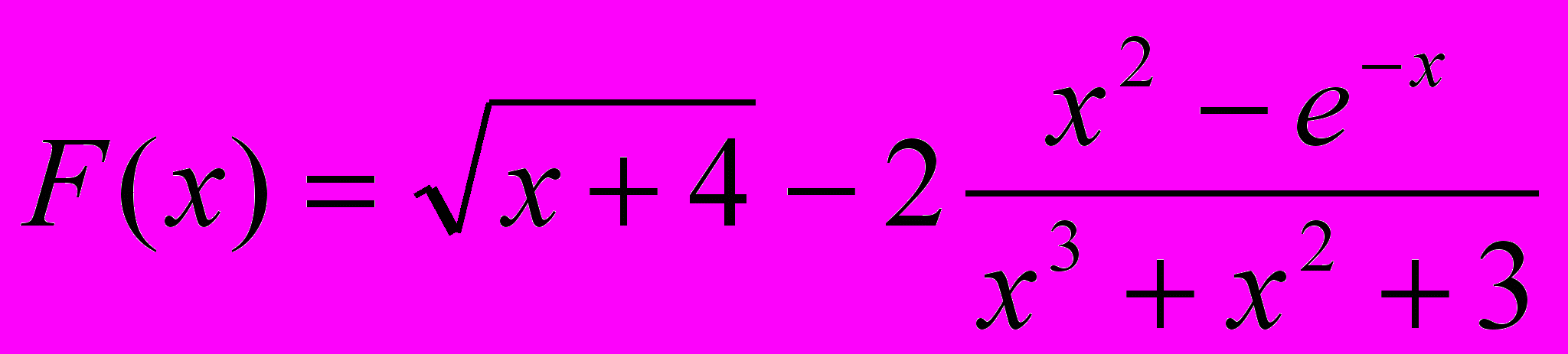
2. Верно ли, что количество положительных значений функции F(x) в три раза меньше суммы ее положительных значений. Х изменяется от 30 до 36 с шагом 0.2
Вариант 36
1. Вывести на печать значения функции
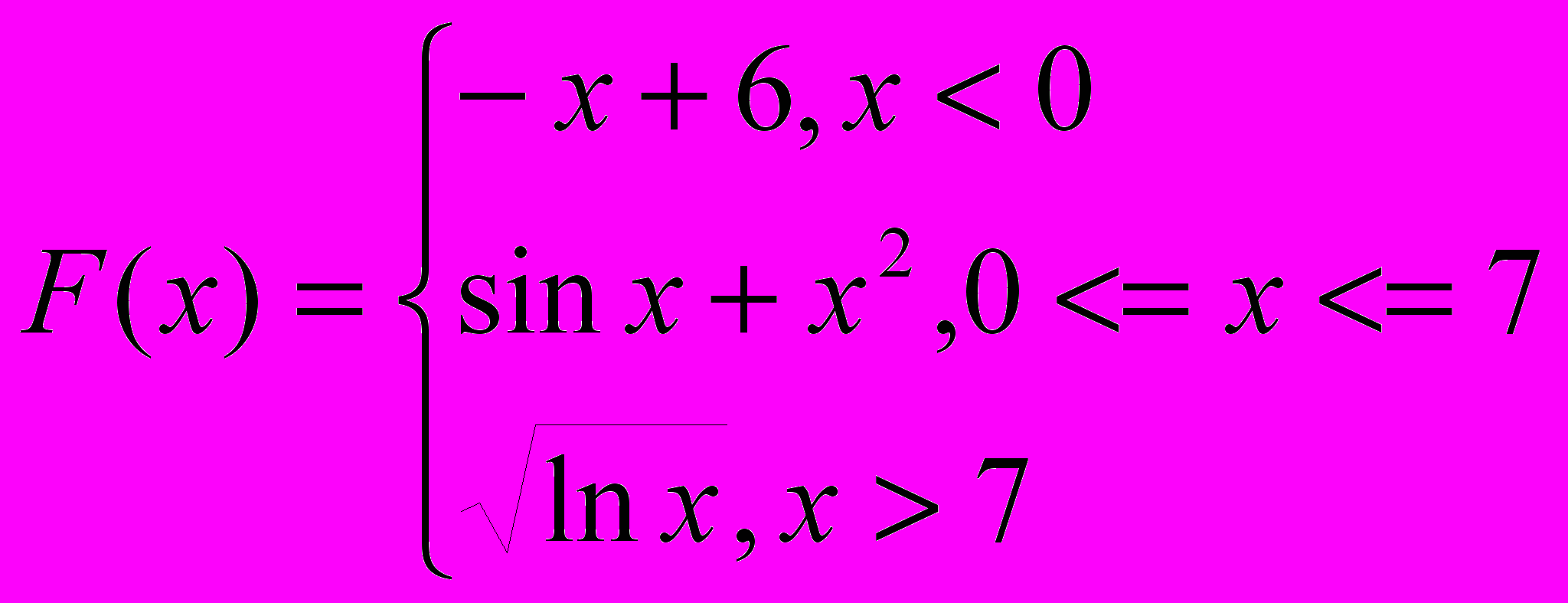 , лежащие в интервале [4;6] . Х изменяется от -5 до 6 с шагом 0.1.
, лежащие в интервале [4;6] . Х изменяется от -5 до 6 с шагом 0.1.2. Подсчитать сумму значений функции F(x), ровно в 2 раза больших минимума функции. Х изменяется от 5 до 30 с шагом 0.3.
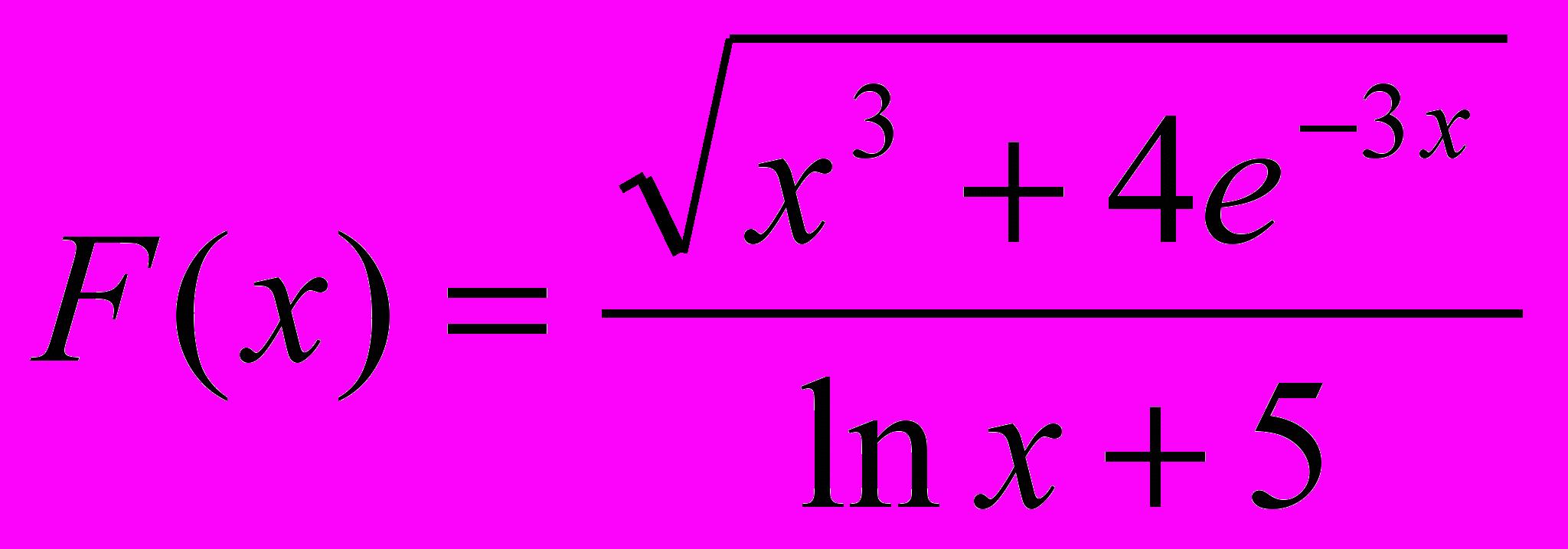
Вариант 37
1. Вычислить величину
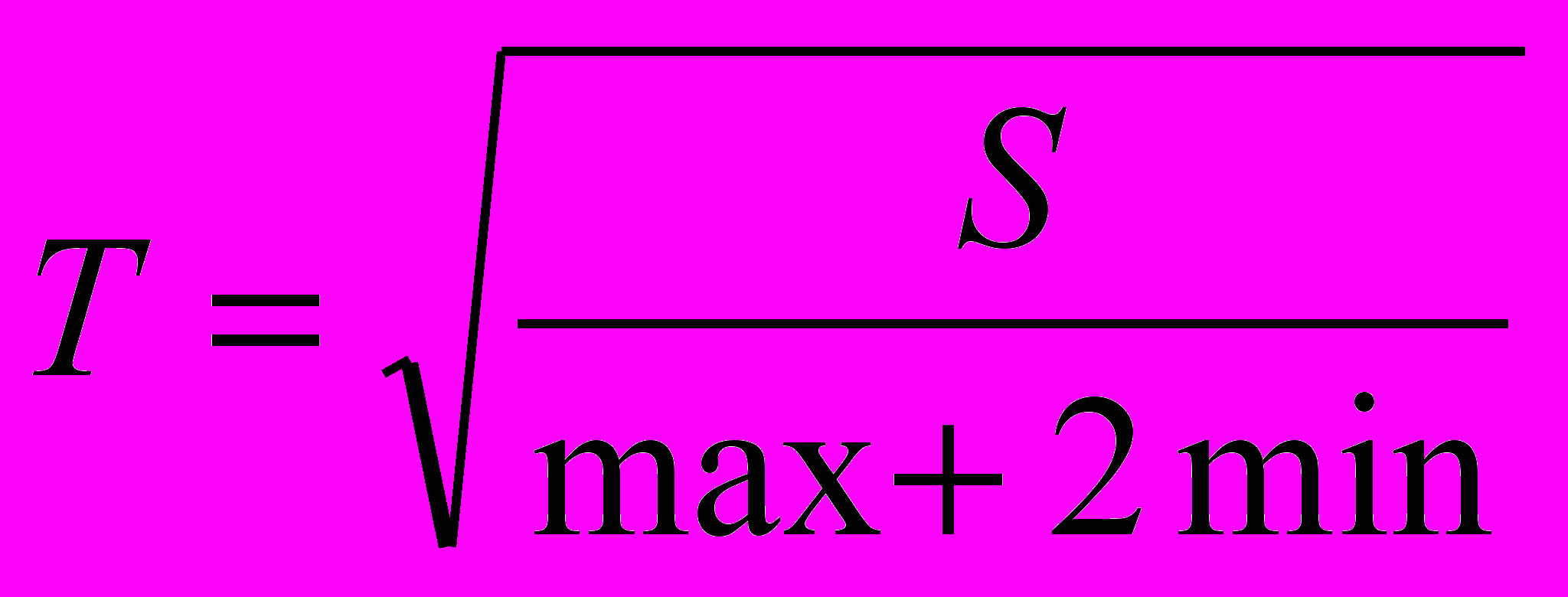 , где S – сумма неотрицательных значений функции F(x), Х изменяется от 4 до 8 с шагом 0.1.
, где S – сумма неотрицательных значений функции F(x), Х изменяется от 4 до 8 с шагом 0.1. 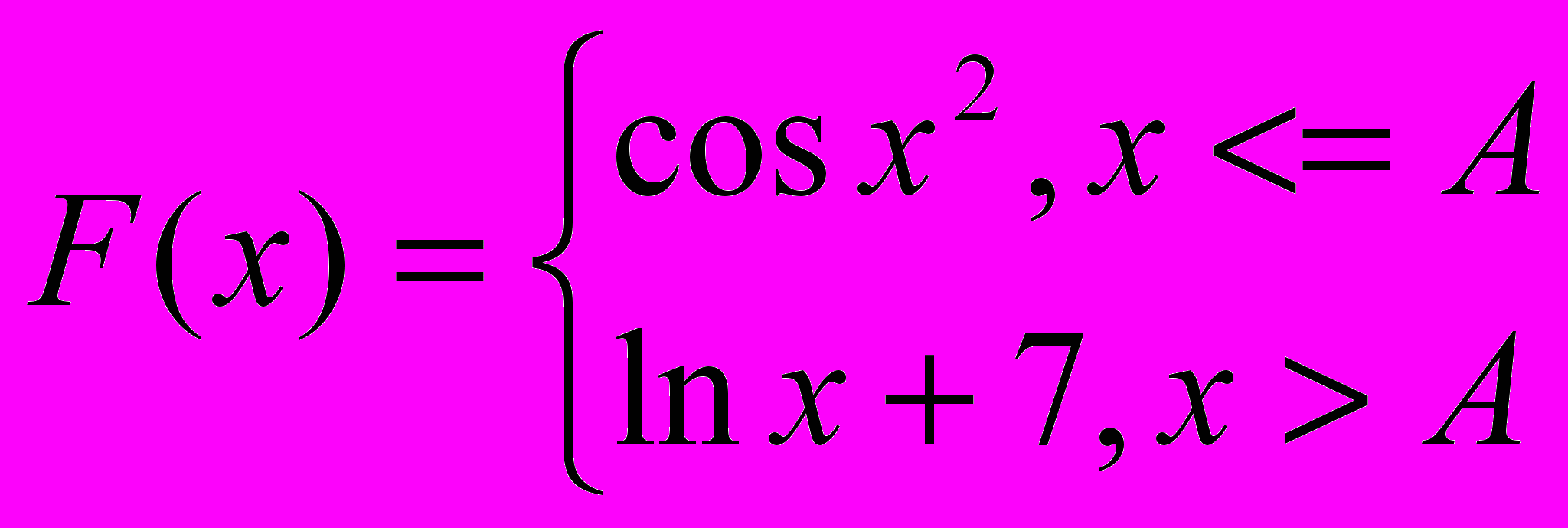
2. Верно ли, что количество положительных значений функции F(x) в три раза меньше суммы ее положительных значений. Х изменяется от 30 до 36 с шагом 0.2
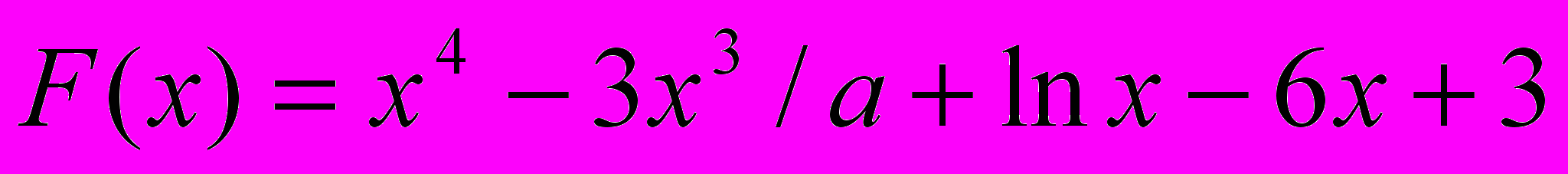
Вариант 38
1. Вывести на печать неотрицательные значения функции
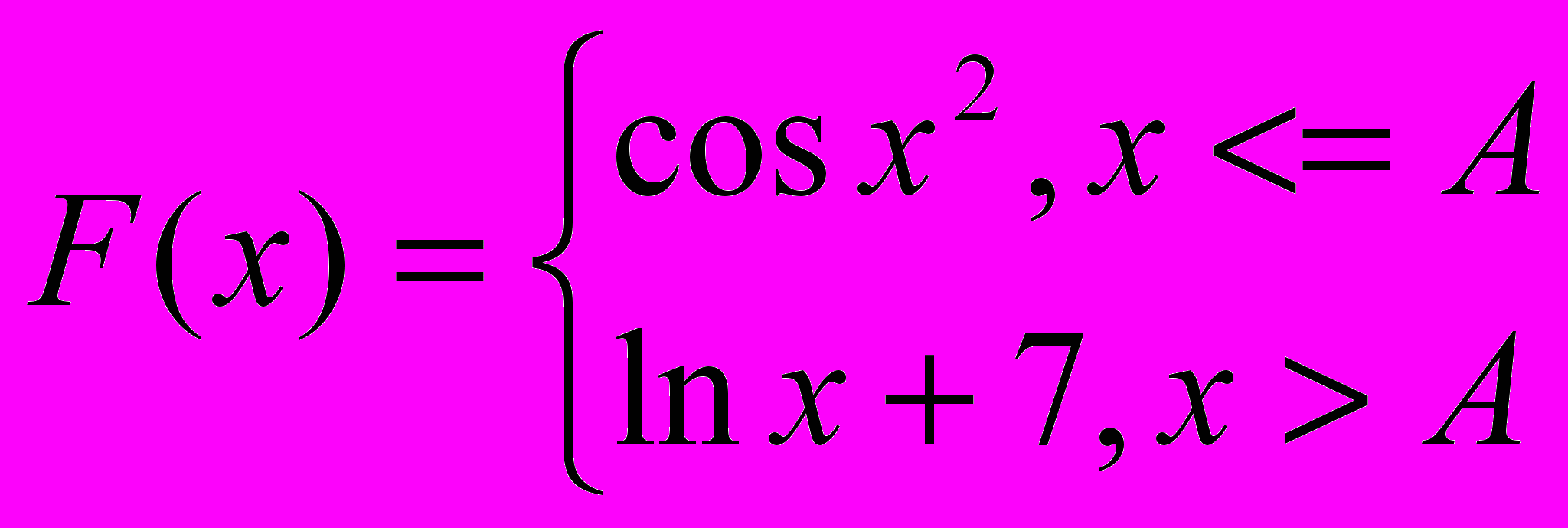 , Х изменяется от 1 до 12 с шагом 0.4 (С помощью всех четырех способов).
, Х изменяется от 1 до 12 с шагом 0.4 (С помощью всех четырех способов).2. Подсчитать сумму значений функции
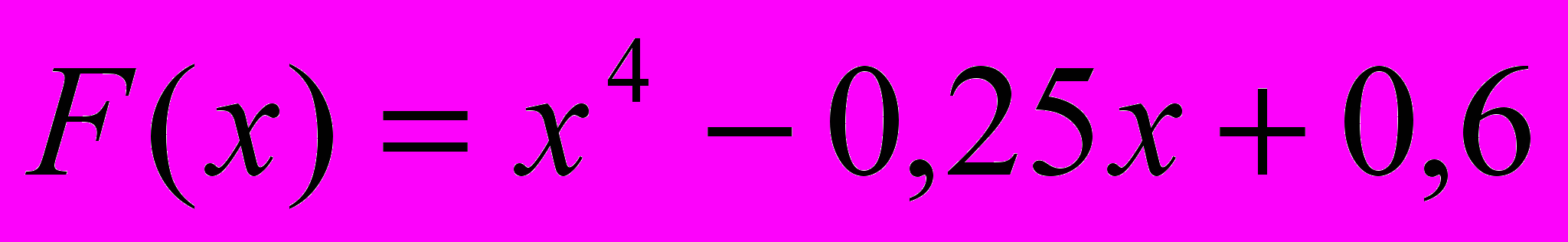 , лежащих в интервале [a;b]. Х изменяется от 10 до 12 с шагом 0.04.
, лежащих в интервале [a;b]. Х изменяется от 10 до 12 с шагом 0.04.Вариант 39
1. Вычислить величину
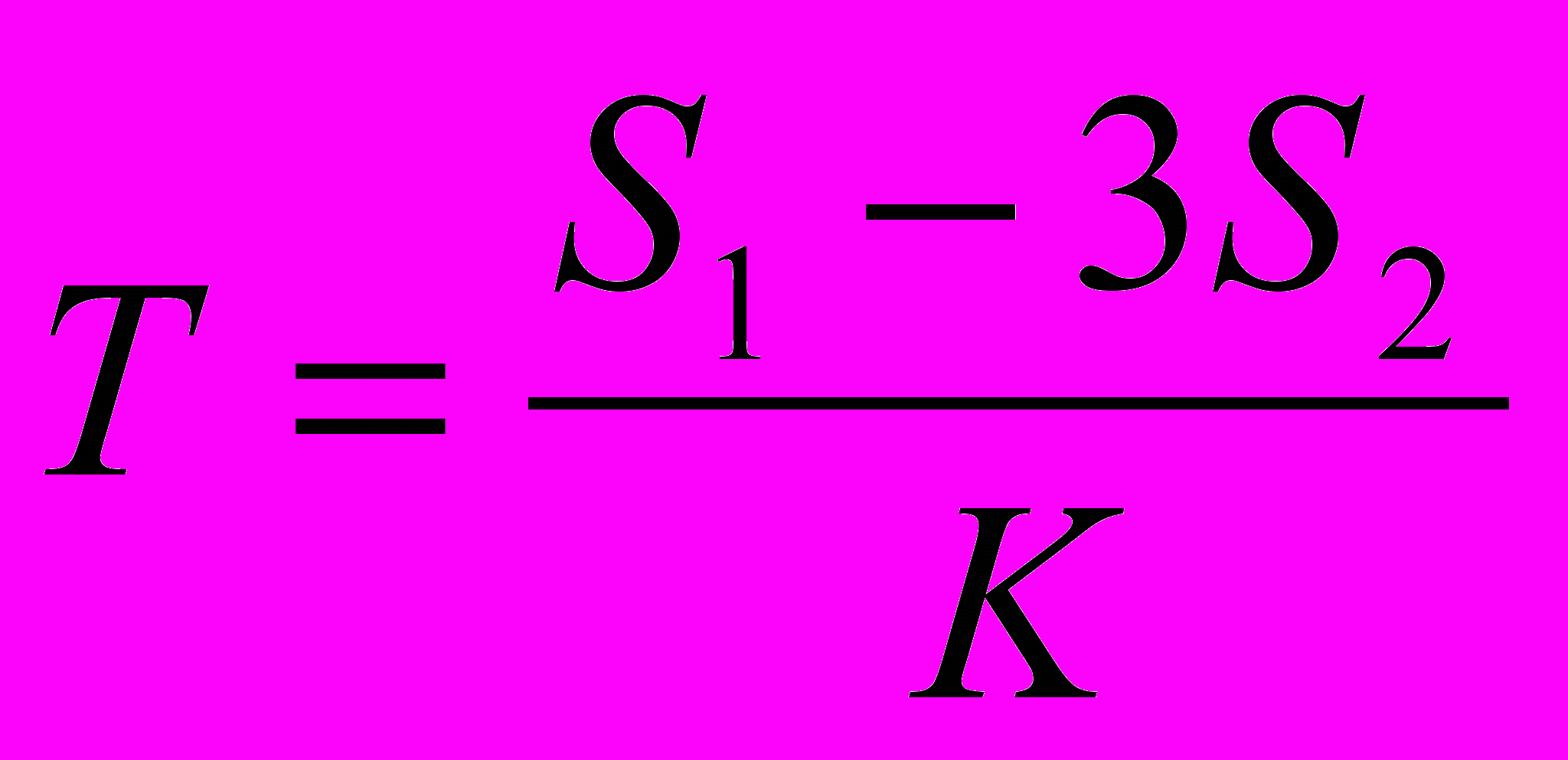 , где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов).
, где S1 – сумма значений функции F(x)>a, S2 – сумма значений F(x)<=b, K – количество неотрицательных значений функции (С помощью всех четырех способов).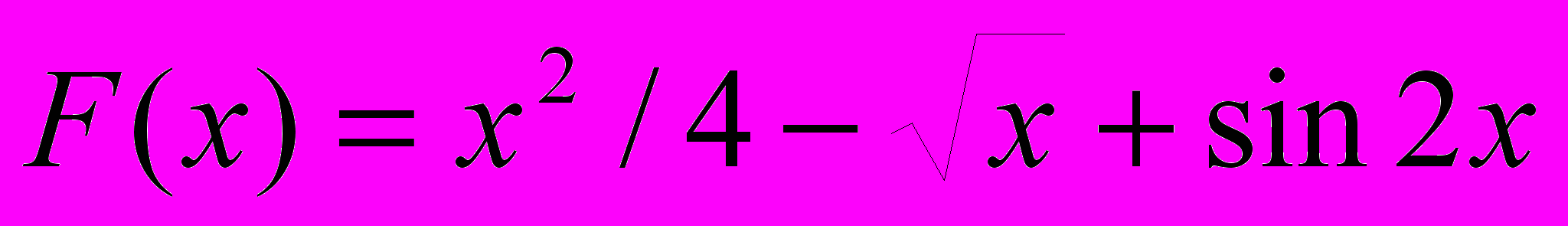
2. Вывести на печать значения функции
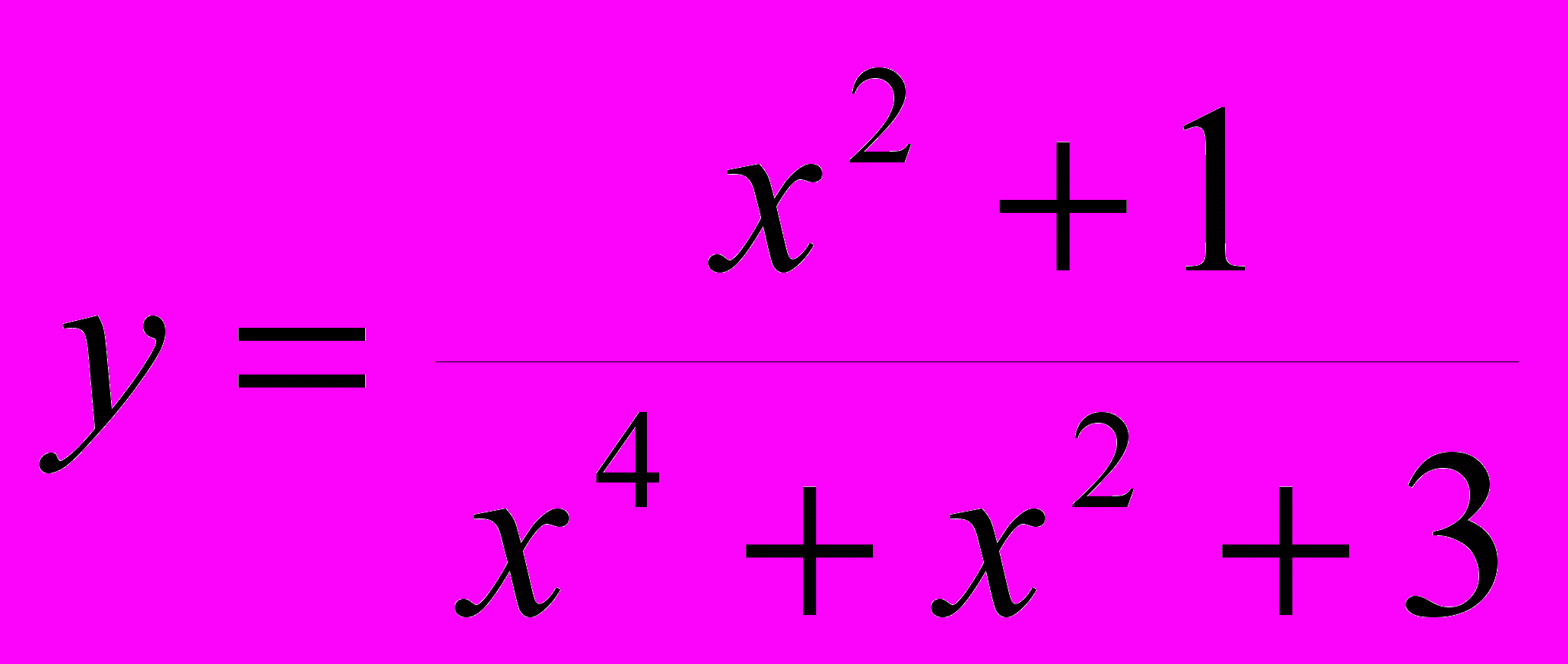 , при x изменяющемся от 0 с шагом 0.5 до y<0.005.
, при x изменяющемся от 0 с шагом 0.5 до y<0.005.Вариант 40.
1. Верно ли, что мах F(X) в 2 раза больше суммы модулей ее отрицательных значений. X изменяется от 1 до 18 с шагом 1 (с помощью всех четырех способов).
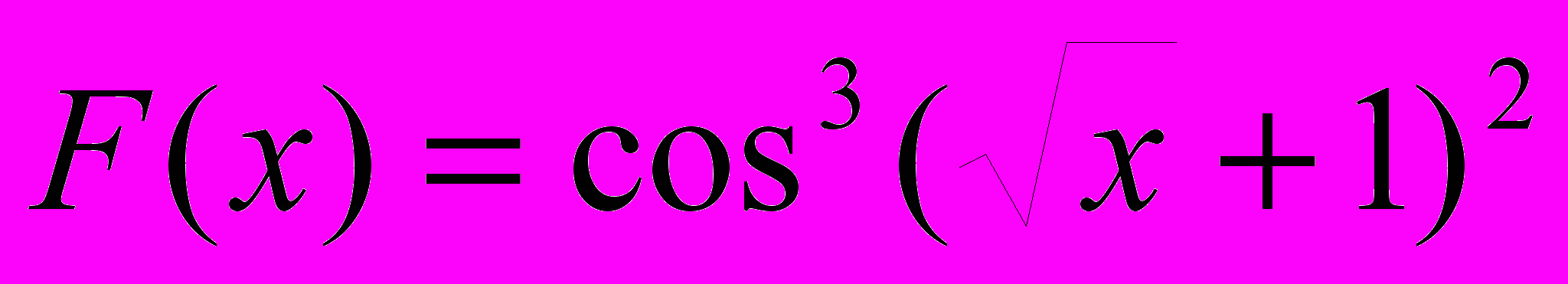
2. Вычислить величину
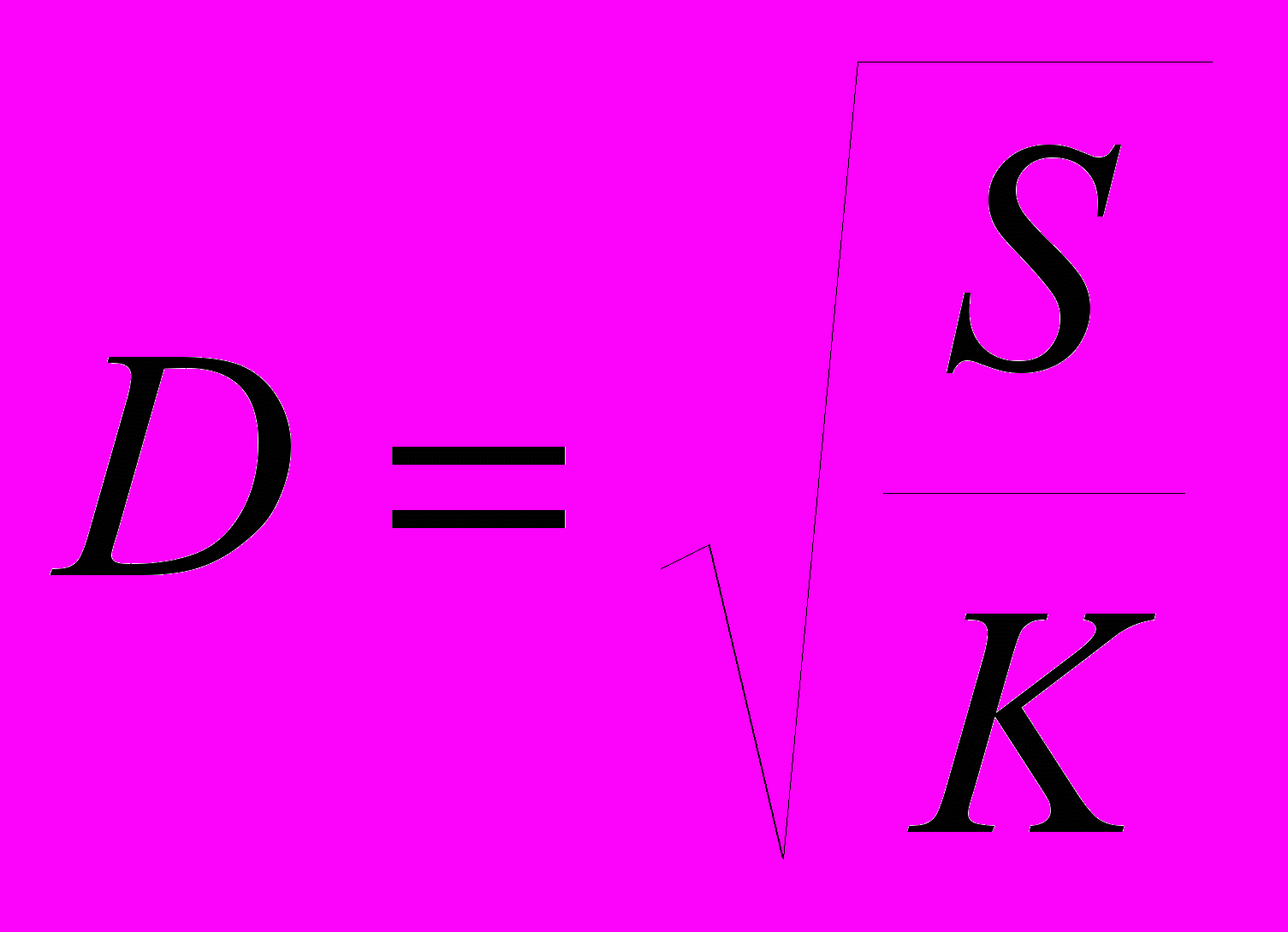 , где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений.
, где S – сумма положительных значений функции F(x), K – количество ее отрицательных значений.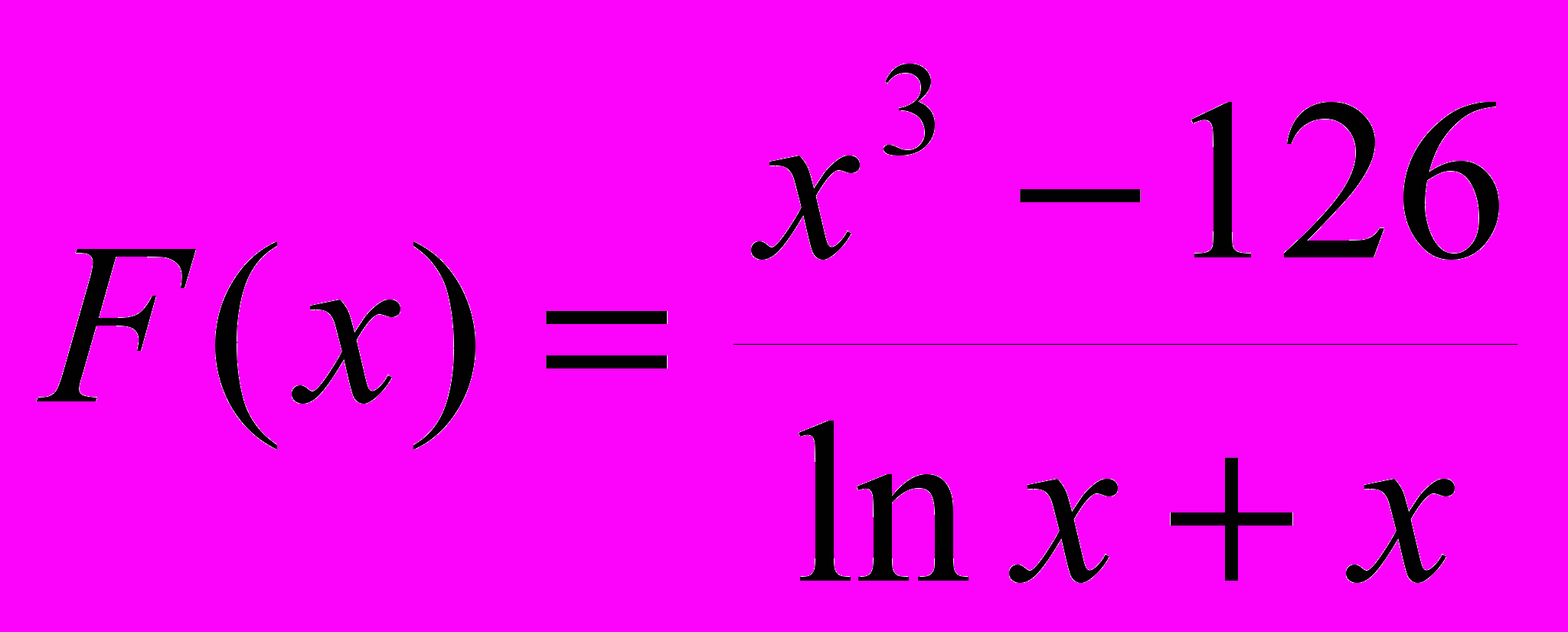 .Х изменяется от 1 до 13 с шагом 0.1
.Х изменяется от 1 до 13 с шагом 0.1Вариант 41.
1. Вывести на печать значений функции F(x), не лежащие в интервале [a,b]. x изменяется от 5 до 16 с шагом 0.2.
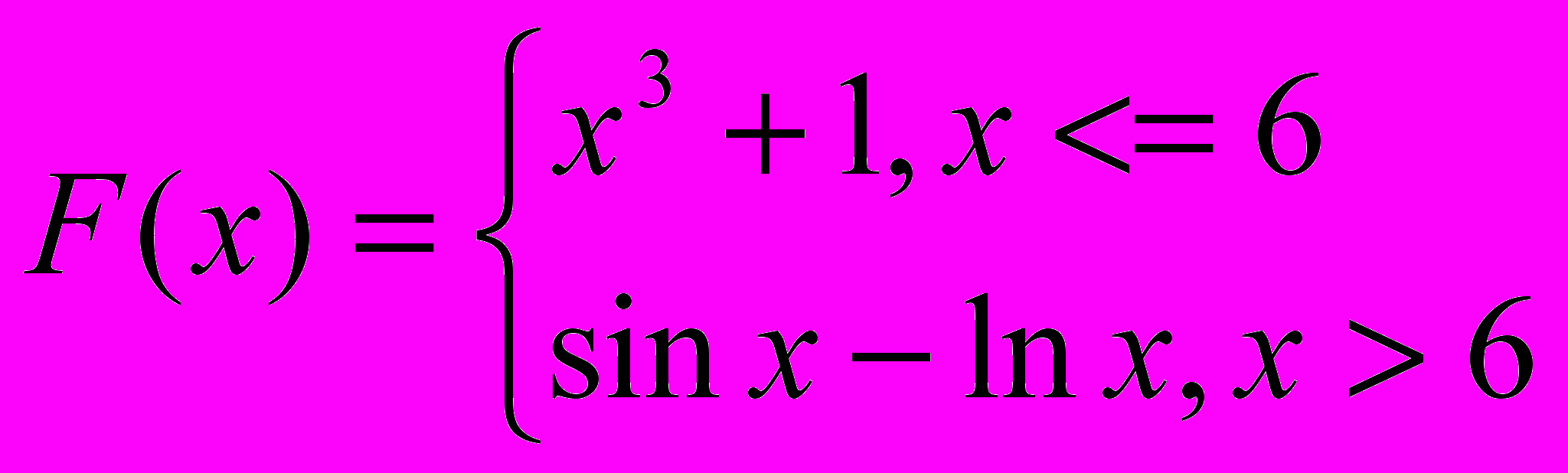
2. Верно ли, что среднее арифметическое неотрицательных значений функции F(x) больше некоторого числа P. x изменяется от 4 до 81 с шагом 2.
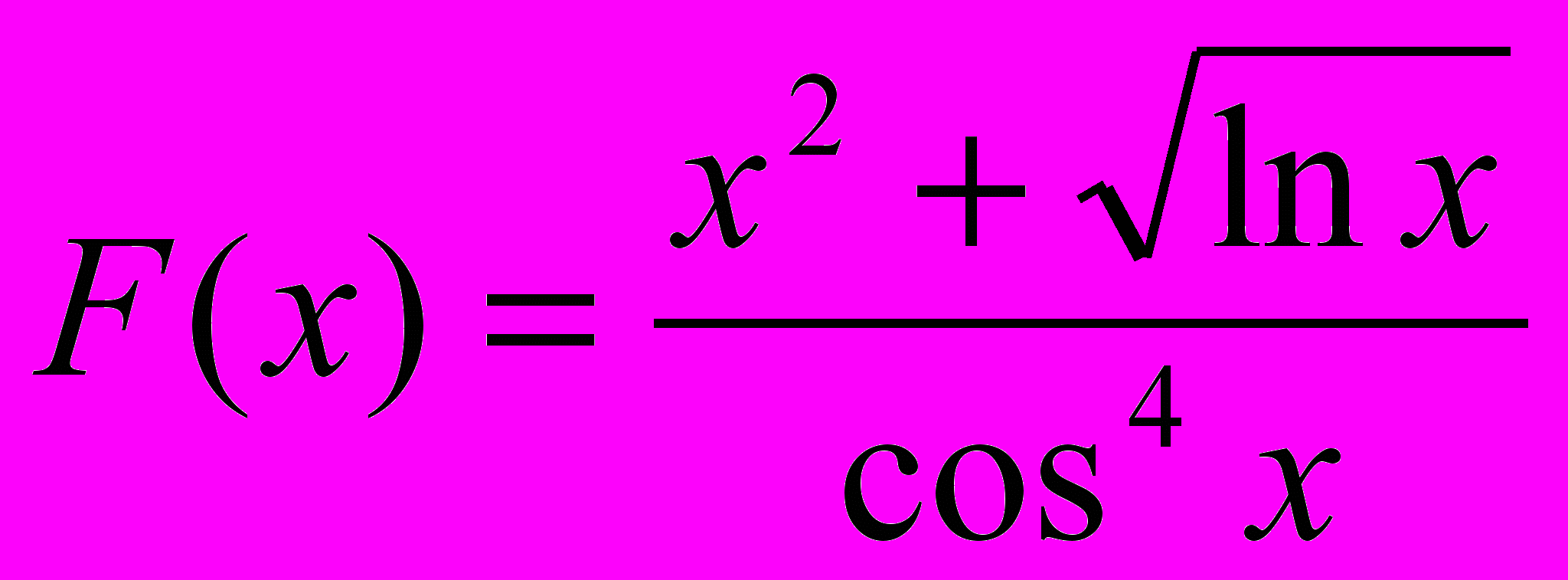
Вариант 42.
1. Верно ли, что функция F(x) на интервале изменения x от 6 от 13 с шагом 0.3 принимает только положительные значения.
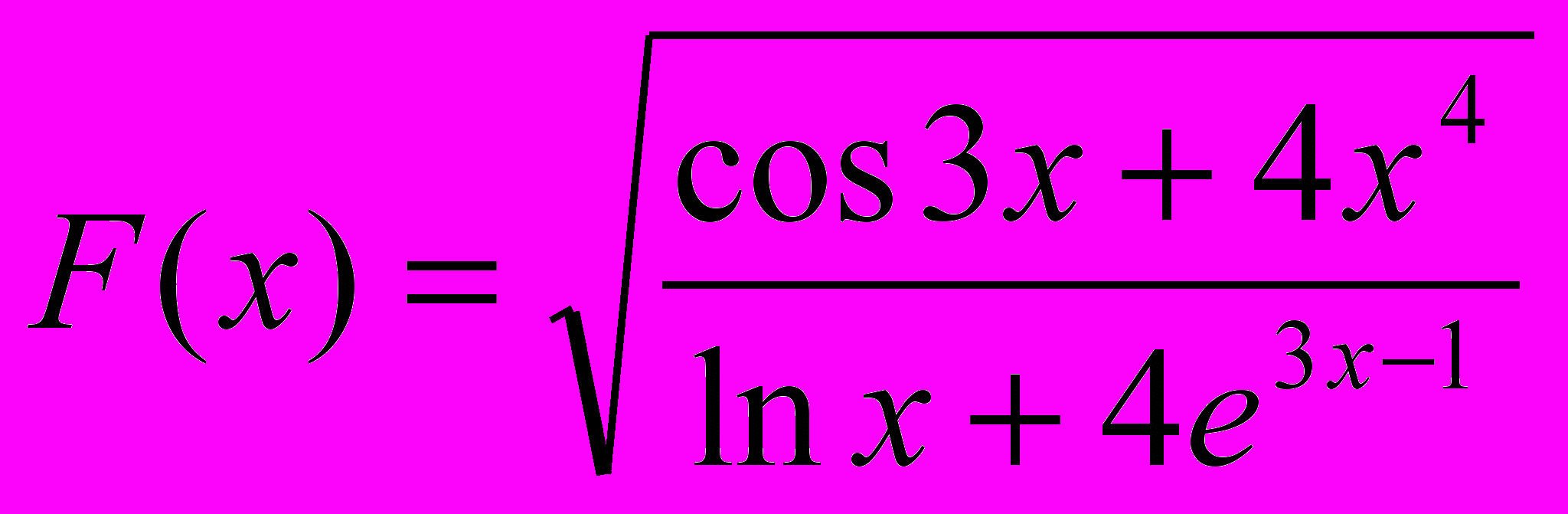
2. Подсчитать сумму значений функции
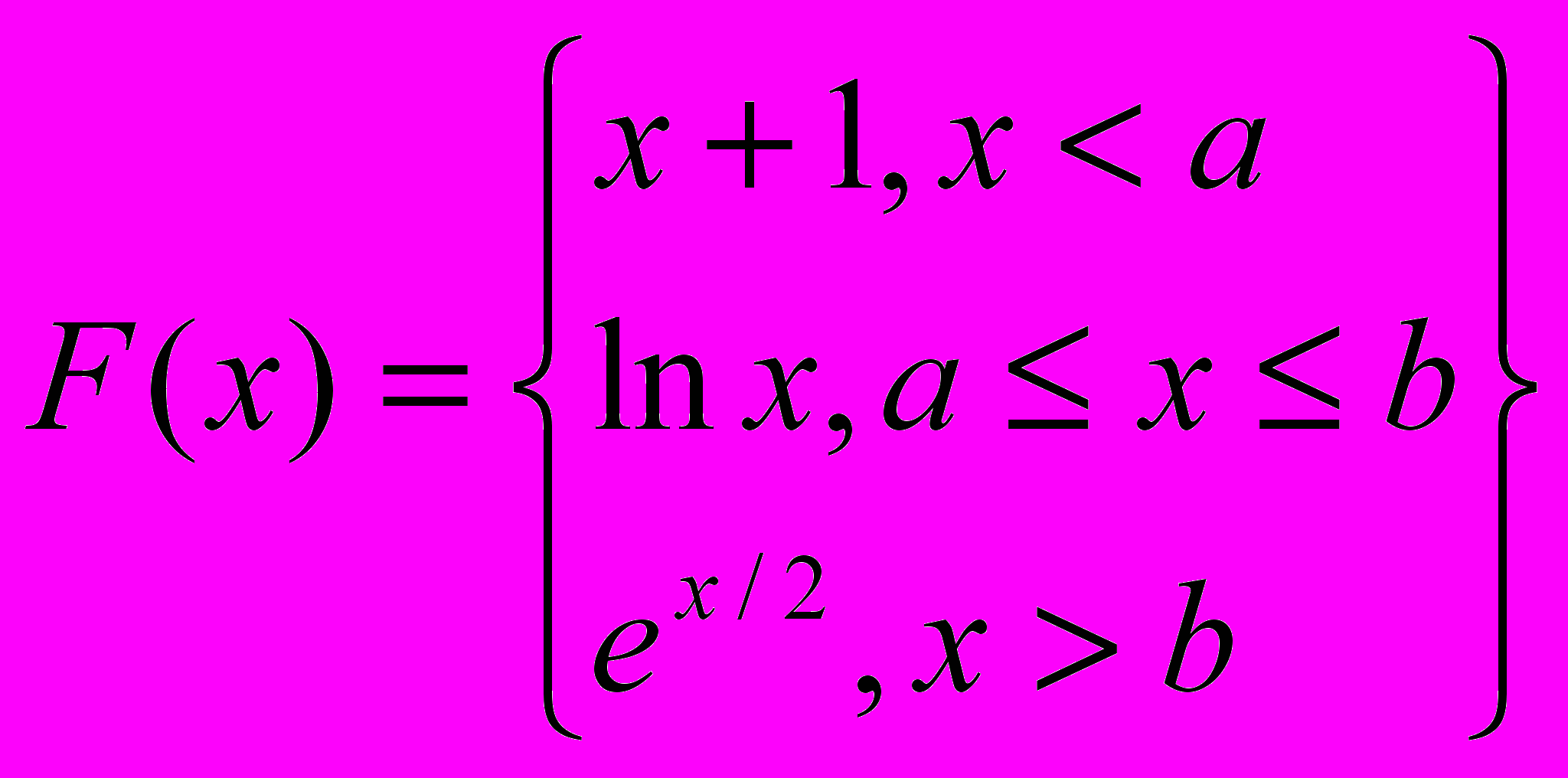 , меньших некоторого числа W. x изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).
, меньших некоторого числа W. x изменяется от1 до 16 с шагом 0.4.( с помощью всех четырех способов).Вариант 43.
1. Верно ли, что сумма положительных значений F(x) в 3 раза больше ее минимального значения ? х изменяется от 1 до 16 с шагом 0.3.
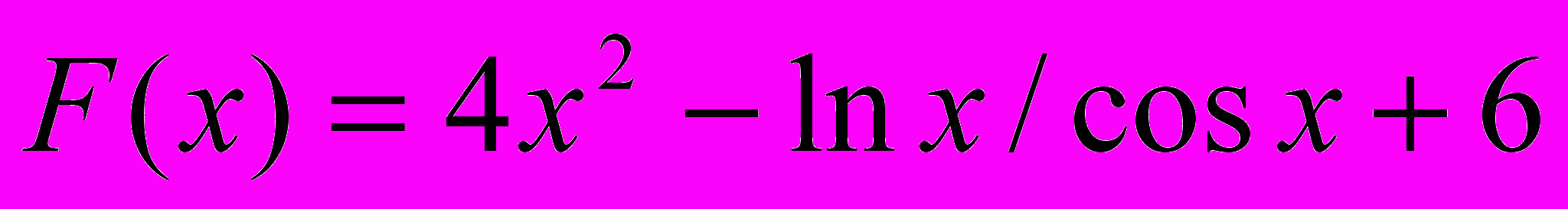
2. Вывести на печать значения функции
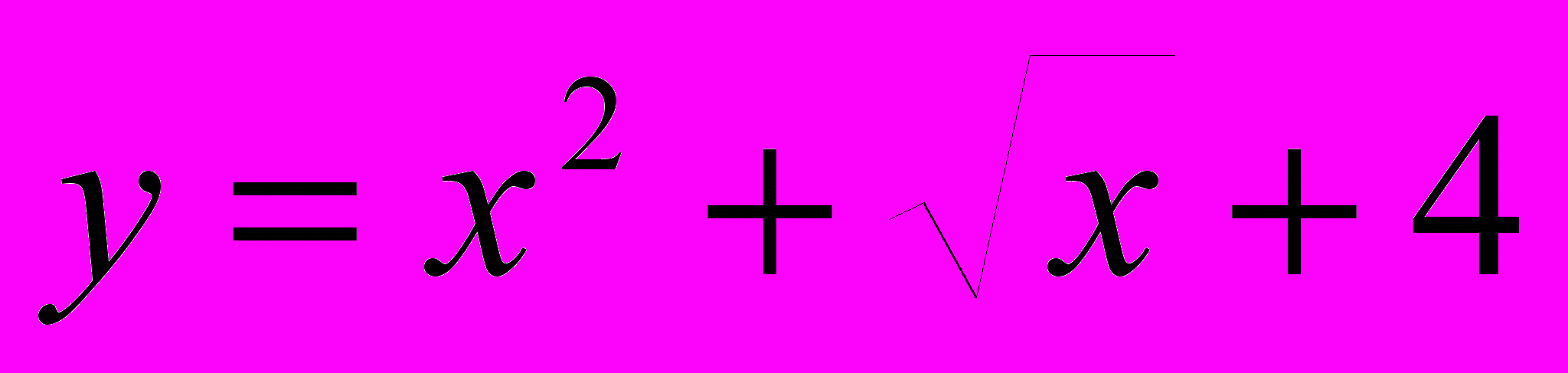 до y> 150. х изменяется от 1 с шагом 0.3.
до y> 150. х изменяется от 1 с шагом 0.3.Вариант 44.
1. Верно ли, что максимум функции F(x) в три раза больше ее минимума. Х изменяется от 4 до 13 с шагом 0.1.
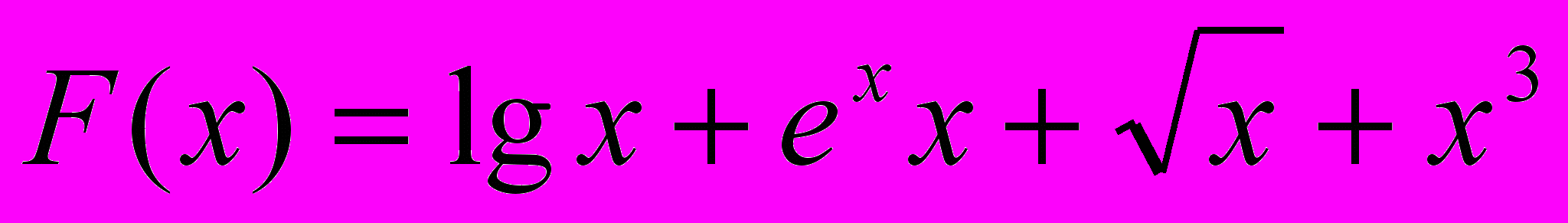
2. Вычислить величину
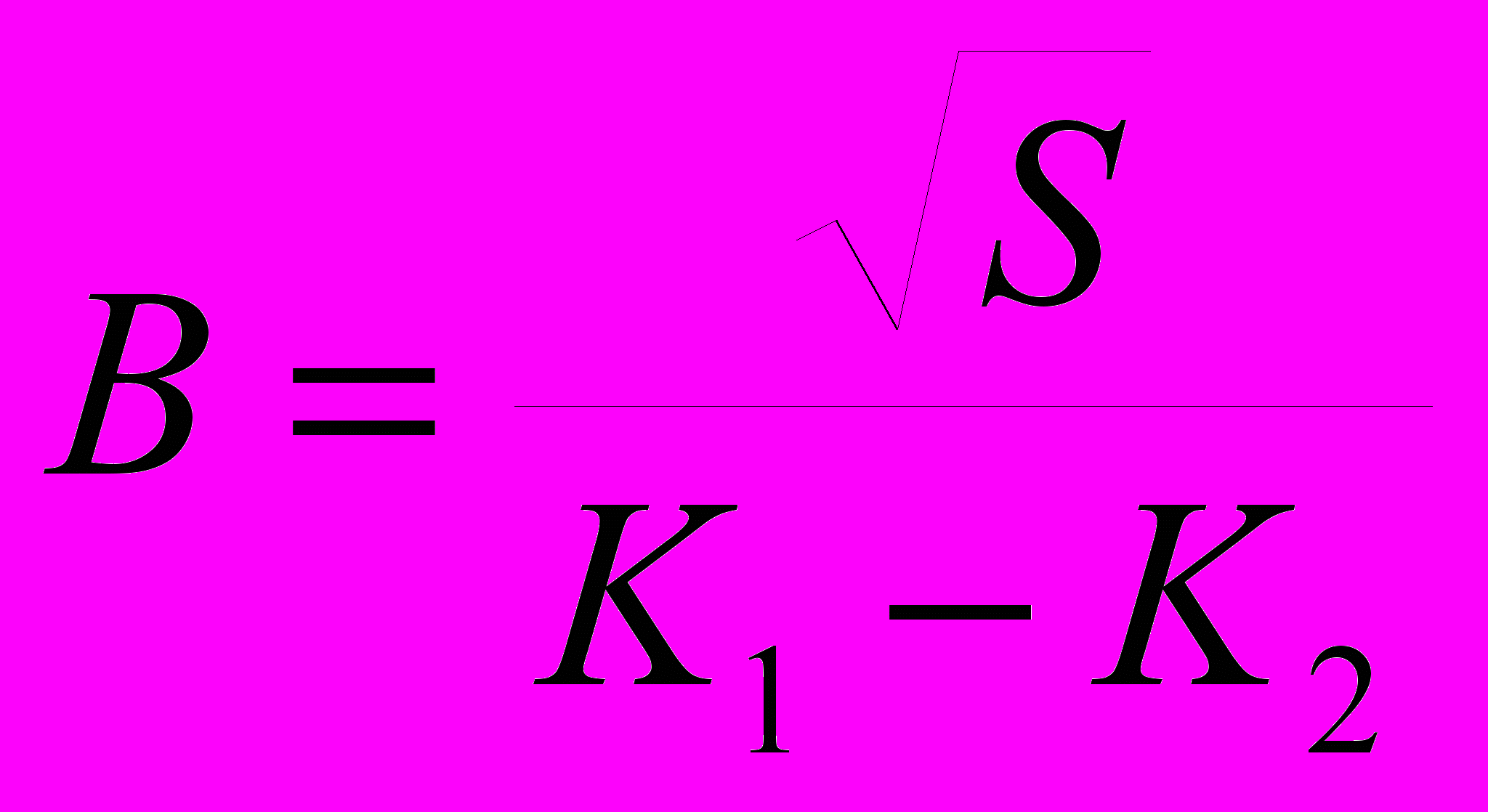 , где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. х изменяется от 5 до 15 с шагом 0.4.
, где S –сумма неотрицательных значений функции F(x), K1- количество ее неотрицательных значений, K2- количество значений функции, меньших числа Р. х изменяется от 5 до 15 с шагом 0.4.
Вариант 45.
1. Верно ли, что максимум функции F(x) лежит в интервале [5;12]. Х изменяется от 4 до 18 с шагом 0.5. (с помощью всех четырех способов).
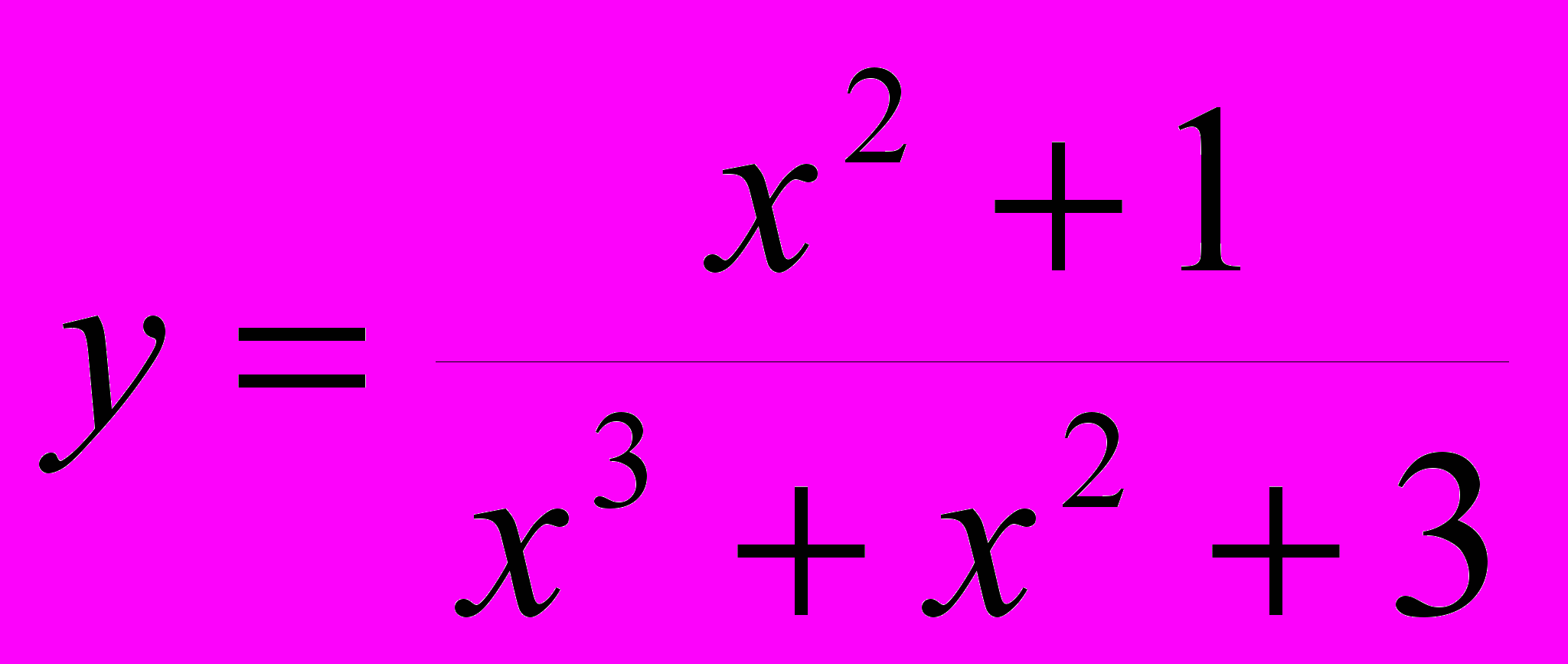 +6х
+6х2. Верно ли, что среднее значение функции
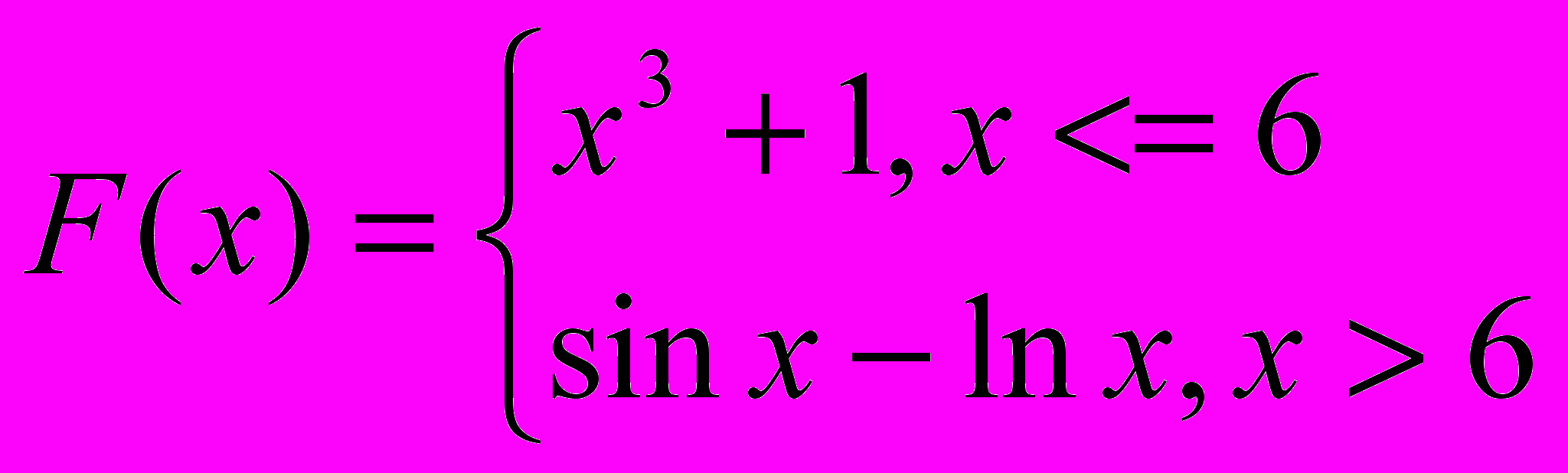 равно полусумме ее максимума и минимума. Х изменяется от 4 до 8 с шагом 0.3.
равно полусумме ее максимума и минимума. Х изменяется от 4 до 8 с шагом 0.3.Вариант 46.
1. Подсчитать количество значений функции F(x), меньших ее среднего значения ровно на 1. Х изменяется от 4 до 15 с шагом 0.2.
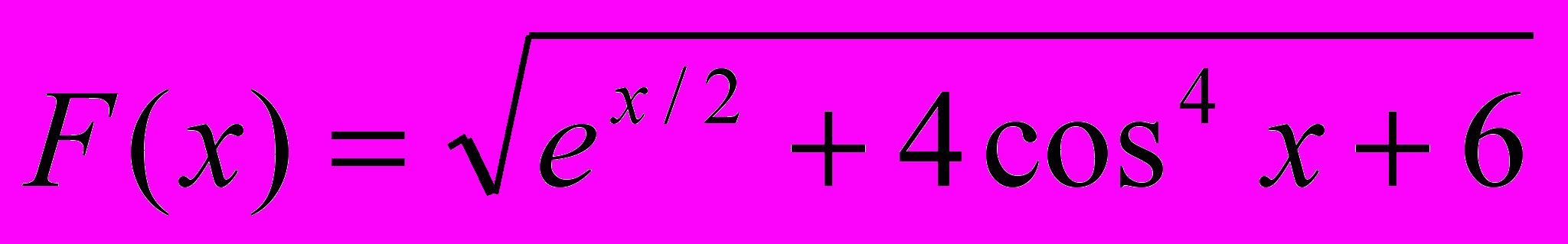
2. Верно ли, что функция F(x) на отрезке изменения х от а до b с шагом 0.2 принимает только отрицательные значения.
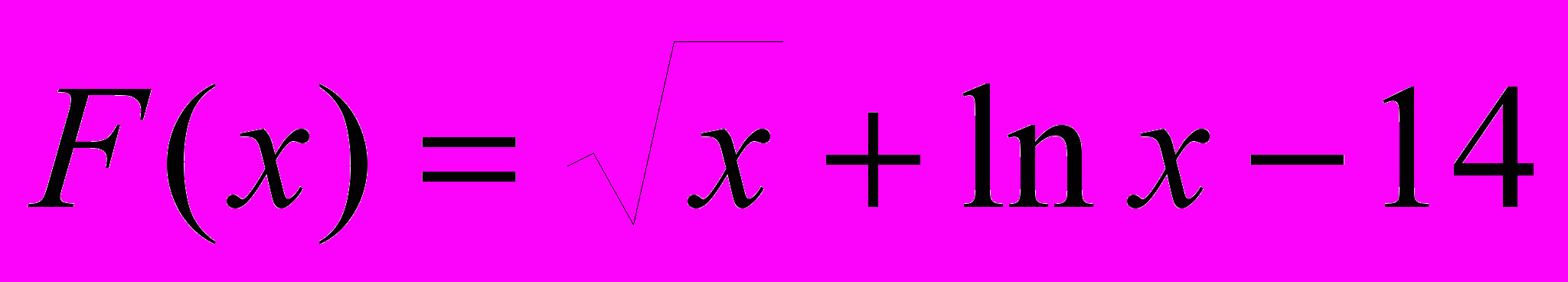
Вариант 47.
1. Вычислить величину
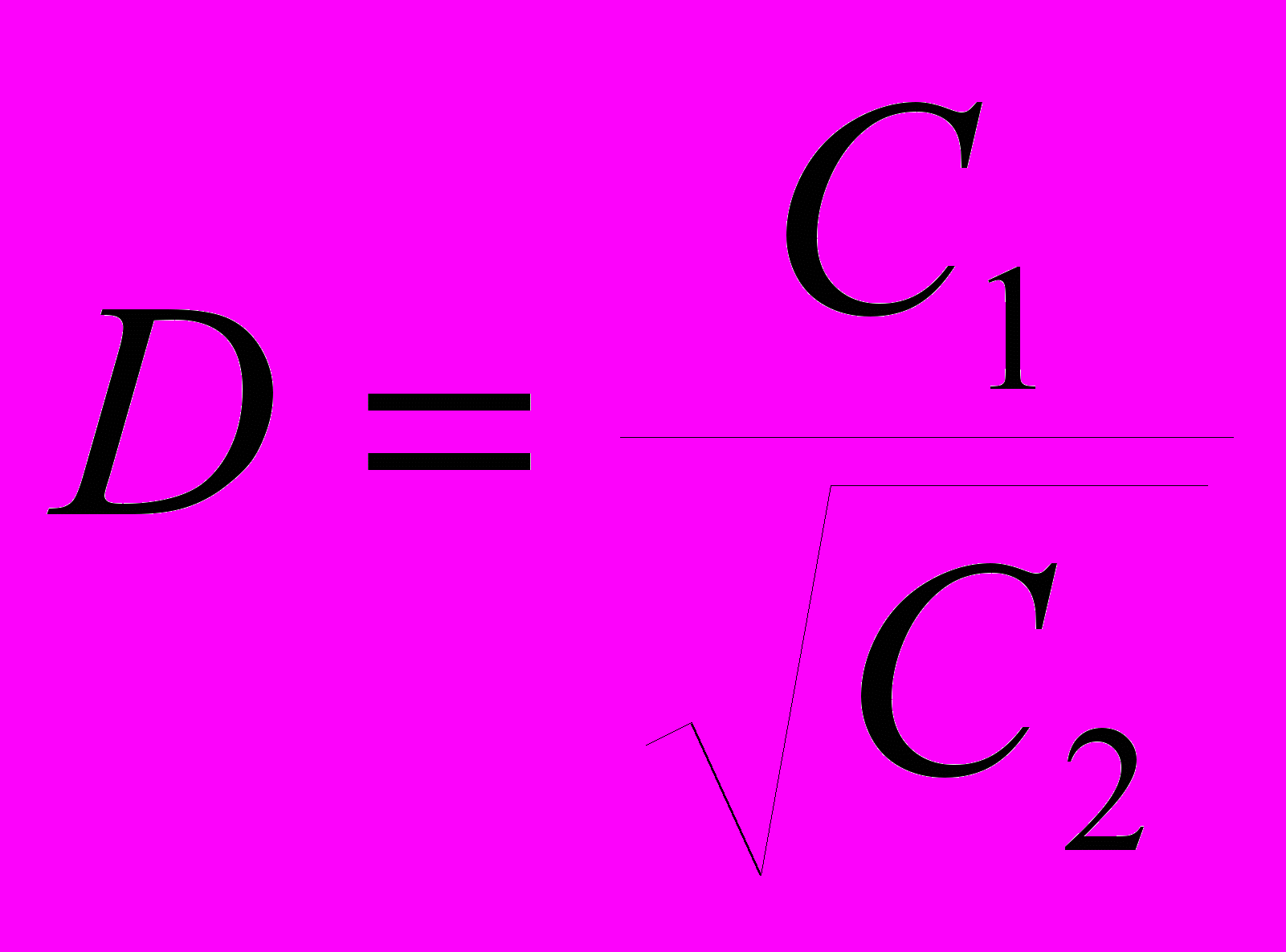 . Где С2- среднее арифметическое положительных значений функции, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 5 до 18 с шагом 0.2.
. Где С2- среднее арифметическое положительных значений функции, С1 – среднее арифметическое ее отрицательных значений. Х изменяется от 5 до 18 с шагом 0.2. 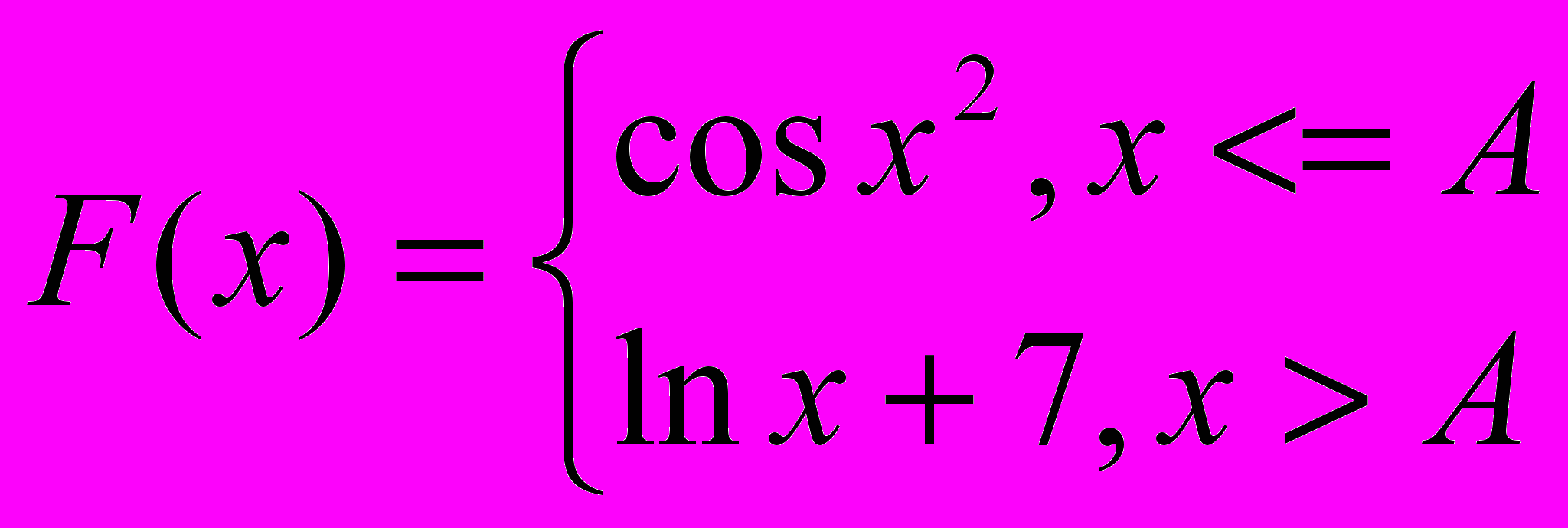
2. Вывести на печать значения функции
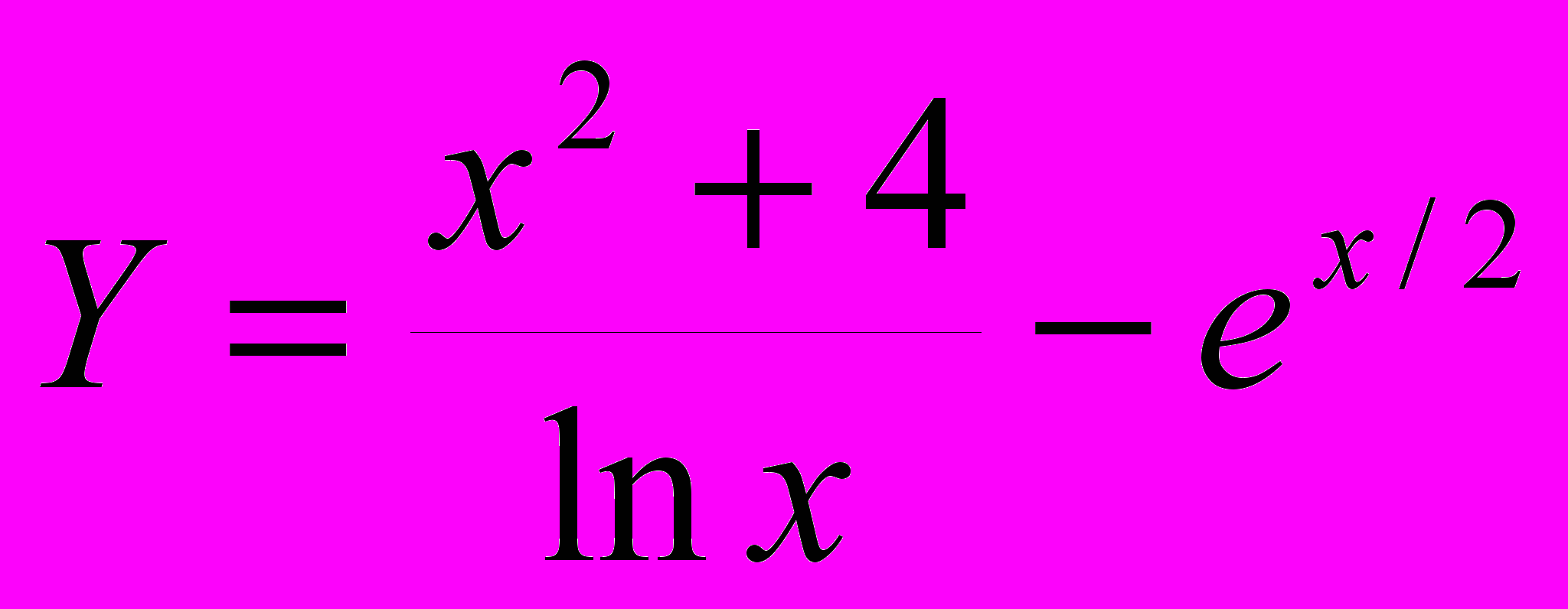 до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.
до ее первого отрицательного значения. Х изменяется от 2 с шагом 0.3.Задание 1. Для каждого вида растений рассчитать стоимость. Если растение берется в количестве большем 120 шт, делается скидка 10% стоисости.
Задание 2. Рассчитать средний период между датой оплаты и выполнением заказа.
Задание 3. С помощью автофильтра вывести все растения, оплаченные в апреле 2007 года.
| наименование | кол-во | цена(руб/шт) | дата оплаты | дата выполнения |
| флоксы | 100 | 1,5 | 16.06.2006 | 20.06.2006 |
| резеда | 80 | 2,8 | 18.04.2006 | 25.04.2006 |
| астры | 120 | 0,95 | 25.07.2006 | 01.08.2006 |
| тюльпаны | 150 | 2,5 | 25.03.2007 | 28.03.2007 |
| нарциссы | 75 | 1,8 | 30.03.2006 | 05.04.2007 |
| ирисы | 80 | 2,4 | 20.04.2007 | 27.04.2007 |
Задание 1. Используя функцию МЕСЯЦ отметить знаком * лиц, родившихся в весенние месяцы
Задание 2. Рассчитать оклад сотрудников следующим образом: сотруднику со стажем более 10 лет выплачивается надбавка 20%
Задание 3. Для каждой должности в алфавитном порядке расположить сотрудников в алфавитном порядке.
| фамилия | дата рождения | должность | стаж | оклад |
| Иванов | 22.12.1960 | конструктор | 15 | 14570 |
| Федосеев | 14.04.1956 | лаборант | 22 | 5600 |
| Лукьянов | 17.10.1981 | программист | 3 | 10000 |
| Кузьмин | 24.05.1982 | программист | 1 | 3400 |
| Аверкиев | 15.08.1976 | конструктор | 14 | 12780 |
| Воронов | 02.07.1969 | нач.группы | 17 | 18300 |
Задание 1. Для каждого врача в алфавитном порядке расположить пациентов в алфавитном порядке.
Задание 2. Вывести с помощью автофильтра всех пациентов врача Окунева с причиной «Заболевание».
Задание 3. Отметить знаком * всех пациентов, больничный лист которым был выдан более чем на 10 дней.
| пациент | врач | дата | причина | б/л по |
| Васин | Петров А.В. | 22.12.2006 | заболевание | 17.12.2006 |
| Шишкин | Морозова К.Т. | 16.09.2006 | травма | 26.10.2006 |
| Иванов | Окунев С.Р. | 17.10.2006 | заболевание | 25.10.2006 |
| Калачев | Петров А.В. | 20.11.2006 | заболевание | 12.12.2006 |
| Лазарев | Морозова К.Т. | 14.12.2006 | травма | 21.12.2006 |
| Муромцев | Окунев С.Р. | 03.02.2007 | травма | 05.03.2007 |
