Рабочая программа Программа лекционного курса План практических занятий

Вид материала

Рабочая программа

Содержание Декартово поизведение множеств. разбиение множества на классы Элементы комбинаторики Высказывания и операции над ними Высказывательные формы (предикаты) Логическая организация математического материала Отношения на множестве Системы счисления Делимость чисел Делимость чисел Аксиоматическое построение Теоретико-множественный подход к построению множества целых неотрицательных чисел Натуральное число как результат

Подобный материал:

• Рабочая программа Программа лекционного курса План практических занятий, 825.14kb.
• Методика преподавания математики рабочая программа Программа лекционного курса Планы, 266.77kb.
• Методика преподавания математики рабочая программа Программа лекционного курса Планы, 384.99kb.
• Рабочая программа Программа лекционного курса Планы лабораторных занятий, 88.79kb.
• Рабочая программа Программа лекционного курса Планы лабораторных занятий, 97.54kb.
• Рабочая программа Тематика и планы семинарских занятий График текущего и промежуточного, 127.07kb.
• Программа курса психологии продажи товара Тематический план лекций, семинаров, практических, 54.58kb.
• Программа лекционного курса для магистрантов факультета философии гу-вшэ цель курса, 174.59kb.
• М к. Аммосова Педагогический институт Рабочая программа, 114.38kb.
• Программа лекционного курса для студентов 5 курса спец. «история», 413.6kb.

Тема: МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ

Литература:

(1) гл. I, § 1 пп. 1,2;3,4 (2) гл. I, § 1, с. 6-9, 11-13, 14-25; (3) гл. I, § 1 пп. 1,2,3,4; (4) гл. I, с. 31-36; (5) гл I, §§ 1.1-1.3, 1.5-1.7.

Контрольные вопросы:

1. Множество. Элемент множества. Пустое множество. Обо­зна­чение.

2. Способы задания множеств. Числовые множества.

3. Отношения между множествами. Подмножества.

4. Универсальное множество. Круги Эйлера.

5. Пересечение множеств. Свойства пересечения множеств.

6. Объединение множеств. Свойства объединения множеств.

7. Разность множеств. Дополнение к подмножеству. Фор­мулы де Моргана.

8. Отношения между множествами и их доказательство.

9. Связь с начальным курсом математики.

10. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 1, 2.

2. (1) гл. I, § 1 №№ 1-13; №№ 14-54; (4) гл. I, с. 53, №№ 1.4-1.8, 1.11., с.54, № 1.15


Занятие № 2

Тема: ДЕКАРТОВО ПОИЗВЕДЕНИЕ МНОЖЕСТВ. РАЗБИЕНИЕ МНОЖЕСТВА НА КЛАССЫ

Литература:

(1) гл. I, § 1 п.5, 6; (2) гл. I, § 1, с. 25-33, 26-27, 38-39; (3) гл. I, § 1 п.5, §5 пп 31,32; (4) гл. I, с. 37-38, с. 45-47; (5) гл. I, §§ 1.4, 1.5, 1.7.

Контрольные вопросы:

1. Декартово произведение двух множеств. Свойства декар­това произведения двух множеств.

2. Способы задания декартова произведения двух множеств.

3. Графическое изображение декартова произведения двух чи­словых множеств.

4. Декартово произведение n множеств.

5. Условия разбиения множества на классы (на попарно не­пере­секающиеся подмноже­ства).

6. Разбиение множества на классы с помощью одного, двух, трех свойств. Классифи­кация.

7. Число элементов в объединении двух конечных множеств и дополнении к подмно­жеству.

8. Применение разбиения множества на классы к решению тек­стовых задач.

9. Из истории развития теории множеств.

Задание на дом:

1. Зачетное задание № 3.,4

2. (1) гл. I, § 1 №№ 55-81; № 107-116; (4) гл. I, с. 54, №№ 1.21-1.24 с. 55, №№ 1.28, 1.30.

3. Примерный вариант к/р № 1.


Первый семестр


Занятие № 3

Тема: ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

Литература:

(1) гл. I, § 2 пп. 8-11; (2) гл. I, § 6, с. 142-149; (3) гл. I, § 2 пп.6-8; (4) гл. V, с. 151-155; (5) гл. IV, §§ 4.1 – 4.7.

Контрольные вопросы:

1. Комбинаторные задачи. Правила суммы и произведения.

2. Перестановки, размещения без повторений и с повторе­ниями.

3. Сочетания без повторений и с повторениями. Свойства чисел .

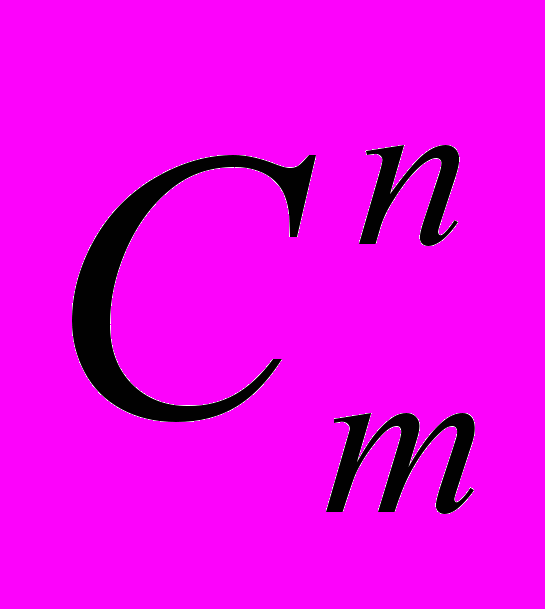4. Число подмножеств конечного множества.

5. Бином Ньютона. Треугольник Паскаля.

5. Связь с начальным курсом математики.

6. Из истории развития комбинаторики.

Задание на дом:

1. Зачетное задание № 4.

2. (1) гл. I, №№ 117-161; (4) гл. V, с. 164, №№ 5.25-5.30.


Занятие № 4

Тема: ВЫСКАЗЫВАНИЯ И ОПЕРАЦИИ НАД НИМИ

Литература:

(1) гл. I, § 3 пп.13-17; (2) гл. I, § 3, с. 53-59, 73; (3) гл. I, § 3, пп.18-20; (4) гл. II, с. 57-59, с. 88-91; (5) гл. II, §§ 2.1, §§ 2.6 – 2.9.

Контрольные вопросы:

1. Понятие высказывания. Примеры, контрпримеры. Обо­значе­ния. Равносильные вы­сказывания.

2. Операции над высказываниями (отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция), их свойства.

3. Формулы логики высказываний. Тавтология. Доказатель­ство равносильностей вы­сказываний.

4. Логические уравнения и их применение к решению задач.

5. Способы решения логических задач.

6. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 5.

2. (1) гл. I, III №№ 175-176, 184-186, 204-209, 219, 240, 242, 244, 246, 247, 255, 256; (4) гл. II, с. 99, №№ 2.1-2.3, 2.26-2.31.


Контроль за самостоятельной работой студентов

(3 час)


Второй семестр


Занятия № 5

Тема: ВЫСКАЗЫВАТЕЛЬНЫЕ ФОРМЫ (ПРЕДИКАТЫ)

Литература:

(1) гл. I, § 3 пп.16-17, § 4 пп.19-21; (2) гл. I, § 3, с. 55-56, 61-62, 67-71, 73; (3) гл. I, § 3 пп. 18-23; (4) гл. II, с. 62-83; (5) гл. II, §§ 2.2, 2.5.

Контрольные вопросы:

1. Понятие высказывательной формы (предиката). Примеры. Область определения, множества истинности и ложности пре­диката.

2. Операции над предикатами.

2.1. Обращение предиката в высказывание. Кванторы.

2.2. Отрицание, конъюнкция, дизъюнкция, импликация, экви­валенция предикатов.

3. Отрицание высказываний, содержащих кванторы.

4. Отношения следования и равносильности. Необходимые и достаточные условия.

5. Теоремы. Строение теоремы. Виды теорем.

6. Способы доказательств методом от противного и методом контрапозиции.

7. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 6.

2. (1) гл. I №№ 173-183, 193-203, 210-218, 220-233, 234-238, 249, 257, 258, 263, 268, 275-287, 288-293, 294-301, 312-314; (4) гл. II, с. 99, №№ 2.6, 2.16-2.17.


Занятие №6

Тема: ЛОГИЧЕСКАЯ ОРГАНИЗАЦИЯ МАТЕМАТИЧЕСКОГО МАТЕРИАЛА

Литература:

(1) гл. I, §§ 5, 6 пп.23-28; (2) гл. I, § 2, с. 46-50, 89-92, 94-97, 99-103; (3) гл. I, § 3 пп.17,24, 25-27; (4) гл. II, с. 75-82; (5) гл. II, §§ 2.3, 2.4, 2.7, 2.8.

Контрольные вопросы:

1. Математические понятия. Определяемые и неопределяе­мые понятия. Объем и со­держание понятия.

2. Отношения между понятиями.

3. Способы определения понятий. Структура определения поня­тий через род и видо­вое отличие.

4. Требования к определению понятий.

5. Умозаключения (рассуждения). Дедуктивные и недедук­тив­ные умозаключения.

6. Простейшие правила вывода. Проверка правильности умозак­лючений с помощью кругов Эйлера.

7. Способы доказательства математических утверждений (пред­ложений). Софизмы.

8. Индуктивные умозаключения. Полная и неполная индукция.

9. Связь с начальным курсом математики.

10. Из истории развития математической логики.

Задание на дом:

1. Зачетное задание № 7.

2. (1) гл. I, №№ 315-320, 321-328, 329-334, 337, 341, 342-345, 346-349, 350-353, 356, 357-364; (4) гл. II, с. 99, №№ 2.10-2.13.


Занятия № 7

Тема: СООТВЕТСТВИЯ

Литература:

(1) гл. I, § 10 пп.44-46; (2) гл. II, § 8, с. 166-170; (3) гл. I, § 2, пп. 9,10; (4) гл. III, с. 103-107; (5) гл. III, §§ 3.1, 3.2.

Контрольные вопросы:

1. Соответствия между элементами двух множеств. Основ­ные понятия. Обозначения. Способы задания соответствий.

2. Виды соответствий (обратное, противоположное дан­ному). Взаимнооднозначные соответствия. Равномощные мно­жества.

3. Отображения, виды отображений.

4. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 8.

2. (1) гл. I, § 10 №№ 487-504, 528-538; (4) гл. III, с. 121, №№ 3.1-3.9.


Занятия № 8

Тема: ОТНОШЕНИЯ НА МНОЖЕСТВЕ

Литература:

(1) гл. I, § 10 пп.44-45; (2) гл. II, § 10, с. 188-190, 198-201; (3) гл. I, § 2 пп. 11-13; (4) гл. III, с. 108-114; (5) гл. III, §§ 3.3 – 3.6.

Контрольные вопросы:

1. Отношения на множестве. Основные понятия. Обозначения.

2. Способы задания отношений.

3. Свойства отношений на множестве.

4. Отношения эквивалентности, их связь с разбиением мно­же­ства на классы.

5. Отношения порядка. Упорядоченные множества.

6. Связь с начальным курсом математики.

7. Из истории развития теории соответствий и отношений.

Задание на дом:

1. Зачетное задание № 9.

2. (1) гл. I, § 10 №№ 505-527, 583-603; (4) гл. III, с. 122, №№ 3.11-3.15.

3. Примерный вариант контрольной работы № 2.


САМОСТОЯТЕЛЬНО:


Тема: СИСТЕМЫ СЧИСЛЕНИЯ

Литература:

(2) гл. II, § 14 п. 60; (3) гл. III, § 17, пп. 80-87; (4) гл. IV, §§ 18-22; (5) гл. II, § 6 пп. 44-49; (6) гл. IX.

Контрольные вопросы:

1. Понятие системы счисления.

2. Непозиционные и позиционные системы счисления (со­обще­ние).

3. Запись и название чисел в десятичной системе счисления.

4. Исторические сведения о возникновении и развитии спо­собов записи целых неот­рицательных чисел (сообщение).

5. Алгоритмы арифметических действий над целыми неот­рица­тельными числами в де­сятичной системе счисления.

6. Связь введенных понятий с начальным курсом математики.

7. Из истории развития систем счисления.

Задание на дом:

1. Зачетное задание № 1.

2. (2) гл. II, №№ 94-114, №№ 139, 150, 151.

3. (6) гл. IX, с. 297-299, №№ 9.1 –9.35.


Занятия № 9

Тема: ДЕЛИМОСТЬ ЧИСЕЛ

Литература:

(2) гл. II, § 15 пп. 64,65; (3) гл. III, § 18, пп 88-89; (5) гл. II, § 7, пп. 51,52; (6) гл. X, с. 300-307.

Контрольные вопросы:

1. Отношение делимости на множестве целых неотрицатель­ных чисел.

2. Свойства отношения делимости.

3. Делимость суммы, разности, произведения целых неотри­ца­тельных чисел.

4. Признаки делимости в десятичной системе счисления.

5. Деление с остатком.

6. Связь введенных понятий с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 2.

2. (2) гл. II, №№ 30-37; №№ 152-160; №№ 161-188; №№ 224-228, 230, 231.

3. (6) гл. X, с. 330-331, №№ 10.1-10.29.


Занятие № 10

Тема: ДЕЛИМОСТЬ ЧИСЕЛ

Литература:

(2) гл. II, § 15 пп. 66-68; (3) гл. III, § 18, пп 90-93; (4) гл. V, §§ 26-30; (5) гл. II, § 7 пп. 53-55; (6) гл. X, с. 308-323.

Контрольные вопросы:

1. Простые и составные числа. Решето Эратосфена.

2. Бесконечные множества простых чисел.

3. Кратные и делители. НОК и НОД чисел, их свойства.

4. Признак делимости на составное число.

5. Основная теорема арифметики.

6. Алгоритмы нахождения НОД и НОК чисел.

Задание на дом:

1. Зачетное задание № 2.

2. (2) гл. II, №№ 189-198; №№ 199-223, №№ 232-239.

3. (6) гл. X, с. 331-332, №№ 10.30-10.54.


Занятие № 11

Тема: АКСИОМАТИЧЕСКОЕ ПОСТРОЕНИЕ

МНОЖЕСТВА ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ

Литература:

(2) гл. II, § 11 пп. 50-52; (3) гл. III, §§ 13, 14; (4) гл. I, §§ 1-9; (5) гл. II, § 4 пп. 28-37; (6) гл. VIII, с. 225-240.

Контрольные вопросы:

1. Понятие об аксиоматическом методе построения теории.

2. Аксиомы Пеано для множества целых неотрицательных чи­сел.

3. Сложение и умножение целых неотрицательных чисел.

4. Вычитание и деление. Невозможность деления на нуль. Деле­ние с остатком.

5. Метод математической индукции. Применение к решению задач.

6. Свойства множества целых неотрицательных чисел.

7. Связь с начальным курсом математики.

6. Из истории развития теории натуральных чисел.

Задание на дом:

1. Зачетное задание № 3.

2. (2) гл. II, №№ 1-11, №№ 12-17, №№ 25-29.

3. (6) гл. VIII, с. 266, №№ 8.1-8.4, 8.8-8.18, 8.45-8.46.


Занятие № 12

Тема: ТЕОРЕТИКО-МНОЖЕСТВЕННЫЙ ПОДХОД К ПОСТРОЕНИЮ МНОЖЕСТВА ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ

Литература:

(2) гл. II, 12 пп 54-56; (3) гл. III, §§ 13, 15; (4) гл. II, 10-15; (5) гл. II, 5 пп 38-43; (6) гл. VIII, с. 240-249.

Контрольные вопросы:

1. Краткие исторические сведения о возникновении понятия на­турального числа и нуля (сообщение).

2. Основные положения количественной теории Г. Кантора.

3. Отношения "равно", "меньше" на множестве целых неот­рица­тельных чисел.

4. Отрезок натурального ряда чисел. Порядковые и количест­венные натуральные числа.

5. Теоретико-множественный смысл арифметических дейст­вий над целыми неотрица­тельными числами. Законы.

6. Связь с начальным курсом математики.

Задание на дом:

1. Зачетное задание № 4.

2. (2) гл. II №№ 38-42, №№ 43-63, №№ 64-76, №№ 77-85.

3. (6) гл. VIII, с. 266, №№ 8.5-8.6, 8.34-8.44, 8.47.


САМОСТОЯТЕЛЬНО:


Тема: НАТУРАЛЬНОЕ ЧИСЛО КАК РЕЗУЛЬТАТ

ИЗМЕ­РЕНИЯ ВЕЛИЧИН

Литература:

(2) гл. II, 13 пп 58,59; (3) гл. III, § 16, пп 76-79; (4) гл. III, 16, 17; (6) гл. VIII, с. 249-250, 263-265.

Контрольные вопросы:

1. Натуральное число как результат измерения величины.

2. Операции над числами.

3. Задачи с именованными числами.

4. Связь с начальным курсом математики.

Выполните упражнения:

1. Зачетное задание № 4.

2. (2) гл. II №№ 86-93.

3. (6) гл. VIII, с. 266, №№ 8.7, 8.47.


Контроль за самостоятельной работой студентов

(3 час)


ПРОГРАММА И СПИСОК ЛИТЕРАТУРЫ К ЭКЗАМЕНУ (1-й курс)


1. Понятие множества. Элемент множества. Пустое множество. Конечные и бесконечные множества.

(1) гл. I, § 1 п. 1; (2) гл. I, § 1, с. 6-8; (3) гл. I, § 1 п. 2; (4) гл. I, c. 31-47; (5) гл. I, п. 1.1.

2. Способы задания множеств. Примеры.

(1) гл. I, § 1 п. 1; (2) гл. I, § 1, с. 9; (3) гл. I, § 1 п. 2; (4) гл. I, с. 31-47; (5) гл. I, п. 1.1.

3. Равные множества. Подмножество. Универсальное множество. Круги Эйлера.

(1) гл. I, § 1 пп. 1, 2; (2) гл. I, § 1, с. 11-13; (3) гл. I п. 2; (4) гл. I, с. 31-47; (5) гл. I, п. 1.1.

4. Пересечение множеств, свойства.

(1) гл. I, § 1 п. 3; (2) гл. I, § 1, с. 14-15, 18-22; (3) гл. I п. 2; (4) гл. I, с. 31-47; (5) гл. I, п. 1.2.

5. Объединение множеств, свойства.

(1) гл. I, § 1 п. 3; (2) гл. I, § 1, с. 16-17, 18-22; (3) гл. I, § 1, п. 3; (4) гл. I, с. 31-47; (5) гл. I, п. 1.2.

6. Разность двух множеств. Дополнение до универсаль­ного множества.

(1) гл. I, § 1 п. 4; (2) гл. I, § 1, с. 23-25; (3) гл. I, § 1 п. 4; (4) гл. I, с. 31-47; (5) гл. I, п. 1.2.

7. Декартово произведение двух и более множеств, свой­ства. Примеры. Число элементов объединения декартова произведения множеств.

(1) гл. I, § 1 п. 6; (2) гл. I, § 1, с. 29-33, 38-39; (3) гл. I, § 1, пп. 5,6; (4) гл. I, с. 31-47; (5) гл. I, п. 1.4.

8. Разбиение множества на попарно-непересекающиеся подмножества (классы). Примеры. Разбиение множества на классы с помощью одного, двух и трех свойств.

(1) гл. I, § 1 п. 5; (2) гл. I, § 1, с. 26-27; (3) гл. I, § 1 п. 5; (4) гл. I, с. 45-47; (5) гл. I, п. 1.3.

9. Соответствие между элементами двух множеств. Основные понятия. При­меры.

(2) гл. II, § 8, с. 166; (3) гл. I, § 2 п. 9; (4) гл. III, c. 105; (5) гл. III, п. 3.1.

10. Способы задания соответствий. Виды соответствий (обратное, противопо­ложное данному).

(2) гл. II, § 8, с. 167-170; (3) гл. I, § 2 п. 9; (4) гл. III, с. 103; (5) гл. III, п. 3.1.

11. Отображения. Виды отображений.

(1) гл. I, § 10 п. 46; (4) гл. III, с. 107; (5) гл. III, п. 3.2.

12. Взаимно-однозначные соответствия. Равномощные множества. Свойства отношения равномощности мно­жеств на множестве множеств.

(2) гл. II, § 8, с. 172-174; (3) гл. I, § 2 п. 10; (4) гл. III, с. 107; (5) гл. I, п. 1.5.

13. Отношения на множестве. Основные понятия. Спо­собы задания.

(1) гл. I, § 10 п. 44; (2) гл. II, § 10, с. 188-190; (3) гл. I, § 2, п. 11; (4) гл. III, с. 108; (5) гл. III, п. 3.3.

14. Свойства отношения на множестве.

(1) гл. I, § 10 п. 45; (2) гл. II, § 10, с. 192-196; (3) гл. I, § 2, п. 12; (4) гл. III, с. 109-111; (5) гл. III, п. 3.3.

15. Отношение эквивалентности. Связь отношения экви­валентности с разбие­нием множества на классы.

(1) гл. I, § 10 п. 45; (2) гл. II, § 10, с. 198-200; (3) гл. I, § 2, п. 13; (4) гл. III, с. 112; (5) гл. III, п. 3.3.

16. Отношение порядка. Упорядоченные множества.

(1) гл. I, § 10 п. 45; (2) гл. II, § 10, с. 200-201; (3) гл. I, § 2, п. 13; (4) гл. III, с. 114; (5) гл. III, п. 3.3.

17. Определяемые и неопределяемые понятия. Объем и содержание понятия. От­ношения между понятиями. Требо­вания к определению понятий.

(1) гл. I, § 5 пп. 23,24; (2) гл. I, § 2, с. 41-44; (3) гл. I, § 3 п. 17; (4) гл. II, с. 66; (5) гл. II, п. 2.3.

18. Способы определения понятий. Структура определе­ния через род и видовое отличие.

(1) гл. I, § 5 п. 25; (2) гл. I, § 2, с. 46-50; (3) гл. I, § 3 пп. 17,24; (4) гл. II, с. 67; (5) гл. II, п. 2.3.

19. Правильные и неправильные рассуждения. Простей­шие формы дедуктивных рассуждений.

(1) гл. I, § 6 пп. 27,28; (2) гл. I, § 4, с. 89-92, 94-97; (3) гл. I, § 3 п. 25; (4) гл. II, с. 75; (5) гл. II, п. 2.4.

20. Способы доказательства математических утвер­ждений.

(2) гл. I, § 4, с. 99-103; (3) гл. I, § 3 пп. 26,27; (4) гл. II, с. 80-82; (5) гл. II, п. 2.5.

21. Высказывания. Конъюнкция двух высказываний. Свой­ства.

(1) гл. I, § 3 пп. 13,14; (2) гл. I, § 3, с. 53-56, 58; (3) гл. I, § 3, пп. 18,19; (4) гл. II, с. 57-58; (5) гл. II, п. 2.1.

22. Высказывания. Дизъюнкция двух высказываний. Свой­ства.

(1) гл. I, § 3 пп. 13,14; (2) гл. I, § 3, с. 53-57, 59; (3) гл. I, § 3, пп. 18,19; (4) гл. II, с. 59; (5) гл. II, п. 2.1.

23. Высказывания. Импликация, эквиваленция двух выска­зываний. Тавтология.

(4) гл. II, с. 59; (5) гл. II, п. 2.1.

24. Высказывания. Отрицание высказываний. Закон двой­ного отрицания. Отри­цание высказываний, содержащих кванторы.

(1) гл. I, § 3 пп. 15-17; (2) гл. I, § 3, с. 73; (3) гл. I, § 3, пп. 20,21; (4) гл. II, с. 58, 63; (5) гл. II, п. 2.1.

25. Высказывательные формы (предикаты). Область оп­ределения, множества истинности и ложности предиката.

(1) гл. I, § 3 пп. 13,14; (2) гл. I, § 3, с. 55-56, 61-62; (3) гл. I, § 3 п. 18; (4) гл. II, с. 62; (5) гл. II, п. 2.2.

26. Предикаты. Кванторы. Обращение предиката в вы­сказывание. Отрицание предиката.

(1) гл. I, § 3 пп. 15-17; (2) гл. I, § 3, с. 67-71, 73; (3) гл. I, § 3, пп. 18,21; (4) гл. II, с. 62-63; (5) гл. II, п. 2.2.

27. Операции над предикатами (дизъюнкция, конъюнк­ция).

(4) гл. II, с. 64; (3) гл. I, § 3 пп. 18-20; (1) гл. I, § 3 п. 14; (5) гл. II, п. 2.2.

28. Операции над предикатами (импликация, эквивален­ция).

(4) гл. II, с. 64; (5) гл. II, п. 2.2.

29. Отношение логического следования и равносильности на множестве предло­жений. Необходимые и достаточные условия.

(1) гл. I, § 4 пп. 19,20; (2) гл. I, § 3, с. 77-81; (3) гл. I, § 3 п. 22; (4) гл. II, с. 85;.

30. Строение теоремы. Виды теорем. Закон контрапози­ции.

(1) гл. I, § 4 п. 21; (2) гл. I, § 3, с. 83-86; (3) гл. I, § 3 п. 23; (4) гл. II, с. 85; (5) гл. II, п. 2.5.

31. Логические задачи и их решение. Примеры.

(4) гл. II, с. 88-91.

32. Комбинаторные задачи. Правила суммы и произведе­ния. Примеры.

(1) гл. I, § 2 п. 8; (2) гл. I, § 6, с. 142-144; (3) гл. I, § 1 п. 6; (4) гл. V, с. 151; (5) гл. IV, п. 4.1.

33. Размещения без повторений и с повторениями.

(1) гл. I, § 2 п. 9; (2) гл. I, § 6, с. 145-147; (3) гл. I, § 1 п. 7; (4) гл. V, с. 153; (5) гл. IV, п. 4.2.

34. Перестановки без повторений и с повторениями.

(1) гл. I, § 2 п. 10; (2) гл. I, § 6, с. 146-147; (3) гл. I, § 1 п. 7; (4) гл. V, с. 154; (5) гл. IV, п. 4.2.

35. Сочетания без повторений и с повторениями.

(1) гл. I, § 2 п. 11; (2) гл. I, § 6, с. 147-149; (3) гл. I, § 1 п. 8; (4) гл. V, с. 154; (5) гл. IV, п. 4.2.

36. Свойства чисел 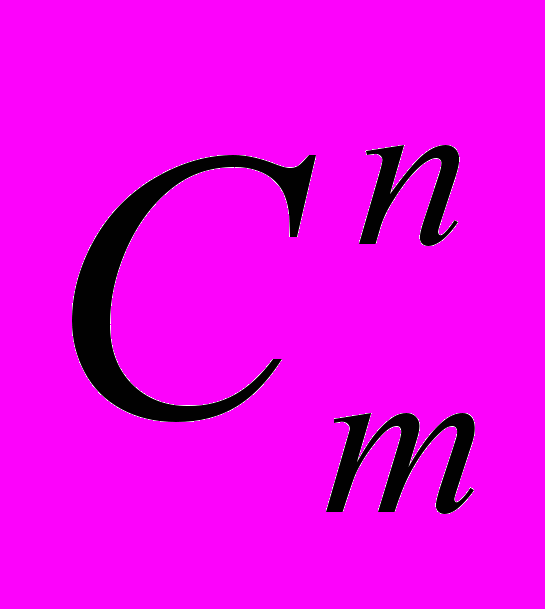. Треугольник Паскаля. Число подмно­жеств конечного мно­жества.

(4) гл. V, с. 155; (5) гл. IV, п. 4.2.


ЛИТЕРАТУРА


Основная

1. Лаврова Н.Н., Стойлова Л.П. Задачник-практикум по мате­матике. - М.: Просвещение, 1985.

2. Стойлова Л.П. Математика. – М.: Издательский центр «Академия», 2000.

3. Стойлова Л.П., Виленкин Н.Я., Лаврова Н.Н. Математика. Часть I.- М.: Просвеще­ние, 1990.

4. Тонких А.П. Математика: Учебное пособие для студентов факультетов подготовки учителей начальных классов. В 2-х книгах. Книга 1. - М.: Книжный дом «Университет», 2002.

5. Тонких А.П., Охременко Д.В. Математика. Часть 1. Основ­ные понятия: Учебное по­собие для студентов педагогических вузов по специальности № 031200 "Педагогика и ме­тодика на­чального образования", - Брянск: Изд-во БГПУ, 1998.


Дополнительная

Аматова Г.М., Аматов М.А. Математика: Учебное пособие для факультетов подготовки бакалавров образования в области начального образования и учителей начальных классов педагогических высших учебных заведений. - М.: Московский психолого-социальный институт, 1999.

Виленкин Н.Я., Пышкало А.М., Рождественская В.В., Стой­лова Л.П. Математика. Учебное пособие для студентов педин­ститутов. - М.: Просвещение, 1977.

Мерзон А.Е., Добротворский А.С., Чекин А.Л. Пособие по математике для студентов факультетов наачльных классов. – М.: Изд-во «Иститут практической психологии»; Воронеж: Изд-во НПО «МОДЕК», 1998.

Стойлова Л.П., Пышкало А.М. Основы начального курса ма­тематики. - М.: Просвеще­ние, 1988.

Тонких А.П. Темы сообщений по математике. Методические рекомендации студентам стационара и ОЗО. - Брянск, 1993.

Тонких А.П., Охременко Д.В., Булохова Р.С. Изучаем математику на пер­вом курсе. Учебно-методическое пособие по организации самостоя­тельной работы студентов I курса. – Брянск: Изд-во БГУ, 2003.

2-й курс


Третий семестр


САМОСТОЯТЕЛЬНО: