Основные законы магнитного поля

Вид материала

Закон

Подобный материал:

• Дефицит магнитного поля, 27.98kb.
• Задание 1 Цель: оценить значение сердечника для получения магнитного поля катушки, 33.68kb.
• Домашнее задание по физике на 4 сессию Учебник, 55.57kb.
• Задачи урока: -обучения: продолжить формирование представлений о магнитном поле; рассмотреть, 35.34kb.
• Урок на тему «Магнитное поле Земли», 31.68kb.
• Лабораторная работа № Исследование магнитного поля модели сверхпроводникового индуктора, 75.13kb.
• Разработка урока в 8-м классе "Магнитное поле. Линии магнитного поля", 33.77kb.
• Магнитное поле. Сила Ампера. Сила Лоренца. Явление электромагнитной индукции, 98.2kb.
• Лекция n 21, 1748.76kb.
• 1. Основные законы электрического поля, 316.07kb.

18.Теорема Гаусса для магнитного поля. Теорема о циркуляции для магнитного поля.


ОСНОВНЫЕ ЗАКОНЫ МАГНИТНОГО ПОЛЯ


1) Теорема Гаусса:



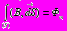
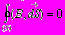 математическое выражение того факта, что

магнитное поле не имеет источника (его силовые линии замкнуты)

Воспользовавшись теоремой Остроградского-Гаусса, запишем теорему Гаусса в дифференциальной форме:

(,B)=0; B=[,A], A  векторный потенциал


ТЕОРЕМА О ЦИРКУЛЯЦИИ


С помощью закона Био-Савара-Лапласа запишем:

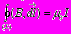; I=I_i ;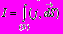

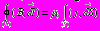 магнитное поле  не потенциальное  циркуляция  0;

Воспользовавшись теоремой Стокса, запишем теорему о циркуляции в дифференциальном виде: [,B]=₀j ;


ПРИМЕНЕНИЕ ТЕОРЕМЫ О ЦИРКУЛЯЦИИ ДЛЯ РАСЧЁТА МАГНИТНЫХ ПОЛЕЙ

Алгоритм:

1. Проводим контур через исследуемую точку поля
   
2. Такой, чтобы в каждой его точке B имел одинаковые значения
   

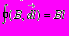
а) Магнитное поле прямого тока: B2r=₀I => B=(₀I)/(B2r)

б) Магнитное поле бесконечного соленоида:

n  число витков на единицу длины; Bl=₀Inl => B=₀In

в) Магнитное поле тороида: B2r=₀IN => B=₀IN/2r

г) Магнитное поле бесконечной плоскости с током: B2l=₀il =>

B=0.5₀i