Geum.ru

Моделирование фазовых диаграмм «состав температура» И«состав ток» солевых и металлических систем 02. 00. 04 физическая химия

Вид материалаАвтореферат диссертации
Максимальные токи растворения сплавов индий-свинец в насыщенном растворе KCl для фазовой области ограниченных твердых растворов
Таблица 15 Парциальные токи растворения α/
Подобный материал:
1   2   3   4

Максимальные токи растворения сплавов индий-свинец в насыщенном растворе KCl для фазовой области ограниченных твердых растворов (α/) (; )

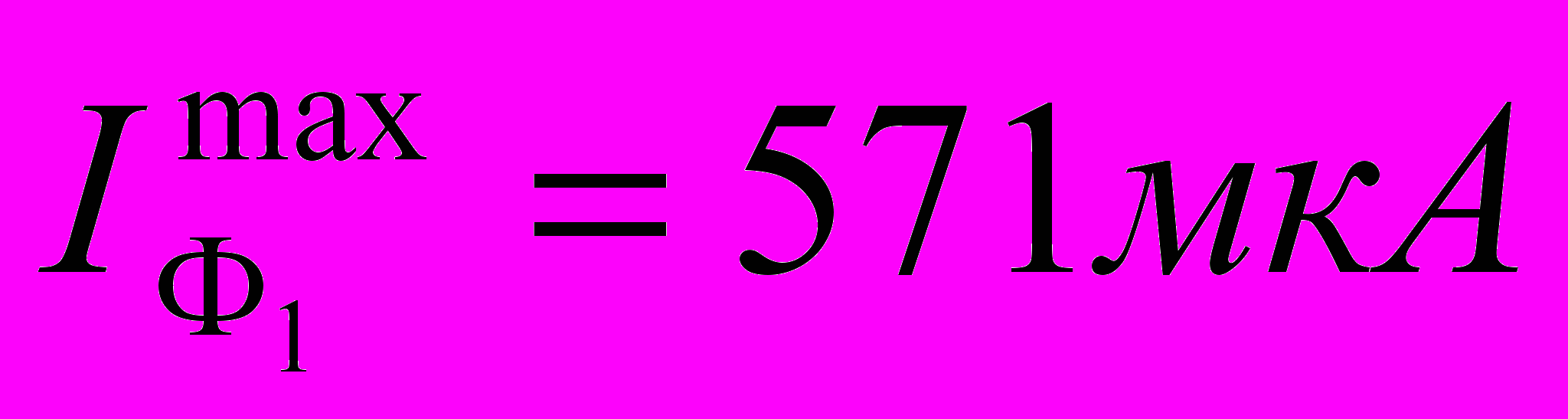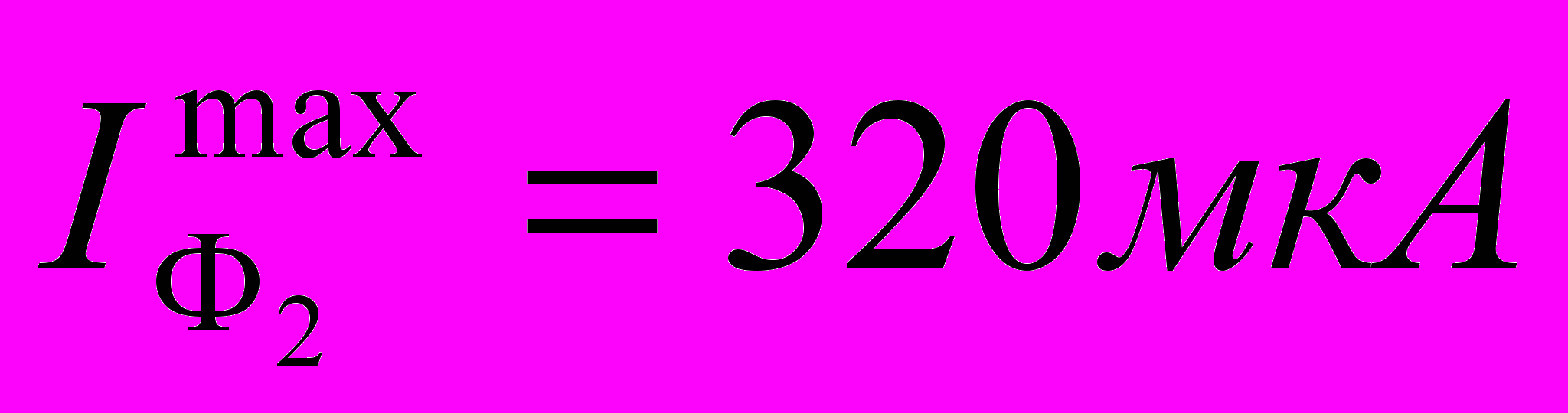Элементный состав, % масс. Pb
Молярная доля Ф1 в фазовой области α/
Ток растворения сплава, мкА

Эксперимент
Теория (ур.2)
Теория (ур.9)

25
0,837
459
530
437

30
0,594
408
469
403

35
0,329
371
402
366

39
0,111
330
348
336

Средняя относительная погрешность вычислений по ур. 2 – 10,99 %.

Средняя относительная погрешность вычислений по ур. 9 – 2,3 %.

Для фазовой области ограниченных твердых растворов (Pb) наблюдается прямопропорциональная зависимость коэффициента активности растворяющейся фазы от ее мольной доли, поэтому f(Pb)=N(Pb), а ур. (9) преобразуется к следующему виду

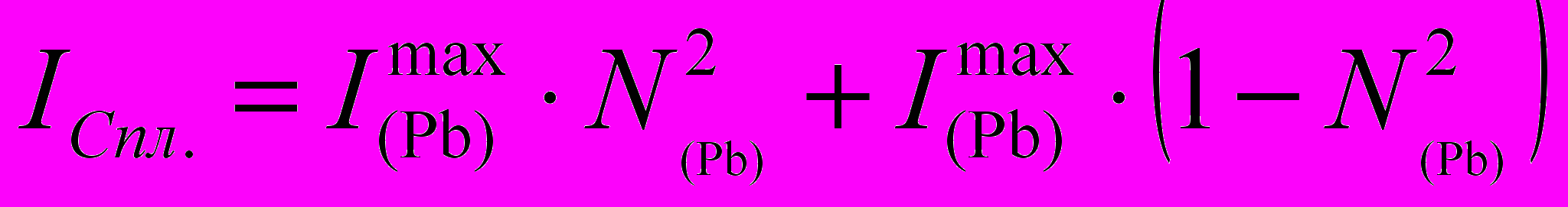(10)

Расчет токов растворения гомогенных сплавов (Pb), произведенный по ур. (10), приведен в табл. 14. Очевидно, что расчетные и экспериментальные данные находятся в хорошем согласии.

Таблица 14

Максимальные токи растворения сплавов индий-свинец в насыщенном растворе KCl для фазовой области ограниченных твердых растворов (Pb) (; )

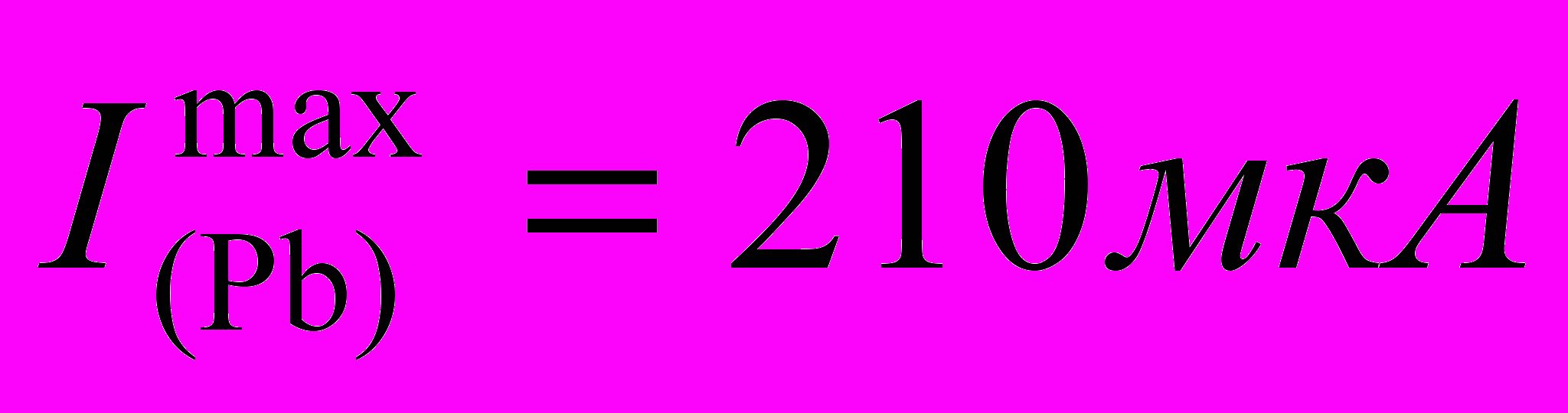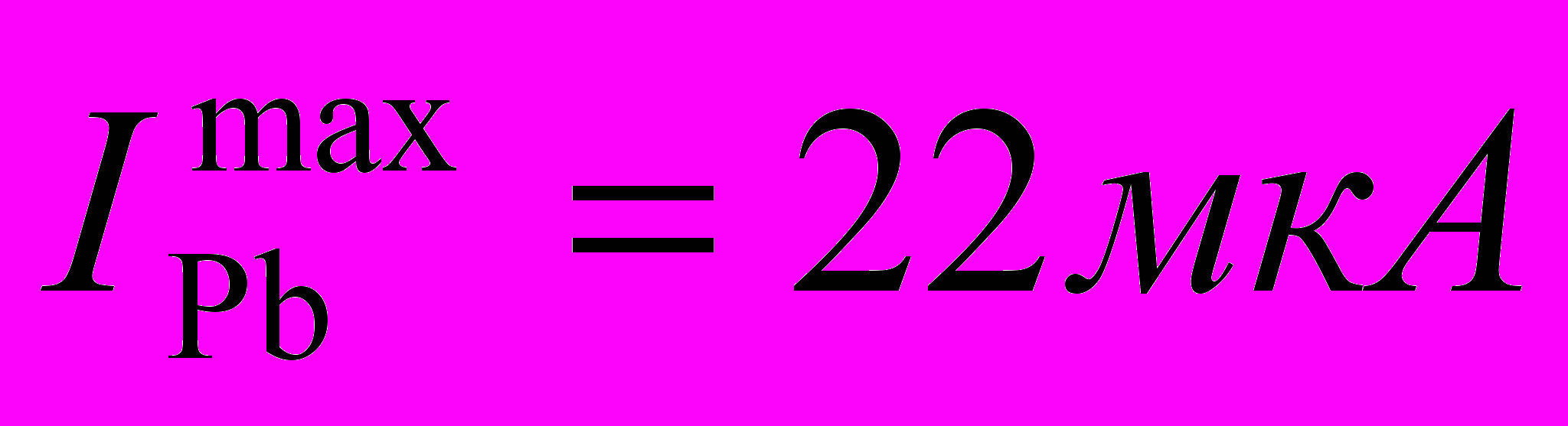Элементный состав, % масс. Pb
Молярная доля (Pb)-фазы
Ток растворения сплава, мкА

Эксперимент
Теория (ур.2)
Теория (ур.10)

60
0,874
170
186
166

75
0,601
89
135
90

80
0,498
74
116
69

90
0,267
37
72
35

Средняя относительная погрешность вычислений по ур. 2 – 53,12 %.

Средняя относительная погрешность вычислений по ур. 10 – 3,91 %.

Гетерогенная фазовая область α/+( Pb) состоит из двух фаз α/ и (Pb), образовавшихся по перитектическим реакциям. Сплавы индий-свинец, соответствующие этой двухфазной области имеют неоднородную кристаллическую структуру, поэтому расчет парциальных токов растворения α/- и (Pb)–фаз проведен по ур. (8), аналогично рассмотренной ранее системе ε-η в сплавах медь-олово – табл. 15.

Таблица 15

Парциальные токи растворения α/- и (Pb)–фаз из матрицы сплава In-Pb в насыщенном растворе KCl для фазовой области α/- и (Pb)

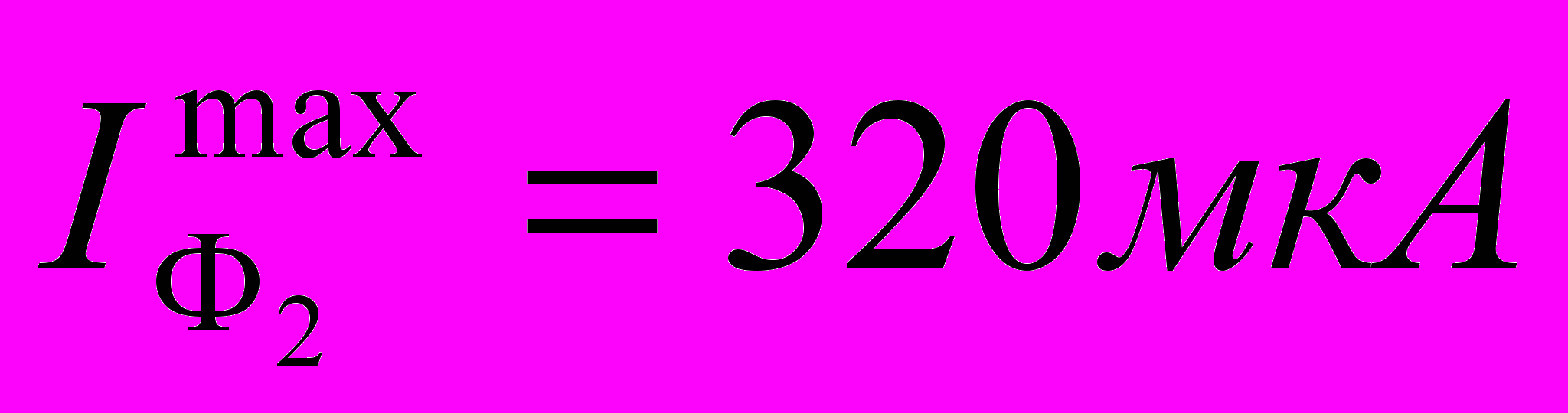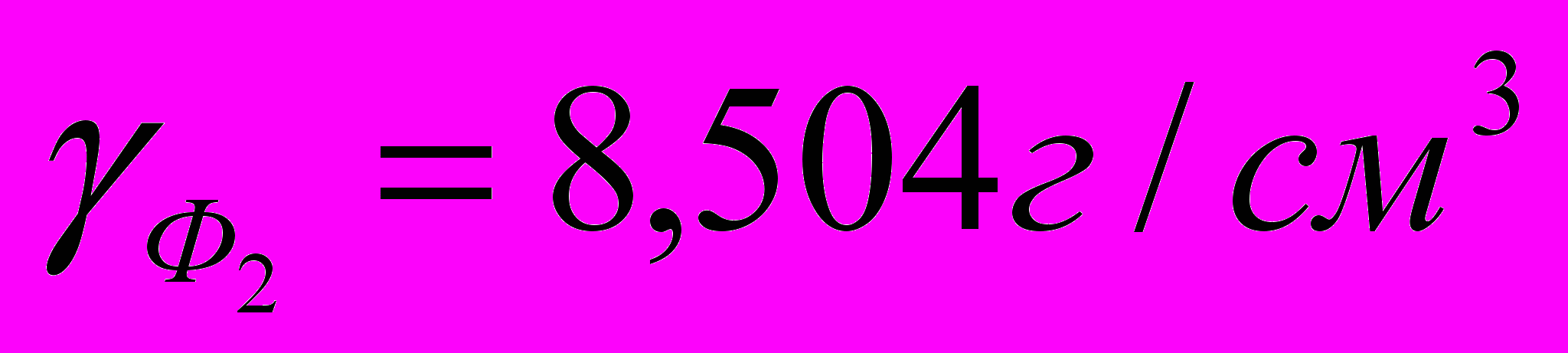(, , a=(2,82±0,01)·10-3, b=0,245±0,001; 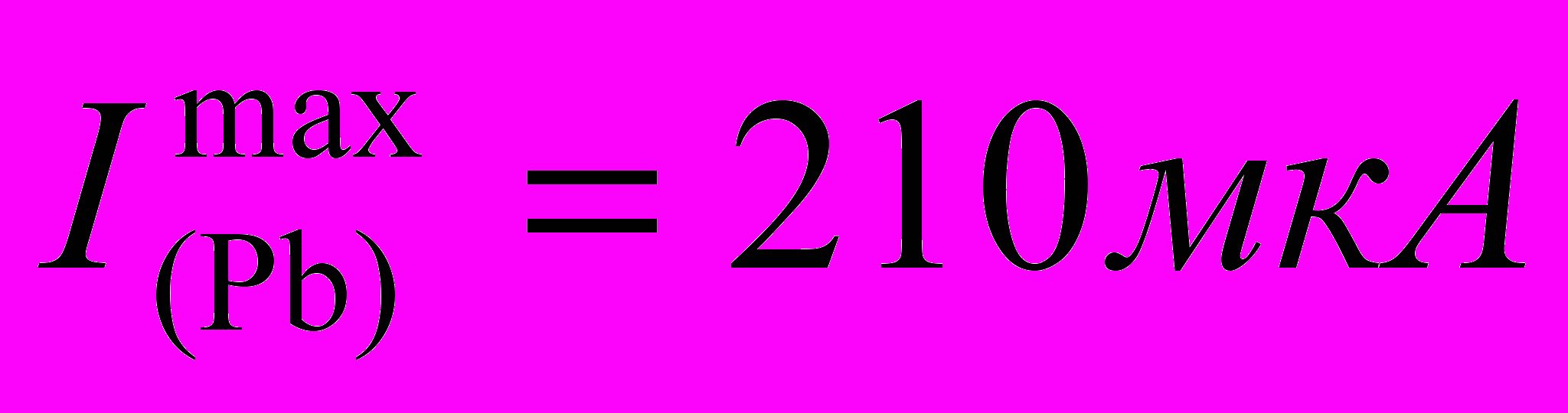, , 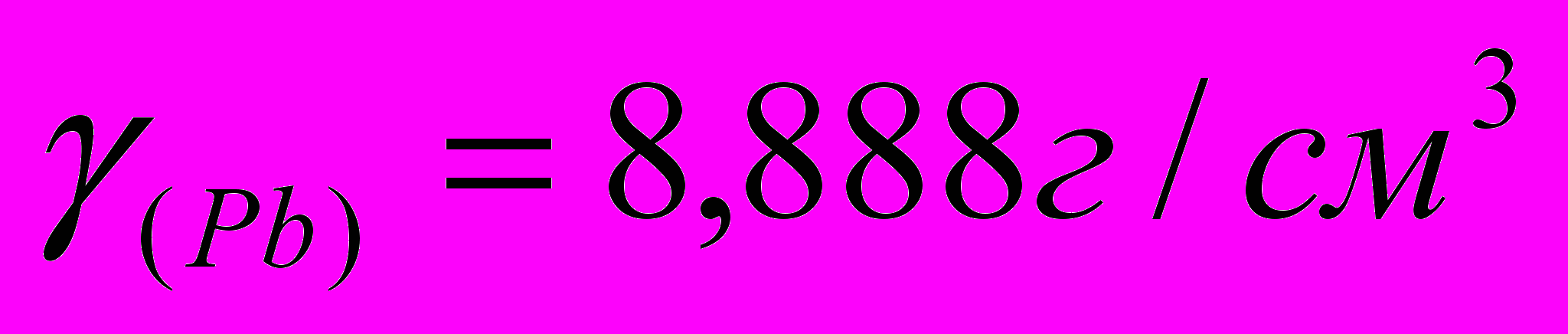a=(4,76±0,01)·10-3, b=1,365±0,001)

Элементный состав, % масс. Pb
Фазовый состав, % масс. α/- фазы
Ток, мкА

α/- фаза
(Pb)–фаза

Эксперимент
Теория (ур.8)
Эксперимент
Теория (ур.8)

42
92,94
319
309
19
10

46
55,76
245
245
74
68

50
18,59
141
142
148
148

Средняя относительная погрешность вычислений по ур. 8 значений парциальных токов растворения для α/- фазы – 1,28 %.

Средняя относительная погрешность вычислений по ур. 8 значений парциальных токов растворения для (Pb)–фазы – 18,49 %.

В четвертой главе проведено обсуждение результатов моделирования фазовых диаграмм «состав-температура» и «состав-ток» солевых и металлических систем в физико-химическом анализе. Обоснован выбор метода расчета характеристик (состава и температуры) эвтектик солевых систем, проведено сравнение результатов расчетов различными методами. Проанализированы результаты расчета парциальных токов, полученные по уравнениям, применявшимся ранее для расчетов токов растворения фаз металлических систем в условиях ЛЭА. Проведено сравнение погрешностей расчетных данных по различным уравнениям.

Дальнейшее развитие АС предполагается, по крайней мере, в трёх направлениях: во-первых, моделирование характеристик эвтектик для систем с числом компонентов более четырех; во-вторых, моделирование не только характеристик эвтектик, но и характеристик других нонвариантных точек (перитектик, минимумов твёрдых растворов), кривых моновариантных равновесий и, наконец, полной поверхности кристаллизации систем в разнообразным морфологическим типом взаимодействия компонентов (обменные реакции, комплексообразования инконгруэнтного характера, твёрдых растворов различной степени устойчивости и др.); в-третьих, моделирование диаграмм «состав – ток» для систем с числом компонентов более двух.

Выводы:
  1. Разработаны алгоритмы расчета состава и температуры эвтектики тройных, тройных взаимных, четверных эвтектических систем, а также тройных и тройных взаимных систем с комплексообразованием конгруэнтного плавления на основе термодинамического метода Мартыновой – Сусарева расчета характеристик тройных эвтектик (температуры и состава) по данным об элементах огранения.
  2. На основе указанных алгоритмов создана автоматизированная система, спроектирована база данных, содержащая экспериментальные сведения по изученным системам и по элементам огранения. Разработанная методика компьютерного моделирования позволила оптимизировать изучение фазовых диаграмм трёхкомпонентных, трёхкомпонентных взаимных, четырехкомпонентных эвтектических систем, трёхкомпонентных, трёхкомпонентных взаимных систем с комлексообразованием.
  3. На примере ряда исследованных ранее модельных трёхкомпонентных, трёхкомпонентных взаимных, четырехкомпонентных эвтектических систем, трёхкомпонентных, трёхкомпонентных взаимных систем с комлексообразованием конгруэнтного плавления проведена апробация разработанной методологии, показавшая удовлетворительные результаты.
  4. Разработаны алгоритмы теоретического расчета значения парциального тока фазовых диаграмм «состав-ток» с помощью данных о максимальном токе анодного растворения чистых металлов, их плотности и содержании металлов в сплаве.
  5. Рассмотрены особенности морфологии диаграмм «состав – ток» неограниченных твердых растворов. Установлены аналитические выражения для зависимости тока растворения сплава от его состава. Установлена взаимосвязь тока растворения гомогенного сплава с работой выхода электрона.
  6. Установлено влияние структуры эвтектики на морфологию фазовых диаграмм «состав – ток» в методе локального электрохимического анализа (ЛЭА). Показано, что для эвтектических структур нормального кристаллического строения расчет парциального тока растворения фазы можно производить по преобразованному соответствующим образом уравнению Гаусса. Для эвтектических структур с аномальной и разъединенной эвтектикой расчет парциальных токов растворения фаз можно производить по уравнению, предложенному ранее для порошковых композиций.
  7. Рассмотрены особенности морфологии диаграмм «состав-ток» металлических систем сплавов с интерметаллическими соединениями и промежуточными фазами. Установлены аналитические выражения для зависимости токов растворения ограниченных твердых растворов, перитектических и эвтектических структур.
  8. Важным достоинством автоматизированной системы (АС) фазовых диаграмм является широкая область ее использования для солевых и металлических систем. Применение АС фазовых диаграмм даёт возможность перейти к принципиально новому виду электронных справочников.

Список цитируемой литературы
  1. Трунин А.С. Комплексная методология исследования многокомпонентных систем. Самара. CамГТУ. СамВен. 1997. 308 с.
  2. Брайнина Х. З., Нейман Е.Я., Слепушкин В.В. Инверсионные электроаналитические методы. М. Химия. 1988. 239 с.
  3. Мартынова Н.С., Сусарев М.П. Выявление концентрационной области расположения тройной эвтектики в простых эвтектических системах по данным о бинарных эвтектиках и компонентах. // Журн. прикл. химии. 1968. Т. 41. № 9. С. 2039-2047.
  4. Сусарев М.П., Мартынова Н.С., Расчет состава четверной эвтектики по данным для тройных и бинарных. // Журн. прикл. химии. 1974. №3. С. 497-500.

Основное содержание диссертации опубликовано:
  1. Трунин.А.С., Будкин А.В., Моргунова О.Е., Мощенская Е.Ю. Компьютерные технологии в физико-химическом анализе. Программа «Эвтектический калькулятор». В кн.: Тр. 4-й Международн. конференции молодых ученых «Актуальные проблемы современной науки». Ч.9. Химическая физика. Физическая химия, физико-химический анализ. Самара. 2003. С. 48-49.
  2. Трунин А.С., Будкин А.В., Мощенская Е.Ю. Алгоритм моделирования характеристик эвтектик по методу Мартыновой – Сусарева В кн.: Тр. 4-й Международн. конференции молодых ученых «Актуальные проблемы современной науки». Ч.9. Химическая физика. Физическая химия, физико-химический анализ. Самара. 2003. С. 44-48.
  3. Трунин А.С., Будкин А.В., Мощенская Е.Ю., Моргунова О.Е., Климова М.В. Автоматизация математического моделирования характеристик нонвариантных эвтектических точек трехкомпонентных систем методом Мартыновой-Сусарева. // Вестник Самарского гос. техн. ун-та. Сер. Физико-математические науки. 2004. № 26. С. 159-164.
  4. Трунин А.С., Мощенская Е.Ю. Расчет составов многокомпонентных систем В кн.: Тр. 5-й Международн. конференции молодых ученых «Актуальные проблемы современной науки». Ч.12. Физико-химический анализ. Самара. 2004. С. 162-165.
  5. Мощенская Е.Ю., Трунин А.С. Идеология расчета составов эвтектик четырехкомпонентных систем В кн.: Тр. 5-й Международн. конференции молодых ученых «Актуальные проблемы современной науки». Ч.12. Физико-химический анализ. Самара. 2004. С. 176-179.
  6. Трунин А.С., Мощенская Е.Ю. Моделирование и расчет характеристик четырехкомпонентных систем // Вестник Самарского гос. техн. ун-та. Сер. Физико-математические науки. 2004. № 30. С. 202-205.
  7. Слепушкин В.В., Рублинецкая Ю.В., Мощенская Е.Ю. Закономерности анодного растворения сплавов с неограниченной взаимной растворимостью компонентов в условиях локального электрохимического анализа. // Известия ВУЗов. Химия и химическая технология. 2005. Т.48. Вып. 10. С. 110-112.
  8. Рублинецкая Ю.В., Слепушкин В.В., Мощенская Е.Ю. Закономерности анодного растворения эвтектических сплавов в условиях локального электрохимического анализа. Эвтектические системы нормального строения с взаимной нерастворимостью компонентов в твердом состоянии // Известия ВУЗов. Химия и химическая технология. 2005. Т. 48. Вып. 10. С. 112-116.
  9. Мощенская Е.Ю., Рублинецкая Ю.В. Закономерности анодного растворения эвтектических сплавов в условиях локального электрохимического анализа. Эвтектические системы нормального строения с повышенной межкристаллитной хрупкостью. // Известия ВУЗов. Химия и химическая технология. 2005. Т. 48. Вып. 10. С. 119-120.
  10. Рублинецкая Ю.В., Слепушкин В.В., Мощенская Е.Ю. Закономерности анодного растворения сплавов c интерметаллическими соединениями и промежуточными фазами в условиях локального электрохимического анализа. // Известия ВУЗов. Химия и химическая технология. 2005. Т. 48. Вып. 10. С. 122-126.
  11. Св-во об офиц регистрации программы для ЭВМ «Моделирование нонвариантных точек трёхкомпонентных эвтектических систем» № 2005611159 от 19.05.2005./ Трунин А.С, Мощенская Е.Ю., Будкин А.В., Моргунова О.Е., Климова М.В.
  12. Мощенский Ю.В., Мощенская Е.Ю., Рублинецкая Ю.В., Слепушкин В.В., Федотов С.В. Анализатор поверхности ЭФА-11. // 2-я Всероссийская конференция «Аналитические приборы». Санкт-Петербург. 2005. С. 194.
  13. Трунин А.С., Мощенская Е.Ю. Моргунова О.Е. Моделирование характеристик эвтектик в трёхкомпонентных необратимо-взаимных системах с подчинённой адиагональю и образованием соединения конгруэнтного плавления. // Вестник Самарского гос. техн. ун-та. Сер. Физико-математические науки. 2006. № 2. С 109-113.
  14. Рублинецкая Ю.В., Слепушкин В.В., Мощенская Е.Ю., Суськина Е.Л. Локальный электрохимический анализ как метод исследования металлов, сплавов, порошковых и композиционных материалов. // XVI Международная конференция «Физика прочности и пластичности материалов». Самара. 2006 г. С. 145.
  15. J.V.Rublinetskaya, V.V.Slepushkin, E.J.Moshchenskaya, E.L.Suskina The General Theory Of An Analytical Signal In A Method Of The Local Electrochemical Analysis Of Alloys. // International Congress on Analytical Sciences ICAS-2006. Russia. Moscow. 2006. P. 446.



Подписано в печать 04.07.2006.

Формат 60x84 1/16. Объем 1,5 печ. л.

Бумага офсетная. Гарнитура «Таймс», печать офсетная.

Заказ № 1221 от 11.07.2006. Тираж 100 экз.


Отпечатано в типографии Самарского государственного технического университета, 443100, г. Самара, ул. Молодогвардейская, 244., корп. 8

_______________________________________________________________

Размножено в соответствии с решением диссертационного совета Д 212.217.05 от 04.07.2006 № 7 в количестве 100 экз.