Моделирование фазовых диаграмм «состав температура» И«состав ток» солевых и металлических систем 02. 00. 04 физическая химия
| Вид материала | Автореферат диссертации |
- Топология фазовых диаграмм тройных расслаивающихся систем соль бинарный растворитель, 1064.84kb.
- План: Введение; Химия Земли; Химический состав метеоритов; Химический состав звезд, 279.93kb.
- План состав нуклеиновых кислот Состав ДНК, 232.1kb.
- Рабочей программы учебной дисциплины физическая химия уровень основной образовательной, 53.86kb.
- Рабочая программа дисциплины (модуля) «математический анализ», 424.74kb.
- Рабочая программа дисциплины (модуля) «Уравнения математической физики», 266.58kb.
- Рабочая программа дисциплины «физическая химия», 80.79kb.
- Темы курсовых работ, предлагаемые кафедрой биофизики, для студентов 2-го курса физического, 134.4kb.
- Лабораторная работа №2 Создание и редактирование диаграмм в документах word, 83.26kb.
- Урок. Тема: Алкины- строение, состав, изомерия, 34.86kb.
Ток растворения гомогенного сплава является суммой парциальных токов растворения компонентов:
(2)где
- максимальный ток анодного растворения сплава A-B; 
и 
– парциальные токи растворения компонентов A и B из матрицы сплава; 
и 
- молярные доли компонентов в сплаве.В качестве примера рассмотрены диаграммы «состав – ток» неограниченных твердых растворов золото – серебро в подкисленном растворе NH4Cl (рис. 7 а) и медь – никель в 3 М KCl (рис. 7 б). Наблюдается непрерывное изменение анодных токов сплавов с составом, что согласуется с фазовой диаграммой указанных систем, в которых образуются ряды твердых растворов. В табл. 5 и 6 представлены соответствующие теоретические расчеты токов растворения, произведенные по уравнению (2).
Учитывая изменение электронной структуры сплавов с изменением их состава, получим:
(3)Как видно из результатов табл. 6, теоретические расчеты находятся в хорошем соответствии с экспериментом (рис. 7 б).
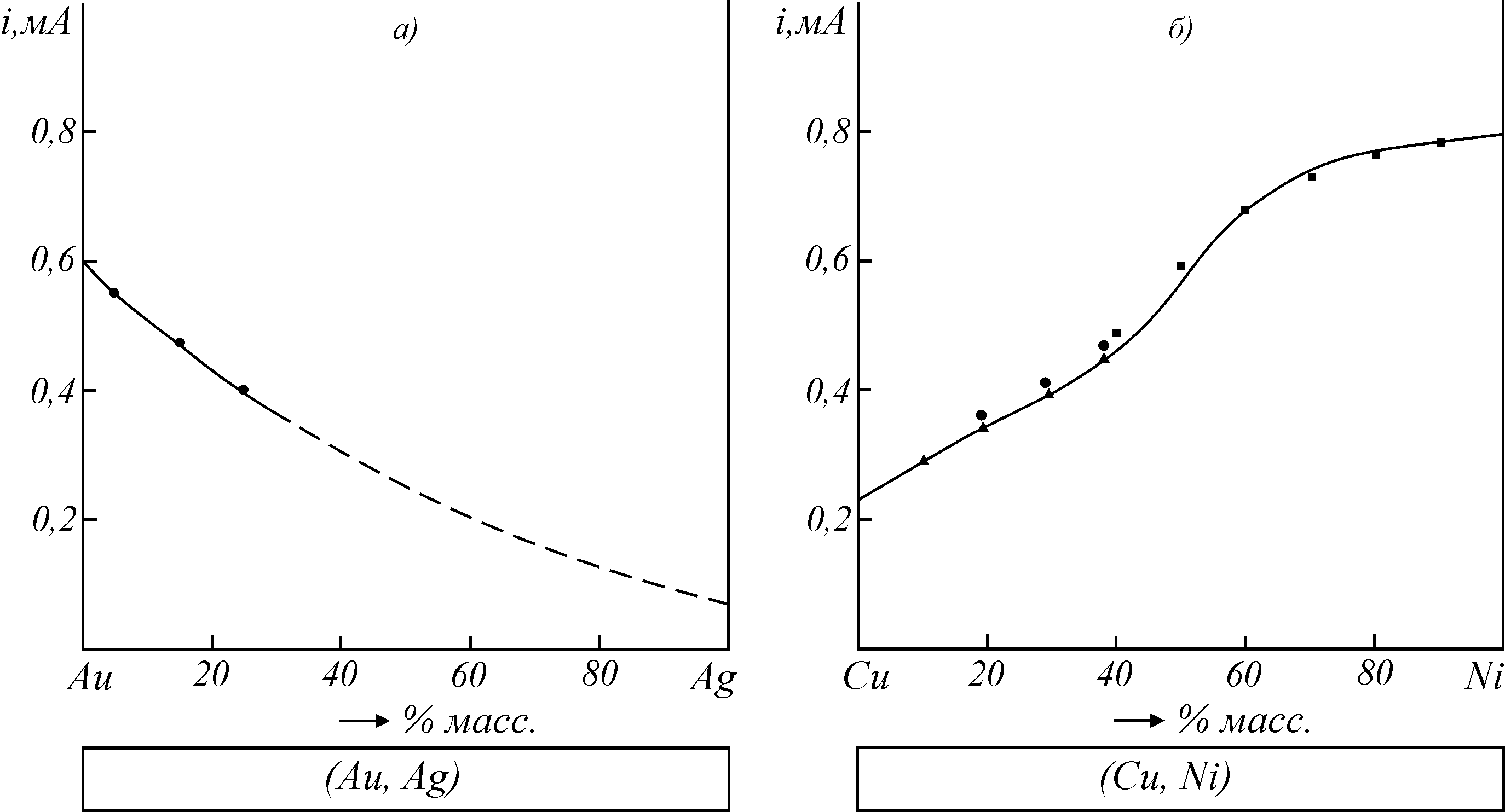
Рис. 7. Диаграммы «состав-ток» для сплавов Au-Ag в подкисленном растворе NH4Cl (а) и сплавов Cu-Ni в 3 М KCl (б) [2]
эксперимент; теория (ур. 2);
теория (ур. 3); - теория (ур. 4).Таблица 5
Максимальные токи растворения сплавов золото – серебро
в подкисленном растворе NH4Cl
(
,
)| Содержание серебра в сплаве, % масс. | Максимальный ток растворения сплава, мкА | |
| Эксперимент | Теория (ур. 2) | |
| 5,0 | 550 | 554 |
| 15,0 | 470 | 473 |
| 25,0 | 390 | 403 |
Средняя относительная погрешность вычислений по ур. 2 – 1,57 %.
Процесс селективного растворения никеля из матрицы сплава в области составов от ~40 до ~100% масс. Ni будет определяться выражением [2]:
(4)где
- максимальный ток анодного растворения чистого никеля, мкА; 
и 
- содержание компонентов в сплаве, % масс.; 
и 
- плотности компонентов сплава, г/см3; a и b – эмпирические постоянные. Для процесса растворения сплавов Cu-Ni в 3 М KCl a=(-6,7±0,1)·10-3, b=0,68±0,01.Таблица 6
Максимальные токи растворения сплавов медь – никель
в 3 М KCl
(
; 
; 
; 
)| Содержание никеля в сплаве, % масс. | Ток растворения сплава, мкА | ||||
| Работа выхода электрона, эВ | Эксперимент | Теория (ур. 2) | Теория (ур. 3) | Теория (ур. 4) | |
| 9,3 | 4,34 | 290 | 296 | 292 | - |
| 18,7 | 4,39 | 340 | 351 | 345 | - |
| 28,4 | 4,44 | 395 | 407 | 396 | - |
| 38,2 | 4,51 | 450 | 462 | 450 | - |
| 40,0 | - | 470 | - | - | 491 |
| 50,0 | - | 566 | - | - | 591 |
| 60,0 | - | 670 | - | - | 670 |
| 70,0 | - | 750 | - | - | 728 |
| 80,0 | - | 766 | - | - | 766 |
| 90,0 | - | 786 | - | - | 786 |
Средняя относительная погрешность вычислений по ур. 2 – 2,76 %.
Средняя относительная погрешность вычислений по ур. 3 – 0,6 %.
Средняя относительная погрешность вычислений по ур. 4 – 1,97 %.
Рассмотрено влияние кристаллического строения эвтектических сплавов на их электрохимические свойства и морфологию фазовых диаграмм «состав – ток». Эвтектики (E) по особенностям кристаллического строения подразделяют на нормальные и аномальные. Нормальные эвтектики бывают пластинчатые, стержневые и глобулярные. Рассмотрены особенности процесса анодного растворения эвтектических структур в условиях локального электрохимического анализа.
Характер кривых iМе=f(CМе) показывает, что парциальные токи более электроотрицательного компонента сплава изменяются с составом по s-образной кривой, характерной для эвтектических сплавов такого типа. При этом следует различать доэвтектические (Ме2+E) и заэвтектические (E+Ме1) сплавы. Для доэвтектических сплавов (Ме2+E) растворение электроотрицательного компонента Ме1 происходит из матрицы эвтектической структуры (E), которая обуславливает достаточно низкую электрохимическую активность составляющих ее фаз (меди и цинка). Компонент как бы «запрятан» в матрицу эвтектической структуры. Этот эффект и обуславливает нелинейность градуировочной характеристики iМе=f(CМе).
Аналитическое выражение для зависимости анодного тока растворения электроотрицательного металла от состава
из матрицы доэвтектических (Ме2+E) и околоэвтектических сплавов нормального строения было выведено при помощи дифференцирования экспериментальной кривой по концентрации на основании сходства кривой производной 
с кривой распределения Гаусса (ур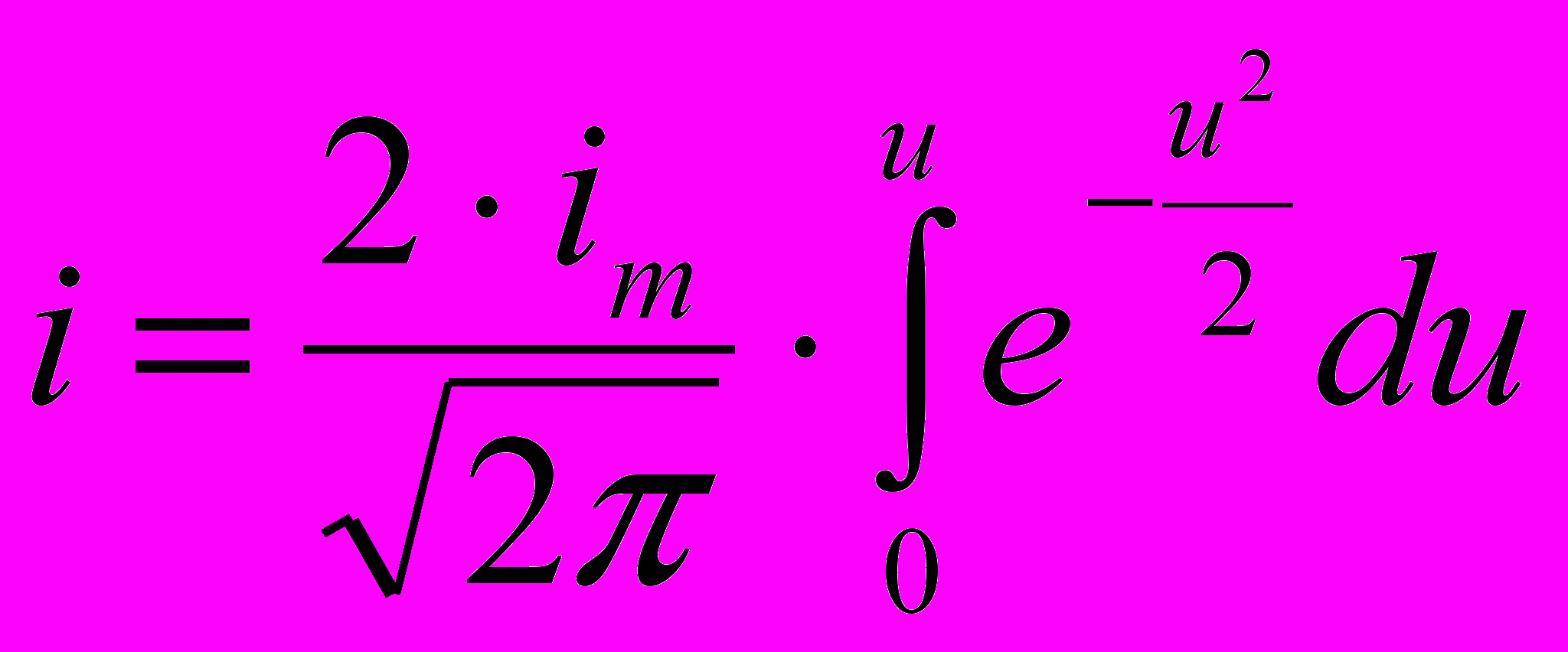. 5):
(5),где
– значение парциального тока растворения электроотрицательного компонента (im) из матрицы сплава при Ci = Cm, u = Ci-Cm/
, для двухфазной области, Cm – это состав сплава по концентрации электроотрицательного компонента, соответствующий максимуму на дифференциальной кривой в % масс.; а 2 – дисперсия генеральной совокупности распределения эвтектической структуры в матрице сплава.Для заэвтектических сплавов (E+Ме1) за счет преимущественного растворения первичных кристаллов Ме1 происходит разрыхление поверхности сплава, и создаются условия для растворения металла из более глубинных слоев, помимо растворения из эвтектической структуры.
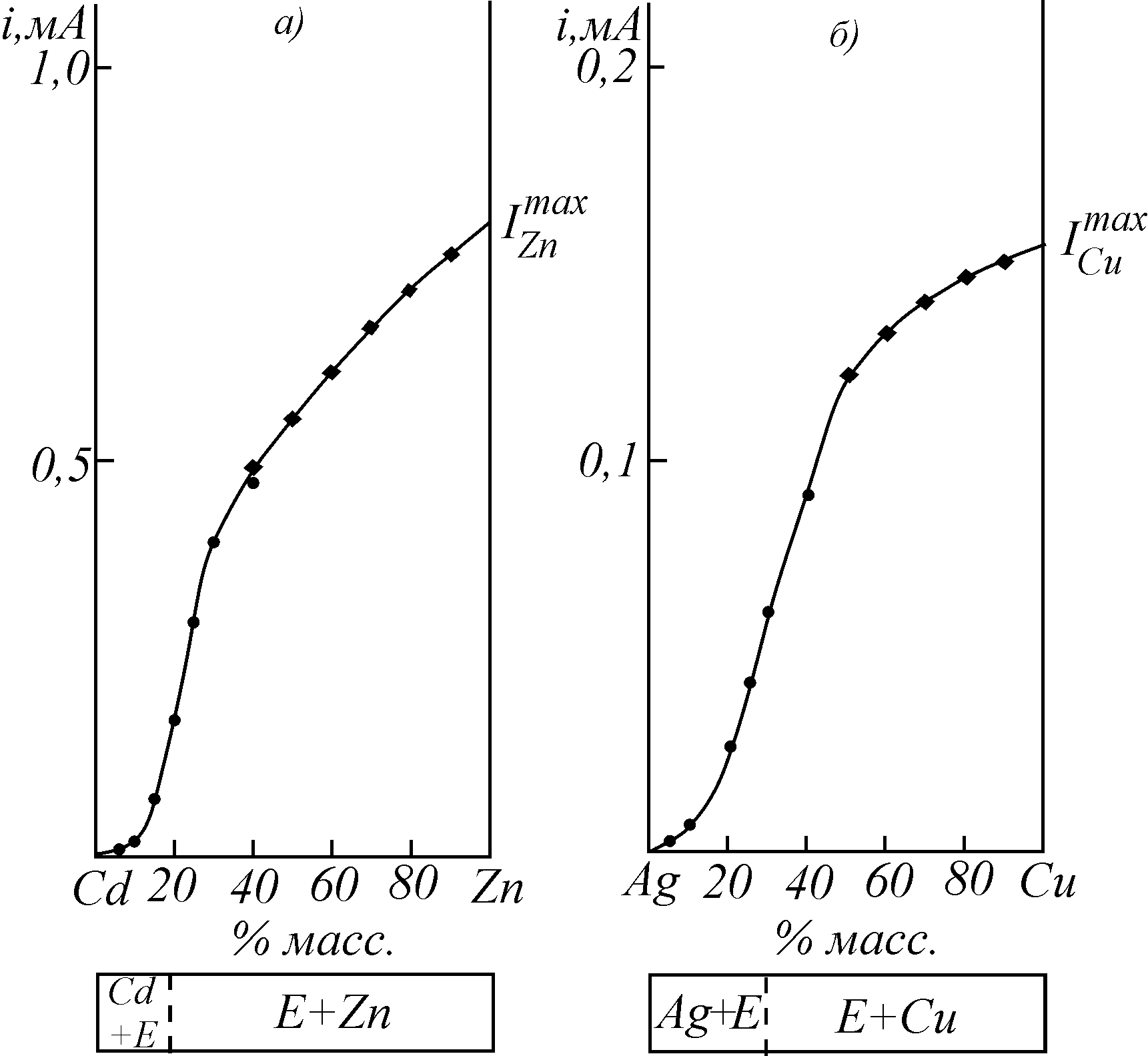
Рис. 8. Диаграммы «состав-ток» (а, б) для процесса анодного растворения цинка из матрицы сплавов Cd – Zn в 1 М NaClO4 (а) и меди из матрицы сплавов Ag – Cu в 2 М NH4F (б) [2].
э
ксперимент; уравнение (5); уравнение (6).Таблица 7
Экспериментальные и расчетные значения парциальных токов растворения цинка из матрицы сплавов кадмий – цинк в 1 М NaClO4
(Cm =22,5 % масс. Zn, , im=238 мкА,
)| Содержание цинка в сплаве, % масс. | Парциальный ток растворения цинка, мкА | ||
| Эксперимент | Теория (ур.5) | Теория (ур.6) | |
| 5 | 5 | 5 | - |
| 10 | 20 | 23 | - |
| 15 | 60 | 75 | - |
| 20 | 160 | 176 | - |
| 25 | 300 | 299 | - |
| 30 | 386 | 400 | 402 |
| 40 | 485 | 471 | 498 |
| 50 | 560 | - | 558 |
| 60 | 637 | - | 620 |
| 70 | 678 | - | 674 |
| 80 | 720 | - | 723 |
| 90 | 771 | - | 767 |
Средняя относительная погрешность вычислений по ур. 5 – 8,12 %.
Средняя относительная погрешность вычислений по ур. 6 – 1,84 %.
Таблица 8
Экспериментальные и расчетные значения парциальных токов растворения меди из матрицы сплавов серебро – медь в 2 М NH4F
(Cm =28 % масс. Cu, im=54 мкА,
)| Содержание меди в сплаве, % масс. | Парциальный ток растворения меди, мкА | ||
| Эксперимент | Теория (ур. 5) | Теория (ур. 6) | |
| 5 | 3 | 3 | - |
| 10 | 7 | 7 | - |
| 20 | 25 | 27 | - |
| 25 | 40 | 43 | - |
| 30 | 58 | 61 | - |
| 40 | 98 | 91 | - |
| 50 | 119 | - | 121 |
| 60 | 131 | - | 132 |
| 70 | 139 | - | 140 |
| 80 | 145 | - | 146 |
| 90 | 151 | - | 150 |
Средняя относительная погрешность вычислений по ур. 5 – 4,63 %.
Средняя относительная погрешность вычислений по ур. 6 – 0,9 %.
В структуре заэвтектических сплавов (E+Ме1) зависимость
будет подчиняться уравнению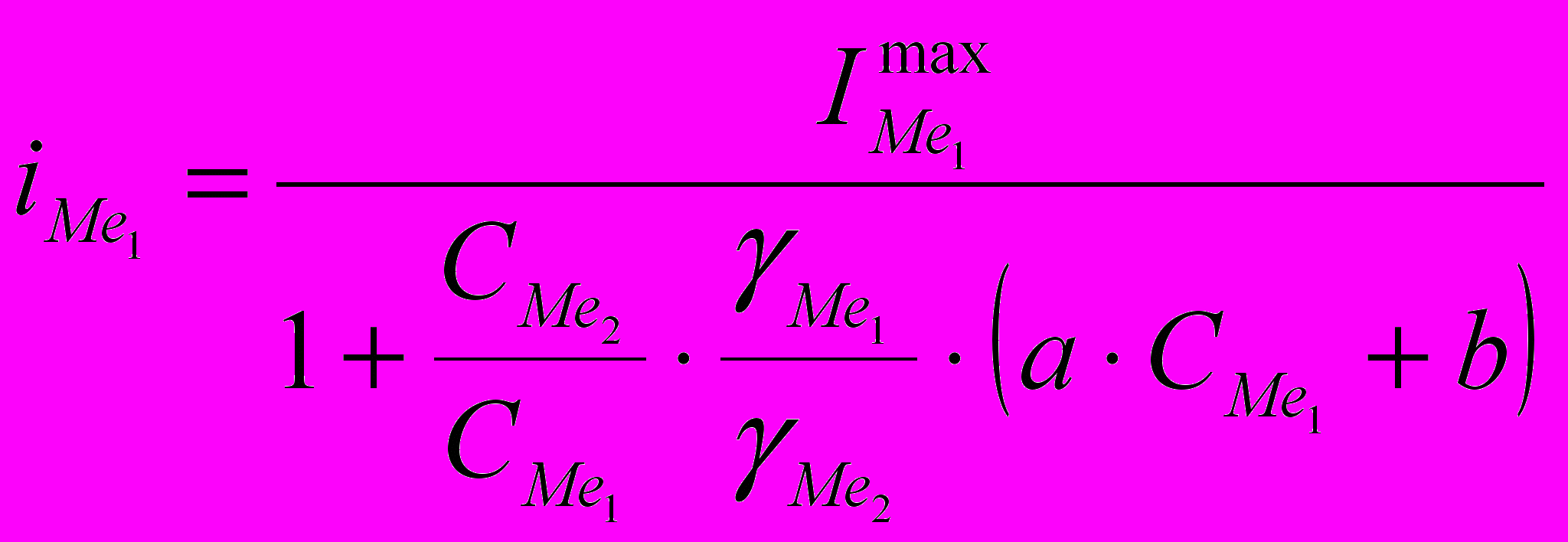
(6),где
- парциальный ток растворения электроотрицательного металла, мкА; 
- максимальный анодный ток растворения чистого металла, мкА; 
- содержание металлов в сплаве, % масс., 
- плотность металлов, г/см3; a и b – эмпирические константы, которые находятся по экспериментальным кривым 
Очевидно, что расчетные и экспериментальные данные находятся в удовлетворительном согласии.
Расчет парциальных токов эвтектических сплавов нормального строения с повышенной межкристаллитной хрупкостью можно также производить при помощи уравнения 6.
Для удобства расчетов парциальных токов эвтектических сплавов был разработан алгоритм с использованием уравнения 6, который реализован в среде визуального программирования Delphi (рис. 9).
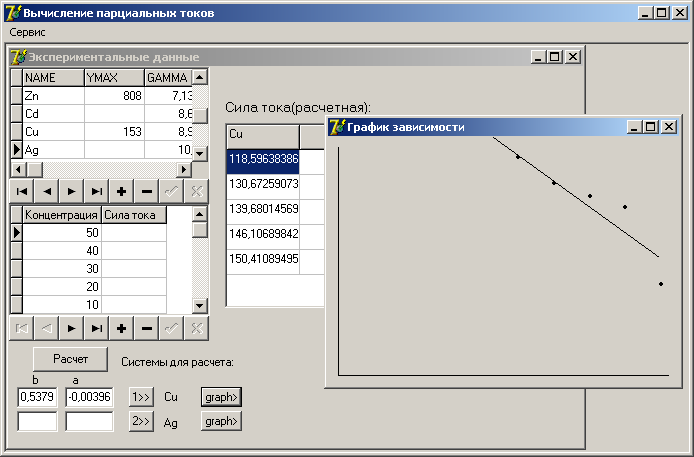
Рис. 9. Вычисление парциальных токов растворения фаз Cu – Ag.
Морфология фазовых диаграмм «состав – ток» сплавов с интерметаллическими соединениями и промежуточными фазами рассмотрена на примере изученных ранее систем сплавов медь-олово, сурьма-индий и индий-свинец.
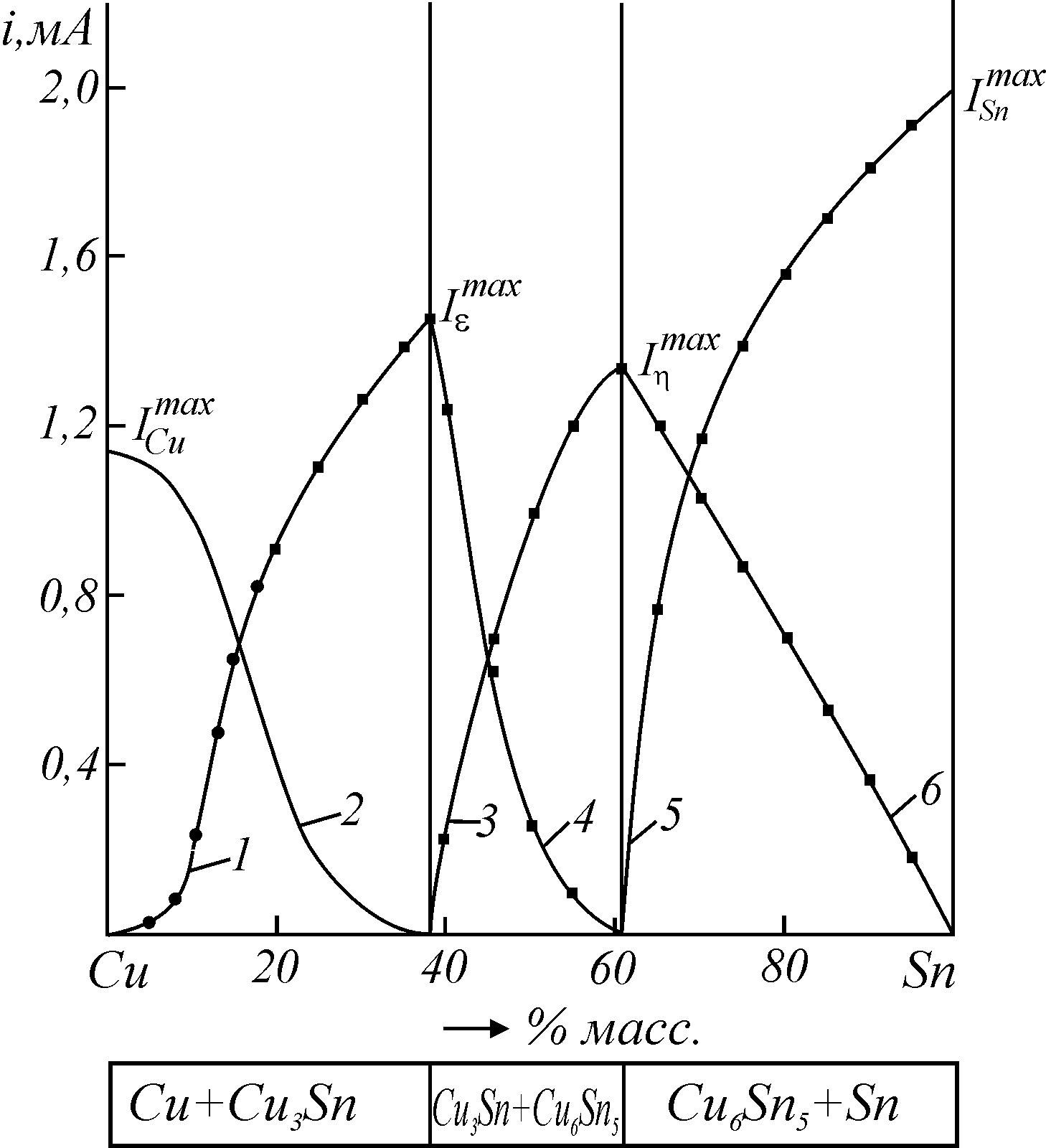
Рис. 10. Диаграмма «состав-ток» для сплавов медь-олово в 1 М NaClO4
1 – iε; 2 – iCu; 3 – iη; 4 – iε; 5 – iSn; 6 - iη.[2]
э
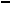
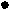
ксперимент; уравнение (7); уравнение (8).S-образный ход кривой
(рис. 10, кр.1.) указывает на то, что расчет парциальных токов ε–фазы (
) можно производить по известным уравнениям:
(7)и
(8)где
- парциальный ток растворения ε–фазы при Ci=Cm, равный 480 мкА; u - Ci-Cm/, для двухфазной области (Cu-Cu3Sn) Cm =33,9 % масс. Cu3Sn, =11,2 %, 
; 
- максимальный ток растворения ε–фазы, равный 1450 мкА; 
и 
- фазовый состав сплава Cu-Sn в двухфазной области Cu- Cu3Sn, % масс.; 
и 
- плотности сосуществующих фаз (Cu3Sn и Cu), г/см3; a и b – эмпирические постоянные. Для процесса растворения ε–фазы в 1 М NaClO4 a=(-4,3±0,1)·10-3, b=0,87±0,01. В табл. 9 представлены результаты теоретического расчета токов растворения электроотрицательной фазы ε (Cu3Sn) из матрицы сплава в двухфазной области Cu-Cu3Sn.Таблица 9
Парциальные токи растворения ε–фазы из матрицы сплава
Cu-Sn в 1 М NaClO4
| Элементный состав, % масс. Sn | Фазовый состав, % масс. Sn | Ток, мкА | ||
| Эксперимент | Теория (ур. 7) | Теория (ур. 8) | ||
| 5,0 | 13,0 | 35 | 30 | - |
| 7,5 | 19,5 | 90 | 94 | - |
| 10,0 | 26,1 | 230 | 232 | - |
| 13,0 | 33,9 | 480 | 480 | - |
| 15,0 | 39,1 | 650 | 650 | - |
| 17,5 | 45,6 | 820 | 817 | - |
| 20,0 | 52,1 | 920 | 910 | 912 |
| 25,0 | 65,2 | 1100 | - | 1105 |
| 30,0 | 78,2 | 1260 | - | 1263 |
| 35,0 | 91,2 | 1390 | - | 1386 |
Средняя относительная погрешность вычислений по ур. 7– 3,01 %.
Средняя относительная погрешность вычислений по ур. 8– 0,46 %.
В фазовой области Cu3Sn-Cu6Sn5 (рис. 10, кр.3 и 4) характер изменения парциальных токов сосуществующих фаз (ε и η) схож с прессованными порошковыми композициями. Следовательно, расчет парциальных токов растворения ε- и η- фаз можно производить по ур. (8) – табл. 10.
Матрица сплавов Cu-Sn в интервале составов от 60,89 до 100 % масс. Sn состоит также из двух фаз η (Cu6Sn5) и Sn. Это эвтектическая система сплавов η-Sn, в которой точка эвтектики смещена к чистому компоненту олову (СЕ=99,3 % масс. Sn). Судя по характеру изменения парциальных токов сосуществующих фаз (η и Sn) с составом (рис. 10, кр. 5 и 6), эвтектическая структура имеет аномальное кристаллическое строение, а процесс растворения фаз должен подчиняться уравнению (8), что и наблюдается в действительности – теоретические и экспериментальные токи растворения фаз находятся в хорошем согласии (табл. 11).
Таблица 10
Парциальные токи растворения η-фазы из матрицы сплава
Cu-Sn в 1 М NaClO4
(
, a=(-0,70±0,01)·10-3, b=0,44±0,01; 
,a=(-3,85±0,01)·10-2, b=5,6±0,1)
| Элементный состав, % масс. Sn | Фазовый состав, % масс. Cu6Sn5 | Ток, мкА | |||
| η-фаза | ε–фаза | ||||
| Эксперимент | Теория (ур. 8) | Эксперимент | Теория (ур. 8) | ||
| 40 | 7,2 | 210 | 217 | 1240 | 1238 |
| 45 | 29,4 | 700 | 695 | 620 | 630 |
| 50 | 51,6 | 990 | 993 | 270 | 272 |
| 55 | 73,8 | 1190 | 1189 | 110 | 104 |
| 60 | 96,0 | 1330 | 1322 | 10 | 10 |
Средняя относительная погрешность вычислений по η-фазе – 1,0 %.
Средняя относительная погрешность вычислений по ε-фазе – 1,59 %.
Таблица 11
Парциальные токи растворения олова и η-фазы из матрицы сплава
Cu-Sn в 1 М NaClO4
(
a=(2,43±0,01)·10-3, b=0,19±0,01; ,a=(1,18±0,01)·10-3, b=0,79±0,01)
| Элементный состав, % масс. Sn | Фазовый состав, % масс. Cu6Sn5 | Ток, мкА | |||
| Sn | η-фаза | ||||
| Эксперимент | Теория (ур. 8) | Эксперимент | Теория (ур. 8) | ||
| 65 | 10,5 | 760 | 763 | 1200 | 1198 |
| 70 | 23,3 | 1170 | 1167 | 1030 | 1030 |
| 75 | 36,1 | 1390 | 1398 | 870 | 870 |
| 80 | 48,7 | 1560 | 1559 | 700 | 702 |
| 85 | 61,6 | 1700 | 1692 | 530 | 535 |
| 90 | 74,4 | 1810 | 1804 | 360 | 364 |
| 95 | 87,2 | 1910 | 1911 | 190 | 187 |
Средняя относительная погрешность вычислений по Sn-фазе – 0,31 %.
Средняя относительная погрешность вычислений по η-фазе – 0,58 %.
Индий и сурьма образуют систему сплавов с одним интерметаллическим соединением InSb (51,48 % масс. Sb), а диаграмма «состав-ток» представляет собой совокупность двух более простых диаграмм на основе InSb и Sb, In и InSb. Парциальные токи растворения фаз сплавов изменяются также, как в эвтектических системах. Система In-InSb относится к сплавам с вырожденной эвтектикой, и процесс растворения сосуществующих фаз (In и InSb) подчиняется ур. (8). На анодное поведение сплавов системы Sb –InSb существенное влияние оказывает высокая межкристаллитная хрупкость, и парциальные токи растворения фаз (Sb и InSb) подчиняются ур. (8) (рис. 11).
Рис. 11. Диаграмма «состав-ток» для сплавов сурьма-индий в 1 М NaClO4 [2]
1 – iInSb; 2 – iSb; 3 – iIn; 4 – iInSb.
э
ксперимент; уравнение (8).В основе диаграммы состояния системы индий - свинец лежат две перитектические диаграммы, а всю систему сплавов можно представить как совокупность четырех фазовых полей – ограниченных твердых растворов на основе индия (In) от 0 до 20 % масс. Pb; ограниченных твердых растворов на основе индия и свинца α/ от 21,5 до 41,24 % масс. Pb; гетерогенной фазовой области α/+( Pb) от 41,24 до 52 % масс. Pb и ограниченных твердых растворов на основе свинца (Pb) от 52 до 100 % масс. Pb (рис. 11).
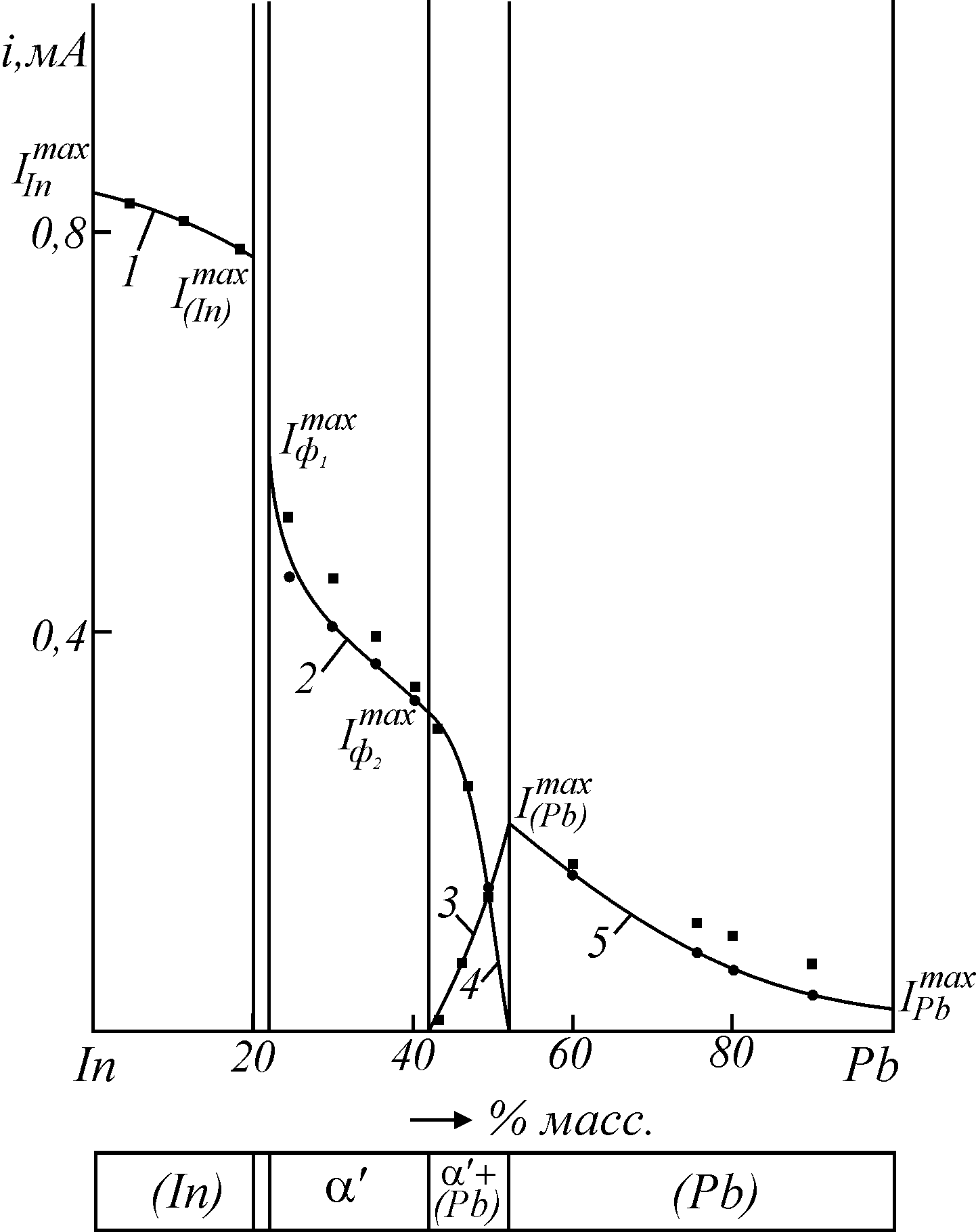
Рис. 12. Диаграмма «состав-ток» для сплавов индий-свинец в насыщенном растворе KCl [2]: 1 – I(In); 2 –
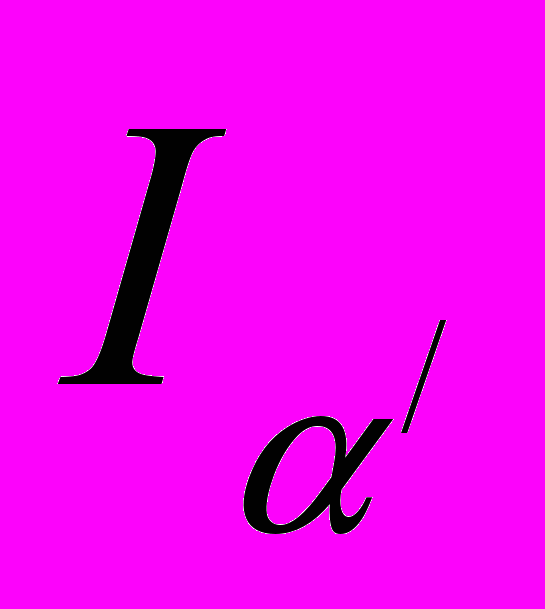; 3 – i(Pb); 4 – 
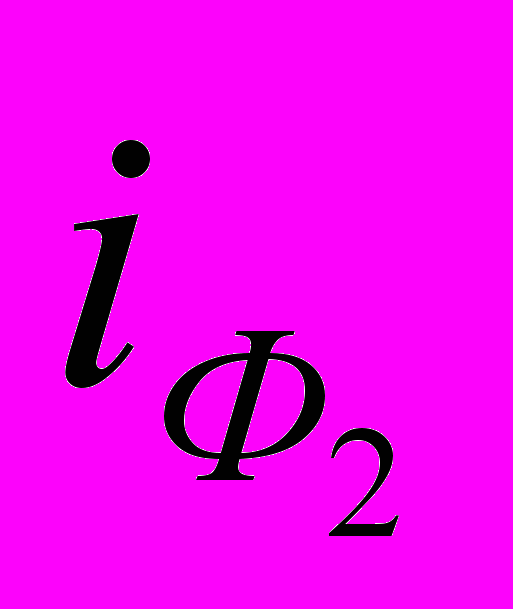; 5 – I(Pb).э
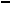
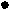
ксперимент; ур. (9, 10); ур. (2); ур. (8).Для трех фазовых полей ограниченных твердых растворов (In), α/ и (Pb) расчет тока раствора проведен по ур. (2), в табл. 12, 13 и 14 приведены результаты соответствующих расчетов.
Таблица 12
Максимальные токи растворения сплавов индий-свинец в насыщенном растворе KCl для фазовой области ограниченных твердых растворов (In) (
; 
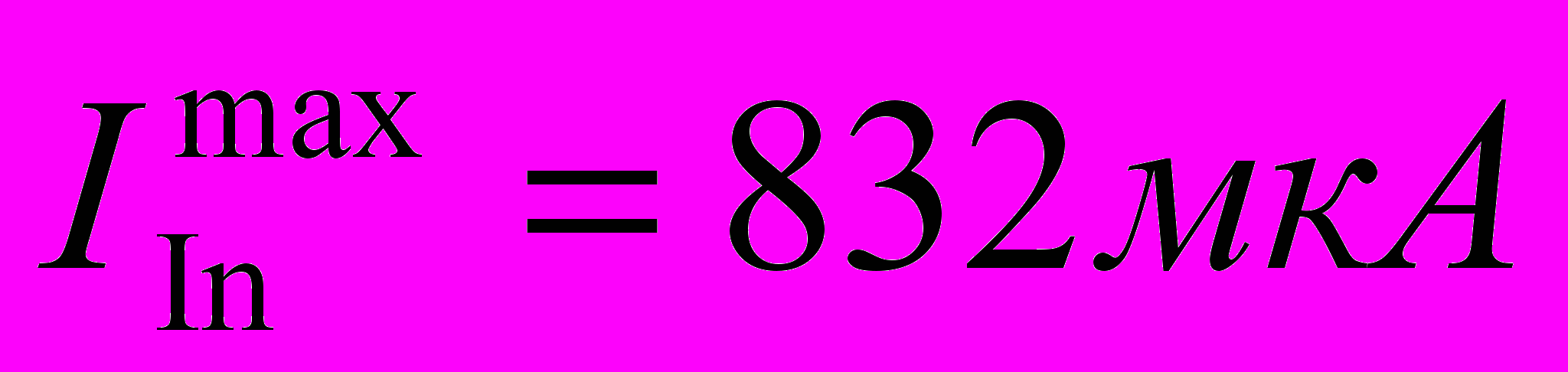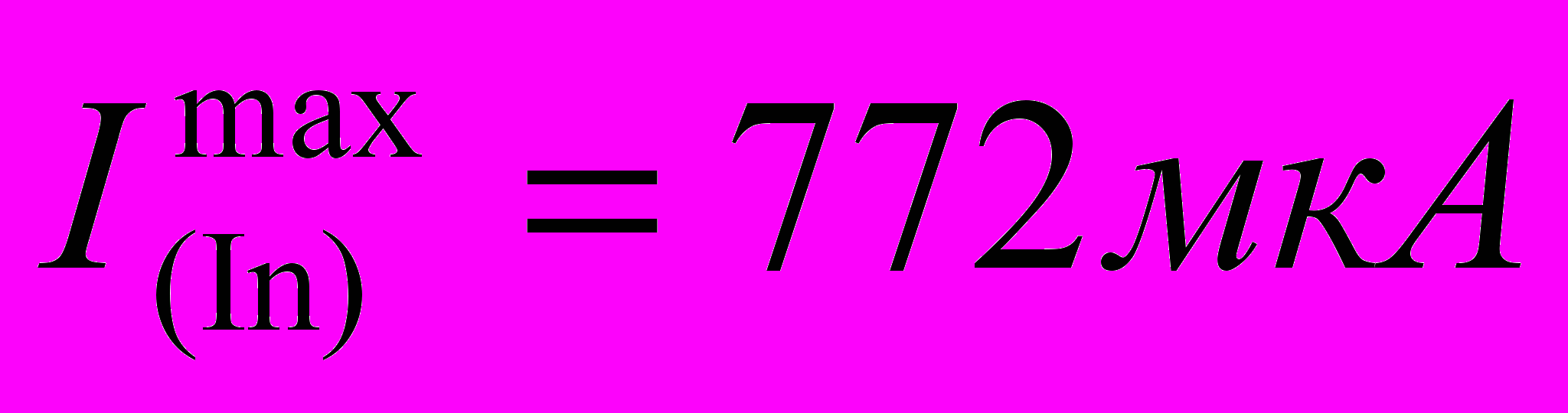)| Элементный состав, % масс. Pb | Молярная доля индия в фазовой области (In) | Ток растворения сплава, мкА | |
| Эксперимент | Теория (ур.2) | ||
| 6 | 0,719 | 819 | 815 |
| 12 | 0,423 | 804 | 797 |
| 18 | 0,109 | 778 | 778 |
Средняя относительная погрешность вычислений по ур. 2 – 0,45 %.
Для фазовых областей ограниченных твердых растворов α/ и (Pb) токи растворения сплавов, рассчитанные по ур. (2) существенно больше экспериментальных – табл. 13 и 14. Для учета этих отклонений введен коэффициент активности растворяющейся фазы в ур. (2)
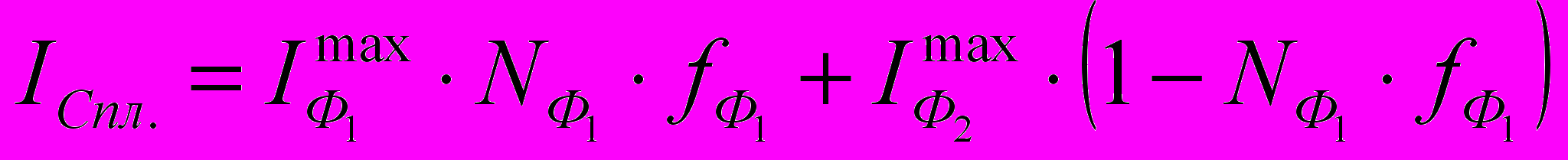(9)Таблица 13