Рабочая программа дисциплины «теория вероятностей и математическая статистика» Рекомендуется для направления подготовки 080100 Экономика
| Вид материала | Рабочая программа |
- Рабочая программа дисциплины «теория вероятностей и математическая статистика» Рекомендуется, 213.97kb.
- Программа дисциплины «Теория вероятностей и математическая статистика» для направления, 243.86kb.
- Рабочая учебная программа дисциплины (модуля) Теория вероятностей и математическая, 217.23kb.
- Примерная программа наименование дисциплины «теория вероятностей и математическая статистика», 165.37kb.
- Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика», 103.07kb.
- Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика», 108.11kb.
- Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика», 96.22kb.
- Рабочая программа дисциплины «теория вероятностей и математическая статистика» Рекомендуется, 152.96kb.
- Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика», 686.98kb.
- Рабочая программа учебной дисциплины «Теория вероятностей и математическая статистика», 165.42kb.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ЭКОНОМИКИ И ФИНАНСОВ
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
«ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Рекомендуется для направления подготовки
080100 Экономика
Квалификация выпускника - бакалавр
Санкт-Петербург
2011 год
- Цели и задачи дисциплины
Накопление необходимого запаса сведений по математике (основные определения, теоремы, правила), а также освоение математического аппарата, помогающего моделировать, анализировать и решать экономические задачи, помощь в усвоении математических методов, дающих возможность изучать и прогнозировать процессы и явления из области будущей деятельности студентов; развитие логического и алгоритмического мышления, способствование формированию умений и навыков самостоятельного анализа исследования экономических проблем, развитию стремления к научному поиску путей совершенствования своей работы.
- Место дисциплины в структуре ООП
Дисциплина «Теория вероятностей и математическая статистика» относится к циклу Б.2.1 Математический цикл, Базовая часть. Входные знания, умения и компетенции студентов должны соответствовать первому курсу математики. Дисциплина «Теория вероятностей и математическая статистика» является предшествующей для следующих дисциплин: «Теория рисков», «Математические методы и модели», «Статистика», «Экономика фирмы», «Статистические пакеты прикладных программ», «Бизнес-планирование», «Рынок ценных бумаг», «Экспертные методы и системы», «Теория выборки и оценка рисков», «Финансовая статистика», «Финансовая математика», «Анализ временных рядов и прогнозирование», «Многомерные статметоды», «Демография и статистика населения», «Статистика фирм и отраслей», «Эконометрическое моделирование», «Статистика цен», «Социальная статистика», «Статистика природопользования», «Статистика страхования», «Страхование», «Социальное страхование», «Инвестиции», «Теория и методы экономического прогнозирования», «Теория игр», «Методы социально-экономического прогнозирования», «Теория рисков и моделирование рисковых ситуаций», «Многомерная статистика в экономике».
- Требования к результатам освоения дисциплины
Процесс изучения дисциплины направлен на формирование следующих компетенций:
- способен понимать сущность и значение информации в развитии современного информационного общества, сознавать опасности и угрозы, возникающие в этом процессе, соблюдать основные требования информационной безопасности, в том числе защиты государственной тайны (ОК-12);
- владеет основными методами, способами и средствами получения, хранения, переработки информации, имеет навыки работы с компьютером как средством управления информацией, способен работать с информацией в глобальных компьютерных сетях (ОК-13);
расчетно-экономическая деятельность
- способен собрать и проанализировать исходные данные, необходимые для расчета экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов (ПК-1);
- способен на основе типовых методик и действующей нормативно-правовой базы рассчитать экономические и социально-экономические показатели, характеризующие деятельность хозяйствующих субъектов, (ПК-2);
- способен выполнять необходимые для составления экономических разделов планов расчеты, обосновывать их и представлять результаты работы в соответствии с принятыми в организации стандартами (ПК-3);
- аналитическая, научно-исследовательская деятельность
- способен осуществлять сбор, анализ и обработку данных, необходимых для решения поставленных экономических задач (ПК-4);
- способен выбрать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, проанализировать результаты расчетов и обосновать полученные выводы (ПК-5);
- способен на основе описания экономических процессов и явлений строить стандартные теоретические и эконометрические модели, анализировать и содержательно интерпретировать полученные результаты (ПК-6);
- способен использовать для решения аналитических и исследовательских задач современные технические средства и информационные технологии (ПК-10);
- организационно-управленческая деятельность
- способен использовать для решения коммуникативных задач современные технические средства и информационные технологии (ПК-12);
- педагогическая деятельность
- способен преподавать экономические дисциплины в образовательных учреждениях различного уровня, используя существующие программы и учебно-методические материалы (ПК-14);
- способен принять участие в совершенствовании и разработке учебно-методического обеспечения экономических дисциплин (ПК-15).
В результате изучения дисциплины студент должен:
Знать:
основы теории вероятностей и математической статистики, необходимые для решения экономических задач;
Уметь:
применять методы математического анализа и моделирования, теоретического и экспериментального исследования для решения экономических задач;
Владеть:
навыками применения современного математического инструментария для решения экономических задач;
методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов.
- Объем дисциплины и виды учебной работы
Общая трудоемкость дисциплины составляет 5 зачетных единиц.
-
Вид учебной работы
Всего часов (третий семестр)
Аудиторные занятия (всего)
90
В том числе:
-
Лекции
42
Практические занятия (ПЗ)
48
Самостоятельная работа (всего)
90
В том числе:
-
Тест №1
20
Тест №2
20
Контрольная работа
7
Индивидуальное задание
7
Экзамен
36
Общая трудоемкость час
зач. ед.
180
4+1
- Содержание дисциплины
5.1. Содержание разделов дисциплины
1. Теория вероятностей.
Случайные события. Предмет теории вероятностей и ее значение для экономической науки. Пространство элементарных событий. Алгебра событий. Понятие случайного события.
Вероятность случайного события. Элементы комбинаторики. Частота события, ее свойства, статистическая устойчивость частоты. Аксиомы теории вероятностей. Простейшие следствия из аксиом. Классическое и геометрическое определения вероятности случайного события. Теорема сложения вероятностей. Условная частота, ее устойчивость. Условная вероятность события. Формула умножения вероятностей. Независимые события. Формула полной вероятности и формула Байеса. Схема Бернулли. Формула Бернулли. Теоремы Муавра-Лапласа (без доказательства).
Случайные величины. Понятие случайной величины. Дискретные случайные величины (ДСВ). Ряд распределения. Биномиальное распределение. Распределение Пуассона. Независимые случайные величины. Системы случайных величин. Функции от случайных величин. Математическое ожидание ДСВ, его вероятностный смысл. Свойства математического ожидания случайной величины. Дисперсия случайной величины, ее свойства. Среднее квадратическое отклонение. Моменты случайных величин. Непрерывные случайные величины (НСВ). Функция распределения случайной величины, ее свойства. Плотность распределения вероятностей случайной величины, ее свойства. Математическое ожидание, дисперсия и среднее квадратическое отклонение НСВ. Моменты НСВ. Равномерное распределение. Нормальное распределение. Мода, медиана, асимметрия, эксцесс. Правило трех стандартов. Распределение Стьюдента, распределение
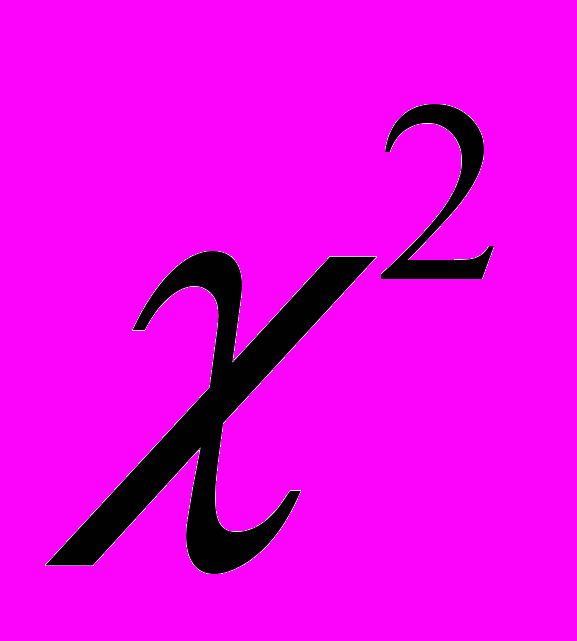 . Функции от случайных величин. Понятие о производящей функции. Двумерные случайные величины.
. Функции от случайных величин. Понятие о производящей функции. Двумерные случайные величины. Элементы корреляционной теории. Функциональная зависимость и корреляция. Функция регрессии. Корреляционный момент и коэффициент корреляции.
Закон больших чисел. Понятие о законе больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. Понятие о теореме Ляпунове.
2. Математическая статистика.
Основы выборочного метода и элементы статистический теории оценивания. Генеральная и выборочная совокупности. Вариационный ряд, интервальный вариационный ряд. Полигон, гистограмма. Выборочная функция распределения. Числовые характеристики выборки. Точечное оценивание параметров распределения. Несмещенность, состоятельность и эффективность оценки. Выборочная средняя как оценка генеральной средней. Оценка генеральной дисперсии. Интервальное оценивание параметров распределения. Доверительный интервал и доверительная вероятность. Интервальное оценивание генеральной средней и генеральной дисперсии.
Статистическое исследование зависимостей. Корреляционный и регрессионный анализ. Корреляционная таблица. Выборочный коэффициент корреляции. Построение выборочных линейных уравнений регрессии. Множественная линейная регрессия. Частные и множественные коэффициенты корреляции. Экономические примеры.
Методы статистической проверки гипотез. Статистическая гипотеза. Нулевая и конкурирующая гипотезы. Критерий проверки статистической гипотезы, критическая область. Ошибки первого и второго рода, уровень значимости, мощность критерия. Проверка гипотезы о среднем значении при известной и неизвестной дисперсии. Гипотеза о равенстве генеральных средних. Гипотеза о равенстве генеральных дисперсий. Понятие о критерии согласия. Критерий согласия Пирсона. Критерий согласия Колмогорова.
5.2 Разделы дисциплины и междисциплинарные связи с обеспечиваемыми (последующими) дисциплинами
| № п/п | Наименование обеспе-чиваемых (последующих) дисциплин | № № разделов данной дисциплины, необходимых для изучения обеспечиваемых (последующих) дисциплин | |
| 1 | 2 | ||
| 1. | Теория рисков | * | * |
| 2. | Математические методы и модели | * | * |
| 3 | Статистика | * | * |
| 4 | Экономика фирмы | * | * |
| 5 | Статистические пакеты прикладных программ | * | * |
| 6 | Бизнес-планирование | * | * |
| 7 | Рынок ценных бумаг | * | * |
| 8 | Экспертные методы и системы | * | * |
| 9 | Теория выборки и оценка рисков | * | * |
| 10 | Финансовая статистика | * | * |
| 11 | Финансовая математика | * | * |
| 12 | Анализ временных рядов и прогнозирование | * | * |
| 13 | Многомерные статметоды | * | * |
| 14 | Демография и статистика населения | * | * |
| 15 | Статистика фирм и отраслей | * | * |
| 16 | Эконометрическое моделирование | * | * |
| 17 | Статистика цен | * | * |
| 18 | Социальная статистика | * | * |
| 19 | Статистика природопользования | * | * |
| 20 | Статистика страхования | * | * |
| 21 | Страхование | * | * |
| 22 | Социальное страхование | * | * |
| 23 | Инвестиции | * | * |
| 24 | Теория и методы экономического прогнозирования | * | * |
| 25 | Теория игр | * | * |
| 26 | Методы социально-экономического прогнозирования | * | * |
| 27 | Теория рисков и моделирование рисковых ситуаций | * | * |
| 28 | Многомерная статистика в экономике | * | * |
5.3. Разделы дисциплин и виды занятий
| № п/п | Наименование раздела дисциплины | Лекц. | Практ. зан. | СРС | Всего час. |
| 1. | Теория вероятностей | 26 | 32 | 47 | 105 |
| 2. | Математическая статистика | 16 | 16 | 7 | 39 |
6. Лабораторный практикум не предусмотрен
7. Практические занятия (семинары)
| № п/п | № раздела дисцип- лины | Тематика практических занятий (семинаров) | Трудо-емкость (час.) |
| 1 | 1 | Случайные события. Операции над случайными событиями. | 2 |
| 2 | 1 | Пространство элементарных событий. Элементы комбинаторики. | 2 |
| 3 | 1 | Задачи на классическое определение вероятности. | 2 |
| 4 | 1 | Геометрическая вероятность. Задача о встрече. | 2 |
| 5 | 1 | Условная вероятность. Независимые случайные события. | 2 |
| 6 | 1 | Вычисление вероятностей случайных событий при помощи теоремы сложения и формулы умножения вероятностей. | 2 |
| 7 | 1 | Использование формулы полной вероятности, формула Байеса. | 2 |
| 8 | 1 | Формула Бернулли и теоремы Муавра-Лапласа. | 2 |
| 9 | 1 | Контрольная работа. | 2 |
| 10 | 1 | Случайные величины. Построение ряда распределения дискретной случайной величины | 2 |
| 11 | 1 | Биномиальное распределение и распределение Пуассона. | 2 |
| 12 | 1 | Вычисление числовых характеристик ДСВ. | 2 |
| 13 | 1 | Функция распределения и плотность распределения вероятностей непрерывной случайной величины. | 2 |
| 14 | 1 | Вычисление числовых характеристик НСВ. Равномерное распределение. | 2 |
| 15 | 1 | Нормальное распределение. Понятие о распределении Стьюдента и распределении 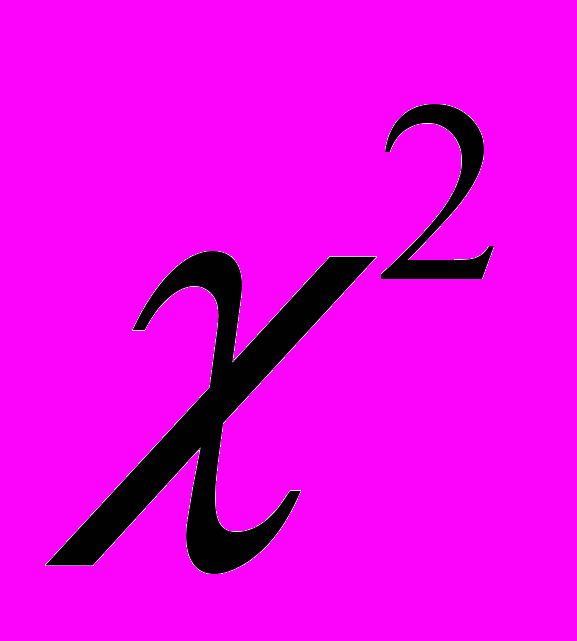 . . | 2 |
| 16 | 1 | Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. | 2 |
| 17 | 2 | Основы выборочного метода и элементы статистической теории оценивания. Выборочная совокупность, выборочная функция распределения. | 2 |
| 18 | 2 | Гистограмма, полигон часто, интервальный ряд. | 2 |
| 19 | 2 | Вычисление точечных оценок параметров распределения. | 2 |
| 20 | 2 | Вычисление интервальных оценок параметров распределения. | 2 |
| 21 | 2 | Статистические исследования зависимостей. Выборочный коэффициент корреляции | 2 |
| 22 | 2 | Построение выборочных линейных уравнений регрессии. | 2 |
| 23 | 2 | Методы статистической проверки гипотез. Гипотеза о равенстве генеральных средних. | 2 |
| 24 | 2 | Гипотеза о равенстве генеральных дисперсий. Критерий согласия Пирсона. | 2 |
8. Примерная тематика курсовых работ – курсовые работы не предусмотрены.
9. Учебно-методическое и информационное обеспечение дисциплины
а) основная литература
- Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2003. – 479 с.
- Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979.
- Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам – М.: Айрис-пресс, 2006. – 288.
б) дополнительная литература
- Вентцель Е.С. Исследование операций. Задачи, принципы, методология. Учебное пособие для студентов ВУЗов. – М.: Высшая школа, 2001.
- Вентцель Е.С. Теория вероятностей: Учебник для ВУЗов. – М.: Высшая школа, 2002.
- Первичная статистическая обработка данных –Л.:ЛФЭИ, 1987 (1,2 части)
- Итенберг В.С., Ковбаса С.И. Кондратьев В.С. Теория вероятностей: Учебное пособие. -Л.:ЛФЭИ, 1990.
- Кремер Н.Ш. Теория вероятностей и математическая статистика. – М.: ЮНИТИ-ДАНА, 2003.
в) программное обеспечение не предусмотрено
г) базы данных, информационно-справочные и поисковые системы:
10. Материально-техническое обеспечение дисциплины
Документ-сканер, принтеры, компьютеры и пакеты программ обработки результатов тестирования.
11. Методические рекомендации по организации изучения дисциплины
Дисциплина «Теория вероятностей и математическая статистика» читается в течение пятого семестра и заканчивается экзаменом. Для контроля обучения в течение семестра проводятся два теста, одна контрольная работа и одна самостоятельная работа. Максимальное количество баллов за каждый тест равно 40. Минимальное количество баллов для того, чтобы тест считался сданным, равно 22. Максимальное количество баллов за контрольную и самостоятельную работы равно 16, минимальное – 6 и 5 соответственно. За работу в течение семестра необходимо набрать от 55 до 100 баллов. Максимальное число баллов, которое можно получить на экзамене, также равно 100. Итоговая оценка (в баллах) вычисляется по формуле
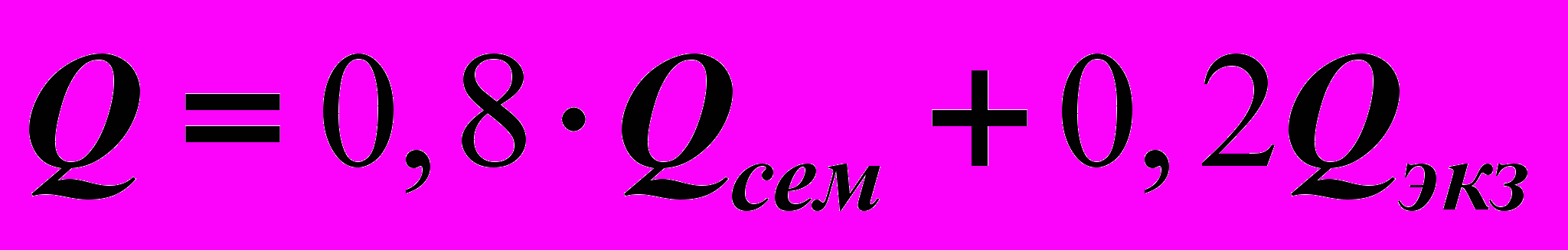 , где
, где 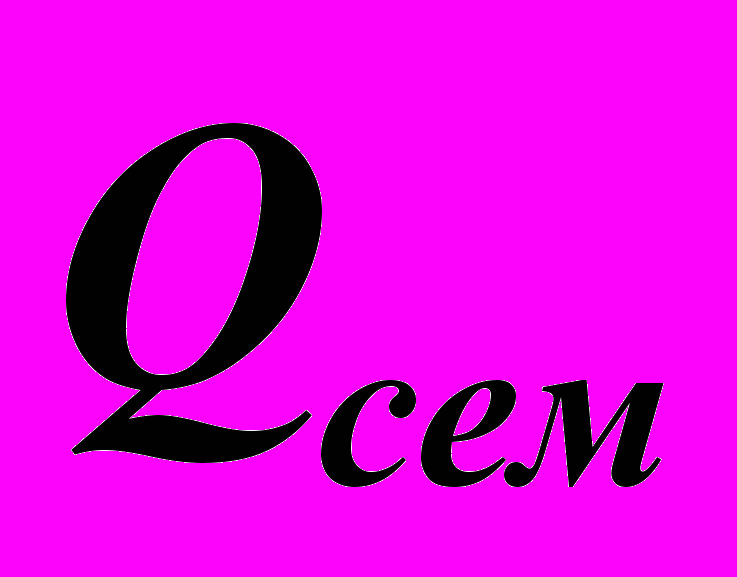 – баллы, полученные за работу в семестре, а
– баллы, полученные за работу в семестре, а 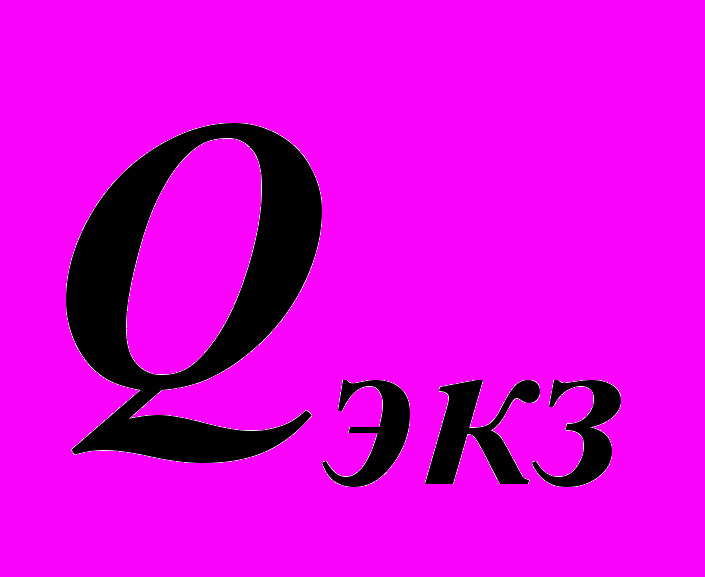 – за экзамен. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:
– за экзамен. Набранное итоговое количество баллов переводится в оценку согласно следующей таблице:| Итоговое количество баллов | оценка |
| до 55  | неудовлетворительно |
| от 55 до 70 | удовлетворительно |
| от 70 до 85 | хорошо |
| от 85 | отлично |
Примеры задач и вопросов теста №1.
Требуется дать ответ ДА или НЕТ.
Пусть
 и
и 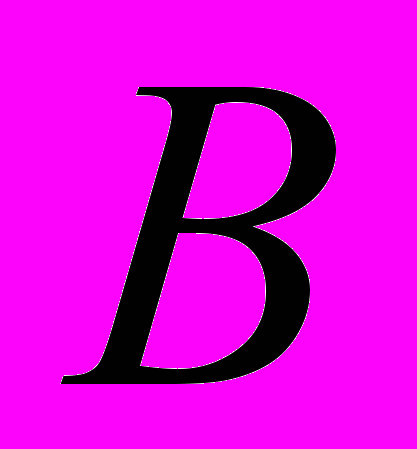 - случайные события, имеющие ненулевые вероятности.
- случайные события, имеющие ненулевые вероятности.Верно утверждение:
если
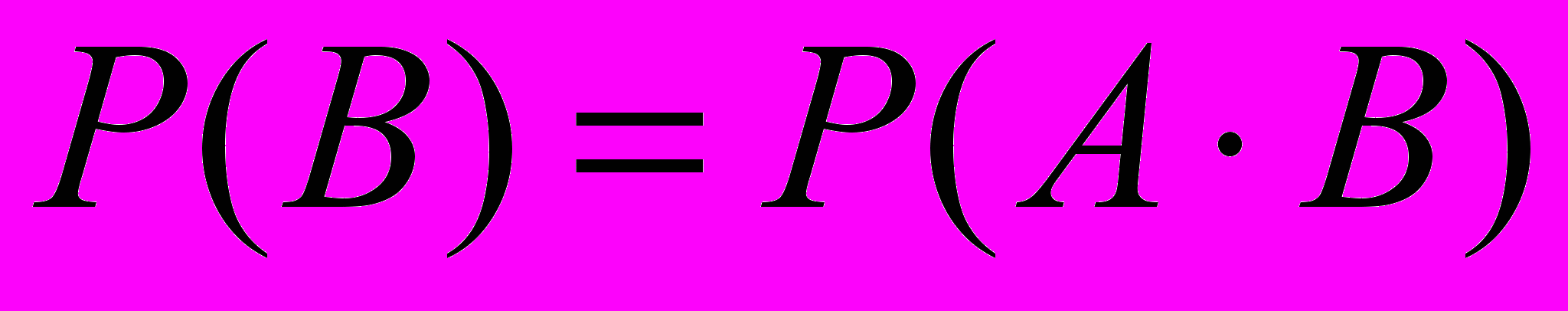 , то
, то 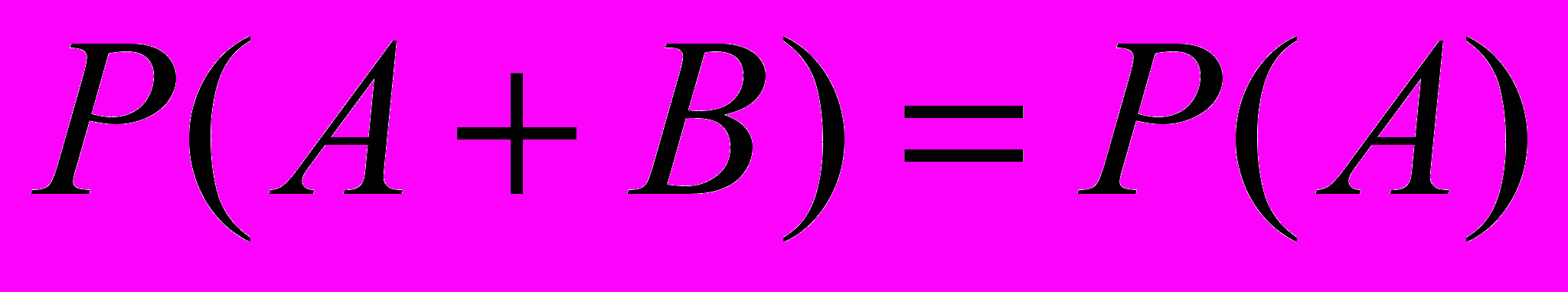 .
.если
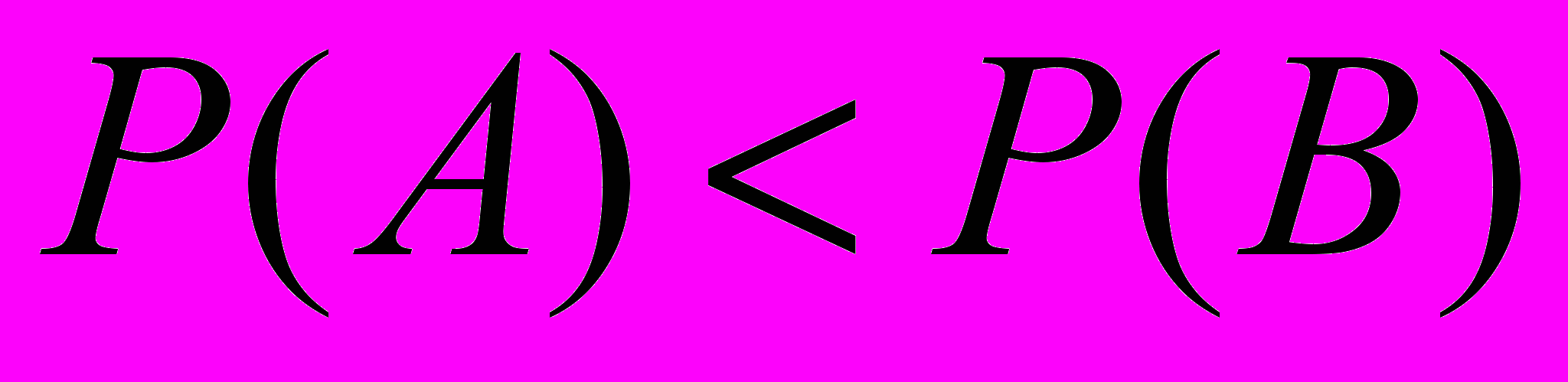 , то
, то 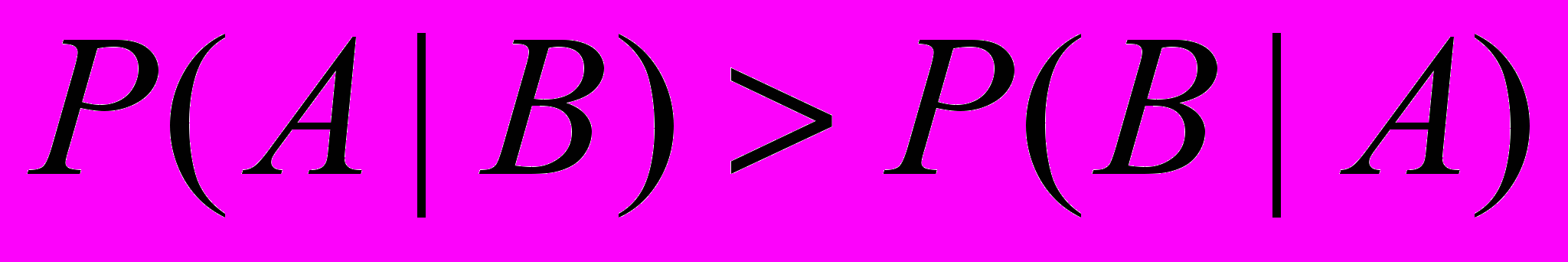 .
.если события
 и
и 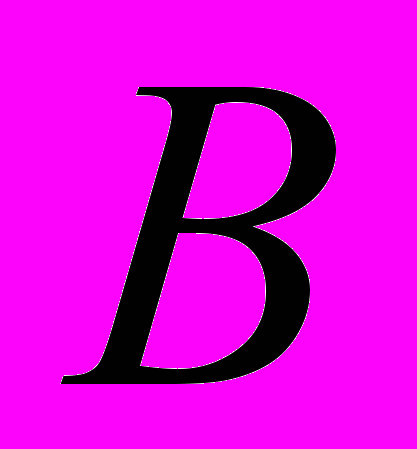 несовместны, то они независимы.
несовместны, то они независимы.Требуется выбрать правильный ответ.
Производится серия независимых испытаний, в каждом из которых с вероятностью
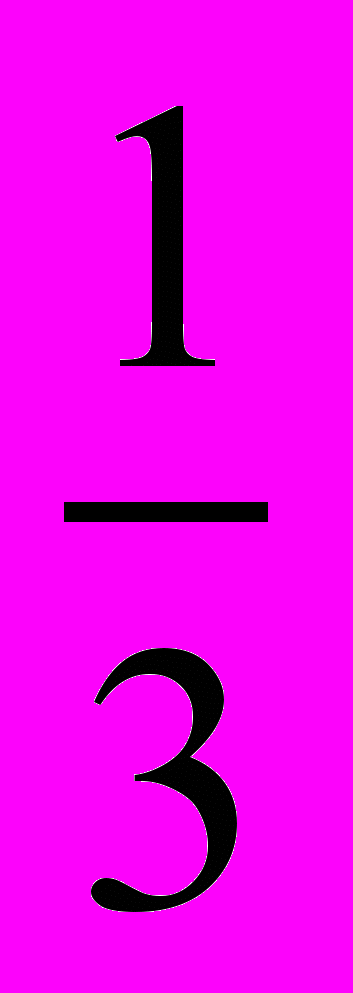 может появиться событие
может появиться событие  . Верно утверждение:
. Верно утверждение:Вероятность того, что при четырех испытаниях событие
 появится ровно три раза, принадлежит промежутку …
появится ровно три раза, принадлежит промежутку …А.
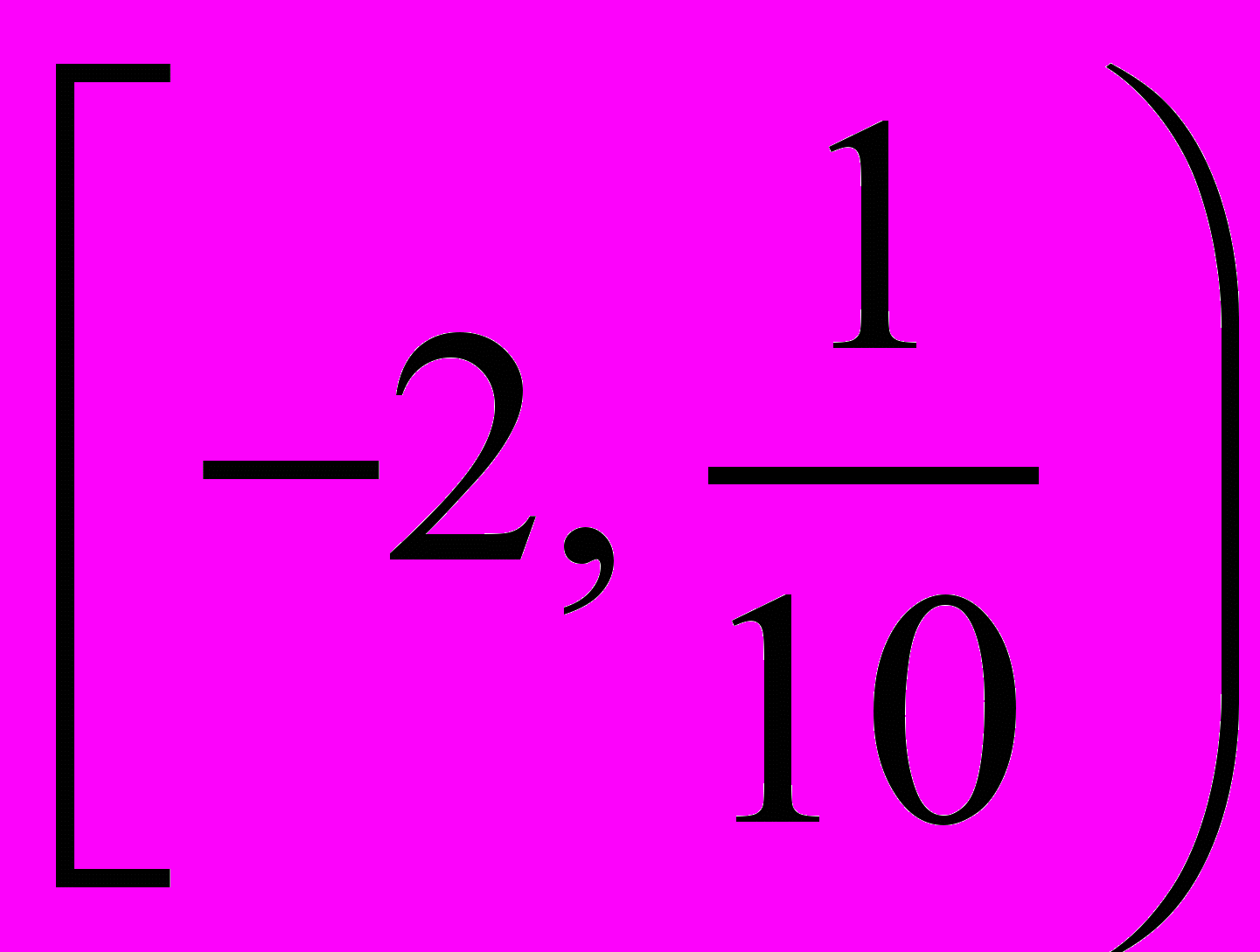 . Б.
. Б. 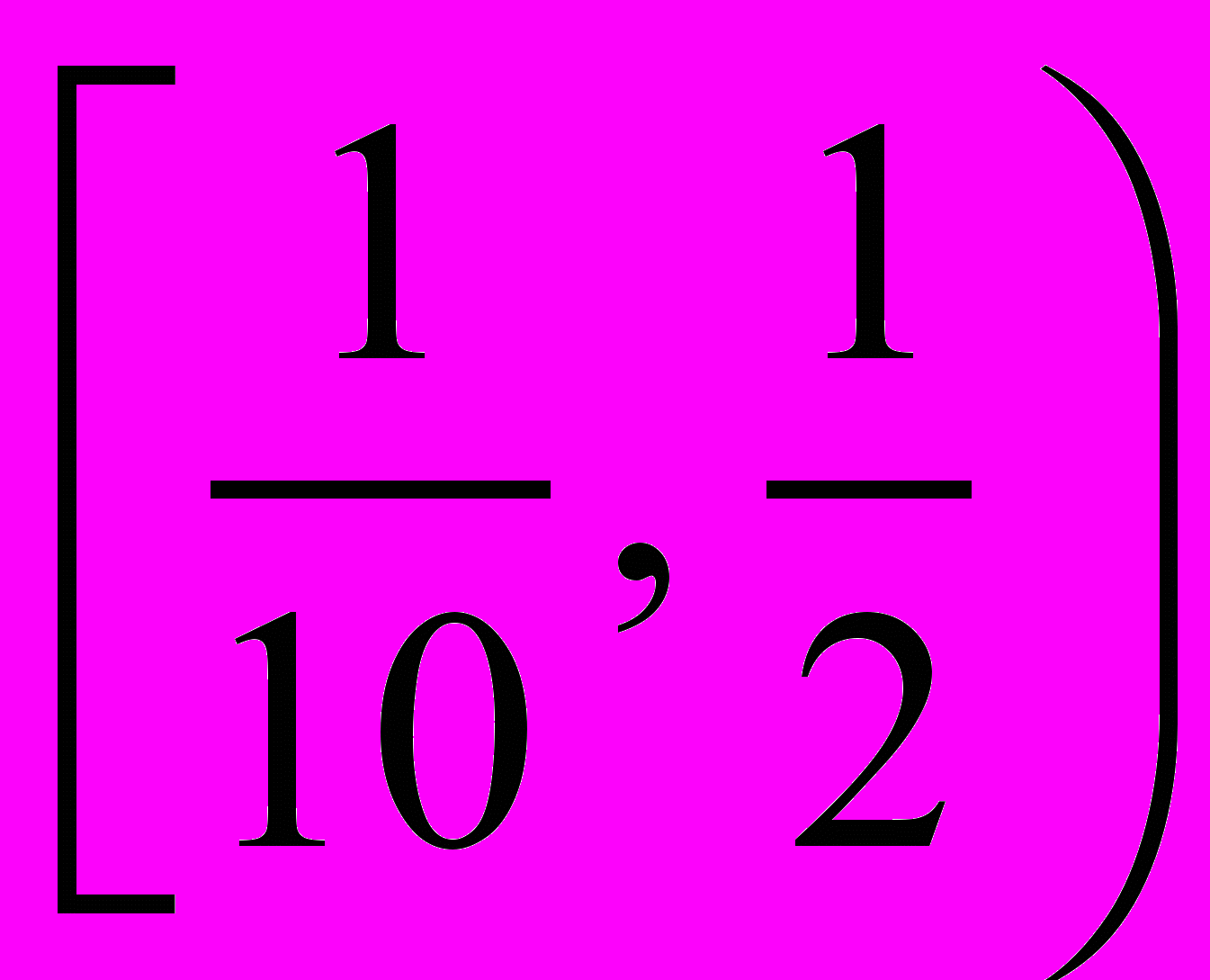 . В.
. В. 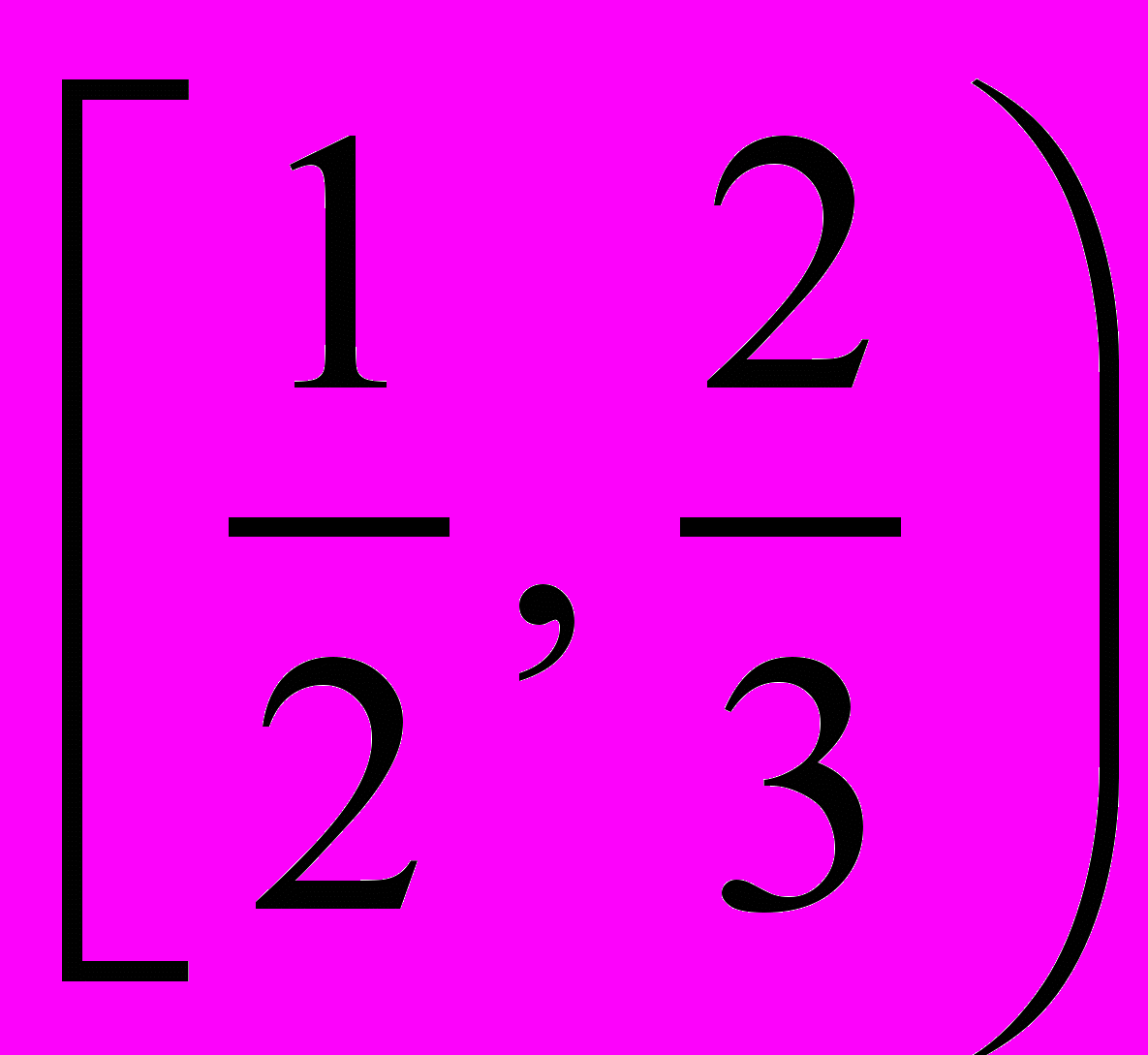 . Г.
. Г. 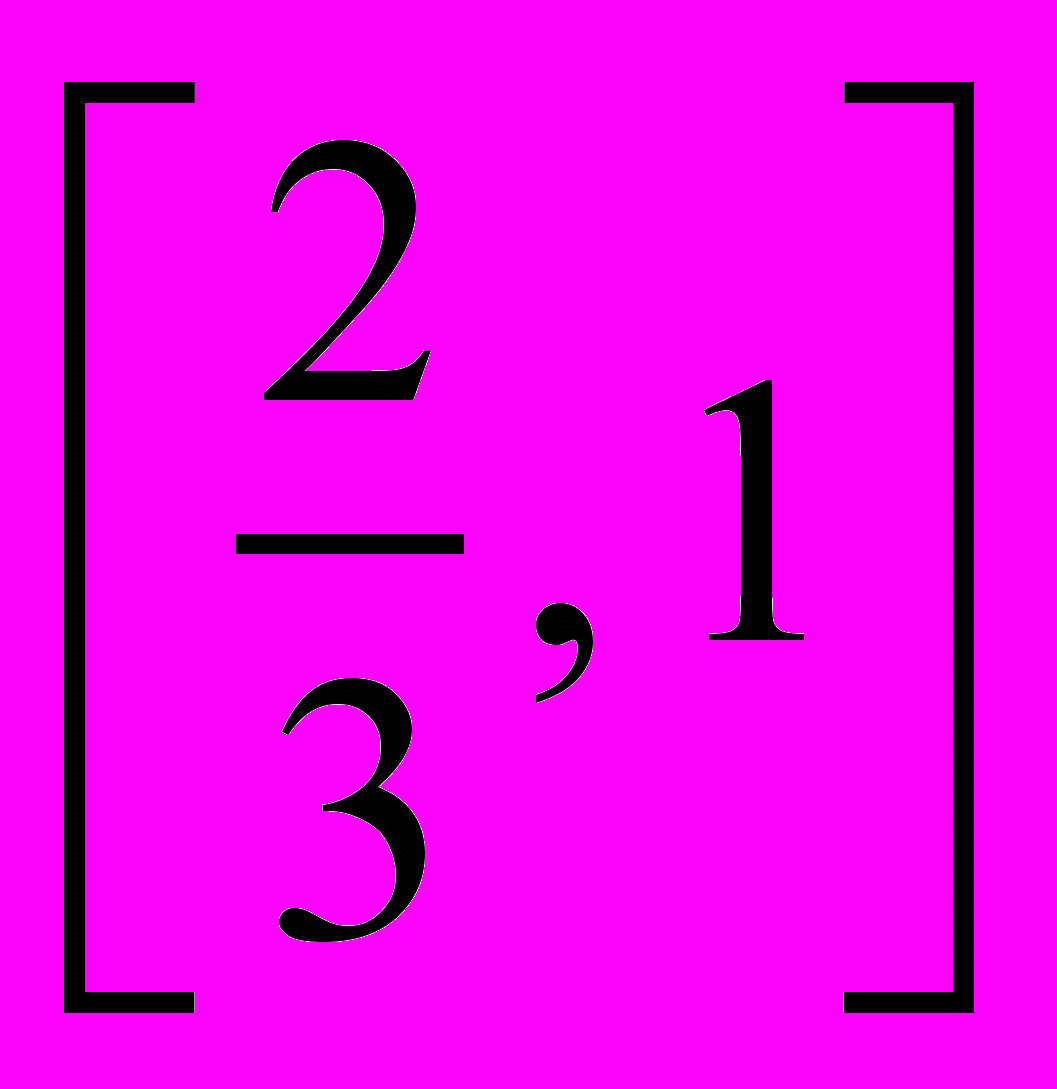 .
.Требуется дать числовой ответ.
В ящике 3 белых, 4 черных и
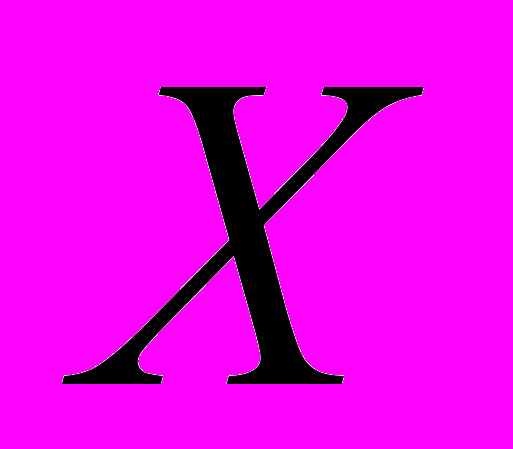 красных шаров. Вероятность вытащить случайным образом белый шар равна 0.2. Тогда вероятность вытащить красный шар равна
красных шаров. Вероятность вытащить случайным образом белый шар равна 0.2. Тогда вероятность вытащить красный шар равнаПримеры задач и вопросов теста №2.
Требуется дать ответ ДА или НЕТ.
Закон распределения двумерной дискретной случайной величины
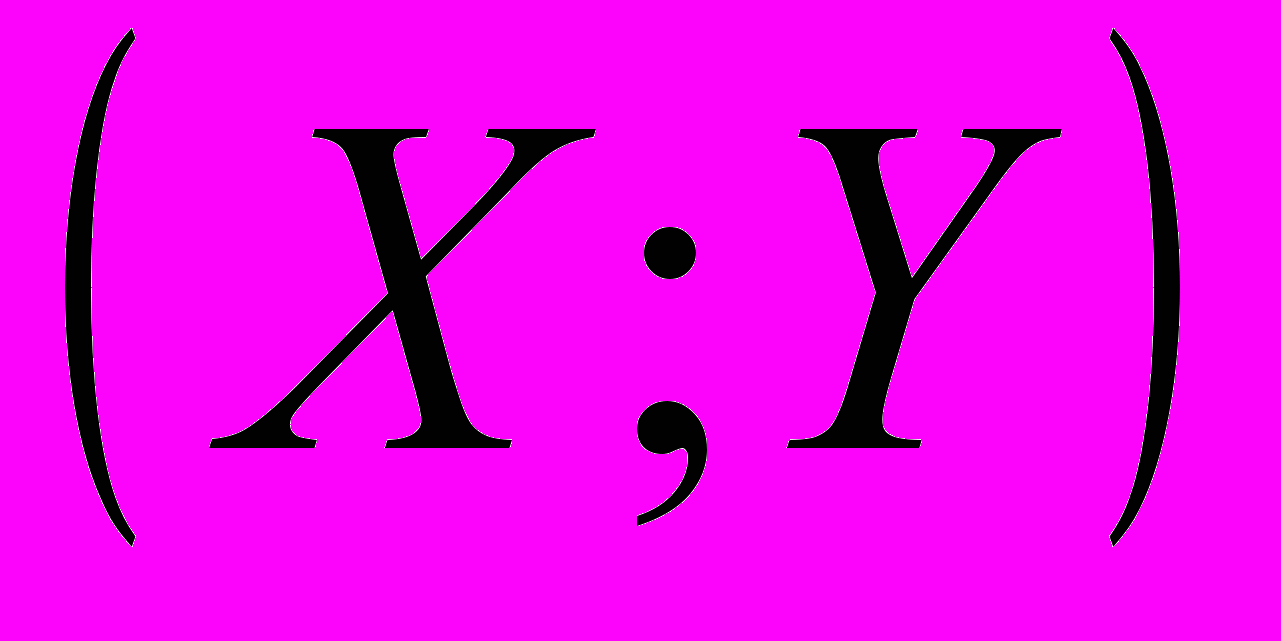 имеет вид:
имеет вид: 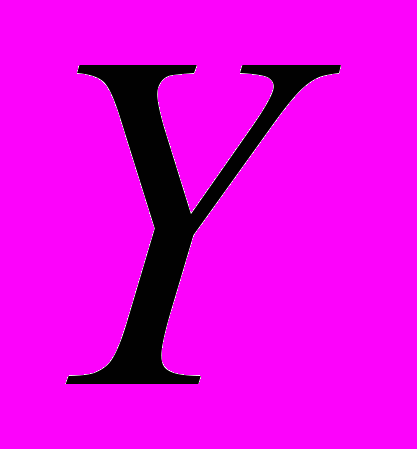 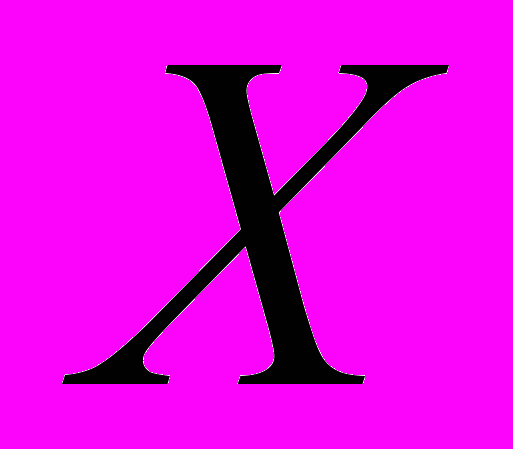 | 0 | 1 |
| -1 | 0.12 | 0.28 |
| 1 | 0.18 | 0.42 |
Тогда верны следующие утверждения:
Случайные величины
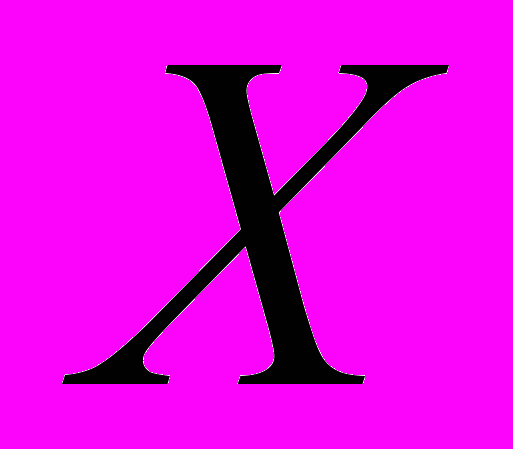 и
и 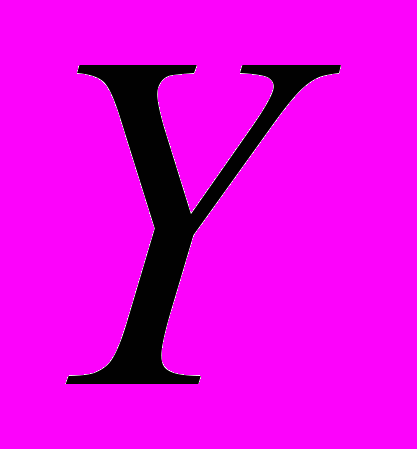 независимы.
независимы.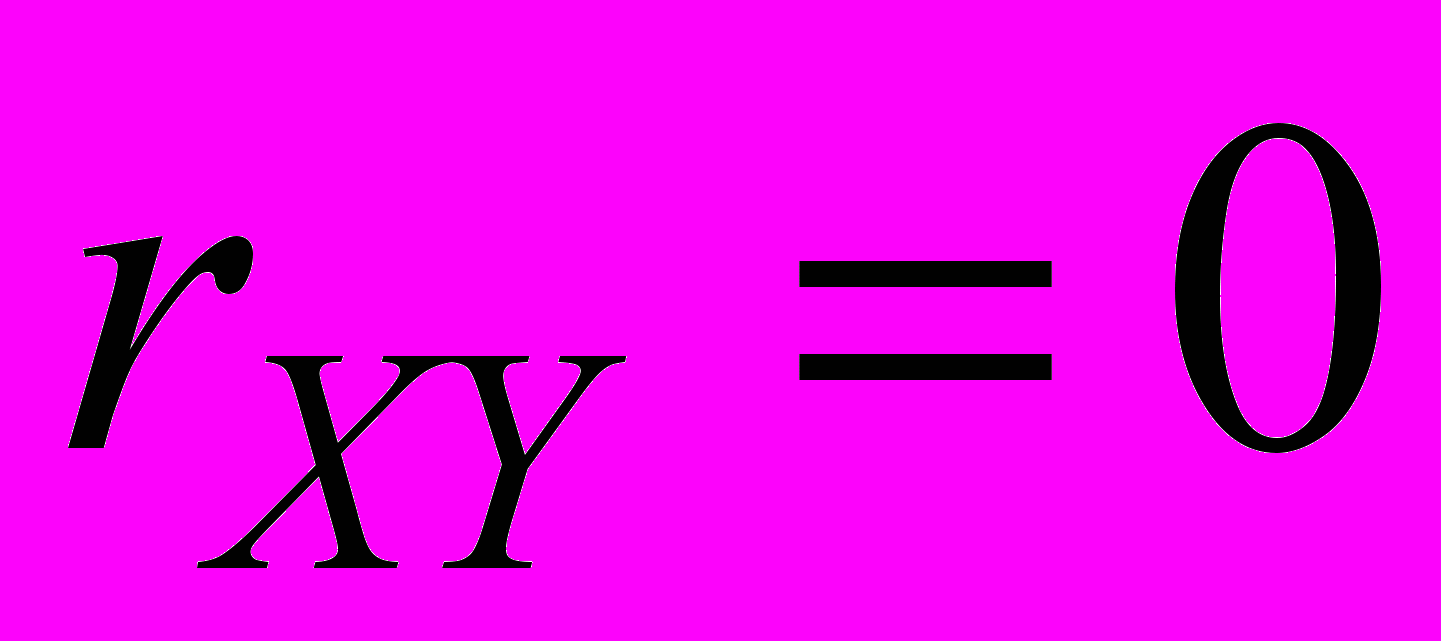 .
.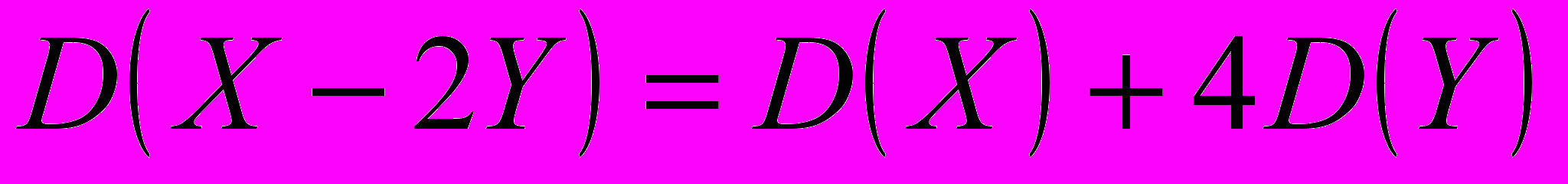 .
.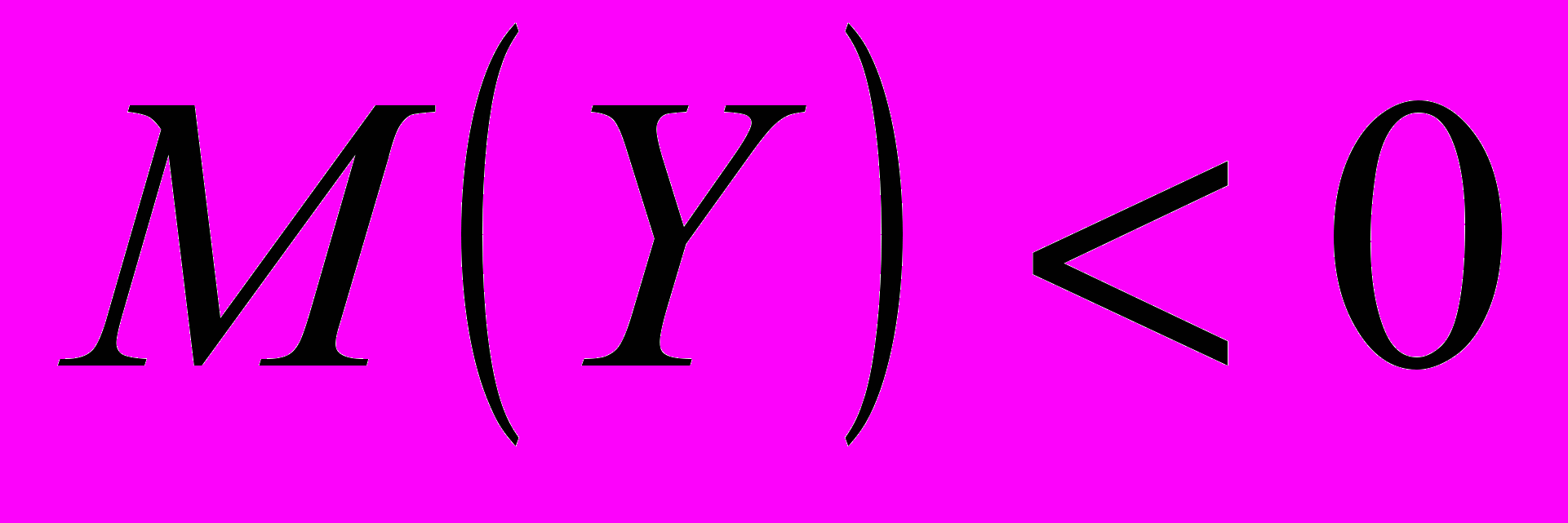 .
.Требуется выбрать правильный ответ.
Пусть
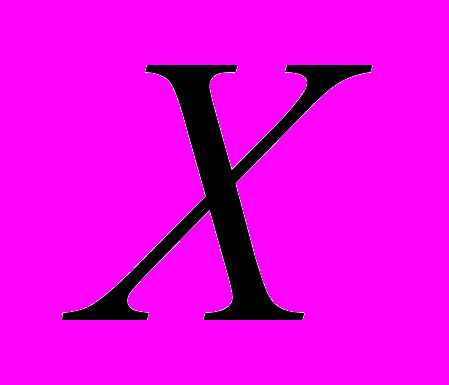 - нормально распределенная случайная величина с математическим ожиданием
- нормально распределенная случайная величина с математическим ожиданием 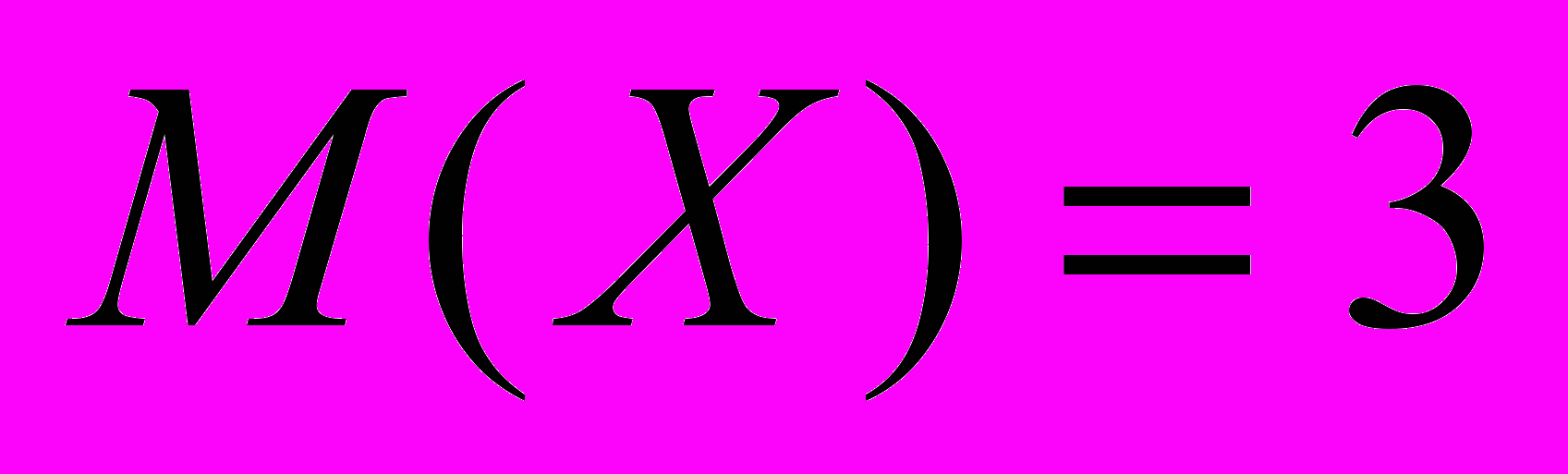 , дисперсией
, дисперсией 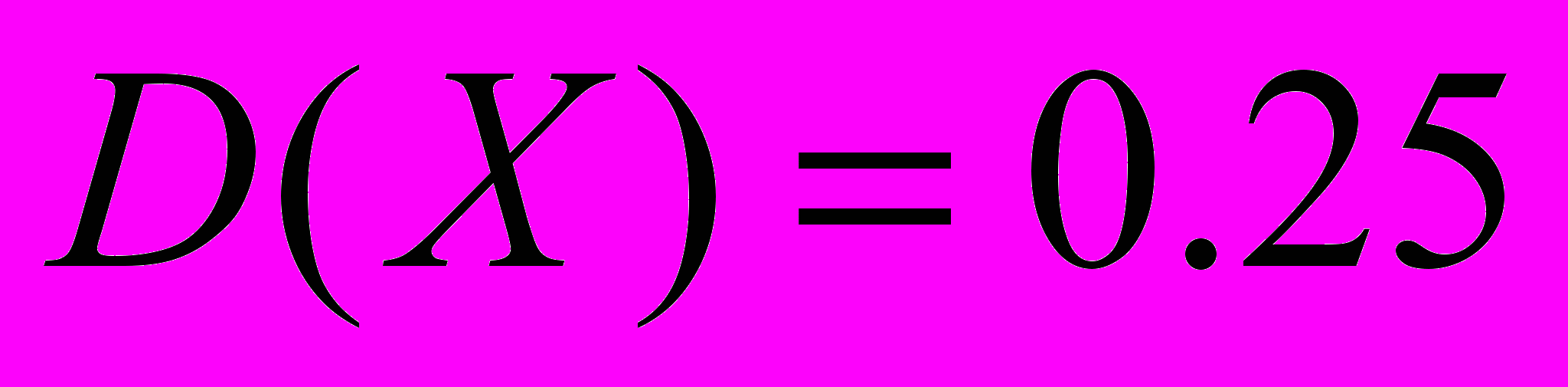 . Пусть
. Пусть 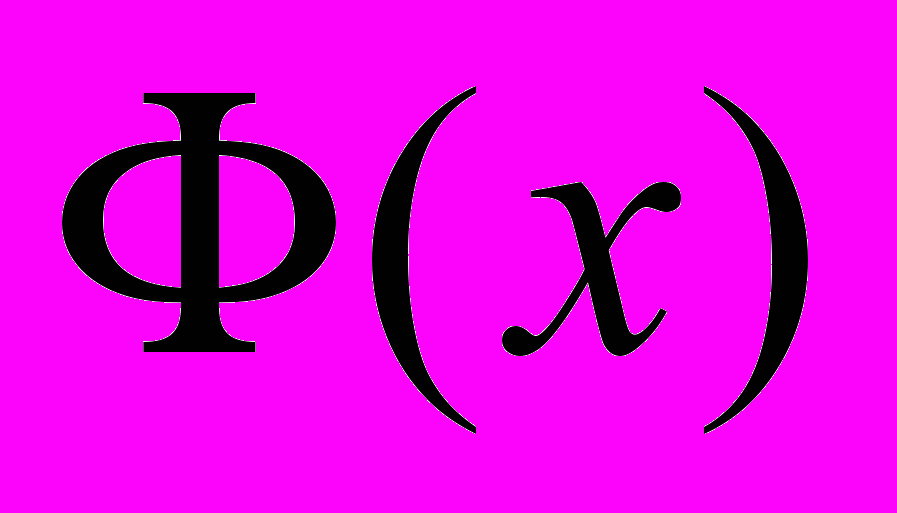 - функция Лапласа. Тогда вероятность попадания
- функция Лапласа. Тогда вероятность попадания 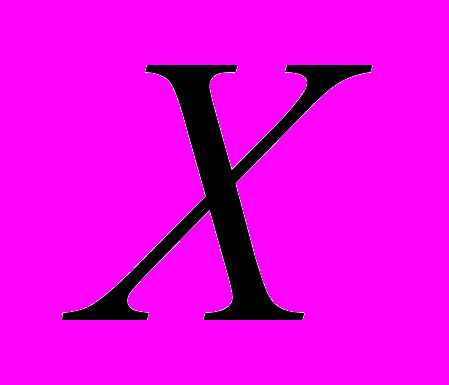 в интервал
в интервал 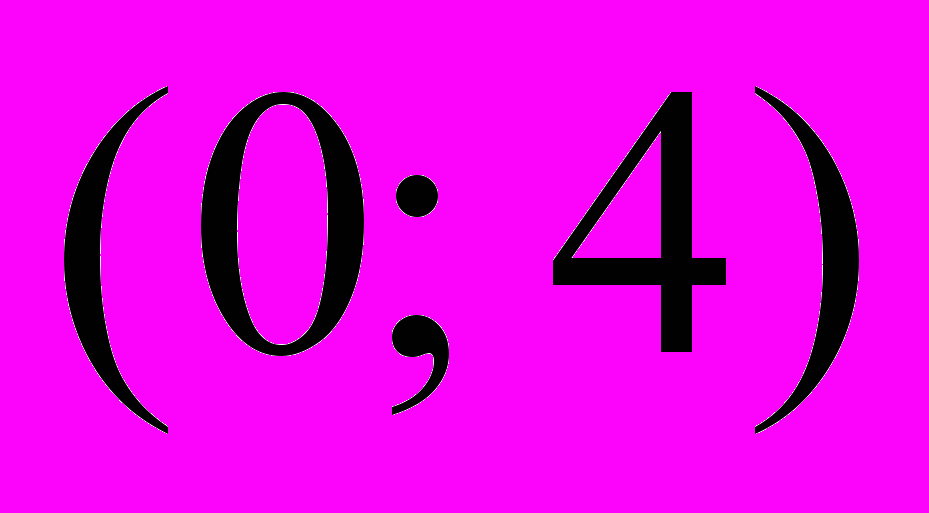 равна …
равна …А.
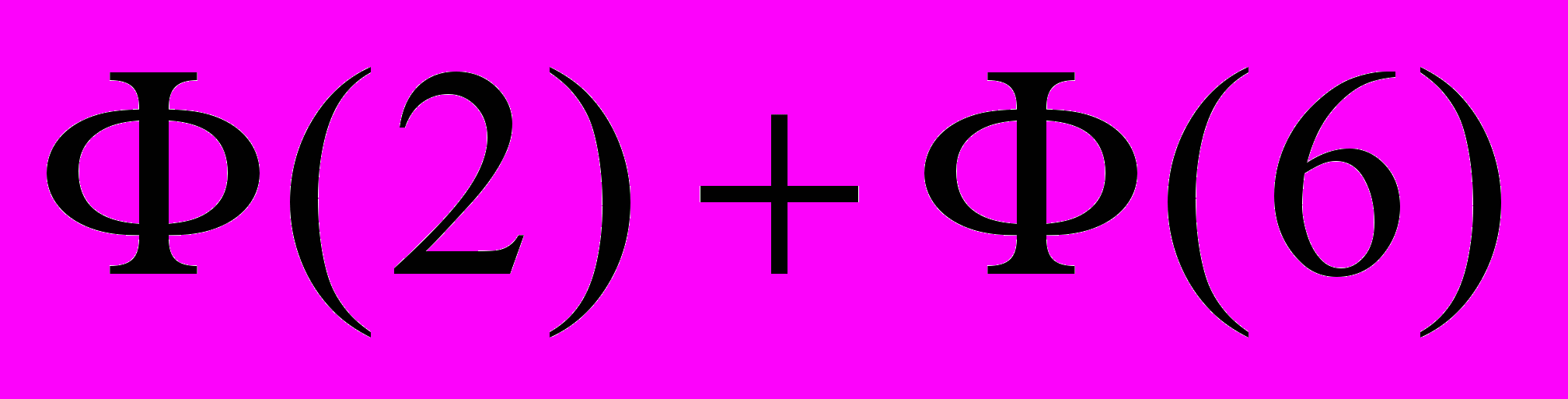 . Б.
. Б. 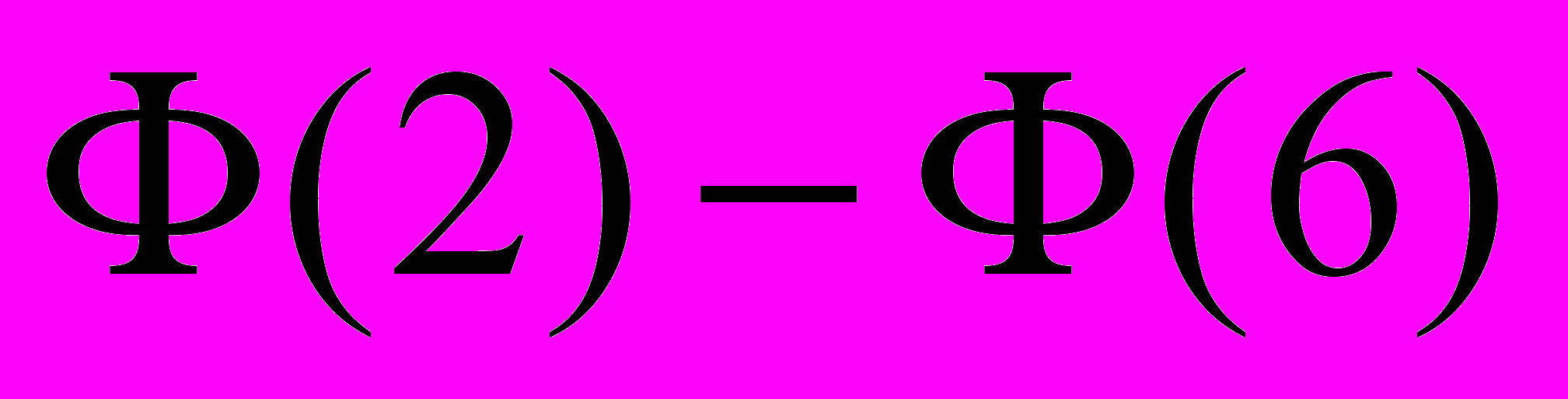 . В.
. В. 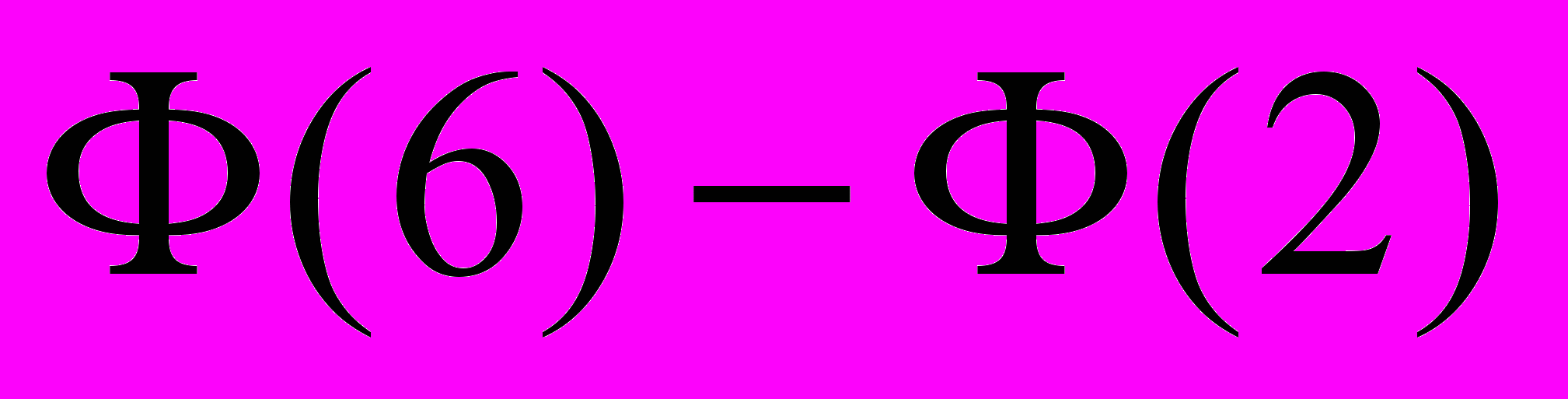 . Г.
. Г. 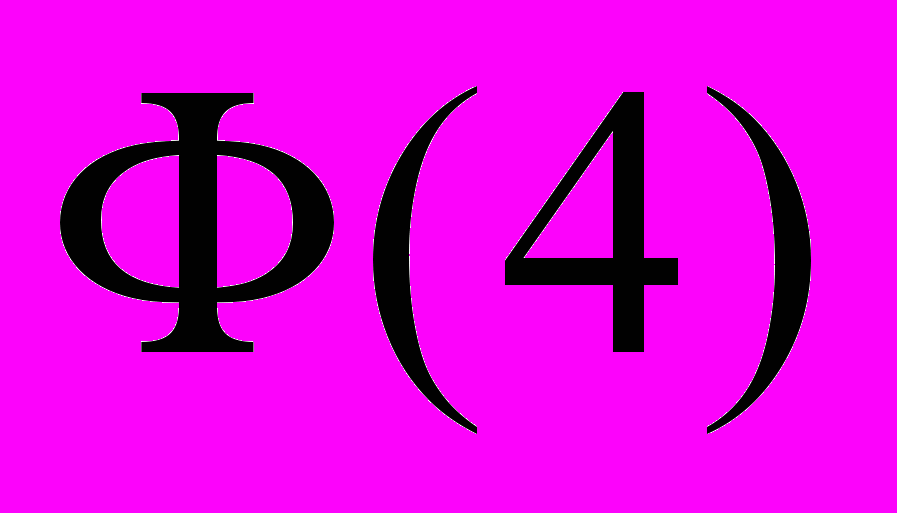 .
.Требуется дать числовой ответ.
Дана функция распределения непрерывной случайной величины
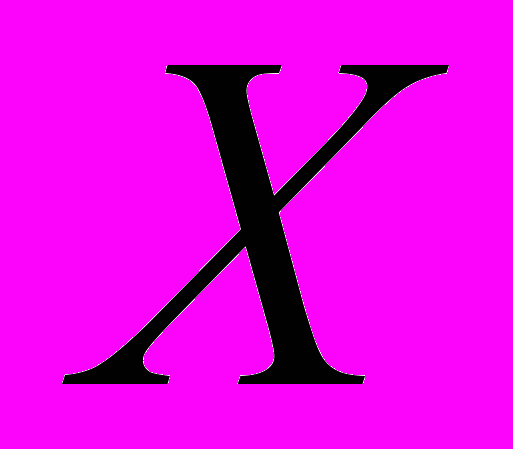 :
: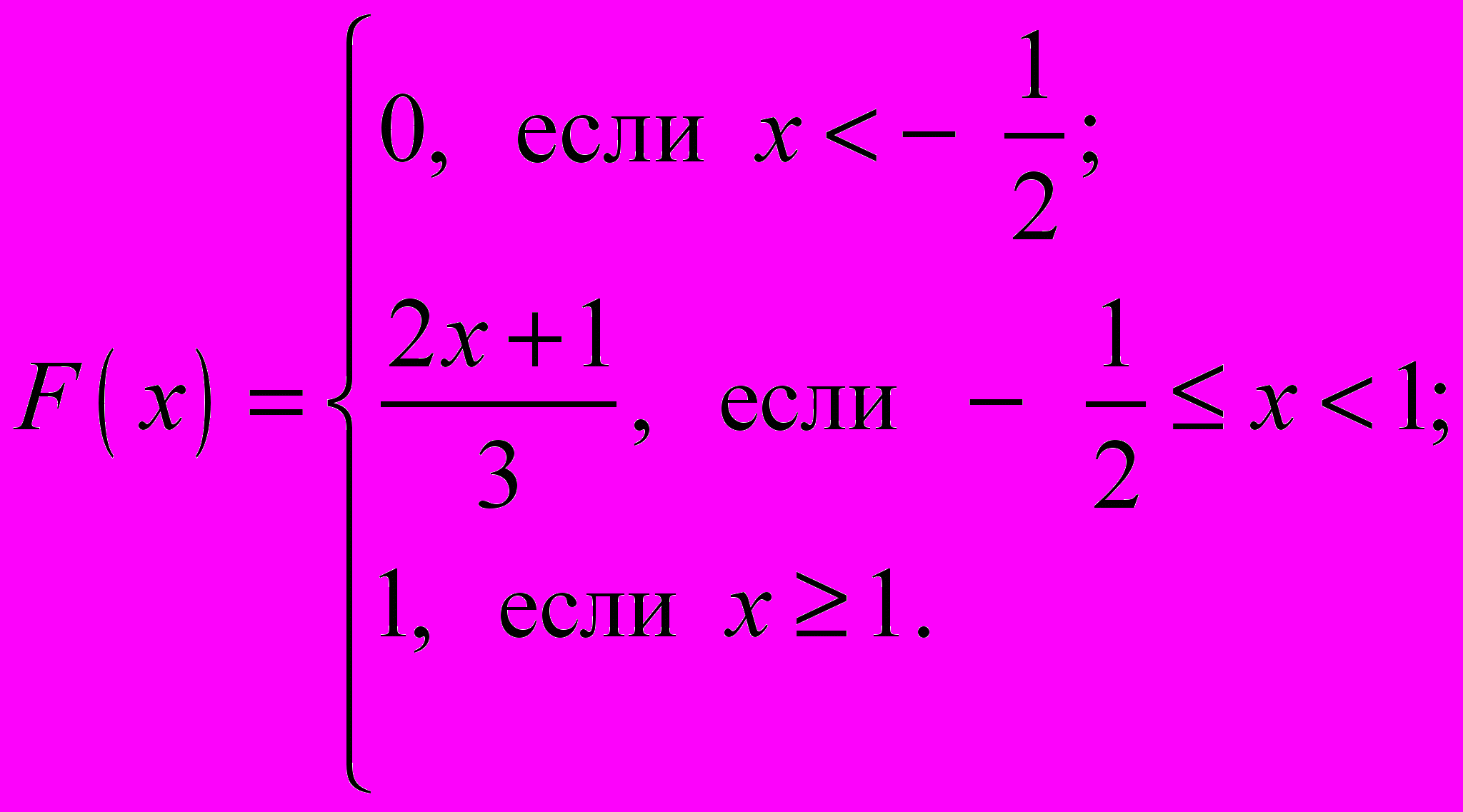
Найти
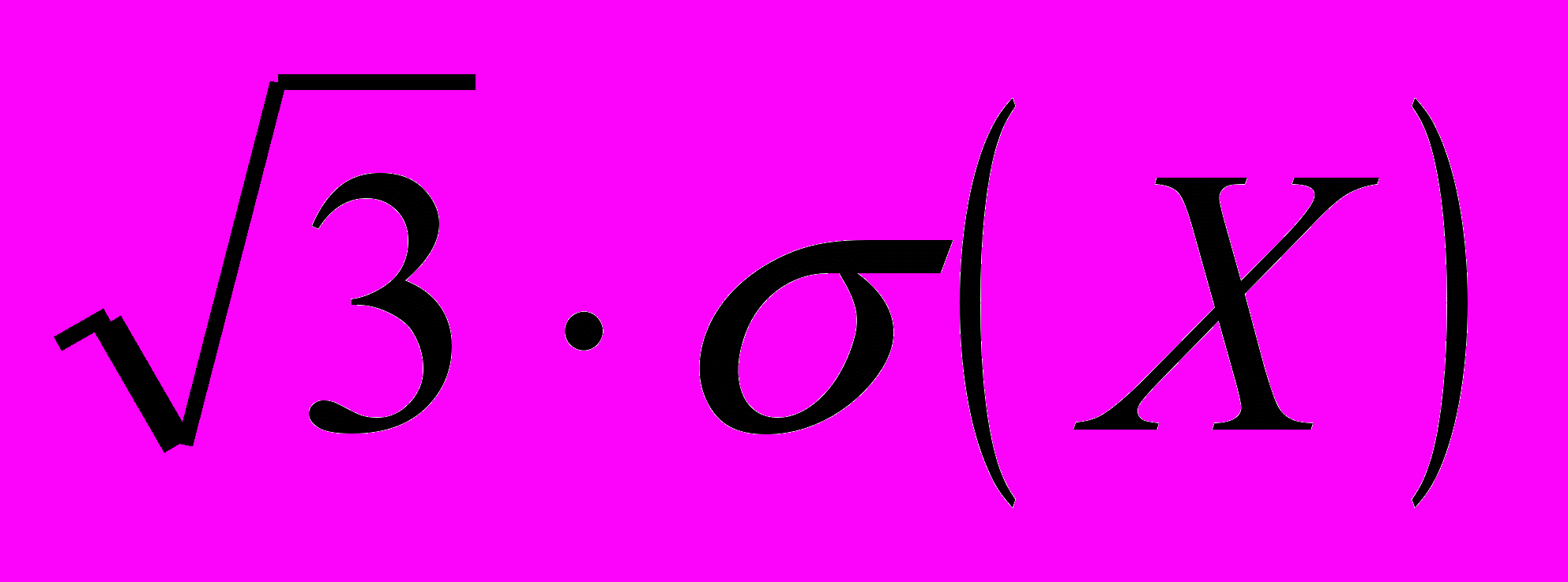 .
.Примеры задач контрольной работы.
Задача №1. Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Задача №2. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна
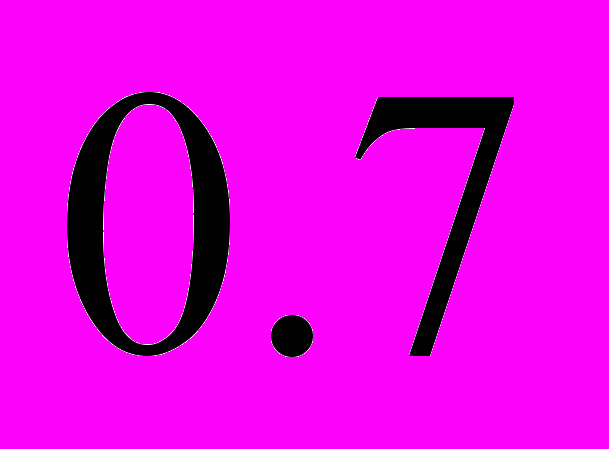 , а для второго -
, а для второго - 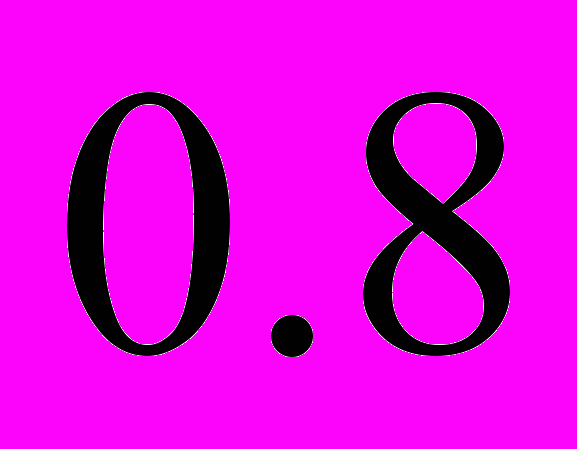 . Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.
. Найти вероятность того, что при одном залпе в мишень попадет только один из стрелков.
Задача №3. В каждой из тех урн содержится
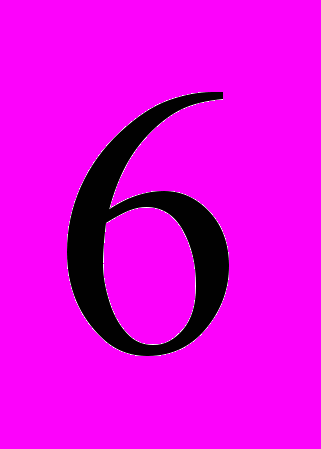 черных и
черных и 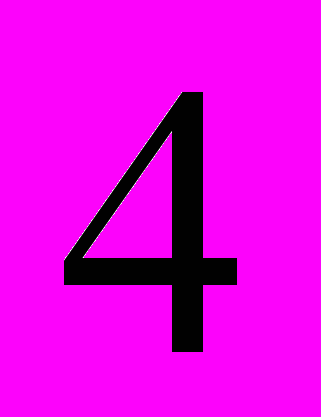 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что, наудачу извлеченный из третьей урны, окажется белым.
белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найти вероятность того, что, наудачу извлеченный из третьей урны, окажется белым.
Задача №4. Три стрелка произвели залп, причем две пули попали в мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятность попадания в мишень первым, вторым и третьим стрелками соответственно равны
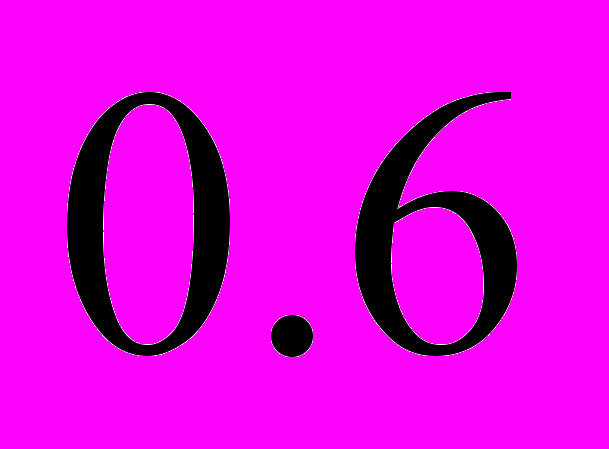 ,
, 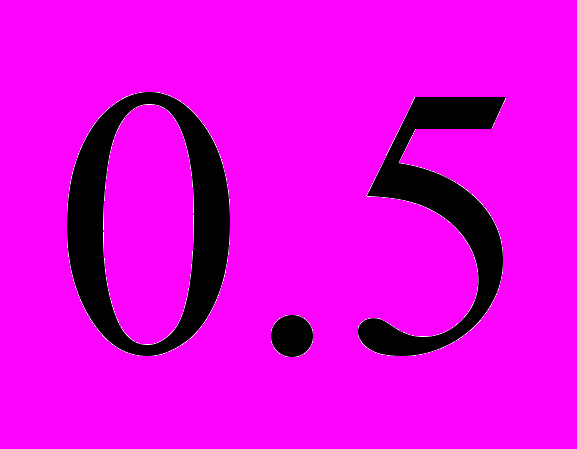 и
и 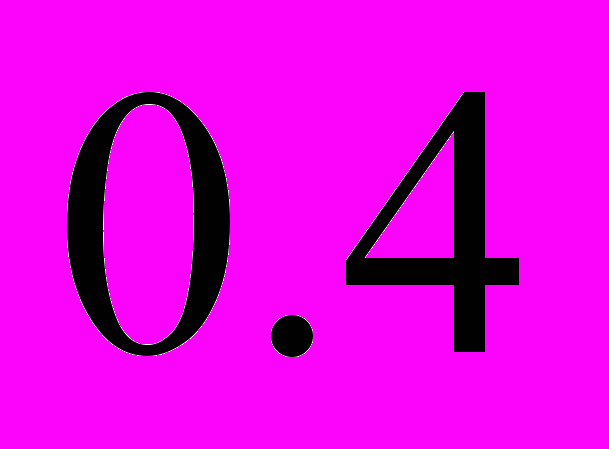 .
.
Задача №5. Монету бросают пять раз. Найти вероятность того, что «герб» выпадет: 1) менее дух раз; 2)не менее двух раз.

Пример индивидуального задания.
Из генеральной совокупности извлечена выборка объема
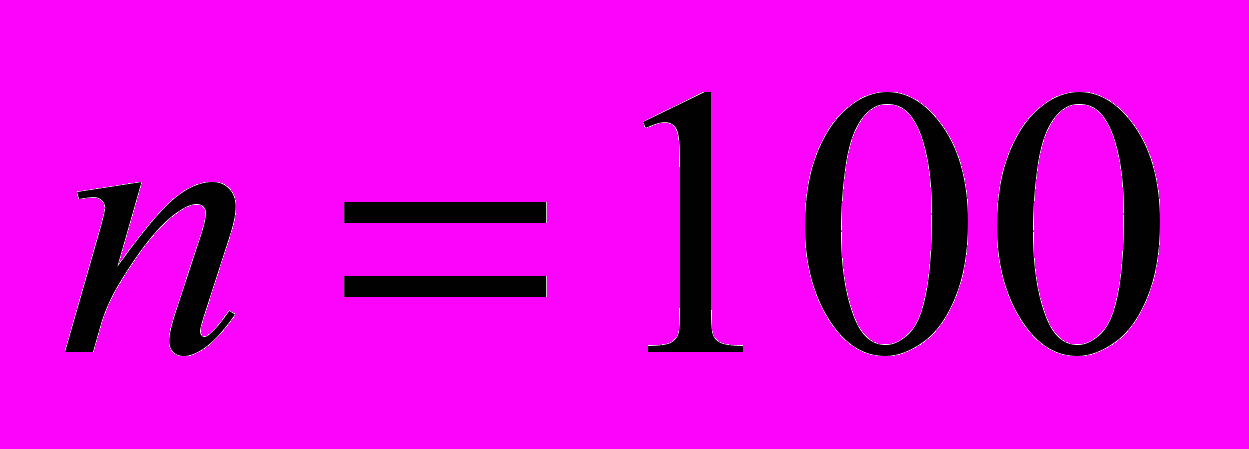 . Результаты представлены в виде интервального ряда.
. Результаты представлены в виде интервального ряда.| интервал | 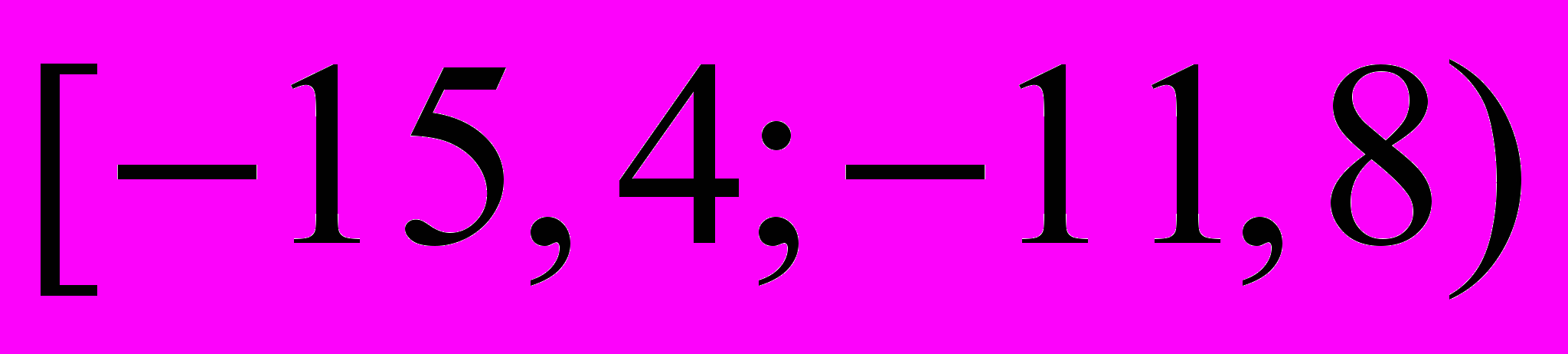 | 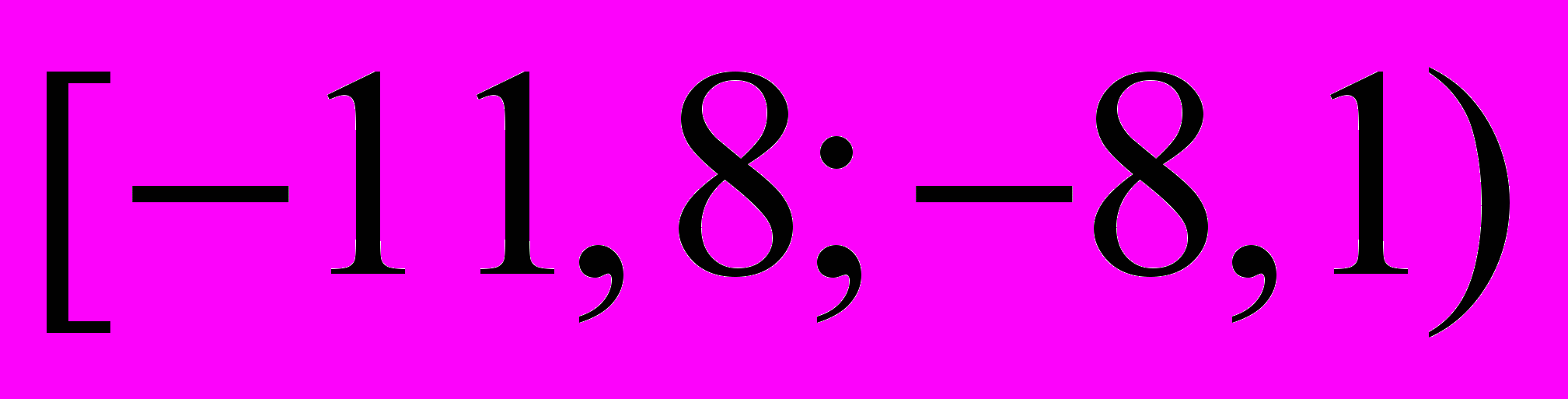 | 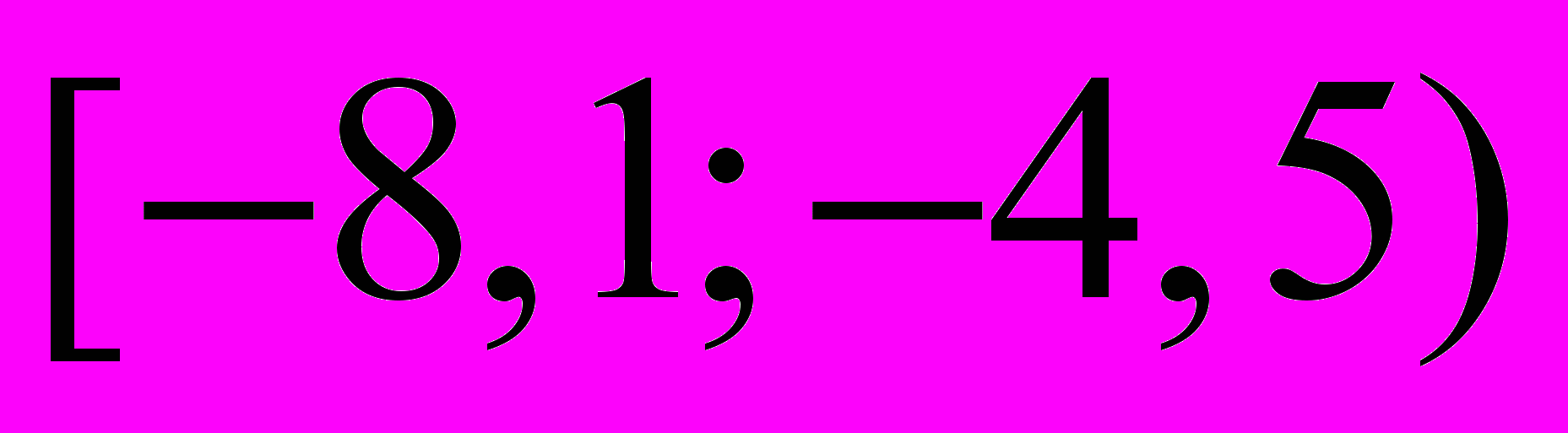 | 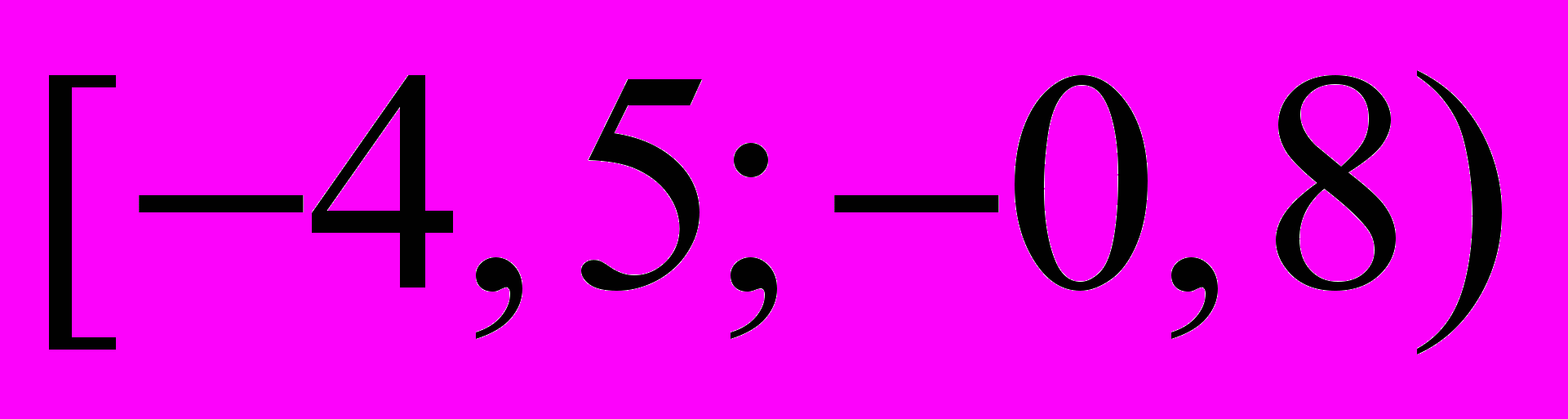 | 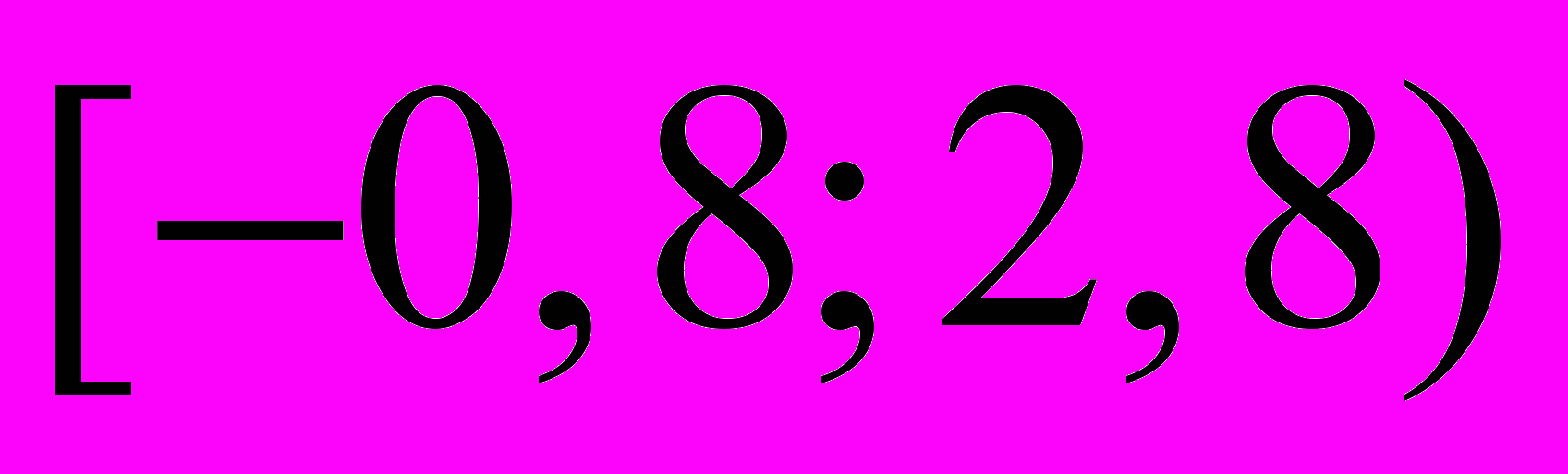 |
| частота | 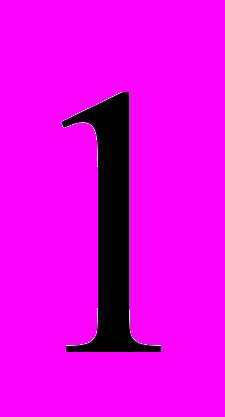 | 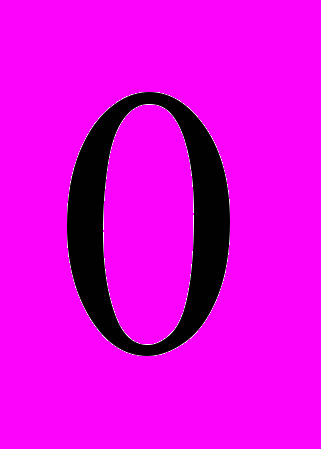 | 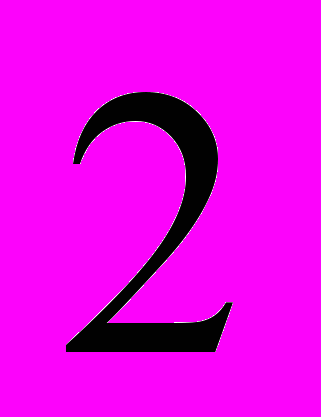 | 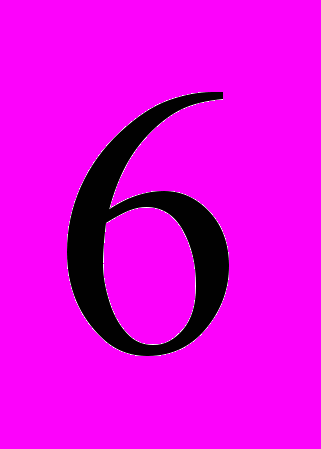 | 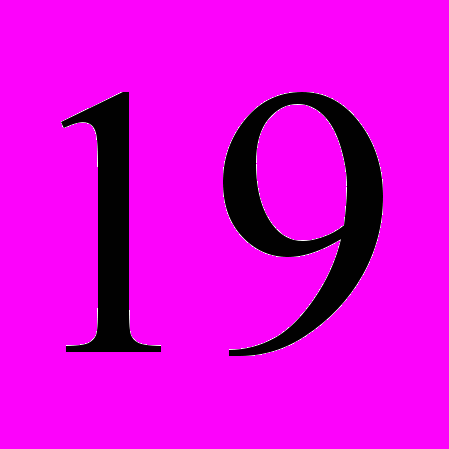 |
| интервал | 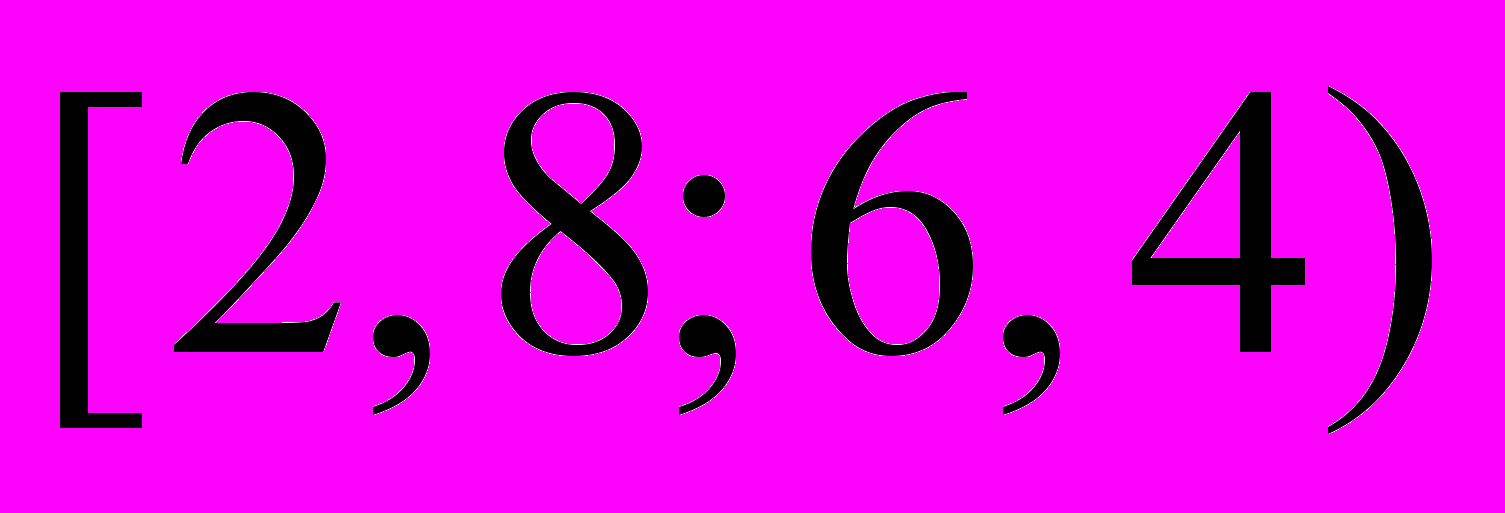 | 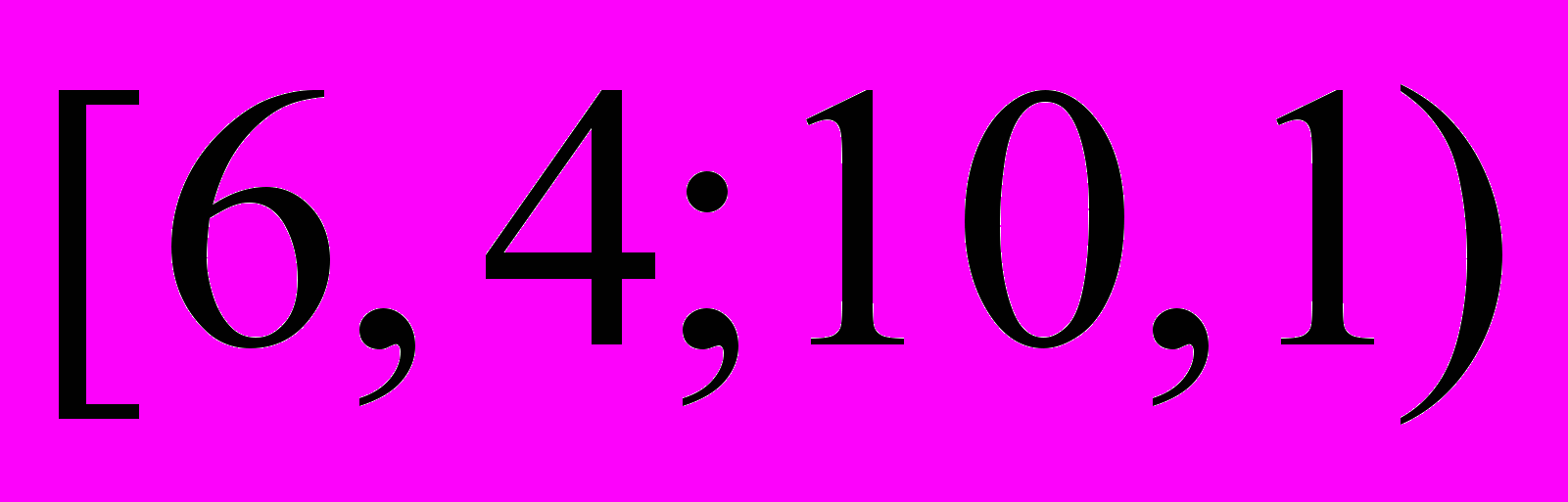 |  | 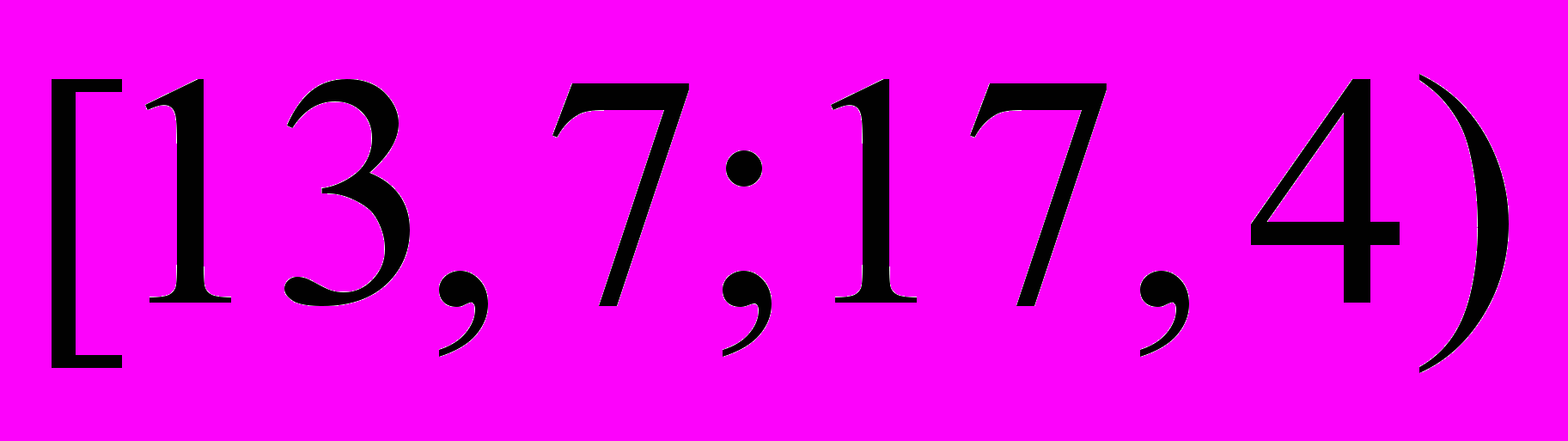 | 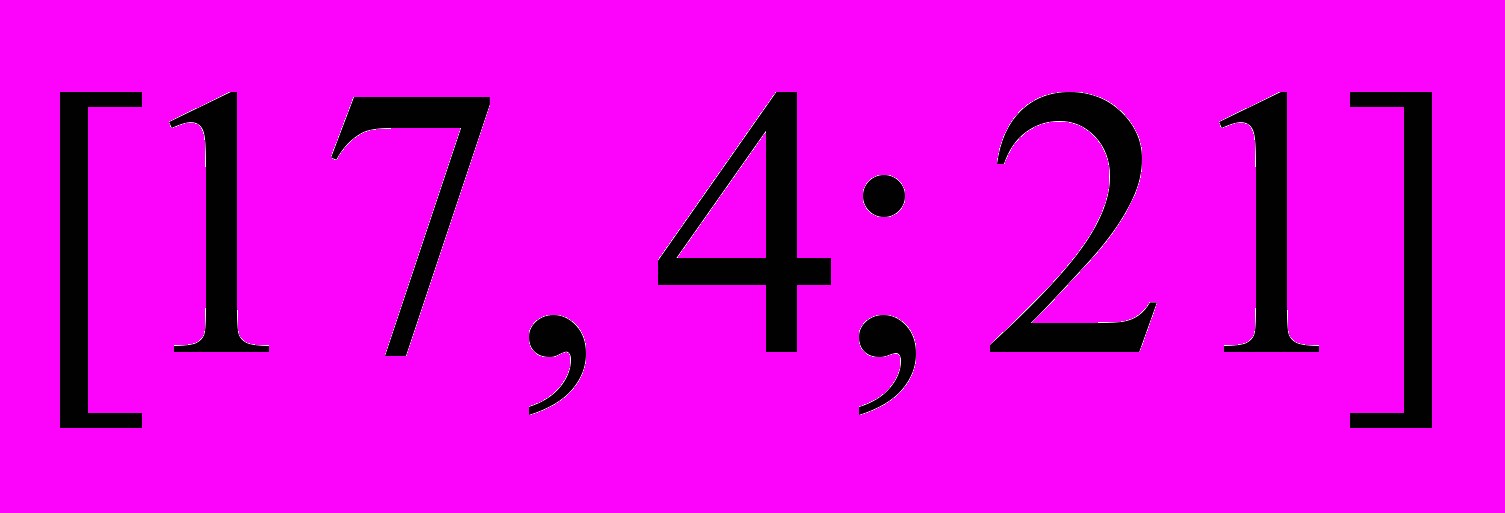 |
| частота | 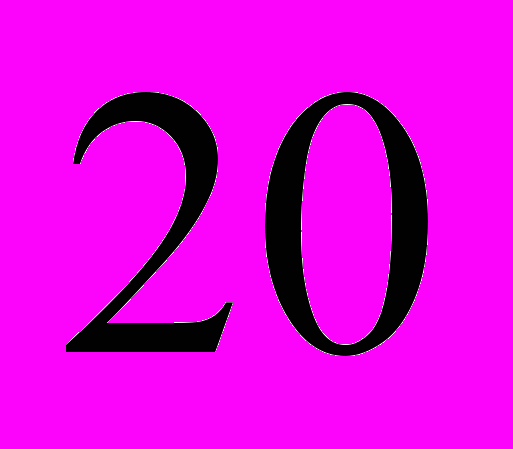 | 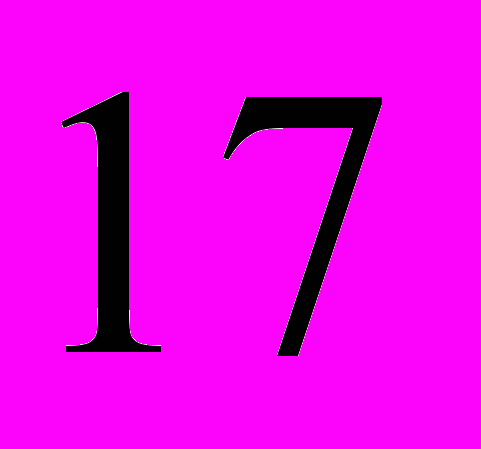 | 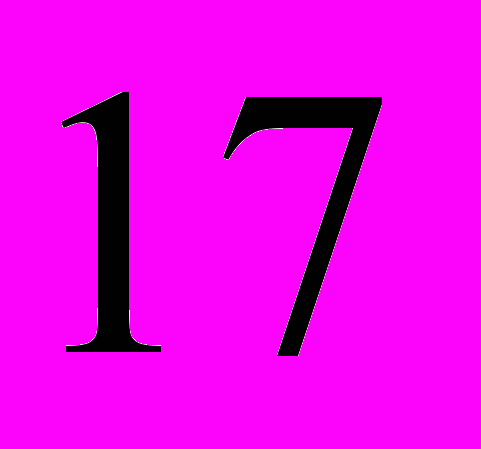 | 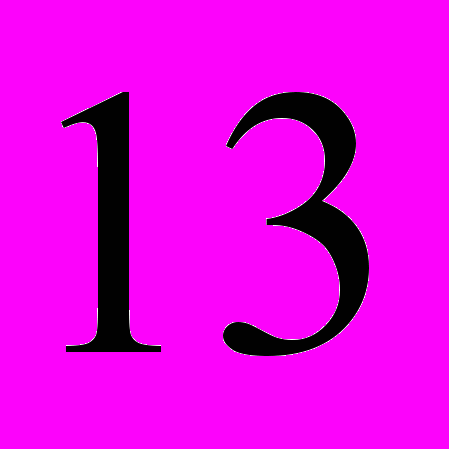 | 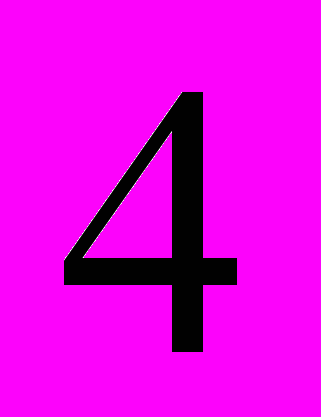 |
1. Построить гистограмму и график выборочной функции распределения.
2. Найти выборочные оценки генеральной средней и генерального СКО.
3. Используя критерий Пирсона, проверить гипотезу о нормальном распределении изучаемого признака в генеральной совокупности, выбрав уровень значимости
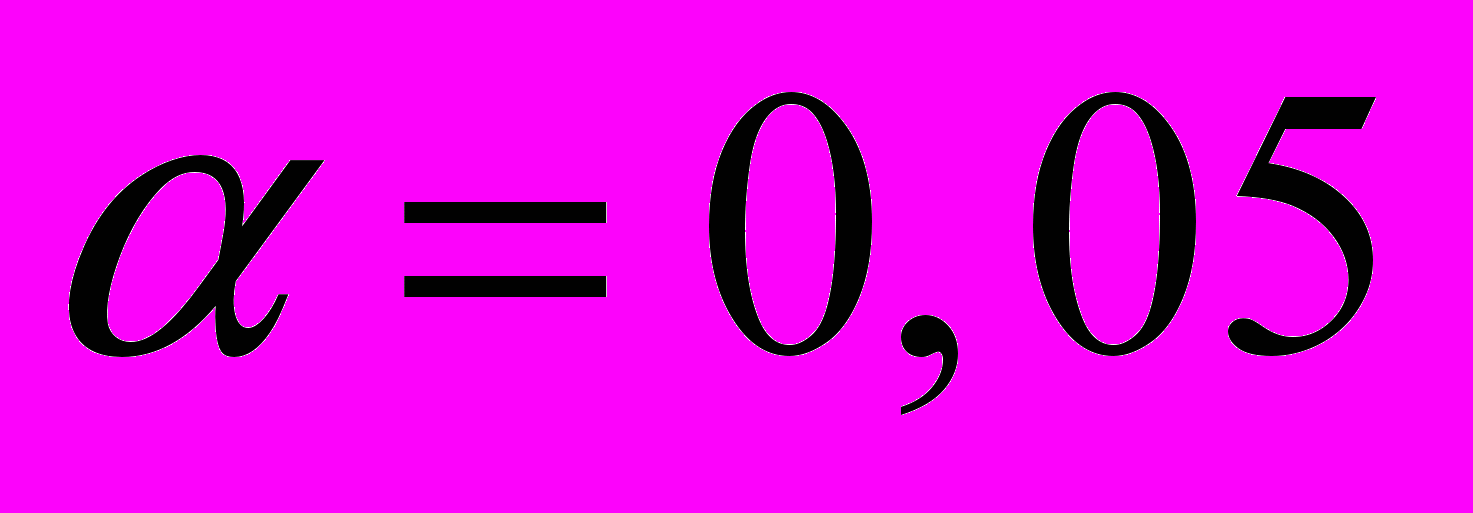 .
.4. Считая распределение признака в генеральной совокупности нормальным с генеральным СКО
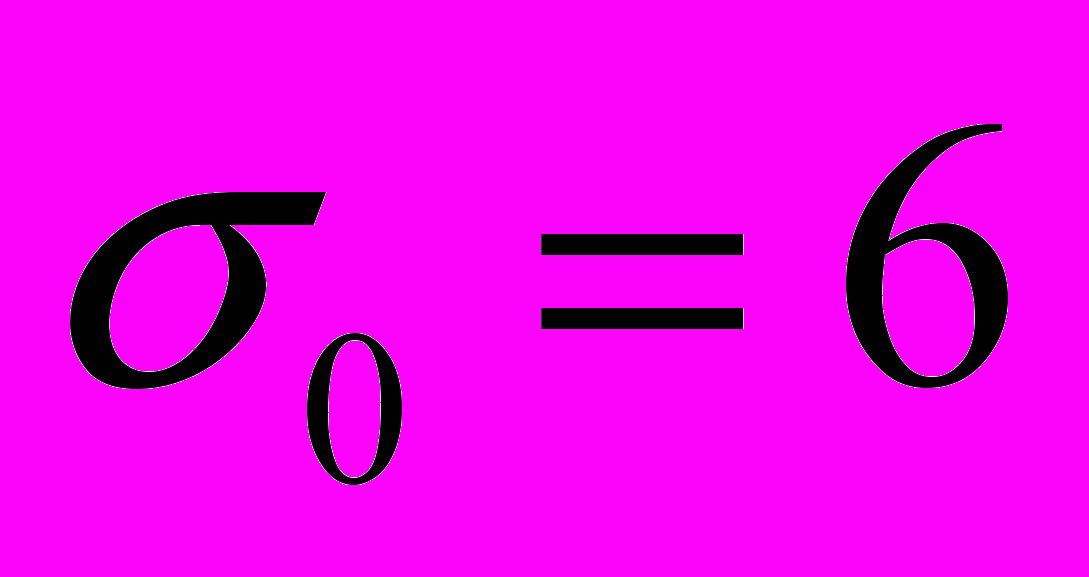 , а) построить доверительный интервал для генеральной средней, выбрав значение доверительной вероятности ; б) проверить гипотезу о равенстве генерального среднего заданному значению
, а) построить доверительный интервал для генеральной средней, выбрав значение доверительной вероятности ; б) проверить гипотезу о равенстве генерального среднего заданному значению 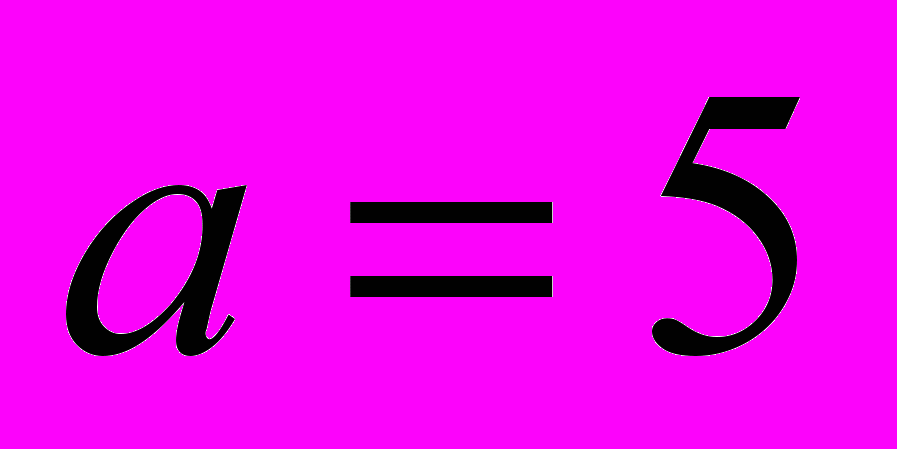 , выбрав
, выбрав 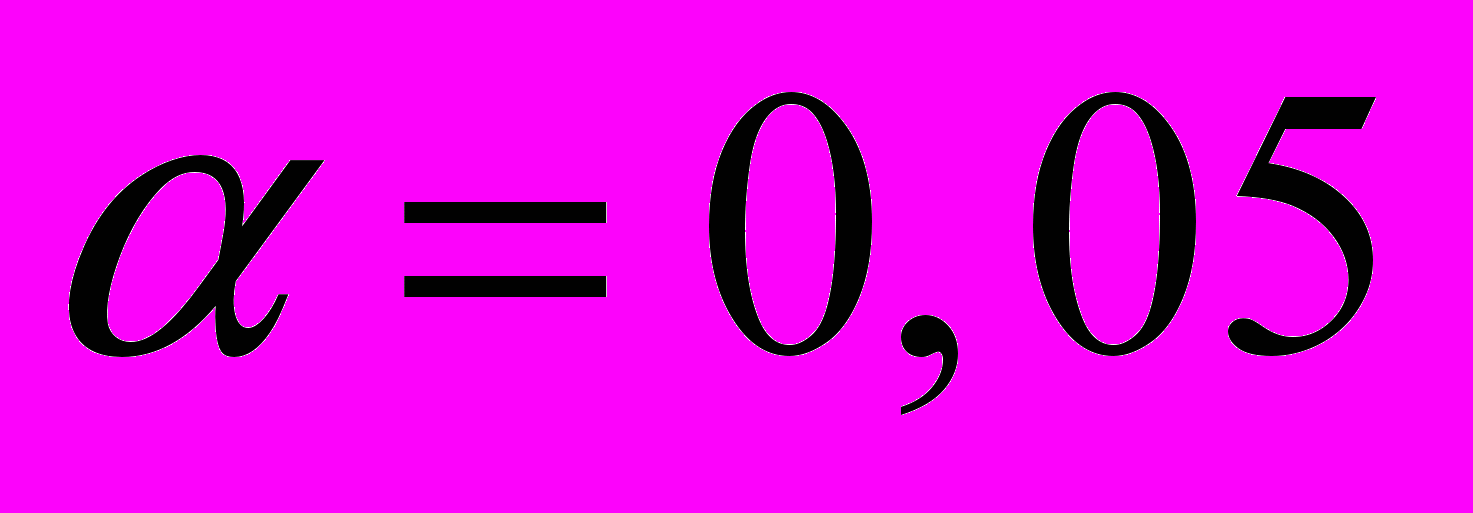 .
.Разработчики:
СПбГУЭФ доцент В. Г. Дмитриев
СПбГУЭФ профессор Г. В. Савинов
Эксперты:
ЭМИ РАН директор Л. А. Руховец
СПбГМТУ профессор В. Б. Хазанов
