Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика» по профилям «Финансы и кредит», «Мировая экономика», «Налоги и налогообложение»
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика», 108.11kb.
- Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика», 103.07kb.
- Рабочая программа учебной дисциплины Для бакалавров направления 080100. 62 «Экономика», 686.98kb.
- Программа «Экономика и финансы» вопросы из курсов «Финансы и кредит», «Налоги и налогообложение»;, 23.41kb.
- Профессиональные компетенции бакалавра по направлению «Экономика» по профилям: «Финансы, 51.78kb.
- Рабочая программа учебной дисциплины Для направления 080100. 62 «Экономика» (программа, 562.39kb.
- Программа дисциплины «Налоги и налогообложение» для направления 080100. 62 «Экономика», 462.63kb.
- Основная образовательная программа подготовки бакалавра по направлению 080100 Экономика, 143.16kb.
- Программа дисциплины «Корпоративные финансы» для направления 080100. 62 «Экономика», 309.78kb.
- Методические указания к практическим занятиям для студентов специальности 080102 «Мировая, 444.73kb.
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве
Российской Федерации»
Кафедра «Теория вероятностей и математическая статистика»
С.А. Зададаев
МАТЕМАТИЧЕСКАЯ ЛОГИКА
И ВЕРОЯТНОСТНЫЕ ПРОСТРАНСТВА
Рабочая программа учебной дисциплины
Для бакалавров направления 080100.62 «Экономика»
по профилям «Финансы и кредит», «Мировая экономика»,
«Налоги и налогообложение»
М
осква 2010 Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«ФинансовЫЙ УНИВЕРСИТЕТ при Правительстве
Российской Федерации»
Кафедра «Финансовый менеджмент»
утверждаю
Ректор
__________ М.А. Эскиндаров
_______ ___________ 2010 г.
С.А. Зададаев
МАТЕМАТИЧЕСКАЯ ЛОГИКА
И ВЕРОЯТНОСТНЫЕ ПРОСТРАНСТВА
Рабочая программа учебной дисциплины
Для бакалавров направления 080100.62 «Экономика»
по профилям «Финансы и кредит», «Мировая экономика»,
«Налоги и налогообложение»
Утверждено кафедрой «Теория вероятностей и математическая
статистика», протокол № ___ от ___ ___________ 2010 г.
М
осква 2010 УДК
ББК
Рецензент: Т.Л.Мелехина, доцент кафедры «Теория вероятностей и математическая статистика»
С.А. Зададаев
«Математическая логика и вероятностные пространства». Программа дисциплины для студентов, обучающихся по направлению «Экономика» по профилям «Финансы и кредит», «Мировая экономика», «Налоги и налогообложение» (программа подготовки бакалавров) – очная форма обучения.– М.: ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», кафедра «Теория вероятностей и математическая статистика», 2010. - 10 с.
Дисциплина «Математическая логика и вероятностные пространства» является специальной дисциплиной по выбору вариативной части дисциплин ФГОС ВПО по направлению 080100.62 «Экономика» по профилям «Финансы и кредит», «Мировая экономика», «Налоги и налогообложение» Приведены организационный учебно-методический раздел, программа дисциплины и
перечень рекомендуемой литературы. УДК
ББК
Учебное издание
Сергей Алексеевич Зададаев
МАТЕМАТИЧЕСКАЯ ЛОГИКА
И ВЕРОЯТНОСТНЫЕ ПРОСТРАНСТВА
Рабочая программа учебной дисциплины
Компьютерный набор, верстка: Зададаев С.А.
Формат 60х90/16. Гарнитура Times New Roman
Усл.п.л.1,1. Изд. № -2010. Тираж ___ экз.
Отпечатано в ФГОУ ВПО «Финансовый университет при
Правительстве Российской Федерации»
С.А. Зададаев, 2010
ФГОБУ ВПО «Финансовый университет при Правительстве Российской Федерации», 2010Содержание
- Цели и задачи дисциплины………………………………………...4
- Место дисциплины в структуре ООП……………………………..4
- Требования к результатам освоения дисциплины………………..5
- Объем дисциплины и виды учебной работы……………………..7
- Содержание разделов дисциплины………………………………..8
- Учебно-методическое и информационное обеспечение
дисциплины…………………………………………………………9
1. Цели и задачи дисциплины
Цель дисциплины –
1. Получение базовых знаний и формирование основных навыков по комбинаторике и математической логике, необходимых для понимания основ теории вероятностей, а также, формирующих общую культуру логических рассуждений.
2. Развитие комбинаторного и логического мышления с формированием элементарной алгебраической подготовки, необходимой для понимания основ математической логики и её применения.
Задача дисциплины –
В результате изучения дисциплины «Математическая логика и вероятностные пространства» студенты должны владеть основными математическими понятиями курса; уметь использовать теоретический и вычислительный аппарат для решения соответствующих прикладных задач экономики, уметь решать типовые задачи, иметь навыки работы со специальной математической литературой.
2. Место дисциплины в структуре ООП
Дисциплина «Математическая логика и вероятностные пространства» является специальной дисциплиной по выбору вариативной части дисциплин Федерального государственного образовательного стандарта высшего профессионального образования (ФГОС ВПО) по направлению 080100.62 «Экономика» (бакалавриат).
Изучение дисциплины «Математическая логика и вероятностные пространства» основывается на базе знаний, полученных студентами на первом курсе в ходе освоения дисциплин «Линейная алгебра» и «Математический анализ» математического цикла базовых дисциплин.
Дисциплина «Математическая логика и вероятностные пространства» изучается на втором году обучения, закладывает фундамент для понимания теории вероятностей, математической и экономической статистики.
3. Требования к результатам освоения дисциплины
В совокупности с другими дисциплинами базовой части математического цикла ФГОС ВПО дисциплина «Математическая логика и вероятностные пространства» обеспечивает инструментарий формирования следующих профессиональных компетенций бакалавра экономики:
- владение культурой мышления, способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения (ОК-1);
- способность собирать и анализировать исходные данные, необходимые для расчёта экономических и социально-экономических показателей, характеризующих деятельность хозяйствующих субъектов (ПК-1);
- способность на основе типовых методик и действующей нормативно-правовой базы рассчитывать экономические и социально-экономические показатели, характеризующие деятельность хозяйствующих субъектов (ПК-2);
- способность выполнять расчёты, необходимые для составления экономических разделов планов. Обосновывать их и представлять результаты работы в соответствии с принятыми в организации стандартами (ПК-3);
- способность осуществлять сбор, анализ и обработку данных, необходимых для решения поставленных экономических задач (ПК-4);
- способность выбирать инструментальные средства для обработки экономических данных в соответствии с поставленной задачей, анализировать результаты расчётов и обосновывать полученные выводы (ПК-5).
В результате освоения содержания дисциплины «Математическая логика и вероятностные пространства» студент должен:
знать
- основы комбинаторики и математической логики, необходимые для решения финансовых и экономических задач;
уметь
- применять комбинаторные методы и формально-логическое мышление для решения экономических задач;
владеть
- навыками применения современного математического инструментария для решения экономических задач;
- методикой построения, анализа и применения математических моделей для оценки состояния и прогноза развития экономических явлений и процессов (в части компетенций, соответствующих методам комбинаторики и математической логики).
4. Объём дисциплины и виды учебной работы
Общая трудоёмкость дисциплины составляет 1 зачётную единицу.
Вид промежуточной аттестации – зачет.
| Вид учебной работы | Часы | Семестры (II курса) |
| 4 | ||
| Общая трудоёмкость дисциплины | 72 | 72 |
| Аудиторные занятия | 34 | 34 |
| Лекции (Л) | 17 | 17 |
| Практические занятия (ПЗ) | 17 | 17 |
| Самостоятельная работа | 38 | 38 |
| В семестрах | 38 | 38 |
| В сессию / форма | - | - |
| | зачет |
5. Содержание разделов дисциплины
Раздел 1. Введение
Понятия множества и элемента. Схема свертки. Парадокс. Операции над множествами и их свойства: объединение, пересечение, дополнение, разность и симметрическая разность, декартово произведение. Диаграммы Эйлера-Венна.
-
Определение бинарного отношения. Свойства бинарных отношений: рефлексия, симметричность и транзитивность. Отношение порядка и эквивалентности. Теорема о разбиении.
Борелевские множества,
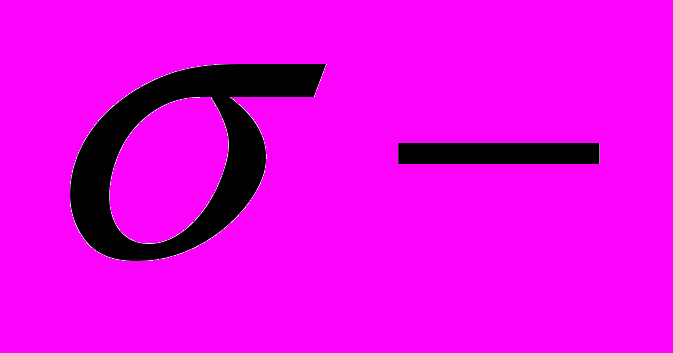алгебра. Аксиоматика вероятностных пространств.
Раздел 2. Математическая логика
2.1. Высказывания. Операции над высказываниями: конъюнкция, дизъюнкция, отрицание и импликация. Формулы алгебры высказываний. Таблицы истинности. Эквивалентность формул. Свойства логических операций, законы де-Моргана. Основные эквивалентности.
2.2. Элементы теории доказательств: принцип двойственности, система натурального вывода, логическое следование и принцип резолюции. Понятие выводимой (доказуемой) формулы.
2.3. Логика предикатов. Логические операции над предикатами. Кванторы общности и существования. Формулы логики предикатов и логические законы.
2.4. Двоичная арифметика. Булевы функции. Таблица двумерных булевых функций. Связь с логическими операциями над высказываниями. Теорема о разложение булевой функции по аргументу. Совершенные дизъюнктивные и конъюктивные нормальные формы.
2.5. Полные системы булевых функций. Важнейшие замкнутые классы булевых функций
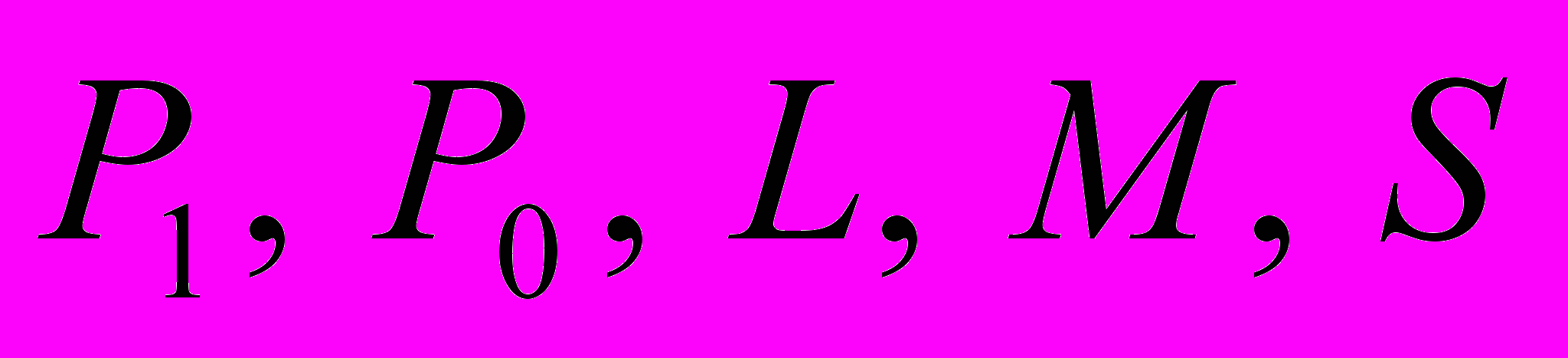. Теорема Поста о неполноте. Полнота класса, содержащего штрих Шеффера или стрелку Пирса.Раздел 4. Функции выбора
4.1. Понятие функции выбора. Скалярный и векторный критерии выбора. Обобщение на случай произвольного отношения предпочтения – функция блокировки
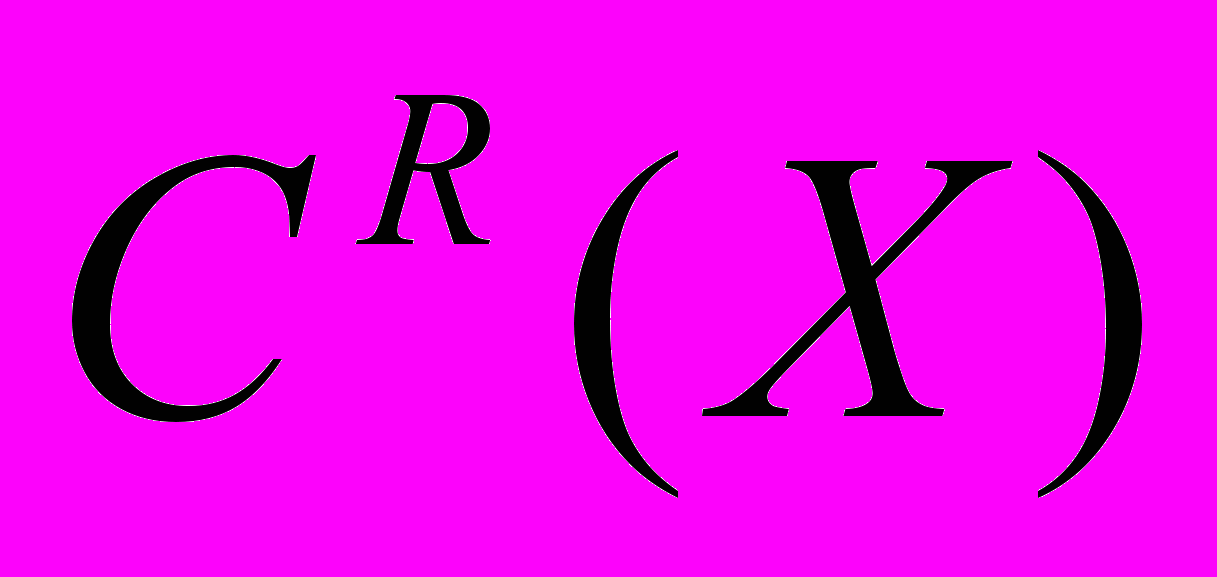и двойственная ей 
. Турнирный выбор.4.2. Характеристические векторы подмножеств конечного множества. Логическое представление произвольных и нормальных функций выбора. Логическое представление турнирного выбора.
4.3. Ранжирование по Парето* (не является обязательной частью).
6. Учебно-методическое
и информационное обеспечение дисциплины
Рекомендуемая литература
а) основная:
- Гисин В.Б. Лекции по дискретной математике. Часть 1. – М.: Финансовая академия, 2001. – 196 c.
- Гисин В.Б. Лекции по дискретной математике. Часть 2. – М.: Финансовая академия, 2003. – 156 c.
- Гисин В.Б., Зададаев С.А., Орел О.Е. Дискретная математика.
Часть 1. – М.: Финансовая академия, 2005. – 96 c.
- Гисин В.Б., Зададаев С.А., Орел О.Е. Дискретная математика.
Часть 2. – М.: Финансовая академия, 2005. – 76 c.
б) Дополнительная:
- Ерусалимский Я.М. Дискретная математика. – М.: Вузовская книга, 1999. – 280 c.
- Москинова Г.И. Дискретная математика. Математика для менеджера в примерах и упражнениях: Учебное пособие. – М.: Логос, 2002. – 240 c.
- Белоусов А.И., Ткачев С.Б. Дискретная математика. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2001. – 744 с.
- Андерсон Джеймс. Дискретная математика. – М. – СПб. - Киев: 2003. – 960 с.
- Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Физматлит, 2002. – 256 c.