В объемные акустические волны
| Вид материала | Учебное пособие |
- Тема Плоские акустические и электромагнитные волны в однородных изотропных средах., 28.93kb.
- Акустические резонаторы, 111.12kb.
- Программа учебной дисциплины сдм. В. 01 05 «Акустические волны в движущихся средах», 84.38kb.
- Программа учебной дисциплины сдм. В. 01-05 «Поверхностные акустические волны» Магистерская, 56.62kb.
- Контрольная работа №4 по теме «Механические колебания и волны. Звук», 35.03kb.
- Его причины и особенности, силовые связи между частицами среды, перенос энергии без, 14.74kb.
- Волновое движение. Электромагнитные волны, 45.73kb.
- Электромагнитные волны. Радиосвязь, 88.78kb.
- «Поляризация света», 79.64kb.
- Тема: Механические волны. Скорость и длина волны, 48.24kb.
4.4.4. Связь КПД контура с измеряемыми величинами в случае, когда
возбуждающей системой является некоторый четырехполюсник.
Рассмотрим теперь общий случай, когда возбуждающей системой пьезопреобразователя служит некоторый четырехполюсник, к выходным клеммам которого подключен пьезоэлемент, а к входным - стандартная передающая линия, соединяющая его с генератором. Таким четырехполюсником в простейшем варианте может быть отрезок линии пониженного волнового сопротивления, соединяющий пьезоэлемент со стандартным передающим трактом, например, четвертьволновый трансформатор.
Будем считать, что четырехполюсник не имеет потерь. В таком случае он трансформирует сопротивление по закону [17]

где a, b и c - некоторые действительные, зависящие от частоты коэффициенты, называемые обычно A-параметрами четырехполюсника, Zвых - импеданс, подключенный к выходным клеммам, Zвх - трансформированный импеданс на входных клеммах. В рабочем состоянии к выходным клеммам подключен пьезоэлемент. Можно считать, что указанный четырехполюсник трансформирует ЭДС и внутреннее сопротивление генератора в плоскость подключения пьезоэлемента. В результате пьезоэлемент оказывается нагрузкой как бы другого генератора с новым значением ЭДС и внутреннего импеданса Zi =Ri +jXi . Тогда в соответствии с определением (86) будем иметь
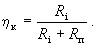
Чтобы определить трансформированный внутренний импеданс генератора Zi , выберем входные клеммы четырехполюсника в максимуме стоячей волны при разомкнутых клеммах на выходе. Назовем эти клеммы сечением “ x x ”. Указанное сечение можно отыскать, если снять с возбуждающей системы звукопровод с напыленным на него пьезоэлементом и найти с помощью зонда измерительной линии максимум стоячей волны. В таком случае будем иметь Zвых = и из (102) получим Zвх = а / jc . Если входные клеммы располагаются в максимуме стоячей волны, то в отсутствие потерь, когда КСВ → ∞, можно записать
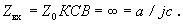
Следовательно, для выбранного четырехполюсника в формуле (102) следует положить c = 0 , и мы будем иметь

Коэффициент a при необходимости можно найти с помощью измерительной линии, если измерить Zвх при некотором известном сопротивлении нагрузки на выходных клеммах Zвых = Rн . Тогда искомый коэффициент будет равен
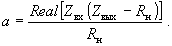
Располагая величиной a, нетрудно, воспользовавшись формулой (103), вычислить активную составляющую внутреннего импеданса Zi трансформированного генератора. Для этого, в случае согласованного с волноводом источника электромагнитной мощности, надо в (103) задать Zвх = Z0 , где Z0 - волновое сопротивление волновода и найти Zвых . Это и будет внутренним импедансом Zi . Его действительная часть равна Real( Zi ) =Z0 / a . В таком случае КПД контура примет вид
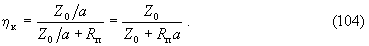
Легко видеть, что величина (Rп a) есть сопротивление потерь преобразователя, трансформированное четырехполюсником в сечение “ x x ”. Этот вывод является следствием линейного характера зависимости Zвх от Zвых в формуле (103). Очевидно, на этом основании трансформированное в сечение “ x x ” сопротивление излучения также можно найти, умножив исходное значение на коэффициент a.
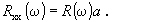
Полное активное сопротивление в сечении “ x x ”, равное [Rп +R(ω)] a , выражается через измеряемые величины - модуль |Γ| и фазу φ коэффициента отражения формулой
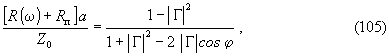
в которой величина |Γ| связана с коэффициентом стоячей волны K известным соотношением
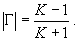
Используя выражение (104) для КПД контура, а также формулы (100) и (105), нетрудно получить
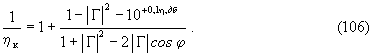
Можно показать, что в случае резонаторной возбуждающей системы формула (106) сводится к формуле (101). Предположим, что мы вывели звукопровод с пьезоэлементом из резонатора. Последний при этом оказался расстроенным. Если теперь найти положение максимума стоячей волны, то это и будет сечение “ x x ”. После возвращения звукопровода с пьезоэлементом в резонатор и его настройки на частоту генератора, в зависимости от величины коэффициента связи, в сечении “ x x ” может появиться либо минимум стоячей волны, либо максимум [18]. Минимум будет в случае сильной связи при β =K0 , а максимум - в случае слабой связи при β = 1/K0 . Здесь K0 = КСВ при резонансе. Расстояние d от минимума до сечения “ x x ” будет в 1-ом случае равно 0, а во 2-ом - Λ/4. Следовательно, в первом случае φ = 4π ( d/Λ) - π = - π, а во втором φ = 0 . Εсли теперь в формуле (106) перейти от модуля |Γ| к КСВ = K0 , а также подставить φ = π , K0 = β или φ=0 , K0 =1/β, то мы получим формулу (101).
Итак, чтобы найти ηк , необходимо измерить величины K, φ θ η. Однако, экспериментальное значение η может быть вычислено по формуле (92), если, в свою очередь, известен ηк . Следовательно, для правильного нахождения η и ЗТ по экспериментальным значениям ПП, A, K и φ необходимо совместно решать уравнения (92), (93) и (106).
4.5. Рекомендуемый порядок проведения исследований
1. Воспользовавшись необходимыми геометрическими размерами и физическими константами, рассчитать зависимости сопротивлений излучения от частоты для пьезоэлементов в двух случаях:
а) преобразователь с объемным резонатором;
б) преобразователь с коаксиальной возбуждающей системой.
Частоту изменять в диапазоне 500...1000 МГц.
2. Рассчитать зависимости коэффициентов преобразования от частоты для тех же случаев, что и в п 1. Считать, что резонатор подстраивается на каждой частоте.
3. Запустить экспериментальную установку, для чего:
а) генератор Г ввести в режим амплитудной модуляции прямоугольными импульсами с длительностью ≤ 2 мкс, с частотой повторения 1...2 кГц и выходной мощностью ≥ 1 мВт. Установить частоту генерации ~800 МГц;
б) к плечу 2 циркулятора ФЦ подключить коаксиальную возбуждающую систему с пьезопреобразователем;
в) ввести импульсный осциллограф ЭO в режим внешнего запуска от
синхронизирующего импульса генератора Г;
г) настроить приемник П на частоту сигнала 800 МГц, плавно изменяя частоту гетеродина ГT вблизи 800 МГц и, наблюдая картину на экране осциллографа, добиться появления эхо-импульсов;
д) измерить чувствительность приемника с помощью встроенного в генератор калиброванного аттенюатора. Тщательно подстроить приемник, добившись, чтобы предельная чувствительность была бы не менее 110 дБ Вт. После этого можно приступить к проведению экспериментальных исследований.
4. Измерить время задержки, воспользовавшись калиброванной разверткой применяемого импульсного осциллографа. Измерения выполнить для тех же двух случаев, что и в п 1.
5. Исследовать экспериментально частотные зависимости коэффициента преобразования и затухания упругой волны в звукопроводе для тех же случаев, что и в п 1.
4.6. Указания по исследованию экспериментальных образцов
преобразователей.
В настоящей работе предлагается исследовать электроакустические преобразователи двух типов. В первом из них возбуждающей системой служит объемный резонатор, а во втором - коаксиальная линия с четвертьволновым трансформатором. Ниже приводятся сведения о преобразователях указанных типов, имеющихся в спецпрактикуме кафедры электроники, колебаний и волн Саратовского университета. Они необходимы для выполнения предлагаемых расчетов и обработки результатов измерений.
1. Преобразователь с объемным резонатором.
1.1. Параметры резонатора. Собственная добротность Q0 и коэффициент связи β с передающей линией.
| f, МГц | 500 | 550 | 600 | 650 | 700 | 750 | 800 | 850 | 900 |
| Q0 | 96 | 75 | 75 | 67 | 57 | 53 | 53 | 49 | 65 |
| β | 1,07 | 1,22 | 1,44 | 1,32 | 1,3 | 1,45 | 1,38 | 1,47 | 1,48 |
Емкость зазора резонатора, (10-12 Ф) 51
1.2 Параметры пьезоэлемента в резонаторной возбуждающей системе.
1.2.1. Подслой
материал медь (Cu) (изотропная)
толщина g, мкм 0,28
плотность (103 кг/м3 ) 8,96
скорость продольных упругих волн (103 м 4,7
удельная электропроводность (107 См/м) 4,5
1.2.2. Пьезослой
материал окись цинка (ZnO) (мозаичный кристалл)
ориентация [0001]
толщина пленки h, мкм 2,8
плотность (103 кг/м3 5,64
скорость продольных упругих волн в направлении [0001] (10 м/с) 6,094
диэлектрическая проницаемость ε0 εs33 (10-11 Ф/м) 7,8234
пьезоэлектрическая константа e , (Кл/м2 ) 1,14
упругая постоянная C3333 , (1010 Н/м2 ) 21,0941
1.2.3. Диаметр контакта пьезоэлемента с центральным проводником
коаксиального резонатора (мм) 0,5
1.3. Параметры кристалла - звукопровода
материал алюмоиттриевый гранат (Y3 Al5 O12 )
ориентация [110]
длина, мм 16,5
сечение, мм2 4х4
плотность (103 кг/м3 ) 4,55
скорость продольных упругих волн (103 м/с) 8,6
2. Преобразователь с коаксиальной возбуждающей системой
2.1. Параметры коаксиальной возбуждающей системы.
2.1.1. Размеры.
Диаметры внешнего и внутреннего проводников коаксиального
трансформатора в мм (соответственно) 2 и 1,5
диаметр контактной площадки на внутреннем проводнике, мм 1,2 длина “четвертьволнового” трансформатора l, мм 87
2.1.2. Коэффициент стоячей волны (K) и фаза коэффициента
отражения φ в плоскости ( x x )
| f, МГц | 500 | 550 | 600 | 650 | 700 | 750 | 800 | 850 | 900 | 950 |
| K | 16,5 | 15,8 | 14,5 | 13,3 | 12,4 | 12,6 | 11,8 | 9,22 | 10,6 | 11,7 |
| φ, рад | -2,95 | -3,03 | -2,81 | -2,73 | -2,98 | -2,97 | -2,71 | -2,84 | -2,74 | -2,97 |
2.2. Параметры кристалла-звукопровода в коаксиальной возбуждающей
системе - те же, что и в резонаторной системе, см. п 1.3.
2.3. Параметры пьезоэлемента в коаксиальной возбуждающей системе
- те же, что и в 1.2.1. и 1.2.2.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Дайте краткую характеристику объемных, поверхностных, волноводных и
канализированных упругих волн. Приведите примеры применения упругих волн на СВЧ.
2.Запишите основные уравнения, описывающие электромеханические процессы в пьезоэлектрическом кристалле.
3. Как выводится уравнение движения упругодеформированной среды?
4. Получите волновое уравнение для плоских объемных акустических волн.
5. Дайте определение плотности потока упругой энергии, акустического импеданса и акустического волнового сопротивления.
6. Что понимается под коэффициентом электромеханической связи?
7. Запишите определение коэффициента электроакустического преобразования.
8. Получите формулу, связывающую коэффициент преобразования с коэффициентом отражения в волноводе и сопротивлением излучения пьезоэлемента.
9. Опишите схему вывода формулы для расчета сопротивления излучения пьезоэлемента.
10. Расскажите в общих чертах как выводятся формулы для расчета коэффициентов преобразования в случаях резонаторной и коаксиальной возбуждающих систем.
11. Как устроены резонаторная и коаксиальная возбуждающие системы?
12. Нарисуйте структурную схему экспериментальной установки и расскажите
как она работает.
13. Дайте вывод рабочих формул, связывающих коэффициент преобразования
и затухания упругой волны с измеряемыми величинами: полными потерями, отношением мощностей соседних эхо-импульсов и КПД контура.
14. Расскажите как правильно измерить полные потери, когда циркулятор
используется за пределами своего рабочего диапазона частот.
15. Как измеряется КПД контура в случаях резонаторной и коаксиальной
возбуждающих систем? Дайте выводы соответствующих рабочих формул.
СПИСОК ЛИТЕРАТУРЫ
1. Ю. А. Зюрюкин, В. И. Наянов, В. А. Полотнягин. К теории возбуждения
гиперзвуковых волн пьезоэлектрическими преобразователями. // Радиотехника и электроника. 1970. Т.15. № 4. С. 797-805.
2. Ю. А. Зюрюкин, В. И. Наянов, В. А. Полотнягин. К теории возбуждения гиперзвуковых волн пьезоэлектрическими преобразователями (тонкопленочные преобразователи). // Радиотехника и электроника, 1970. Т.15. № 5. С. 1059-1067.
3. Э. Дьелесан, Д. Руайе. Упругие волны в твердых телах. М. Наука, 1982.
4. Дж. Най. Физические свойства кристаллов. М. Мир, 1967.
5. Дж. Мак-Фи. Распространение и усиление звуковых волн в пьезоэлектрических полупроводниках. // Физическая акустика, под ред. У. Мэзона. Т. 4А. С. 13. М. 1969.
6. Д. Берлинкур, Д. Керрон, Г. Жаффе. Пьезоэлектрические и пьезомагнитные материалы и их применение в преобразователях. // Физическая акустика, под ред. У. Мэзона. Т. 1А. С. 204. M. 1966.
7. М. А. Григорьев, В. В. Петров, А. В. Толстиков. Сверхвысокочастотный пьезопреобразователь с электродами конечной толщины в качестве нагрузки коаксиальной линии. // Радиотехника и электроника, 1990, Т. 35, N 9, С. 1977-1987.
8. М. А. Григорьев, С. С. Курышов, А. В. Толстиков. О влиянии конечной толщины электродов при возбуждении объемных упругих волн пьезоэлектриками класса 6mm с произвольной ориентацией оси 6. // Акустический журнал. 1990. Т. 36. N 2.С.255-261.
9. Х. Мейнке и Ф. Гундлах. Радиотехнический справочник. M. Госэнергоиздат, 1960.
10. Р. А. Браже, М. А. Григорьев. Влияние потерь в электродинамической системе на коэффициент преобразования СВЧ электроакустического преобразователя. // Электронная техника. Сер. 1. Электроника СВЧ. 1972. Вып. 3. С.16-21.
11. Б. С. Данилин, Б. Ф. Мочалов, Н. Н. Стрельцова, Т. Д. Шермергор. Осаждение пьезоэлектрических пленок окиси цинка в магнетронной системе ионного распыления. // Электронная техника. Сер. 3. Микроэлектроника. 1980. Вып.3 (87). С. 62-65.
12. М. А. Григорьев, Б. Д. Зайцев, А. В. Цыбин. Затухание продольных упругих волн в тонких пленках на частоте 9.4 ГГц. // Письма в ЖТФ. 1979. Т. 5. N1. С. 50.
13. В. И. Калинин, Г. М. Герштейн. Введение в радиофизику. M. ГИЗ Тех.-теор.лит. 1957.
14. А. Л. Фельдштейн, Л. Р. Явич, В. П. Смирнов. Справочник по элементам
волноводной техники. Гос. энергоизд. М. Л. 1963.
15. М. А. Григорьев, Б. Д. Зайцев, В. В. Петров, А. В. Толстиков. Об ошибках при измерении на СВЧ коэффициента электроакустического преобразования и затухания упругих волн эхо-методом. // Акустический журнал. 1983. Т. 27. N 3. C. 351-357.
16. М.А. Григорьев, Ю.Н. Навроцкая. Эхо-импульсный метод исследований с
применением эффективных гиперзвуковых преобразователей. // Акустический журнал. 1996. Т.42. №2. С. 276-278.
17. К. Шимони. Теоретическая электротехника. М. Мир. 1964.
18. Э. Л. Гинзтон. Измерения на сантиметровых волнах. М. И. Л. 1960.
