В объемные акустические волны

Вид материала

Учебное пособие

Содержание 2.8. Коэффициент электромеханической связи. 3.2. Импеданс излучения.

Подобный материал:

• Тема Плоские акустические и электромагнитные волны в однородных изотропных средах., 28.93kb.
• Акустические резонаторы, 111.12kb.
• Программа учебной дисциплины сдм. В. 01 05 «Акустические волны в движущихся средах», 84.38kb.
• Программа учебной дисциплины сдм. В. 01-05 «Поверхностные акустические волны» Магистерская, 56.62kb.
• Контрольная работа №4 по теме «Механические колебания и волны. Звук», 35.03kb.
• Его причины и особенности, силовые связи между частицами среды, перенос энергии без, 14.74kb.
• Волновое движение. Электромагнитные волны, 45.73kb.
• Электромагнитные волны. Радиосвязь, 88.78kb.
• «Поляризация света», 79.64kb.
• Тема: Механические волны. Скорость и длина волны, 48.24kb.

       
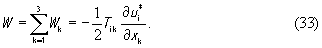
В этом выражении предполагается суммирование по повторяющимся индексам i и k . Если индексы поменять местами и принять во внимание симметрию тензора упругого напряжения (T_{i k} =T_{k i} ), то будем иметь
 
 Складывая выражения (33) и (34) с учетом (7) и находя среднюю за период плотность упругой энергии, получим окончательно
                                     

2.7. Акустический импеданс.

      Для чистых мод плоских упругих волн, распространяющихся вдоль одной из координатных осей, из выражения (32) для компонент вектора Умова, опуская индексы, будем иметь
                                     
Под T и u здесь следует понимать выраженные в комплексном виде чисто продольные, либо чисто поперечные волны напряжения и смещения. Сопоставим фрмулу (36) с выражением для мощности, переносимой электромагнитной волной, в некоторой передающей линии
                                         
где электрическое напряжение V и ток J в общем случае обусловлены суммой прямых и обратных волн. Сравнение формул (36) и (37) позволяет сделать вывод, что плоскую волну величины (-du/dt) можно принять аналогом волны электрического тока J, а волну упругого напряжения T - аналогом волны электрического напряжения. Это дает основание подобно электрическому импедансу в некотором сечении передающей линии ввести понятие акустического импеданса
                                 В общем случае, когда в среде одновременно присутствуют прямые и обрат-ные акустические волны, импеданс Z_ак будет комплексной величиной, зависящей от  координаты вдоль звукопровода. Если же имеют место чисто бегущие волны, то эта величина становится действительным числом, называемым акустическим волновым сопротивлением Z_0,ак .
                               
где знак + означает прямую бегущую волну. Для пьезоэлектрика из (28) и (29) имеем
        
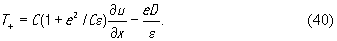
 Здесь индукция D, как следует из (30), не зависит от координаты x и поэтому может быть функцией только времени D=D₀e^jωt . Если же пьезоэлектрик используется как простой звукопровод и не включен в какую-либо электрическую цепь, то ток в нем должен отсутствовать, т.е ∂D/dt = jωD=O. На этом основании, полагая в (40) D=O и подставляя в (39), для бегущей волны получим

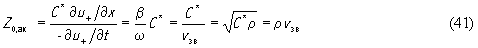
 где C* =C(1+k² ) - ужесточенная за счет пьезоэффекта упругая кoнстанта, k²=e²/Cε - квадрат коэффициента электромеханической связи. Используя понятие акустического волнового сопротивления, можно плотность потока мощности, переносимой бегущей акустической волной, записать в виде

   

Понятие акустического импеданса широко используется при описании распространения плоских объемных упругих волн в различных контактирующих между собой средах. Так, например, если акустические волновые сопротивления двух сред равны, то при прохождении упругой волны из одной среды в другую не будет возникать отраженной волны. Если же некоторую среду с акустическим волновым сопротивлением Z_0,ак соединить с другой средой, акустический импеданс которой      равен Z_ак   , то в месте соединения комплексный коэффициент отражения будет равен

    

Также, как и в электромагнитных волноводах, акустический импеданс трансформируется отрезком звукопровода по закону

    
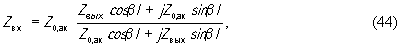
где Z_вх, Z_вых - акустические импедансы на входе и выходе трансформирующего отрезка длины  l ,  β- пοстоянная распространения упругой волны. Для звукопроводов с потерями акустическое волновое сопротивление становится комплексным. Если
                                                     
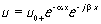
где α- коэффициент затухания, то из (39) следует
                 
Эта формула может быть использована, например, для нахождения коэффициента акустического затухания α в некоторой среде по измеренному коэффициенту отражения от границы раздела между звукопроводом и исследуемой средой.

2.8. Коэффициент электромеханической связи.

 

      Выше были использованы безразмерные величины (24) и (26), названные коэффициентами электромеханической связи. Они определяются физическими константами пьезоэлектрика e ,C и ε и служат его обобщенной характеристикой, во многом определяющей свойства устройств, в которых используется данный пьезоэлектрик. В литературе имеются различные определения этой величины. В [5], например, определение коэффициента электромеханической связи сопровождается следующими рассуждениями. На распространение плоских упругих волн в пьезоэлектрической среде оказывают влияние лишь продольные компоненты электростатических полей, вызванных поляризацией пьезоэлектрика. Упругие волны, сопровождаемые продольными пьезополями, называются “пьезоактивными”.Для них эффективный модуль упругости “ужесточается”. Величина этого “ужесточения” и определяет коэффициент электромеханической связи, который дается формулой
                                                  
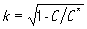
где C - “неужесточенный” модуль упругости пьезоэлектрика, C^* - “ужесточеный” за счет пьезоэффекта модуль упругости.
       Из рассмотренных выше чистых мод упругих волн “пьезоактивными” будут продольные волны вдоль оси x₃ и поперечные волны вдоль оси x₁. В [6] коэффициент электромеханической связи определяется как отношение плотности взаимно упругой и электрической энергии к среднему геометрическому значению плотности внутренних упругой и электрической энергий. Плотность внутренней энергии кристалла ( в пренебрежении тепловыми и магнитными членами) можно записать как сумму механической и электрической энергий
                                                   
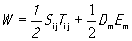
 Если подставить сюда выражения для T_{i j} и D_m из (6) и (8), то будем иметь
                     

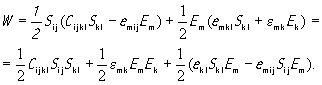
 Первое слагаемое в этом выражении представляет собой плотность упругой     энергии, второе - плотность электрической энергии и третье - плотность  так называемой   взаимной энергии или энергии электромеханического взаимодействия.        В соответствии с  высказанным определением можно получить

                                

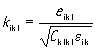
Существуют и другие определения понятия коэффициента   электромеханической связи [6], на которых мы не будем здесь останавливаться.

 3. ЭЛЕКТРОАКУСТИЧЕСКОЕ ПРЕОБРАЗОВАНИЕ

3.1. Постановка задачи.

      Ниже мы рассмотрим вариант возбуждения объемных упругих волн с помощью пьезоэлектрика, как показано на рис. 2,б. В этом случае упругая волна возбуждается пьезоэлектрическим слоем, нанесенным на торец звукопровода, причем последний может быть как пьезоэлектриком, так и непьезоэлектриком. Для концентрации электрического поля в пьезоэлектрике, между ним и звукопроводом, как правило, располагается металлический электрод, называемый обычно “подслоем”. С той же целью на внешнюю поверхность пьезоэлектрика может наноситься другой электрод, называемый “надслоем”. В другом варианте, обычно называемом “возбуждением с поверхности”, упругая волна генерируется непосредственно в звукопроводе, который сам является пьезоэлектриком и вводится в переменное электрическое поле, создаваемое какими-либо внешними электродами, как показано на рис. 2,а. При этом возбужденная волна начинает свой путь от поверхности плоского торца, находящегося в переменном электрическом поле. Строгий теоретический анализ этого случая наталкивается на математические трудности в силу сложности геометрии. Поэтому здесь мы не будем его рассматривать. В любом случае пьезоэлемент, введенный в зазор между электродами, может быть охарактеризован некоторым импедансом, активная составляющая которого поглощает электромагнитную (ЭМ) мощность.Последняя расходуется как на возбуждение в звукопроводе акустической волны, так и на различного рода потери (джоулевы, акустические и др.). Для простоты будем считать, что все потери могут быть описаны некоторой действительной, зависящей в общем случае от частоты, добавкой R_п (ω) κ импедансу пьезоэлемента

                                                  

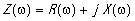
найденному без учета потерь. Тогда мощность акустической волны P_{ак ,} излученная в звукопровод и мощность потерь P_п будут выражаться следующими формулами:
                                   
где J - амплитуда тока, текущего через преобразователь. Величина Z(ω) обычно называется импедансом излучения, а R(ω) сопротивлением излучения. Эффективность преобразователя в целом, включая возбуждающую систему, подводящую к нему ЭМ мощность, характеризуется обычно коэффициентом электроакустического преобразования η, определяемым как отношение η =P_ак/P_{сн ,} где   P_сн - мощность , отдаваемая генератором в согласованную с волноводом (неотражающую) нагрузку. Чтобы найти величину η , будем считать в дальнейшем , что генератор характеризуется ЭДС с фиксированной амплитудой и согласован с передающим трактом, т.е. его внутреннее сопротивление Z_i чисто активно и равно волновому сопротивлению волновода Z_i = Z₀ . Покажем, что в этом случае при произвольной нагрузке будет выполняться равенство P₊ =P_{сн ,} где P₊ - мощность прямой волны. Если генератор с эффективным значением ЭДС=E_эф нагружен на согласованную       нагрузку Z_н = Z₀ , то он будет отдавать в нее мощность P_сн = (E_эф /2Z₀)²Z₀ = E²_эф /4Z₀ .            В случае произвольной нагрузки с импедансом Z_н= =R_н+jX_{н ,} в волноводе возникнет            стоячая волна, образованная прямой волной с мощностью P₊ и отраженной - с мощностью P_- . В нагрузке будет выделяться мощность
                                          
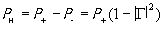
где |Γ | - модуль коэффициента отражения в подводящем волноводе. Если учесть, что
      
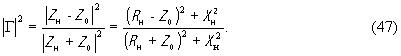
то                                                               


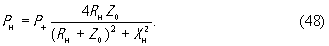
 Эту же мощность можно найти как P_н =J²_эфR_{н ,} где J - эффективное значение тока в цепи нагрузки. Величина J²_эф может быть выражена как

J²_эф =E²_эф /|Z₀ +Z_н |² .

Тогда
                              
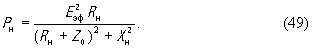
Приравнивая правые части (48) и (49), получим
                                                
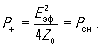
На этом основании определение коэффициента электроакустического преобразования можно записать в виде
                            
Поскольку P_ак +P_п = P₊ (1-|Γ|²) , то из (50) с учетом (46) будем иметь

                               
где величина
                                      

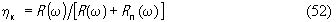
называется коэффициентом полезного действия (КПД) контура. Такое название связано с тем, что R_п(ω) определяет электрические потери главным образом в подслое и надслое, что можно отнести к потерям в электрической цепи




(контуре), тогда как акустическое затухание и собственная проводимость пьезоэлектрика обычно пренебрежимо малы.              Модуль коэффициента отражения |Γ| нетрудно найти по формуле (47), если известен импеданс нагрузки Z_н(ω) в некотором сечении передающего тракта и его волновое сопротивление Z₀ . В нашем случае Z_н(ω) вычисляется как результат трансформации возбуждающей системой импеданса излучения преобразователя и сопротивления потерь R_п. Таким образом, первоочередной задачей при анализе работы пьезопреобразователя является нахождение импеданса излучения Z(ω) .Лишь после этого можно приступить к рассмотрению конкретной возбуждающей системы и к нахождению коэффициента электроакустического преобразования и других характеристик преобразователя.


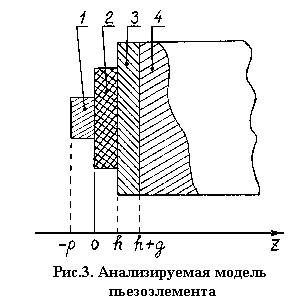
3.2. Импеданс излучения.

      Анализируемая модель представлена на рис. 3. Пьезоэлемент состоит из пьезослоя 2 и металлических обкладок 1 (наслоя) и 3 (подслоя). Последний находится в акустическом контакте со звукопроводом 4. Рассмотрим в соответствии с работой [7] наиболее важные в практическом отношении случаи преобразователей на основе пьезоэлектрика класса 6mm (например CdS, ZnO) с осью 6 , перпендикулярной или параллельной поверхностям электродов. В первом случае возбуждаются чисто продольные упругие волны, а во втором- сдвиговые. Надслой, подслой и звукопровод будем считать изотропными или ориентированными продольной нормалью перпендикулярно торцу последнего. В противном случае преобразователь будет одновременно возбуждать квазипродольные и квазипоперечные волны. (Случай произвольной ориентации пьезоэлектрика рассмотрен в работе [8].) Полагая d/dx=d/dy=0, для непроводящего пьезоэлектрика из уравнения Пуассона получим dD/dz=0, где D - электрическое смещение. Это означает, что величина D не зависит от координаты z и может быть функцией только времени t. При выбранной ориентации уравнения состояния пьезоэлектрика сводятся к скалярным

                          
где T и u - упругое напряжение и механическое смещение в пьезоэлектрике, C и e - упругая и пьезоконстанты, ε- диэлектрическая проницаемость, E - напряженность электрического поля. Если ось 6 пьезоэлектрика перпендикулярна (параллельна) торцу звукопровода, то физические константы в уравнениях (53) и (54), как показано в разделе 2.4, представляют собой следующие компоненты тензоров: e=e₃₃₃ (=e₁₁₃) , ε=ε₃₃ (=ε₁₁) , C=C₃₃₃₃ (=C₁₃₁₃). Импеданс пьезоэлемента в квазистатическом приближении определяется следующим образом:


        


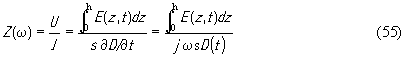
где s - площадь подслоя. Если найти E из (54) и подставить в (55), то получим


        
                              

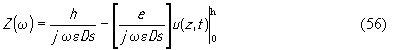
Первый член в этом выражении представляет собой чисто реактивное сопротивление, определяемое статической емкостью C₀ =εs/h . Действительная часть второго члена является сопротивлением излучения R(ω) , а мнимая - входит в реактивное сопротивление преобразователя как некоторая добавка, вызванная пьезоэффектом. Функция u(z,t) есть решение волнового уравнения (18) для пьезоэлектрика:

                           
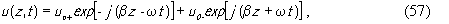
где u₀₊ и u_0- - комплексные амплитуды, определяемые граничными условиями,   β=ω(ρ/(C(K² +1)))^1/2 , ρ- плотность, K - коэффициент электромеханической связи. В случае нормальной ориентации пьезоэлектрика
                                                          
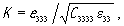
а в случае тангенциальной -
                                                
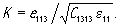
Если исходить из непрерывности на границах двух сред механических смещений и упругих напряжений, то при z=0 и z=h должны быть равны акустические импедансы, определяемые формулой (38), найденные в пьезоэлектрике и в контактирующей с ним среде. Тогда для звукопровода, имеющего бесконечную длину, получим следующие граничные условия:

                                         




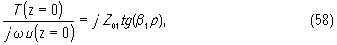
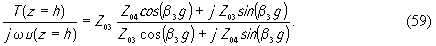
         Формула (58) означает, что пьезоэлемент нагружен надслоем, как короткозамкнутым отрезком волновода, а последнее равенство выражает тот факт, что подслой является трансформатором сопротивления, включенным между бесконечно длинным звукопроводом с волновым сопротивлением Z₀₄ и пьезоэлементом (см. формулу (44). Здесь Z₀₁, Z₀₃, Z₀₄- акустические волновые сопротивления соответственно надслоя, подслоя и звукопровода , β₁ и β₃- волновые числа в первой и третьей среде (см рис. 3). Для того, чтобы выразить в (58) и (59) величину T при z=0 и z=h через смещения u , воспользуемся следующим из (53) и (54)соотношением