В объемные акустические волны

Вид материала

Учебное пособие

Содержание 2.Уравнения, описывающие электромеханические 2.2. Уравнения состояния пьезоэлектрика 2.3. Уравнения Максвелла. 2.4. Волновое уравнение для плоских ОАВ в пьезоэлектрике. 2.5. Поток упругой энергии. 2.6. Плотность упругой энергии.

Подобный материал:

• Тема Плоские акустические и электромагнитные волны в однородных изотропных средах., 28.93kb.
• Акустические резонаторы, 111.12kb.
• Программа учебной дисциплины сдм. В. 01 05 «Акустические волны в движущихся средах», 84.38kb.
• Программа учебной дисциплины сдм. В. 01-05 «Поверхностные акустические волны» Магистерская, 56.62kb.
• Контрольная работа №4 по теме «Механические колебания и волны. Звук», 35.03kb.
• Его причины и особенности, силовые связи между частицами среды, перенос энергии без, 14.74kb.
• Волновое движение. Электромагнитные волны, 45.73kb.
• Электромагнитные волны. Радиосвязь, 88.78kb.
• «Поляризация света», 79.64kb.
• Тема: Механические волны. Скорость и длина волны, 48.24kb.

2.УРАВНЕНИЯ, ОПИСЫВАЮЩИЕ ЭЛЕКТРОМЕХАНИЧЕСКИЕ
                                        ПРОЦЕССЫ В ПЬЕЗОЭЛЕКТРИКЕ

2.1. Уравнение движения упругодеформированной среды.

Если в твердом теле существуют упругие волны, то отдельные частицы, из которых состоит это тело, испытывают колебательное движение. В теории упругости вещество рассматривается как непрерывная, сплошная среда (континуум). В таком случае колебательному движению будет подвержен любой выделенный в среде элементарный объем и к нему можно применить 2-й закон Ньютона. Чтобы это сделать, рассмотрим в окрестности точки с радиусом-вектором r (см. рис.1) элементарный объем среды в виде


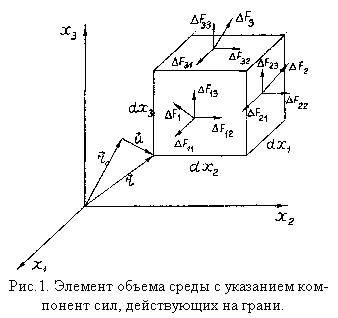
прямоугольного параллелепипеда, ребра которого параллельны осям прямоугольной системы координат x₁, x₂, x₃ и имеют длины dx₁,dx₂,dx₃. Со стороны окружающей среды на вещество, заключенное в объеме
dV=dx₁ dx₂ dx₃ , действуют силы, обеспечивающие его ускорение. Пусть ∆F_i - сила, действующая на одну из обращенных к нам граней обьема dV, перпендикулярную i-ой оси. На противоположную грань будет действовать сила-(∆F_i-d(∆F_i)), где d(∆F_i) - приращение, обусловленное расстоянием dx_i . Суммарная сила, действующая на весь объем , может быть записана как векторная сумма



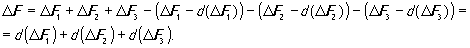
Тогда 2-й закон Ньютона, описывающий движение элементарной массы, заключенной в объеме dV , примет в векторной форме вид

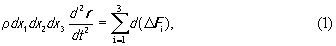
где ρ - плотность среды, которую для волн малых амплитуд можно считать постоянной величиной.
      Радиус-вектор r, имеющий компоненты x₁, x₂, x₃ , отсчитывается от некоторого фиксированного начала координат и является функцией времени и начального радиуса-вектора r₀ (см. рис.1) с компонентами x₁₀, x₂₀, x₃₀. Смещение элементарного объема dV из начального положения характеризуется вектором u. Легко видеть, что
 
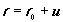
Если за начальное положение точек среды принять их невозмущенное состояние, то u будет вектором смещения из положения равновесия. Поскольку для рассматриваемого объема r₀ = const , то d²r/dt²=d²u/dt². На этом основании (1) примет вид

 
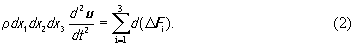
      При заданных d(∆F_i) это уравнение имеет решение u(t), описывающее движение некоторой материальной точки с начальными координатами x₁₀, x₂₀, x₃₀ .Чтобы найти закон движения другой точки, необходимо в (2) сменить координаты x_i0 и соответствующие приращения сил d(∆F_i). Если проделать такую замену многократно, то из уравнения (2) может быть получено дискретное распределение вектора смещения u в пространстве.
      Наша задача заключается в нахождении волн, которые могут существовать в данной упругой среде. Волна описывается непрерывной функцией от времени и координат, характеризующей точки пространства, не связанные с конкретной материальной частицей среды. Такое описание называется пространственным. Чтобы решить поставленную задачу, необходимо уравнение (2) видоизменить так, чтобы оно давало пространственное описание поля смещений. Такое видоизменение обычно называют переходом от материального описания (переменные Лагранжа) к пространственному (переменные Эйлера).
      Смещение u в данный момент времени для различных частиц среды будет различным, т.е. u есть функция радиуса-вектора r , характеризующего начальное положение точек среды. Начальные координаты этих точек, по сути дела, совпадают с координатами точек пространства. Поэтому величину u можно представить в пространственном описании как функцию времени и пространственных координат. В таком случае для компонент скорости в пространственном описании поля смещений будем иметь  


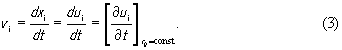
 Компоненты скорости v_i в пространственном описании также представляют собой некоторую функцию v_i(t, x₁, x₂, x₃). Тогда компоненты ускорения dv_i /dt , входящего в уравнение (2), можно записать следующим образом
 
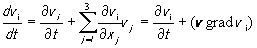
где круглые скобки означают скалярное произведение. Если считать, что дрейфовое движение частиц среды отсутствует, то в случае волн малой амплитуды можно принять (v grad v_i) = 0. На этом основании, переходя в (2) к пространственному описанию поля смещений, полную производную dv/dt следует приближенно заменить частной производной ∂v/dt . Учитывая также выражение (3), получим из (2)

 

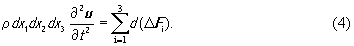
       Обратимся теперь к правой части полученного уравнения. На рис.1 показаны компоненты сил ∆F_i , действующих на грани, перпендикулярные осям x_i . Например, для грани, перпендикулярной оси x_i, будем иметь следующие компоненты: ∆F_{i 1}, ∆F_{i 2},∆F_{i 3}. Первый индекс указывает номер оси, перпендикулярной грани, а второй - оси, параллельно которой направлена соответствующая компонента. В общем случае будем иметь∆F_ij. Воспользуемся понятием тензора упругого напряжения, компоненты которого определяются формулой
 
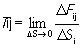
где ∆S_i- элементарная площадка, перпендикулярная i-й оси. По смыслу величина T_{i j} является компонентой упругой силы, приходящейся на единицу площади соответствующей грани. Упругое напряжение как физическая величина представляется тензором второго ранга и в общем случае характеризуется 9-ю компонентами, величины которых зависят от выбора системы координат.
      Учитывая, что d(∆F_ij)=dT_ij dS_i из (4) для j-й компоненты смещения получим в пространственном описании уравнение движения в окончательном виде:
 
Для сокращения записи знак суммы в правой части полученного уравнения опущен, а свидетельством суммирования служит повторяющийся индекс i.


2.2. Уравнения состояния пьезоэлектрика.

        Имеется два феноменологических уравнения, описывающих в линейном приближении электромеханическое состояние пьезоэлектрической среды. Первое уравнение связывает компоненты тензора упругого напряжения T _{i j} с компонентами тензора деформации S _{k l} и компонентами вектора напряженности электрического поля E _m .
                                       
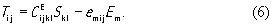
         В нем C^E_{i j k l} и e_{m i j} - коэффициенты пропорциональности, являющиеся материальными константами. C^E_{i j k l}- компонента тензора четвертого ранга, называемого тензором модулей упругости (жесткости); верхний индекс E означает, что эта величина получена при E = const;      e_{m i j}- компонента тензора третьего ранга, называемого тензором пьезомодулей; S_{k l} - безразмерная деформация, связанная с компонентами вектора смещения u , формулой
                                                  
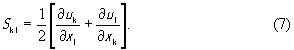
           Первое слагаемое в правой части уравнения (6) выражает известный закон Гука для упругой среды. Второе слагаемое описывает пьезоэффект, заключающийся в том, что электрическое поле порождает в пьезоэлектрике упругое напряжение. Заметим, что для кристалла и первое, и второе слагаемые в формуле (6) представляют собой суммы по повторяющимся индексам k , l и m , каждый из которых может принимать значения 1, 2, 3.
      Второе уравнение состояния пьезоэлектрика связывает компоненты вектора электрического смещения (индукции) D с компонентами тензора деформации S и вектора напряженности электрического поля E

                               

Коэффициентами пропорциональности здесь служат компоненты пьезоэлектрического тензора (пьезомодули) e_{n k l} и компоненты тензора диэлектрической проницаемости ε^S_{n m}, найденные при S=const. В правой части уравнения (8) второе слагаемое связывает электрическую индукцию с напряженностью электрического поля как в диэлектрике. Первое слагаемое отражает опытный факт поляризации пьезоэлектрика под действием деформации даже в отсутствие внешнего электрического поля.

2.3. Уравнения Максвелла.

      При построении теории пьезоэлектрического преобразователя уравнения Максвелла используются в следующем виде:


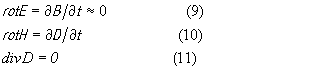
       Первое из этих уравнений означает, что теория строится в квазистатическом приближении. Для обоснования этого можно привести следующие соображения. Электрические поля, порождаемые в пьезоэлектрике упругой волной возникают благодаря перераспределению этой волной положительных и отрицательных зарядов в объеме среды. Созданный при этом зарядовый “рельеф” переносится упругой волной со скоростью звука. Последняя в ≈10⁵ раз меньше скорости распространения электромагнитных волн. Поэтому указанные заряды можно считать неподвижными, а электрические поля, создаваемые ими - потенциальными, подчиняющимися законам электростатики.
      В уравнении (10) отсутствует плотность тока проводимости и оставлена только плотность тока смещения ∂D/dt . Это связано с тем, что пьезоэлектрик, используемый в электроакустическом преобразователе, должен быть непроводящим. В противном случае он будет шунтироваться собственной проводимостью, которая снизит в нем амплитуду переменного поля.   Равенство нулю дивергенции в (11) следует из того, что пьезоэлектрик считается непроводящим и плотность объемного заряда в нем равна нулю.

2.4. Волновое уравнение для плоских ОАВ в пьезоэлектрике.       Рассмотрим случай, когда в переменное электрическое поле введен конец пьезоэлектрического звукопровода, либо пьезоэлектрическая пластина,




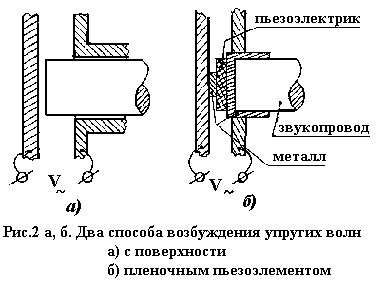
закрепленная на непьезоэлектрическом звукопроводе (см.рис.2). Предположим, что пьезокристалл ориентирован осью x₃ кристаллофизической системы координат параллельно вектору электрического поля, а его торцевая поверхность перпендикулярна этой оси. В таком случае в пьезоэлектрике будут возбуждаться практически плоские ОАВ с фазовой скоростью, направленной вдоль оси x₃ и можно положить ∂/dx₁ =∂ /dx₂ =O. Уравнения (5), (6), (8) , (11) с учетом (7) примут вид
                                
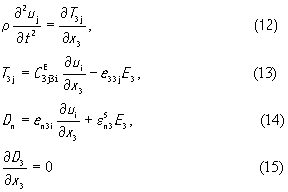
Из последнего уравнения следует, что D₃ не зависит от координаты x₃ и, следовательно, является лишь функцией времени. Выразим из (14) напряженность электрического поля E₃
                                       

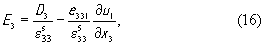
                подставим ее в (13)
                                       


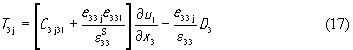
  и, используя полученное выражение, найдем из (12) следующее волновое уравнение.                                                                   




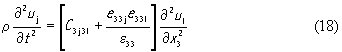
      Поскольку j здесь может принимать значения 1,2,3, формула (18) представляет собой    три уравнения, в которых неизвестными служат компоненты вектора смещения   u_j (x₃, t).
        Рассмотрим случай, когда пьезоэлектриком является кристалл класса 6mm, например, ZnO или CdS. Если воспользоваться матрицами упругих,       пьезоэлектрических и диэлектрических постоянных для таких кристаллов [4], то нетрудно убедиться, что во всех приведенных выше уравнениях неравными нулю   будут  только константы C₃₁₃₁ = C₃₂₃₂ , C₃₃₃₃  , e₃₃₃ и ε₃₃. Тогда из (13) и (14) будем   иметь
                     а из (18) получим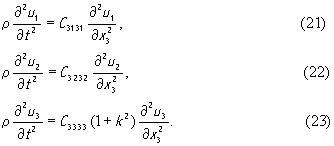


 В последнем уравнении величина       k = (e²₃₃₃ / C₃₃₃₃ ε₃₃ )^1/2
называется коэффициентом электромеханической связи. Таким образом, в пьезоэлектрике класса 6mm в направлении оси x₃ возможно распространение двух чисто поперечных волн со смещениями вдоль x₁ и x₂ (см.(21) и (22)) и чисто продольной волны со смещением вдоль оси x₃ (см.(23)). Скорости этих волн, как следует из дисперсионных уравнений, которые нетрудно получить из (21), (22) и (23), соответственно, равны (C₃₁₃₁/ρ)^{1/2 ,} (C₃₂₃₂/ρ)^1/2 и (C₃₃₃₃  ( 1+k²)/ρ)^1/2 . Заметим, что обе поперечные волны имеют одинаковые скорости, так как C₃₁₃₁ = C₃₂₃₂ . Переменным электрическим полем, направленным вдоль оси x₃ , будет возбуждаться лишь одна из этих трех волн, а именно продольная волна. Действительно, если в (12) подставить (13) и воспользоваться матрицами материальных констант [4], то из трех уравнений, которые мы при этом получим, два точно совпадают с (21) и (22), а третье примет вид


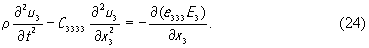
 Правая часть этого неоднородного уравнения представляет в нем источник возбуждения акустических волн. Следовательно, для возбуждения упругой волны в пьезоэлектрике необходимо, чтобы производная ∂(e₃₃₃E₃ )/∂x₃ была бы отлична от нуля, т.е. произведение (e₃₃₃E₃ ) должно изменяться в зависимости от координаты x₃ .Если, например, плоская граница пьезоэлектрика перпендикулярна оси, то значение e₃₃₃ испытывает на ней скачок и будет иметь место так называемое “возбуждение с поверхности”.В случае пьезоэлектрика класса 6mm возможен также другой случай, когда переменное электрическое поле, направленное перпендикулярно торцу звукопровода, возбуждает чисто поперечную волну. Для этого необходимо сориентировать пьезоэлектрик таким образом, чтобы ось x₃ кристаллофизической системы координат оказалась бы перпендикулярной вектору электрического поля E и, следовательно, параллельной собственному торцу кристалла. В этом случае чисто поперечная волна может возбуждаться в любом направлении, лежащем в плоскости x₁O x₂ . Например, для волн, распространяющихся вдоль оси x₁, тензорные уравнения (5), (6) и (8) сводятся к следующим скалярным
                            
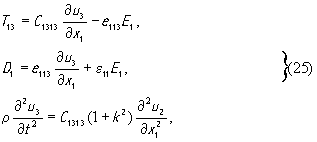
где k - коэффициент электромеханической связи, равный


Решением уравнения (25) является чисто поперечная волна, распространяющаяся вдоль оси x₁ со смещением частиц среды параллельно оси x₃ . Две другие волны, существование которых также возможно, не возбуждаются при заданном направлении электрического поля. Таким образом, в рассмотренных двух случаях тензорные уравнения, описывающие электромеханические свойства пьезоэлектрика, сводятся к скалярным. Обобщая оба случая, будем в дальнейшем необходимые нам уравнения записывать, опуская индексы, в следующем виде


                                         

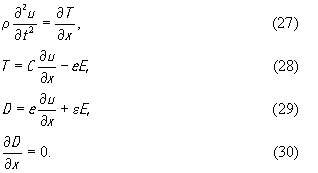
2.5. Поток упругой энергии.

Распространение акустической волны сопровождается переносом энергии. Этот перенос характеризуется вектором Н.А.Умова (1874г., Одесский университет), величина которого равна количеству энергии, переносимой волной за единицу времени через единицу площади (плотность потока мощности). Компоненты этого вектора выражаются формулой



 где подразумевается суммирование по повторяющемуся индексу i от 1 до 3. В случае, если используется комплексное представление векторов синусоидально изменяющихся полей, то среднюю за период плотность потока мощности, переносимой упругой волной в направлении оси x_k ,можно записать следующим образом



Здесь под T_ik и u_k понимаются комплексные амплитуды компонент тензора упругого напряжения и вектора смещения. u_i* означает комплексно сопряженную величину.

   2.6. Плотность упругой энергии.

      Воспользовавшись формулой (32) для компонент вектора Умова, можно найти выражение для величины упругой энергии, заключенной в единице объема. За время dt через единичную площадку, перпендикулярную оси x_k протекает в направлении оси упругая энергия P_k dt. Если при этом фронт k-й компоненты потока мощности перемещается на расстояние dx_k , то указанную энергию можно считать заключенной в объеме dx_k∙1 м² .Тогда часть плотности упругой энергии, приходящаяся на k-ю ось, будет равна
                                       
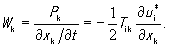
      Заметим, что здесь нет суммирования по индексу k. Складывая плотность упругой энергии для всех трех координатных осей, будем иметь полную плотность