Математическая модель укладки армирующих волокон в сферической оболочке
| Вид материала | Документы |
- Л. М. Чирок Математическая модель электрохимического датчика, 44.36kb.
- Игра как математическая модель конфликтной ситуации. Антагонистические игры, 56.39kb.
- Д. А. Силаев 1/2 года Физическое явление и математическая модель. Математическое исследование, 20.76kb.
- Математическая модель процессов взаимодействия диоксида серы со структурными элементами, 348.91kb.
- Правила и технология укладки уравнительных стыков на мостовых переходах Москва 2011, 1060.5kb.
- Гагарин В. Г., Козлов В. В. Математическая модель и инженерный метод расчета влажностного, 113.96kb.
- Журавлев С. Д., Жуков Р. А. Математическая модель эффективного использования земельных, 39.41kb.
- Вестник Брянского государственного технического университета. 2011. №4(32), 125.71kb.
- Содержание машиностроение, 267.31kb.
- Курсовой проект по дисциплине «технология научного исследования» на тему «методы программно-целевого, 122.89kb.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ УКЛАДКИ АРМИРУЮЩИХ ВОЛОКОН В СФЕРИЧЕСКОЙ ОБОЛОЧКЕ
Копытов Н.П., Митюшов Е.А.
Екатеринбург, Россия
В
 данной статье рассмотрена процедура получения математической модели укладки армирующих волокон при создании сферической оболочки, которая обеспечивает ее однородность и трансверсальную изотропию. Процесс укладки волокон при моделировании происходит по окружностям большого радиуса, плоскости которых поворачиваются таким образом, чтобы обеспечивалась их равновероятная ориентация.
данной статье рассмотрена процедура получения математической модели укладки армирующих волокон при создании сферической оболочки, которая обеспечивает ее однородность и трансверсальную изотропию. Процесс укладки волокон при моделировании происходит по окружностям большого радиуса, плоскости которых поворачиваются таким образом, чтобы обеспечивалась их равновероятная ориентация.Запишем уравнение окружности лежащей в плоскости
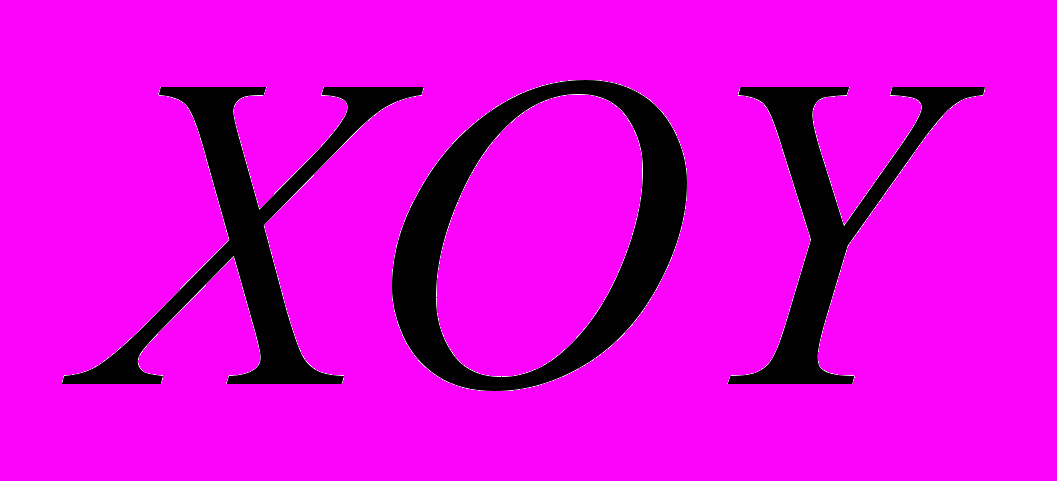 и c центром в начале системы координат, следующим образом:
и c центром в начале системы координат, следующим образом: , где
, где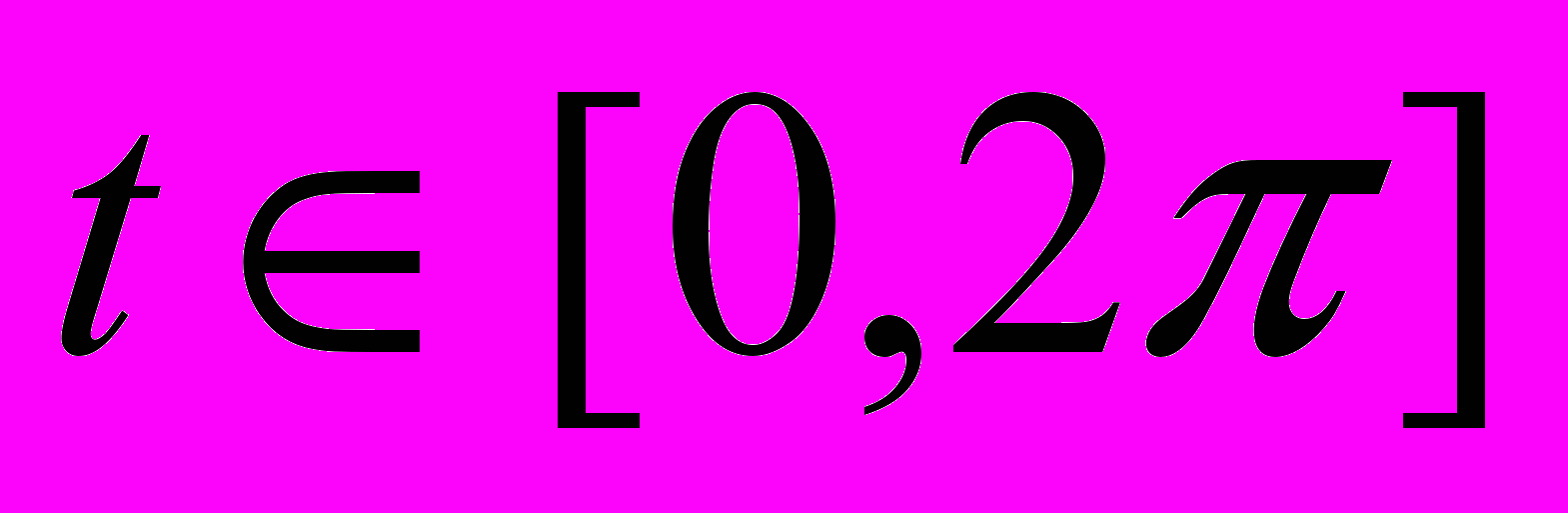 , а
, а  - радиус окружности.
- радиус окружности. Используя матрицу поворота относительно оси
 на угол
на угол  и матрицу поворота относительно оси
и матрицу поворота относительно оси  на угол
на угол  , получим уравнение окружности:
, получим уравнение окружности: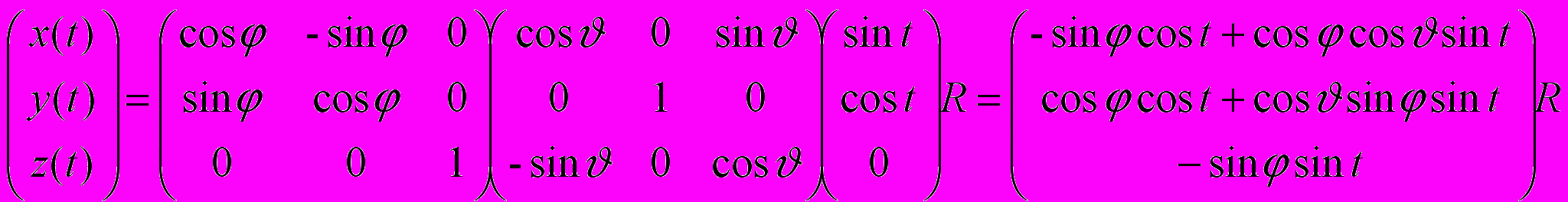 .
.Сферические углы, определяющие пространственное распределение окружностей, в случае равновероятного их распределения имеют следующую совместную плотность распределения:
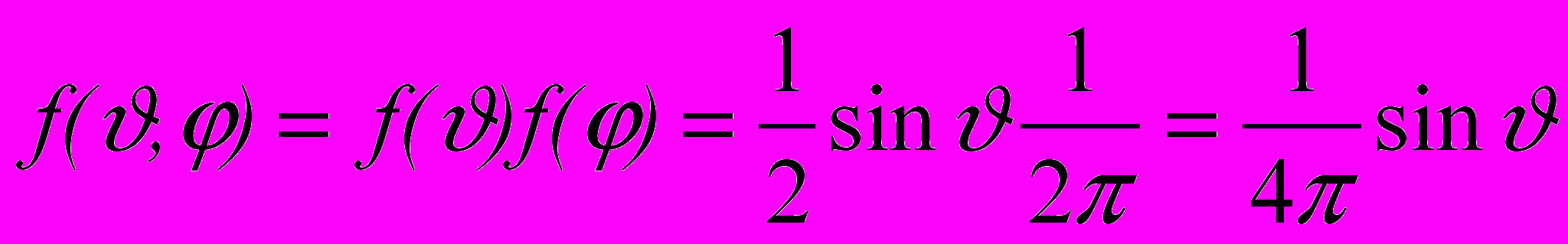 , где
, где 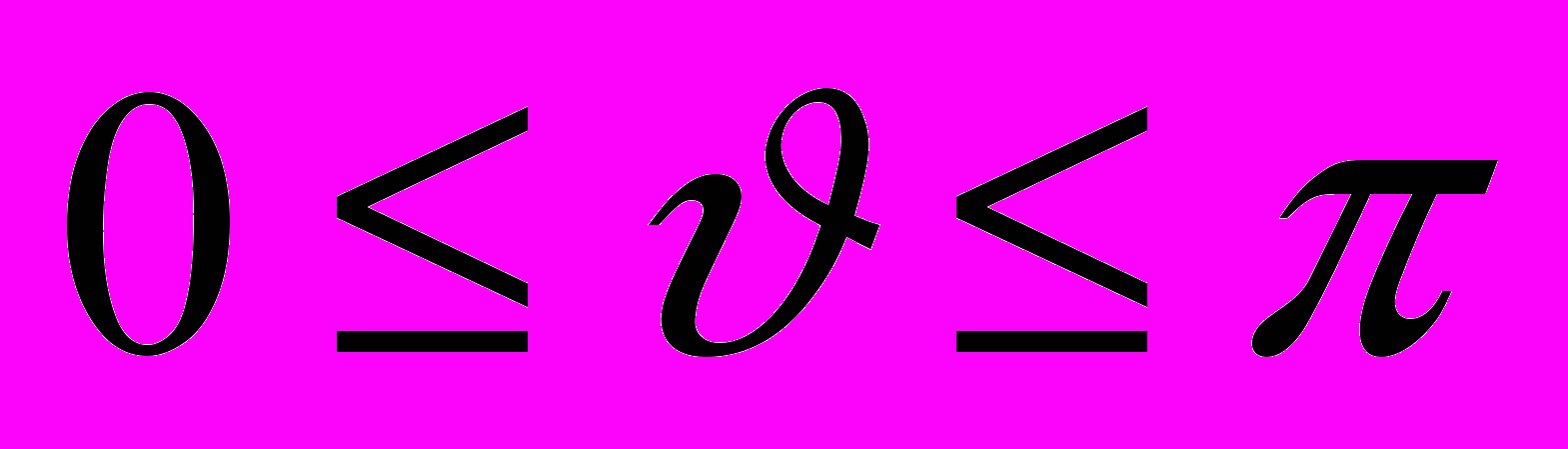 ,
, 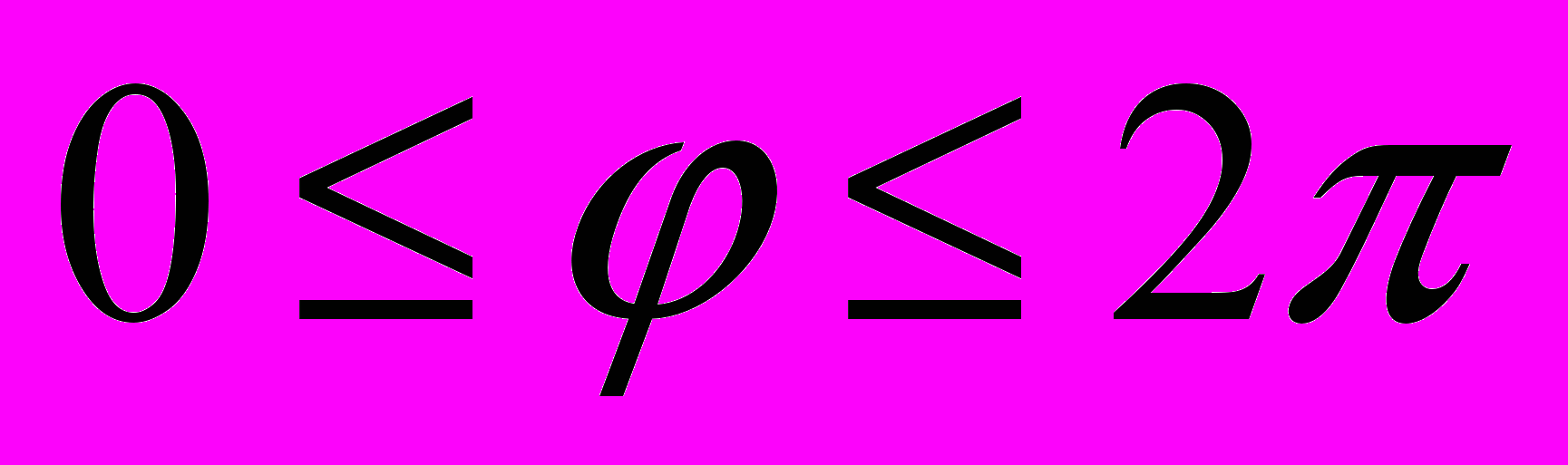 .
.П
 ри генерировании случайных чисел
ри генерировании случайных чисел  и
и , удовлетворяющих указанному закону, получается модель оптимального армирования сферической оболочки. В данной работе значения
, удовлетворяющих указанному закону, получается модель оптимального армирования сферической оболочки. В данной работе значения  и
и  генерировались согласно формулам:
генерировались согласно формулам: ,
, 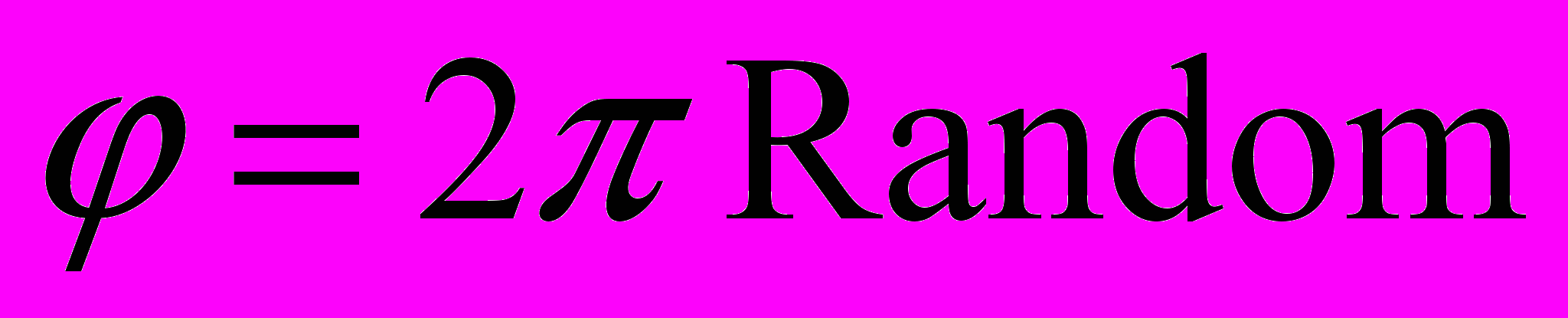 , где
, где  - случайное число с равномерным распределением на интервале
- случайное число с равномерным распределением на интервале 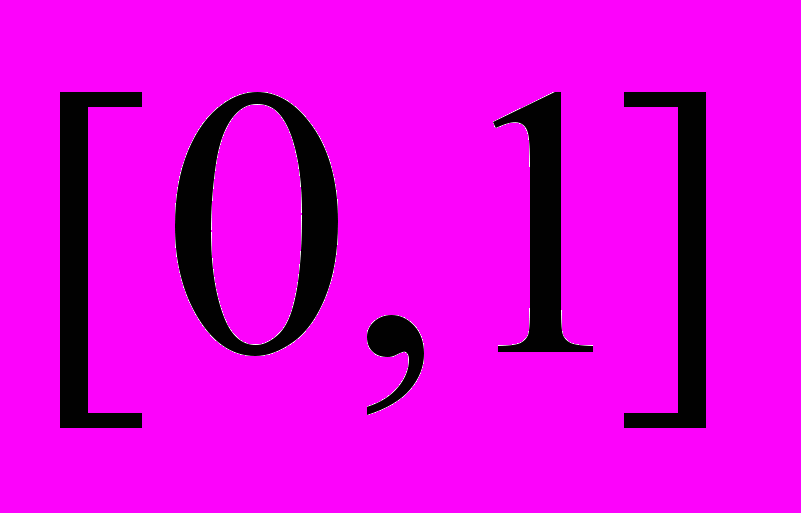 .
.Расчеты и визуализация выполнены с использованием программного комплекса Mathematica 5.0. На рисунке сверху представлено распределение точек по поверхности сферы, на рисунке снизу – распределение полуокружностей по поверхности полусферы. Оба рисунка получены на основании описанной выше математической модели.
Литература
1. Isotropic distribution in Spherical polar coordinate, ссылка скрыта
2. Sphere Point Picking, ссылка скрыта
3. Моделирование случайной величины с заданным законом распределения, ссылка скрыта
