Geum.ru

Журавлев С. Д., Жуков Р. А. Математическая модель эффективного использования земельных ресурсов. // Проблемы информатики в образовании, управлении, экономике и технике: Сб

Вид материалаДокументы

Содержание


Zhuravlev S.D., Zhukov R.A. The mathematical model of effective use of land resources.
Подобный материал:
Журавлев С.Д., Жуков Р.А. Математическая модель эффективного использования земельных ресурсов. // Проблемы информатики в образовании, управлении, экономике и технике: Сб. статей XI Междунар. научно-техн. конф. – Пенза: ПДЗ, 2011. – С.  44 47.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭФФЕКТИВНОГО ИСПОЛЬЗОВАНИЯ ЗЕМЕЛЬНЫХ РЕСУРСОВ

С.Д. Журавлев, Р.А. Жуков

Тульский филиал Российской академии народного хозяйства
и государственной службы при Президенте РФ,
г. Тула, Россия, ZhuravlSD@yandex.ru
Тульский институт экономики и информатики,
г. Тула, Россия, pluszh@mail.ru

Представлена математическая модель эффективного использования земельных ресурсов, разработанная на основе корреляционно-регрессионного и факторного анализа.


Zhuravlev S.D., Zhukov R.A. The mathematical model of effective use of land resources. The mathematical model of an effective use of the land resources, constructed on the basis correlation-regressive and the factorial analysis is represented.


Рассмотрим два множества и 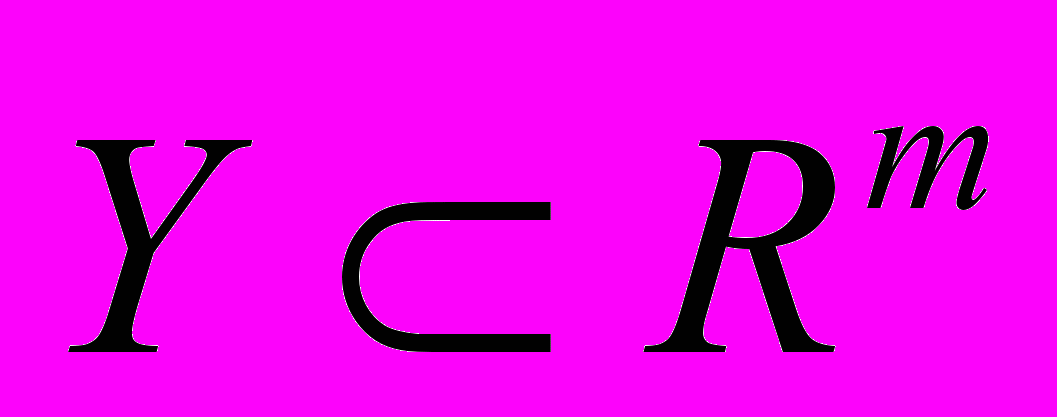. При этом существует некоторый n-мерный вектор 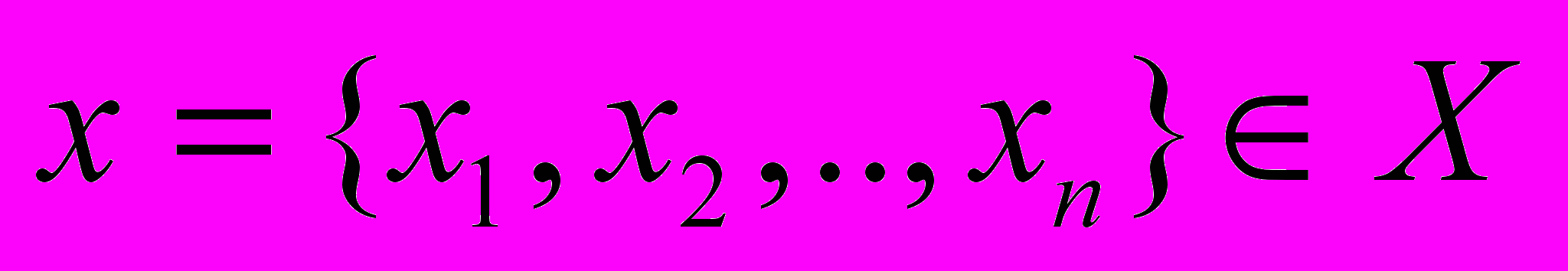, отражающий факторные признаки, и m мерный вектор 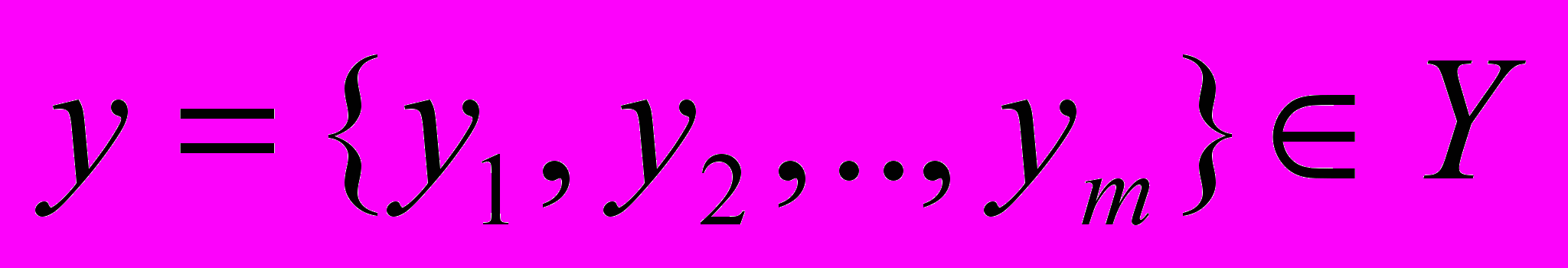, характеризующий результаты производственной деятельности сельскохозяйственных организаций. Пусть имеется некоторая функция f такая, что каждому значению 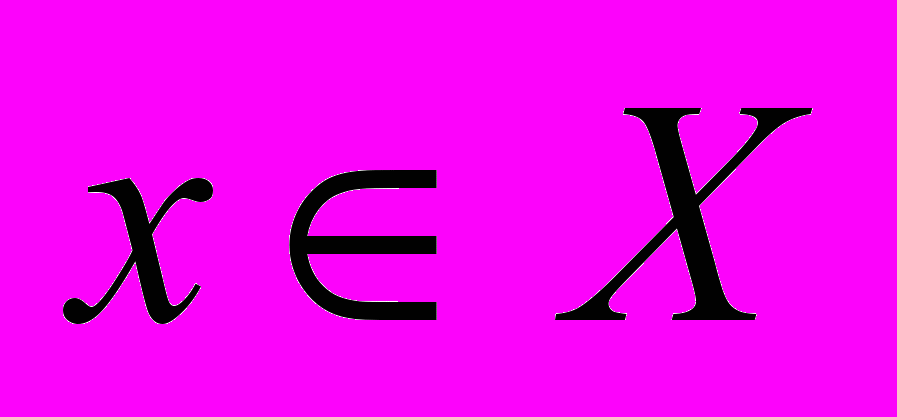ставит в соответствие значение :

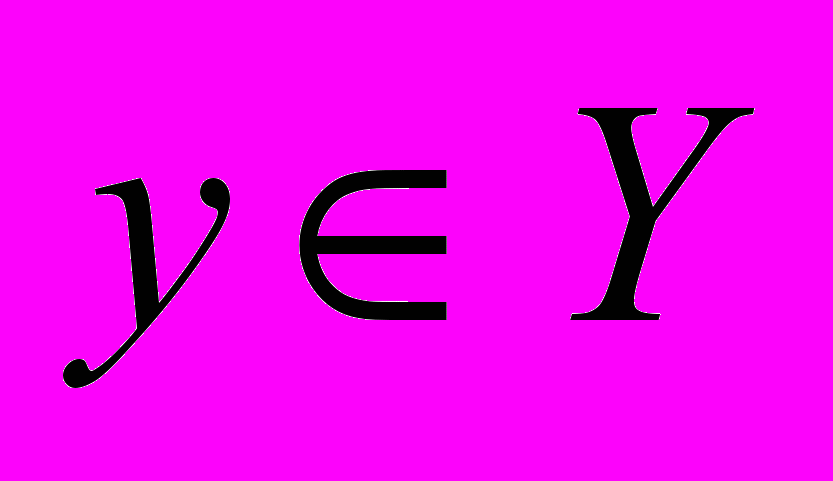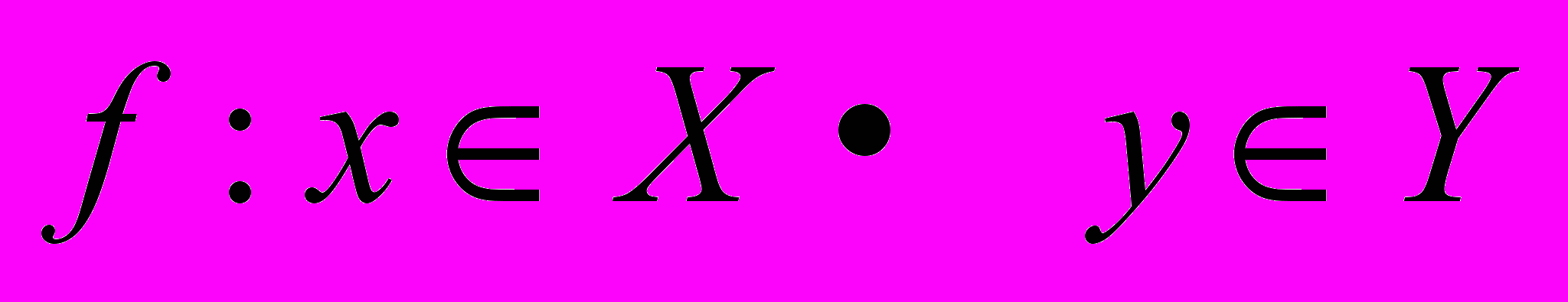(1)

Используя традиционную форму записи, выражение (1) можно представить как

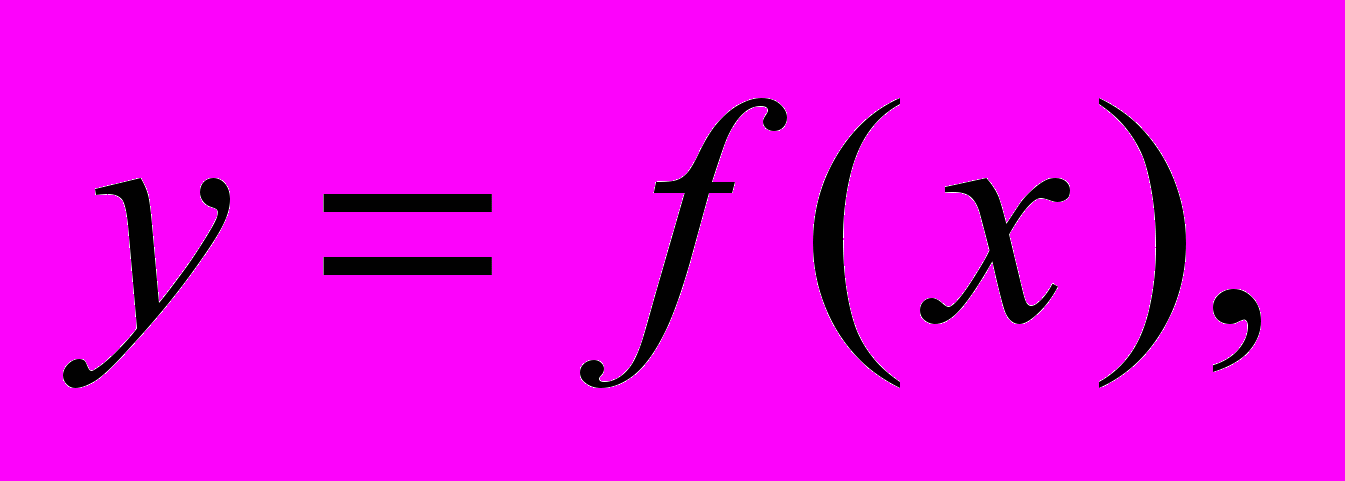(2)

где , .

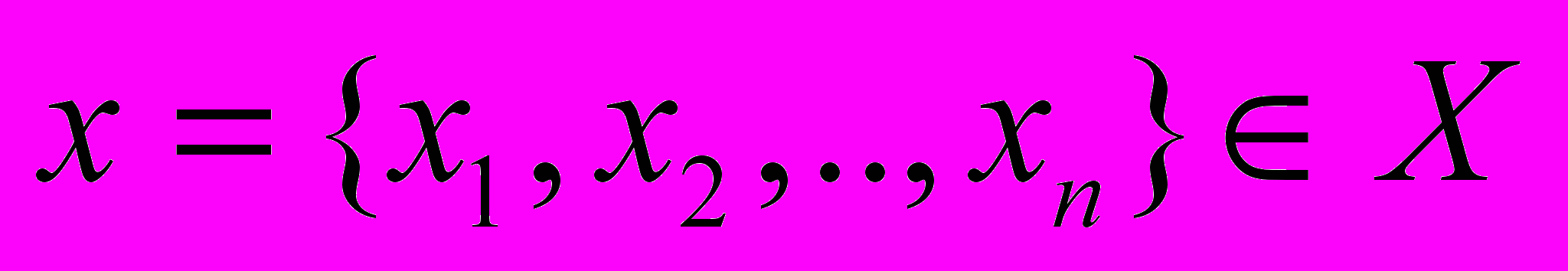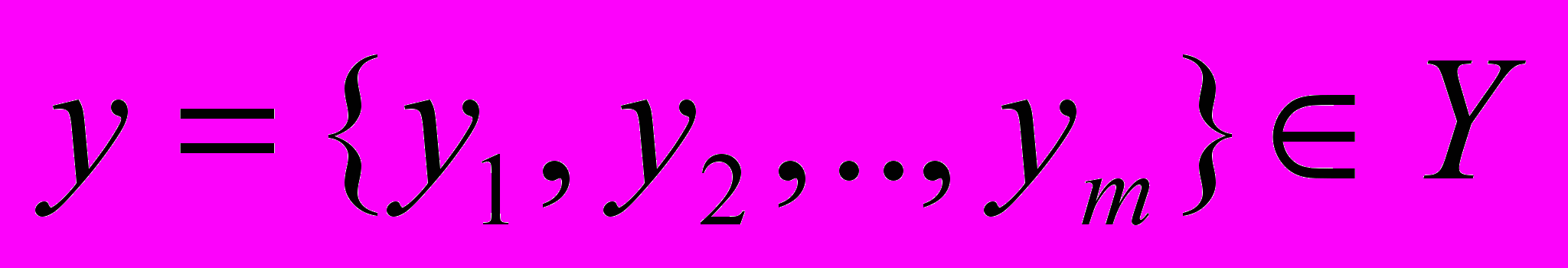В линейном случае уравнение (2) можно представить в матричной форме:

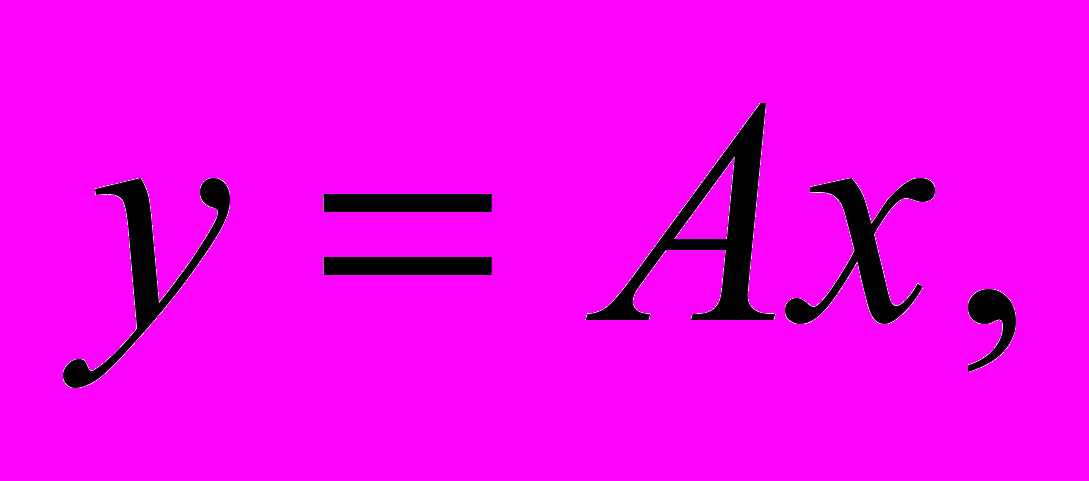(3)

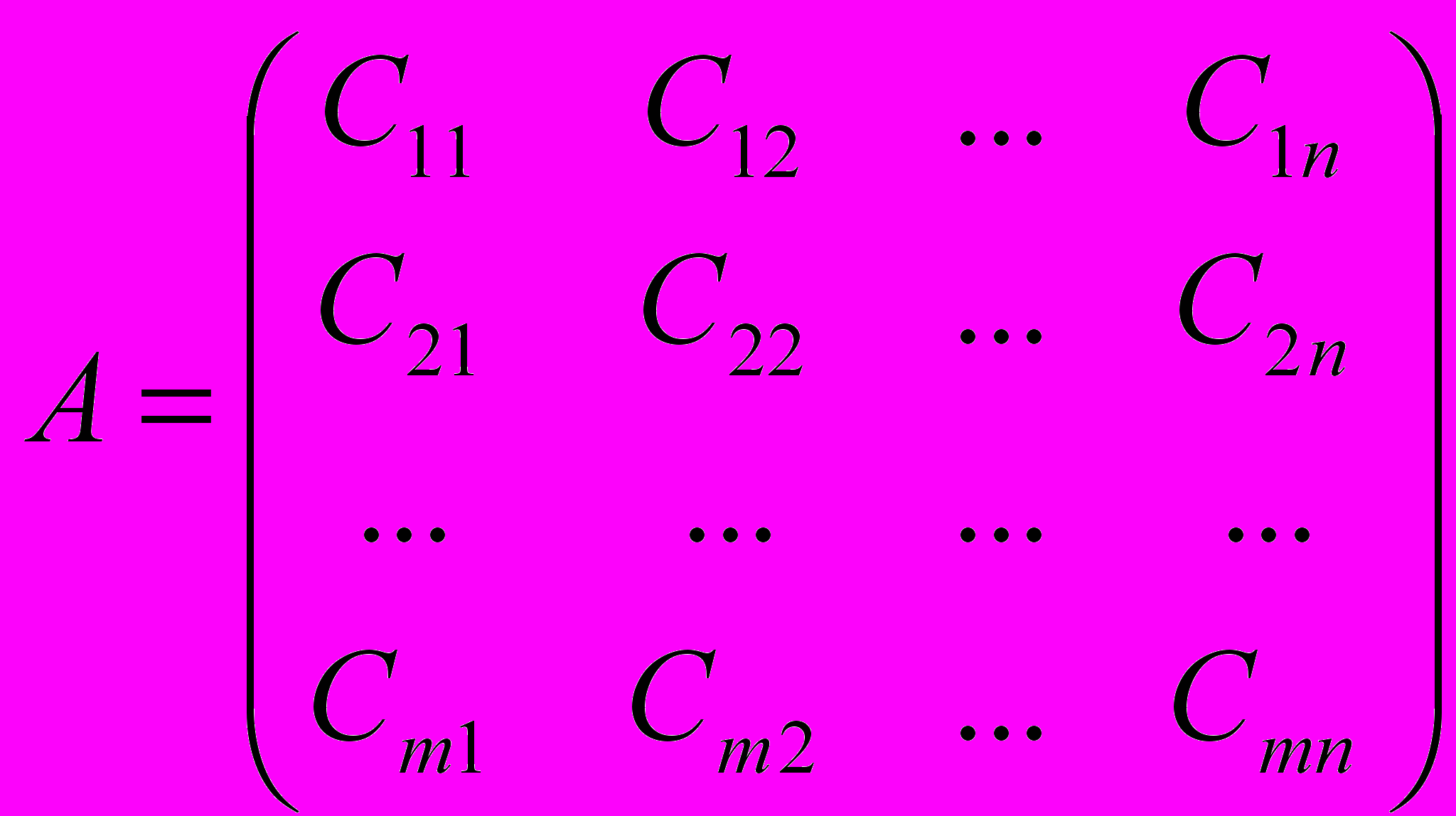где . (4)

Здесь 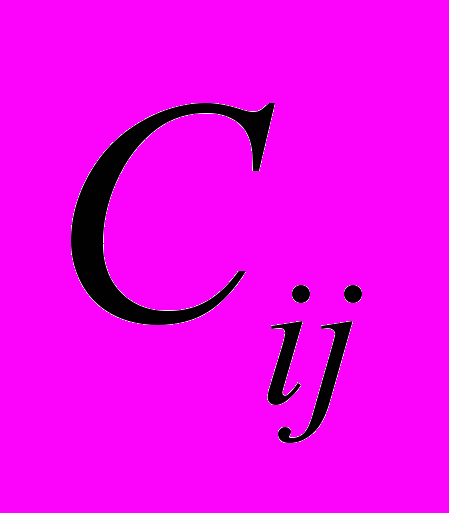– некоторые постоянные коэффициенты, которые определяются на основании корреляционно-регрессионного анализа, i=1..m, j=1..n.

Рассмотрим выражение, аналогичное (2), и представим каждый из компонентов вектора 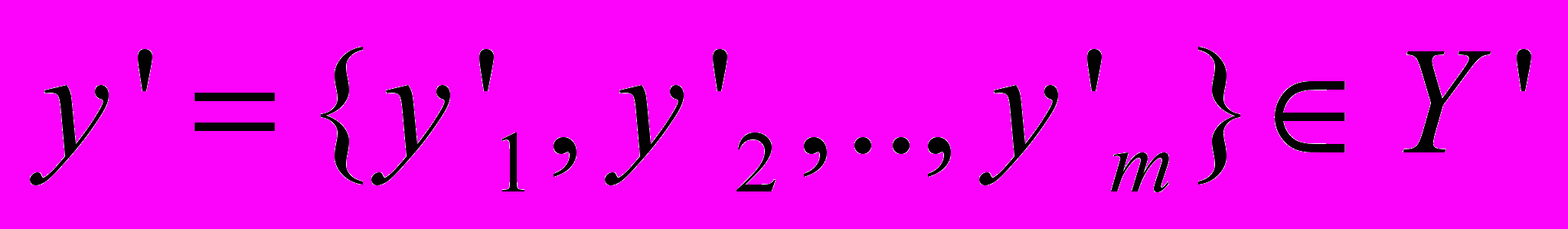, в виде линейной зависимости. Для простоты рассмотрим зависимость 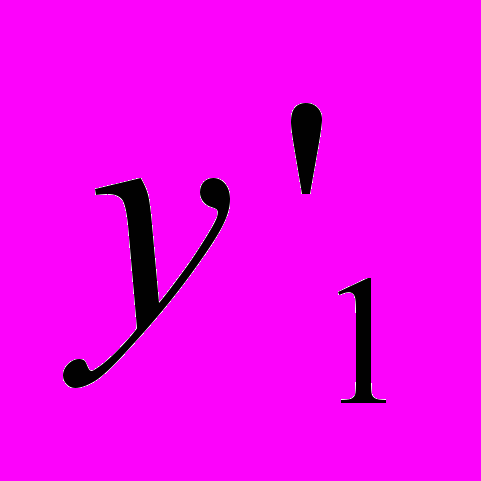от .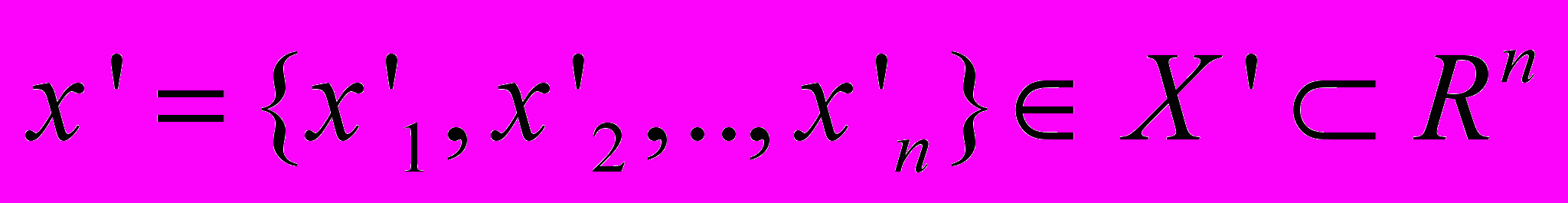

Представим данное соотношение в линейном виде:

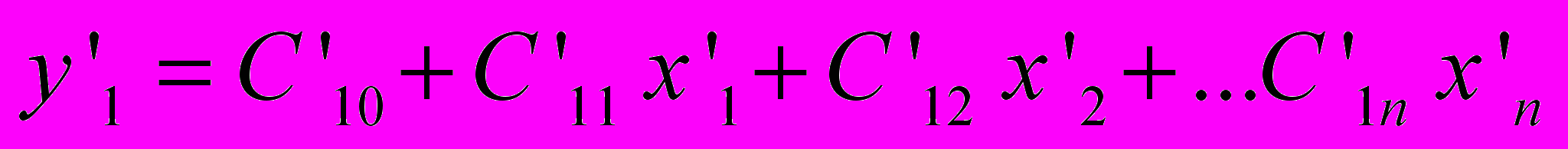, (5)

где 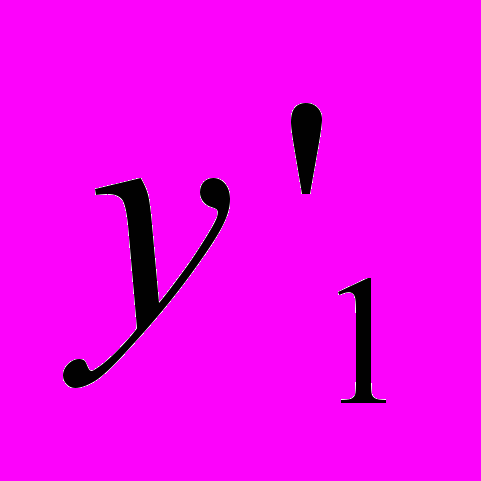– результативный показатель (наблюдаемое явление); 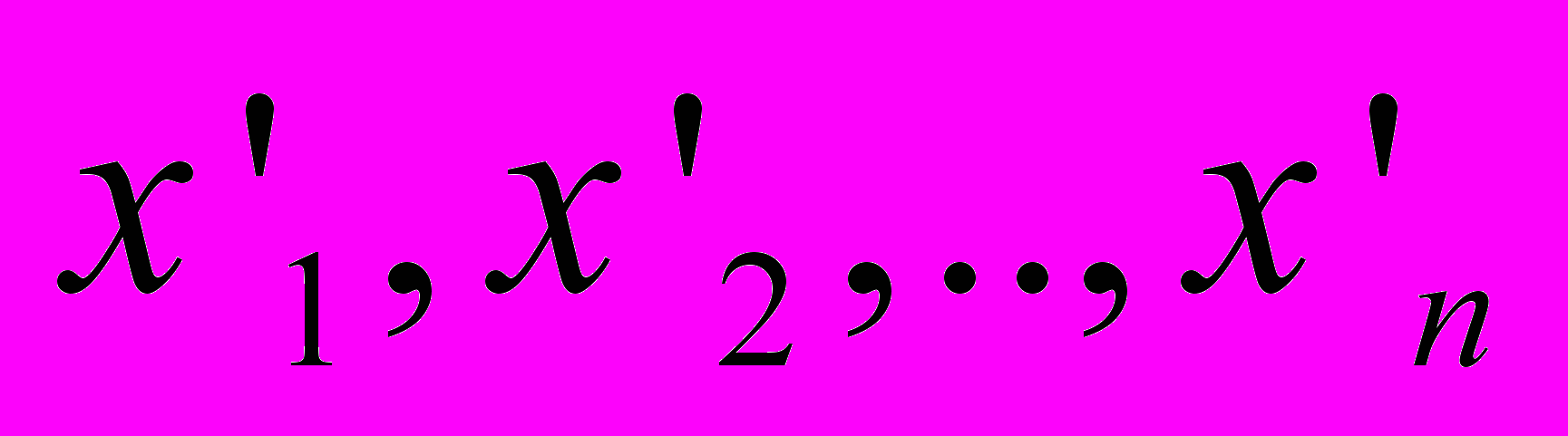– факторные признаки (условия, при которых наблюдается явление), выраженные в натуральных или стоимостных единицах измерения (множественная регрессия, причем некоторыми факторными признаками можно управлять).

Для отыскания параметров в (5) воспользуемся методом наименьших квадратов:

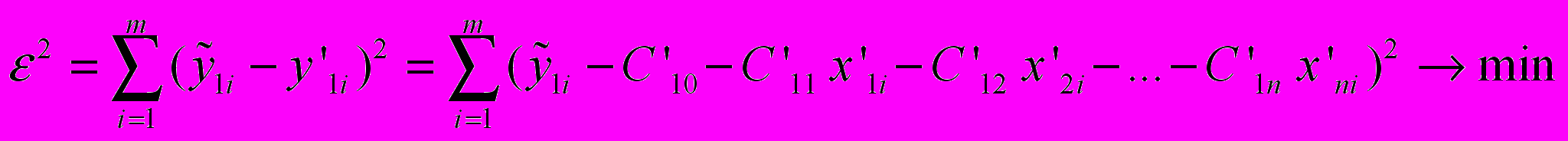, (6)

где 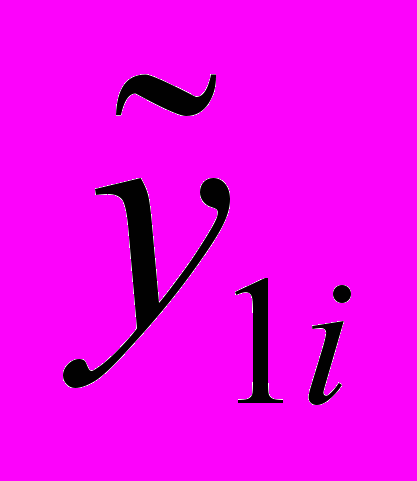– фактические значения результативного признака, выраженные в натуральных или стоимостных единицах измерения; 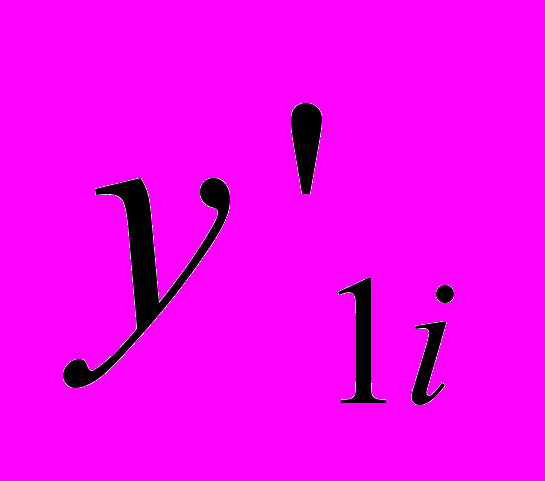– значение результативного показателя, рассчитанное по регрессионной модели; – сумма квадратов ряда остатков; m – число наблюдений.

Для анализа силы воздействия факторных признаков на результат с целью сравнения влияния на зависимую переменную объясняющих переменных, когда они представлены в разных единицах измерения, возникает необходимость использования безразмерных величин. Тогда в уравнении (5) вместо 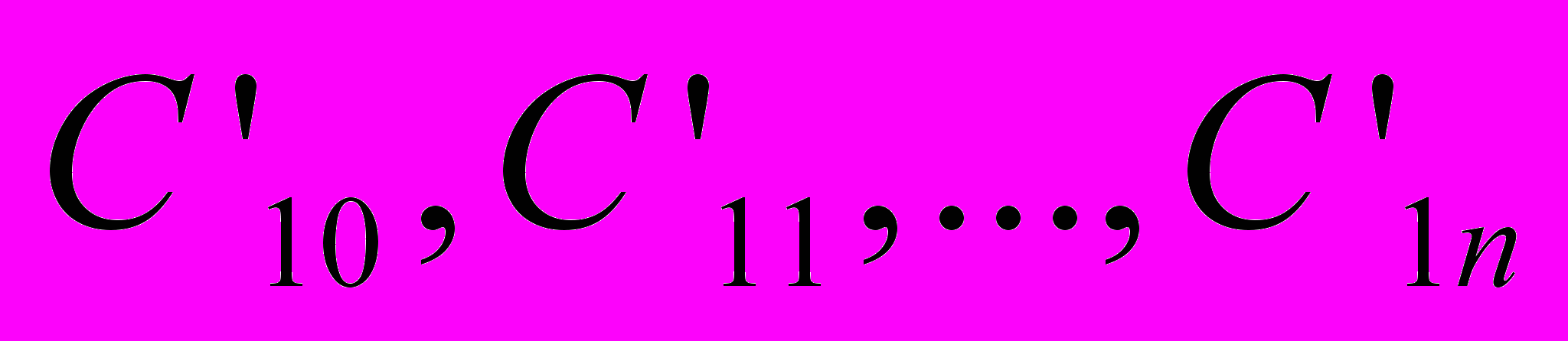должны фигурировать стандартизованные коэффициенты регрессии 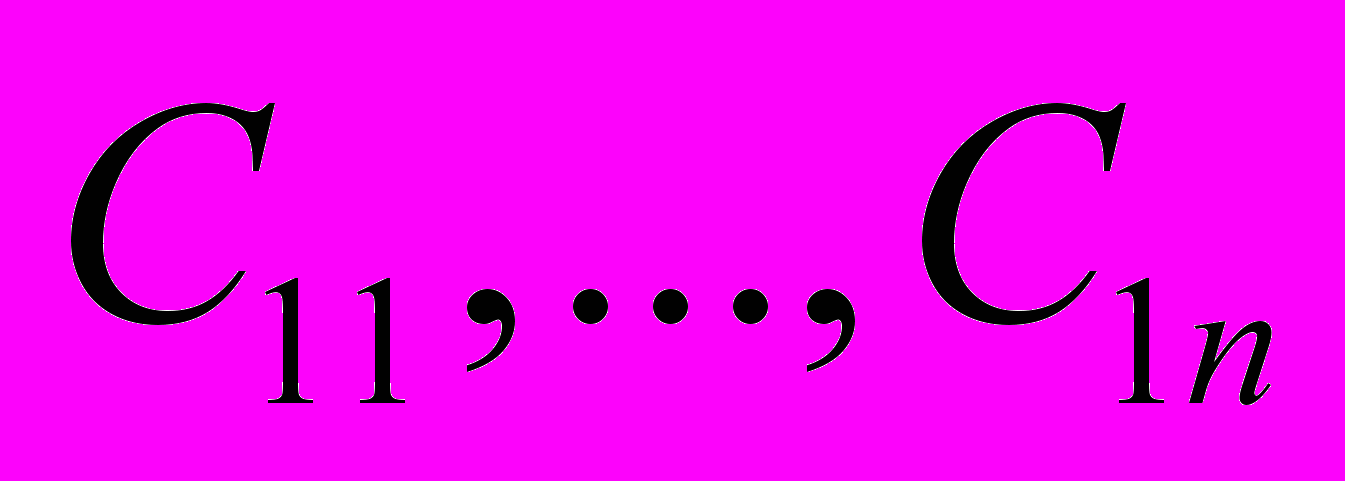и стандартизованные переменные:

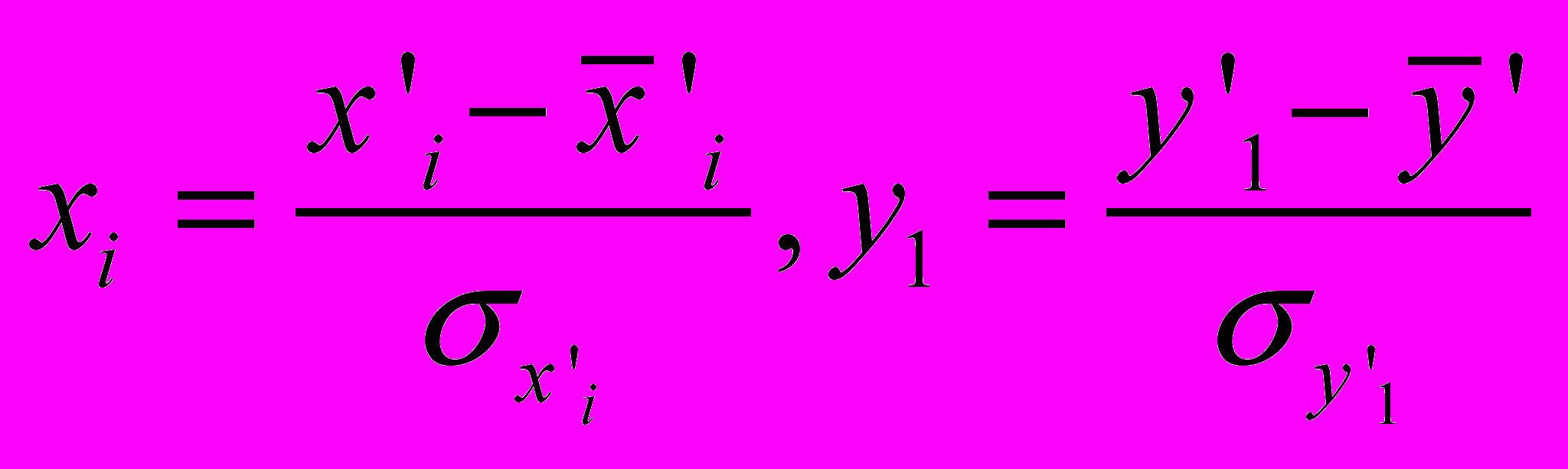, (7)

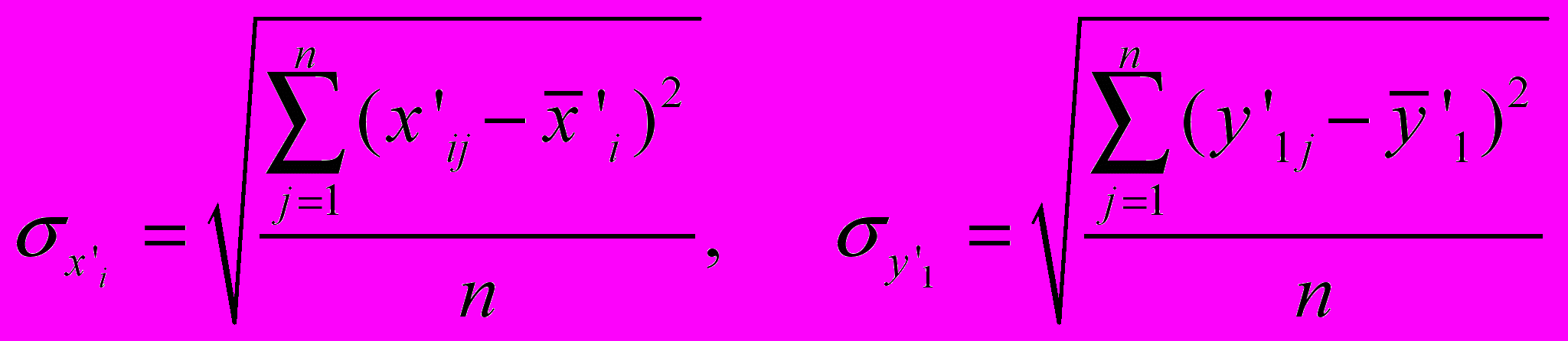где , (8)

соответствующие среднеквадратические отклонения (для количества наблюдений меньше 30 в знаменателе следует использовать выражение (n-1), а

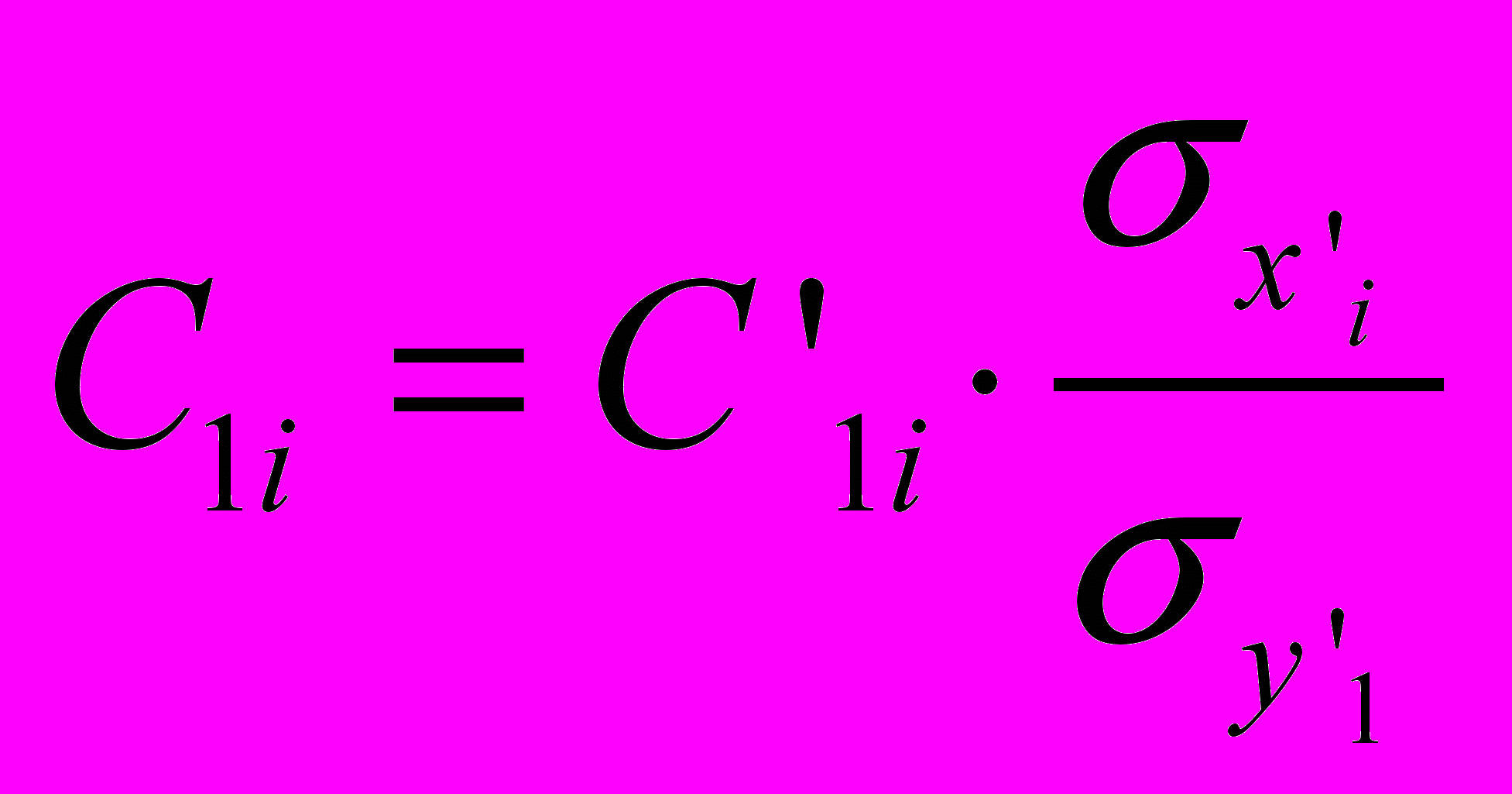. (9)

Стандартизованный коэффициент регрессии показывает, на сколько величин 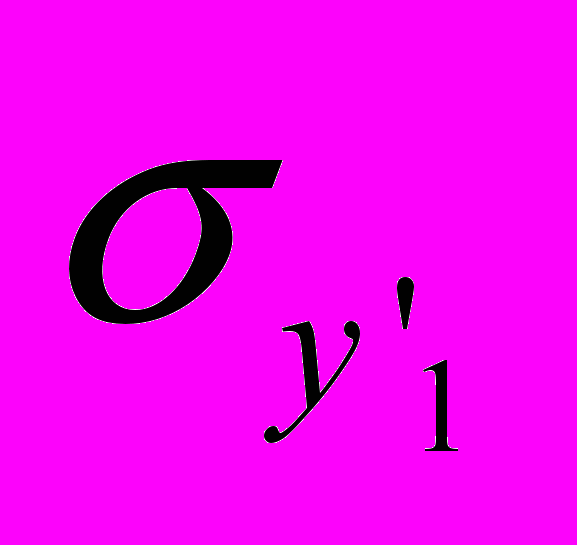изменится в среднем результативный показатель 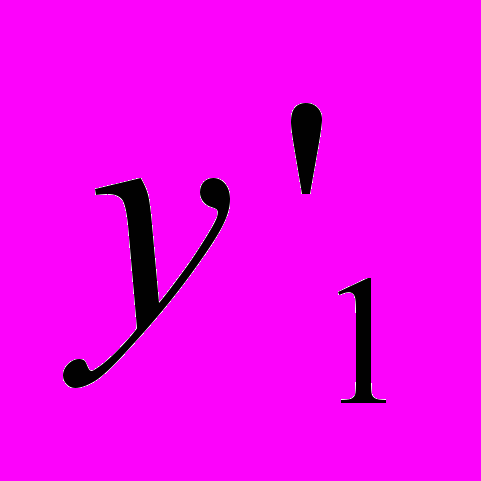при увеличении факторного признака 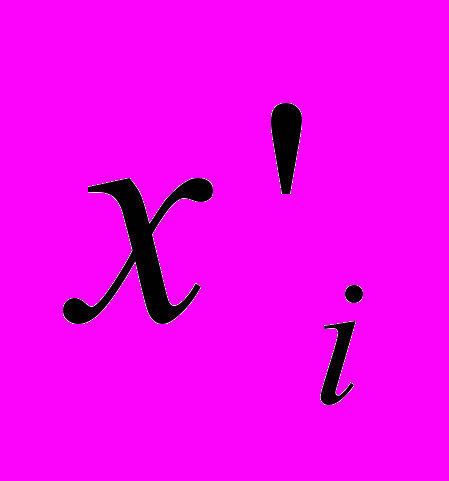на величину .

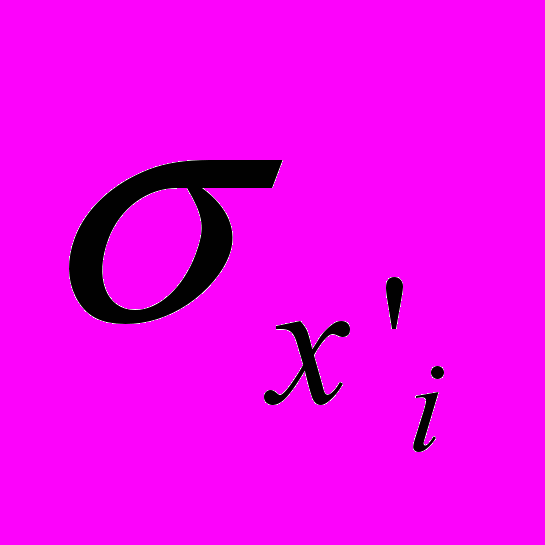Применяя преобразования (7) – (9), суть которых в приведении показателя к стандартизованному виду, приходим к следующему виду регрессионной модели:

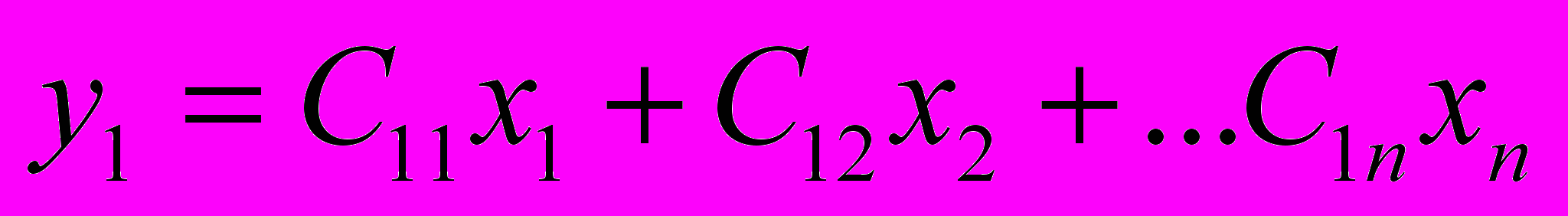, (10)

Обобщая представленную методику на случай m результативных признаков, имеем:

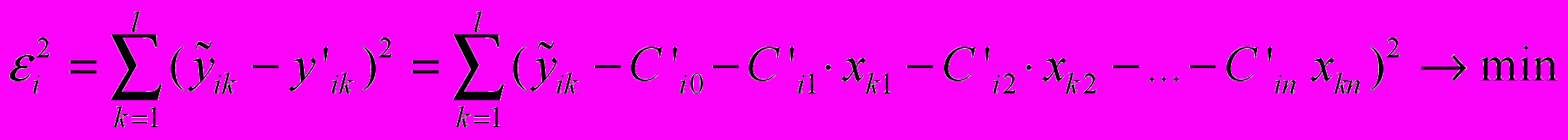(11)

или

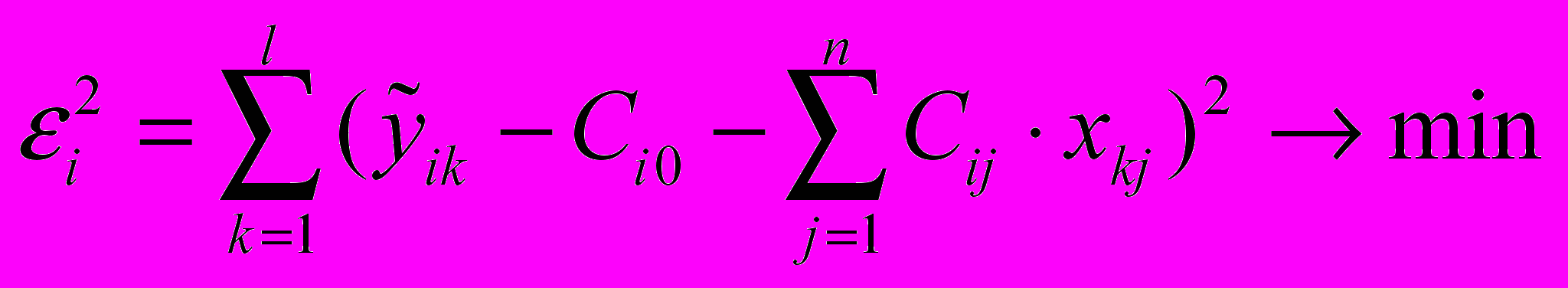. (12)


Здесь l – число наблюдений (количество взятых в рассмотрение единиц совокупности): i=1..m – индекс результативного показателя. Для отыскания минимума возьмем частные производные по неизвестным параметрам и приравняем их к нулю:

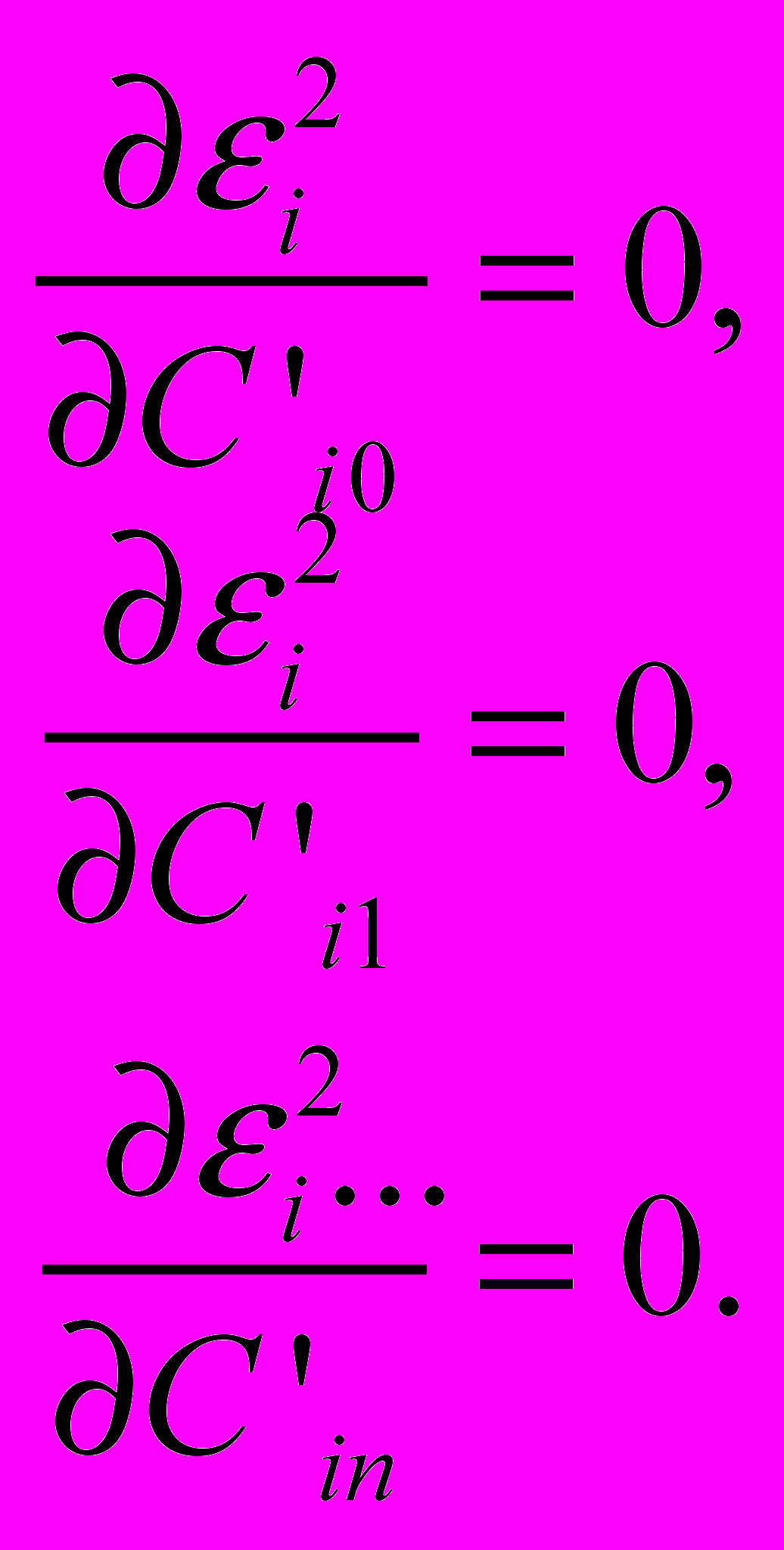(13)

Тогда полученная система линейных уравнений примет вид:

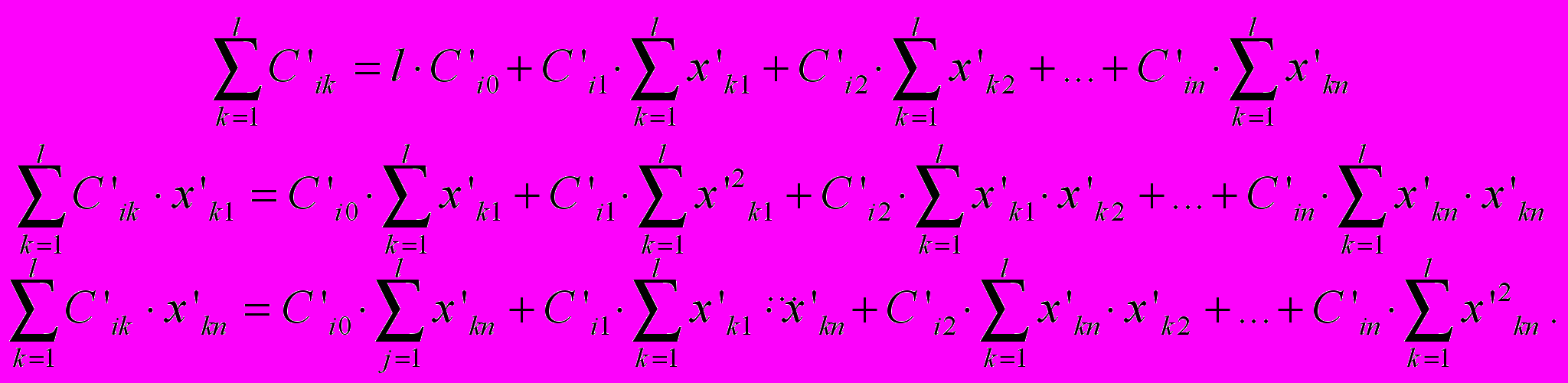(14)

Из (14) однозначно находятся параметры 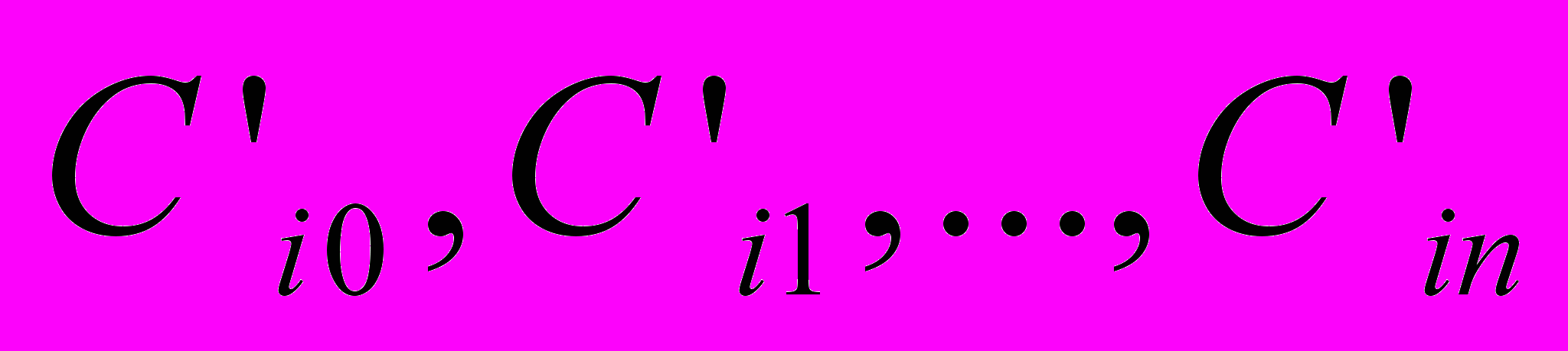, причем такие соотношения формируются для каждого i=1..m.

Для решения системы алгебраических уравнений (14) можно воспользоваться одним из известных методов, например, методом Крамера, методом Гаусса, Жордано и др. Переходя к стандартизованному виду и используя соотношения (7)-(9), имеем набор моделей, каждая из которых характеризует выбранный результативный признак:

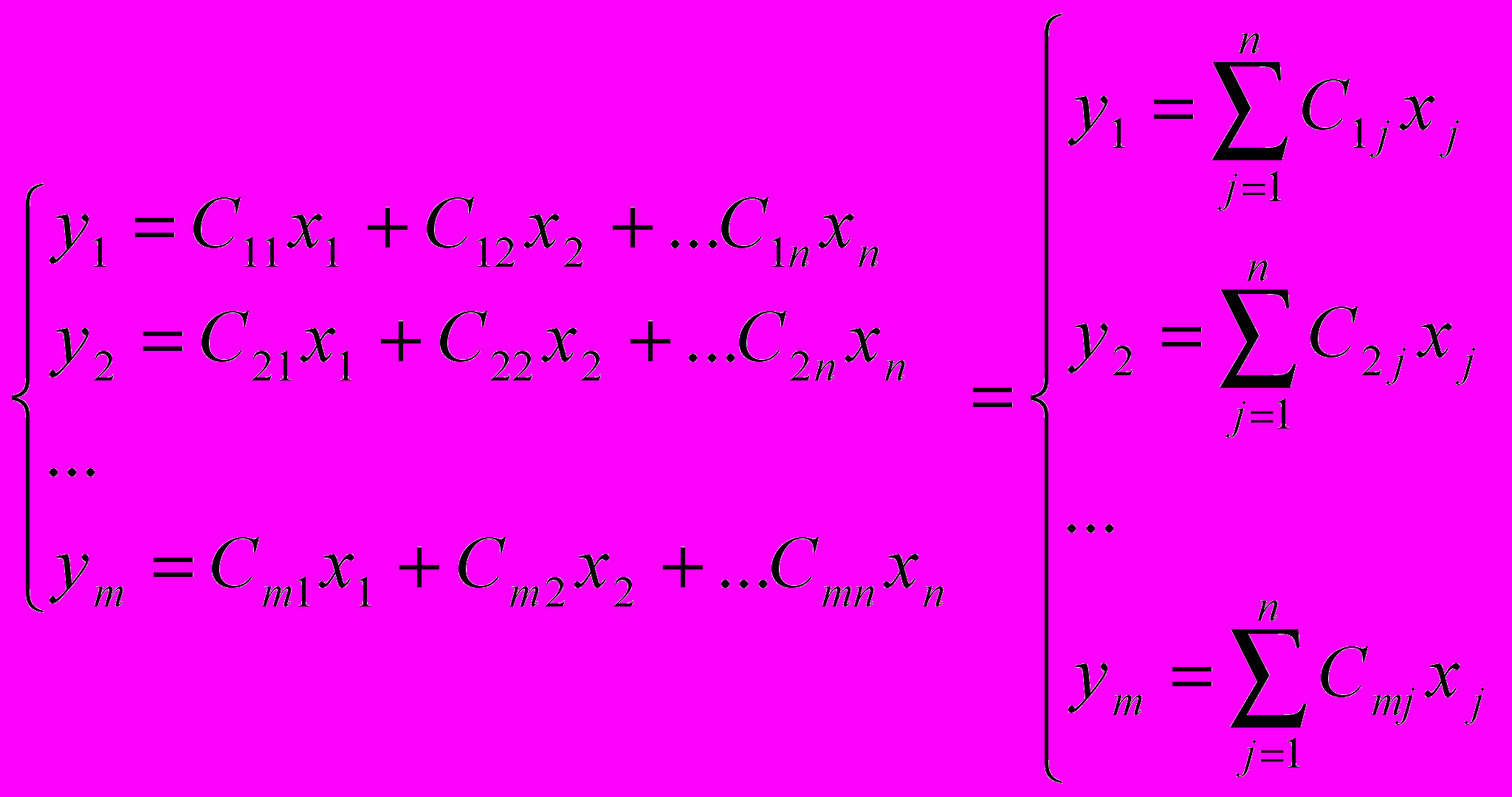, (15)

Модели, представленные в форме (15) (в матричном виде используется соотношение (3), позволяют вычислить средние значения результативных показателей по исследуемому объекту: муниципальному образованию, региону, федеральному округу и т.д. В этом аспекте будем считать их «нормативными» и использовать для последующего анализа хозяйственной деятельности объектов на обособленной территории, в частности, для анализа эффективности использования земельных ресурсов.

Представляется, что разработанный подход является универсальным для анализа показателей, имеющих различную природу, и его можно применять для изучения процессов деятельности подсистем экологического, социального и экономического характера.

Следует отметить, что в моделях должны фигурировать существенные факторы, оказывающие наибольшее влияние на результативный признак, что определяется на основе факторного анализа. Это является необходимым (но недостаточным) условием для формирования оптимальных управляющих воздействий, направленных на эффективное использование земельных ресурсов.