Прошина Р. Д., Слесарев Ю. Н. Методы построения математических моделей в пространстве состояний. // Проблемы информатики в образовании, управлении, экономике и технике: Сб
| Вид материала | Анализ |
- Прошина Р. Д., Слесарев Ю. Н. Математическое моделирование асинхронного электропривода, 40.5kb.
- Об использовании Нобелевских лекций в информационных технологиях. // Проблемы информатики, 110.52kb.
- Поддубный А. П., Юрков Н. К., Якимов А. Н. Фрактальный подход к сжатию информации., 47.01kb.
- Журавлев С. Д., Жуков Р. А. Математическая модель эффективного использования земельных, 39.41kb.
- Дрождин В. В., Масленников А. А., Сергеев А. С. Использование протоколов запросов для, 63.12kb.
- Н. Н. Яремко Пензенский государственный педагогический университет им. В. Г. Белинского, 53.48kb.
- Демидова Л. А., Коротаев А. Н. Генетический алгоритм настройки параметров системы нечеткого, 38.47kb.
- Титов Д. В., Кобак В. Г. Анализ подходов к улучшению результатов работы генетического, 82.51kb.
- Кацюба О. А., Тимонин Д. В. Нахождение параметров нелинейных класса Гаммерштейна динамических, 21.38kb.
- Герасимов А. Ф., Федотов Н. Г. Опотоковом методе анализа движений денежных средств, 28.85kb.
Прошина Р.Д., Слесарев Ю.Н. Методы построения математических моделей в пространстве состояний. // Проблемы информатики в образовании, управлении, экономике и технике: Сб. статей XI Междунар. научно-техн. конф. – Пенза: ПДЗ, 2011. – С. 56 59.
МЕТОДЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ
В ПРОСТРАНСТВЕ СОСТОЯНИЙ
Р.Д. Прошина, Ю.Н. Слесарев
Пензенский государственный педагогический университет
им. В.Г. Белинского,
г. Пенза, Россия, proshin@pgta.ru
Представлена система методов математического моделирования технических объектов в пространстве состояний. Приведены алгоритм и синтезированные математические модели систем управления в нормальной форме пространства состояний.
Proshina R.D., Slesarev Yu.N. The methods of construction of mathematical models in state space. A system of mathematical modeling of technical objects in the space of states is shown. The algorithms and mathematical models of the synthesized control system in the normal form of the state space are given.
Анализ и синтез систем управления (СУ) различных технических объектов (ТО) в условиях интегрированного комплекса сетевых автоматизированных лабораторий (ИКСАЛ) [1, 2] наиболее эффективно проводить на компьютерах с использованием методов математического моделирования в форме пространства состояний (ПС). При этом множество и специфика решаемых при исследовании технических объектов в ИКСАЛ задач часто приводит к противоречивым требованиям, предъявляемым к математическим моделям элементов СУ, что обусловливает необходимость применения для их анализа и синтеза различных методов моделирования [3].
Алгоритм построения моделей одномерных САУ в нормальной форме (НФ) пространства состояний основан на преобразовании математической модели “вход – выход” в виде передаточной функции канонической формы. В соответствии с введёнными методами предлагаемый алгоритм включает построение двух групп моделей вложенной структуры:
– с обратными связями по переменным состояния и с суммированием на входе;
– с местными обратными связями по выходу.
В первой группе на вход системы поступает взвешенная сумма переменных состояния, во второй группе – каждая переменная состояния формируется с учётом последней координаты состояния системы для моделей с прямой причинно-следственной связью и по первой координате состояния для моделей с обратной причинно-следственной связью.
Для первой группы моделей НФ с прямой и обратной причинно-следственной связью матрицы системы формируются в виде:
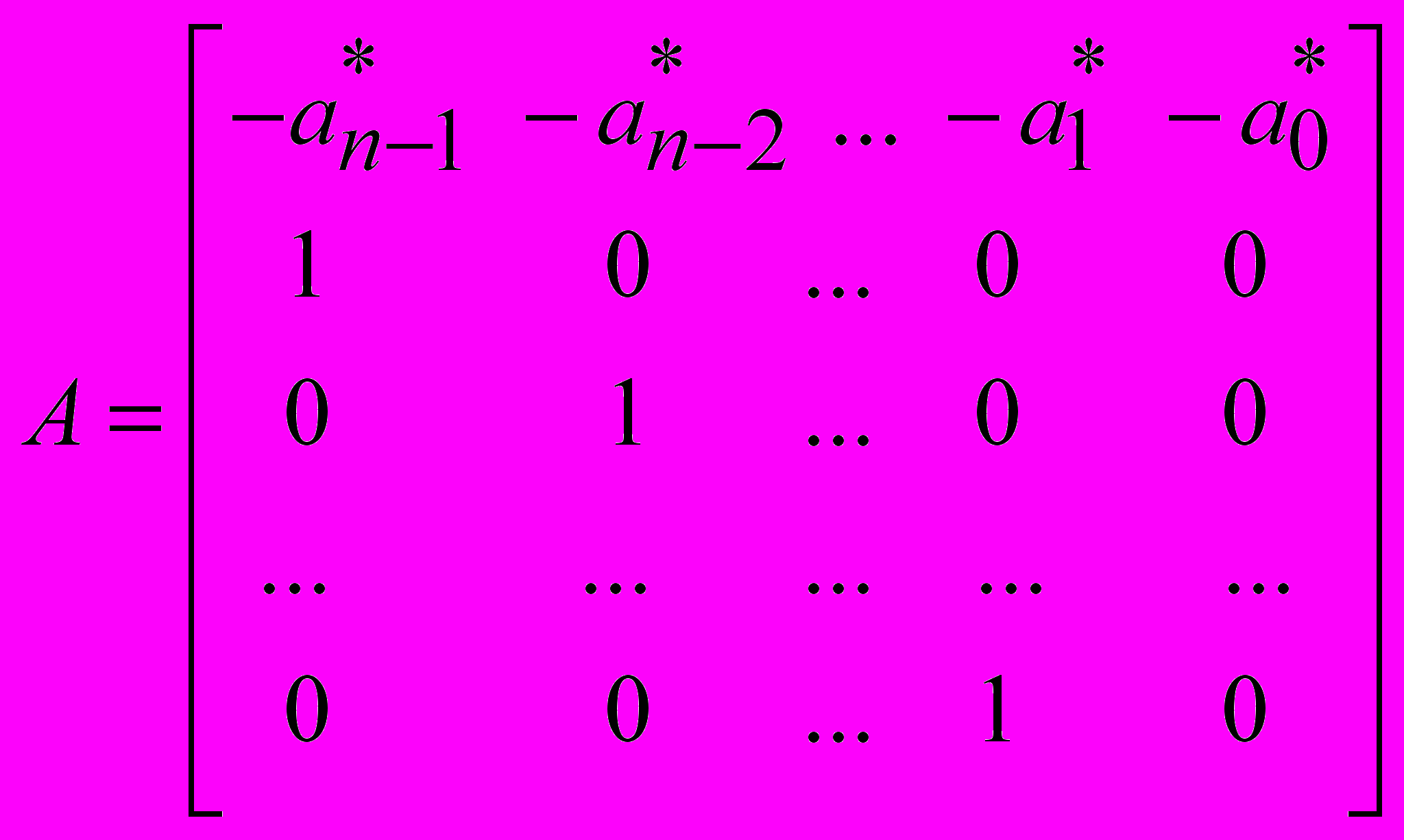 ;
;  . (1)
. (1)Для второй группы соответственно в моделях с прямой и обратной причинно-следственной связью задаётся так
 ;
;  . (2)
. (2)Матрицы управления и наблюдения для первой модификации первой группы моделей:
 ;
;  ,
,  ;
;  (3)
(3)формируются с использованием коэффициентов
 :
: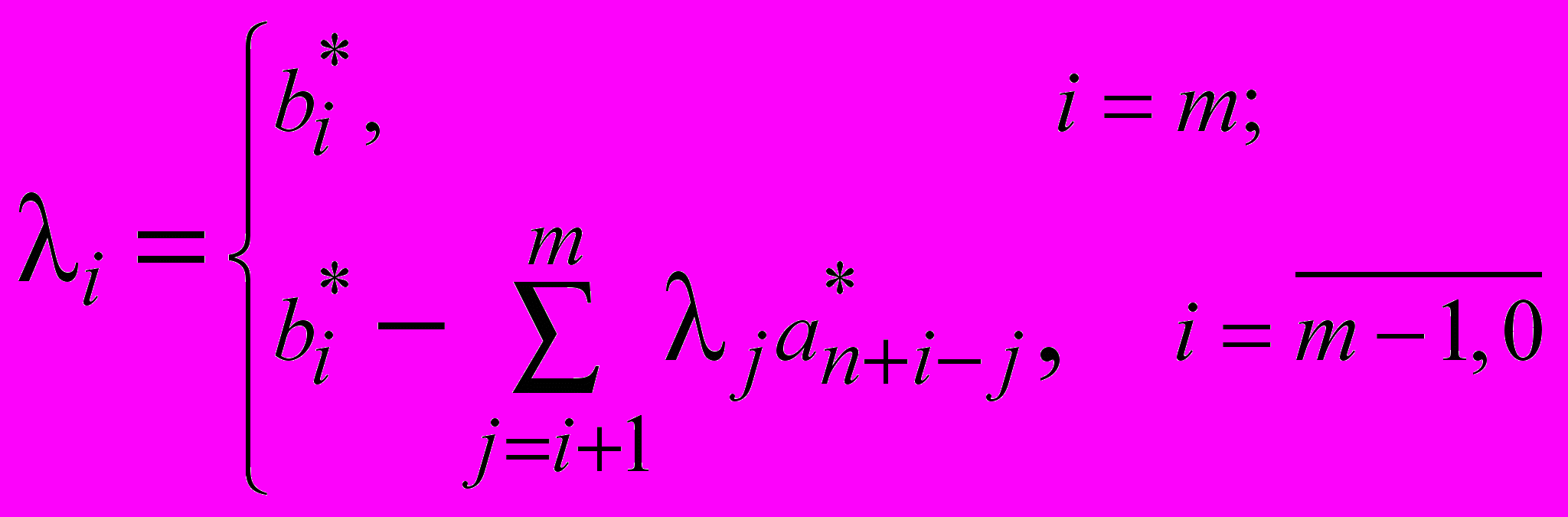 ,
,а для второй группы посредством коэффициентов
 :
: ,
,  .
. ;
;  ,
,  ;
;  . (4)
. (4)Формирование матриц управления и наблюдения второй модификации, наоборот, обеспечивается для первой группы применением коэффициентов
 :
: ;
; ,
,  ;
;  ,
,а для второй группы – коэффициентов
 :
: ;
; 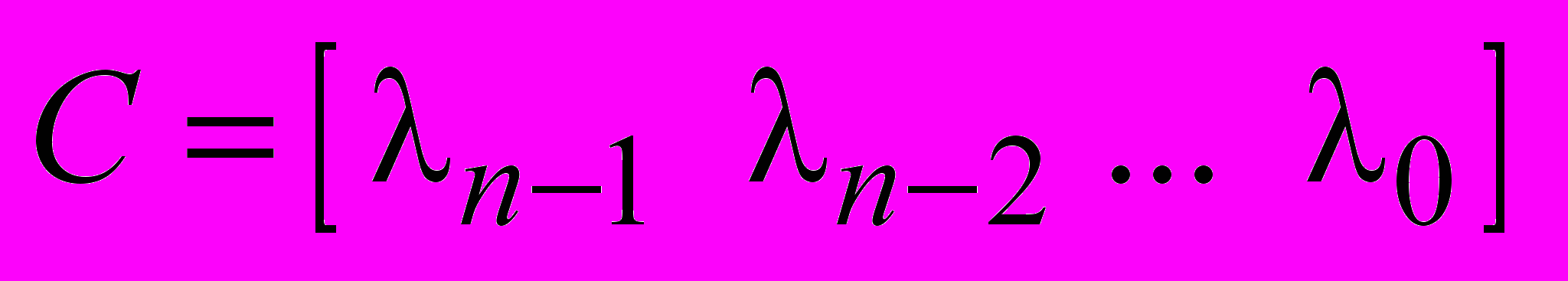 ,
,  ;
; 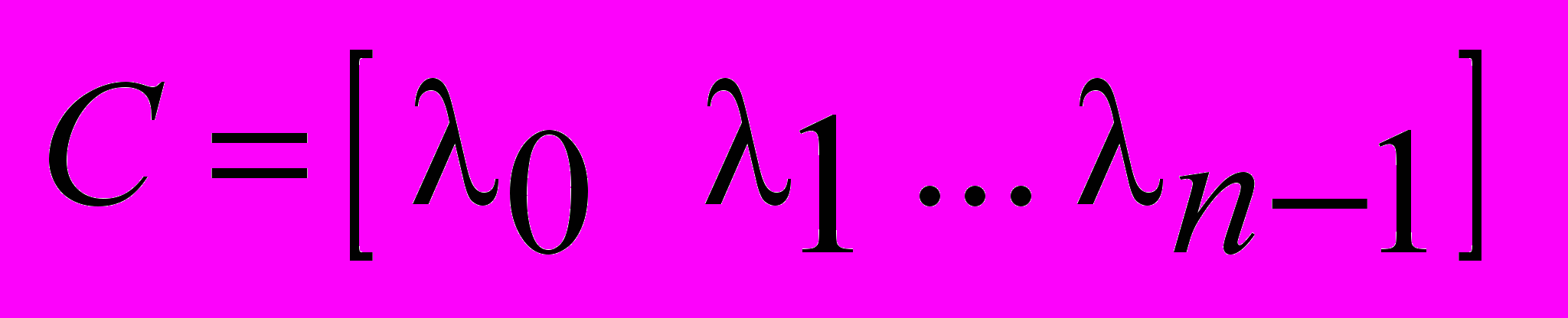 .
.Порядок следования коэффициентов в матрицах управления и наблюдения для моделей с прямой и обратной причинно-следственной связью взаимно противоположен.
Таким образом, разработан единый комплекс методов построения математических моделей в нормальной форме пространства состояний, обеспечивающий синтез семейства из восьми модификаций моделей и повышающий эффективность математического моделирования систем управления с различной структурой при использовании всевозможных сочетаний методов, отражающих особенности отдельных компонентов исследуемой системы. Предложены вычислительные алгоритмы формирования математических моделей с прямой и обратной причинно-следственной связью двух групп моделей вложенной структуры: с обратными связями по переменным состояния и с суммированием на входе; с местными обратными связями по последней и первой координате состояния соответственно.
Библиографический список
1. Прошин И.А., Прошин Д.И., Прошина Р.Д. Концепция построения интегрированных комплексов сетевых автоматизированных лабораторий. // Известия Самарского научного центра Российской Академии наук. –
2009. – №2. – С. 527–530.
2. Прошин И.А., Прошин Д.И., Прошина Р.Д. Программная платформа для построения интегрированного комплекса сетевых автоматизированных лабораторий (ИКСАЛ). // Известия Самарского научного центра Российской Академии наук. – 2009. – №2. – С. 531–536.
3. Прошина Р.Д. Математическое моделирование технических систем в нормальной форме пространства состояний. // Известия Самарского научного центра Российской Академии наук. – 2011. – №1. – С. 613–616.
