Кацюба О. А., Тимонин Д. В. Нахождение параметров нелинейных класса Гаммерштейна динамических систем при наличии помех в выходных сигналах. // Проблемы информатики в образовании, управлении, экономике и технике: Сб

Вид материала

Документы

Подобный материал:

• Демидова Л. А., Коротаев А. Н. Генетический алгоритм настройки параметров системы нечеткого, 38.47kb.
• Об использовании Нобелевских лекций в информационных технологиях. // Проблемы информатики, 110.52kb.
• Поддубный А. П., Юрков Н. К., Якимов А. Н. Фрактальный подход к сжатию информации., 47.01kb.
• Журавлев С. Д., Жуков Р. А. Математическая модель эффективного использования земельных, 39.41kb.
• Прошина Р. Д., Слесарев Ю. Н. Методы построения математических моделей в пространстве, 34.51kb.
• Титов Д. В., Кобак В. Г. Анализ подходов к улучшению результатов работы генетического, 82.51kb.
• Прошина Р. Д., Слесарев Ю. Н. Математическое моделирование асинхронного электропривода, 40.5kb.
• Дрождин В. В., Масленников А. А., Сергеев А. С. Использование протоколов запросов для, 63.12kb.
• С. О. Токмаджян Ереванский государственный университет архитектуры и строительства, 50.2kb.
• Герасимов А. Ф., Федотов Н. Г. Опотоковом методе анализа движений денежных средств, 28.85kb.

Кацюба О.А., Тимонин Д.В. Нахождение параметров нелинейных класса Гаммерштейна динамических систем при наличии помех в выходных сигналах. // Проблемы информатики в образовании, управлении, экономике и технике: Сб. статей Всерос. научно-техн. конф.– Пенза: ПДЗ, 2008. – С. 52-55.

НАХОЖДЕНИЕ ПАРАМЕТРОВ НЕЛИНЕЙНЫХ
КЛАССА ГАММЕРШТЕЙНА ДИНАМИЧЕСКИХ СИСТЕМ
ПРИ НАЛИЧИИ ПОМЕХ В ВЫХОДНЫХ СИГНАЛАХ

О.А. Кацюба, Д.В. Тимонин

Самарский государственный университет путей сообщения,
г. Самара

Рассмотрим стационарную нелинейную динамическую систему, которая описывается следующим разностным уравнением:

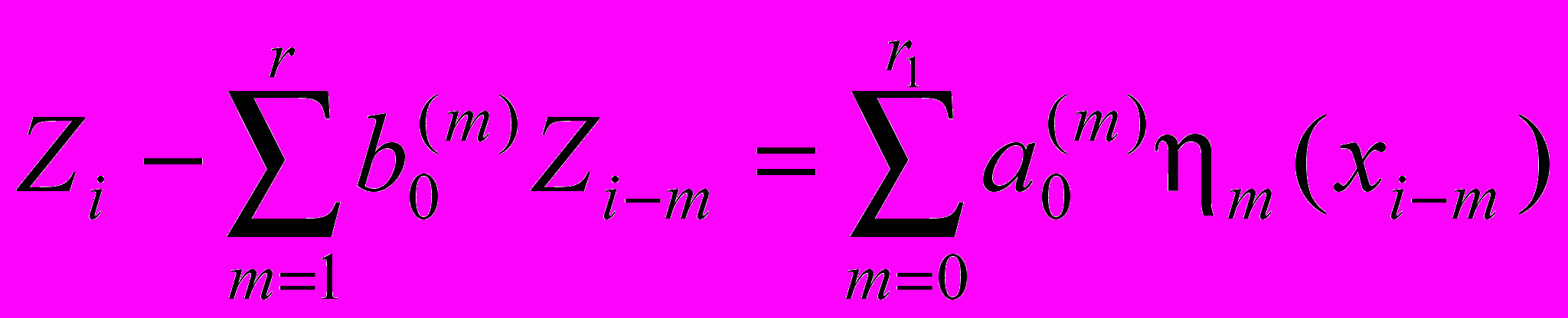, (1)

где выходная переменная 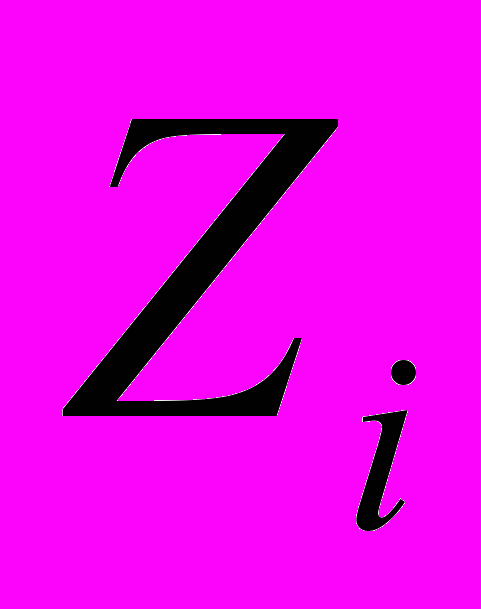наблюдается с аддитивными помехами в виде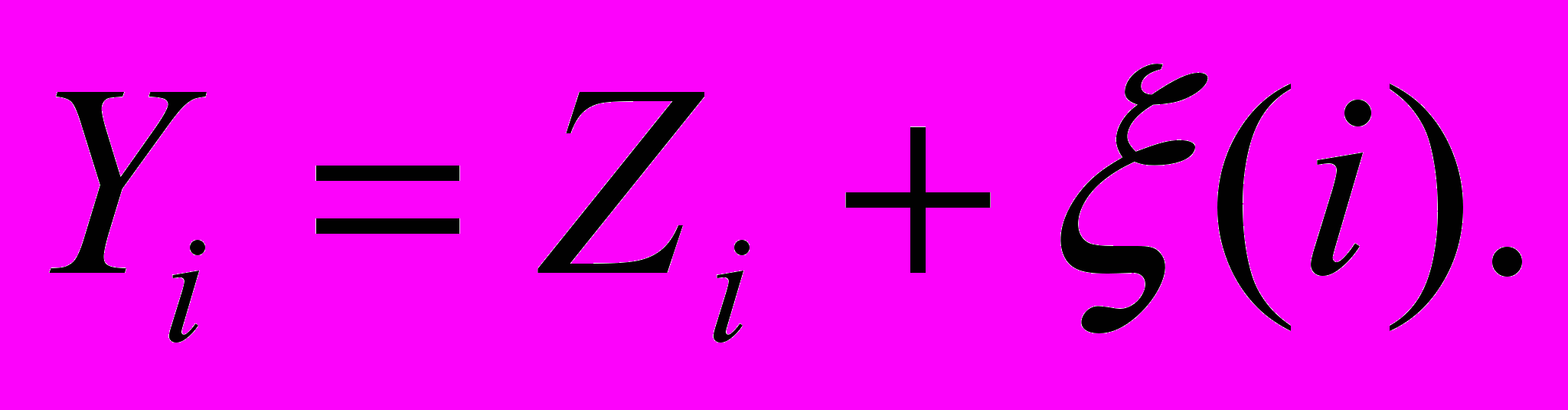

Требуется по наблюдаемым конечным выборочным реализациям последовательносте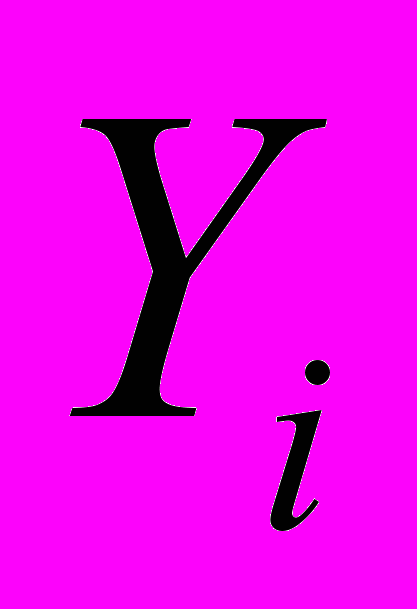й и 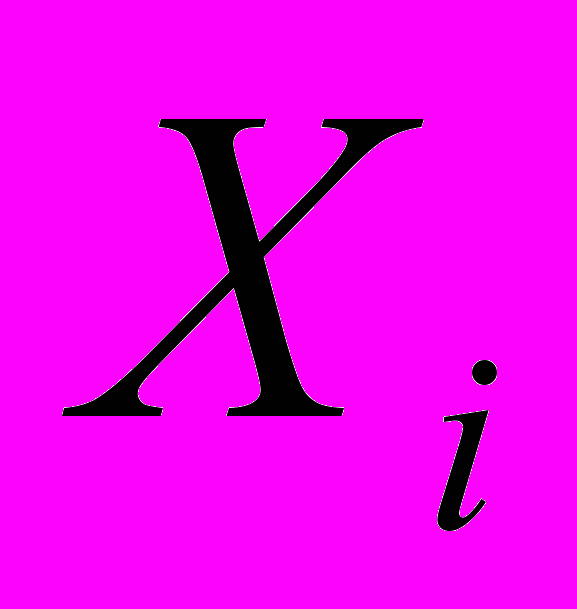при известных порядках 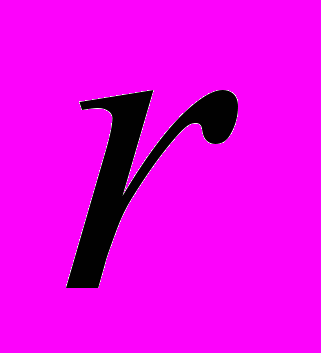и 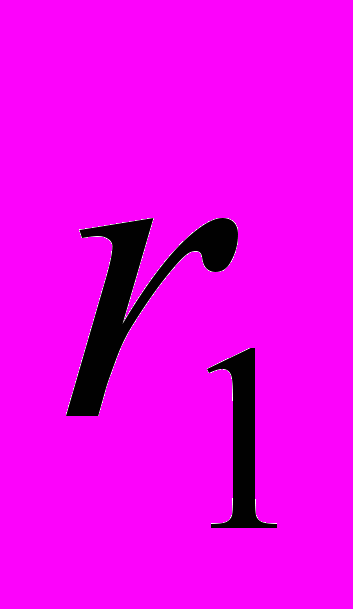(1) определить оценки истинных значений параметров.

В [1] показано, что для получения состоятельных оценок параметров (1) применим следующий критерий:

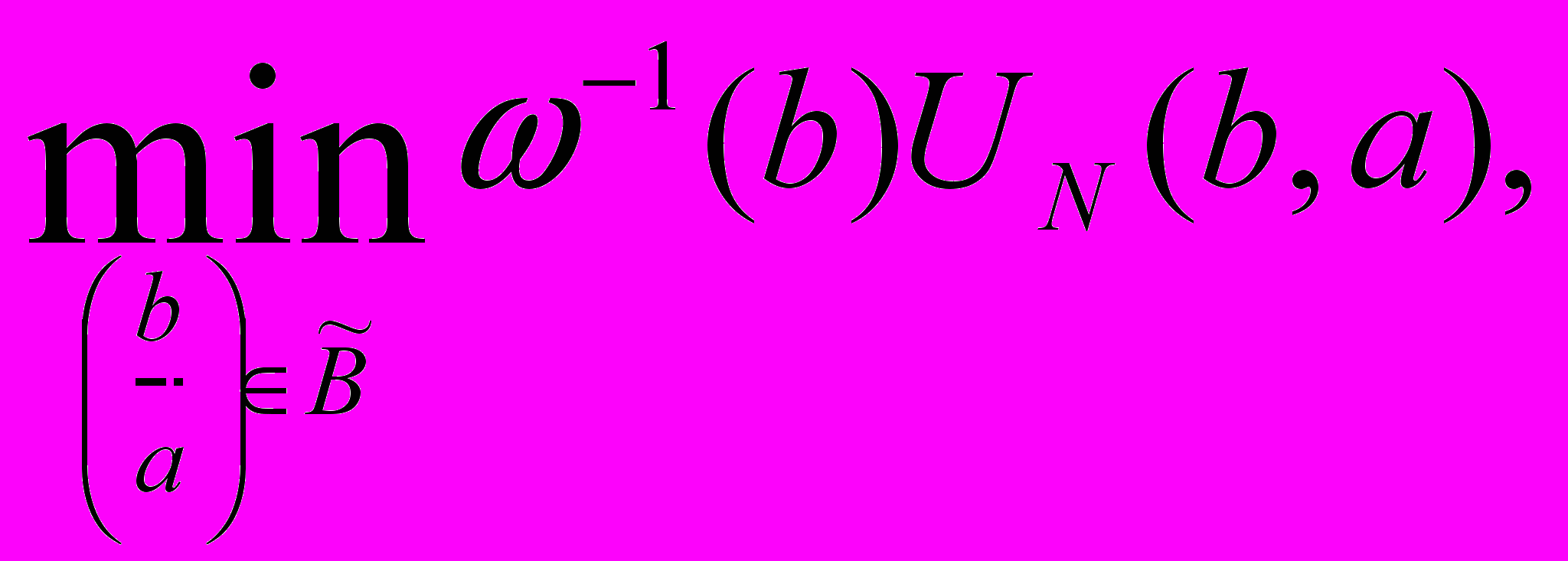(2)

где – компакт, ,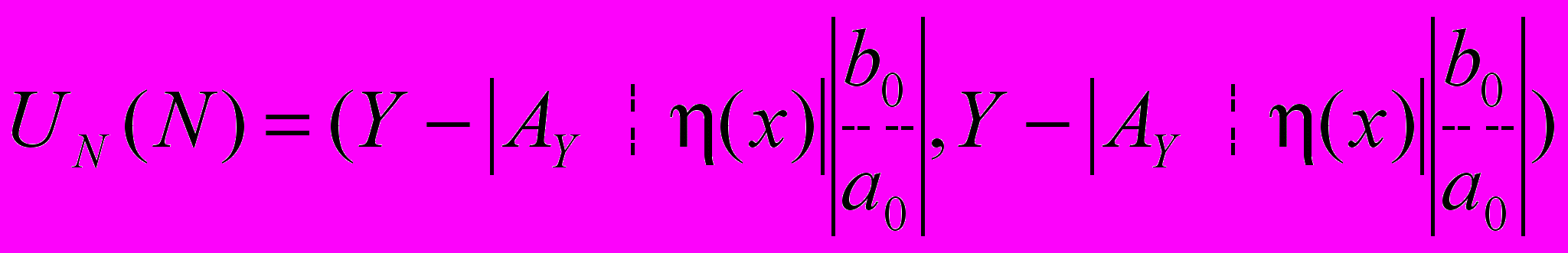

где 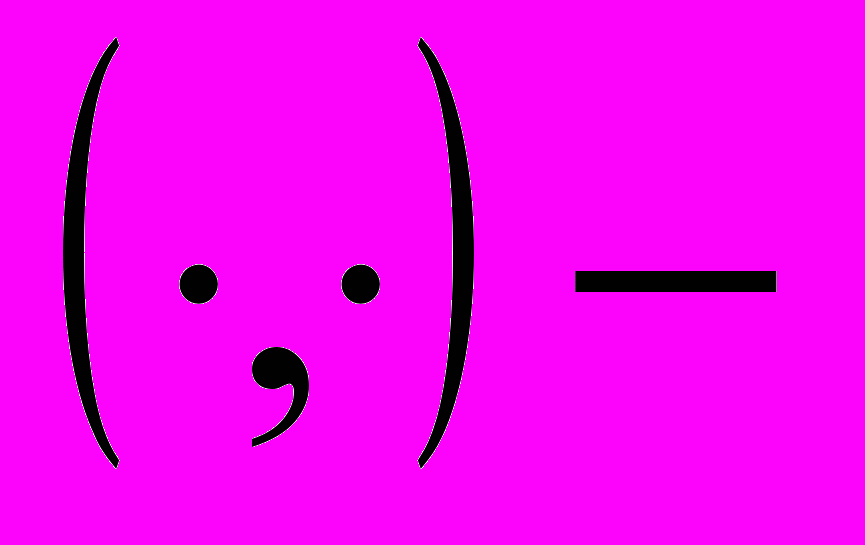скалярное произведение, ,

, , ,

, ,

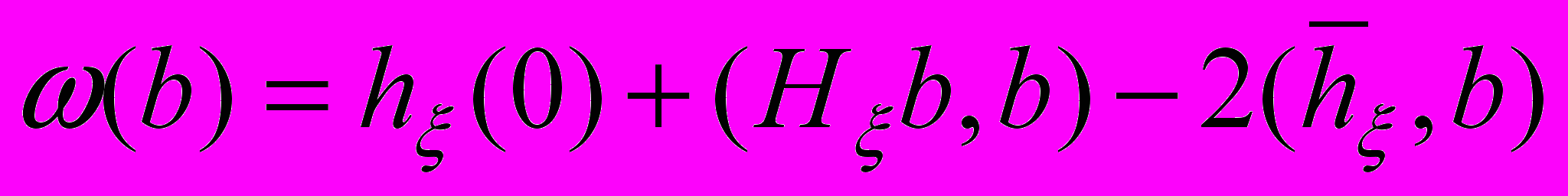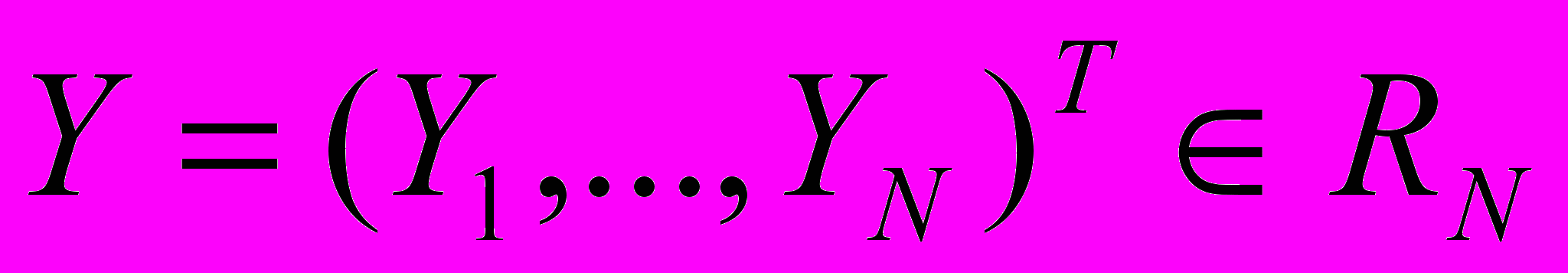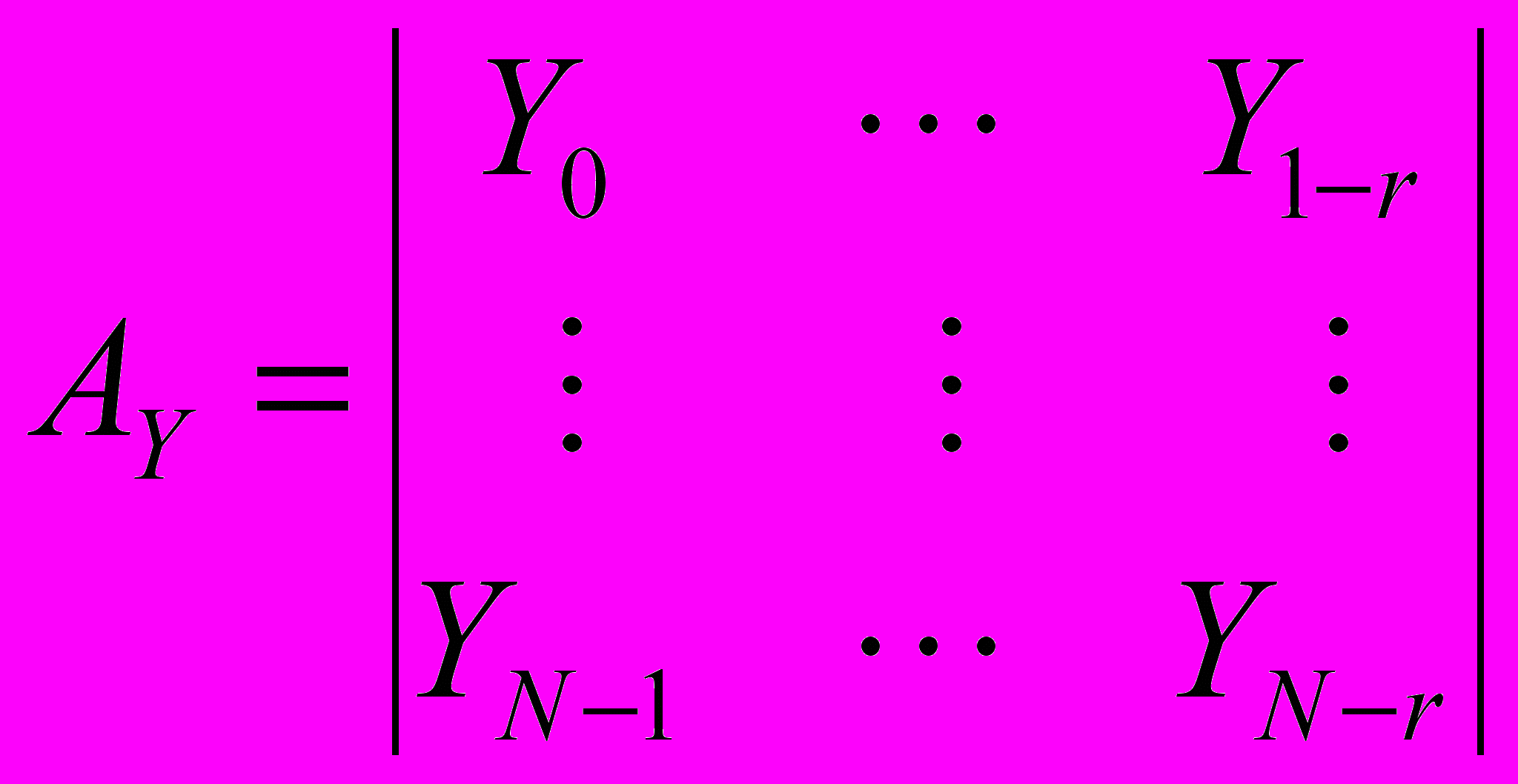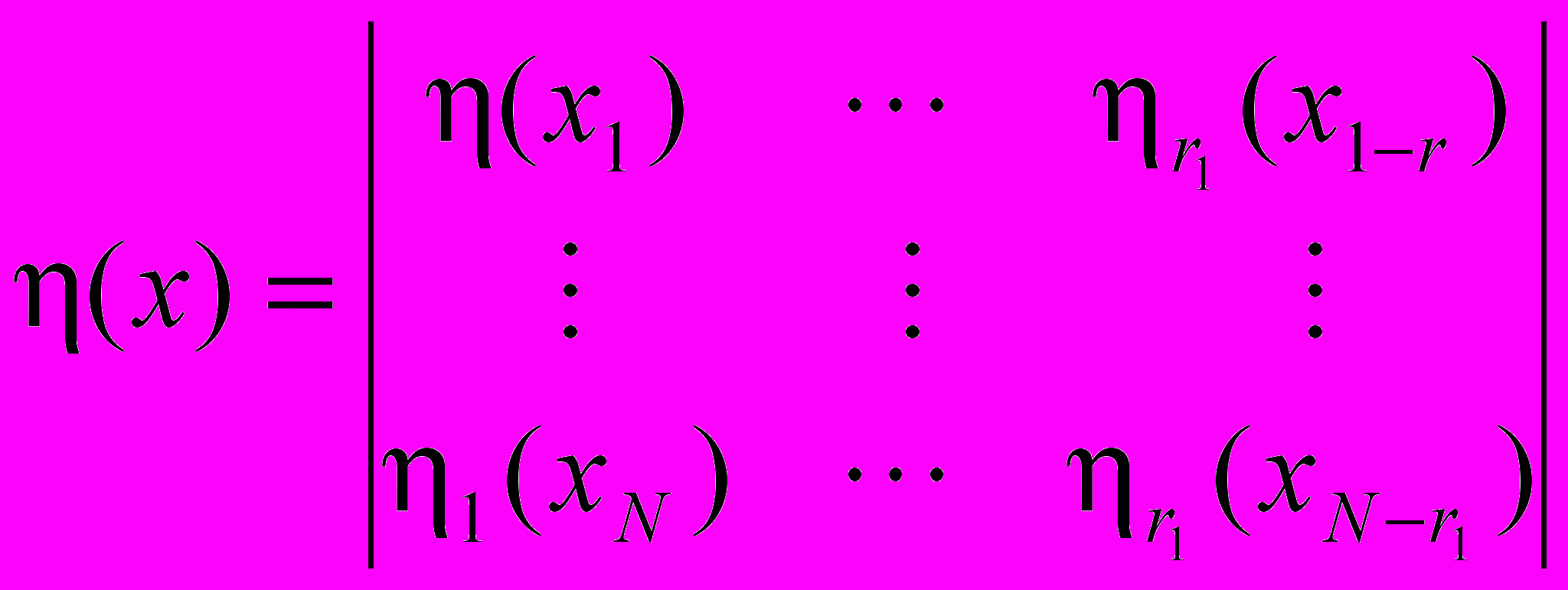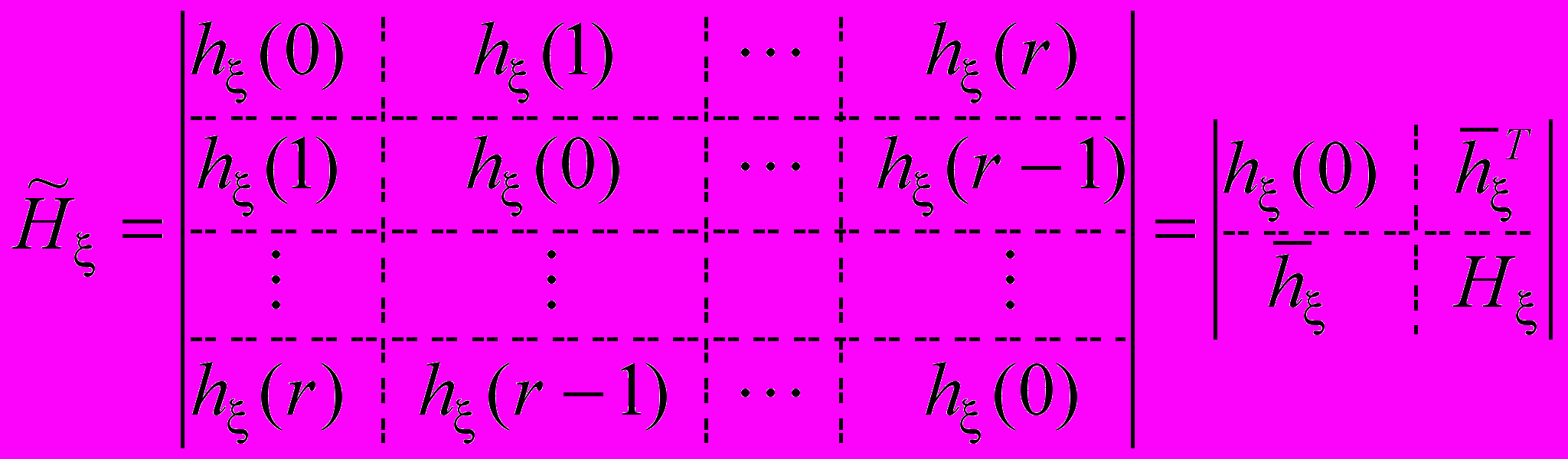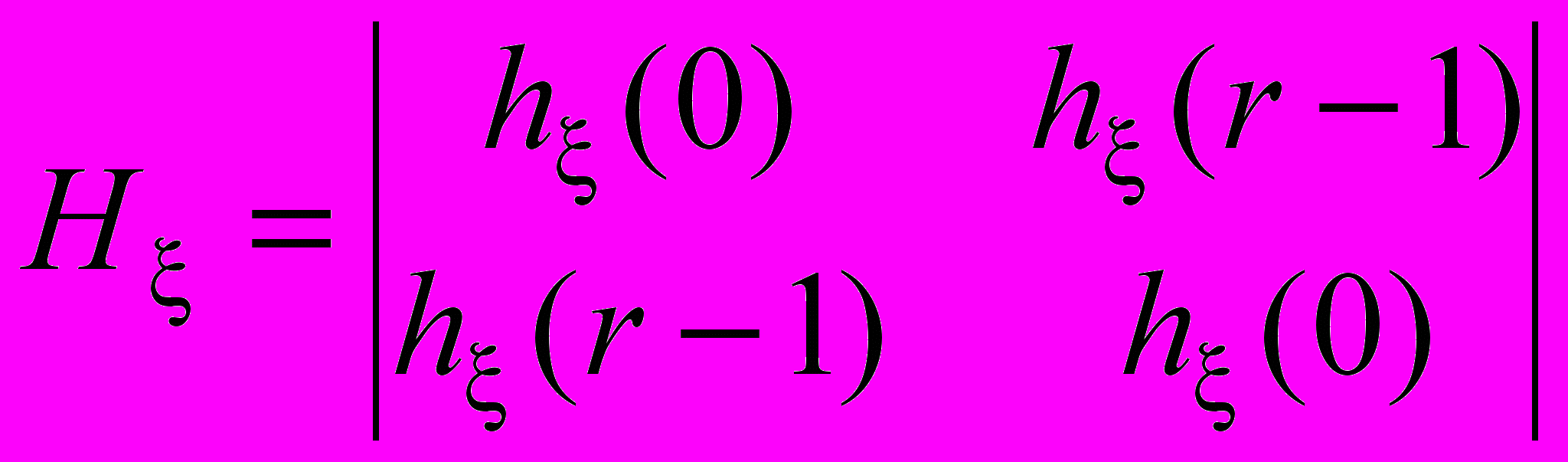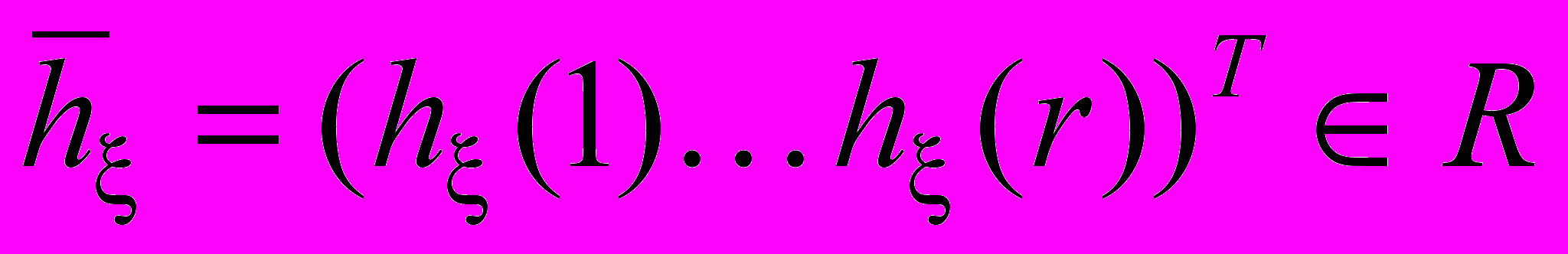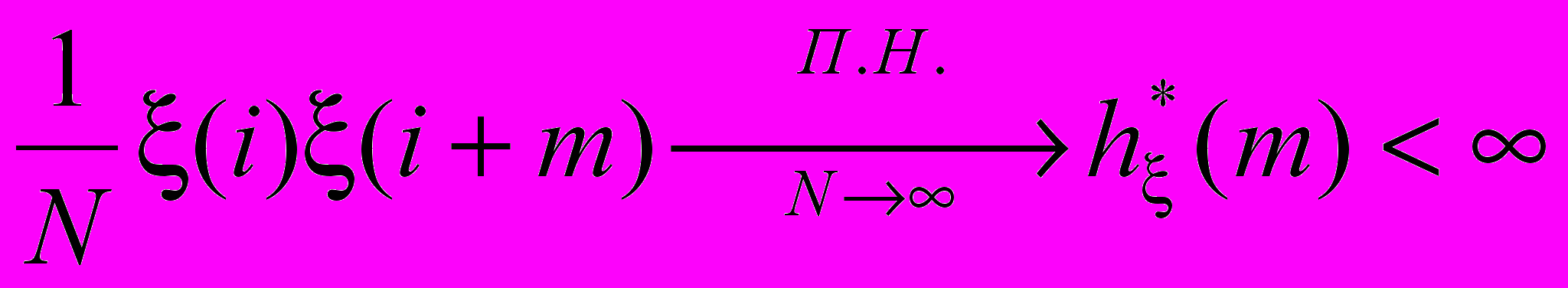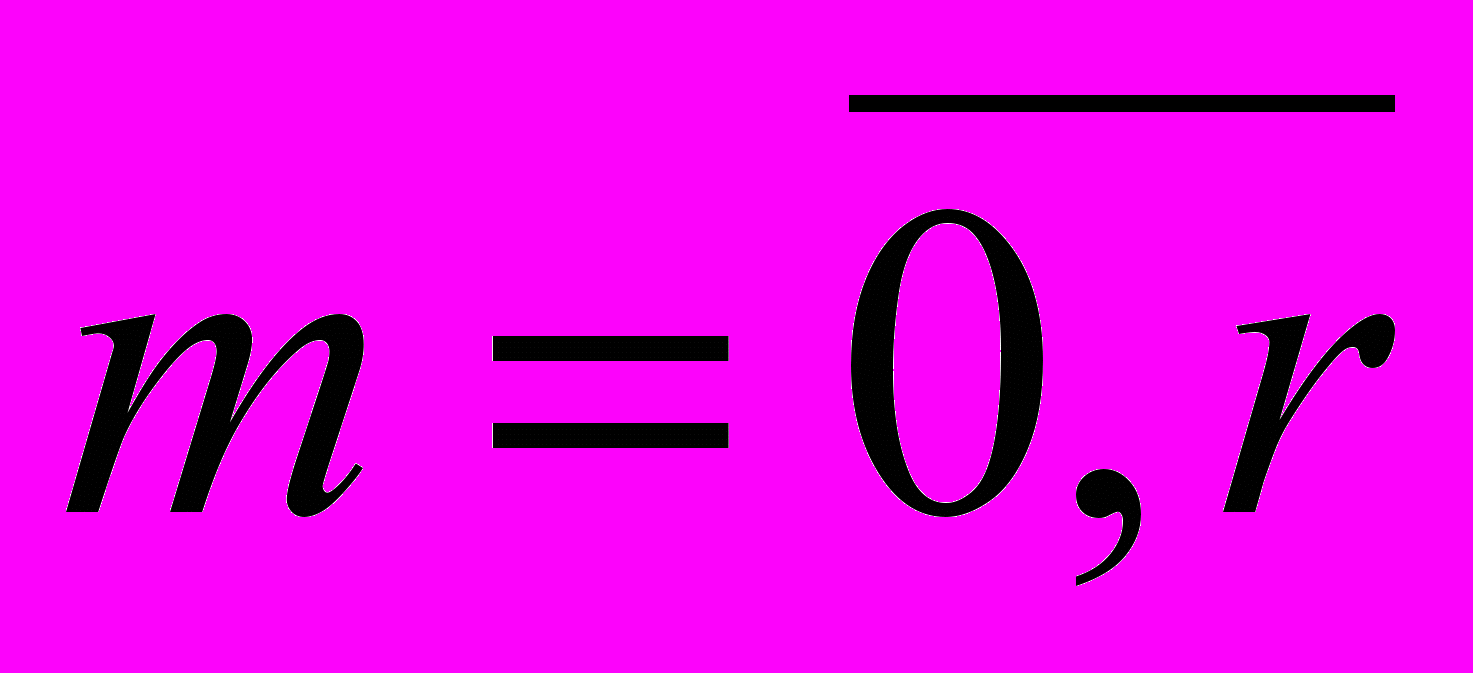, , , где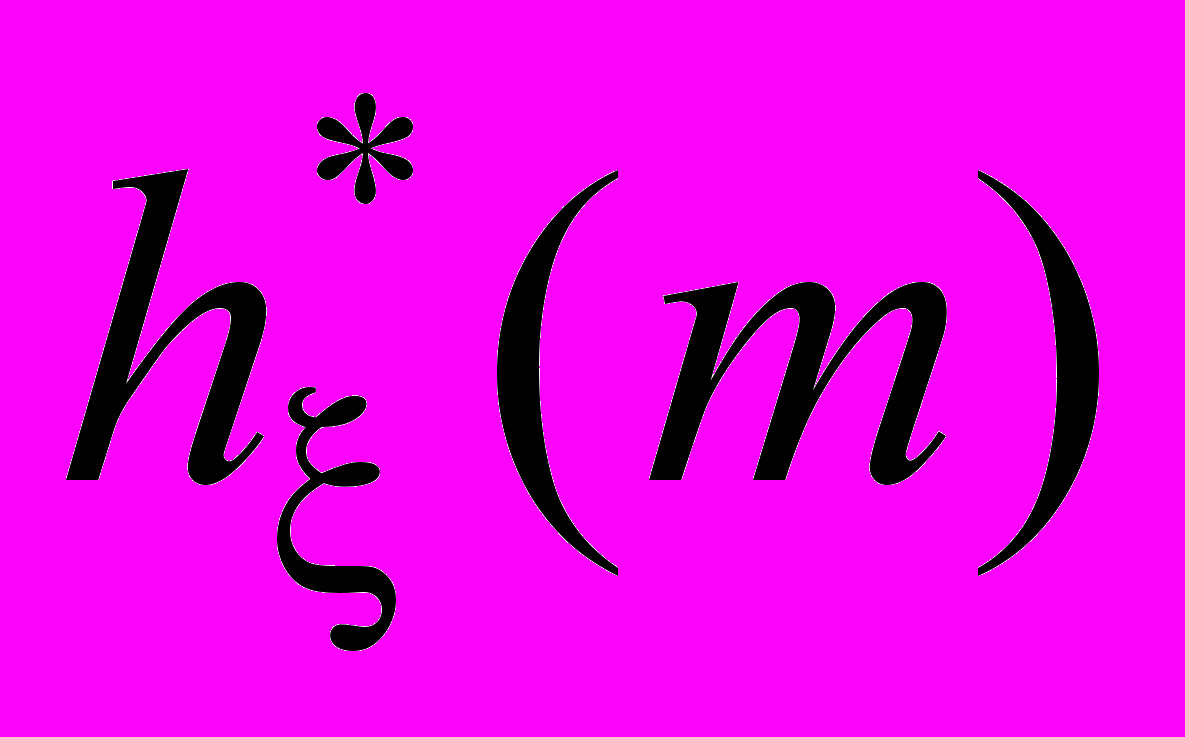

– локальная автокоррелированная функция.

Для получения численного метода вычисления оценок параметров из критерия (2) рассмотрим функцию

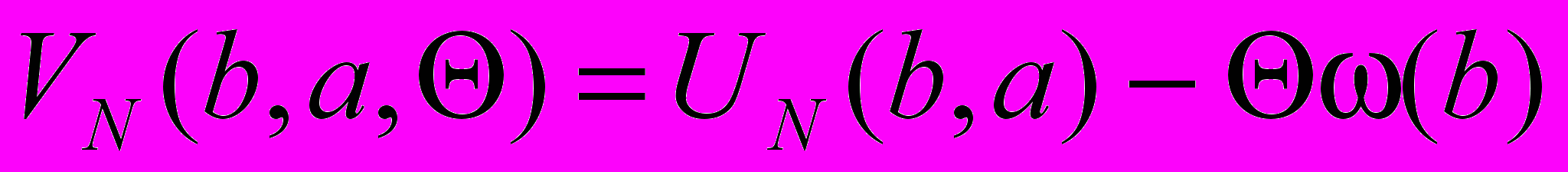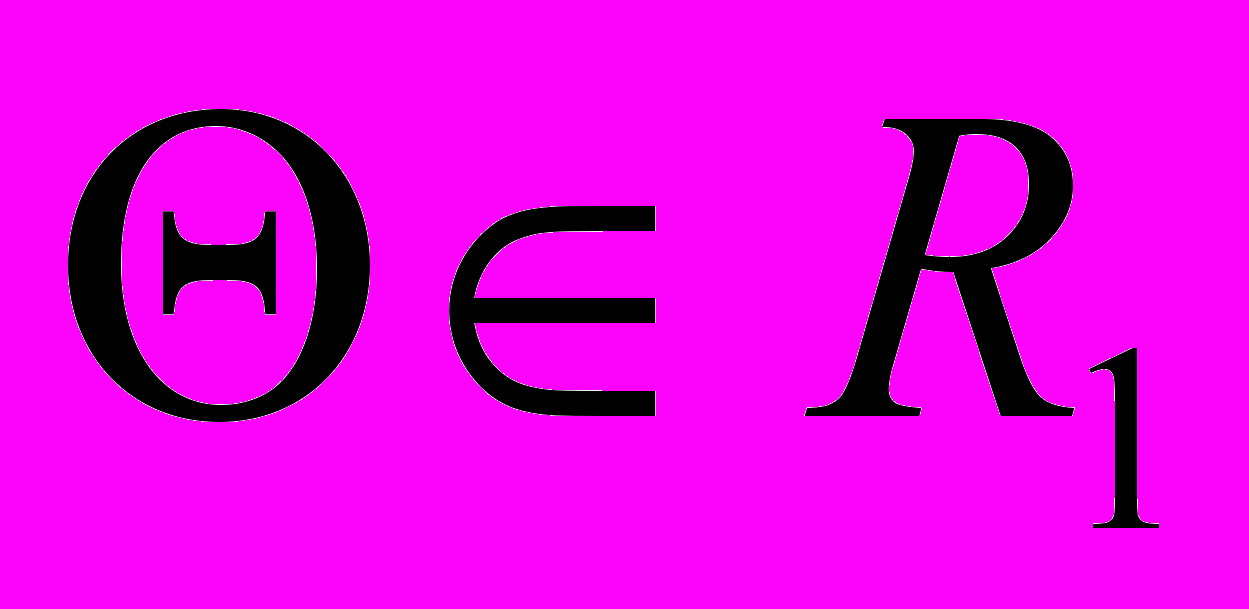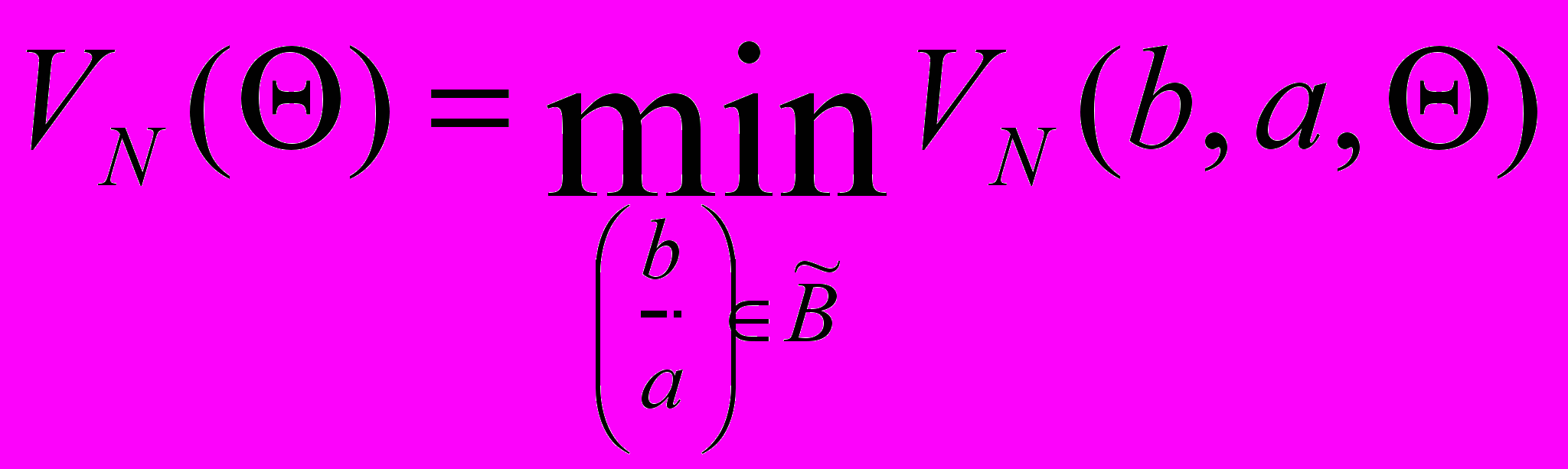, , , тогда *

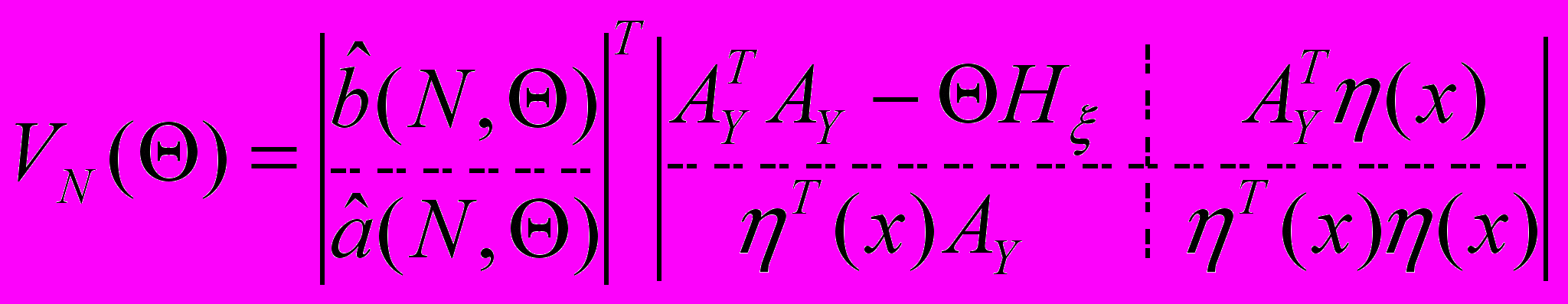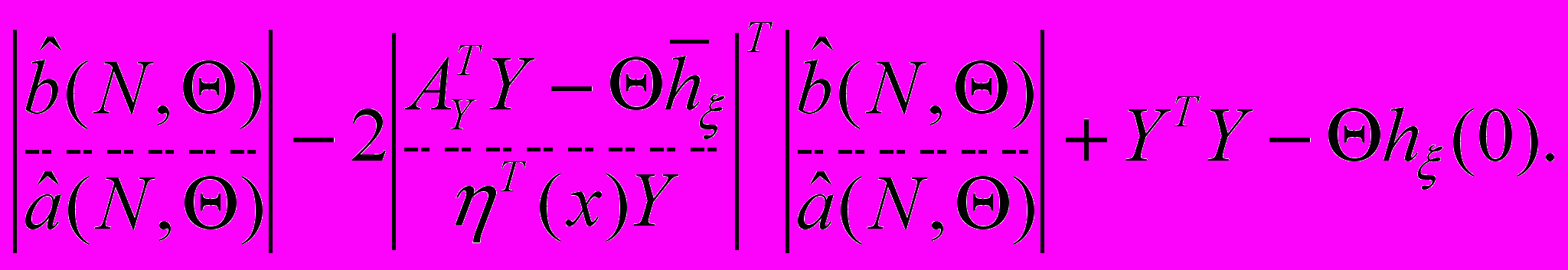* (3)

Это позволяет определить параметр , а затем и оценки параметров 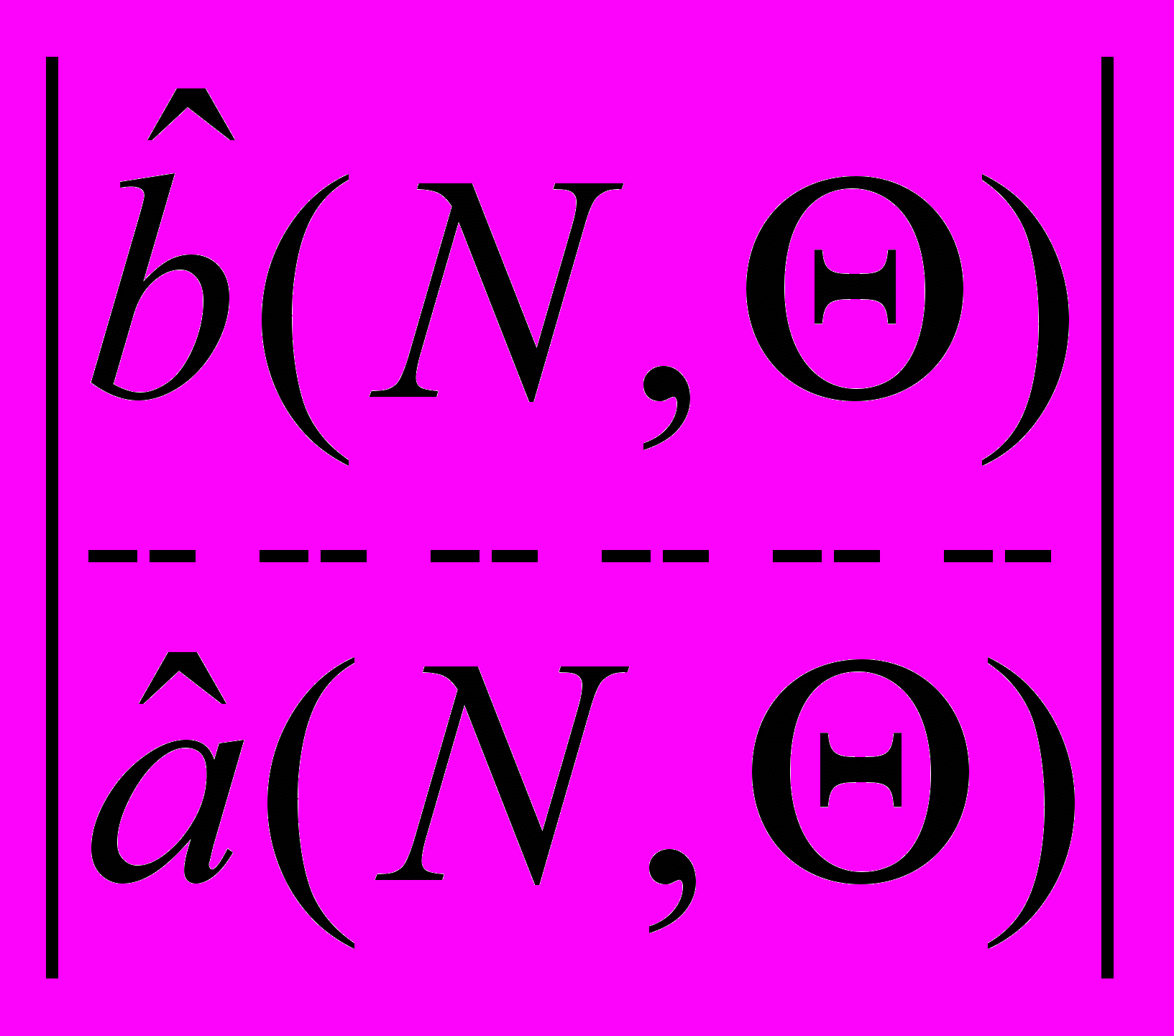на основе применения метода Ньютона: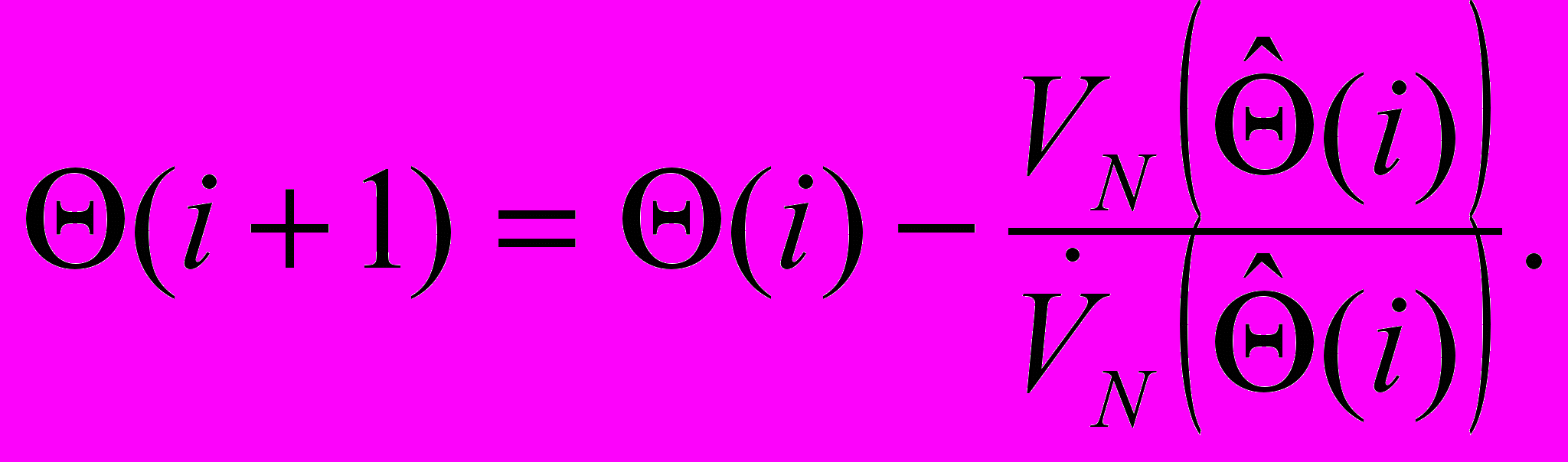



Обоснованность использования метода Ньютона вытекает из того, что функция 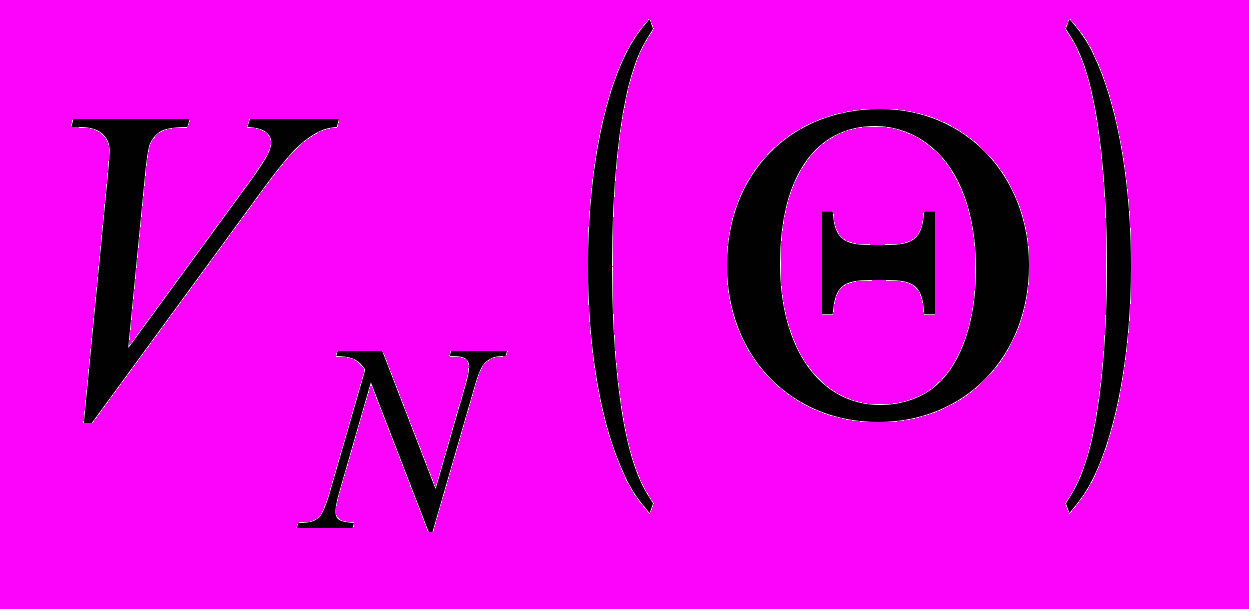непрерывна на интервале 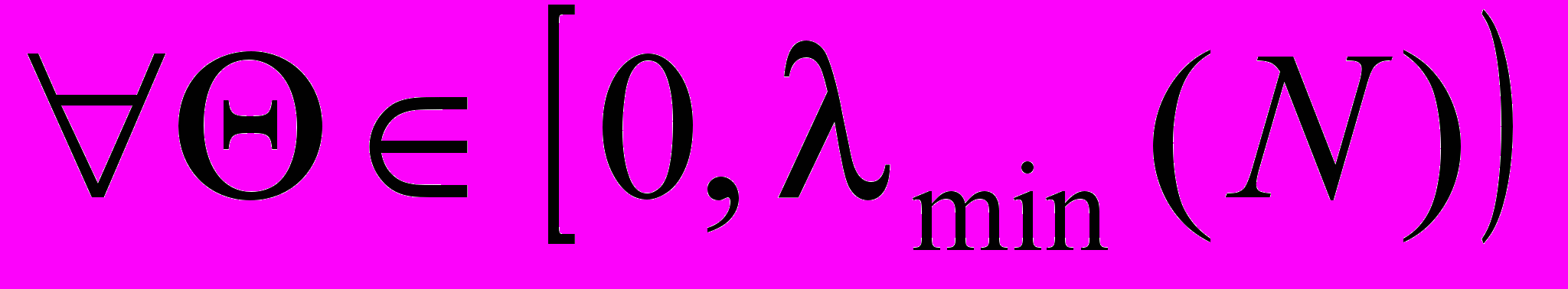и и на интервале .





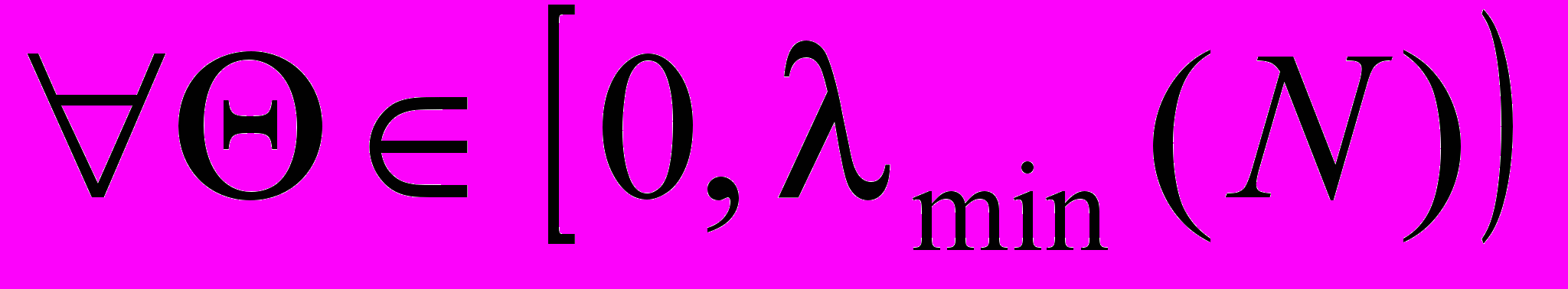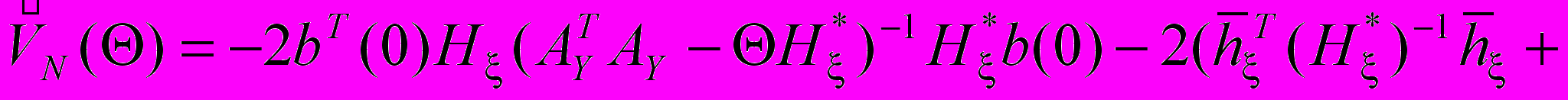
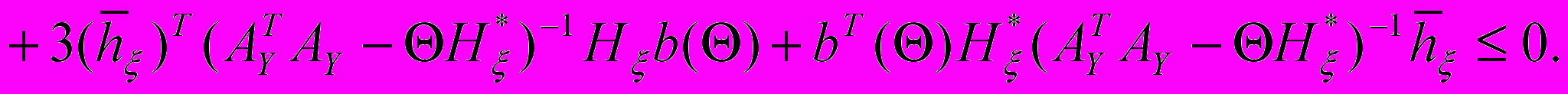
На основе вышеописанного алгоритма в среде Mathcad создано программное обеспечение, позволяющее получать оценки матриц параметров. В качестве результата работы приложения Identification на рис.1 и рис.2 приведены графики значений последовательности 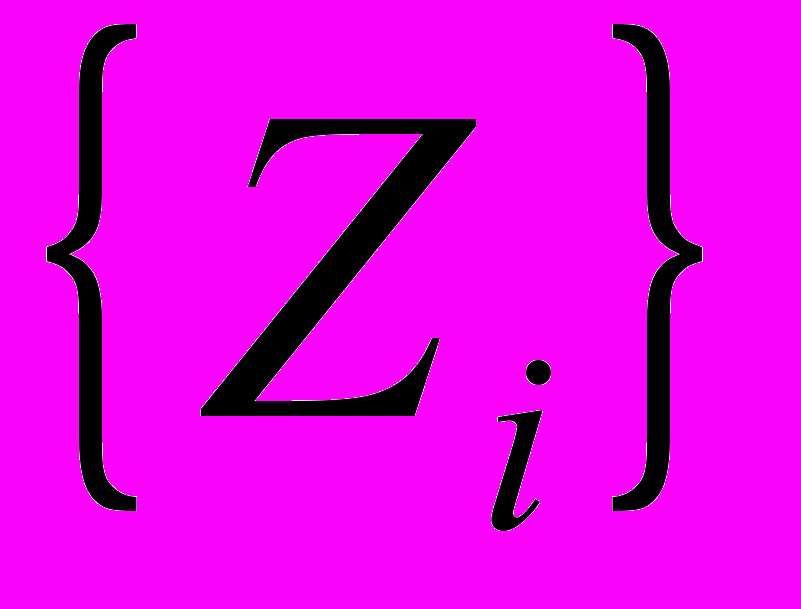, а также значений последовательностей моделей и .




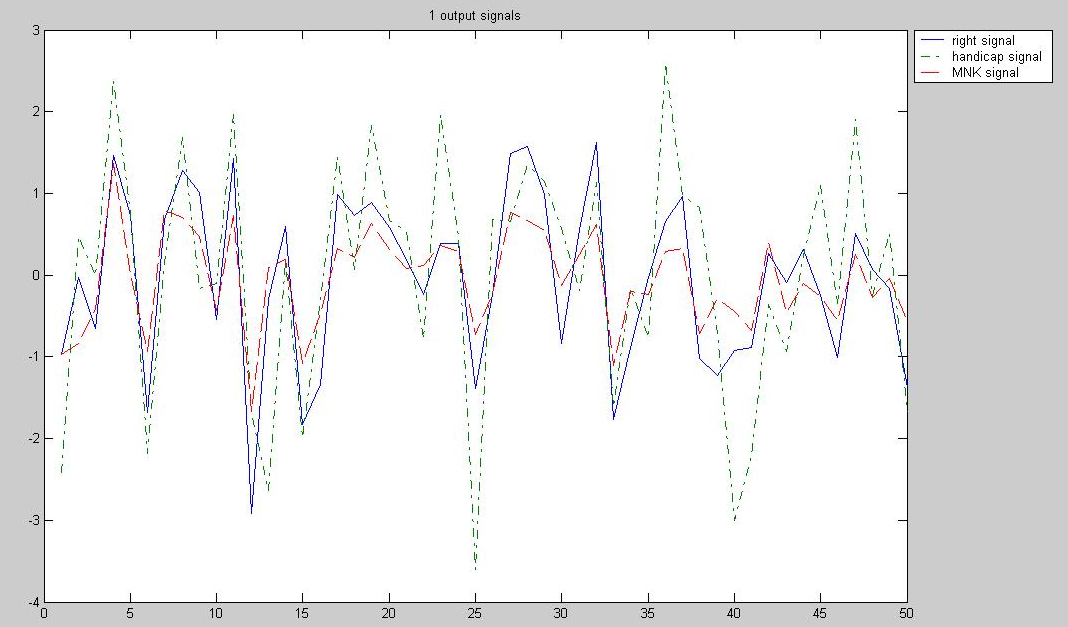
Рис. 1. Графики значений последовательносте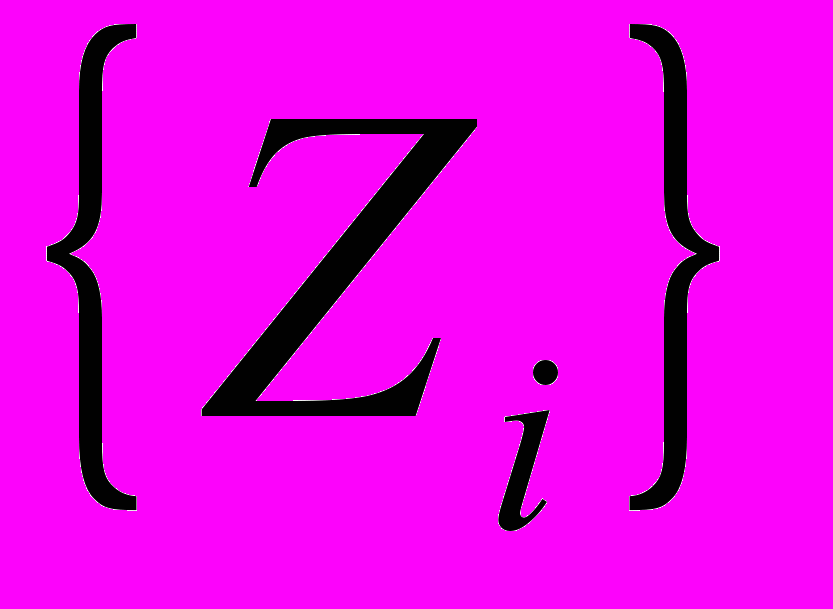й и



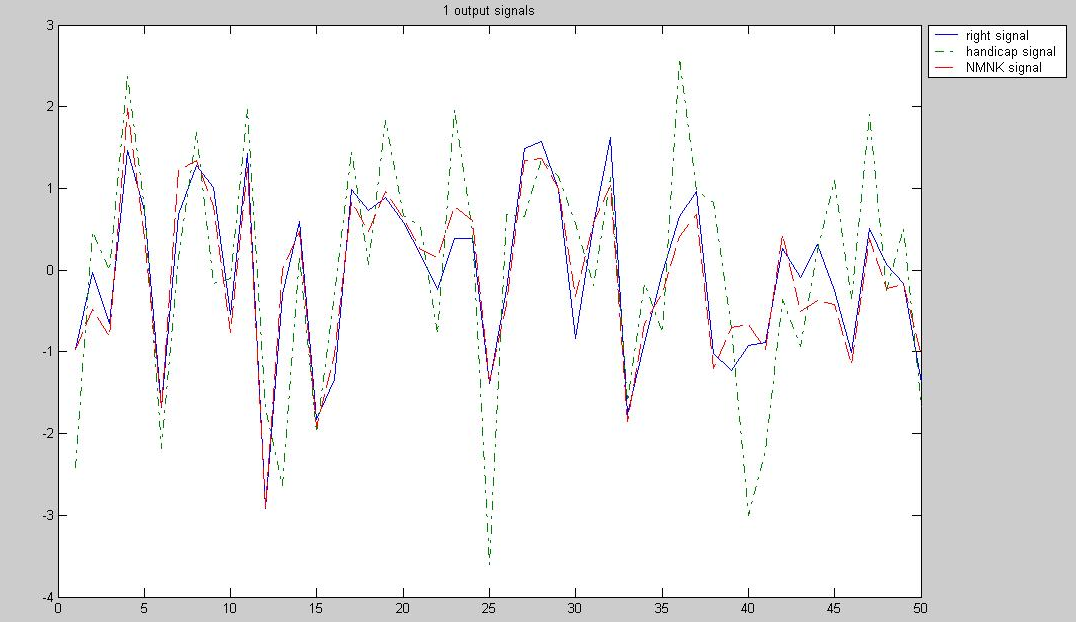
Рис. 2. Графики значений последовательносте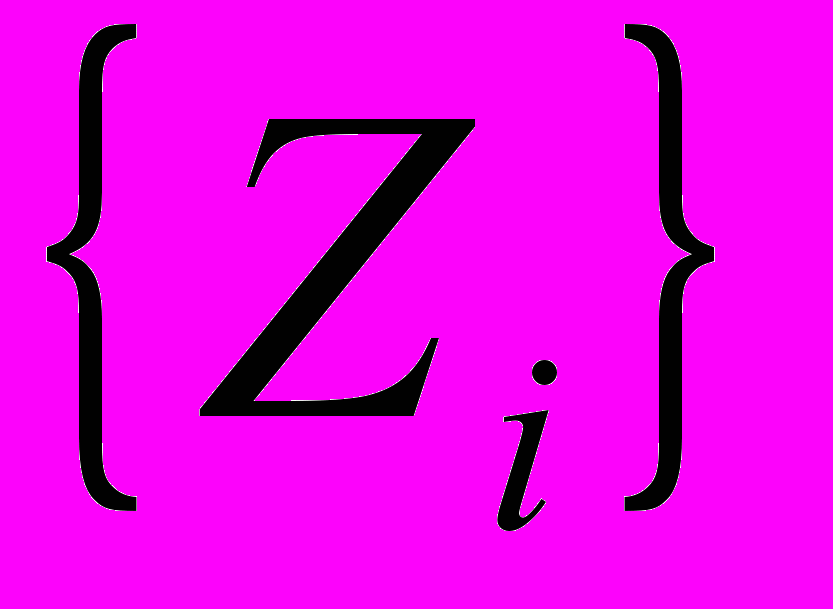й и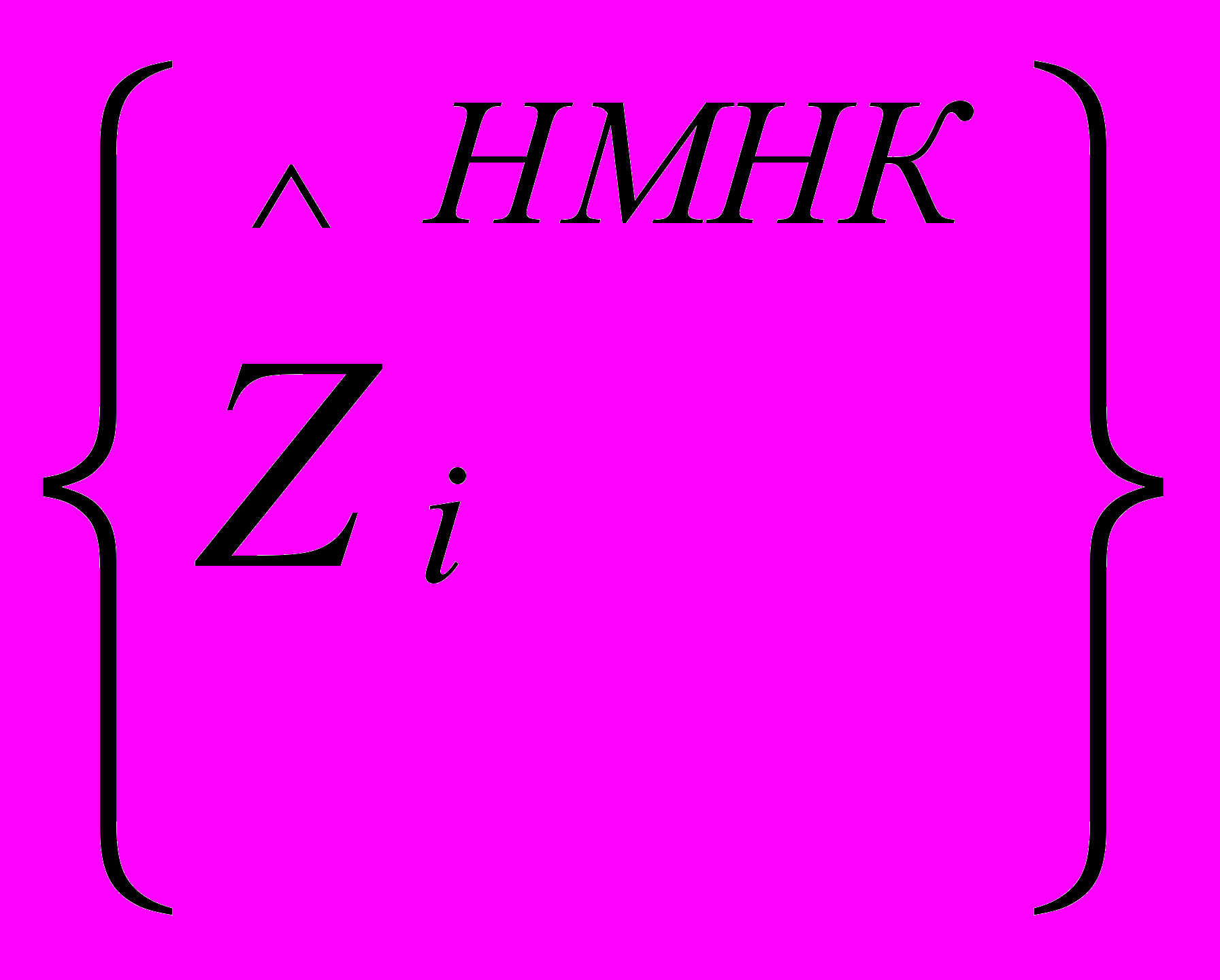

На этих рисунках дисперсии по МНК составляют 0,2248, а по НМНК – 0,0823.

Библиографический список

1. Кацюба, О.А., Тимонин, Д.В. Численный метод идентификации параметров нелинейных динамических систем при наличии помех наблюдений // Сборник трудов «Математические методы в технике и технологиях – ММТТ-21». – Саратов, 2008. – Т. 2.