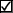Пояснительная записка 4 Тематическое планирование 7
| Вид материала | Пояснительная записка |
- Тематическое планирование курса «География. Землеведение» в 6 классе, 456.77kb.
- Пояснительная записка Ктематическому планированию по музыке Развернутое тематическое, 212.47kb.
- Пояснительная записка развернутое тематическое планирование составлено на основе, 470.14kb.
- Пояснительная записка Календарно-тематическое планирование по изобразительному искусству, 989.33kb.
- Пояснительная записка развернутое тематическое планирование составлено на основе, 311.29kb.
- Пояснительная записка врезультате изучения данных тем курса математики учащиеся должны, 237.64kb.
- Пояснительная записка. Количество часов в неделю-2, в год-34. Контрольные работы-2,, 126.14kb.
- Пояснительная записка развернутое тематическое планирование составлено на основе, 4318.59kb.
- Пояснительная записка развернутое тематическое планирование составлено на основе, 3834.55kb.
- Пояснительная записка Календарно тематическое планирование по алгебре в 8 классе, 158.23kb.
Содержание
1. Пояснительная записка 4
2. Тематическое планирование 7
3. Схематический план отчета по курсу геометрии 12
4. Приложения 13
4.1. Вопросы к экзамену по геометрии 13
4.2. “Прямая на плоскости. Векторы” 15
4.3. “Линии 2-го порядка” 16
4.4. “ Векторы. Система координат” 17
4.5. Памятка для самостоятельной работы 18
студентов I курса по высшей геометрии 18
Приложение 5.2 20
4.6. “Прямая на координатной плоскости” 20
4.7. Семинар 3 “Линии второго порядка” 21
4.8. Преобразование системы координат и 22
уравнения линии 2-го порядка. 22
4.9. “Циклоида. Циклоидальные кривые” 23
4.10. “Специальные кривые” 24
4.11. “Линии второго порядка” 25
1. Пояснительная записка
ИНДИВИДУАЛЬНО - ОРИЕНТИРОВАННЫЙ ПЛАН
ИЗУЧЕНИЯ ГЕОМЕТРИИ НА ФАКУЛЬТЕТЕ МАТЕМАТИКИ
2 СЕМЕСТР, 1 КУРС, ПРЕПОДАВАТЕЛЬ Е.И. ТКАЧЕНКО
Индивидуально-ориентированный план является рабочей программой для преподавателя и студента. В плане указаны темы лекций, семинаров, задания для практических занятий(тренировочных) и зачетных – индивидуальной работы студента.
В плане указаны примерные сроки изучения тем, количество часов аудиторных плюс внеаудиторных, отводимых на самостоятельную работу студента. Отчетом по самостоятельной работе является участие в семинарах и выполнение зачетных заданий. Возникающие в ходе самостоятельной работы вопросы можно вынести на семинарские или практические занятия, а также на индивидуальные консультации ( 1 час в неделю на группу). К семинарским занятиям указан примерный перечень вопросов, который может быть изменен самим студентом, и перечень дополнительной литературы по теме семинара .
В графе “примечание” предполагается отметка результатов оценки по зачету, самооценки по теме, в том числе проблемы возникающие в начале изучения темы и трудности отмеченные преподавателем и студентом в конце изучения темы. Эти проблемы (трудности) являются объектом для планирования индивидуального повторения вопросов курса.
Курс данного семестра содержит следующие разделы:
- векторы и действия с ними на координатной плоскости. 13+3
- прямая на плоскости - 15+3
- линии второго порядка - 15+4
- преобразования координатной плоскости - 14+6
- Критерий разрешимости задач на построение циркулем и линейкой - 7+2
- Основными понятиями курса являются:
- вектор направленный отрезок (
 или
или  );
);
- модуль вектора - число являющееся длиной вектора (отрезка);
- коллинеарность векторов - принадлежность их одной прямой или параллельным прямым;
- аналитическая геометрия - теория, устанавливающая связь между линиями на плоскости и алгебраическими уравнениями с двумя переменными;
- алгебраическая линия - множество точек определяемых уравнением F(х,у)=0, где F (х,у) - многочлен, состоящий из слагаемых вида ахp уq где a-действительное число, p, q - целые неотрицательные числа;
- порядок линии определяется степенью многочлена F (х,у),т.е. числом p + q
| - окружность: |
где а, b, k - действительные числа. |
| - эллипс: | 1. Сечение конической поверхности плоскостью, пересекающей все ее образующие под углом к оси, отличным от 90. 2. Множество точек, сумма расстояний от которых до двух фиксированных точек постоянная
где а и b-действительные числа (полуоси эллипса). |
| - парабола: |
где р - действительное число. |
| - гипербола: |
где а и в- действительные числа. |
| - циклоида: | плоская кривая, которая является траекторией точки окружности, катящейся по прямой без скольжения. |
| - циклоидальная кривая: | плоская линия, которая является траекторией точки окружности, катящейся без скольжения по неподвижной окружности (вне неподвижной окружности - эпициклоида, внутри неподвижной окружности - гипоциклоида. |
В разделе “Векторы и действия на ними” обобщаются и углубляются знания школьного курса геометрии и курс высшей алгебры по системе координат, координатной плоскости, координатах точки и вектора;
определения и свойства действий над векторами, виды векторов и условия взаимного расположения векторов на плоскости. Знания этого раздела является основой усвоения курса аналитической геометрии.
В разделе “Прямая на плоскости” систематизируются и расширяются знания об уравнении прямой на плоскости, полученные в школьном курсе геометрии.
Рассматриваются различные способы задания прямой и виды ее уравнений, устанавливаются способы определения взаимного расположения точки и прямой, двух прямых, прямой и оси координат. Вводится понятие пучка прямых. Рассматриваются задачи на составление уравнения прямой и исследования прямой по ее уравнению.
В разделе “Линии второго порядка” рассмотрены линии - конические сечения: их уравнения, свойства, способы построения.
В разделе “Преобразование системы координат” рассматривается зависимость между координатами точки в исходной и полученной системах координат, что позволяет рассмотреть порядок приведения любого уравнения линии второго порядка каноническому (общепринятому) виду, способствующему изображению любой линии на координатной плоскости.
В разделе “ Циклоида. Циклоидальные кривые” рассматриваются способы составления уравнений любой линии - траектории точки подвижной окружности; использование угла поворота в качестве параметра, способы приведения параметрического уравнения к каноническому виду, использования уравнений для построения кривых.
В разделе “Специальные кривые” завершается курс “Построение фигур на плоскости”, рассматривается критерий разрешимости задач на построение циркулем и линейкой и способы решения классических задач: о трисекции угла, квадратуре круга( спрямлении окружности) и удвоении куба с помощью специальных кривых.
Курс геометрии завершается зачетом и устным экзаменом (вопросы в приложении N 1)
Зачет выставляется на основе результатов двух контрольных работ (“Прямая на плоскости” (приложение N 2), “Линии 2-го порядка (приложение N 3)
В курсе предусмотрены семинарские занятия по каждому разделу (приложения 4,5,6,7,8,9) и “Коллоквиум по теме “Линии 2-го порядка” (приложение 9)
Тема “Специальные кривые” может быть рассмотрена глубже в курсовой работе (VI семестр), с включением компьютерной графики.
Темой курсовой работы может стать аналитическая геометрия с аффинной системой координат.(основные отличия решения задач от их решения в декартовой системе координат).
Литература
Основная:
С.А.Анищенко “Лекции по геометрии ч.1, КГПУ. 1998.
Дополнительная:
- М.Я.Выготский “Справочник по высшей математике” М., Наука.1 1972.
- Журнал “Математика в школе”
- Математическая энциклопедия”
- “Геометрия” под редакцией Г.Н. Яковлева. М.Н. Наука.1990. 320с.
2. Тематическое планирование
| Содержание | Количество часов | Дата | Практические задания | Примечание | ||
| | | План | Факт | Тренировочные | Зачетные – индивидуальные | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| I.Векторы. Система координат. Знать: понятия: координатная прямая (плоскость), координаты точки (вектора), длина вектора, коллинеарные векторы, радиус-вектор, линейная комбинация векторов, равные векторы, правила и свойства действий с векторами, условия коллинеарности и перпендикулярности векторов. Уметь формулировать и доказывать свойства действий над векторами, эквивалентность геометрического и координатного определений действий над векторами; определять взаимное расположение векторов и расположение вектора в системе координат; Обосновывать и применять формулу вычисления длины вектора, угла между векторами. Навык изображение точки и вектора в системе координат; выполнение действий с векторами, определение координат точки и вектора, изображенных на плоскости II.Прямая на плоскости. Знать: уравнения прямой на плоскости различного вида (смысл постоянных величин в каждом виде уравнения)формулу расстояния от точки до прямой; угол между прямыми. Уметь: составлять и исследовать уравнение прямой на плоскости; определять взаимное расположение прямых на плоскости, в том числе на координатной плоскости; определять угол между прямыми; расстояние от точки до прямой и между параллельными прямыми; доказывать эквивалентность различных уравнений одной прямой. Навык: построение прямой на плоскости по ее уравнению, нахождение угла наклона к оси ОХ, Составление и чтение общего уравнения прямой. .III Линии 2-го порядка Знать: знать различные определения конических сечений - линий второго порядка; канонические уравнения каждой из линий; параметрические уравнения окружности и эллипса. Уметь: составить уравнение линии 2-го порядка по ее характеристическим свойствам. Уметь составлять параметрические уравнения окружности и эллипса, приводить их к каноническому виду. Уметь строить линию по характеристическим свойствам и по уравнению. Навык: схематичное изображение каждой линии второго порядка. IV. Общее уравнение линии 2-го порядка. Преобразование системы координат Знать; определения и свойства преобразований плоскости: Симметрия относительно точки (оси), параллельный перенос, поворот вокруг точки. Общее уравнение линии 2-го порядка и порядок приведения его к каноническому виду. Уметь: определить координаты точки в преобразованной системе координат, приводить уравнение линии 2-го порядка к каноническому виду, выполнять схематичный чертеж линии 2-го порядка и образа системы координат. Навык Схематичное изображение образа системы координат при преобразованиях и схематичный чертеж линии 2-го порядка по ее каноничному уравнению V.Критерий разрешимости задач на построение циркулем и линейкой. Знать: Критерий разрешимости задач на построение циркулем и линейкой, Определение циклоиды Диоклеса, конхоиды Никомеда, квадратрисы Динострата. Уметь обосновывать неразрешимость классических задач на построение циркулем и линейкой, решать их с помощью специальных кривых Навык: формулировка классических задач, неразрешимых циркулем и линейкой. | 13+3 час. Лекция 1. “Векторы в системе координат на плоскости. Декартова система координат”, 2 ч. Лекция 2 “Действия над векторами, использование их свойств в решении задач”, 2ч. Семинар 1 (приложение 4) “Векторы. Система координат”, 4 ч. 15+3 час. Лекция 3 “Прямая на плоскости”, 2ч. Лекция 4 “Взаимное расположение прямой. Пучки прямых”, 4 ч. Семинар 2 (приложение 5) “Прямая на плоскости”, 4ч. 15+4 час. Лекция 5 “Коническое сечение, эллипс, его уравнение и свойства”, 1ч. Лекция 6 “ Виды конических сечений и их уравнения”, 2ч. Лекция 7. “Задачи приводящие к линиям 2-го порядка», 1ч. Семинар № 3 (приложение 6) “Линии 2го порядка- конические сечения”, 2ч. Коллоквиум “Линии 2го порядка” (приложение 10), 2ч. 14+6 Лекция 8”Преобразование системы координат и ее практическое использование для выполнения чертежей”, 2ч. Лекция 9 Приведение общего уравнения линии 2-го порядка к каноническому виду”, 4ч. (Семинар 4), 4ч. 7+2 Лекция “Критерий разрешимости задач на построение циркулем и линейкой”, 4ч. Семинар 6 “Специальные кривые” (приложение 9). 2ч. | январь 3 январь 4 февраль1 февраль 2 февраль 3 февраль 4 март 1 март 2 март 3 март 4 апрель 1 апрель 2 апрель 3 апрель 4 май 1 май 2 май 3 май 4 май 4 июнь 1 июнь 2 | | 5 ч. 1)стр.85-86 С.А.Анищенко “Лекции…..” NN 1 – 30
5 ч. Лекции – С.А.Анищенко стр.92-93 NN 1-24 Контрольная работа 1 Прямая на плоскости (приложение 2), 2ч. 6 ч. Лекции С.А.Анищенко стр.108-110 №№ 1-40 4 ч. Лекции ч.1 С.А.Анищенко стр. 116-117 № 1-4 Контрольная работа №2 “Линии 2-го порядка” (приложение 3) 1 ч. Построение специальных кривых в т.ч. с помощью ЭВМ | 3 ч.
3 ч.
4 ч. 1.”Блок схема “Линии 2го порядка”
6 ч.
2 ч. Решение задач о трисекции угла, удвоении куба и квадратуре круга. | Блок схема “Векторы в курсе геометрии 7-9 классов” Блок схема Векторы на координальной плоскости” Блок схема “Уравнение прямой на плоскости” Структурно-логическая схема “Расстояние от точки до прямой” Анализ трудностей и ошибок в контрольной работе для планирования индивидуального повторения. Блок-схема “Конические сечения и их уравнения” Блок-схема “Линии 2-го порядка и ихпреображение” Блок-схема Решение задач с помощью специальных кривых” |
3. Схематический план отчета по курсу геометрии
I курс (II семестр) «Аналитическая геометрия на плоскости» (63 часа)
| № | Наименование раздела | Кол-во часов | Зачетные занятия и задания | Общеучебные умения | Индивид. допол. задания | ||||||||||
| 1 | Векторы и действия над ними на координатной плоскости | 13+3 | С.№4 | 5 шк. задач | 5 своих задач | | СЛС. ""Классификация векторов на плоскости" "Векторы в шк. курсе геометрии"" Действия над векторами" О О О | | |||||||
| | | | |||||||||||||
| 2 | Прямая на координатной плоскости | 15+3 | С. №2 | Л,О,№ 5 задач | 5 шк. задач | 5 своих | К/р № 1 | | СЛС "Уравнение прямой" (классификация). "Расстояние от точки до прямой" О О О | | |||||
| | | | | | | ||||||||||
| 3 | Линии 2-го порядка | 15+4 | С. №3 | Чертежи всех линий | сочинение "Моя линия" | коллоквиум | СЛС "Линия 2-го порядка (классификация) "Полные сведения о линии 2-го порядка" О | | |||||||
| | | | теория | практика | |||||||||||
| 4 | Преобразования координатной плоскости | 14+6 | С. № 4. | 6 задач | К/р № 2 | Моделирование | Алгоритм проведения линии 2-го порядка к каноническому виду и построение чертежа. О | | |||||||
| | | | О О О О | ||||||||||||
| | | | |||||||||||||
| 5 | Специальные кривые | 7+2 | С. №6 | Построение для решения классических задач | СЛС «Способы решения одной из классических задач» О | | |||||||||
| спрямление | квадратура | удвоение | трисекция | ||||||||||||
Итог: зачет; устный экзамен (см. вопросы). Заполните для себя последнюю колонку
4. Приложения
ПРИЛОЖЕНИЕ 1
4.1. Вопросы к экзамену по геометрии
(I курс, II семестр)
- Вектор. Действия сложения и вычитания векторов (определение, свойства).
- Определение и свойства умножения вектора на число. Применение в задачах.
- Скалярное произведение векторов, свойства его. Определение взаимного расположения векторов по их произведению.
- Уравнение прямой, заданной направляющим вектором и точкой (каноническое и параметрические).
- Общий вид уравнений прямой, заданной на координатной плоскости. Исследование прямой по ее уравнению.
- Расстояние от точки до прямой.
- Уравнение прямой, проходящей через две точки. Эквивалентность его другим уравнениям прямой (1 по выбору).
- Уравнение прямой, заданной нормальным вектором и точкой. Эквивалентность его общему виду уравнения прямой.
- Уравнение прямой, заданной направляющим вектором и точкой. Эквивалентность его общему виду уравнения прямой.
- Уравнения прямой с угловым коэффициентом. Эквивалентность его общему виду уравнения прямой.
- Параметрические уравнения прямой. Эквивалентность их общему виду уравнения прямой.
- Взаимное расположение прямых на плоскости.
- Пучки прямых на плоскости, общее уравнение.
- Парабола. Вывод канонического уравнения. Исследование по уравнению. Построение параболы по уравнению.
- Гипербола. Вывод уравнения, исследование по уравнению. Построение гиперболы уравнению.
- Эллипс. Вывод уравнения, исследование по уравнению. Построение эллипса по уравнению.
- Изменение координат в результате поворота координатной плоскости вокруг 0 (0;0).
- Каноническое и параметрические уравнения окружности.
- Эллипс как проекция окружности. Параметрические уравнения эллипса, построение эллипса по ним.
- Изменение координат в результате геометрических преобразований координатной плоскости (симметрии, параллельный перенос).
- Общий вид уравнения линии 2-го порядка, порядок приведения его к каноническому виду.
- Критерий разрешимости задач на построение циркулем и линейкой. Неразрешимость задач о квадратуре круга, спрямление окружности, удвоение куба и трисекции угла.
- Уравнение прямой “в отрезках” Эквивалентность его общему виду уравнения прямой.
- Эллипс как коническое сечение. Характеристическое свойство эллипса в построении его.
- Парабола как коническое сечение. Характеристические свойства параболы в построении ее.
- Гипербола как коническое сечение. Характеристические свойства гиперболы в построении ее.
- Окружность как коническое сечение. Характеристические свойства окружности. Точка как вырожденная окружность.
- Пара прямых как образ линии 2-го порядка.
Приложение 2
4.2. “Прямая на плоскости. Векторы”
Контрольная работа
(примерное содержание)
| I | | II |
| 1. Составьте уравнение прямой, проходящей через F перпендикулярно 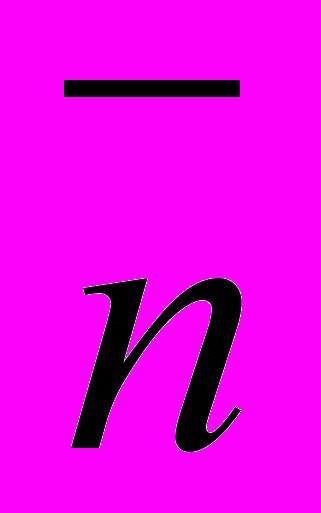 (2; 5), если F симметрична, К(3; -4) относительно оси ОХ. (2; 5), если F симметрична, К(3; -4) относительно оси ОХ. | | 1. Составьте уравнение прямой, проходящей через точку пересечения прямой 5х-2у-10=0 с осью ОУ и перпендикулярной данной прямой. |
| 3. Даны уравнения двух сторон параллелограмма х-4у+11=0; 2х+у-5=0 и уравнение одной его диагоналей х-у-1=0. Найти координаты вершин этого параллелограмма и его площадь. | | 3. Даны вершины треугольника: А(2; 1), В (-2; 3) и С (-10; -13). Вычислите длину перпендикуляра, опущенного из вершины В на медиану, проведенную из вершины С. |
| 4. Составьте уравнение прямой, проходящей через точку (1; 2) что расстояние до этой прямой от точек (2; 3) и (4; –5) одинаковые. | | 4. Запишите уравнение прямых, параллельных прямой 4х + 3у + 1 + 0 так, и отстоящих от нее на расстоянии 3 единиц. |
| 2. Дан правильный шестиугольник, 2 стороны которого 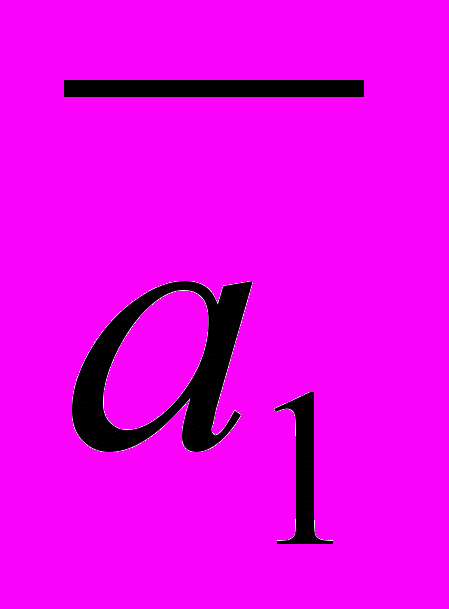 и и  Выразите через Выразите через 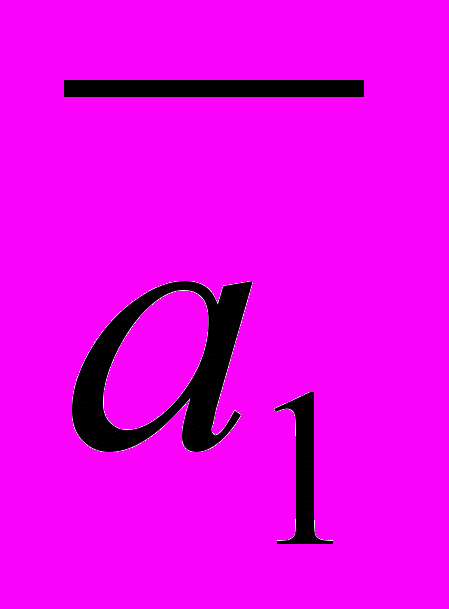 и и 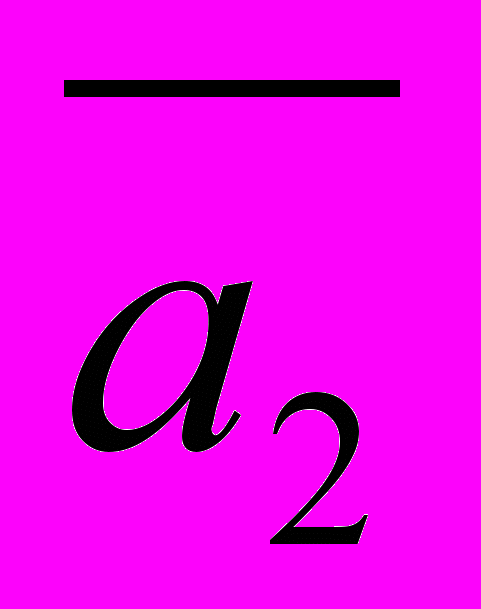 все векторы, определяемые вершинами шестиугольника и выходящие из одной вершины. Определите его площадь. все векторы, определяемые вершинами шестиугольника и выходящие из одной вершины. Определите его площадь. | | (пятиугольник) (пятиугольника) |
Приложение 3
4.3. “Линии 2-го порядка”
Контрольная работа 2
Вариант 1
- Составьте уравнение касательной к гиперболе
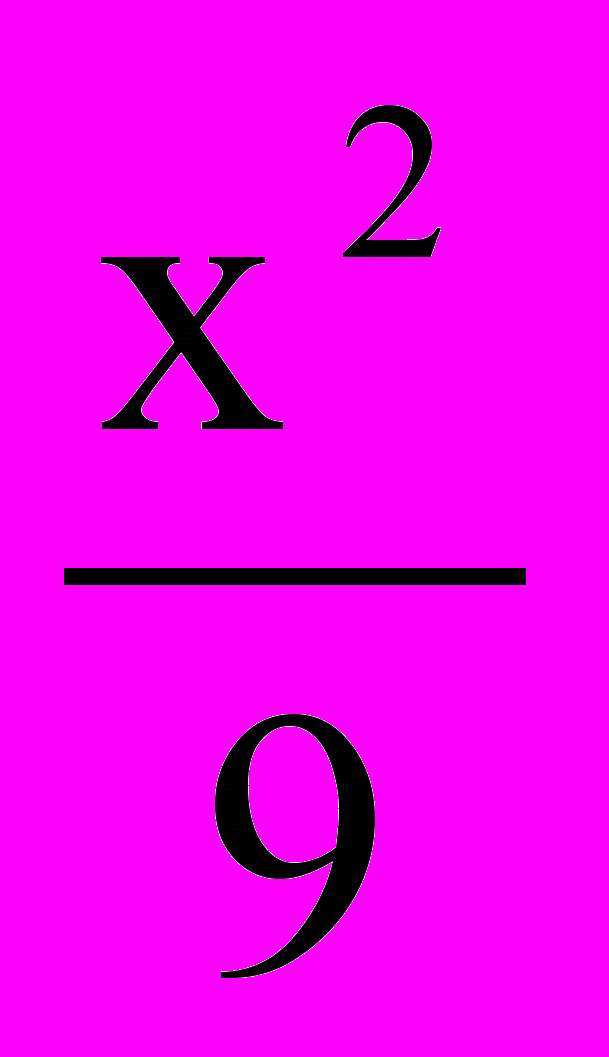 -
-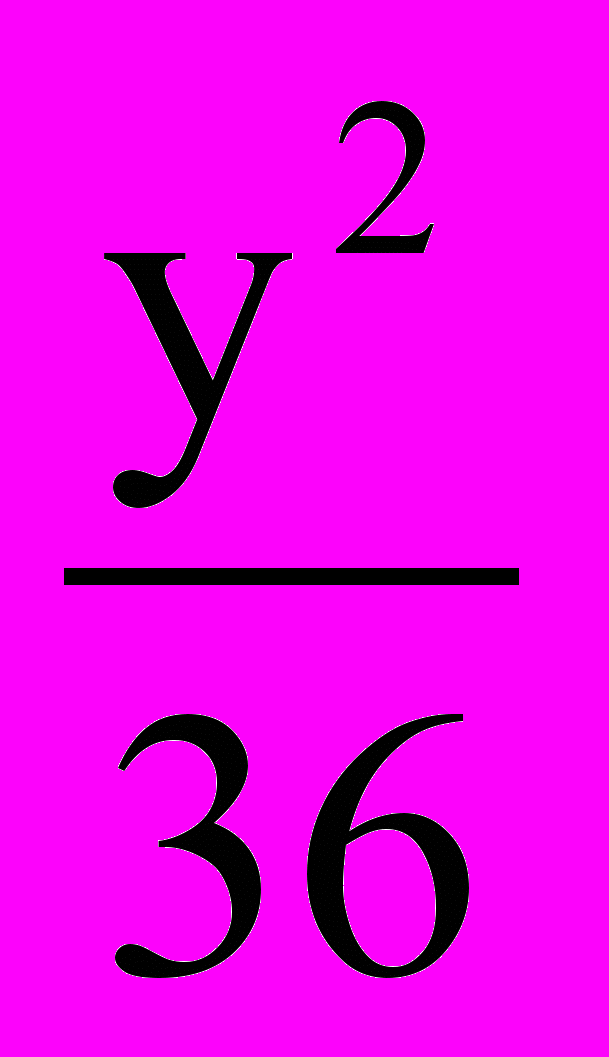 =1, если касательная параллельна прямой 3х - у -17= 0
=1, если касательная параллельна прямой 3х - у -17= 0
- Составьте каноническое уравнение параболы, которая делит отрезок АВ пополам, если А(6;0); В(0;12).
- Уравнение 6x2+4xy+3y2+3x+4y-3=0 привести к каноническому виду, Постройте линию, заданную уравнением.
Вариант 2
- Дан прямоугольник со сторонами 12 и 16. Найдите эксцентриситет гиперболы, которая касается двух его противоположных сторон, а диагонали прямоугольника являются ее асимптотами.
- Напишите уравнение касательной к параболе y2=8x, которая образует с осью абсцисс угол в 450
Уравнение 5x2+8xy+5y2-18y+9=0 привести к каноническому виду. Постройте линию, заданную уравнением.
ПРИЛОЖЕНИЕ 4
4.4. “ Векторы. Система координат”
Лист опроса 4 (семинар 1)
- Система координат на плоскости.
- Виды системы координат.
- 3.Координаты точки на плоскости.
- Вектор.
- Координаты вектора на плоскости.
- Длина вектора.
- Равные векторы.
- Радиус - вектор.
- Единичный вектор.
- Коллинеарные векторы.
- Условие коллениарности векторов.
- Произведение вектора на число.
- Сумма векторов.
- 14.Разность векторов.
- Скалярное произведение векторов.
- Угол между векторами.
- Перпендикулярность (ортогональность) векторов.
- Условие перпендикулярности векторов.
- Векторный метод решения задач.
а) а||в
б)А, В и С - принадлежат одной прямой
в)а в
г) длина отрезка
д) угол между прямыми.
- Координатный метод решения задач (алгебраический)
а) расстояние между точками; б) угол треугольника.
- Свойства сложения векторов.
- Свойства вычитания векторов.
- Свойства умножения вектора на число.
24. Свойства скалярного произведения векторов.
- Линейная комбинация векторов.
26. Линейная зависимость векторов.
- Блок - схема “Векторы на плоскости”
Литература:
1. В.А. Гусев и др. Практикум по элементарной математике (геометрия) М. Просвещение 1992. 352 с.
2. Геометрия под редакцией Г.Н. Яковлева М., Наука. 1990. 320 с.
Приложение 5.1
4.5. Памятка для самостоятельной работы
студентов I курса по высшей геометрии
Тема: “Прямая на плоскости” должна быть усвоена за 20 учебных часов
4 часа - лекция
12 часов - практики
2 часа - рефлексия /подведение итогов/
2 часа - контрольная работа по решению задач
Лекцию вы прослушали, где были разобраны примеры отдельных задач. Дома вам нужно проработать лекцию по памятке “Как работать с учебным текстом”. Подобрать свои примеры элементарных задач.
Дома решаете задачи из темы “Координатная плоскость” (Геометрия 7-9кл.) и задачи из “Геометрии Яковлева для техникумов ( гл.2) и лекции по геометрии С.А. Анищенко стр. 92-93.Трудные задачи можно обсудить с учителем на любом из практических занятий.
По итогам изучения темы Вы должны уметь:
- рассказать по уравнению о положении прямой на плоскости;
- составить уравнение прямой:
а) по направляющему вектору и точке,
б) по двум точкам /координатам этих точек,
в) по нормальному вектору и точке,
г) по отрезкам, отсекаемым прямой на осях координат,
3) перейти от одного вида уравнения прямой к другому виду,
4) определить взаимное расположение точки и прямой, двух прямых,
5) найти расстояние от точки до прямой, между двумя точками,
6) найти угол между прямыми,
При необходимости надо быть готовым обосновать свой путь рассуждениями с теоретических позиций.
Зачетом является: 1. Самоотчет по листу №,5,
- Контрольная работа по решению задач, проверяемая учителем.
Работа предлагает в двух стилях / или вариантах/ В1 - от теории к практике /дедуктивный стиль мышления/
в2 от задач к теории /индуктивно-дедуктивный/
Вы выбираете тот, который Вам подходит. Если затрудняетесь сразу определить свой стиль мышления, начните с В1, т.к. он соответствует методике обучения в ВУЗе.
Надеюсь, что Вы успешно подготовитесь к итоговой контрольной работе.
В добрый путь!
В1. Ответь на вопросы: Лист №.5
- Если смогли ответить на все вопросы, то решите задачи на карточках 5 из группы В, 3 из группы А.
- Оцените свою работу:
За все задачи группы В - “4”
За все задачи группы В и 1-3 группы А - “5”
Правильность решения обсудите с товарищем, ответы проверьте по карточке преподавателя.
Итог подводим вместе /март 3/
После обсуждения к/р /март 3/
Вариант 2 попробуйте решать задачи 5 гр. В, затем 3 гр. А. В случаях затруднения в решении задач обратитесь за помощью.
2.1.К лекции. После прочтения нужной части вернитесь к задаче.
- К однокурснику, после обсуждения с ним теоретической основы задач /математической модели/, вернитесь к решению задач.
- Если лекция и однокурсник не помогли, обратитесь к преподавателю.
- Ответьте на вопросы листа №.5
- Обсуждать итоги будем вместе /март 3/.
Приложение 5.2
4.6. “Прямая на координатной плоскости”
ЛИСТ ОПРОСА 5 (семинар 2)
- Где можно линейную зависимость векторов использовать в теме “Прямая на координатной плоскости.(3 варианта ответа) ?
- Как использовать знания о векторах в следующих задачах?
а) составление уравнения прямой
б) определение взаимного расположения двух прямых
в) определение расстояния от точки до прямой.
- Какой вид может иметь уравнение прямой на плоскости? Что по нему можно сказать о положении прямой на координатной плоскости?
- каноническое
- параметрические
- “в отрезках”
- с угловым коэффициентом
- Каким набором элементов можно задать прямую?
- Нормальный вектор прямой
- Направляющий вектор прямой.
- Точка принадлежит прямой.
- Назовите возможные случаи расположения двух прямых на плоскости.
- Как определить угол между двумя прямыми?
- Как установить параллельность прямых? (4 способа: через направляющие векторы /нормальные/, через угол, через коэффициенты общего уравнения, через систему уравнений/.
- Как установить перпендикулярность прямых? ( 3 способа)
- Как определить точку пересечения двух прямых?
- Как определить расстояние от точки до прямой? / 2 способа/
- Как найти точки, расположенные по одну сторону от прямой?
- Блок-схема “Вектор и прямая на координатной плоскости”
Литература:
- С.А. Анищенко. Лекции по геометрии Ч.1. КГПУ, 1998.
- Г.Н. Яковлев. Геометрия. М.: Наука, 1972.
- Л.С. Атанасян. Геометрия. 2 Ч.1
- Математическая энциклопедия
- В.С. Крамор. Повторяем и систематизируем школьный курс математики. М.: Просвещение, 1992.
Приложение 6
4.7. Семинар 3 “Линии второго порядка”
1.Окружность
а) определение, характеристическое свойство
б) каноническое уравнение
в) параметрические уравнения
г) касательная прямая
д) построение окружности по 3 точкам
2.Эллипс
а) определение, характеристическое свойство
б) каноническое уравнение
в) параметрические уравнения
г) оси эллипса
д) сопряженные диаметры
е) эллипс как проекция окружности
ж) построение эллипса
з)касательные к эллипсу
3.Гипербола
а) определение, характеристическое свойство
б) каноническое уравнение
в) асимптоты гиперболы
г) оси гиперболы
д) касательные к гиперболе
е)построение гиперболы
4.Парабола
а) определение, характеристическое свойство
б) каноническое уравнение
в) уравнение директрисы
г) ось параболы
д) касательная к параболе
е) построение параболы
5. Линии второго порядка как конические сечения, в том числе точка, пара прямых пересекающихся.
6. Пара параллельных прямых как линия 2 - го порядка
7. Диаметр конического сечения (гиперболы, эллипса, параболы)
8. Эксцентриситет линии 2-го порядка
9. Общее определение эллипса, гиперболы, параболы.
10. Блок - схема “Линии 2-го порядка”
Дополнительная литература:
1. Л.С. Атанасян. Геометрия. Ч.1. М.: Просвещение, 1962.
- Математическая энциклопедия
- М.Я. Выготский. Справочник по высшей математике. М.: Наука. 1972. с.872
Приложение 7
4.8. Преобразование системы координат и
уравнения линии 2-го порядка.
- Общий вид уравнения линии 2-го порядка
- Поворот осей системы координат на угол вокруг О
- Параллельный перенос системы координат на
 (x0,y0)
(x0,y0)
- Отражение системы координат от оси ОХ
- Отражение системы координат от оси ОУ
- Отражение системы координат от точки О
- Алгоритм приведения общего уравнения линии 2-го порядка к каноническому виду
- Построение схематичного чертежа линии 2-го порядка с учетом преобразования системы координат.
Дополнительная литература (см. в приложении 6)
Приложение 8
4.9. “Циклоида. Циклоидальные кривые”
Семинар 5
1.Циклоида.
а) определение
б) параметрические уравнения
в) трансцендентное уравнение
г) построение циклоиды (в т.ч. на дисплее ЭВМ)
д) Блок-схема “Вывод уравнения циклоиды”
2. Циклоидальные кривые
а)эпициклоида (определение, параметрические уравнения)
б) гипоциклоида (определение, параметрические уравнения, построение, в т.ч. на ЭВМ)
в) кардиоида
г)астроида
д) кривая Штейнера
3. Блок-схема “ Циклоидальные кривые”
Литература (дополнительная)
- Математическая энциклопедия
- М.Я. Выгодский. Справочник по высшей математике. М.: Наука 1992, 382с.
- Л. С. Атанасян. Геометрия. Ч.1. М.: Просвещение, 1962.
- Н.И. Пак, В.В. Рогов. Практика работы на языке Турбо-Паскаль. Красноярск, КГПУ, 1992, 155 с.
Приложение 9
4.10. “Специальные кривые”
Семинар 6
- Критерий разрешимости задач на построение циркулем и линейкой.
- Примеры задач на построение, разрешимых циркулем и линейкой.
- Классические задачи на построение, неразрешимые циркулем и линейкой (формулировка, обоснование неразрешимости)
а) о трисекции угла
б) об удвоении куба
в) о квадратуре круга
г) о спрямлении окружности.
4. Циссоида Диоклеса (определение, уравнение, построение, практическое использование)
5. Конхоида Никомеда (определение, уравнение, построение, практическое использование)
6. Квадратриса Динострата (определение, уравнение, построение, практическое использование)
7. Блок схема:
“Классические задачи на построение, неразрешимые циркулем и линейкой и способы их решения другими средствами”
Литература : ( см. приложение 8)
5. В.Д. Чистяков. Старинные задачи. Минск, “Высшая школа” 1966.
Приложение 10
4.11. “Линии второго порядка”
Коллоквиум
- Смотри вопросы теоретические в приложении 6
- Практические задания - узнай и изобрази заданную линию
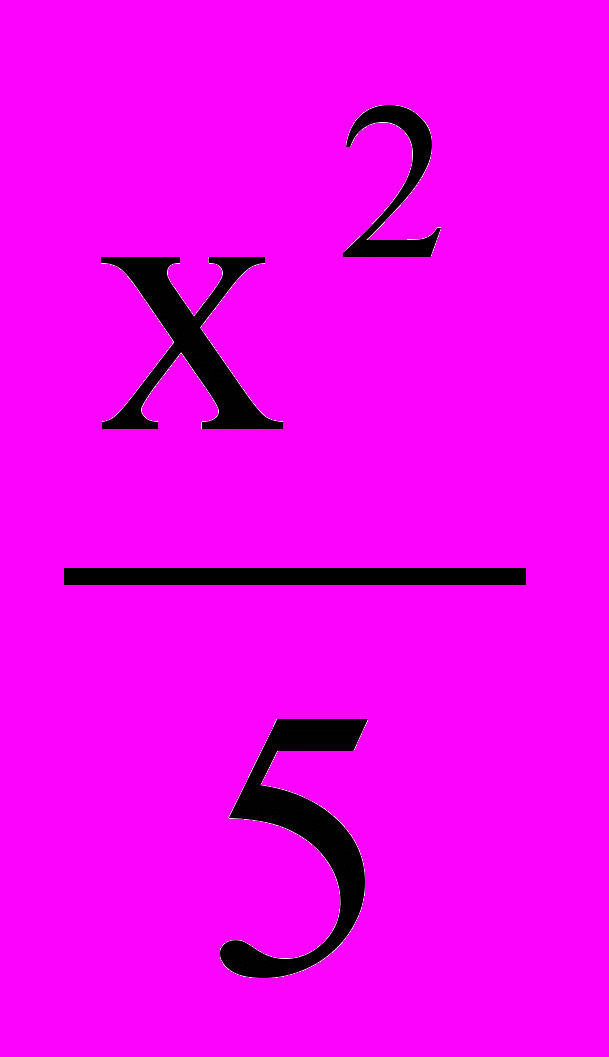 +
+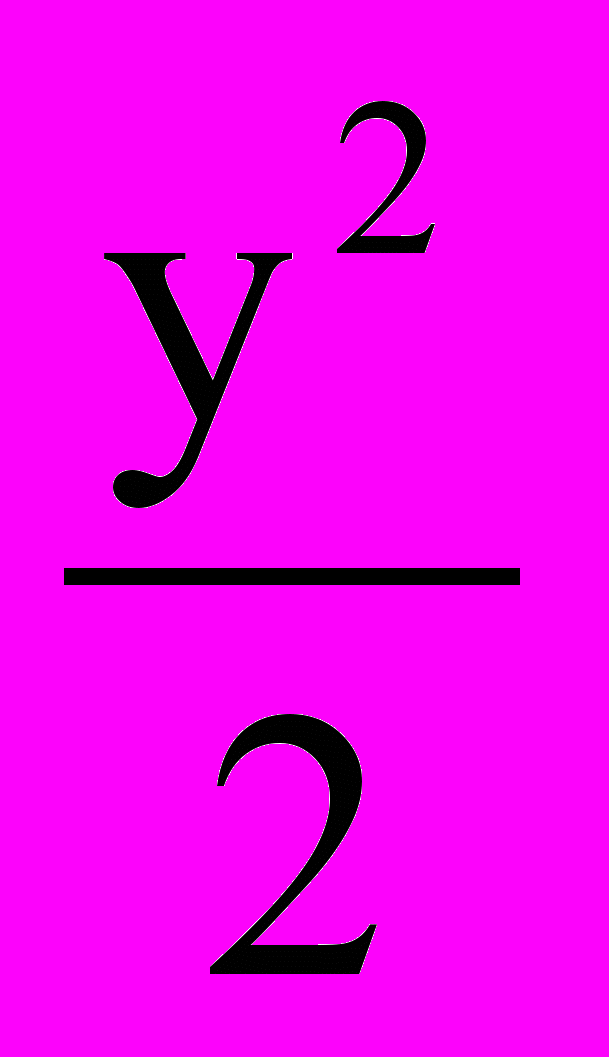 =1; б)
=1; б) 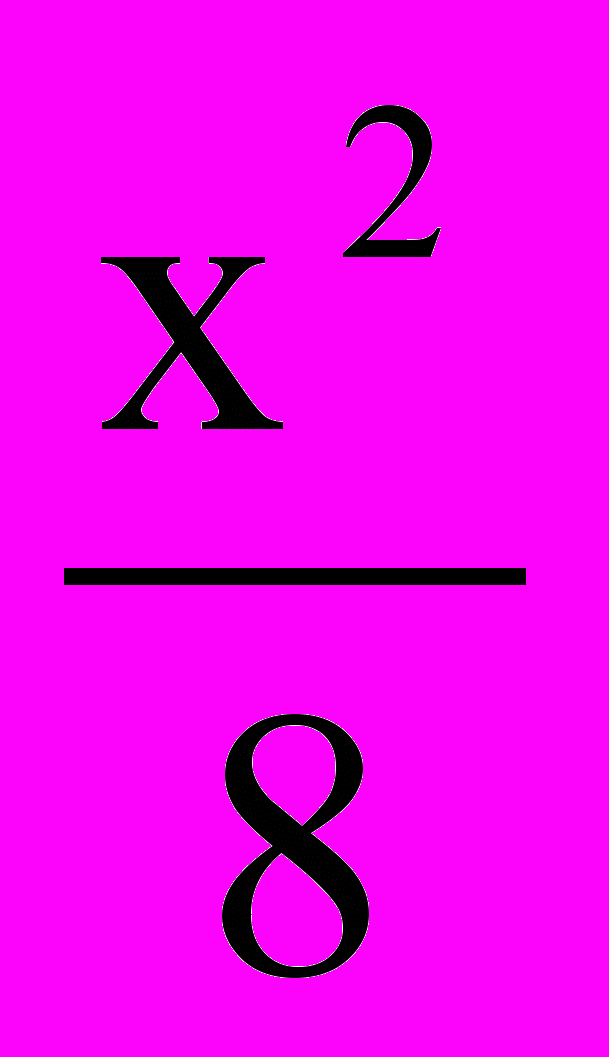 –
–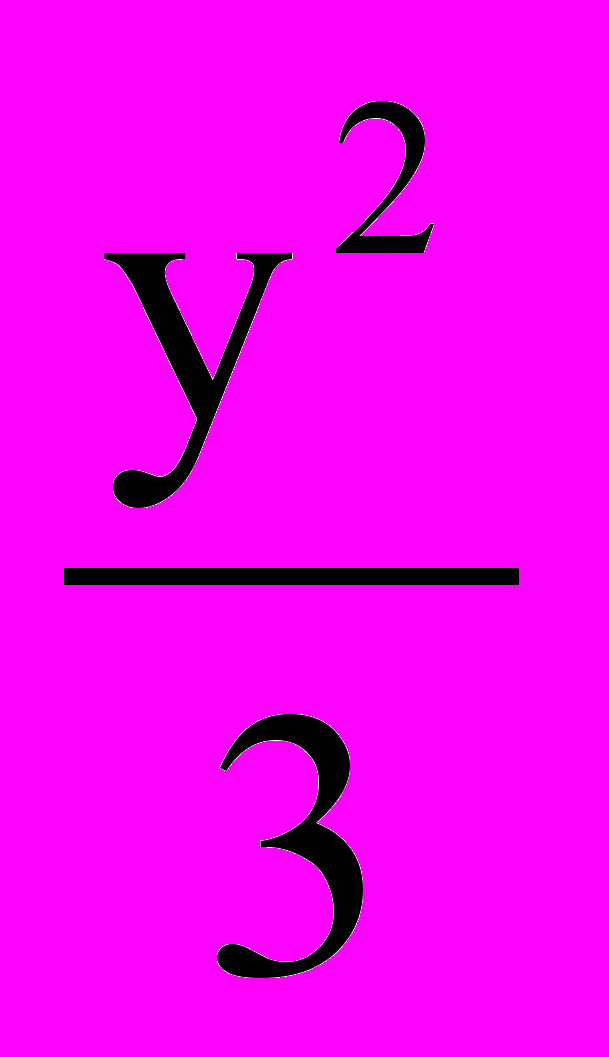 =1; в)
=1; в) 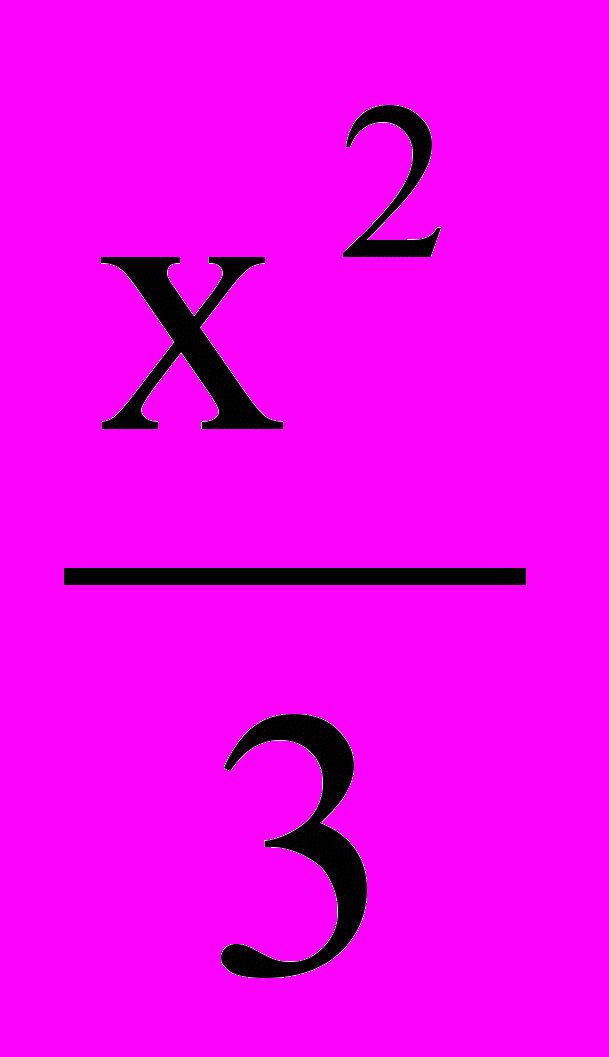 –
–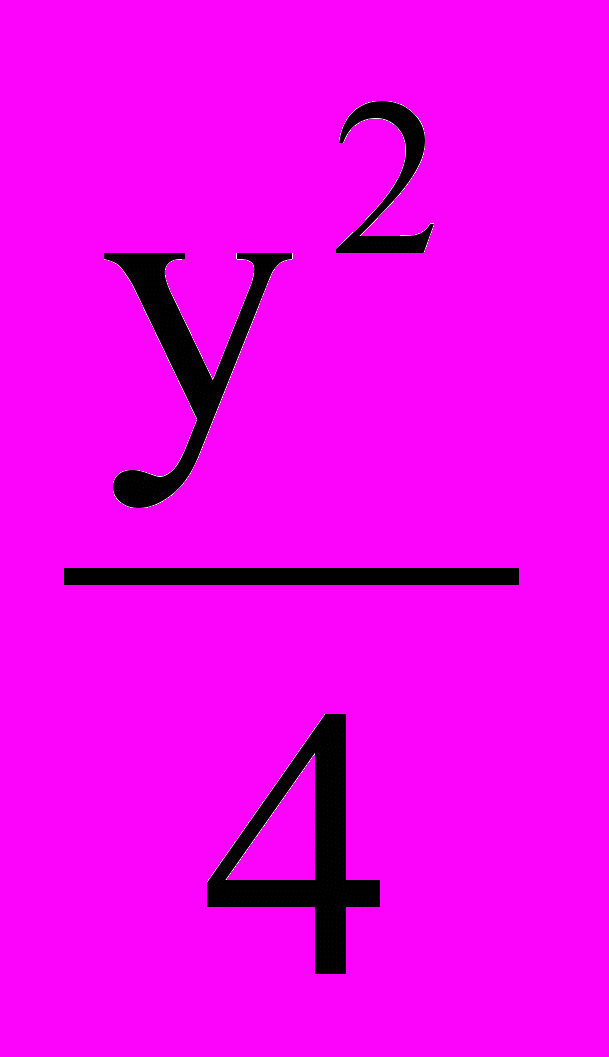 =0;
=0;
г) –
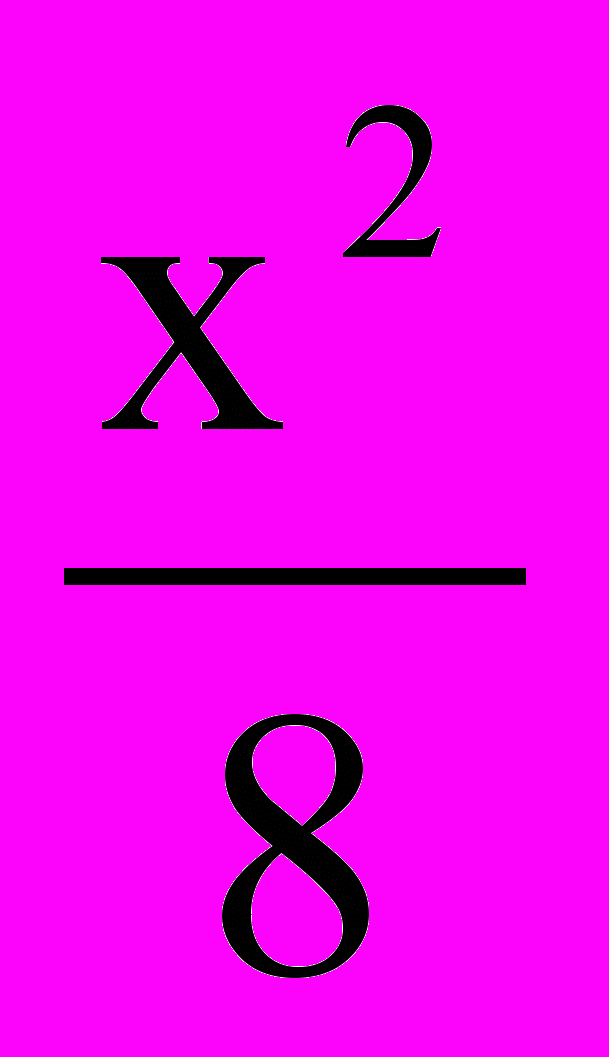 –
–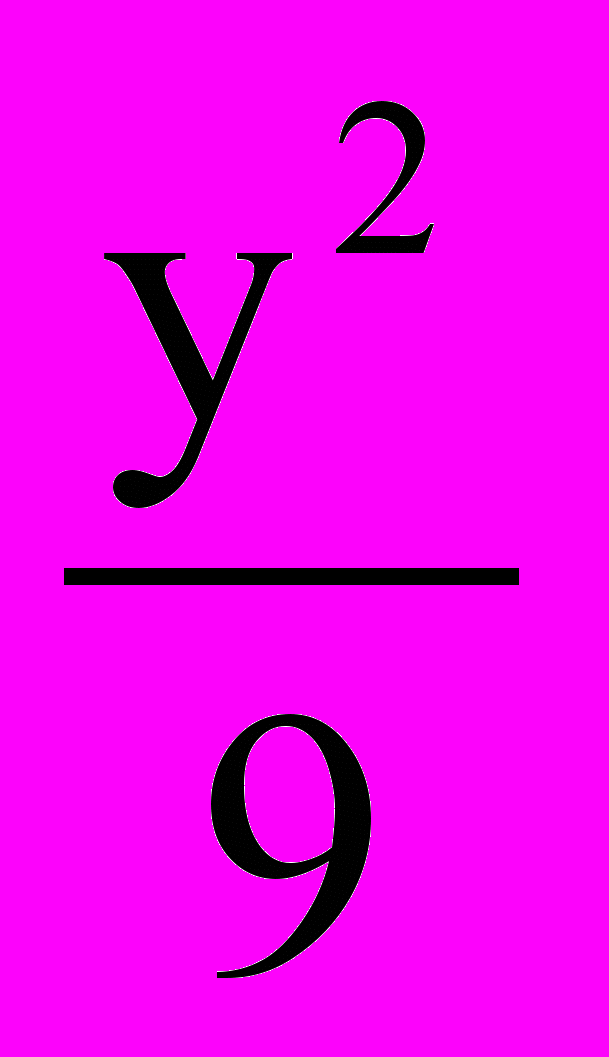 =–1; д)
=–1; д) 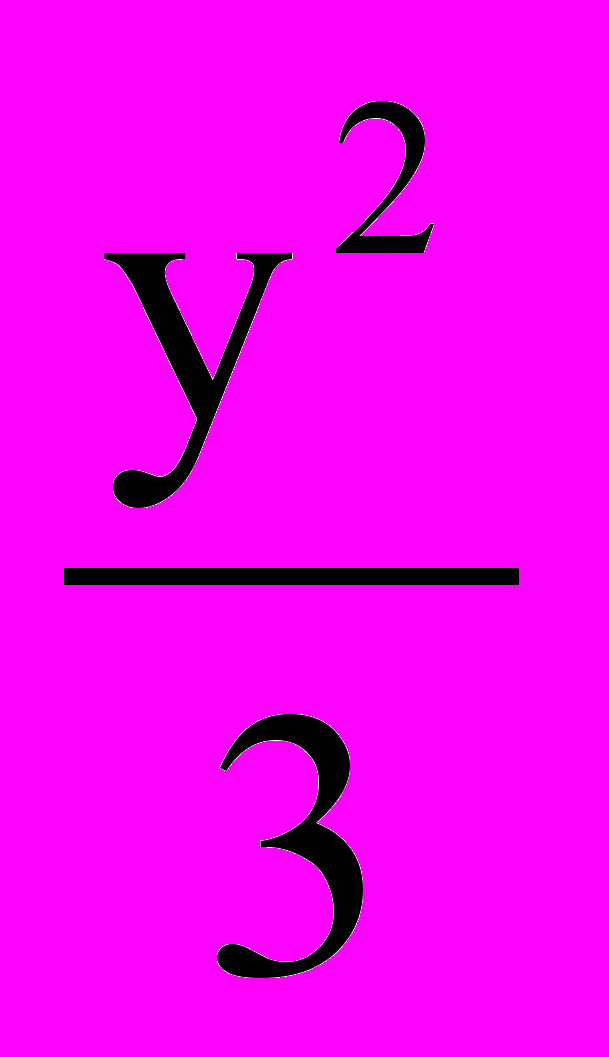 –
–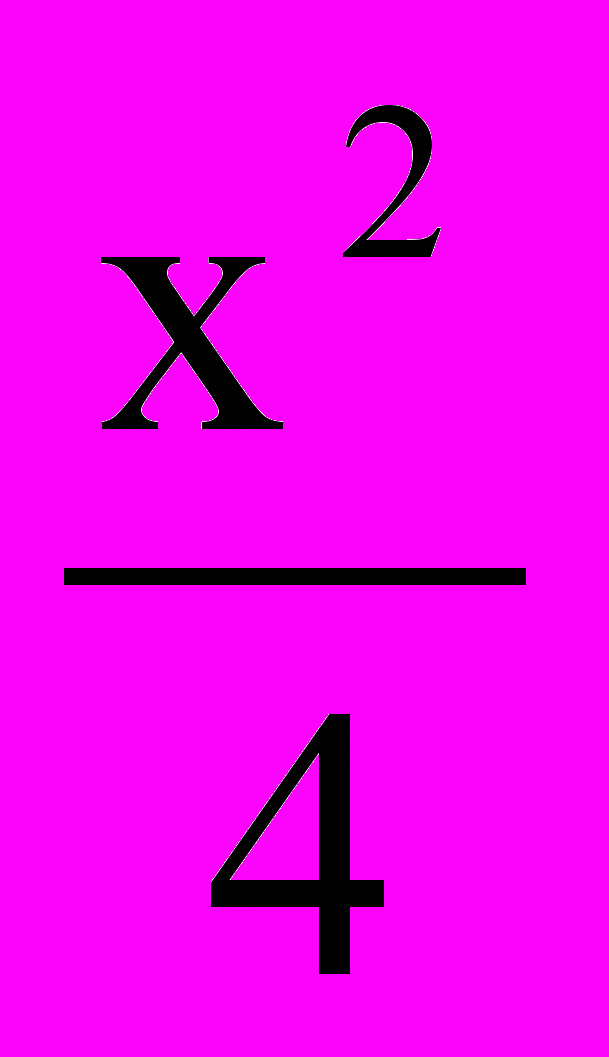 =2; е) 3x2 + 4y2 = 8;
=2; е) 3x2 + 4y2 = 8;ж) (x – 5) 2 + (y – 3)2=8; з)
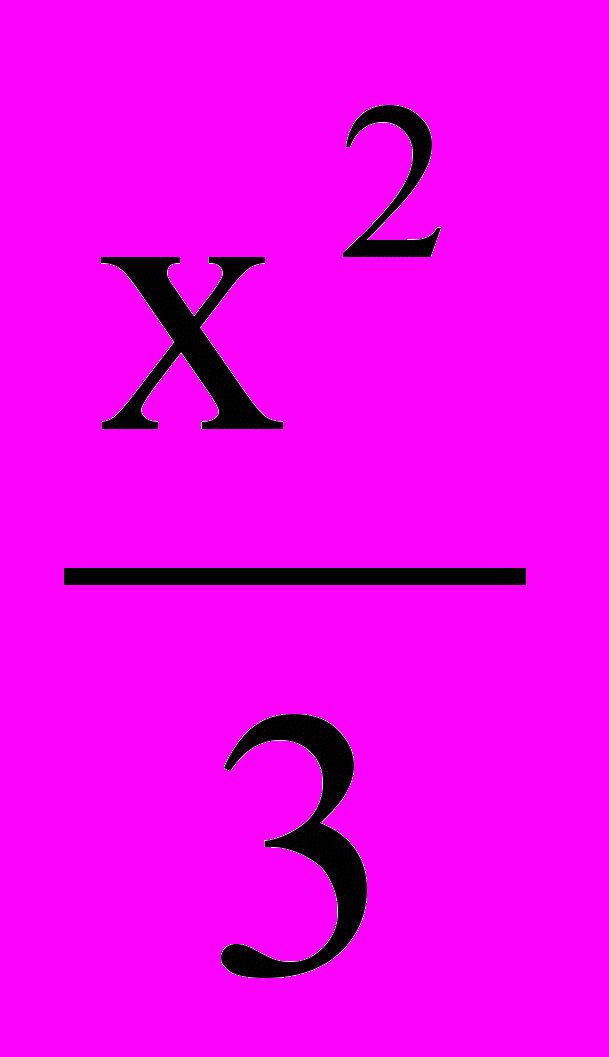 +
+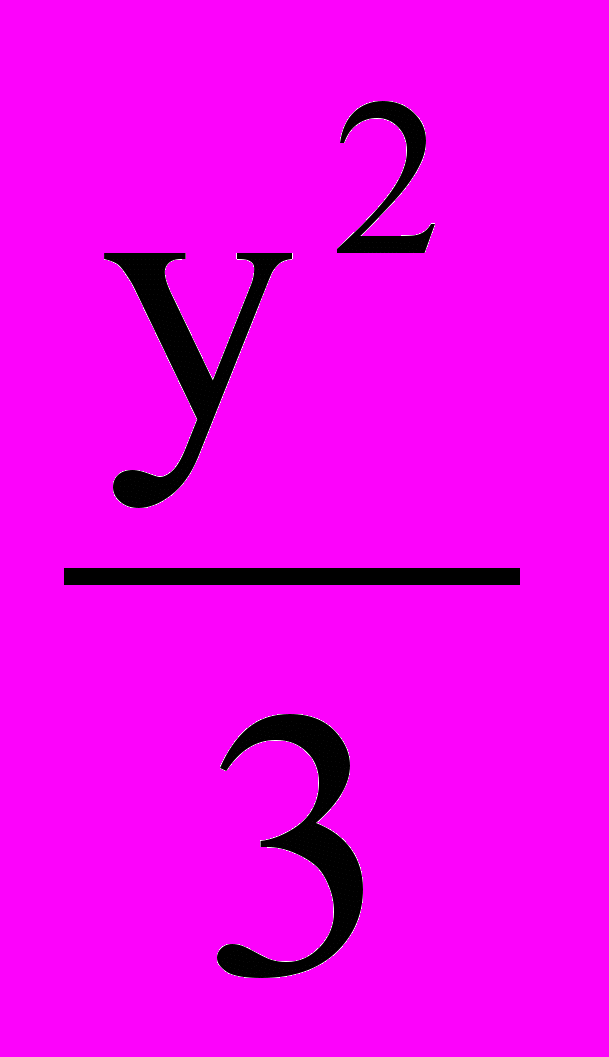 =1; и) 5x2 – 20 = 0;
=1; и) 5x2 – 20 = 0;к) x2 = 8y; л) y =
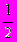 x2
x23. Изобрази и запиши уравнение линии:
а) эллипс с осями 8 и 6
б) гиперболу с осями 8 и 6
в) окружность с центром (0; 5) и радиус r
г) гиперболу с мнимой осью 3 и действительной осью 2.
д) эллипс с эксцентриситетом 1/3 и большей осью 4
ж) гиперболу с эксцентриситетом 3/2 и действительной осью 4
з) параболу с фокусом (0; 4) и директрисой у–8=0
и) параболу с осью х = 3 и директрисой у = –5
- Запишите уравнение касательной
а) к окружности 5x2+5y2=15: 1) в точке (
 ;0)
;0)2) параллельную оси ОХ
3) параллельную ее диаметру,
лежащему на прямой у=х
4) перпендикулярную ее диаметру,
лежащему на прямой у=-х
б) к эллипсу
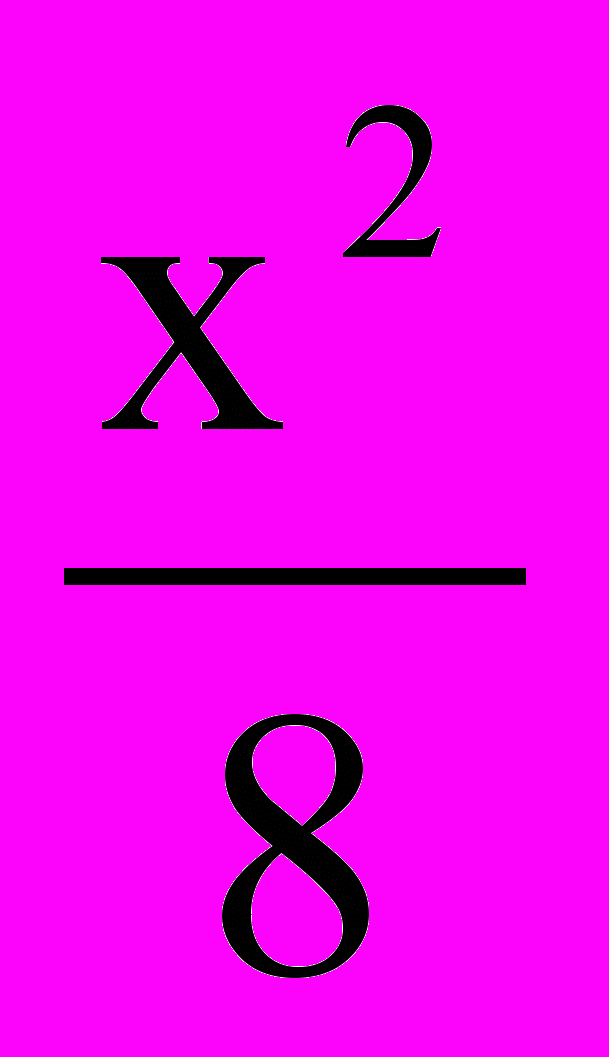 +
+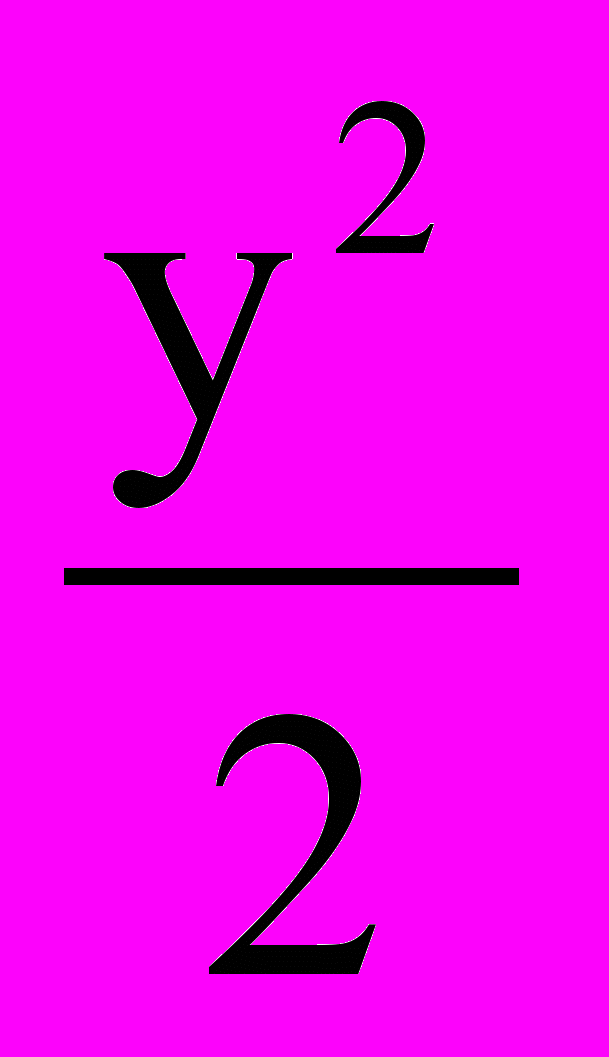 =1 в точке (2
=1 в точке (2 ; 0);
; 0);в) к гиперболе
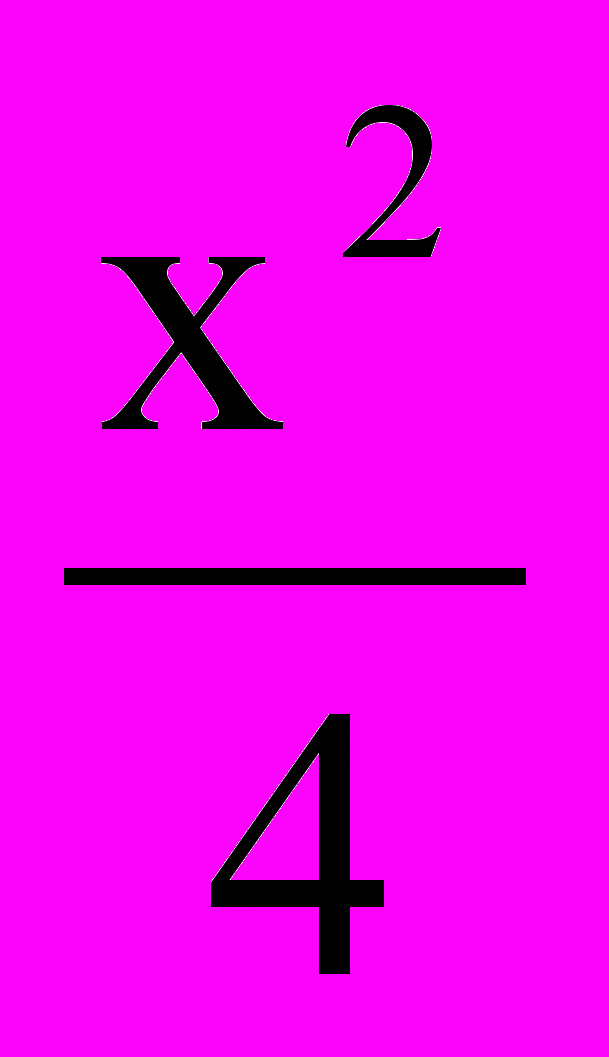 –
–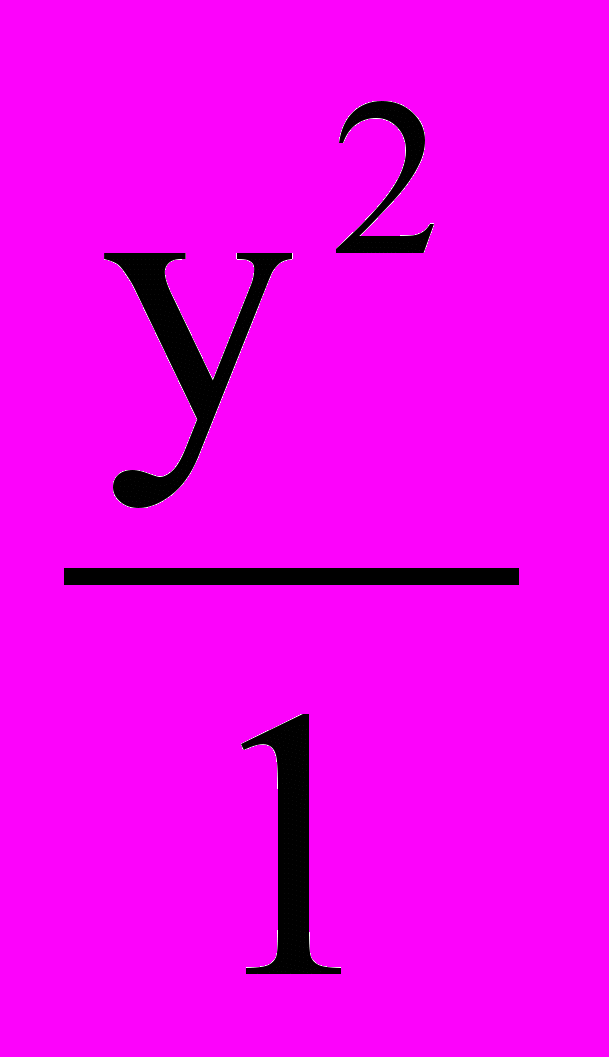 =1 в точке (4;
=1 в точке (4;  );
);г) к параболе y2=4x в точке (5; 2
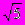 ).
).5. Напишите уравнение асимптот гиперболы:
а)
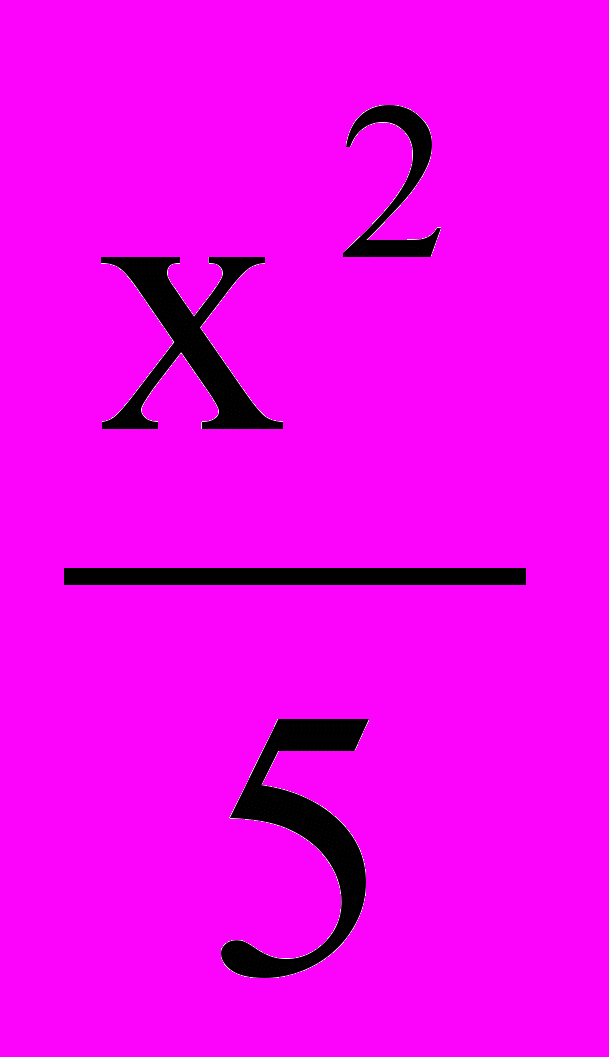 –
–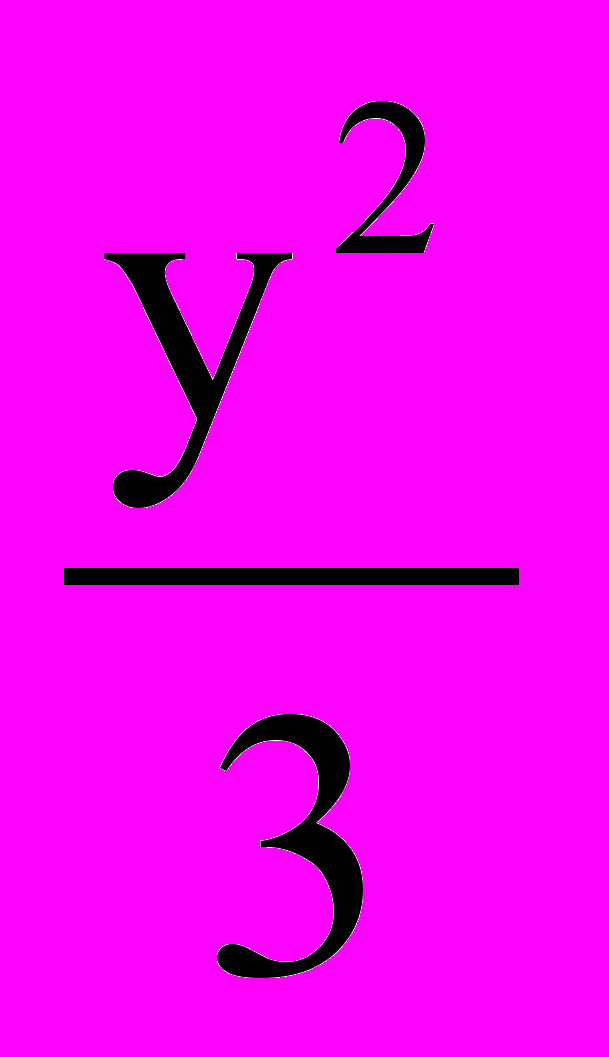 =1; б)
=1; б) 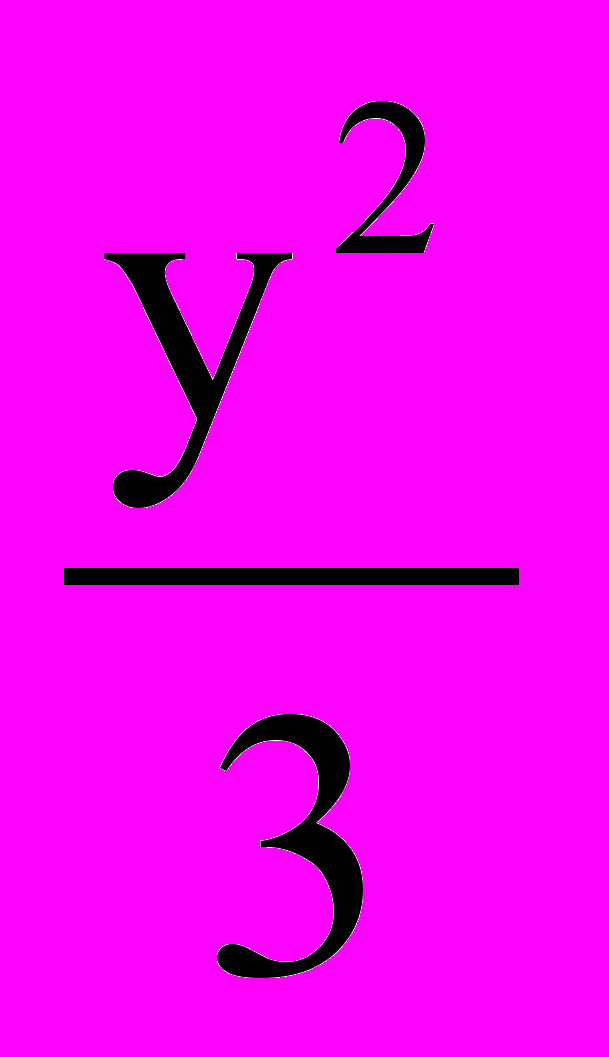 –
–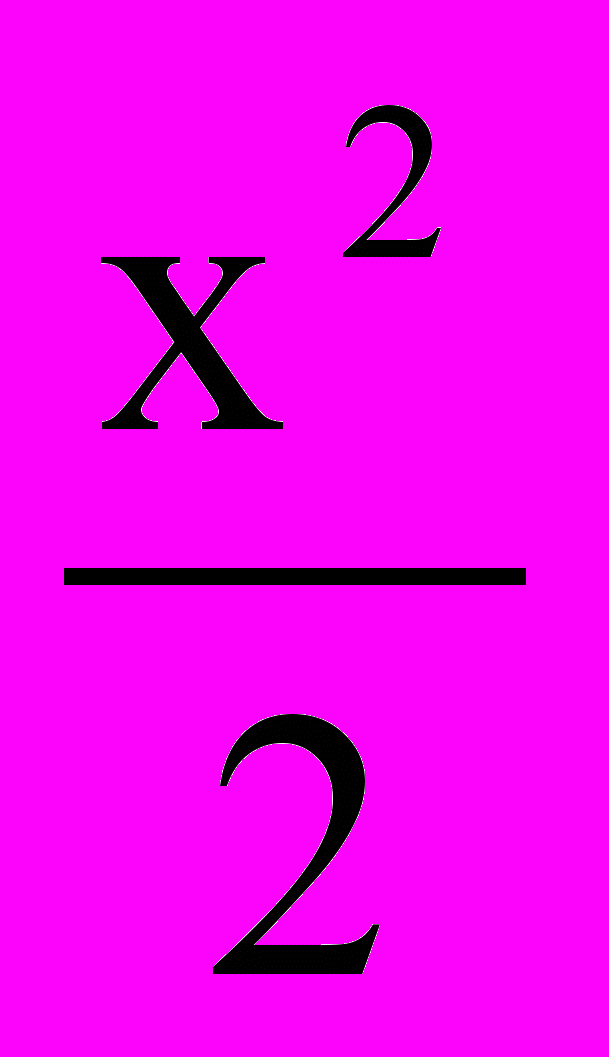 =1.
=1.Литература (в приложении № 6).