Программа и задание на контрольную работу по дисциплинам "Моделирование систем" для студентов IV курса специальности

Вид материала

Содержание

Рабочая программа
071900. Информационные системы и технологии
Комплексы, системы и сети (эвм
1. Цель изучения дисциплины
2. Требования к уровню освоения содержания дисциплины
3. Объем дисциплины и виды учебной работы
4. Содержание дисциплины
4.2.Содержание разделов дисциплины
Информационно-методическое обеспечение дисциплины
Задание на контрольную работу
Т=А+В+2 мкс, и с фронтом и срезом по h

Подобный материал:

МПС РОССИИ

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ

20/53/1

Согласовано: Утверждаю:

Зав. кафедрой ВТ Декан факультета УПП

_________ В.Ю.Горелик _________ Г.М.Биленко

МОДЕЛИРОВАНИЕ СИСТЕМ

для студентов IV курса специальности

071900. ИНФОРМАЦИОННЫЕ СИСТЕМЫ И ТЕХНОЛОГИИ (ИСЖ)

и

Модели информационных процессов

для студентов V курса специальности

230101(220100). ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ,

КОМПЛЕКСЫ, СИСТЕМЫ И СЕТИ (ЭВМ)

Рабочая программа

и задание на контрольную работу

с методическими указаниями

Москва – 2007

Рабочая программа и задание на контрольную работу

по дисциплинам "Моделирование систем"

для студентов IV курса специальности

071900. ИНФОРМАЦИОННЫЕ СИСТЕМЫ И ТЕХНОЛОГИИ

(ИСЖ)

и "Модели информационных процессов"

для студентов V курса специальности

230101(220100). ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ,

КОМПЛЕКСЫ, СИСТЕМЫ И СЕТИ (ЭВМ)

Программа составлена в соответствии с Государственным образовательным стандартом высшего профессионального образования и в соответствии с государственными требованиями к минимуму содержания и уровню подготовки инженеров по указанным специальностям.

С о с т а в и т е л ь: д.т.н., проф. Осипов Л.А.

1. Цель изучения дисциплины

Целью изучения дисциплины является обучение студентов общим вопросам теории моделирования, формального описания систем и процессов, методам построения математических моделей и применению их для проведения вычислительных экспериментов и решения задач исследования или проектирования.

2. Требования к уровню освоения содержания дисциплины

В результате изучения дисциплины студент должен:

2.1. Ознакомиться с основными понятиями моделирования и теории подобия и аналогий, теоретическими положениями и методикой экспериментальных исследований, используемых для построения математических моделей;

2.2. Получить навыки в области постановки задачи моделирования, математического описания моделируемого процесса (систем), численных методов реализации математических моделей на ЭВМ и применения интегрированных пакетов;

2.3. Освоить методы подхода к математическому моделированию процессов и систем, начиная с постановки задачи и кончая составлением программ и реализацией математических моделей на ЭВМ.

Материал данной дисциплины основывается на знаниях, полученных студентами при изучении курсов "Информатика", "Высшая математика", "Учебная практика", "Теория вероятностей, статистика и случайные процессы", общенаучных и общеинженерных дисциплин.

3. Объем дисциплины и виды учебной работы

Специальность - Курс	ИСЖ - IV	ЭВМ - V
Всего часов	119	85
Аудиторные занятия:	12	12
Лекции	8	8
Лабораторные занятия	4
Практические занятия		4
Самостоятельная работа	90	58
Контрольная работа	1 (15 час.)	1 (15 час.)
Вид итогового контроля
Зачет	1
Экзамен	1	1

4. Содержание дисциплины

4.1. Перечень тем лекционных и лабораторно-практических занятий

№ п/п	Наименование тем лекций	Количество часов
1.	Моделирование, математические модели и их особенности. Средства и методика моделирования. Построение математических моделей. Уравнения Колмогорова и их решение.	4
2.	Имитационное моделирование информационно-вычислительных систем. Разработка схем алгоритма моделей. Вычислительный эксперимент. Методика выполнения контрольного задания	4

№ п/п	Название лабораторно-практической работы	Количество часов
1.	Решение на ЭВМ задачи имитационного моделирования по разработанной программе на одном из языков программирования (по выбору студента)	4

4.2.Содержание разделов дисциплины

Раздел 1. Общие вопросы теории моделирования.

1.1. Система, её структура, принципы функционирования и модель. Основные понятия теории моделирования. Классификация видов моделирования систем. Методы реализации моделей (аналоговые, численные, аналитические, имитационные). Использование моделирования при проектировании, обучении эксплуатации сложных систем, анализе нештатных ситуаций и в тренажерных комплексах.

1.2. Модели и средства моделирования, применяемые в процессе проектирования информационно-вычислительных систем на разных стадиях проекта и его детализации. Инструментальные средства и языки моделирования систем. Формализация и алгоритмизация процессов обработки информации. Вычислительный эксперимент.

1.3. Основные понятия теории аналогий. Соответствие уравнений, описывающих функционирование системы и её модели. Способы представления моделей. Показатели эффективности и критерии качества систем. Способы оценки точности и достоверности результатов моделирования.

1.4. Обзор математических методов качественного и количественного моделирования систем (объектов и процессов). Математические схемы моделирования информационных систем. Аналитическое и имитационное моделирование.

[1-5 ].

Раздел 2. Методы построения математических моделей

2.1. Суть математического моделирования. Аналитическое и имитационное моделирование. Основные этапы математического моделирования систем.

2.2. Описание объектов моделирования. Упрощение модели объекта и условий его функционирования (идеализация, допущения). Исследование условий подобия модели и моделируемого объекта (процесса). Оценка ожидаемых результатов моделирования. Определение областей устойчивости модели. Методы исследования на полноту, непротиворечивость, адекватность и устойчивость по отношению к возмущениям.

2.3. Аналитическое моделирование информационных систем. Математическое описание функционирования системы. Составление системы дифференциальных уравнений. Определение начальных условий и диапазона изменения параметров.

2.4. Аналитическое моделирование процессов в электрических цепях, в системах связи и передачи данных. Составление дифференциальных уравнений, моделирующих процессы в каналах связи. Определение краевых условий и процесса изменения параметров сигналов.

2.5. Моделирование процессов в электронных устройствах. Определение переходных процессов в импульсных и цифровых устройствах. Моделирование и расчет надежности информационно-вычислительных систем.

2.6. Моделирование систем автоматического управления. Составление дифференциальных уравнений, моделирующих функционирование систем автоматического управления. Определение качества управления и допустимого диапазона изменения параметров системы.

2.7. Методы решения систем алгебраических и дифференциальных уравнений (методы итераций, Гаусса, метод Рунге-Кутты и др.). Применение конечно-разностных преобразований для дифференциальных уравнений. Применение пакетов прикладных программ.

2.8. Имитационное моделирование систем. Характеристики статистического моделирования. Процедуры генерации случайных последовательностей для статистического моделирования на ЭВМ. Оценка качества закона распределения случайных чисел. Получение заданного закона распределения через последовательность равновероятно распределенных чисел.

2.9. Планирование имитационных экспериментов с моделями. Логическая структура моделей. Разработка моделирующих алгоритмов, описание их на машинном языке. Анализ и интерпретация результатов вычислительных экспериментов на ЭВМ. Оценка адекватности моделей, универсальности и экономичности.

[1-3,5-7].

Раздел 3. Моделирования информационных процессов

3.1. Математическое моделирование функционирования систем массового обслуживания (СМО). Потоки требований (запросов) и средства их обработки. Модели СМО с очередями и с отказами. Понятие об оптимизационных задачах. Производительность процессора и время обработки требований. Критерии оптимальности и оценка методов оптимизации.

3.2. Моделирование вычислительных систем и сетей. Поток требований, каналы коммуникаций, очереди, приборы обслуживания (процессоры) и их описание. Многопроцессорные системы и оценка их производительности. Разработка общего алгоритма функционирования модели системы. Реализация вычислительного эксперимента. Сравнение данных моделирования с натурным (физическим) экспериментом. Выработка требований к проектируемым системам и рекомендаций по совершенствованию существующих систем.

3.3. Моделирование каналов передачи информации. Обеспечение помехоустойчивой работы каналов. Определение пропускной способности и требований к каналам передачи цифровой информации.

3.4. Имитационное моделирование информационной системы реализации железнодорожных билетов типа “Экспресс”. Оценка потока заявок. Задание максимальной длины очереди и среднего времени обработки одной заявки. Разработка алгоритма модели и ее машинной программы. Определение среднего времени обслуживания заявки, количества отказов и загрузки центрального процессора. Оптимизация модели.

[1,5-7].

ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ

О с и п о в Л. А. Моделирование информационных процессов: Учебное пособие.-М.: РГОТУПС, 2007.
Ш е л у х и н О. И., Т е н я к ш е в А. М., О с и н А. В. Моделирование информационных систем.-М.: Радиотехника, 2005.
С о в е т о в Б. Я., Яковлев С.А. Моделирование систем: Учебник для вузов. М.: Высшая школа, 2001.
С о в е т о в Б. Я., Яковлев С.А. Моделирование систем: Практикум. М.: Высшая школа, 2006.
Информационные технологии на ж.-д. транспорте: Учебник для вузов ж.-д. транспорта/ Под ред. Э.К.Лецкого, Э.С.Поддавашкина, В.В.Яковлева. М.: УМК МПС РФ, 2001.
О с и п о в Л. А. Эффективные алгоритмы и программы цифровой обработки сигналов: Учебное пособие. М.:РГОТУПС, 1999.
О с и п о в Л. А. Обработка сигналов на цифровых процессорах. Линейно-аппроксимирующий метод: Справочное пособие. М.: Горячая линия-Телеком, 2001.

Задание на контрольную работу

Общие указания

Задание составлено на основе знаний студентами материалов по построению информационно-вычислительных систем, навыков составления алгоритмов и программ и работы на ЭВМ, полученными при изучении дисциплин "Теория вероятностей, статистика и случайные процессы", “Применение интегрированных пакетов в инженерных расчетах”, "Основы алгоритмизации и программирования", "Теория массового обслуживания", "Теория информационных процессов и систем".

Контрольная работа состоит из трех задач и выполняется по варианту, который определяется двумя цифрами учебного шифра студента. Исходные данные рассчитываются по шифру и в числовом виде приводятся в начале контрольной работы. Контрольная работа, выполняется после изучения дисциплины минимум в объеме данного учебного пособия.

Задача 1. Составить схему алгоритма и программу и выполнить исследования методом имитационного моделирования показателей эффективности типовой многопользовательской информационной системы для определения требований к центральному процессору. В качестве примера рассмотреть определение характеристик функционирования централизованной многокассовой системы продажи ж.-д. билетов.

Структурная схема информационной системы приведена на рис. 1. Она состоит из N кассовых терминалов (К₁, К₂, ..., К_N), соединенных каналом связи с вычислительным центром (ВЦ). Основным устройством ВЦ является центральный процессор (ЦП), обрабатывающий заявки от абонентов. ЦП хранит в памяти банк данных о наличии свободных мест на поезда. При ЦП имеется накопитель, память которого обеспечивает хранение в очереди до М заявок, поступивших на обслуживание. После обработки очередной заявки ЦП выдает сведения об имеющихся местах на поезда через канал связи в соответствующую кассу и приступает к обработке следующей заявки из очереди.

Данная система является типовой системой массового обслуживания (СМО). Физически такая система является замкнутой, так как абонент К_jне подает новых заявок, пока не получит ответ от ЦП и не обработает его до определенной формы. Однако, при количестве абонентов N значительно большем емкости М накопителя систему можно рассматривать разомкнутой при среднем потоке заявок на входе устройства обработки. При таком соотношении и рационально выбранных параметрах системы обработки событие пустой очереди перед ЦП будет маловероятным.Аналогичным образом работают многие информационные СМО.

ЦП

t₂

t_m

t_M-1

t₁

t₀

К₁

К₂

К_N

Рис. 1

В задаче требуется определить следующие параметры работы системы количество заявок (n), обслуживаемых за период исследования в Т часов, среднее время обслуживания одной заявки (s), процент отказов в приеме заявок (r) и процент загрузки ЦП (q). Время обслуживания заявки (время ожидания ответа на запрос) слагается из времени ожидания в очереди и времени обработки в процессоре. При отказе в обслуживании обычно выдается сообщение: “Система занята, повторите запрос через некоторое время”. Загрузка процессора говорит о рациональности выбора соответствующего компьютера (она должна быть более 50% , остальное время процессор может использоваться для решения “фоновых задач”).

В работе принять следующие исходные данные (полагая, что шифр студента оканчивается двумя цифрами АВ):

- средний интервал между заявками z=0,001(В+1) час.;

- среднее время обработки процессором одной заявки w задать тремя значениями 0,8z; 0,6z и 0,4z;

- емкость накопителя (очереди) задать двумя значениями М₁=3+А и М₂=7+А;

- период исследования Т=В+2 час.

Задаваясь параметрами М и варьируя w, рассчитать s(w), r(w), q(w), провести их статистическую обработку и построить соответствующие графики. В имитационном моделировании вычислительный эксперимент проводится 5-10 раз при одних и тех же исходных данных и находятся средние значения показателей эффективности (s, r, q) для построения графиков.

Определить при каких значениях w (оно обратно пропорционально производительности ЦП) среднее время ожидания ответа s не более 10 c, обеспечивается средняя загрузка q процессора не менее 50 % , а количество отказов r в среднем не превышает 1% от общего количества поступивших заявок (n).

При решении задачи считать, что поток заявок подчиняется экспоненциальному закону распределения. Плотность вероятности экспоненциального закона имеет максимум при нулевом аргументе, что хорошо согласуется с практикой потоков в СМО. Распределение времени обработки информации в ЦП обычно концентрируется около некоторого среднего значения, поэтому для времени обработки заявок принять закон Рэлея, так как экспоненциальный закон здесь не подходит. Оба принятые законы распределения достаточно просто генерируются через равновероятное распределение случайных величин, имеющееся во всех языках программирования.

Законы равномерной плотности распределения случайных чисел (от 0 до 1) f(x), экспоненциальный f₁(x) и Рэлея f₂(x) описываются в [1-3]. Случайные величины для законов f₁(x) и f₂(x) находятся через их обратные функции распределения (квантили) с помощью процедуры закона равной плотности вероятности f(x).

В контрольной задаче представить следующие материалы:

а) формулировку задания и исходные данные, соответствующие варианту;

б) схему алгоритма решения задач с кратким пояснением;

в) программу решения задачи на языке программирования или с помощью интегрированного пакета;

г) результаты статистической обработки имитационного моделирования задачи на ЭВМ, анализ полученных результатов и выводы (с какими параметрами требуется наиболее экономичный процессор для разрабатываемой ИС).

Задача 2. Описать процессы системы рис. 1 дифференциальными уравнениями Колмогорова и рассчитать решение этих уравнений по формулам вероятности состояний для установившегося режима. Все данные взять из задачи 1. По найденным вероятностям определить среднее время обслуживания заявок s, проценты отказов r и загрузки процессора q.

В контрольной задаче представить следующие материалы:

а) формулировку задания и исходные данные, соответствующие варианту;

б) систему дифференциальных уравнений;

в) программу решения задачи на языке программирования или с помощью интегрированного пакета;

г) сравнить результаты аналитического вероятностного моделирования с результатами решения задачи 1 имитационным моделированием и сформулировать выводы (пояснить причины расхождений и оценить методики исследований).

Задача 3. Методом детерминированного аналитического моделирования исследовать процесс передачи информации по каналам связи. Цифровые сигналы представляются сериями прямоугольных импульсов. В данной задаче требуется определить задержку и уменьшение амплитуды входного импульса на выходе проводной линии связи определенной длины. Процессы в такой электрической цепи можно описать передаточной функцией [6,7]

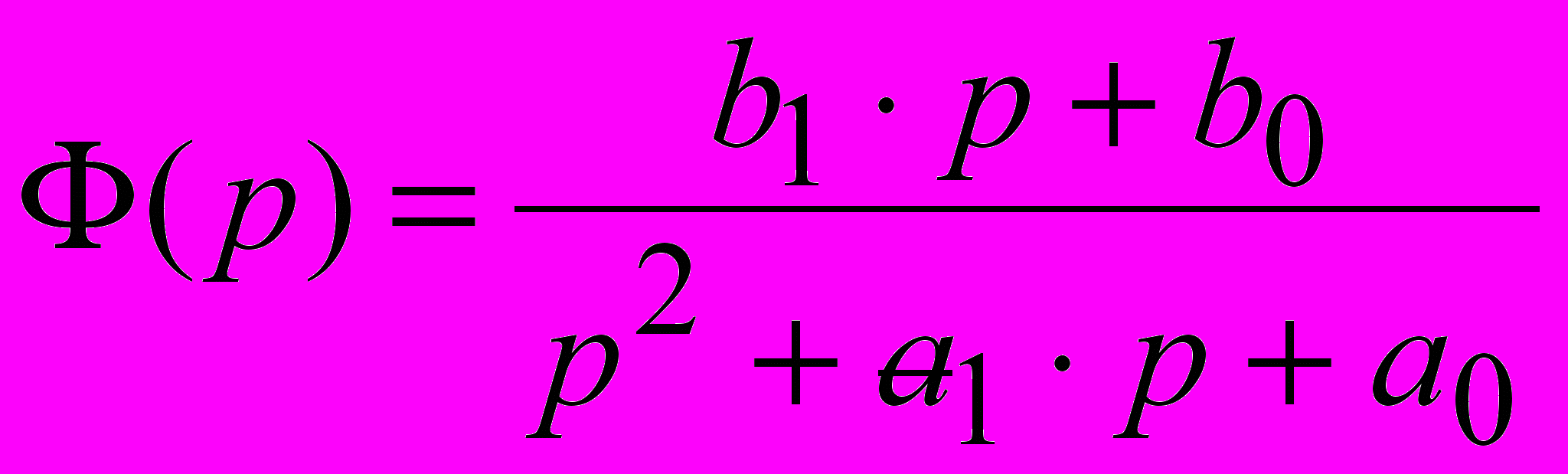, (1)

где p – оператор дифференцирования p=

;

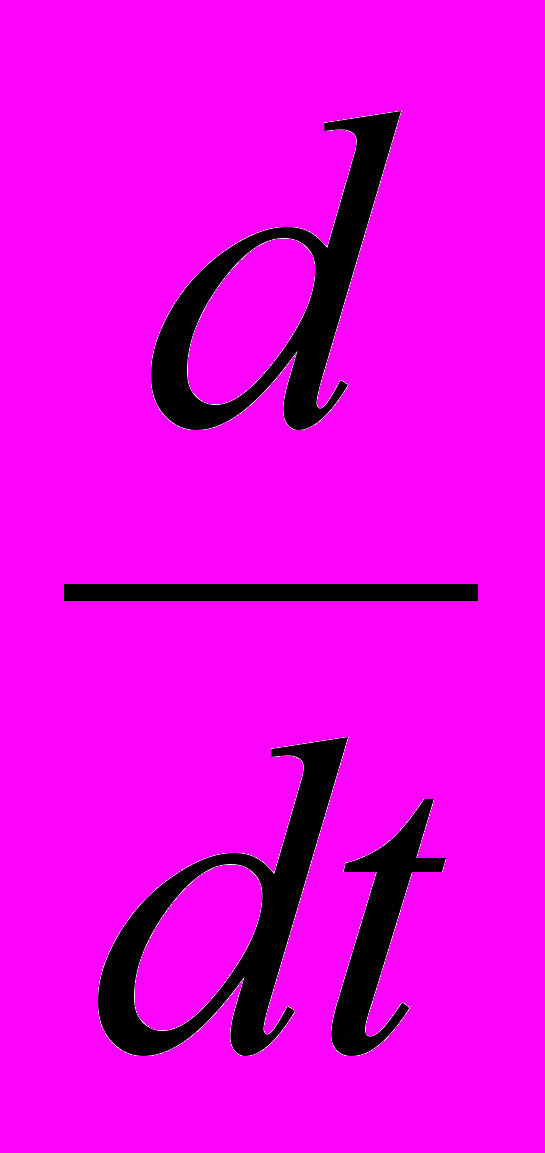b₁, b₀, a₁, a₀ –постоянные коэффициенты, определяются по шифру студента: b₀=В+1; b₁=0,5b₀; a₀=1,1b₀; а₁=3 .

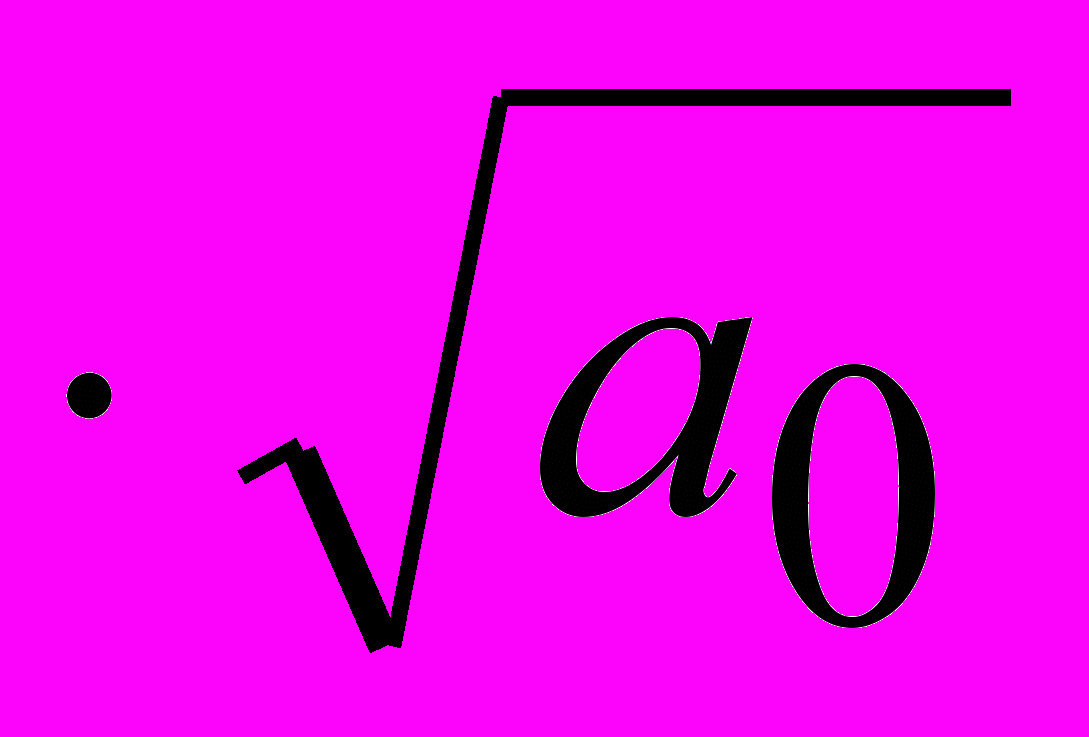Входной импульс полагать трапецеидальным с длительностью по вершине, равной Т=А+В+2 мкс, и с фронтом и срезом по h=0,01T.

Т р е б у е т с я: 1. Составить дифференциальное уравнение системы, описывающей процесс преобразования входного сигнала.

2. Преобразовать передаточную функцию (1) заменой p=i, где i=

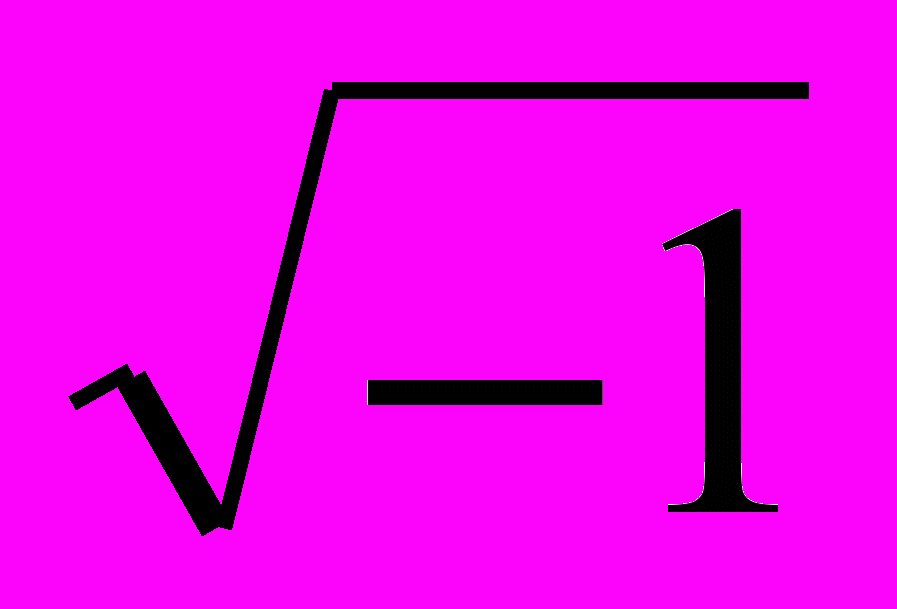,  - круговая частота, в частотную характеристику в виде комплексной суммы Ф(i)=z₁()+iz₂().

3. Разработать графическую схему алгоритма определения переходного процесса дискретным частотным методом и дать пояснения операторам этой схемы.

4. Решить полученные уравнения с помощью интегрированного пакета Mathcad с построением графика для выходного сигнала.

5. Сделать выводы по проведенному исследованию.

В контрольнойзадаче представить следующие материалы:

а) исходные данные, соответствующие варианту;

б) вывод частотной характеристики системы и формулы дискретного преобразования Фурье для определения формы импульса на выходе линии связи;

в) графическую схему алгоритма решения уравнений с пояснением;

г) программу решения с помощью интегрированного пакета уравнений со своими исходными данными и графики входного и выходного импульсов;

д) анализ результатов решения и выводы по проведенному исследованию.

В контрольной работе дать список использованной литературы.

Методические материалы c примерами выполнению подобных задач излагаются в [1].

Blog

Программа и задание на контрольную работу по дисциплинам "Моделирование систем" для студентов IV курса специальности

Содержание

МОДЕЛИРОВАНИЕ СИСТЕМ

Задание на контрольную работу