Geum.ru

Учебное пособие по экоинформатике (сокращенный

Вид материалаУчебное пособие
Устойчивость и полная реакция орграфа
Многокритериальная оценка
Анализ системных весов факторов
Задание (зачетное)
Требования к выполнению курсового проекта
Подобный материал:
1   2   3   4   5

Устойчивость и полная реакция орграфа


Особенностью рассматриваемых нами систем, управляемых человеком, является их стабильность (устойчивость). При этом значения вершин должны стремиться к какому-то конечному пределу при увеличении числа шагов. Этот предел и показывает полную реакцию системы на одноразовый начальный импульс: 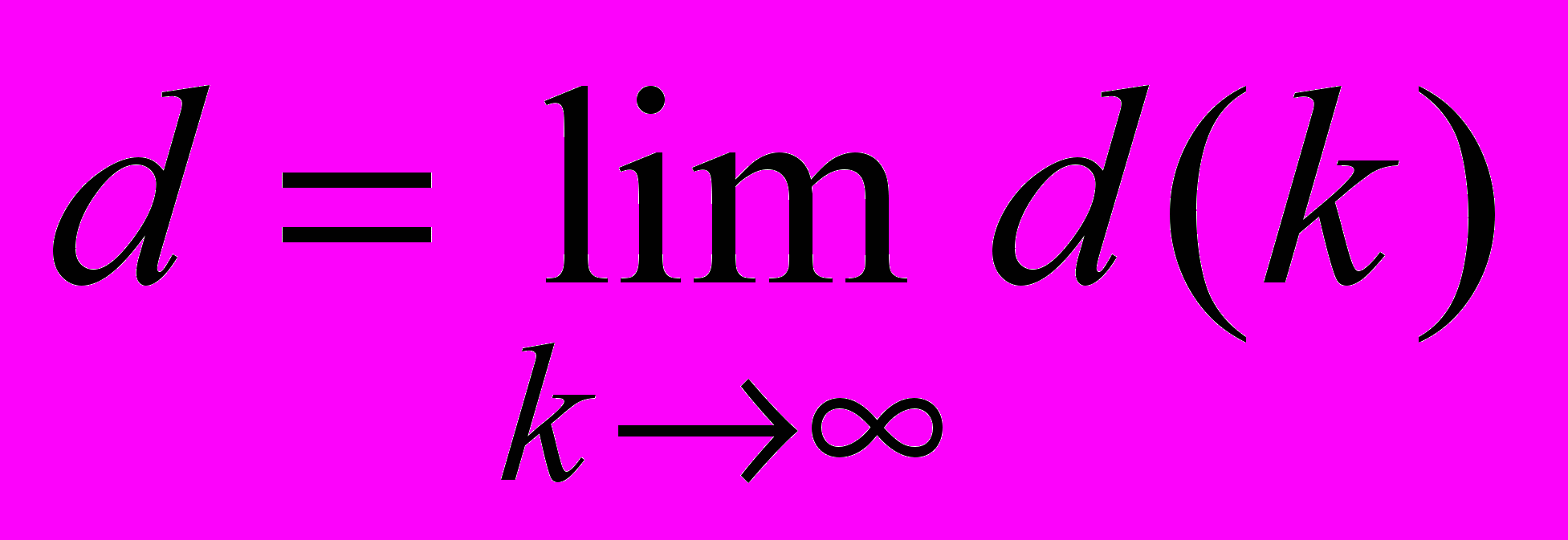. Можно считать, что эта реакция осуществляется за некоторый заданный период времени (например, за год или за 5 лет – в зависимости от рассматриваемой системы).


Рассмотрим воздействие на систему одноразовыми единичными начальными импульсами, направленными на каждую из вершин:

.

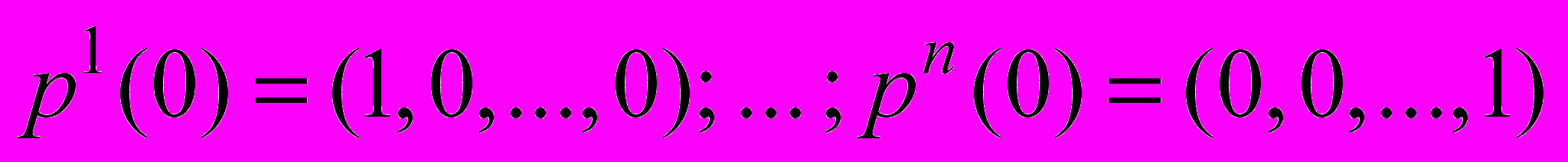Этим импульсам, согласно формуле (5), соответствуют вектора реакций на k-м шаге:

.

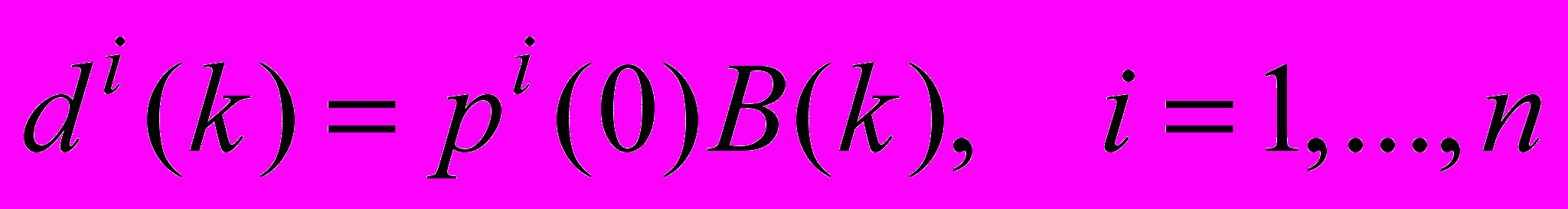Нетрудно убедиться, кстати, что строки матрицы B(k) представляют собой реакции di(k).


Результат единичного воздействия произвольным начальным импульсом 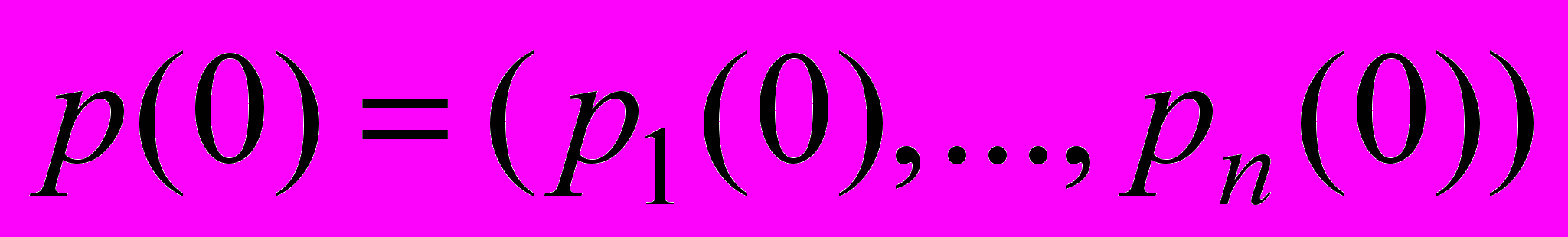равен линейной комбинации результатов воздействия единичными начальными импульсами: 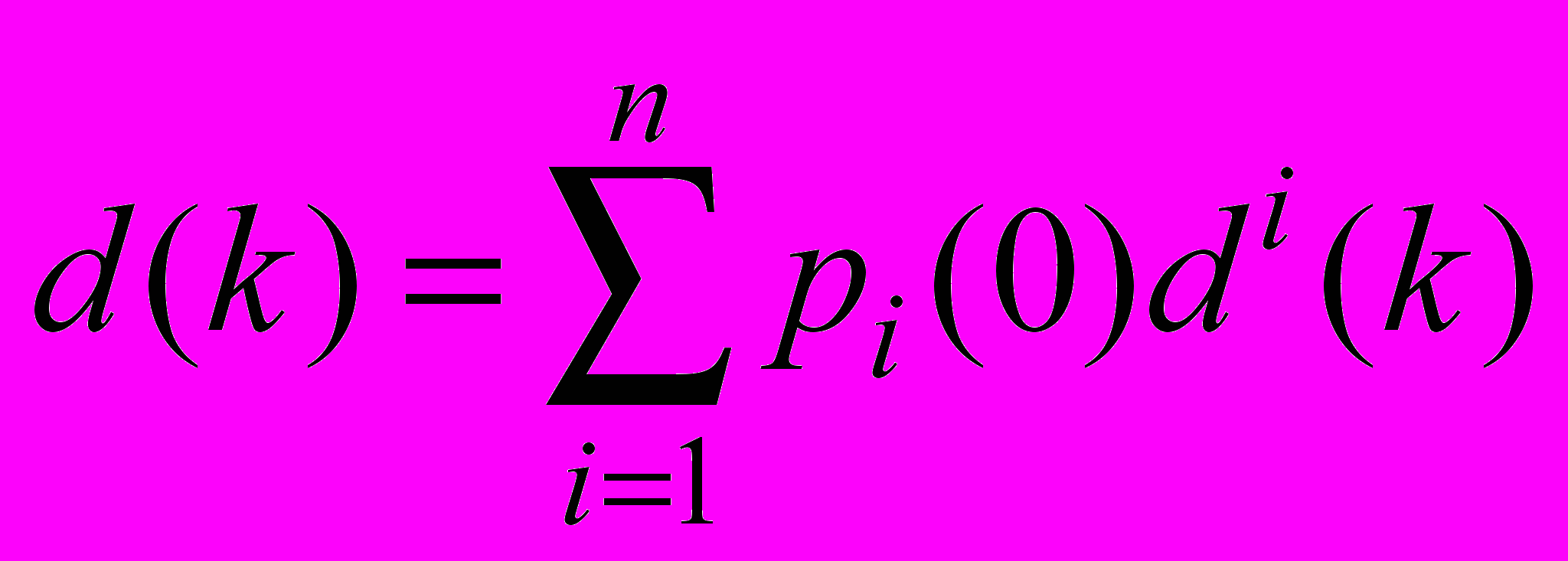; соответственно, для полной реакции: . Поэтому для исследования поведения системы не нужно применять различные произвольные начальные импульсы, достаточно найти реакции системы на единичные импульсы в отдельные вершины.


Технически за полную реакцию системы можно принять реакцию на k-м шаге, если k достаточно велико, чтобы значения реакций стабилизировались с необходимой для целей исследования точностью (например, три знака после запятой). При этом все элементы матрицы Ak должны стать равны нулю также в трех знаках после запятой.

Если стабилизации не происходит, значит, неверно определены весовые коэффициенты связей.

Многокритериальная оценка


Итак, полученные строки di характеризуют состояние системы в результате применения того или иного воздействия на нее. Возникает вопрос: можно ли сравнить эти состояния, выбрать из них лучшее, а соответственно, выбрать лучший вариант начального воздействия?

Если сравнивать альтернативные полные реакции системы (альтернативы) di по какому-то одному из факторов, то, конечно, их легко можно ранжировать от лучшего к худшему. Так например, при оценке состояния региона по фактору заболеваемости (число заболеваний населения по отношению к общей численности населения в год), то чем меньше значение этого фактора, тем лучше признается альтернатива. Если сравнивать альтернативы по фактору средней заработной платы, то чем больше значение фактора, тем лучше и т.д.

Но нам требуется при сравнении альтернатив учитывать все факторы в совокупности, причем, как правило, альтернативы, которая была бы лучшей по всем факторам сразу, не бывает. Таким образом, перед нами стоит задача многокритериальной оценки и сравнения альтернатив. Существуют различные методы решения этой задачи, применимые в различных областях. Мы не будем подробно на них останавливаться, рассмотрим только так называемый метод парных сравнений, который достаточно широко применяется в теории принятия решений


Метод парных сравнений альтернатив.

Построим для каждого фактора m матрицу парных сравнений 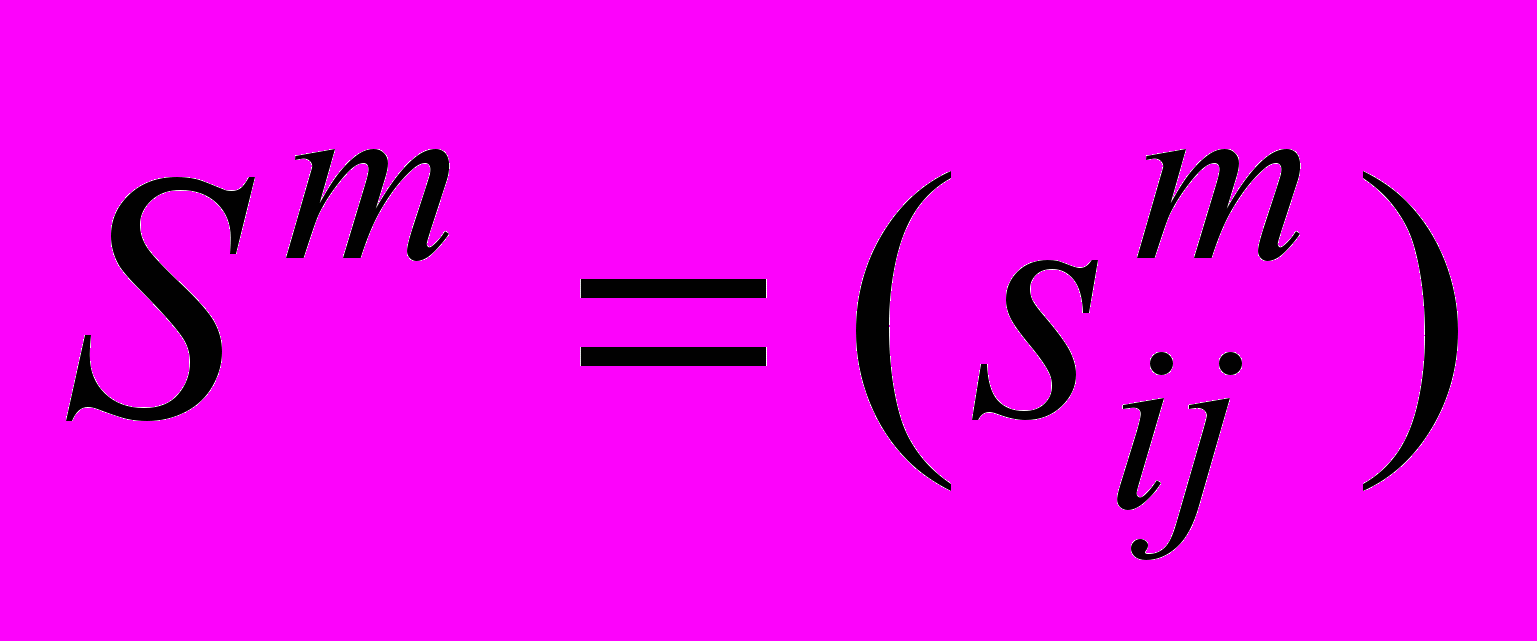по следующему правилу:

, если альтернатива i лучше альтернативы j при сравнении по фактору m и в противном случае. (Заметим, что при этом надо строго следить за тем, требуется для фактора увеличение или уменьшение значения!)

Затем сложим все полученные матрицы в результирующую матрицу парных сравнений .

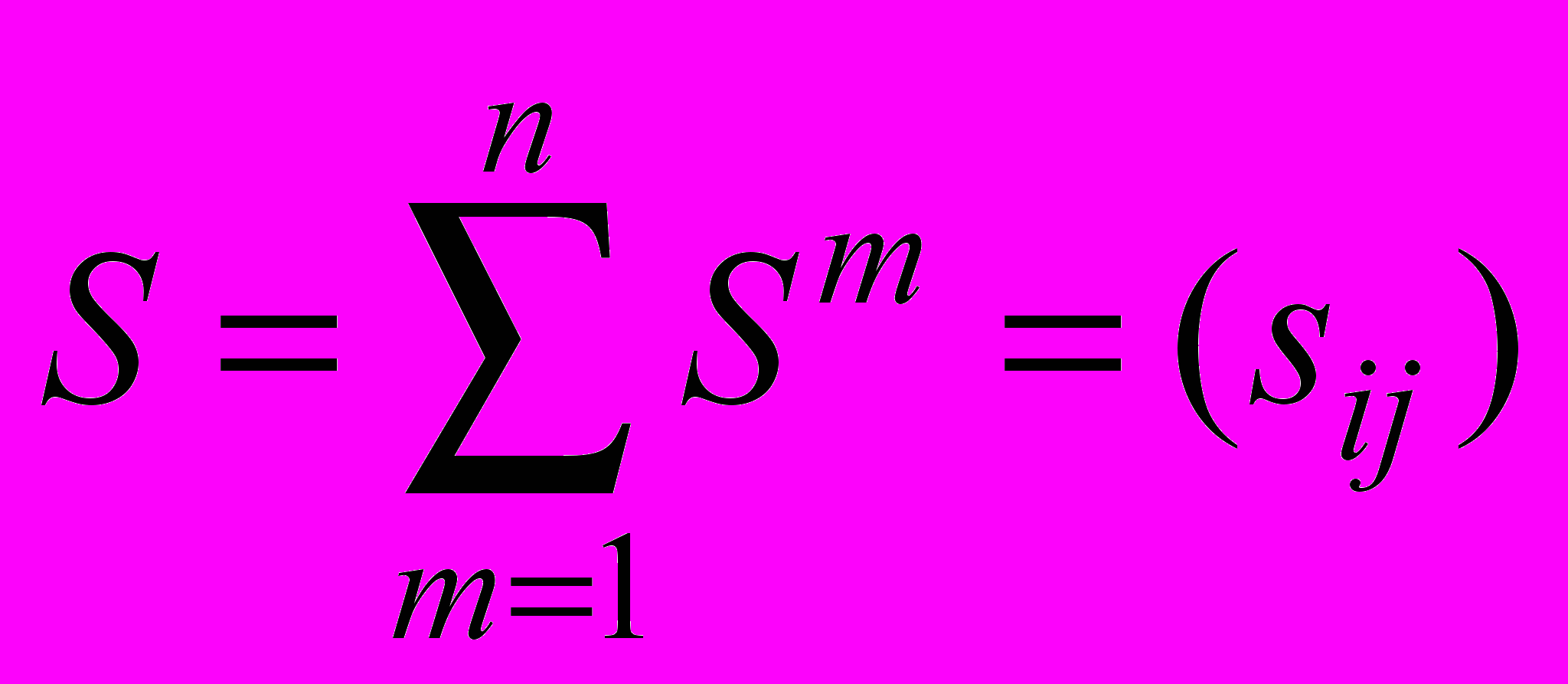Оценкой альтернативы di назовем сумму элементов матрицы S в i-й строке: .

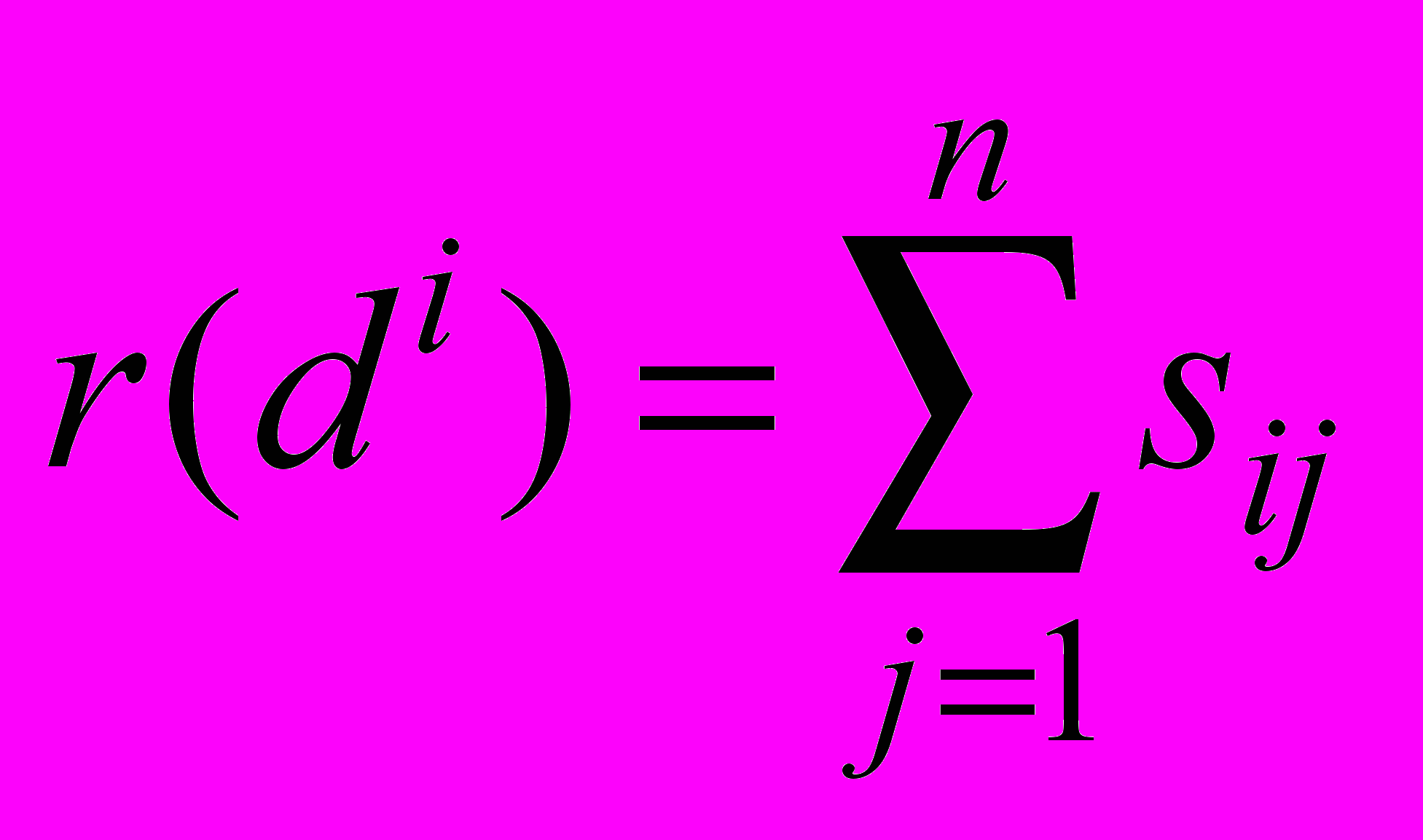Таким образом, все альтернативы можно проранжировать согласно полученным оценкам: чем выше оценка, тем лучше альтернатива.


Этот метод достаточно прост и может применяться при принятии решений (не только при анализе поведения орграфов), если достаточно провести качественное сравнение альтернативных вариантов по каждому фактору. Однако мы имеем больше информации для сравнения: все альтернативы у нас выражены численно, так что хотелось бы провести не только качественное, но и количественное сравнение альтернатив по каждому фактору: не просто «лучше», а «насколько лучше».


Метод парных сравнений с весами.

Прежде всего следует нормировать имеющиеся альтернативы. Оказывается, более удобным является нормирование не по уже приведенным формулам, а по следующему правилу (без смещения):

,

,

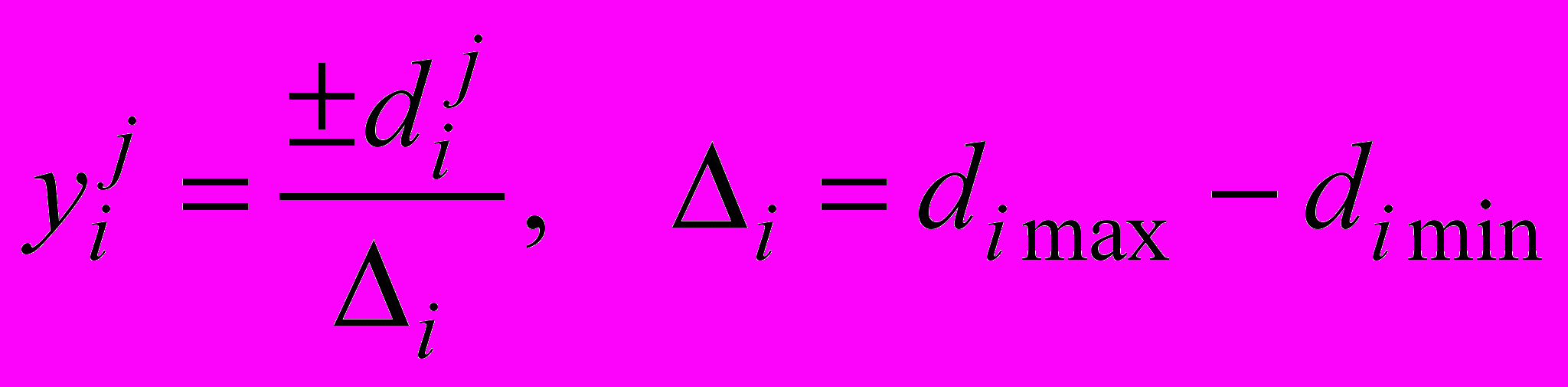где знак “+” ставится для факторов из множества I1,
знак “–“ ставится для факторов из множества I2.

Далее, составляем матрицы парных сравнений с весами и оценки альтернатив:

; ; .

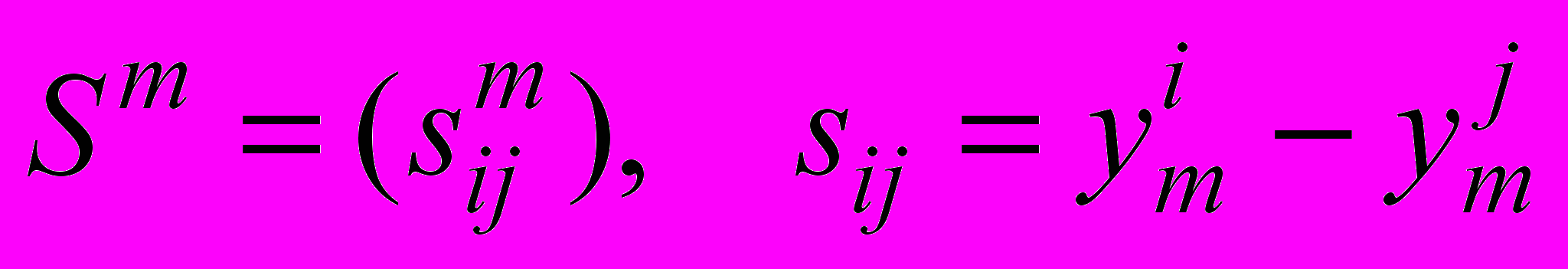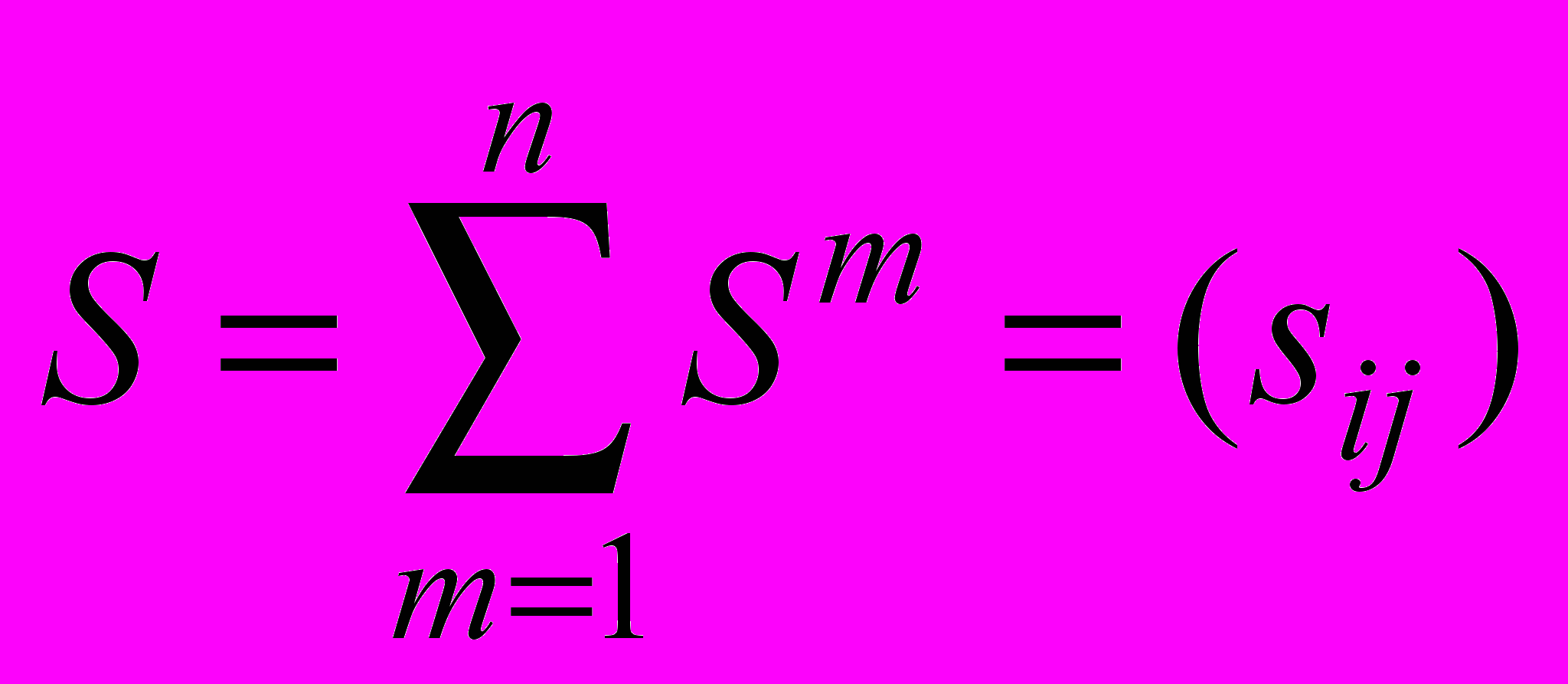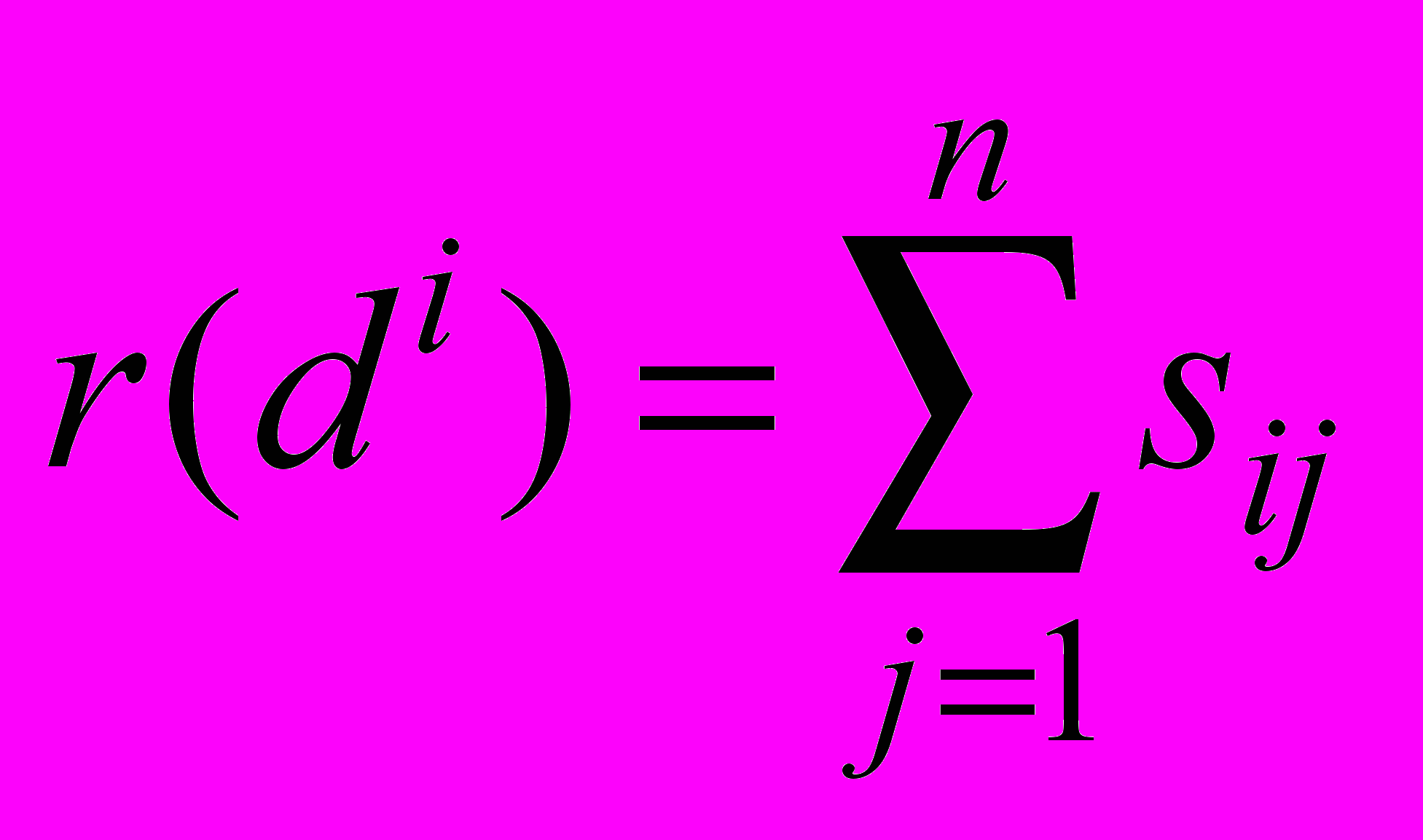Оказывается, такие оценки 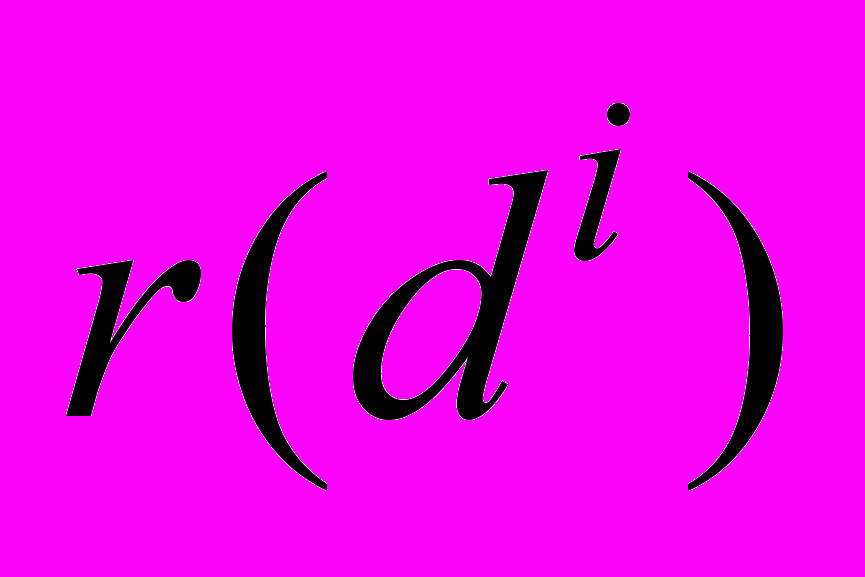эквивалентны оценкам 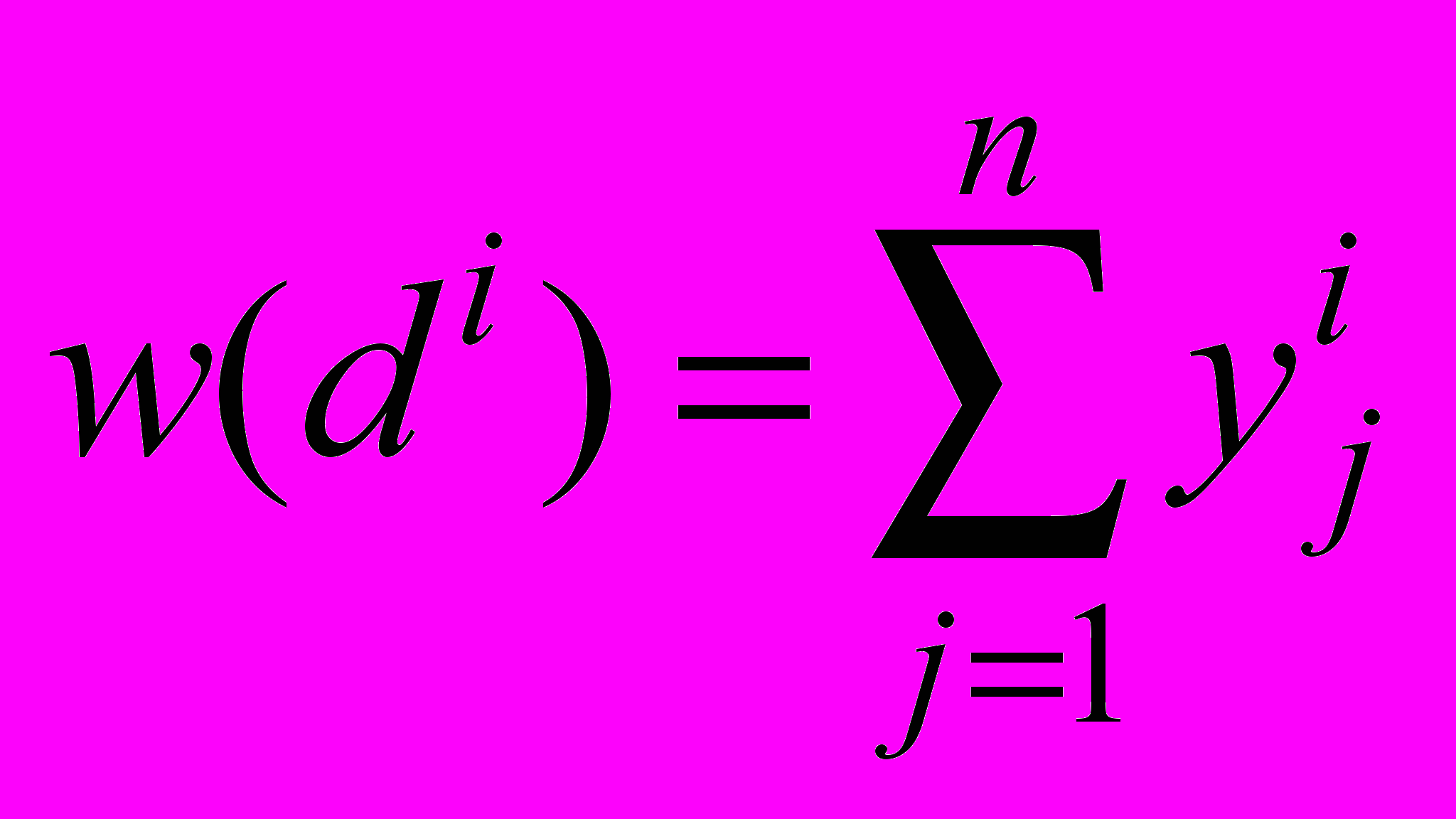, вычислять которые, конечно, проще.
  • Итак, оценки

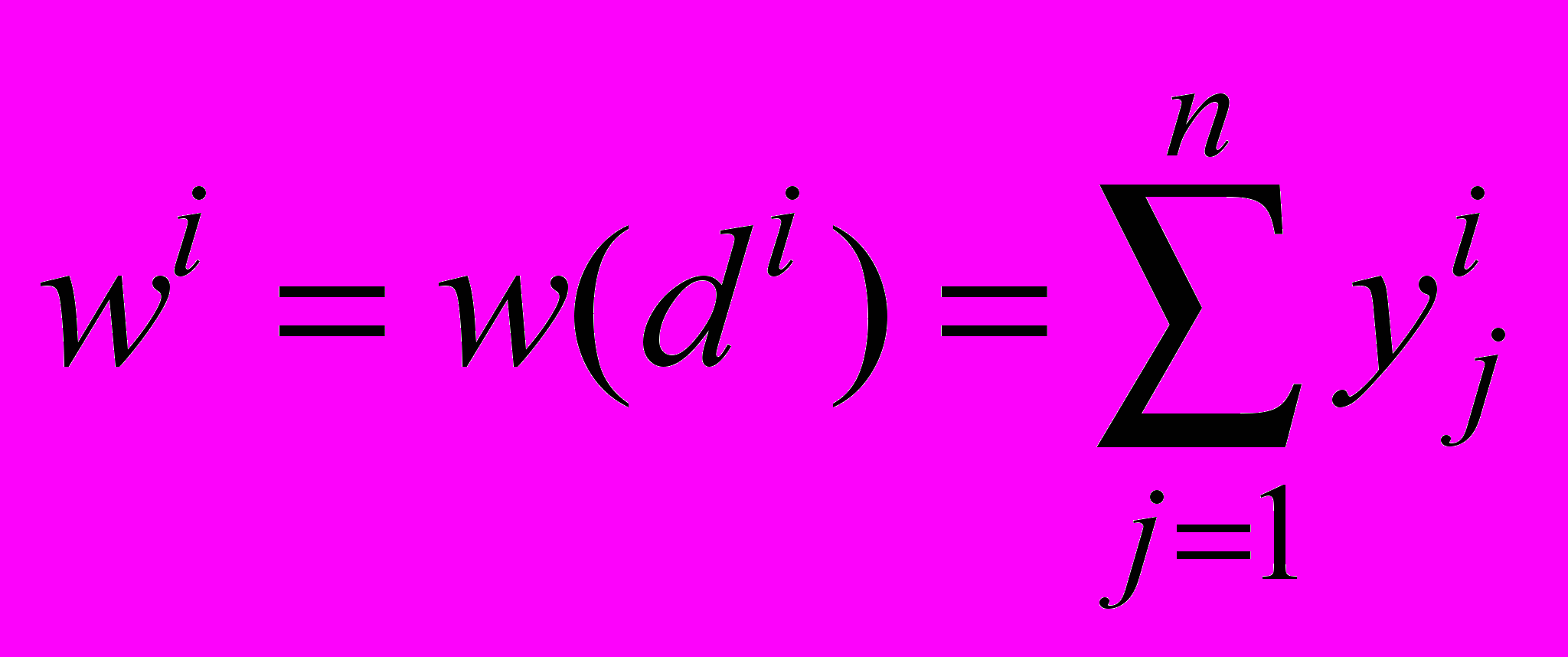, где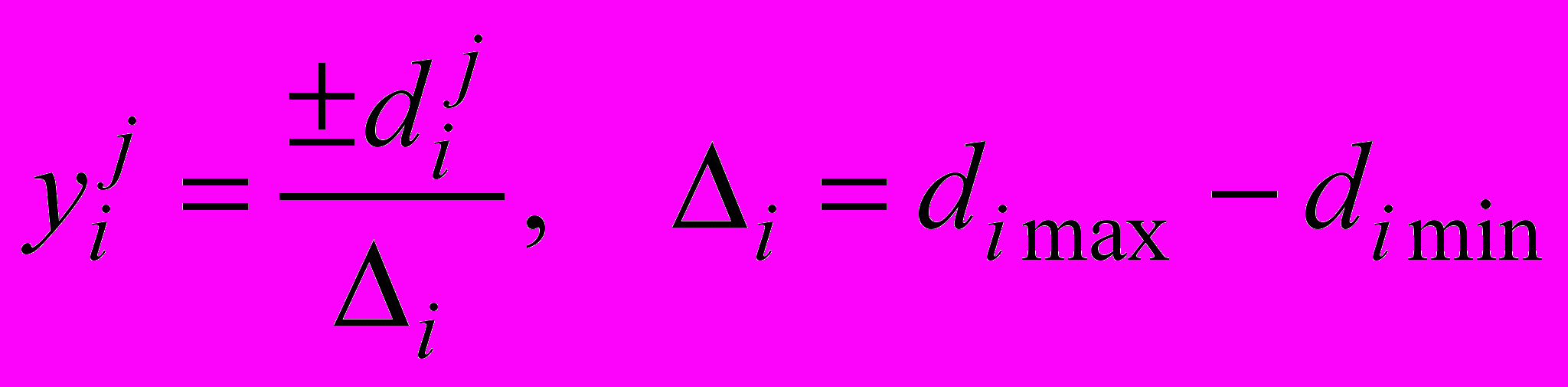

характеризуют ценность различных альтернативных состояний системы, полученных в результате воздействия единичными начальными импульсами на соответствующие вершины, а значит, и степень влияния соответствующих факторов на всю систему в целом. Эти оценки будем называть системными весами факторов и

использовать для управления системой.


Пример

Проводился анализ воздействия автотранспорта на окружающую среду в г. Москве. Рассматривалось 3 варианта:

- система нейтрализации отработанных газов с эжекторной подачей воздуха. Эффективность установки этой системы по снижению токсичности составляет 65%, стоимость – 200 у.е.

- система нейтрализации отработанных газов с нагнетателем воздуха. Эффективность установки этой системы по снижению токсичности составляет 50%, стоимость – 150 у.е.

- система нейтрализации отработанных газов с нагнетателем воздуха и одновременное увеличение площади зеленых насаждений.

В таблице приведены данные изменения значений основных показателей через три года по каждому из вариантов.

показатель
Затраты
Выбросы
Заболев-ть
Растит-ть
Кач-во жизни

тип

вариант
I2.
I2.
I2.
I1.
I1.

1
380
-1,719
-0,59
0,456
0,467

2
280
-0,127
0,081
-0,1
-0,115

3
300
-0,07
0,01
2,139
1,07


Если воспользоваться методом парных сравнений, получим матрицы парных сравнений для всех показателей соответственно:

; ; ; ; .

Суммарная матрица:

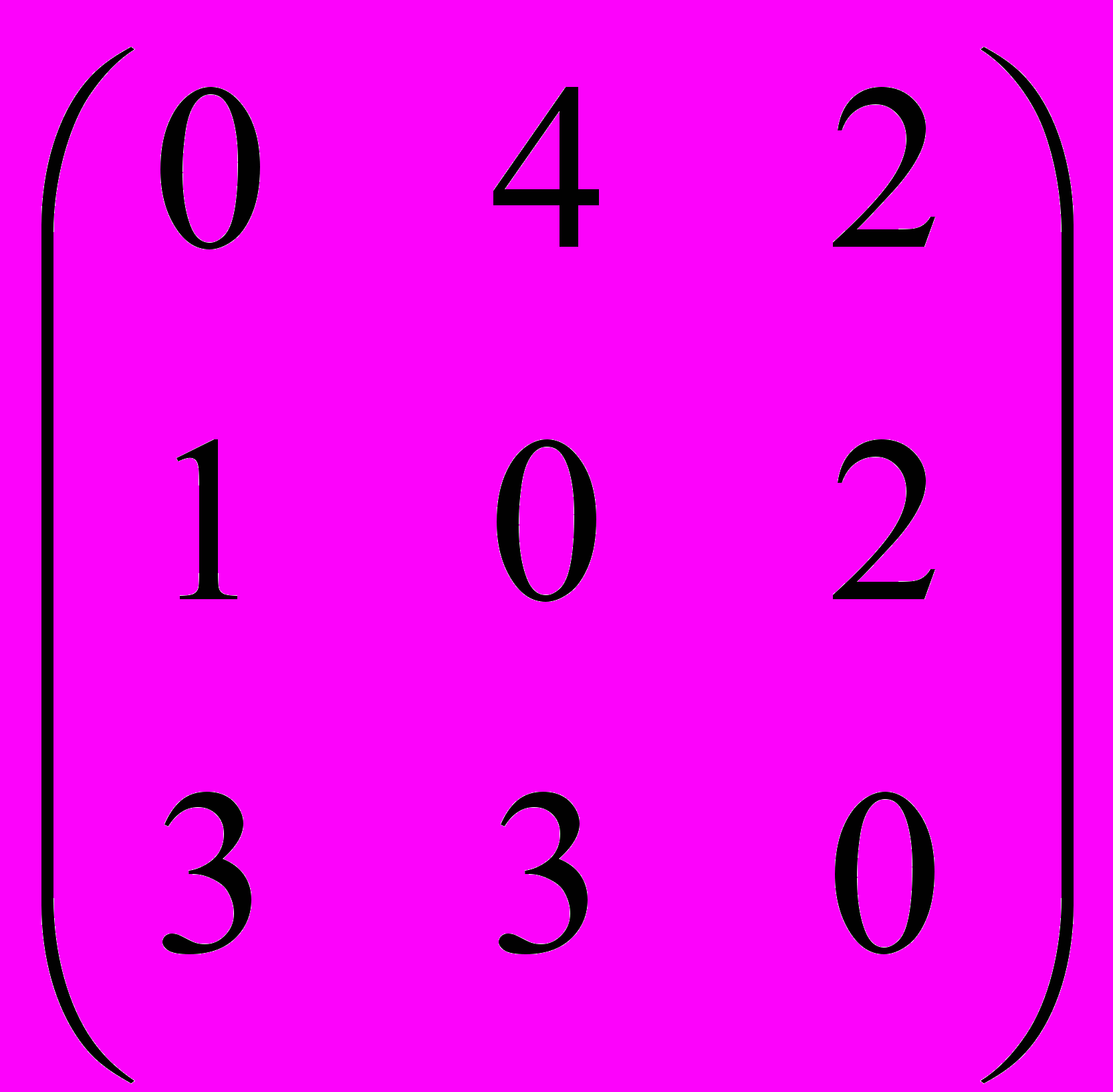
Оценки вариантов: первый – 6, второй – 3, третий – 6. Таким образом, следует признать первый и третий варианты равноценными. Такой результат вызван только качественным, а не количественным сравнением.


Воспользуемся теперь оценкой при помощи метода парных сравнений с весами (точнее, эквивалентной ей); для вычислений используем таблицы Excel. При этом применяются функции МАКС, МИН, СУММ, а формула для нормирования задается непосредственно в строке формул:



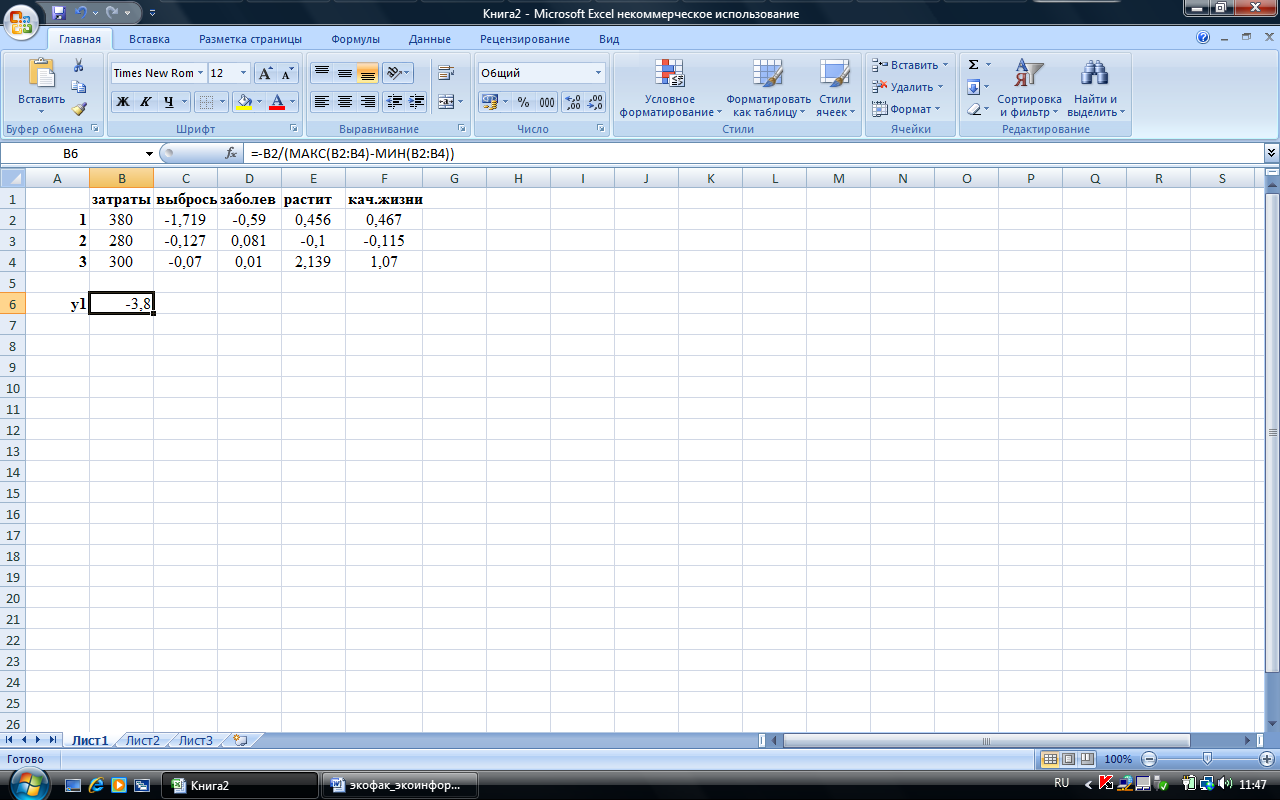
Напомним, что при нормировании надо следить за типом показателя; поскольку первый показатель – затраты – типа I2, в формуле ставится «-». Зафиксируем в формуле для ячейки В6 номера ячеек в диапазонах вычисления значений МАКС и МИН для того, чтобы эту формулу можно было скопировать как по горизонтали (буквы ячеек должны при этом изменяться), так и по вертикали (цифры ячеек не должны изменяться). Строка формул для ячейки В6 примет вид:

=-В2/(МАКС(В$2:B$4)-МИН(В$2:B$4)) .


Теперь содержимое ячейки В6 скопируем далее по строке, вычисляя остальные нормированные значения для варианта 1. Но при этом для показателей типа I1 формулу придется скорректировать, убрав знак «-»:




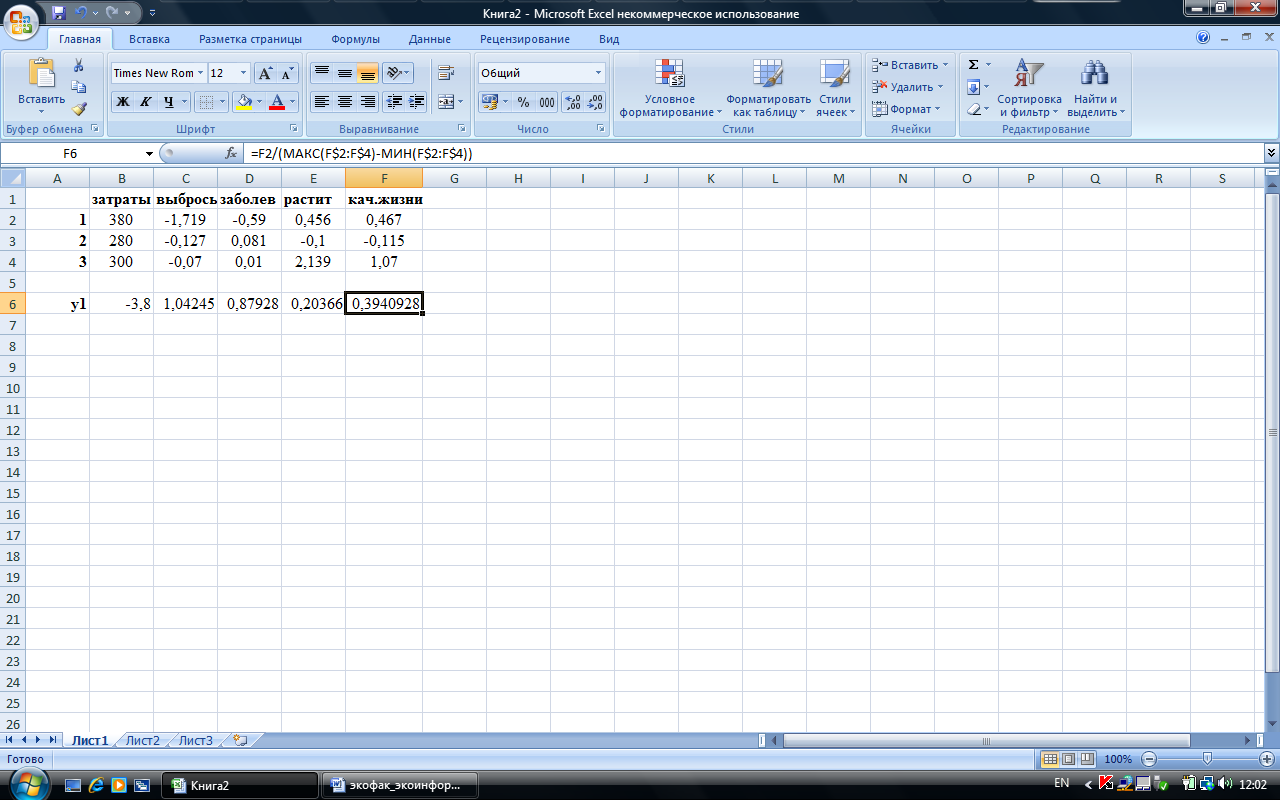
Теперь мы можем скопировать содержимое ячеек вниз, вычисляя таким образом нормированные значения вариантов 2 и 3:



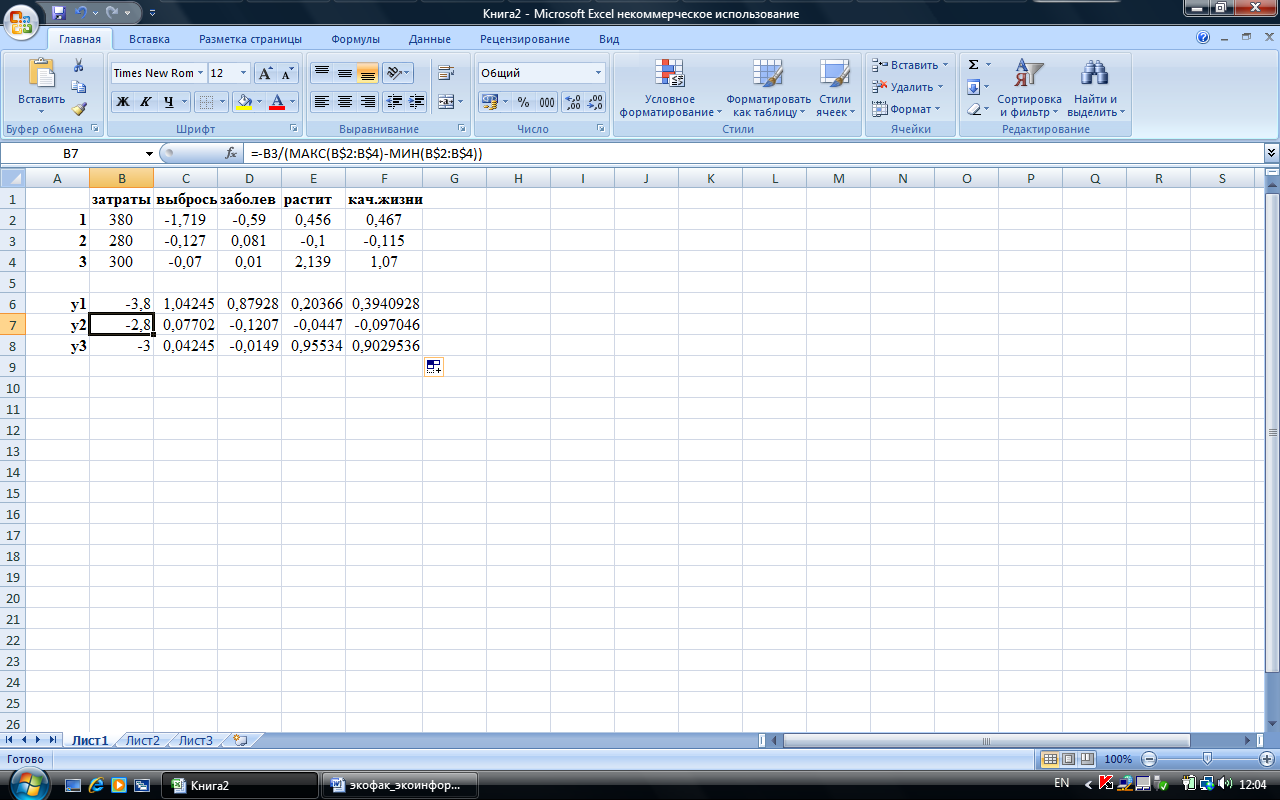
Наконец, вычислим суммы значений в строках y1, y2, y3, получив искомые оценки вариантов:




Таким образом, наиболее эффективным оказывается третий вариант, его оценка оказалась наибольшей (хотя и отрицательной, т.е. полностью вред от выбросов не нейтрализуется).


Если этот метод применяется к сравнению вариантов развития орграфа единичными начальными импульсами в разные вершины (то есть, фактически, к строкам матрицы Bk, где k достаточно велико, чтобы матрицы стабилизировались в третьем знаке после запятой), то полученные оценки являются системными весами соответствующих факторов.


Анализ системных весов факторов

Рассчитанные при помощи метода парных сравнений с весами системные веса факторов позволяют нам определить приоритеты развития исследуемой системы на настоящий момент. Именно, системный вес каждого фактора означает, что увеличение значения этого фактора на 1% влечет изменение (улучшение или ухудшение, согласно знаку веса) состояния всей системы на соответствующее число процентов. Таким образом, для оптимального управления системой следует направлять усилия на изменение параметров, имеющих наибольшие по абсолютной величине системные веса.

Кроме того, анализ полученных для данной системы на данный момент времени системных весов факторов позволяет сделать некоторые дополнительные выводы о стабильности системы или близости ее к кризису. Признаками критического состояния системы являются:

- большой разброс, т.е. разница между самым большим и самым маленьким значениями системных весов факторов;

- перемена знака влияния фактора.

Для примера приведем некоторые выдержки из исследования В.И.Горелова (Управление развитием общества, 2007)


Пример 1. Сравнение приоритетов развития мира в 1995 и 2000 годах

В приведенной ниже диаграмме указаны системные веса факторов, влияющих на развитие стран мира, вычисленные по описанной в настоящем курсе методике.

Разброс весов влияния критериев в 2000 году существенно больше, чем в 1995. Создается впечатление, что до 1995 разброс был небольшим, и критерии почти не менялись.

В целом, наверное, допустимо сказать, что мировое сообщество в 1995 году жило по отработанной за века технологии. Имелся запас энергетических и сырьевых возможностей для развития, было достаточно сырья и электроэнергии, расслоение общества не вызывало серьезных возмущений, большее расслоение общества в странах – энергетических и сырьевых реципиентов компенсировалось большим вниманием к качеству жизни. В странах - энергетических донорах расслоение общества было сравнительно невелико, а общая нищета не ставила вопроса о повышении качества жизни. Мир четко делился на богатые и бедные страны, причем собственных возможностей развития у бедных стран было весьма мало.





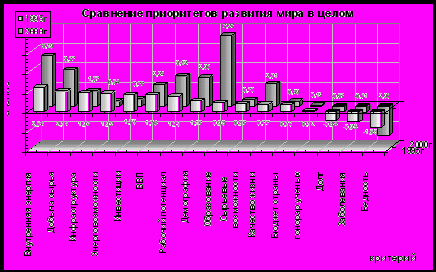
Быстрое развитие новых технологий, увеличение потребления, информационная доступность мира вызвали очень большую напряженность системы. Из сравнения видно, что системное влияние главных критериев увеличилось почти в три раза. Это означает, что мировое сообщество приближается к критической точке. Можно с уверенностью утверждать, что мировое сообщество находится в критической ситуации. Выходом из этого кризиса, скорее всего, либо будет война, либо мировой экономический кризис. Точный ответ о виде кризиса и характере путей выхода из него можно получить только при помощи дополнительных расчетов. Сегодня, к сожалению, мы видим попытки задержать развитие мирового сообщества поиском «врага», идут локальные войны, и, в случае, если они не дадут эффекта, вполне возможна мировая война. Адаптация к таким резким потрясением крайне тяжела, а развитые страны ее перенесут гораздо болезненнее.

В 2000 году, потеснив традиционные приоритеты развития, на первое место в мире вышел уровень образования, системный вес которого с 1995 года увеличился более чем в 7 раз. Возросла роль энергетических и сырьевых запасов, хотя они несколько сдали свои позиции. Их системные коэффициенты влияния на развитие увеличились, в общем, примерно в два раза и возросли до 5,19 и 3,77 соответственно.

Происходит уменьшение влияния сырьевых и энергетических возможностей стран на развитие. Фактически имеет место следующая картина: в странах - энергетических реципиентах практически исчерпаны энергетические возможности и необходимо срочно искать пути их развития, а в странах – энергетических донорах наблюдается почти полное использование сырьевых ресурсов, а они не возобновляемы. Как следствие, усиливается борьба за энергетические ресурсы и сырьевые ресурсы стран – энергетических доноров. Давление таково, что у стран - энергетических доноров по-прежнему главным приоритетом остается развитие энергетических ресурсов. Такое давление весьма опасно.

По сути, первые четыре позиции в развитии территории занимает ресурсный блок, поскольку на четвертом месте с системным весом 3,12 располагается численность рабочих территории. Общее уменьшение природных ресурсных запасов заставляет для сохранения темпов развития обратиться к последнему ресурсу – человеку. За это надо платить. Поэтому повышается влияние качества жизни более чем в три раза.

Как следствие, в мировом сообществе незначительно растет влияние ВВП, уменьшается общее влияние инфраструктуры. Увеличивается влияние численности населения, с ростом качества жизни уменьшается в полтора раза влияние социальной заболеваемости. В целом уменьшается влияние бюджета, в два раза уменьшается влияние инвестиций на развитие территории. Все эти преобразования, к сожалению, вызывают усиление влияния расслоения общества, что ведет к росту социальной напряженности. Вспомните волнения в США и странах Европы.

Заметим, что более точный анализ позволяет провести сравнение весов влияния факторов на развитие стран-доноров и стран-реципиентов по отдельности.


Пример 2. Анализ состояния общества в Европе


Критерий
Системный вес

Образование
9,896

Добыча сырья
1,214

Внутренняя энергия
2,584

Демография
1,950

Рабочий потенциал
2,384

Качество жизни
-0,060

ВВП
0,589

Инфраструктура
0,431

Инвестиции
0,209

Сырьевые возможности
0,009

Бюджет страны
0,157

Гонорар ученых
0,103

Энерговозможности
0,078

Заболевания
-0,429

Долг
-0,392

Бедность
-0,768



Сравнивая системные веса критериев развития Европы с системными весами критериев развития мирового сообщества за 2000 год, можно увидеть, что веса практически всех приоритетов развития ниже, чем в регионах мира.

Расслоение общества (бедность) в странах ЕС незначительно, однако его низкое, по сравнению с мировым сообществом, значение провоцирует большое иммиграционное давление на страны ЕС.

Небольшой, по сравнению с образованием, вес рабочего потенциала показывает, что потребность в рабочей силе не так велика, как недостаток в образовании, поэтому приток неквалифицированных мигрантов является нежелательным.

В ресурсном отношении ЕС находится на грани своих внутренних возможностей (практически они исчерпаны). На это указывают парные показатели: добыча сырья/сырьевые возможности и внутренняя энергия/энерговозможности. Так, добыча сырья оказывала бы достаточно весомое влияние на систему (1,214), но сырья на территории так мало, что оно влияния практически не оказывает (0,009). (Напомним, такое значение веса означает, что гипотетическое увеличение запасов сырья на территории в два раза (!) влечет улучшение системы всего на 0,9%). Значит, имеют место проблемы с внутренней энергетической и сырьевой базой.

В целом, казалось бы, что в благополучной Европе больших проблем нет.

Однако веса ряда параметров резко выделяются. Рассмотрим веса параметров «образование» и «качество жизни».

Вес параметра «качество жизни» отрицателен и, следовательно, он отрицательно влияет на развитие региона. Этот показатель интегрированный, в него входят уровень образования, продолжительность жизни и приведенное значение ВВП на душу населения. Веса показателей «ВВП» и «Образование» положительны. При этом вес показателя «Образование» самый большой и воздействие на него дает наибольший вклад в развитие системы. Следовательно, для эффективного развития необходимо воздействовать на параметр «Образование», но такое воздействие приводит к усилению отрицательного влияния показателя «качество жизни» на развитие системы. Мы получаем противоречие. Это противоречие показывает, что в 2000 году в Европе, как едином сообществе, имел место системный кризис, и в рамках системы не существовало стратегии развития. С большой долей вероятности можно утверждать, что, оставаясь в прежнем составе, Европа стала бы формализованной и нежизненной структурой. Как мы можем видеть, Европа пошла по пути структурных изменений через расширение сообщества, изменения налоговой базы, привлечения к своим проблемам научного сообщества других стран.


Задание (зачетное)

Для системы, смоделированной вами ранее в виде знакового орграфа:

1) Проставить весовые коэффициенты связей (опираясь на непосредственное вычисление и собственный здравый смысл)

2) Вычислить реакции системы на единичные начальные импульсы при помощи таблиц Excel, сделав столько шагов, сколько необходимо для стабилизации в третьем знаке после запятой. При этом проверяется устойчивость системы. Также здесь можно проверить и сильную связность орграфа: она имеется, если итоговая матрица Bk не содержит нулевых элементов

3) Вычислить системные веса факторов и сделать выводы о состоянии системы и оптимальных путях управления системой в данный момент времени.


Приложение


Система оценки работы студента по курсу экоинформатики


Посещение лекций – 8 баллов

Контрольная работа – 12 баллов

Первое зачетное задание – 25 баллов. Максимальное количество баллов ставится за своевременное (по согласованному для группы графику, не позднее недели до промежуточной аттестации) представление ориентированного графа, моделирующего выбранную студентом систему, для обсуждения в форуме (файл с орграфом должен быть прислан преподавателю), если орграф не содержит грубых ошибок (см. лист 4). Участие автора в обсуждении его проекта обязательно!

Участие в обсуждении проектов – 10 баллов. Обсуждение представленных проектов проводится в режиме off-line в форуме на странице преподавателя в течение недели со времени опубликования. Одновременно обсуждаются 4-5 проектов. Можно: задавать вопросы по поводу непонятных вершин или связей представленного графа; предлагать новые вершины и связи или указывать на лишние с Вашей точки зрения; помогать автору отстаивать его точку зрения, если Вы с ней согласны и т.п. Нельзя: переходить на личности, высказываться в некорректной форме или не по теме. Преподаватель высказывает свое мнение, как правило, в конце обсуждения. Автор проекта волен принимать или отвергать предложенные изменения – это не влияет на его оценку (если речь не идет о грубых ошибках моделирования).

Второе зачетное задание – 35 баллов. Максимальное количество баллов ставится за своевременно (по крайней мере за неделю до зачета) представленный преподавателю (без вынесения на открытое обсуждение) курсовой проект, отвечающий указанным ниже требованиям

Зачет – 10 баллов. Эти баллы могут быть заработаны также за счет высокой (и осмысленной) активности в обсуждении проектов и перевыполнения требований к курсовому проекту – например, качества оформления, или выполненной статистической оценки весов части связей (см. полную версию учебного пособия), или интересных (нетривиальных) выводов,…


Требования к выполнению курсового проекта


В выполненном курсовом проекте по моделированию социо-эколого-экономических систем должны быть:
  1. Сформулирована цель
  2. Построен знаковый орграф. Описаны вершины, в т.ч. указаны единицы измерения параметров, описаны связи.
  3. Построенный орграф проверен на сильную связность
  4. Оценены веса связей (по крайней мере часть – экспертно)
  5. Проверена устойчивость взвешенного орграфа
  6. Найдены системные веса факторов (без ошибок)
  7. Сформулированы выводы.


Расчеты должны быть представлены в электронном виде (файл Excel), работа оформлена и готова к печати (файл Word или распечатка).


Вопросы и проекты направлять: Ледащева Татьяна Николаевна

адреса:

e-mail: tledascheva@mail.ru

страницы на Учебном портале: .rudn.ru/web-local/prep/prep_1105/

страницы vkontakte: .ru/id13907401?63152



Ледащева Т.Н., Пинаев В.Е. Управление когнитивными системами