Geum.ru

Учебное пособие по экоинформатике (сокращенный

Вид материалаУчебное пособие
Моделирование больших систем при помощи орграфов
Подобный материал:
1   2   3   4   5

ГРАФЫ


Принято считать, что начало теории графов было положено Л. Эйлером в 1736 году в его знаменитом рассуждении о кенигсбергских мостах.

Город Кенигсберг имел семь мостов, соединяющих острова на реке Перголь с берегами и друг с другом. Жителям хотелось узнать, можно ли, выйдя из произвольной точки вернуться в нее, проходя по каждому мосту только один раз.

В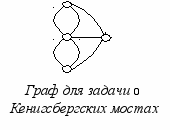ы можете узнать в этой задаче известную головоломку: можно ли обвести фигуру, не отрывая карандаша от бумаги и проводя каждую линию только один раз.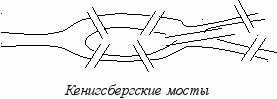




Теория графов позднее применялась Кирхгофом при исследовании электрических сетей, Кели в органической химии, Гамильтоном для решения головоломок и многими картографами, занимавшимися задачей раскраски карт. Как самостоятельная дисциплина теория графов сформировалась в 30-х годах XX века и всегда была ориентирована на приложения. Методы теории графов успешно используются в генетике, химии, теории информации, планировании производства и транспорта.

  • Граф представляет собой объект, состоящий из множества V={vi} вершин, которые соответствуют элементам реального объекта или явления, и множества G={(vi;vj)} линий (ребер), которые соединяют вершины и отражают связь между ними.
  • Если рассматриваются упорядоченные пары {vi;vj}, то они называются дугами и изображаются стрелками от вершины vi к вершине vj, а сам граф называется ориентированным графом или орграфом.
  • Любой орграф имеет матричное представление. Именно, матрицей смежности (или матрицей смежности вершин) орграфа (V;G) называется квадратная матрица

.

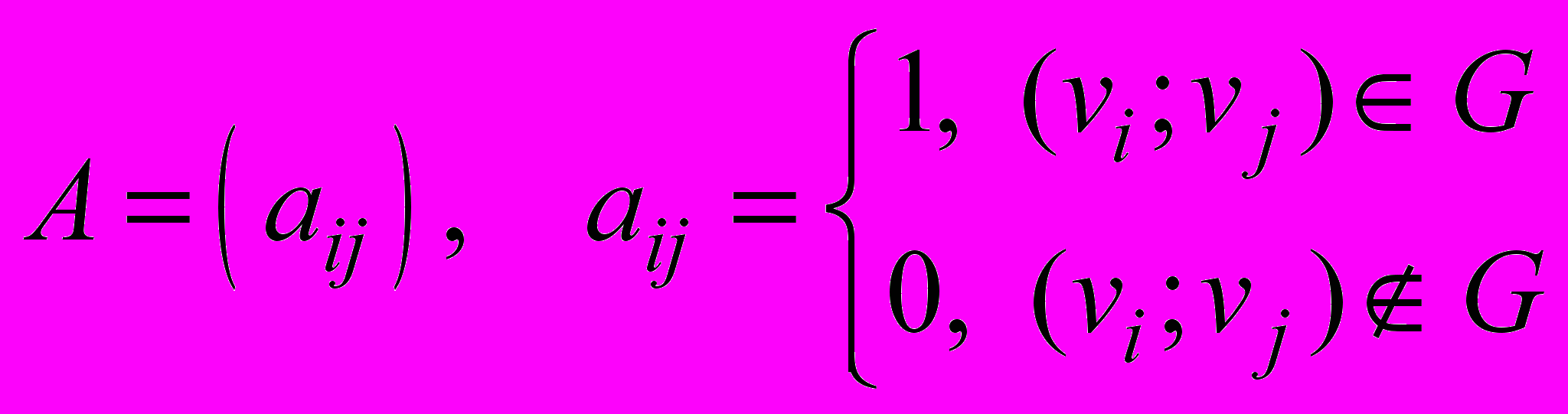П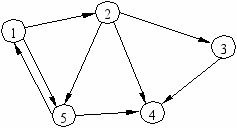ример Составим матрицу смежности вершин орграфа


Сначала заполним таблицу взаимного влияния вершин, двигаясь по строкам: «1» не влияет на «1» – ставим 0, «1» влияет на «2» – ставим 1, «1» не влияет на «3» - ставим 0 и т.д.


вершины
1

2

3

4

5

1
0
1
0
0
1

2
0
0
1
1
1

3
0
0
0
1
0

4
0
0
0
0
0

5
1
0
0
1
0


Получили матрицу смежности вершин орграфа:

А=


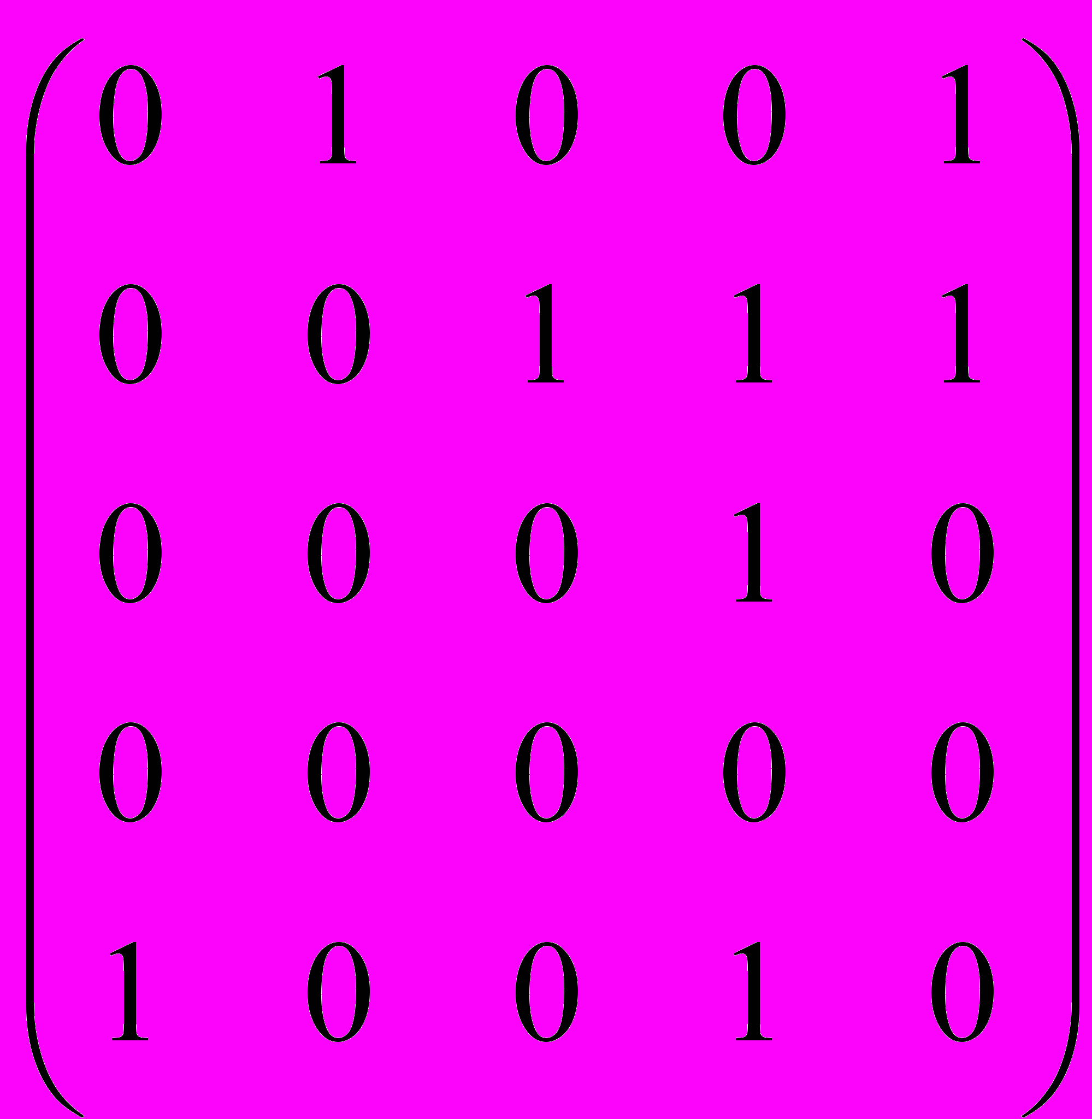
Моделирование больших систем при помощи орграфов

Будем строить модель системы при помощи орграфа следующим образом.

Вершины орграфа представляют элементы системы. Точнее, выделенные с точки зрения целей исследования подсистемы – факторы.

Дуги орграфа представляют прямые связи между факторами. Именно, дуга от вершины А к вершины В проводится, если фактор А прямо (непосредственно, то есть не задействуя другие выделенные факторы) влияет на фактор В.

Таким образом, множество вершин орграфа представляет состав системы, а множество дуг – ее структуру.
  • Систему, смоделированную при помощи орграфа, будем называть когнитивной системой.


П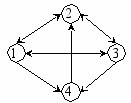ример. Рассмотрим схематическую задачу изучения развития промышленного центра и состояния окружающей среды. Чем больше промышленных предприятий, тем больше население города. При этом рост населения и увеличение промышленных мощностей вызывает необходимость развития инфраструктуры города и создания дополнительных рабочих мест. Развитая инфраструктура города, в свою очередь, способствует росту промышленности. Промышленные предприятия и инфраструктура города отрицательно влияют на состояние окружающей среды. Ухудшение состояния окружающей среды негативно сказывается на здоровье населения. Получаем орграф:


1 – число предприятий

2 – население

3 – инфраструктура центра

4 – состояние окружающей среды.


Как видите, орграф является графическим представлением вербальной модели.

  • Путем в орграфе называется такая конечная последовательность дуг, в которой начало каждой последующей дуги совпадает с концом предыдущей.

В приведенном выше орграфе, например, существует путь между вершинами 2 и 4: {(2,3);(3,4)}. Это означает, что в рассматриваемой системе фактор 2 влияет на фактор 3, а фактор 3 – на фактор 4, так что фактор 2 косвенно влияет на фактор 4.
  • Граф называется сильно связным, если между каждой парой его вершин существует такой путь, что одна вершина будет начальной, а вторая – конечной.

Вспомним, что модель системы также является системой, в частности, обладает свойством целостности (все влияет на все). Таким образом, справедливо

Утверждение. Если орграф является моделью системы, то он сильно связен.

Следствие. В частности, если орграф является моделью системы, то он не имеет начальных и конечных вершин, т.е. для каждой вершины существуют дуги, входящие в нее и из нее исходящие.


Пример

З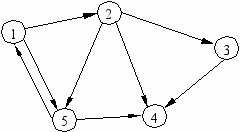аметим, что в рассмотренном ранее орграфе вершина 4 не является начальной ни для какого пути (в матрице смежности это выражается нулевой четвертой строкой). Значит, данный орграф не может служить моделью никакой системы, т.к. нарушается свойство целостности (или т.н. сильной связности орграфа).