Geum.ru

Учебное пособие по экоинформатике (сокращенный

Вид материалаУчебное пособие
Виды ориентированных графов
Моделирование больших систем в виде знакового орграфа
Подобный материал:
1   2   3   4   5

Виды ориентированных графов


Полученная с помощью орграфа модель отражает взаимодействие вершин. Однако самым интересным с точки зрения исследователя является характер взаимодействия и его количественные характеристики. Для того, чтобы их можно было отразить в орграфе, условимся, что каждому фактору в каждый момент времени соответствует некоторое числовое значение – характеристика. Например, если в исследовании учитывается здоровье населения города, то значение соответствующей вершины орграфа можно определять, как относительное число случаев заболевания горожан за определенный период времени.

Тогда дуги орграфа могут отражать характер взаимодействия вершин. В зависимости от способа задания дуг различают следующие виды орграфов.
  • Знаковый орграф. Присвоим каждой дуге знак плюс или минус. Знак плюс присваиваем, если возрастание значения начальной вершины вызывает возрастание значения конечной вершины дуги. Знак минус присваивается, если возрастание значения начальной вершины вызывает убывание значения конечной вершины дуги. Орграф с дугами, размеченными таким образом, называется знаковым орграфом. При матричном представлении знаковых орграфов дуге со знаком плюс соответствует число 1, со знаком минус – число -1.

Пример.

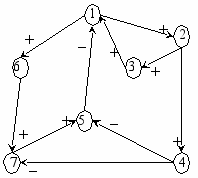Орграф, описывающий проблему удаления отходов из города (Maruyama, 1963) (знаковый)

1 – число жителей города

2 –условия жизни в городе

(средний прямой и непрямой доход)

3 – миграция в город в ед.времени

4 – число очистных сооружений

5 – число заболеваний в ед. времени

6 – количество мусора

на единицу площади

7 – бактериологическая зараженность

на единицу площади


  • Взвешенный орграф. В знаковом орграфе взаимодействие вершин отражено только качественно. Для количественного описания модели дугам присваиваются весовые коэффициенты, отражающие степень влияния одной вершины на другую. Орграф, дугам которого присвоены весовые коэффициенты, называется взвешенным орграфом. При матричном представлении взвешенного орграфа дугам соответствуют значения весовых коэффициентов (со знаком). Взвешенный орграф будет являться уже мягкой моделью системы.
  • Функциональный орграф. Весовые коэффициенты могут изменяться со временем. В этом случае они задаются функциями времени, а взвешенный орграф называется функциональным.
  • Вероятностный орграф. Орграф, имеющий случайные возмущения при взаимодействии вершин, называется вероятностным. Дугам ставится в соответствие вероятность случайной величины (или случайного события из набора гипотез).


Моделирование больших систем в виде знакового орграфа

Итак, подытожим правила моделирования социо-эколого-экономической системы в виде знакового орграфа:
  • вершины орграфа представляют собой факторы (подсистемы), выделенные исследователем в данной системе, и охватывающих все аспекты ее функционирования в рамках поставленной задачи;
  • каждой вершине сопоставляется числовая характеристика, значение которой может быть измерено тем или иным способом (указываются единицы измерения);
  • дуги орграфа представляют прямые связи между факторами;
  • орграф сильно связен, т.е. каждая вершина влияет на все остальные, прямо или косвенно (через другие вершины);
  • каждой дуге приписан знак: «+», если увеличение значения начальной вершины влечет увеличение значения конечной вершины, «-», если увеличение значения начальной вершины влечет уменьшение значения конечной вершины.

К этому можно добавить еще одно правило, выполнение которого не обязательно, но весьма желательно:
  • в орграфе не должно быть двойных связей (типа «А влияет на В, В влияет на А»).Последнее требование обусловлено тем, что при переходе от вербальной модели (которой является знаковый орграф) к мягкой в виде взвешенного орграфа необходимо оценивать весовые коэффициенты связей (об этом будет рассказано ниже). Наиболее общим способом для этого является статистическая оценка, но двойные связи статистически оценить невозможно.

Конечно, двойные связи неизбежно возникают, например, в пищевых связках типа «больше волков – меньше зайцев, больше зайцев – больше волков». В этом случае избавиться от них нельзя, но и необязательно, так как весовые коэффициенты достаточно легко оцениваются непосредственно.

Другой часто встречающийся случай возникновения двойных связей - построение модели, одним из факторов которой является бюджет: например, «больше бюджет – больше платим зарплату, больше зарплата – меньше денег в бюджете». Но в таких случаях от двойных связей избавиться можно, если более четко сформулировать смысл вершины «бюджет».

Иногда от двойных связей избавиться нельзя, но можно ввести дополнительную вершину, с тем, чтобы одна из связей стала косвенной.


Рассмотрим следующий знаковый орграф, призванный служить моделью спортивно-оздоровительного комплекса и разберем на этом примере некоторые часто встречающиеся при моделировании ошибки.




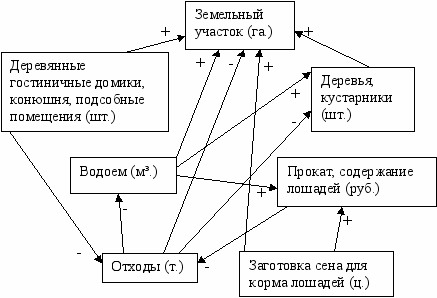
  1. В первую очередь бросается в глаза отсутствие сильной связности орграфа. Именно, нет исходящих дуг у вершины «земельный участок» и входящих дуг у вершин «деревянные домики и т.п.» и «заготовка сена». Попробуем разобраться в возможных причинах подобной ситуации.

Если это не является следствием недостаточной проработки вопроса о связях, а вершина действительно ни на что не влияет, значит, это не фактор системы, а некоторая вторичная характеристика (и ее из модели следует убрать).

Если же на вершину не влияет ни одна другая вершина, это может произойти по одной из двух причин:

- Возможно, не все необходимые для моделирования системы факторы перечислены. Так, часто забывают ввести в модель экономические факторы типа «бюджет», тогда как именно они являются основой функционирования социо-эколого-экономических систем. Это, кстати, и произошло в данном случае (откуда возьмутся лошади, домики и т.п., если в предприятии нет денег?)

- Возможно, это не фактор системы, а часть внешней среды. Так, часто в моделях появляются вершины «географическое положение», «климат» и т.п. которые, конечно, влияют на систему, но мы изнутри системы не можем на них повлиять и воспринимаем как данность. В подобном случае вершину из модели следует убрать.
  1. При более подробном рассмотрении дуг орграфа выявляются следующие несоответствия:

- У вершины «земельный участок» много входящих дуг. Но, учитывая придаваемый этой вершине исследователем смысл (площадь участка в га), ни один из перечисленных факторов не может на нее влиять! Возможно, такая ситуация возникла из-за нечетко понимаемого смысла вершины и на самом деле она должна характеризовать качество участка (например, оценка его рыночной стоимости).

- Похожая ситуация с вершиной «водоем», понимаемой как объем в м3. В такой интерпретации это, скорее, фактор внешней среды, данность, на которую мы повлиять не можем. Но, поскольку автор считает, что на эту вершину влияет фактор «отходы» (со знаком «-»), можно предположить, что опять произошла подмена смысла и имеется в виду не объем водоема, а качество воды, которое можно измерить, например, в загрязненности (мг/м3).

- В орграфе дугам «прокат лошадей»-«отходы» и «деревянные домики…»-«отходы» придан знак «-». Видимо, автор имел в виду, что чем больше отходов, тем хуже, то есть эти связи носят «отрицательный» характер. Но такой эмоциональный подход противоречит принципам моделирования: так, чем больше лошадей, тем больше отходов, значит, следует поставить знак «+».


Задания. 1. Проанализировать на соответствие правилам моделирования знаковый орграф, построенный студентом для анализа деятельности московского нефтеперерабатывающего завода (МНПЗ):




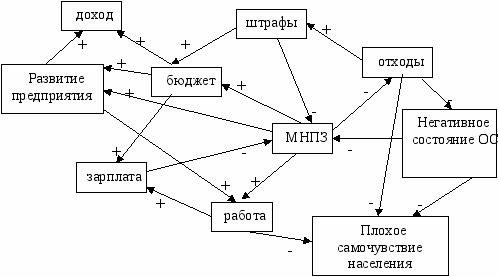
2. Составить матрицу смежности данного орграфа

3. (зачетное задание) Построить модель в виде знакового орграфа для какой-либо социо-эколого-экономической системы


ЧАСТЬ 2

Исследование реакции орграфа на возмущения.

Существует методика исследования и оптимизации систем только по их знаковым орграфам. Но мы в дальнейшем будем использовать взвешенные орграфы, считая, что на текущий момент времени и в ближайший рассматриваемый период структура системы неизменна и весовые коэффициенты постоянны. После этого структура может измениться – могут появиться или пропасть связи, измениться их веса; на новый период времени придется строить новую модель.


Итак, пусть некоторая социо-эколого-экономическая система смоделирована при помощи взвешенного орграфа. Текущее состояние системы описывается набором значений характеристик системы. На момент моделирования система находится в состоянии равновесия, то есть текущие значения характеристик постоянны при отсутствии внешнего воздействия. Пронормируем характеристики, заменив их безразмерными величинами, так что текущему значению каждой характеристики отвечает начальное значение xi(0)=1 соответствующей вершины орграфа. Таким образом, возможные изменения значений вершин (или характеристик) будут вычисляться в долях от текущего состояния.

Управление орграфом состоит в целенаправленном изменении значений одной или нескольких вершин. Эти изменения передаются по дугам к соседним вершинам и далее пошагово. Для описания изменений значения i-ой вершины орграфа xi(k) на k-том шаге после воздействия необходимо задать правило, определяющее переход от xi(k) к xi(k+1) через веса дуг aij.

Рассмотрим правило импульсного процесса, часто применяемое при моделировании социо-эколого-экономических систем. Согласно ему, изменение значения вершины определяется изменениями значений всех ее входных вершин на предыдущем шаге. При этом изменения значений вершины накапливаются. Следует отметить, что такое правило подходит не для всех орграфов. Например, если орграф отражает круговорот какого-либо вещества или энергии в природе, то значения вершин будут не накапливаться, а расходоваться на изменение соседних вершин.

Обозначим изменение значения i-ой вершины на k-том шаге 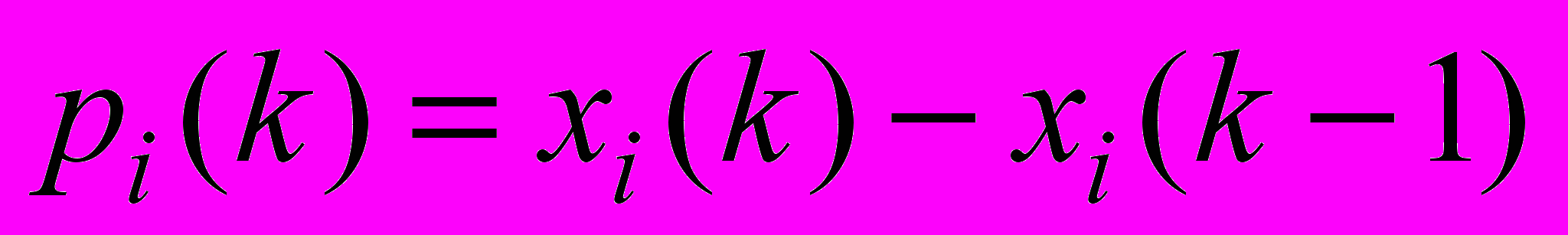и назовем эту величину импульсом.

Пусть вес дуги aij показывает отношение приращения значения конечной вершины дуги xj, полученному ей за один шаг, к вызвавшему его приращению значения начальной вершины дуги xi.

Тогда правило изменения значений задается формулой:

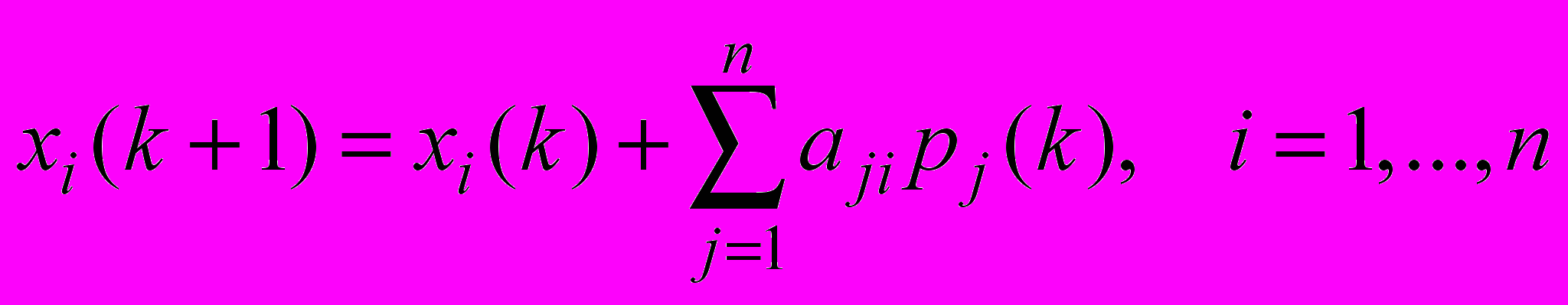(1)

(где n – число вершин орграфа)

Перепишем систему (1) в виде

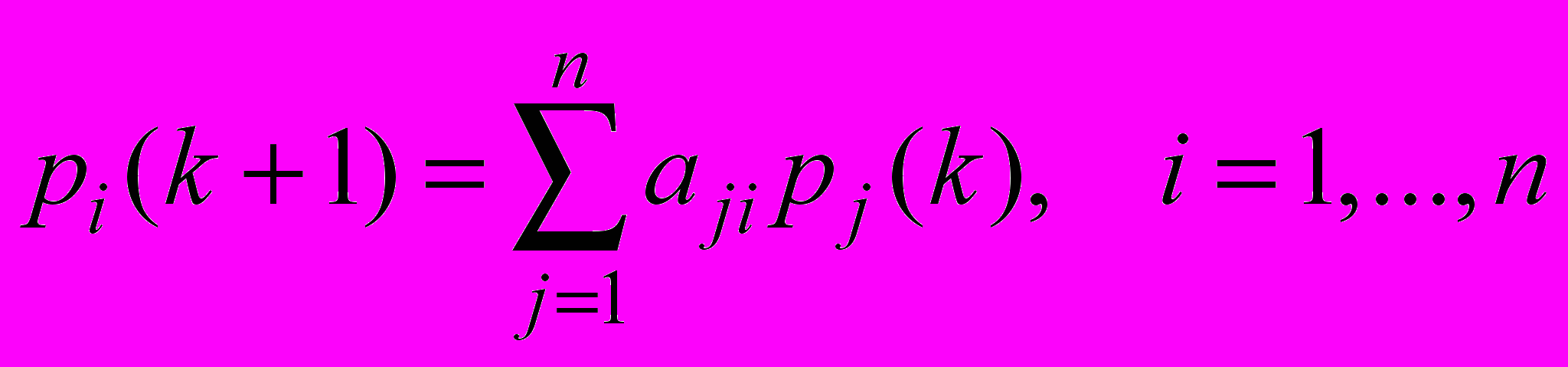(2)

и предположим, что известны начальные импульсы .

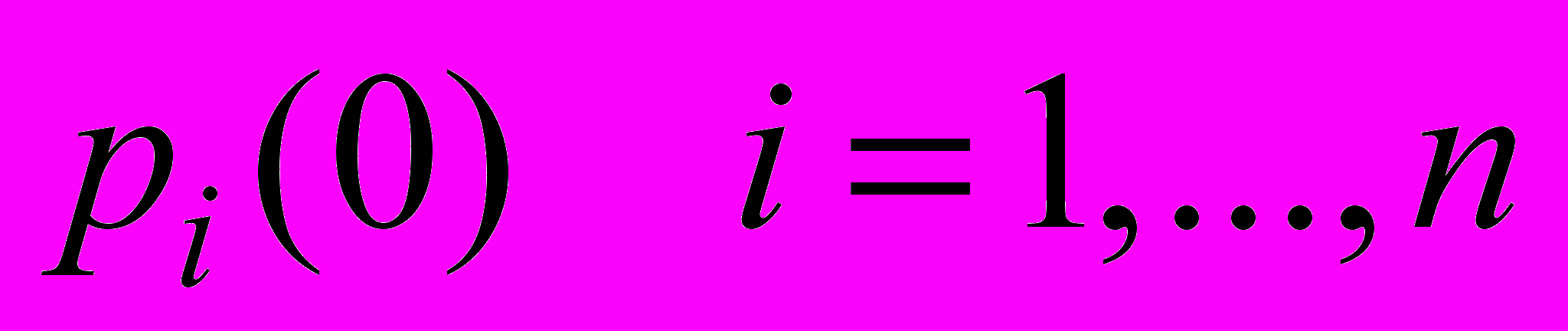Соотношение (2) удобно записать в матричной форме:

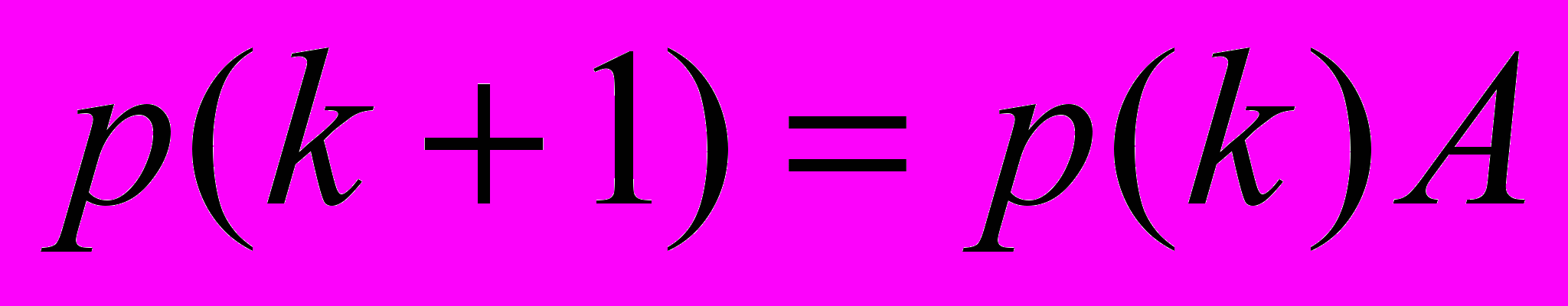, (3)

где

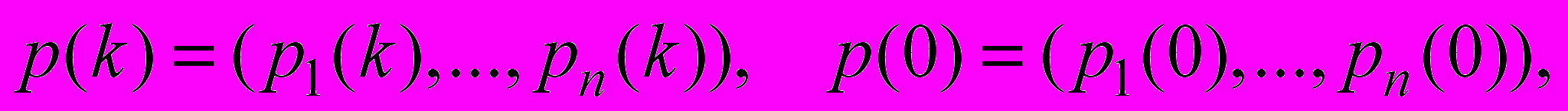
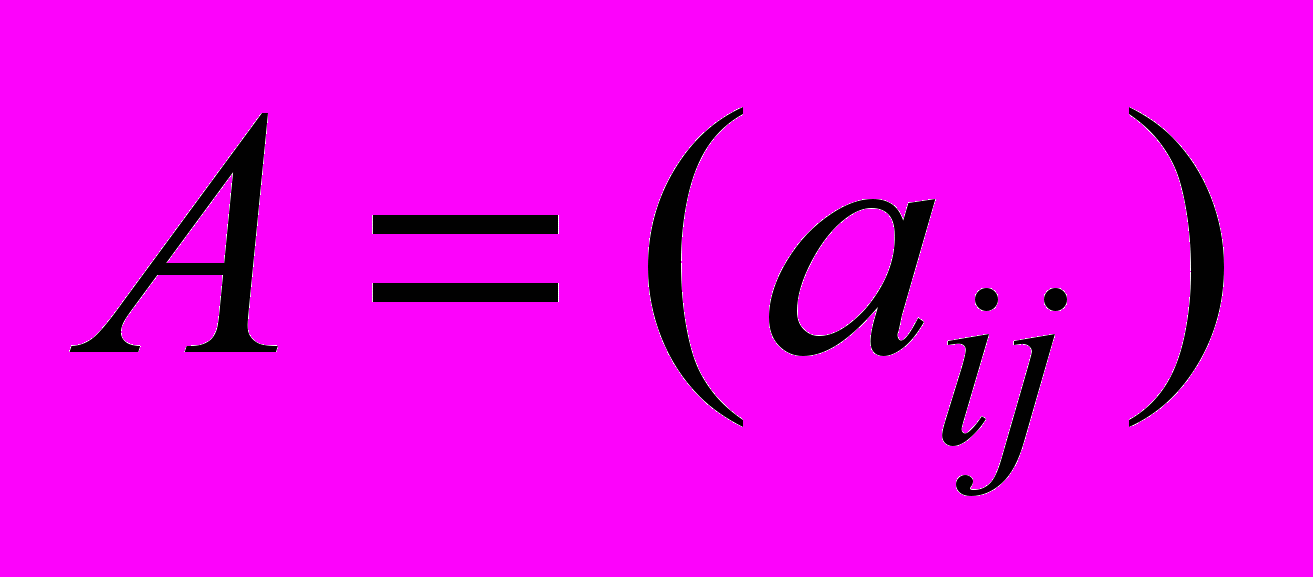- матрица смежности орграфа.

Таким образом,

,

,

…

.

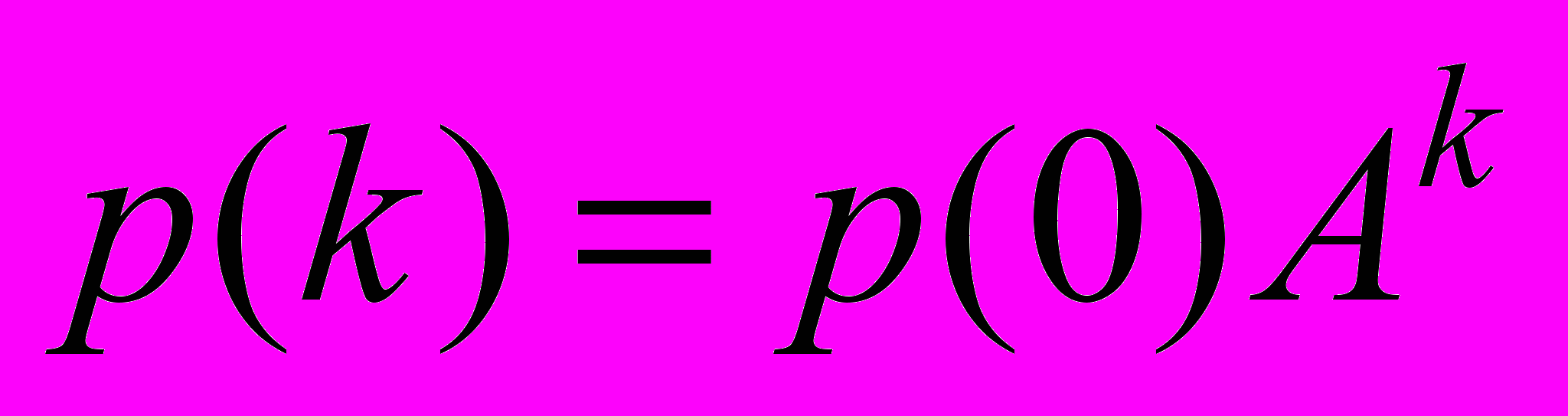Возвращаясь к переменным 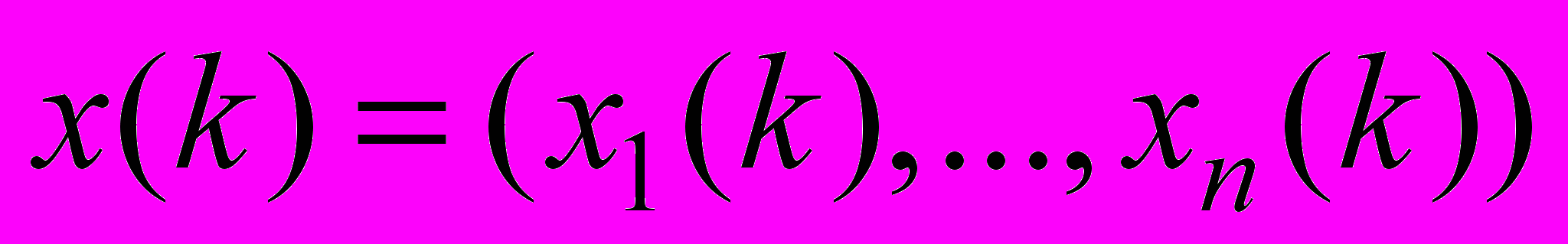, получаем

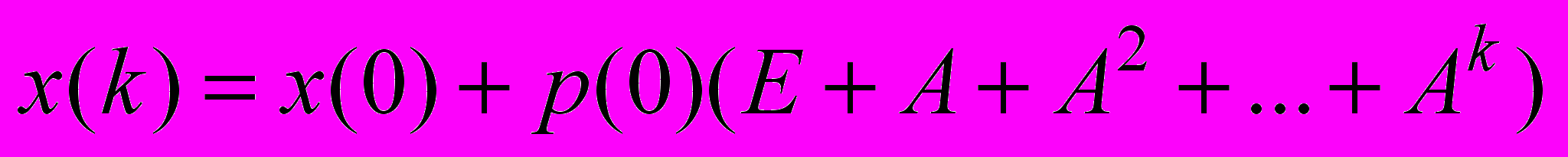(4)

Это правило позволяет найти значения вершин орграфа через любое число шагов после начального воздействия, т.е. дает возможность прогнозировать развитие системы, описываемой данным орграфом, при одноразовом начальном импульсе.
  • Назовем реакцией орграфа на начальный импульс на k-м шаге абсолютное изменение значений вершин за k шагов после начального воздействия: .

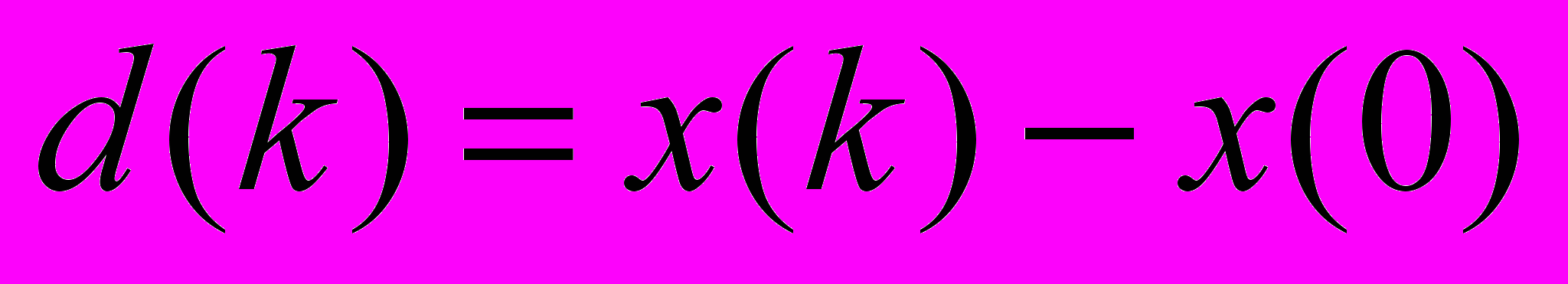Реакция орграфа на k-м шаге вычисляется по формуле:

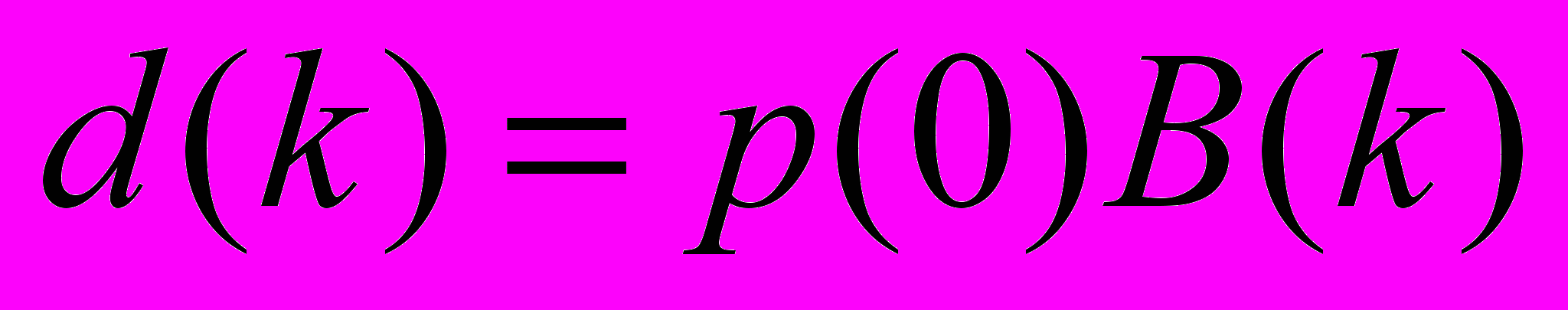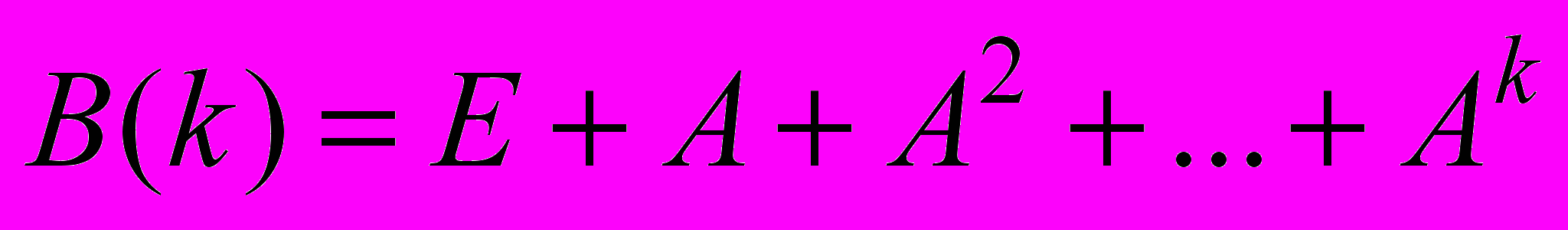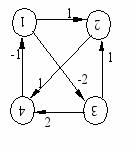
, где (5)


Пример Рассмотрим взвешенный орграф:

Текущие значения вершин орграфа, находящегося в равновесном состоянии, считаются равными 1.


Рассмотрим воздействие на орграф единичным начальным импульсом в первую вершину (т.е. значение первой вершины изменяется на 100%):

р(0)=(1;0;0;0)

Это изменение передается в вершину 2 с коэффициентом 1 и в вершину 3 с коэффициентом –2, так что после одного шага прохождения импульса по орграфу изменение вершин выражается вектором

р(1)=(0;1;-2;0),

а реакция орграфа (общее изменение относительно начального равновесного состояния) становится равна

d(1)=(1;1;-2;0).

Изменение вершины 2 провоцирует на следующем шаге изменения вершины 4 с коэффициентом 1: (0;0;0;1), а изменение вершины 3 провоцирует изменение вершины 2 с коэффициентом 1 и вершины 4 с коэффициентом 2: (0;-2;0;-4). Таким образом, в сумме изменения вершин орграфа после второго шага прохождения импульса выражаются вектором

р(2)=(0;-2;0;-3),

а реакция d(2)=(1;-1;-2;-3)