Учебное пособие по экоинформатике (сокращенный
| Вид материала | Учебное пособие |
- Учебное пособие Житомир 2001 удк 33: 007. Основы экономической кибернетики. Учебное, 3745.06kb.
- Учебное пособие, 2003 г. Учебное пособие разработано ведущим специалистом учебно-методического, 794.09kb.
- Учебное пособие, 2003 г. Учебное пособие разработано ведущим специалистом учебно-методического, 454.51kb.
- Учебное пособие, 2003 г. Учебное пособие разработано ведущим специалистом учебно-методического, 783.58kb.
- Е. Г. Непомнящий Учебное пособие Учебное пособие, 3590.49kb.
- Учебное пособие Сыктывкар 2002 Корпоративное управление Учебное пособие, 1940.74kb.
- Учебное пособие г. Йошкар Ола, 2007 Учебное пособие состоит из двух частей: «Книга, 56.21kb.
- Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
- Общий курс физики т-1 Механика: учебное пособие М.: Физматлит, 2002. Сивухин Д. В.,, 679.32kb.
- Учебное пособие Бишкек 2008 Учебное пособие «Права женщин на землю», 3306.04kb.
На третьем шаге изменение вершины 2 провоцирует изменение
(0;0;0;-2), а изменение вершины 4 провоцирует изменение (3;0;0;0). В сумме
р(3)=(3, 0, 0, -2), d(3)=(4, -1, -2, -5).
Вычисление реакции орграфа при помощи компьютера
Вычисления реакции орграфа на начальный импульс удобно проводить в программе Excel. Проиллюстрируем процесс на примере уже рассмотренного выше взвешенного орграфа. (Заметим, что предлагаемая последовательность действий отнюдь не является единственно возможной.)
Для этого прежде всего следует заполнить на листе Excel матрицу А. (В дальнейшем удобно делать это, начиная с ячейки В2, чтобы в первой строке и первом столбце указывать названия факторов.) Далее, под матрицей А следует выделить массив такого же размера (отступив для удобства одну строку) для матрицы А2=А2 и вычислить ее, применяя функцию МУМНОЖ (значок вставки функции выглядит как fx):
Следует иметь в виду, что, заполнив окно функции, требуется нажать не Enter, а Ctrl+Shift+Enter для возвращения значения массива. Иначе вы получите не матрицу, а только первый ее элемент.
Под матрицей А2 вычисляется матрица А3=А3 путем умножения матицы А2 на матрицу А. Это можно сделать при помощи той же функции МУМНОЖ, а можно – скопировав матрицу А2. Но при копировании массива, заполненного при помощи функции, номера ячеек, используемых в функции, смещаются на то же расстояние, что и сам массив. Поэтому, во-первых, матрицу А3 следует выделять, отступив на 1 строку, так же как и при выделении матрицы А2; во-вторых, следует предварительно зафиксировать в строке формул для массива А2 один из умножаемых массивов при помощи значка $ (используя при этом также не Enter, а Ctrl+Shift+Enter). Строка формул для массива А2 будет иметь вид:
{=МУМНОЖ($B$2:$E$5;B2:E5)} ,
а для массива А3, после смещения формулы на 5 ячеек вниз:
{=МУМНОЖ($B$2:$E$5;B7:E10)} .
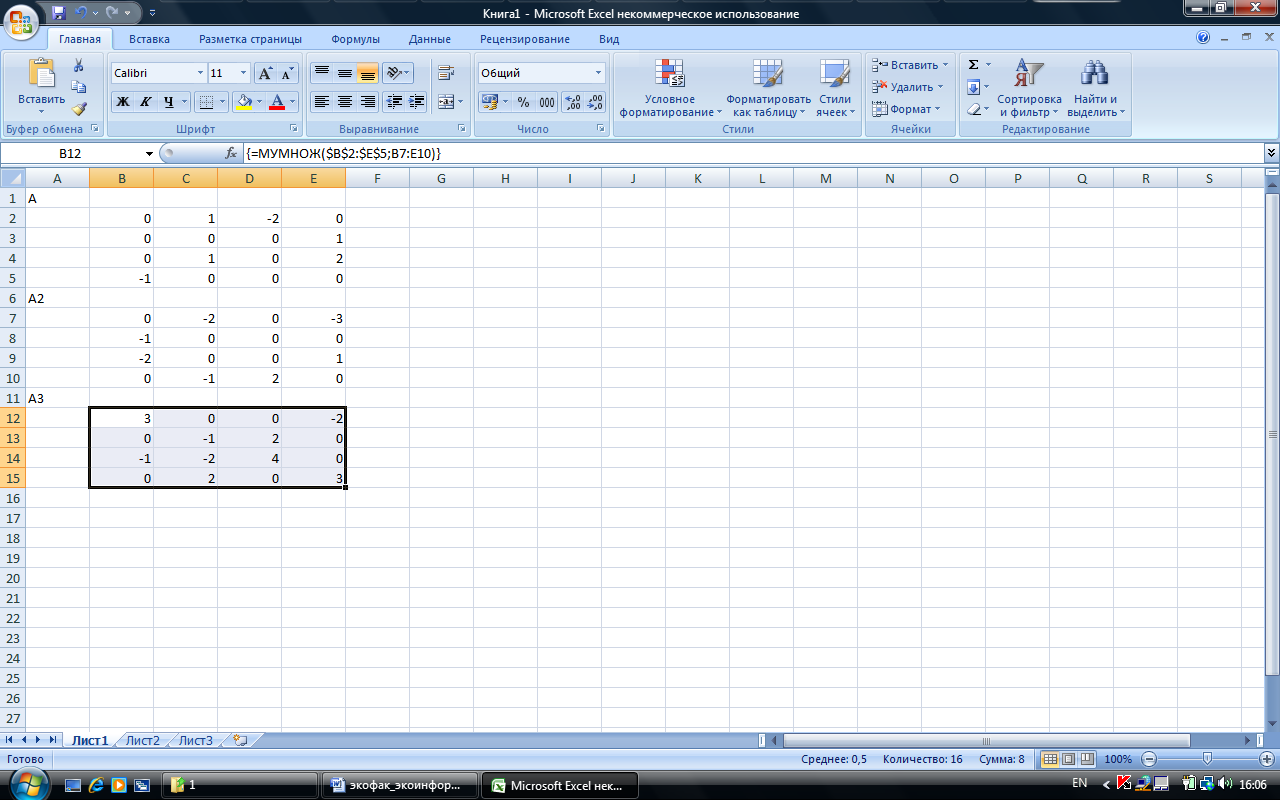
Копирование производится столько раз, сколько шагов прохождения импульса по орграфу требуется выполнить.
Теперь найдем последовательно матрицы Вk=B(k). Сначала заполним единичную матрицу Е того же размера, то и А. Затем выделим место для матрицы В1 и в строке формул введем
=G2:J5+B2:E5 ,
нажав далее снова Ctrl+Shift+Enter:
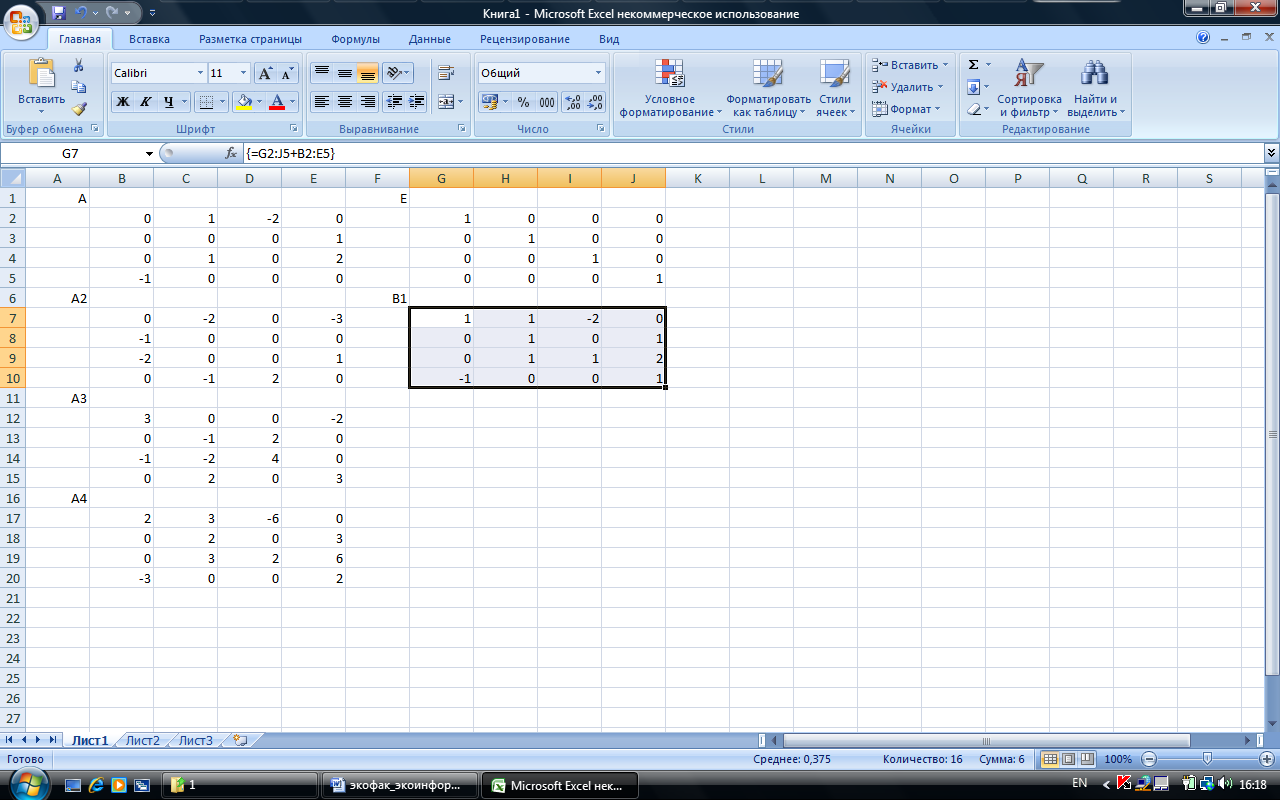
Для вычисления матрицы В2=В1+А2 достаточно скопировать матрицу В1 (без фиксации ячеек в строке формул), отступив на 1 строку. Далее копируем столько раз, сколько требуется шагов.
Если требуется, например, найти реакцию d(3) на произвольный начальный импульс р(0)=(-1;1;2;-2), можно воспользоваться снова функцией МУМНОЖ для умножения р(0)В(3):
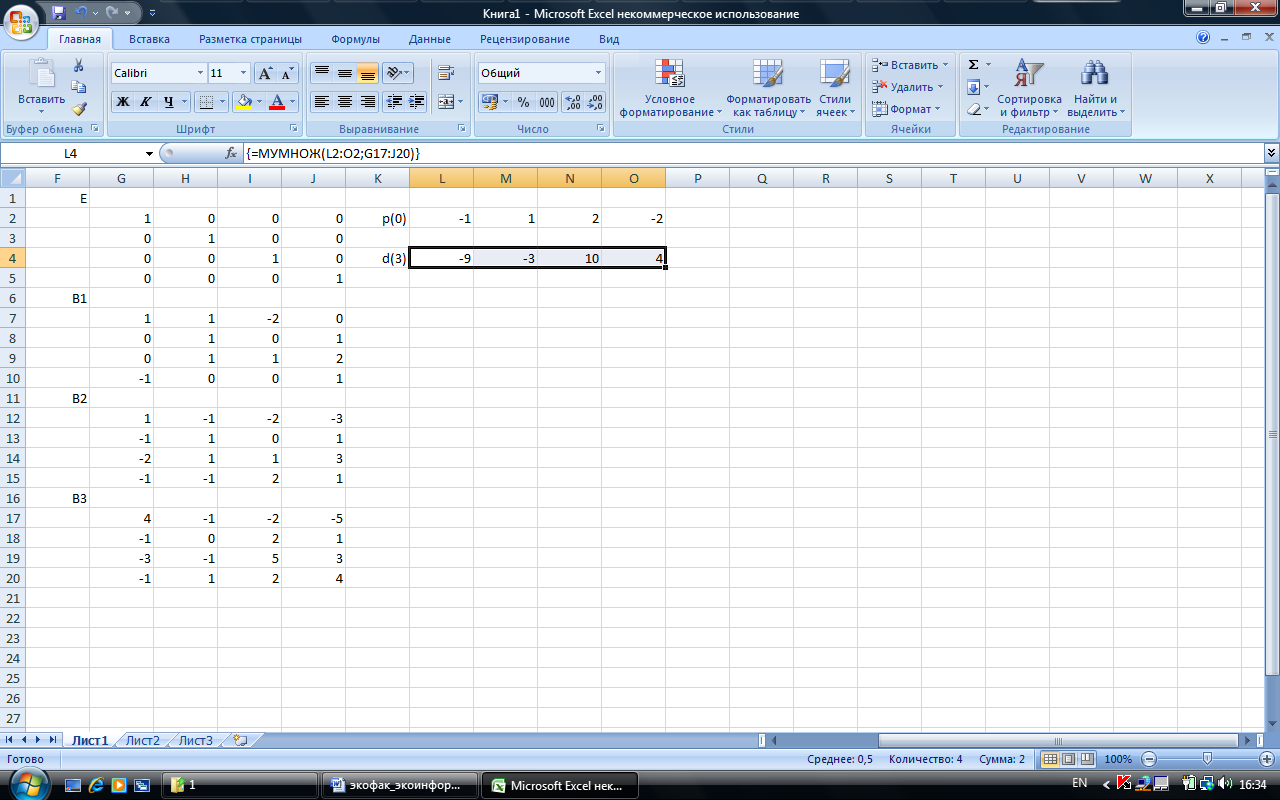
Результат проведенных таким образом расчетов автоматически изменяется при изменении исходных данных – матрицы смежности А и вектора начального импульса р(0).
Оценка весов связей системы при построении взвешенного орграфа.
Одной из сложнейших задач в процессе моделирования систем в виде взвешенного орграфа является установление весовых коэффициентов связей. При этом используют, по мере возможности и в различных комбинациях, один из трех методов: непосредственное вычисление, статистический метод, метод экспертных оценок. Рассмотрим их подробнее.
1. Метод непосредственного вычисления коэффициентов.
Напомним, что под весовым коэффициентом дуги (xi, xj) мы подразумеваем число
, где 
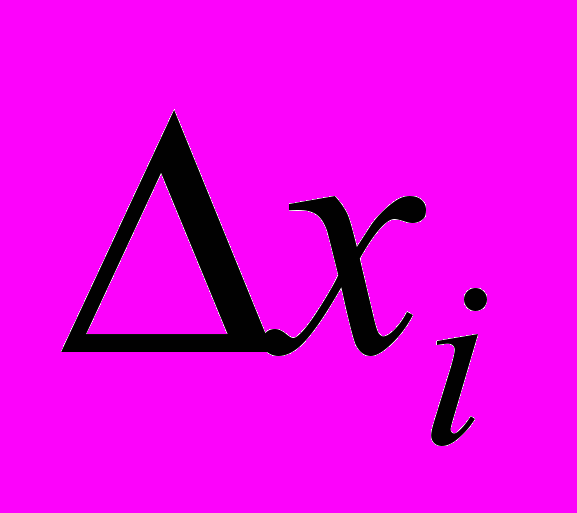- изменение значения вершины xi (в долях от текущего значения), 
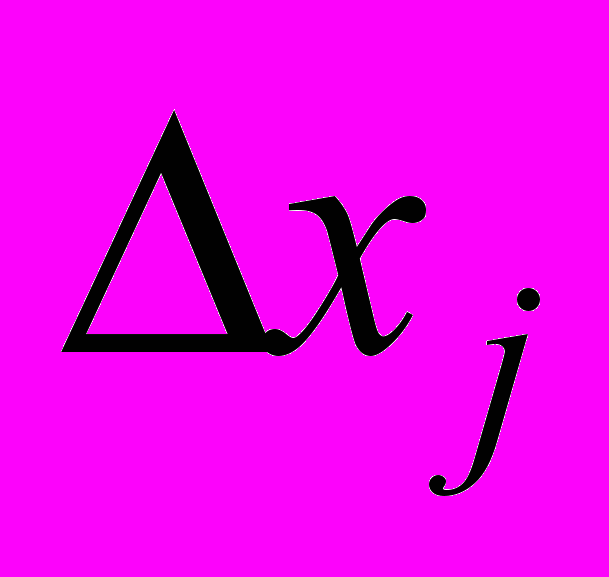- вызванное им непосредственно изменение значения вершины xj (также в долях от текущего состояния). Иногда (к сожалению, довольно редко) эта связь достаточно прозрачна (чаще всего это случается при оценке чисто экономических, финансовых связей).Например, пусть xi – средний доход населения региона, xj – бюджет региона. Одним из источников наполнения бюджета служит подоходный налог; пусть известно, например, что эта статья составляет 15% общего бюджета. Тогда при увеличении значения вершины xi на 100% (в два раза) поступление подоходного налога в бюджет также увеличится в 2 раза, что составит дополнительно 15% от текущего состояния бюджета. Таким образом,
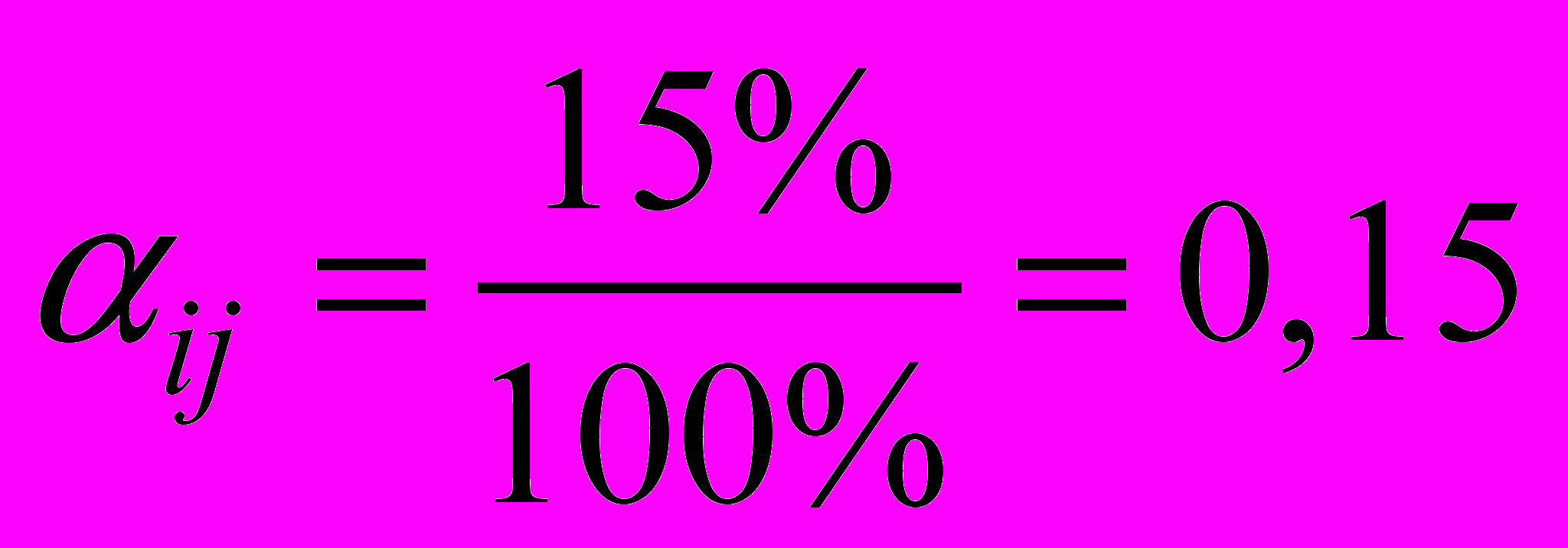.Такая оценка весового коэффициента наиболее достоверна, но, как правило, наименее доступна. Чаще связь между факторами осуществляется не по таким очевидным законам.
2. Статистический метод оценки весовых коэффициентов.
Как показывает практика, достаточно достоверный результат дает статистическая оценка связи между факторами. Для того, чтобы ей воспользоваться, требуется собрать статистику – ряд парных значений вершин для различных состояний моделируемой системы. При этом статистику можно собирать по территориальному или временному признаку. Например, оценивая связь между числом жителей города (вершина x1) и средним доходом (x2) составляем таблицу:
| данные за 2000 год | | данные по Рязани | ||||
| Город | x1=A | x2=B | | Год | x1=A | x2=B |
| Москва | а1 | b1 | | 1980 | а1 | b1 |
| Рязань | а 2 | b 2 | или | 1985 | а 2 | b 2 |
| … | … | … | | … | … | … |
| Норильск | а n | b n | | … | а n | b n |
При этом важно соблюдать принципиальную инвариантность (неизменность) системы на разных территориях либо в разные годы. Действительно, устанавливать зависимость между этими факторами, пользуясь данными, например, из США, Европы и Африки было бы неразумно. Для Европы коэффициент один, для Африки – другой.
Далее, нормируем значения признаков, заменяя каждое значение его долей в суммарном значении данного признака по всем территориям (на всем временном интервале)
Далее, проверяем наличие связи, вычисляя коэффициент корреляции rAB между значениями А и В:
Коэффициент корреляции указывает на наличие связи. Он может находиться в пределах от –1 до 1, при этом если
связь считается сильной, если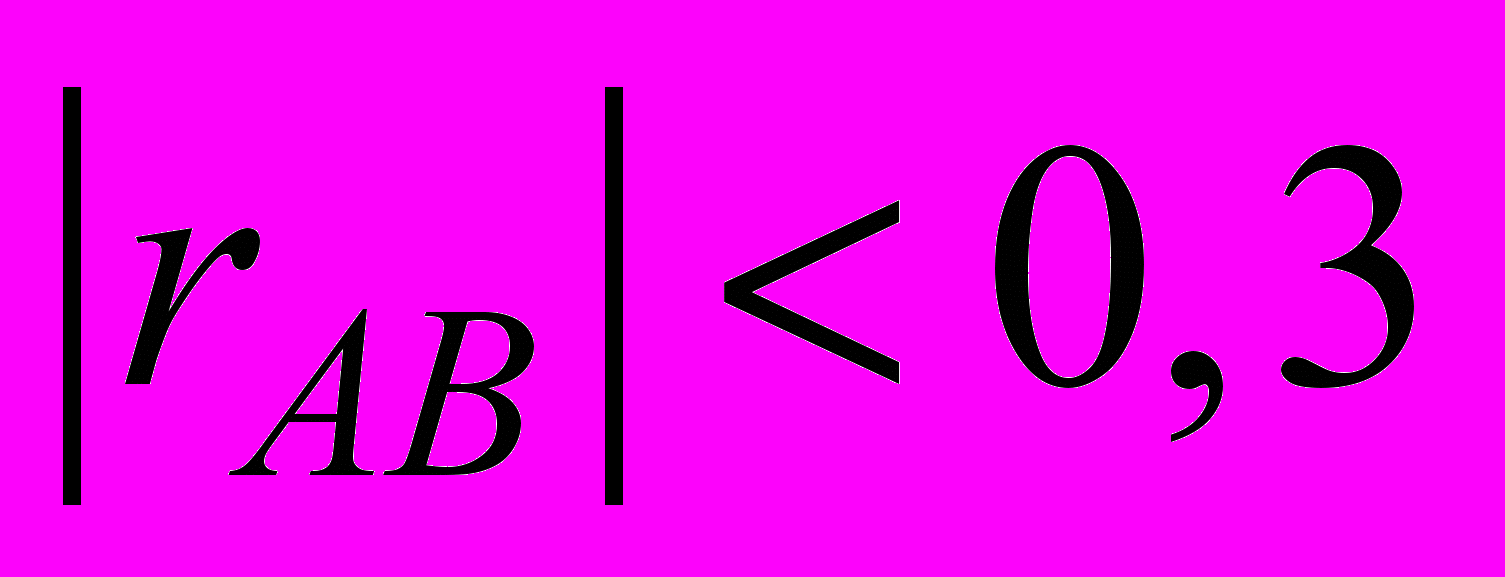 
, связь считается слабой и ее наличие недостоверно, скорее всего, придется ее убрать из орграфа. Знак коэффициента корреляции указывает на знак связи, но направление связи (от А к В или от В к А) никак не указывается; коэффициент корреляции служит только для проверки наличия тех прямых связей, которые исследователь уже построил при помощи логического анализа системы. При этом необходимо заранее исключить двойные связи вида «А влияет на В, В влияет на А»Далее, если коэффициент корреляции имеет достаточно большое значение, оценивается весовой коэффициент связи при помощи коэффициента линейной регрессии RAB между величинами А и В. Именно, если рассматривается связь от А к В (А влияет на В), то ее весовой коэффициент считается равным
Если соблюдено условие инвариантности системы при сборе статистики, этот метод дает достаточно корректные результаты. Однако не всегда удается собрать удовлетворительные статистические данные по всем рассматриваемым факторам. Тогда для оценки значений факторов или самих весовых коэффициентов связей приходится пользоваться экспертной оценкой.
3) методы экспертных оценок
Привлечение экспертов при моделировании системы производится на обоих этапах построения орграфа: при выделении факторов, определяющих поведение системы (с точки зрения целей исследования), то есть построении знакового орграфа и при установлении связей между факторами, то есть при определении весовых коэффициентов дуг (построении взвешенного орграфа).
На втором этапе методы экспертных оценок используются в случае, когда нет достаточной информации об изменении показателя и влияющих на него факторов или показатель не измеряется численно, а выражается качественными оценками. То есть экспертная группа может оценивать как значения факторов, так и весовые коэффициенты связей между ними. Очень важно при этом, чтобы задача, стоящая перед экспертами, была четко сформулирована. Например, при оценке весовых коэффициентов все эксперты должны понимать смысл весового коэффициента дуги взвешенного орграфа.
Пусть n экспертов оценивают m объектов, пользуясь при этом одной и той же шкалой (то есть присваивают оценки в определенном диапазоне: от 1 до 100, от 1 до m, от 0 до 1 и т.п.). Все присвоенные оценки сводят в таблицу:
| эксперты объекты | 1 | 2 | … | n |
| 1 | a11 | a 12 | | a 1n |
| 2 | a21 | a 22 | | a 2n |
| … | | | | |
| m | a m1 | a m2 | | a mn |
где a ij – оценка, присвоенная i-му объекту j-м экспертом.
Далее, вычисляется средняя арифметическая оценок для каждого объекта, которая и присваивается этому объекту в качестве групповой оценки:
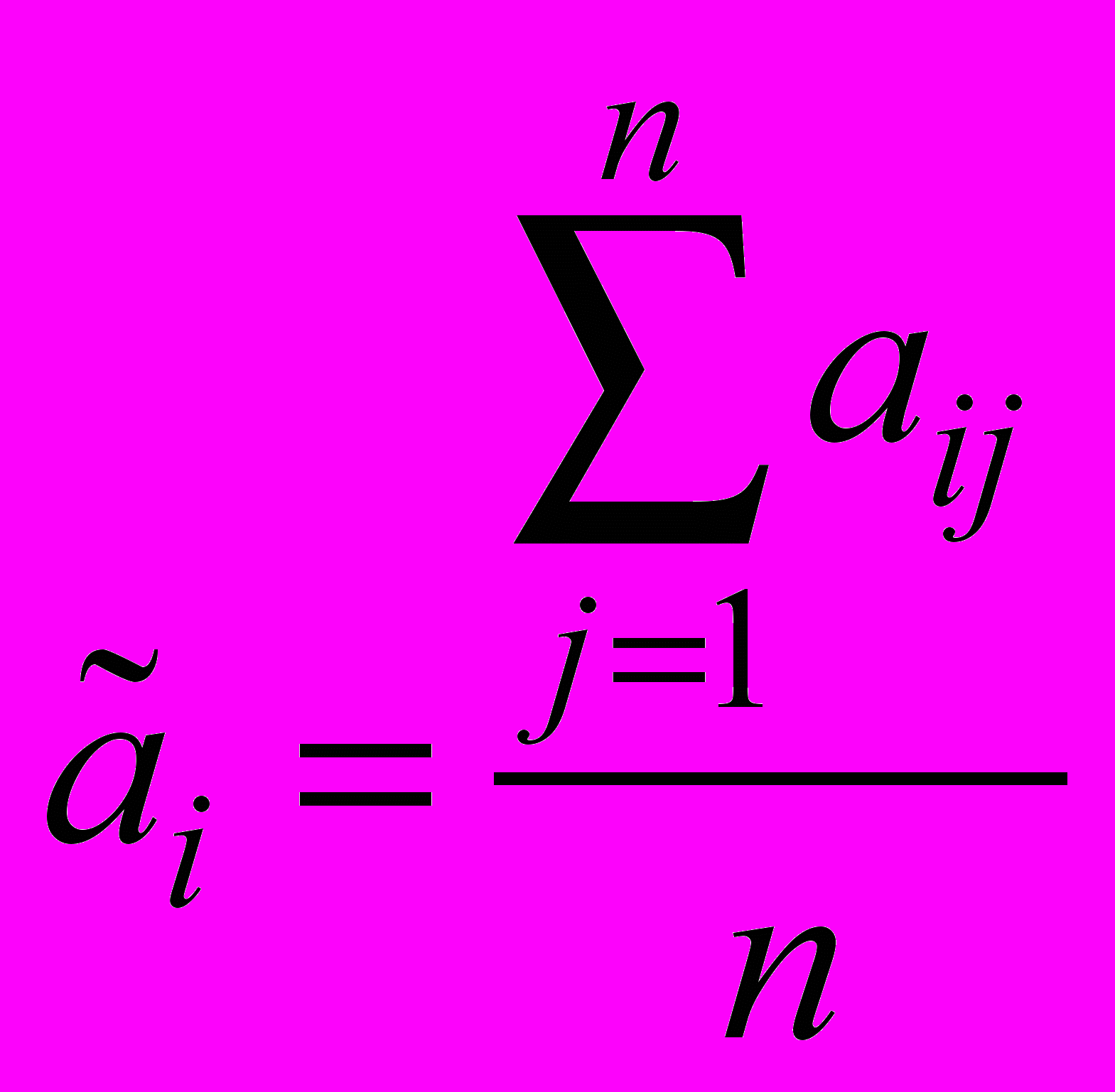. | эксперты объекты | 1 | 2 | … | n | Групповая оценка |
| 1 | a11 | a 12 | | a 1n | ã 1 |
| 2 | a21 | a 22 | | a 2n | ã 2 |
| … | | | | | |
| m | a m1 | a m2 | | a mn | ã m |
Однако такая оценка может быть признана справедливой лишь в том случае, когда мнения экспертов согласованы (т.е. не противоречат друг другу слишком сильно). Для выяснения степени согласованности мнений экспертов вычисляют коэффициент конкордации Кендалла. На практике мы можем считать, что при значении этого коэффициента>0,6 мнения экспертов признаются согласованными.
Следует упомянуть, что при применении описанного метода экспертных оценок желательно, чтобы число экспертов превышало число оцениваемых объектов.
Говоря об оценке весовых коэффициентов дуг, как правило, применяют шкалу от 0 до 1 (0,9 – очень сильная связь, 0,7 – сильная, 0,5 – средняя, 0,3 – умеренная, 0,1 – слабая). Но возможны случаи, когда весовой коэффициент какой-либо связи по абсолютной величине даже превышает единицу. Правда, такие случаи довольно редки и обычно попадают в разряд непосредственного или статистического вычисления коэффициентов.