Geum.ru

Применение моделей опционного ценообразования в оценке бизнеса банковского сектора

Вид материалаКурсовая
2. 2. Численные модели
2. 2. 1. Биномиальные модели
2. 2. 2. Метод конечных разностей
2. 3. Монте-Карло симуляция
2. 4. Модели аналитической аппроксимации
Подобный материал:
1   2   3   4

2. 2. Численные модели


Численные модели основаны на трех подходах. Первый подход известен как биномиальный, второй подход основан на использовании метода конечных разностей, третий — на использовании метода Монте-Карло симуляции.

2. 2. 1. Биномиальные модели


Этот подход был предложен William Sharpe в 1978 году и разработан J. Сох, S. Ross и М. Rubinstein. Его идея заключается в том, что время до погашения опциона разбивается на интервалы. В каждом интервале, как предполагается, цена актива следует биномиальному процессу: цена или возрастает на заданную величину, или падает на заданную величину. Таким образом получают множество возможных значений цены актива в момент исполнения опциона, для каждого значения цены цена опциона известна. После этого, используя возможность построения безрискового портфеля из актива и опционов, производят свертку полученного дерева цен. Преимущество такого подхода состоит в возможности его использования для любых видов опционов.

Наибольшее распространение биномиальные модели получили при оценке опционов на процентные инструменты. Первая модель была предложена Richard Rendleman и Brit Bartter. В 1986 году Thomas Но и Sang-Bin Lee рассмотрели модель изменения структуры процентных ставок, но волатильность всех процентных ставок была одинакова. В 1990 Fischer Black, Derman и Toy устранили это ограничение.

Попробуем построить модель цены опционов с одним периодом для случая, когда цена акции в следующем периоде может принимать только два значения. В следующем периоде акция, которая сейчас продается по цене S, будет продаваться либо по цене uS, либо по цене dS, причем, uS >dS. Величины u и d—это коэффициенты изменения цены акции.

Имеется возможность выпустить или купить облигации на сумму В под процент rf причем r определяется как r = 1 + rf

Риск облигаций равен 0. Величина r больше d, но меньше и. Это условие необходимо для того, чтобы не было возможности без всякого риска получить прибыль только на операциях с акциями и облигациями. Например, если бы и u, и d были больше r, покупка акций на деньги, полученные от выпуска облигаций, принесла бы гарантированную прибыль (без всякого риска). Никто не захотел бы покупать облигации.

Кроме того, если бы r было больше u и d, инвестор, вложив свои деньги в облигации, с полной уверенностью получил бы более весомую прибыль, чем держатель акций. Никто не захотел бы покупать акции.

Чтобы таких крайних случаев не было, предположим, что u>r>d. Представим себе опцион покупателя с ценой исполнения К, срок которого истекает через один период. Пусть С — стоимость опциона в момент 0. Наша цель — рассчитать разумную величину С. Начнем с того, что запишем значения стоимости опциона в момент 1. Стоимость опциона к концу срока будет зависеть от цены акции в этот момент.

Пусть Сu — стоимость опциона к концу срока, если цена акции в этот момент достигнет uS:

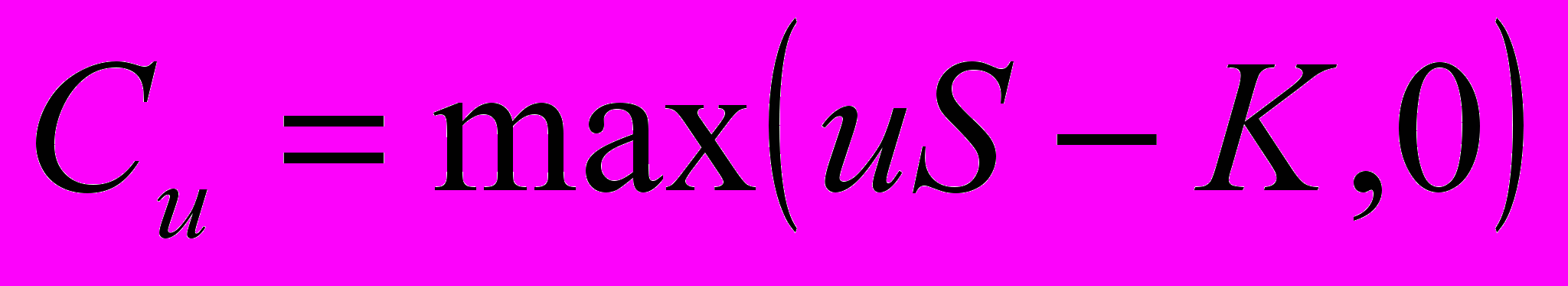(18)

Аналогично пусть Cd — стоимость опциона к концу срока, если цена к этому времени снизится до dS:

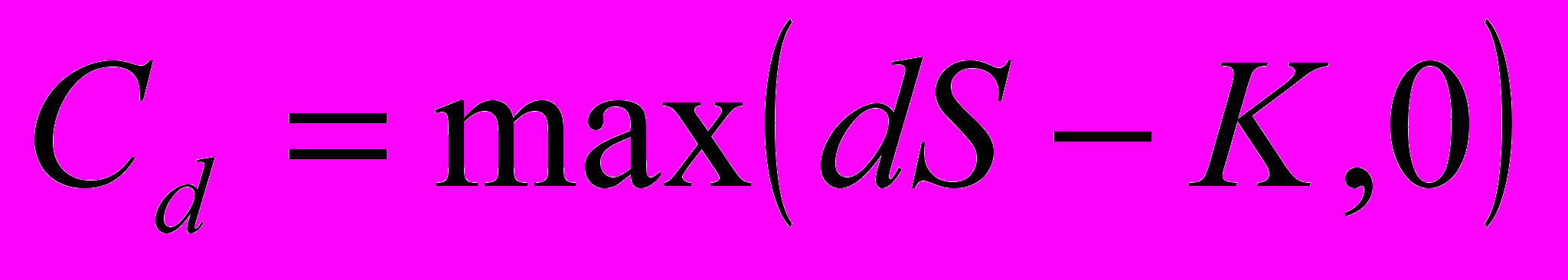(19)

Чтобы определить стоимость опциона в момент 1 за один период до окончания срока, покажем, что доходы от опциона покупателя можно в точности промоделировать доходами от соответствующим образом выбранного портфеля акций и облигаций, который называется хеджированным портфелем. Так как опцион покупателя полностью эквивалентен портфелю, их стоимости должны быть одинаковы. Стоимость хеджированного портфеля можно определить, зная рыночные цены акций и облигаций, из которых он составлен. На этом основан расчет стоимости опциона покупателя.

2. 2. 2. Метод конечных разностей


Этот подход заключается в нахождение численного решения дифференциального уравнения для стоимости опциона. Первая работа была предложена Eduardo Schwartz и расширена Courtadon в 1982. Brennan и Schwartz показали, что этот подход можно рассматривать как триномиальное дерево цен. John Hull и Alan White модифицировали их модель, доказав, что методология триномиального дерева цен и дифференциальное уравнение приводят к одному решению [2, 147].

2. 3. Монте-Карло симуляция


Это принципиально другой подход. Все описанные выше методы оценки опционов сводились к необходимости решать стохастическое дифференциальное уравнение. Подход Монте-Карло симуляции заключается в непосредственной прямой оценке ожидаемой стоимости опциона посредством симуляции возможных значений цены актива в момент исполнения опциона. Правда этот подход также требует предположения о виде стохастического процесса, которому следует цена базового актива.

Первая модель появилась в 1977 году в работе Phelim Boyle. Сегодня этот метод оценки опционов получил наибольшее распространение и продолжает динамично развиваться. Так, Jim Tilley в 1993 году впервые предложил метод оценки опционов американского типа. После этого последовали модели Grant, Vora и Weeks (1994), Barraquand и Martineau (1995), Broadie и Glasserman (1995) [2, 149].

2. 4. Модели аналитической аппроксимации


Эти модели основаны на сочетании аналитического и численного подходов. Обычно они применяются для оценки американских видов опционов. Подход заключается в получении аналитической оценки стоимости опциона в момент исполнения, а затем с помощью численных методов оценивается добавка к стоимости опциона из-за возможности раннего исполнения.

Lionel Macmillan предложил оценку опционов, используя подход квадратичной аппроксимации, эта идея получила отражение в работе Giovanni Barone-Adesu и Robert Whaley.

Все модели оценки стоимости опционов требуют знания напрямую ненаблюдаемых параметров рынка. А именно, необходимо знать вид процесса, которому следует изменение цены актива, лежащего в основе опциона, во-вторых, необходимо знать параметры этого процесса. Основным влияющим параметром является волатильность базового актива.

Эти параметры, как уже отмечалось, нельзя напрямую наблюдать на рынке, как остальные величины (цена актива, безрисковая ставка). Их оценку получают на основе исторических данных. В этом кроется главная проблема теории стоимости опционов: волатильность рынка не является постоянной величиной, и ее изменения носят часто скачкообразный характер. Адекватно учесть будущие изменения волатильности ни одна из моделей не в состоянии [2, 150].