Исследование по результатам решенных задач «Копилка методов и советов Мода Исследование по теме «Техника чтения школьников» Наибольшее и наименьшее значение. Размах
| Вид материала | Исследование |
- Исследование функций на монотонность и экстремумы. Построение графиков, 13.79kb.
- Лекция 15. Определённый интеграл, 71.1kb.
- Е. В. Чепин Московский инженерно-физический институт (государственный университет), 32.43kb.
- Исследование методов и методик развития математических способностей младших школьников, 724.06kb.
- Исследование электрофизических свойств сельскохозяйственных продуктов и материалов, 34.96kb.
- Исследование методов приема сигналов данных, 68.73kb.
- Л. В. Шипова Саратов, сгу им. Н. Г. Чернышевского Исследование, 107.95kb.
- «Исследование и сопоставительный анализ численных методов решения задач не линейного, 321.81kb.
- В. А. Каверина «Картины мира» школьников. Итоги исследования. Исследование, 82.72kb.
- Иванов Петр Алексеевич ввт-406 тудент группа т исследование, 71.44kb.
Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 80»
РЕФЕРАТ
по теме: Статистические характеристики на уроке алгебры.
Выполнили
ученики 7«Б» класса:
Коварж Галина Юрьевна,
Лебедев Александр Станиславович
Руководитель:
Ласточкина Ольга Геннадьевна-
учитель математики
2009г.
Содержание
Введение………………………………………………………………..................3
- «Начала» исследования…………….………………………………………….5
- Первые шаги в исследовании……………………………………………........6
- Среднее арифметическое…………………………………………….…..........7
3.1.Упражнения…………………………………………………….................8
3.2.Исследование из серии «Школьная статистика»……………….............9
- Медиана……………………………………………………………………….10
4.1.Задачи………………………………………………………..…………..12
4.2Исследование по результатам решенных задач «Копилка
методов и советов………………………......................................................12
- Мода…………………………………………………………………………...13
5.1.Исследование по теме «Техника чтения школьников»……………….14
- Наибольшее и наименьшее значение. Размах……..……………………..…15
6.1. Исследовательская мини-задача из серии «Школьная
статистика»………………………………………………………………..15
6.2. Упражнения……………………………………………………………...16
7. Отклонения…………………………………………………………………...17
- Дисперсия……………………………………………………………..……....18
8.1. Примеры и упражнения…………………………………………….......18
8.2. Исследовательский социологический мониторинг по ЕГЭ………….19
- Статистика вокруг нас……………………………………..............................20
9.1 Эконометрика. Расчет средней заработной платы…………….……....20
9.2 Линейный тренд температуры……………………………………….....22
9.3 Анализ отклонения прибыли…………………………………………....23
9.4 Резюме: Оценка «здоровья здорового человека»……………………...24
- Заключение……………………………………………………………………25
- Список литературы…………………………………………………………...26
- Приложение
12.1. Словарь для тех, кто хочет знать больше……….………………........27
Введение.
На уроке алгебры мы познакомились с темой «Статистические характеристики». Среднее арифметическое, медиана, размах и мода. Мода в математике? А медиана в алгебре? Удивительно!
Мы провели математическое исследование, где, задавая вопросы один за другим, определяли направление пути исследования. Нас эта тема очень заинтересовала. Материал был живой, современный и увлекательный.
Поэтому мы решили написать по этой теме реферат и сделать компьютерную презентацию. Нам было интересно узнать о том, что такое мода и среднее значение, их применение в жизни человека. Для чего нужна медиана? Мы занялись поисками, исследованиями. Оказывается, она является одним из показателей средней зарплаты работников на предприятии. Мы открыли, что при массовом пошиве одежды обязательно в расчетах используются описательные статистические характеристики. Следующим нашим открытием были отклонения и дисперсия.
И так, пошив одежды, производство пшеницы в стране, среднемесячные температуры, выдача зарплаты, качество сдачи экзаменов, подсчёт населения городов и многое другое в жизни современного человека характеризуется с помощью описательной статистики.
Мы встречались с выпускниками нашей школы, беседовали и читали их лекции. Они учатся в разных вузах: политехническом университете медицинском, педагогическом, университете, ТУСУРе и им всем приходится выполнять расчеты и обрабатывать результаты, находя среднее значение, медиану, размах, моду, наибольшее и наименьшее значения, отклонения и дисперсию. А они будущие экономисты, психологи, инженеры, менеджеры, врачи. Значит, где бы мы не продолжили свое образование, скорее всего нам придется заниматься статистическими расчетами.
Оказывается, описательная статистика в нашей жизни сейчас занимает не малую роль. Поэтому продолжим исследование и побудем в роли открывателей научных сокровищ и глубин статистики в математике.
Наша цель:
Раскрыть особенности статистических характеристик.
Задачи:
1. Изучить и обобщить собранный материал по теме.
2. Создать творческую разработку в виде реферата, медиапродукта и приложений к ним.
3. Научиться решать и составлять задачи по статистике.
4. Выявить удивительное.
Гипотеза:
Если начать исследование с рассмотрения основных положений описательной статистики с разных точек зрения, то отыщутся различные объяснения и ключи понимания её значимости.
Объект исследования:
Описательная статистика
Предмет исследования:
Среднее арифметическое, медиана, размах и мода, наибольшее и наименьшее значения, отклонения и дисперсия.
1. «Начала» математического исследования
Проблемные вопросы
- Если ты профессиональный статист, то чем бы тебе пришлось заниматься?
- Какие бы ты решал статистические задачи и как?
- Какой области знаний человечества они принадлежат?
- Роль данных характеристик в описательной статистике.
????? ?????
Мы такие проблемы выдвигаем
- -Что нужно понимать под терминами статистика, числовой ряд, среднее арифметическое, медиана, размах и мода, наибольшее и наименьшее значения отклонения и дисперсия?
- - Зачем нужны эти статистические характеристики?
- - Можно ли их сравнивать? Чем объясняются отличия?
- - Какая из характеристик наиболее полно отражает явление?
- - Какие задачи можно решать?
- -Можем ли сами составлять задачи по статистике?
- - Поиски подхода к решению задач.
- - Как выяснить, существуют ли различные способы и методы решения?
- -Какой области научных знаний принадлежат задачи описательной статистики?
????? ?????
2. Первые шаги исследования
Мы познакомились с определениями среднего арифметического, медианы, моды и размаха. И подумали, а смогут ли ребята, зная только определение среднего арифметического, определить, что такое размах, медиана и мода. Мы составили для них вот такое задание, которое назвали «Испорченные определения и предложили найти верные ответы.
«Испорченные» определения
|
|
Верные определения
|
|
Выводы эксперимента:
- Задание вызвало большой интерес.
- Все справились успешно.
- Можно приступить к более глубокому рассмотрению вопросов.
- Среднее арифметическое
Рассмотрим данные о производстве пшеницы в России в 1995-2001гг.(в миллионах тонн).Они приведены в таблице 1.
Таблица 1.Производство пшеницы в России в 1995-2001гг.
| Год | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 |
| Производство, млн. тонн | 30,1 | 34,9 | 44,3 | 27,0 | 31,0 | 34,5 | 47,0 |
Как видно из таблицы 1, производство пшеницы в разные годы различается.
Оно зависит от погодных условий, площади посева и других обстоятельств. Поэтому производство пшеницы за один год не даёт полного представления об уровне производства пшеницы в стране. Для этой цели лучше использовать среднее значение за ряд лет.
По данным таблицы мы можем вычислить среднее производство пшеницы за 7 лет. Для этого надо сложить годовые сборы пшеницы и затем сумму разделить на число слагаемых.
В данном случае получаем
(30,1+34,9+44,3+27,0+31,0+34,5+47,0)/7=35,5
Получаем, что среднее производство пшеницы в России за рассматриваемый период 1995-2001гг. составляло приблизительно 35,5 млн. тонн в год.
Вычисленное нами значение называется средним арифметическим или просто средним.
- Определение. Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
Другими словами, среднее арифметическое - это дробь, в числителе которой стоит сумма чисел, а в знаменателе - их количество.
К вычислениям средних значений прибегают во многих подобных задач.
Можно нанести данные о производстве пшеницы из таблицы 1 на числовую ось в виде точек, а среднее значение в виде вертикальной черты.
Значит, среднее арифметическое числового набора характеризует в целом положение этого набора на числовой прямой. [1]
3.1. Упражнения.
- Каким было производство пшеницы в 1996г., в 2000г.?
- В каком году производство пшеницы было:
А) наибольшим; б) наименьшим?
3.Совпадает ли производство пшеницы в среднем за 7 лет со значением в каком-нибудь году?
Предлагаем задачи для самостоятельного решения:
- Придумайте четыре таких числа, что их среднее арифметическое равно:
А) второму по величине числу; б) третьему по величине числу;
В) полусумме второго и третьего по величине из этих чисел.
2. В таблице 3 приведено число жителей шести крупнейших городов
Московской области в разные годы в тысячах человек. Города указаны в алфавитном порядке.
Таблица 3.Население шести крупнейших городов Московской области в разные годы, тыс. человек.
| Города | 1959 | 1970 | 1981 | 2002 |
| Коломна | 118 | 136 | 150 | 147 |
| Люберцы | 95 | 139 | 163 | 163 |
| Мытищи | 99 | 119 | 145 | 158 |
| Подольск | 129 | 169 | 205 | 190 |
| Химки | 47 | 85 | 121 | 136 |
| Электросталь | 97 | 123 | 143 | 146 |
А) Найдите среднее число жителей крупнейших городов Московской области в 1959г.
Б) Найдите среднее число жителей крупнейших городов Московской области в 1970г.
В) Найдите среднее число жителей крупнейших городов Московской области в 1981г.
Г) Найдите среднее число жителей крупнейших городов Московской области в 2002г.
Д) Сравните число жителей в данных городах в 1959г. и в 1970г. Верно ли, что число жителей возросло за эти годы?
Е) Сравните число жителей в данных городах в 1981г. и в 2002г. Можно ли заключить, что число жителей возросло за эти годы? Сравните среднее число жителей этих городов в 1981 и 2002гг. [1]
3.2. Исследование из серии «Школьная статистика»
Мини - задача
В школе открыты классы по некоторым образовательным направлениям.
Составьте упорядоченный набор чисел, вычислите среднее арифметическое, медиану, размах и моду.
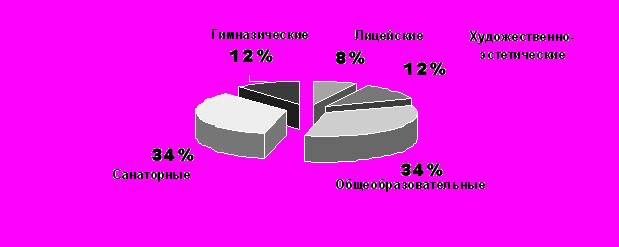
Выводы: Данные для нахождения статистических характеристик могут быть оформлены в виде диаграмм, а могут - в виде таблиц.
Социологическое исследование
по теме «Читательский интерес современного подростка»
Мы провели анкету среди учащихся 5-11 класса, взяв по одному классу в каждой параллели. Учащиеся выбирали те библиотеки, которые они посещают.
1. Нужны ли современным подросткам библиотеки?
-
Школьная библиотека
35%
Среднее арифметическое: (35+29+25+11):4= 50(%)
Моды нет
Размах: 35-11=24(%)
Медиана 27%
Общественная библиотека
29%
Интернет-библиотека
25%
Домашняя библиотека
11%
Выводы:
Медиана не совпадает со средним арифметическим. Однако медиана ближе к значениям 29% и 25% , значит, лучше даёт преставление о посещении библиотеки, как «средней», «типичной». Надо проверить это утверждение, поэтому поближе познакомимся с понятием медиана и рассмотрим некоторые примеры.
