Исследование по результатам решенных задач «Копилка методов и советов Мода Исследование по теме «Техника чтения школьников» Наибольшее и наименьшее значение. Размах
| Вид материала | Исследование |
- Исследование функций на монотонность и экстремумы. Построение графиков, 13.79kb.
- Лекция 15. Определённый интеграл, 71.1kb.
- Е. В. Чепин Московский инженерно-физический институт (государственный университет), 32.43kb.
- Исследование методов и методик развития математических способностей младших школьников, 724.06kb.
- Исследование электрофизических свойств сельскохозяйственных продуктов и материалов, 34.96kb.
- Исследование методов приема сигналов данных, 68.73kb.
- Л. В. Шипова Саратов, сгу им. Н. Г. Чернышевского Исследование, 107.95kb.
- «Исследование и сопоставительный анализ численных методов решения задач не линейного, 321.81kb.
- В. А. Каверина «Картины мира» школьников. Итоги исследования. Исследование, 82.72kb.
- Иванов Петр Алексеевич ввт-406 тудент группа т исследование, 71.44kb.
6.Наибольшее и наименьшее значение. Размах.
Иногда интересные не только средние значения или медианы, но и другие величины, связанные с наборами различных чисел.
Если мы хотим узнать, победил в прыжках в длине в соревнованиях класса, то выберем того, кто пробежал быстрее всех, т.е. показал наименьшее время.
Наибольшие и наименьшие значения часто интересуют нас в самых разных областях.
- Определение. Разность между наибольшим и наименьшим числом называется размахом набора числа.
Мы узнали, что размах показывает, насколько велико рассеивание значений в числовом наборе.
6.1. Исследовательская мини - задача из серии
«Школьная статистика»
Составьте упорядоченный набор чисел, вычислите среднее арифметическое, медиану, наибольшее и наименьшее значения, размах и моду, если учащиеся считают, что в учебе предпрофильная подготовка:
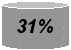
- Помогает значительно-31%

- Помогла, но не значительно-60%
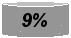
- Практически не помогла-9%
6.2.Упражнения.
- Найдите наибольшее и наименьшее значение, размах, среднее значение и медиану набора чисел;
а) 12, 7, 25, 3, 19, 15; б) 17, 19, 5, 41, 47, 13, 19.
2. В таблице 7 приведены данные о производстве зерновых в России в 1996-2002гг.
Таблица 1.
Производство зерна в России.
-
Показатель
1996
1997
1998
1999
2000
2001
2002
Производство зерновых, млн. т
69,3
88,6
47,9
54,7
65,5
85,2
86,6
Урожай зерновых, ц/га
14,9
17,8
12,9
14,4
15,6
19,4
19,6
Производство пшеницы, млн. т
34,9
44,3
27,0
31,0
34,5
47,0
57,7
По таблице 1 найдите наибольшее, значение и размах:
а) производство зерновых в 1996-2002 гг.;
б) производство пшеницы в 1996-2002 гг.;
в) урожайности зерновых в 1996-2002 гг. [1]
Из лекций наших выпускников:
Студент юридического факультета
При подсчете доходов россиян Правительственная (администрация) партия выберет среднее значение, а оппозиционная - значение медианы, так как для администрации выгодно использовать среднее значение, так как хочет показать доход россиян высоким, а оппозиционная - медиану, так как хочет показать реальные факты о доходах россиян.
Студент экономического факультета
Предположим, что шьется партия готовой одежды без снятия мерок. Для этого полезно знать средний размер группы людей, но важно знать и разброс их размеров. Зная вариацию можно рассчитать, как должны варьироваться изготовляемые размеры.
Студентка психологического факультета
В психологии меры центральной тенденции (среднее значение, медиана, мода) и меры вариативности ( размах, дисперсия, отклонения ) используются для обработки результатов исследования, тестов, для определения выборки и генеральной совокупности. Меры вариативности также называются мерами рассеивания и мерами изменчивости.
7. Отклонения
Попробуем узнать, как числа некоторого набора расположены по отношению к своему среднему арифметическому. Зная только размах, разность между наибольшим и наименьшим значением, мы не можем судить о том, как расположены числа в имеющемся наборе. Для примера возьмём набор 1, 6, 7, 9, 12. Вычислим среднее арифметическое: (1+6+7+9+12):5=7. Найдём отклонение каждого числа от среднего:
1 -7= - 6,
6 -7= - 1,
7 – 7 = 0,
9 – 7 = 2,
12 – 7 = 5.
Получился новый набор, который состоит из отклонений. Если число меньше среднего, то его отклонение отрицательного, если число больше среднего, то его отклонение положительно.
В одном случае – для числа 7, которое совпало со средним арифметическим, - отклонение равно нулю. По набору отклонений можно судить о том, насколько разнообразны числа в наборе.
Если отклонения малы, то числа в наборе расположены близко к среднему арифметическому. А если среди отклонений есть большие по модулю, то числа в наборе сильно разбросаны.
Для любого набора, если только не все числа в нём равны, часть отклонений будет положительно, а часть – отрицательна. При этом сумма всех отклонений равна 0. Убедимся в этом на нашем примере:
-6–1+0 +2+5=0
В этом состоит основное свойство отклонений: сумма отклонений чисел от среднего арифметического этих чисел равна нулю.
В этом пункте рассказывалось об отклонениях величины от среднего значения. Кроме того, мы узнали, что сумма всех отклонений в наборе от среднего равна нулю. [1]
8. Дисперсия.
Наиболее полной характеристикой разброса набора чисел является набор их отклонений от среднего арифметического. Но когда набор чисел велик, рассматривать набор отклонений практически неудобно. Нужно описать разнообразие чисел в наборе одной характеристикой, одним числом.
Размах - слишком грубая мера разброса чисел в наборе, поскольку учитывает только два из них – наибольшее и наименьшее. Можно попробовать взять «среднее отклонение». Но сумма отклонений всегда равна нулю, поэтому среднее арифметическое отклонений тоже равно нулю и его нельзя использовать как меру разброса.
Чтобы судить о разбросе, принято складывать не сами отклонения, а их квадраты. Квадраты отклонений неотрицательны, поэтому сумма квадратов отклонений зависит только от абсолютных величин отклонений, а не от их знаков.
Чем больше отклонения чисел от среднего арифметического, тем больше будет сумма квадратов отклонений. Для того чтобы мера разброса чисел не зависела от их количества в наборе, в качестве такой меры берут среднее арифметическое квадратов отклонений. Эту величину называют дисперсией.
- Определение. Среднее арифметическое квадратов отклонений от среднего значения называется в статистике дисперсией набора чисел.
8.1. Примеры и упражнения
Пример 1.
Покажем на простом примере, как дисперсия характеризует разброс наблюдений. Возьмём два набора чисел 1, 2, 3 и 0, 2, 4. Среднее арифметическое значение обоих наборов равно 2. Для обоих наборов вычислим отклонения и квадраты отклонений, и все данные занесём в таблицу.
| 1-й набор | Отклонение от среднего | Квадрат отклонения | 2-й набор | Отклонение от среднего | Квадрат отклонения |
| 1 | -1 | 1 | 0 | -2 | 4 |
| 2 | 0 | 0 | 2 | 0 | 0 |
| 3 | 1 | 1 | 4 | 2 | 4 |
Дисперсия первого набора: (1+0+1)=
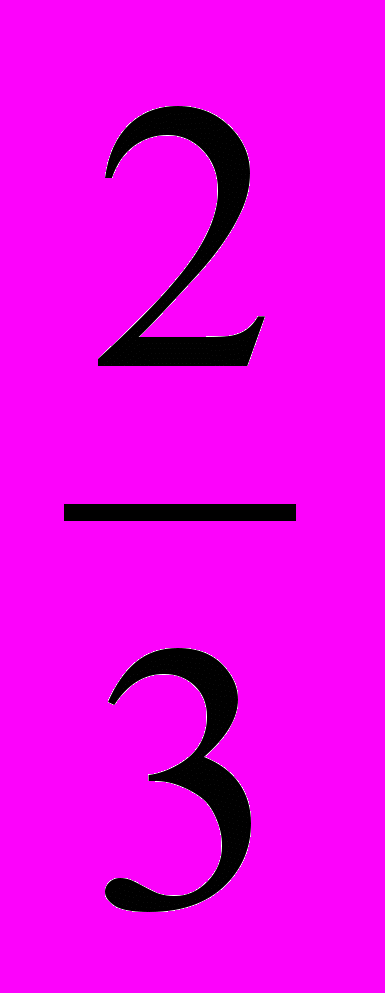
Дисперсия второго набора: (4+0+4)=

Числа в первом наборе расположены более кучно – ближе друг к другу и к своему среднему,- чем числа во втором наборе. Поэтому дисперсия первого набора получилась меньше, чем второго.
Упражнения.
- Даны два набора чисел. Отметьте их на числовой прямой. Вычислите дисперсию каждого из наборов. Дисперсия, какого набора больше?
а) 2, 3, 7 и 1, 2, 3; б)2, 3, 4, 7 и 1, 5, 6, 8.
- Даны два набора чисел. Отметьте их на числовой прямой. Вычислите дисперсию каждого из этих наборов. Сравните дисперсии:
а) 2, 3, 4 и 6, 7, 8; б) 3, 5, 7, 9 и 12, 14, 16, 18. [1]
8.2. Исследовательский социологический мониторинг
Проведены в последние годы два массовых исследования старшеклассников: международное исследование PISA (Program for International Student Assessment, 2003) и Анализ результатов ЕГЭ, 2002-2004гг. Оба исследования позволяют выделить сформированность основных навыков грамотного чтения и грамотного читателя у старших школьников.
Выделим некоторые из них (в скобках указан процент школьников, имеющих соответствующий навык по PISA), далее в нашей школе:
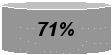
- умение выделить главную мысль текста (71%),
(69 - 71%);
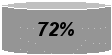
- умение находить заданную информацию в тексте (77 %),
(73 - 78%);
- понимание связности и последовательности событий (63%),
(81-90%).
Задача №1: Составьте два набора чисел. Вычислите отклонения от среднего и их квадраты.
| Исследования PISA 2003 | Школьные исследования |
|  нет снижения нет сниженияна том же уровне 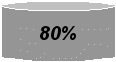 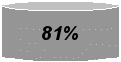 выше выше |
9. Статистика вокруг нас
9.1. ссылка скрыта [2]
Расчет средней заработной платы
Говоря о средней зарплате, среднем доходе и других средних для конкретных экономических данных, подразумевают под "средним" среднее арифметическое. Такая традиция может приводить к ошибочным выводам.
Покажем это на примере расчета средней заработной платы (среднего дохода) работников условного предприятия (табл.1).
| № п/п | Категория работников | Число работников | Заработная плата | Суммарные доходы |
| 1 | Низкоквалифицированные рабочие | 40 | 100 | 4000 |
| 2 | Высококвалифицированные рабочие | 30 | 200 | 6000 |
| 3 | Инженеры и служащие | 25 | 300 | 7500 |
| 4 | Менеджеры | 4 | 1000 | 4000 |
| 5 | Генеральный директор (Владелец) | 1 | 18500 | 18500 |
| 6 | Всего | 100 | | 40000 |
Первые три строки в табл.1 вряд ли требуют пояснений. Менеджеры - это директора по направлениям, а именно, по производству (главный инженер), по финансам, по маркетингу и сбыту, по персоналу (по кадрам). Владелец сам руководит предприятием в качестве генерального директора. В столбце "заработная плата" указаны доходы одного работника соответствующей категории, а в столбце "суммарные доходы" - доходы всех работников соответствующей категории.
Фонд оплаты труда составляет 40000 единиц, работников всего 100, следовательно, средняя заработная плата составляет 40000/100 = 400 единиц. Однако эта средняя арифметическая величина явно не соответствует интуитивному представлению о "средней зарплате". Из 100 работников лишь 5 имеют заработную плату, ее превышающую, а зарплата остальных 95 существенно меньше средней арифметической. Причина очевидна - заработная плата одного человека - генерального директора - превышает заработную плату 95 работников - низкоквалифицированных и высококвалифицированных рабочих, инженеров и служащих.
Ситуация напоминает описанную в известном рассказе о больнице, в которой 10 больных, из них у 9 температура 40 °С, а один уже отмучился, лежи в морге с температурой 0 °С. Между тем средняя температура по больнице равна 36 °С - лучше не бывает!
Сказанное показывает, что среднее арифметическое можно использовать лишь для достаточно однородных совокупностей (без больших выбросов в ту или иную сторону).
А какие средние использовать для описания заработной платы? Вполне естественно использовать медиану. Для данных табл.1 медиана - среднее арифметическое 50-го и 51-го работника, если их заработные платы расположены в порядке неубывания.
Сначала идут зарплаты 40 низкоквалифицированных рабочих, а затем - с 41-го до 70-го работника - заработные платы высококвалифицированных рабочих. Следовательно, медиана попадает именно на них и равна 200. У 50-ти работников заработная плата не превосходит 200, и у 50-ти - не менее 200, поэтому медиана показывает "центр", около которого группируется основная масса исследуемых величин.
Еще одна средняя величина - мода, наиболее часто встречающееся значение. В рассматриваемом случае это заработная плата низкоквалифицируемых рабочих, т.е. 100. Таким образом, для описания зарплаты имеем три средние величины - моду (100 единиц),
медиану (200 единиц)
и среднее арифметическое (400 единиц).
Для наблюдающихся в реальной жизни распределений доходов и заработной платы справедлива та же закономерность: мода меньше медианы, а медиана меньше среднего арифметического. [2]
ссылка скрыта

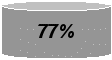 мение находить заданную информацию в тесте
мение находить заданную информацию в тесте  онимание связности и последовательности событий
онимание связности и последовательности событий