Исследование по результатам решенных задач «Копилка методов и советов Мода Исследование по теме «Техника чтения школьников» Наибольшее и наименьшее значение. Размах

Вид материала

Линейный тренд температуры
11. Список литературы.
12.1 Словарь для тех, кто хочет знать больше
Среднее значение или арифметическое среднее
Среднее значение
Наибольшее и наименьшее значения функции

Подобный материал:

1 2 3 4

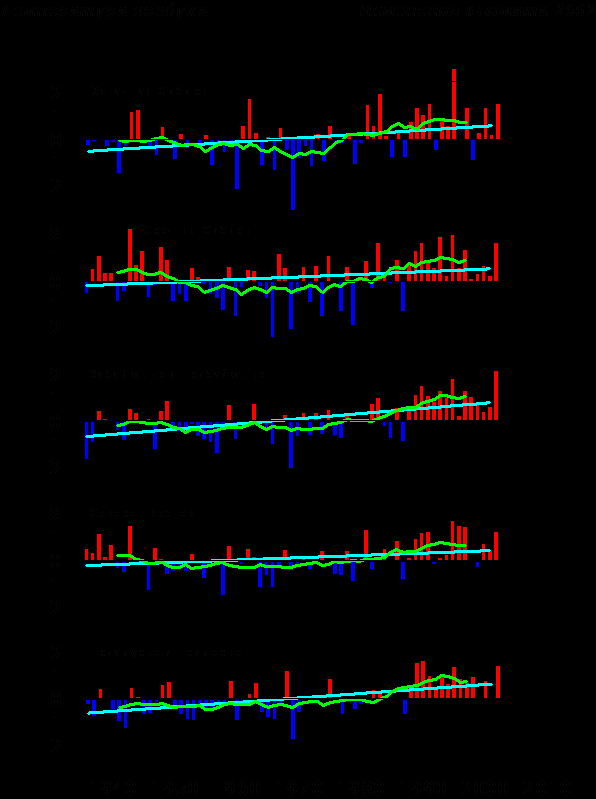
Линейный тренд температуры

Средняя по регионам РФ аномалия среднегодовой температуры воздуха

(отклонение от средней температуры базового периода)

Жирная кривая показывает 11-летнее скользящее среднее.

Показан линейный тренд температуры.

ссылка скрыта

9.3. Анализ отклонения прибыли

При анализе валовой прибыли изучаются причины, вызывающие ее изменение, соответствующие факторы отражаются в отчете и позволяют принять корректирующие меры.

Причины отклонения прибыли:

Изменения в цене продажи и в затратах на единицу продукции.
Изменения в объеме продаж.
Изменения в ассортименте продаж.

Данные для согласования фактических операций с бюджетными значениями получаются на основе анализа изменений между фактическими и бюджетными операциями за текущий год, между фактическими операциями предыдущего года и соответствующими операциями текущего года. Могут рассматриваться изменения в валовой прибыли всей компании или выбранной продуктовой линии.
ссылка скрыта

9.4. Резюме:

Оценка «здоровья здорового человека»

Показатели ВРС у здоровых людей. Оценка «здоровья здорового человека».

Суммируются собственные наблюдения и результаты ряда работ, которые позволяют следующим образом сформулировать основные параметры ВРС, характерные для здорового человека. В таблицах 5-2 - 5-4 приведены показатели математического анализа ВРС, полученные при обследовании практически здоровых лиц молодого возраста. Учитывая, что распределение показателей ВРС отличается от нормального, все данные представлены в виде медианы и интерквантильного размаха. Интерквантильный размах указывается в виде 25% и 75% перцентилей.
ссылка скрыта

10. Заключение

Работая над темой реферата,

«Статистические характеристики на уроках алгебры», мы

изучили учебные пособия;
познакомились с материалами по нашей теме в Интернете, выполнили их отбор, проанализировали и обобщили;
заключили, что статистика - огромное поле смысложизненных ориентиров;
научились решать и создавать статистические задачи,
провели социологические исследования в школе;
познакомились с технологией исследования в математике, оформлять выводы и результаты;
научились наглядно представлять результаты исследования в виде таблиц, диаграмм;
провели презентацию реферата Статистические характеристики на уроке алгебры» на родительском собрании «Математика для родителей»;
создали фото - вернисаж с уроков алгебры по изучению статистических характеристик, выполненный на компьютере;
познакомили учащихся нашего класса с результатами исследования в статистике школы;
подготовили компьютерную презентацию реферата, сделанную в редакторе Microsoft Power Point;
выявили удивительное: неожиданно многое в жизни человека описывается статистическими характеристиками, да как интересно;
поняли, что изучать статистику необходимо и это нам пригодиться при обучении в вузе, а так же в выборе профессии;
сделали вывод из приложений и словаря, которые мы посмотрели в сети Интернет, что статистика тесно связана с непростыми математическими расчетами, которые нам еще предстоит преодолеть,
думаем, что знания, полученные при работе над данной темой, пригодятся нам в дальнейшей учебе и в жизни.
научились работать в команде, распределять обязанности, работать в сотрудничестве.

Наше математическое исследование – это путешествие в глубины неизвестного и интересного в статистике. Задавая вопросы один за другим, главное не останавливаться, мы определяли направление пути исследования. Путей было много, направление выбирали сами. Мы открыли тайны большой и интересной науки статистики и математики.

Исследование наше не заканчивается. Возникают новые вопросы, есть желание вновь открывать научные сокровища и глубины математики.

11. Список литературы.

1) Алгебра : учеб. для 7 кл. общеобразоват. учреждений / (Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова); под ред. С. А. Теляковского. – 16-е изд. – М. : Просвещение,2007. – 240 с. : ил. – ISBN 978-5-09-016309-5

2) Теория вероятности и статистика / Ю. Н. Тюрин, А. А. Макаров, И. Р. Высоцкий, И.В. Ященко. – М.: МЦНМО: АО «Московские учебники», 2004.-256с., ил. ISBN 5-94057-161-1

3) ссылка скрыта. ссылка скрыта. Учебник. М.: Издательство "Экзамен", 2002. Глава 3. Основы теории измерений 3.2. Инвариантные алгоритмы и средние величины

4) ссылка скрыта [Электронный ресурс] / Медиана –16.02.2009 – Режим доступа : ссылка скрыта

5) Википедия – свободная энциклопедия [Электронный ресурс] /Медиана– Электрон. дан. –16.02.2009. – Режим доступа: ссылка скрыта

6)Информационно-развлекательная социальная сеть ссылка скрыта

7) История возникновения медианы ссылка скрыта

8) Наибольшее и наименьшее значения функции ссылка скрыта

9) Словари и энциклопедии по Академики ссылка скрыта

10)Словарь. Яндекс. Размах. ссылка скрыта

11) Википедия – свободная энциклопедия [Электронный ресурс] Среднее значение ссылка скрыта

12)Викизнание ссылка скрыта

12. Приложение

12.1 Словарь для тех, кто хочет знать больше

Взгляд в свое будущее

Среднее значение — числовая характеристика множества чисел или функций; — некоторое число, заключённое между наименьшим и наибольшим из их значений. (ссылка скрыта)

Среднее значение или арифметическое среднее наиболее широко используется в статистике. Это одно значение может использоваться для представления некоторого набора данных. В этом случае среднее значение можно назвать "центром тяжести" этого набора. Среднее значение вычисляется следующим образом: складываются все значения выборки и результат делится на общее число значений. Например, сумма набора значений. (ссылка скрыта)

Среднее значение — числовая характеристика множества чисел или числовых функций; — некоторое число, заключенное между наименьшим и наибольшим из их значений; а также множественно – значная характеристика совокупности множеств или сет-функций; — некоторое множество, содержащее пересечение и содержащееся в объединении этих множеств.

(ссылка скрыта)

Медиана— в статистике - значение варьирующего признака, которое делит ряд распределения на две равные части по объему частот или частостей. Сумма абсолютных величин линейных отклонений от медианы минимальна.…

ссылка скрыта

Медиана - (термин был впервые введен Гальтоном, 1882) выборки - это значение, которое разбивает выборку на две равные части (при ранжировании). Половина наблюдений лежит ниже медианы, и половина наблюдений лежит выше медианы. Если число наблюдений в выборке нечетно, то медиана вычисляется как среднее двух средних значений.

МЕДИАНА - один из показателей центра распределения для порядковых и количественных переменных обозначается Ме. Представляет собой значение переменной, которое делит выборку пополам таким образом, чтобы для 50% объектов из выборки значения переменной не превосходили Ме, а для других 50% объектов - были не меньше, чем Ме.

Для небольшой выборки М. может быть найдена как середина ряда упорядоченных значений переменной (указываются все повторяющиеся значения). Например, в ряду из 9 значений 27 29 30 30 32 37 46 50 52 М. будет число 32, расположенное в центре ряда (Ме = 32).

Для выборки значительного размера М. можно найти как значение хi, соответствующее накопленной частоте Fi = 50% (см. Распределение частот). Если переменная является дискретной и ее значения повторяются, М. может быть найдена только приблизительно, по значению накопленной частоты, наиболее близкому к 50%. Например, при объеме выборки n = 120 М. будет соответствовать накопленная частота Fi = n/2 = 60. В приведенном ниже распределении наиболее близким к 60 значением накопленной частоты является F2 = 45, поэтому М. в данном случае будет соответствующее ей значение x2 = 2. Таким образом, Me ≈ 2 (балла).

Наибольшее и наименьшее значения функции - понятия математического анализа. Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке функция не имеет большего (меньшего) значения. (ссылка скрыта)

Наибольшее и наименьшее значения функции, понятия математического анализа. Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке множества функция не имеет большего (меньшего) значения. Н. и н. з. ф. по сравнению с её значениями во всех достаточно близких точках называются экстремумами (соответственно максимумами и минимумами) функции. Н. и н. з. ф., заданной на отрезке, могут достигаться либо в точках, где производная равна нулю, либо в точках, где она не существует, либо на концах отрезка. Непрерывная функция, заданная на отрезке, обязательно достигает на нём наибольшего и наименьшего значений; если же непрерывную функцию рассматривать на интервале (т. е. отрезке с исключенными концами), то среди её значений на этом интервале может не оказаться наибольшего или наименьшего. Например, функция у = x, заданная на отрезке [0; 1], достигает наибольшего и наименьшего значений соответственно при x = 1 и x = 0 (т. е. на концах отрезка); если же рассматривать эту функцию на интервале (0; 1), то среди её значений на этом интервале нет ни наибольшего, ни наименьшего, так как для каждого x0 всегда найдётся точка этого интервала, лежащая правее (левее) x0, и такая, что значение функции в этой точке будет больше (соответственно меньше), чем в точке x0. Аналогичные утверждения справедливы для функций многих переменных. (ссылка скрыта)

Дисперсия

(от лат. dispersio — рассеяние), в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистическом понимании Д.

есть среднее арифметическое из квадратов отклонений величин xi от их среднего арифметического

Blog