Введение в дескриптивную теорию множеств

Вид материала

Документы

Содержание Aоперация. Суслинские множества. Результат A

Подобный материал:

• Джон Р. Хикс. "Стоимость и капитал", 4314.44kb.
• Введение в общую топологию и топологическую алгебру, 25.85kb.
• Алгебра высказываний, 83.28kb.
• Критерии и методы оценок использования информационных систем и технологий dorokhov, 125.26kb.
• А. В. Корицкий введение в теорию человеческого капитала учебное пособие, 1340.03kb.
• Г. В. Мелихов миф. Идентичность. Знание: введение в теорию социально-антропологических, 741.74kb.
• Ответы на экзаменационные вопросы интернет-курсов интуит (intuit) : Введение в теорию, 197.01kb.
• Анализ и планирование трудовых показателей Аудит и контроллинг персонала Введение, 12.45kb.
• Календарный план учебных занятий по обязательной дисциплине «Дискретная математика, 109.62kb.
• Государственный университет высшая школа экономики л. Л. Любимов введение в экономическую, 3625.38kb.

ВВЕДЕНИЕ В ДЕСКРИПТИВНУЮ ТЕОРИЮ МНОЖЕСТВ

проф. В.И. Пономарев

1 год, 2-5 курс

1. Теоретико-множественное введение. Счетные и несчетные множества. Частичный, линейный и полный порядок. Континуум-проблема. Аксиома выбора, принцип максимального элемента и принцип полной упорядоченности.

2. 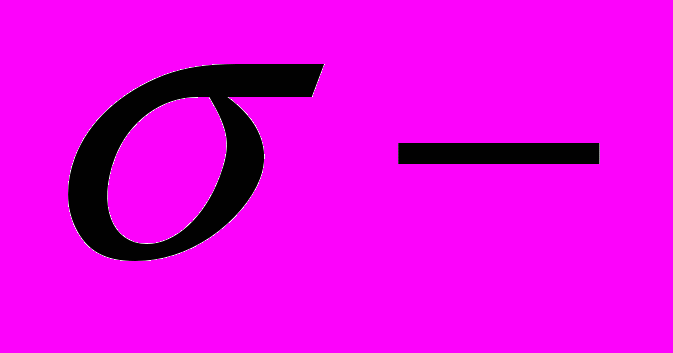кольца и 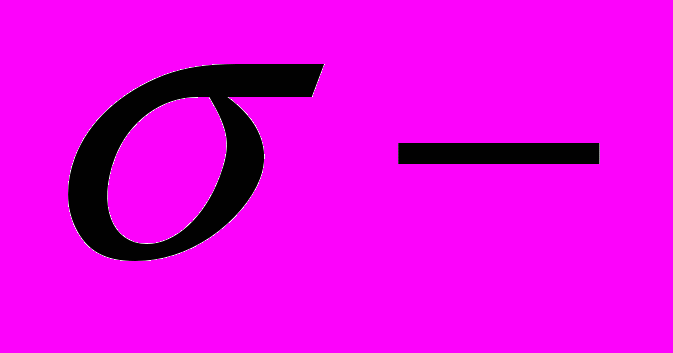алгебры подмножеств данного множества. Борелевские системы. Операции над множествами. 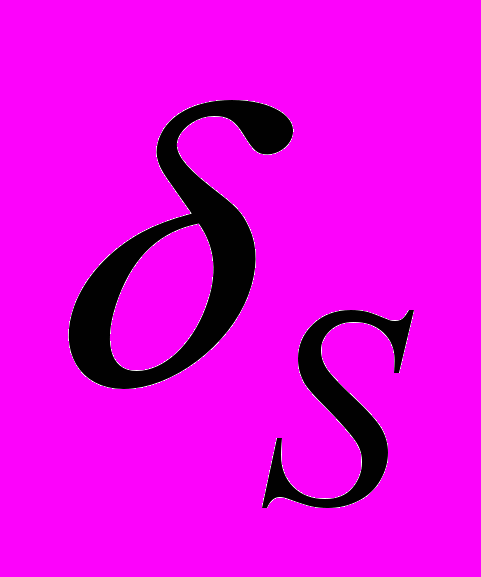операция. Aоперация. Суслинские множества. Результат Aоперации над суслинскими множествами – суслинское множество.

3. Топология. Непрерывные и топологические отображения. Топология метрических пространств. Полная метрика. Компактность. Свойство Бэра. Множества 1-й и 2-й категории. Пространства 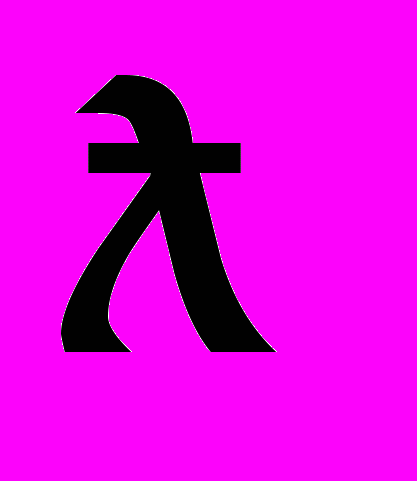рациональных чисел и пространство иррациональных чисел. Паракомпактность метризуемых пространств.

4. Топологическая характеристика рациональных и иррациональных чисел. Пространства Бэра веса . Пространство гомеоморфно .

5. Абсолютные 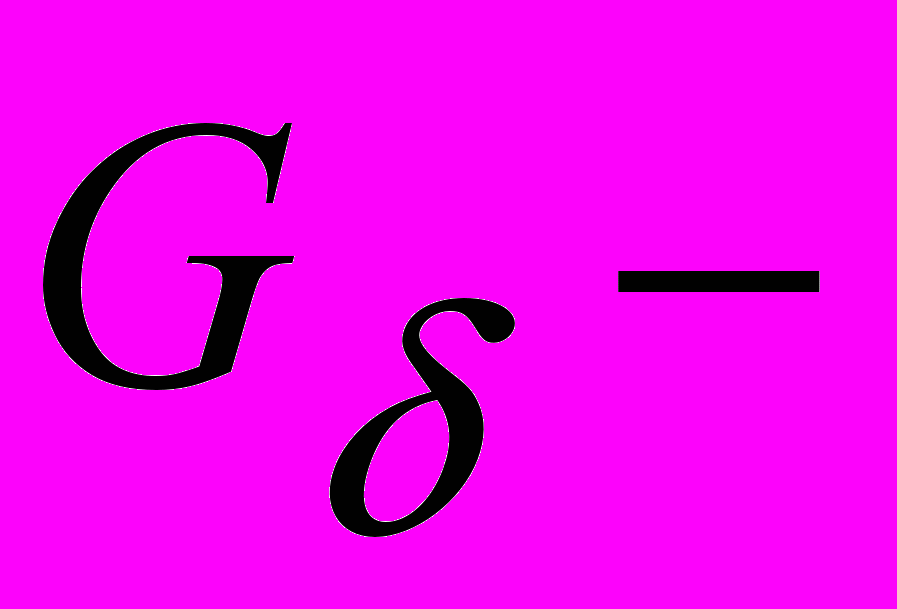множества в классе метризуемых пространств. Характеристика абсолютных 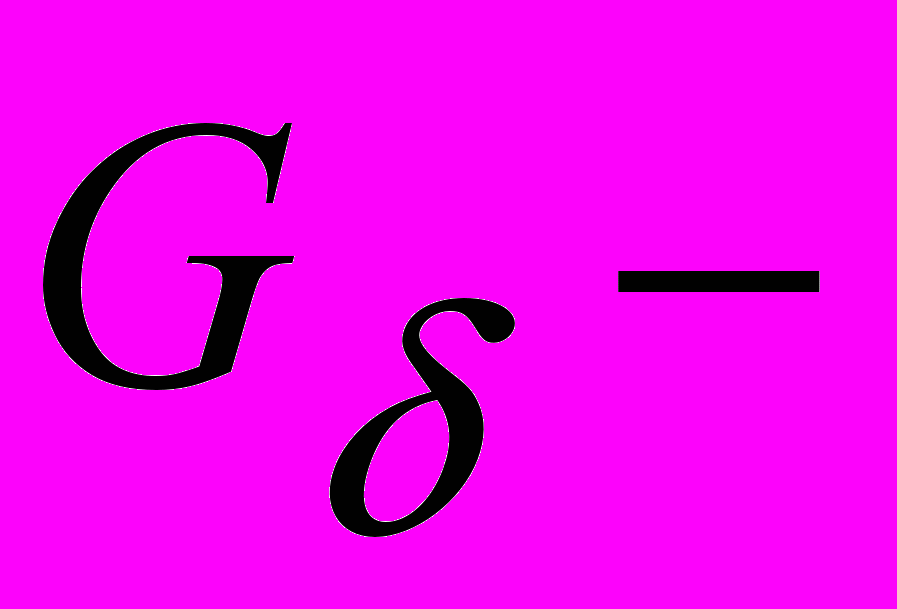множеств (теорема Александрова-Хаусдорфа и теорема Чеха).

6. Абсолютные 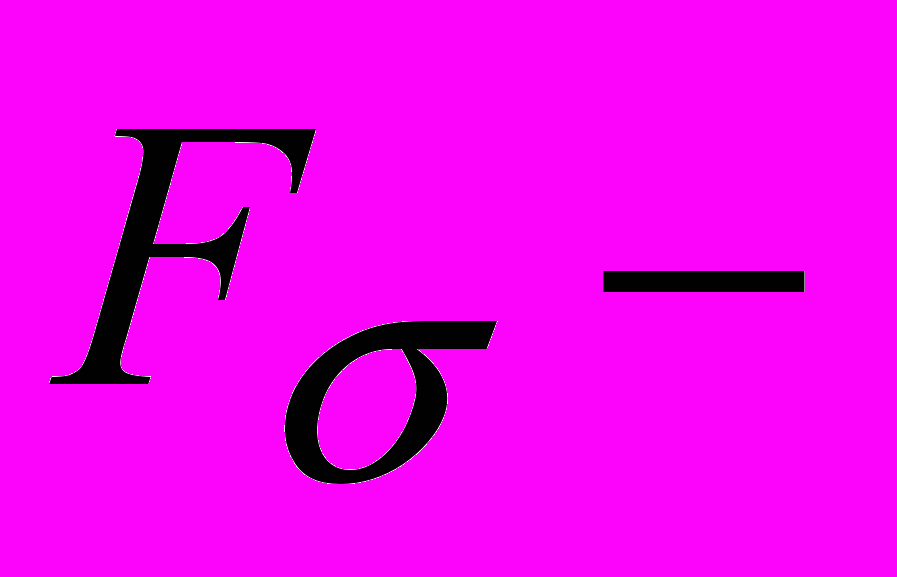множества в классе метризуемых пространств со счетной базой и в классе любых метризуемых пространств (теорема А. Стоуна).

7. Борелевские и суслинские множества в классе метризуемых пространств со счетной базой. Торема Александрова-Хаусдорфа о мощности Aмножеств. Анализ этого доказательства. Теорема А. Елькина.

8. Теорема Суслина о существовании A-множества, не являющегося борелевским.

9. Критерии для борелевских множеств Суслина и Лузина.

10. Непрерывные образы борелевских и суслинских множеств. Каждое абсолютное суслинское множество – непрерывный образ , а каждое абсолютно борелевское множество взаимно-однозначный непрерывный образ замкнутого в множества.

11. Теорема М. Лаврентьева. Топологическая инвариантность классов множеств.

12. Борелевская классификация борелевских множеств. Непустота класов.

13. Теорема К. Куратовского о борелевском изоморфизме несчетных абсолютно борелевских (в классе сепарабельных метризуемых пространств).

14. Теоремы редукции и отделимости. Теорема П. Новикова об отделимости.

15. Теорема П. Новикова и Сент-Раймонда о борелевском сечении.

16. Абсолютные как образы при открытом отображении и как образы при замкнутом отображении.

17. Две теоремы В. Гуревича. Пространство 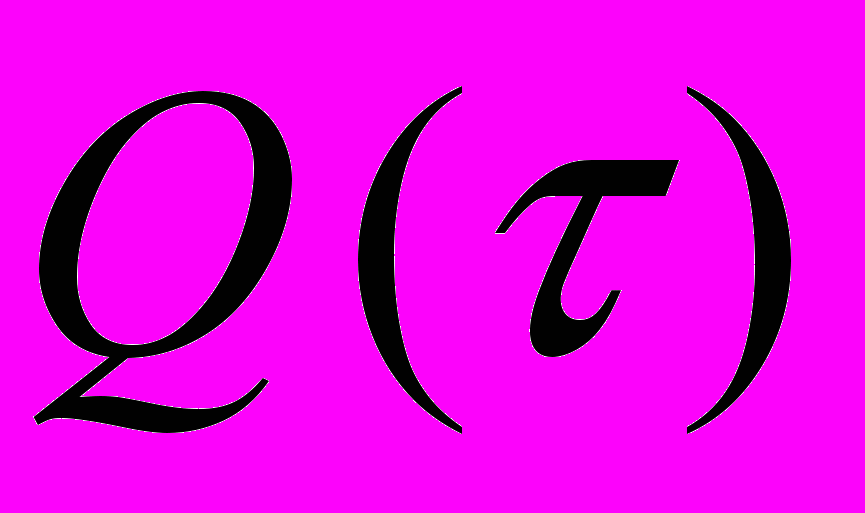и его топологическая характеристика. Теоремы С. Медведева как обобщения теорем Гуревича на несепарабельные метризуемые прострнаства.

18. Элементы дескриптивной теории множеств в неметризуемом случае. 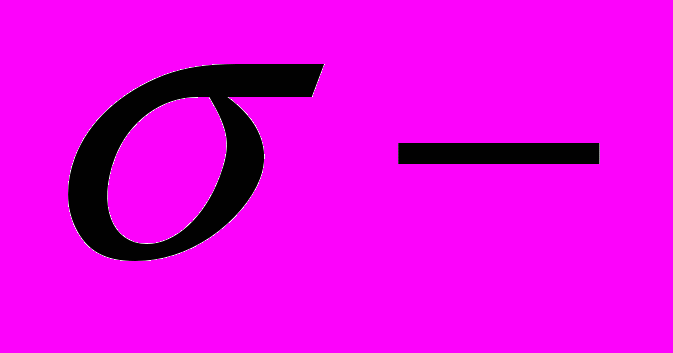алгебра бэровских множеств. Условие совпадения 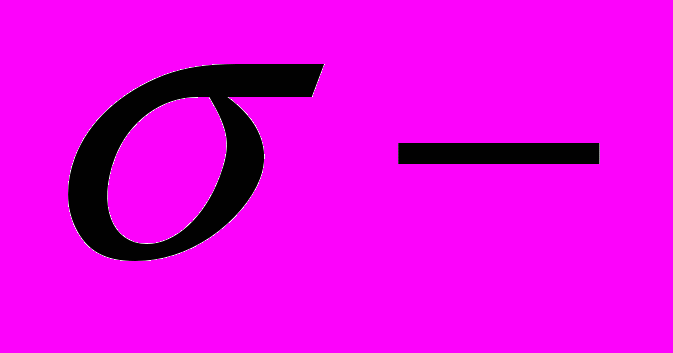алгебры борелевских множеств и 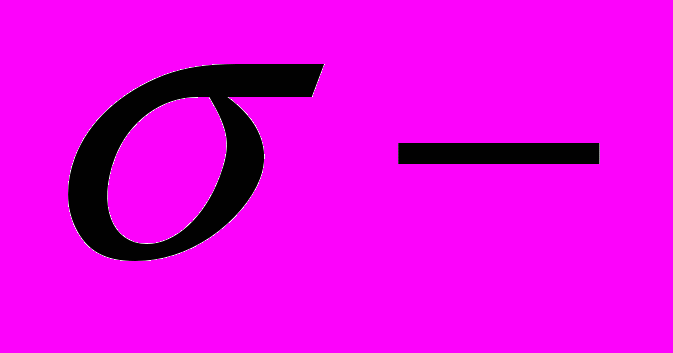алгебры бэровских множеств. Пространства, являющиеся бэровскими множествами в своем бикомпактном расширении.

19. Аналитические, K-аналитические и аналитические по Чеху пространства.

20. Разреженность и неразреженность в разных смыслах и связь этих понятий с проблемой совершенного ядра у A-множеств в полных по Чеху пространствах.