Алгебра высказываний
| Вид материала | Документы |
СодержаниеИНВЕРСИЯ (отрицание) ЭКВИВАЛЕНЦИЯ (равнозначность) Логические операции имеют следующий приоритет Алгоритм определения набора входных переменных |
- Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.
- Алгебра логики. Определение формы сложных высказываний, построение таблиц истинности, 132.48kb.
- Курсовая работа по информатике на тему: «применение алгебры высказываний в информатике», 221.48kb.
- Лекция Логические основы компьютеров , 369.25kb.
- «алгебра высказываний», 30.82kb.
- Алгебра логики высказываний, 428.51kb.
- Методические рекомендации по использованию учебных пособий «Алгебра и математический, 181.08kb.
- Тема 1-2 курс, 31.03kb.
- Программа курса «Математическая логика и теория алгоритмов», 37.76kb.
- Программа курса лекций по математике для учащихся 10-11 «Е» класса гимназии №1 Лектор, 84.04kb.
Алгебра высказываний
| Логическая операция | Обозначения | Таблица истинности | Диаграмма Эйлера-Венна | |||||||||||||||||
| в естественном языке | в алгебре высказываний обозначение | в языках программирования обозначение | ||||||||||||||||||
| КОНЪЮНКЦИЯ (логическое умножение): - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны. | и | &, Λ | And |
| 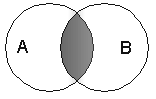 В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам. В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам. | |||||||||||||||
| ДИЗЪЮНКЦИЯ (логическое сложение) - это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно. | или | | Or |
| 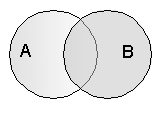 В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В. В алгебре множеств дизъюнкции соответствует операция объединения множеств, т.е. множеству получившемуся в результате сложения множеств А и В соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В. | |||||||||||||||
| ИНВЕРСИЯ (отрицание): - это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается. | неверно, что... и частице не; |  , ¬ , ¬ | Not; |
| 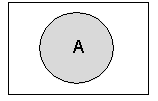 В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества А соответствует множество  , дополняющее его до универсального множества. , дополняющее его до универсального множества. | |||||||||||||||
| ИМПЛИКАЦИЯ (логическое следование): -это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. | если ..., то ...; | . | |
| | |||||||||||||||
| ЭКВИВАЛЕНЦИЯ (равнозначность): – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. | тогда и только тогда; в том и только в том случае; | , ~ , ≡. | |
| | |||||||||||||||
Логические операции имеют следующий приоритет:
действия в скобках, инверсия, &, , , .
Алгоритм построения таблицы истинности
- подсчитать количество переменных n в логическом выражении;
- определить число строк в таблице, которое равно m= 2n;
- подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;
- ввести название столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;
- заполнить столбцы входных переменных наборами значений;
- провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п,4 последовательностью.
Алгоритм определения набора входных переменных
- разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями, а нижнюю единицами;
- разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц, начиная с группы нулей;
- продолжит деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группа нулей и единиц не будет состоять из одного символа.
Пример
Для формулы A&(B
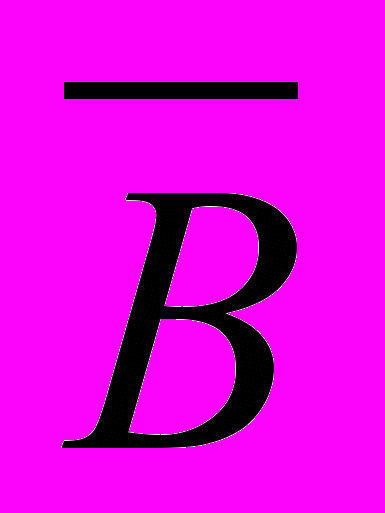 &
&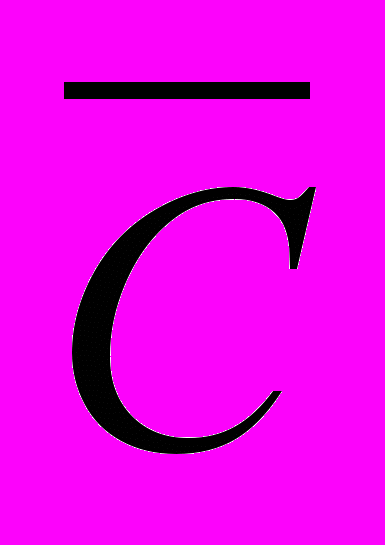 ) построить таблицу истинности.
) построить таблицу истинности. Количество логических переменных 3, следовательно, количество строк - 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов - 3 + 5 = 8.
| A | B | C | 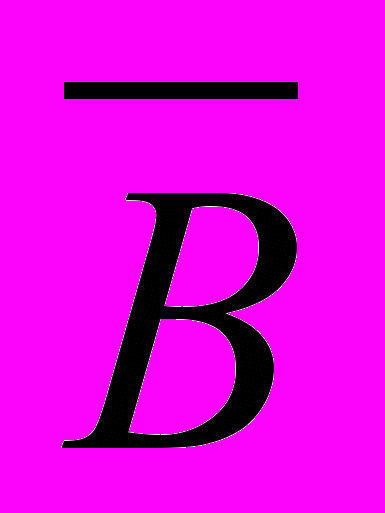 | 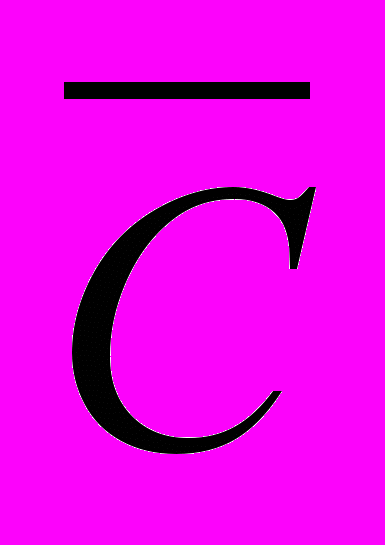 | 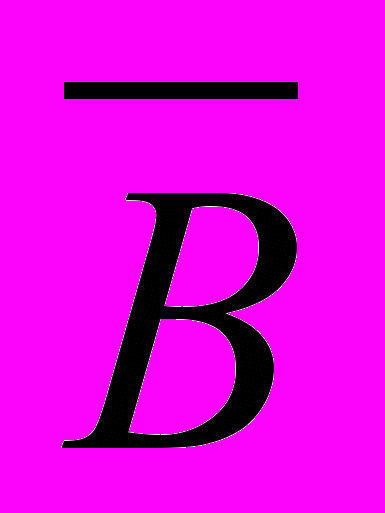 & & 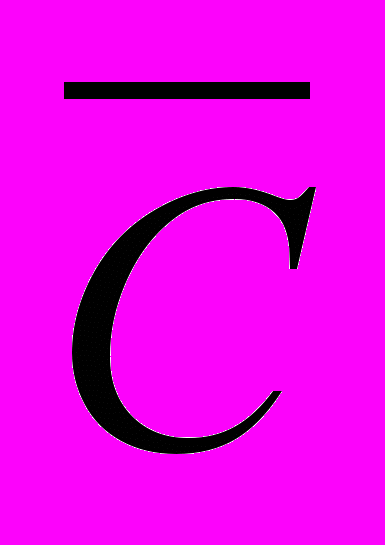 | B 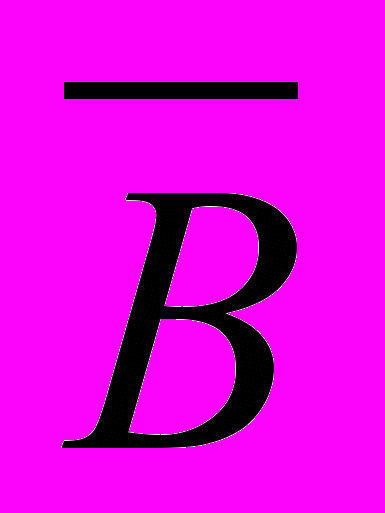 & &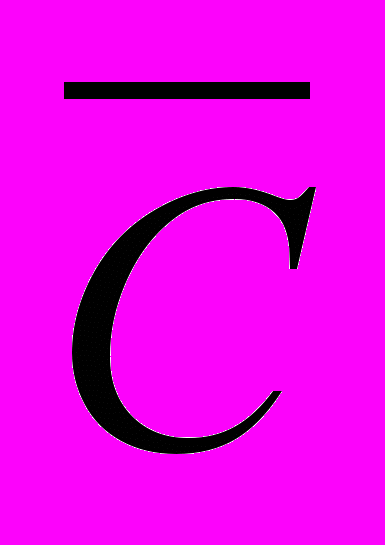 | A&(B 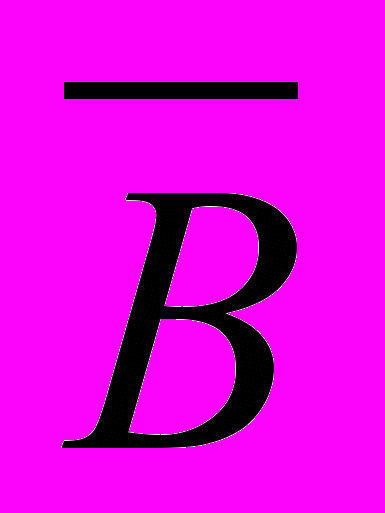 & &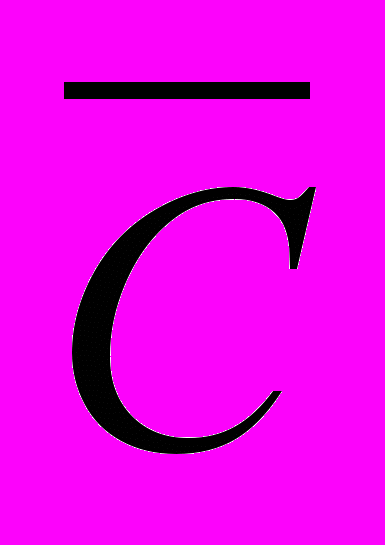 ) ) |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |

