Программа по теоретическим основам начального курса математики
| Вид материала | Программа |
- Вопросы к экзамену по Теоретическим основам начального курса математики, 18.18kb.
- Сборник задач по „теоретическим основам электротехники М.: Высшая школа, 2000. Сборник, 164.59kb.
- Краткий курс лекций учебной дисциплины «Методика преподавания начального курса математики», 631.78kb.
- Руководство курсовыми работами по «теоретическим основам поисков и разведки нефти, 31.49kb.
- М. К. Аммосова Институт математики и информатики Кафедра методики преподавания математики, 112.18kb.
- Методика преподавания математики рабочая программа Программа лекционного курса Планы, 266.77kb.
- Методика преподавания математики рабочая программа Программа лекционного курса Планы, 384.99kb.
- Методика преподавания начального курса математики История Москвы, 1230.51kb.
- Программа вступительного экзамена по приему в магистратуру по специальности 6М010200-, 426.27kb.
- Программа курса опирается на знания, полученные студентами-психологами при изучении, 253.47kb.
Рабочая модульная программа
по теоретическим основам начального курса математики
Выписка из стандарта об обязательном содержании дисциплинЫ.
Множества и операции над ними; соответствие ; отношения и их свойства; особенности математических понятий; целые неотрицательные числа; теоретико- множественный подход к построению множества целых неотрицательных чисел; смысл натурального числа и действий над числами , являющимися результатами измерения величины; делимость целых неотрицательных чисел;; расширение понятий о числе; положительные рациональные числа; система счисления; действительные числа; уравнения и неравенства с одной переменной; числовые функции; прямая и обратная пропорциональности и их свойства; величины и их измерение.
Пояснительная записка
Курс теоретических основ математики должен обеспечить единство теории и практики обучения, дать необходимую математическую подготовку для успешного обучения младших школьников.
Основные задачи курса:
1.Дать студентам необходимые теоретические знания, которые являются основой построения начального курса математики, сформировать умения необходимые для овладения этим содержанием.
2.Раскрыть мировоззренческое значение математики, раскрыть роль и место математики в изучении окружающего мира.
3.Способствовать развитию математического мышления студентов.
Основными базисными понятиями курса являются целое неотрицательное число и операции над числами, величины и их измерение. Натуральное число должно быть рассмотрено с различных позиций – порядковое, числительное, мера величины, компонент вычислений. Для формирования этих понятий необходимо, чтобы студенты освоили некоторые общие понятия математики, обобщили и расширили ранее известные. К таким понятиям относятся понятия множества, соответствия, функции, элементов логики и др. Необходимо знакомить студентов с идеей расширения множества натуральных чисел до множества рациональных и действительных чисел.
В содержании курса условно можно выделить следующие разделы:
1. Общие понятия.
2. Целые неотрицательные числа.
3. Уравнения и неравенства.
4. Расширение понятия натурального числа.
5. Величины и их измерение.
6. Элементы геометрии.
Для изучения курса предлагается следующая система модулей:
- Входной модуль;
- Базовые модули N 1-7;
- Дополнительный модуль;
- Итоговый модуль.
Содержание теоретического курса
Расчет рейтинга
| № модуля | Название модуля | Стоимость модуля (в %) | min (баллы) | max (баллы) |
| 0 | Входной | 2 | 0 | 20 |
| 1 | Базовый модуль № 1. Множества и операции над ними. | 10 | 60 | 100 |
| 2 | Базовый модуль № 2. Отношения. Соответствия. Функции. | 10 | 60 | 100 |
| 3 | Базовый модуль № 3. Целые неотрицательные числа. | 20 | 125 | 200 |
| 4 | Базовый модуль № 4. Делимость натуральных чисел. | 10 | 60 | 100 |
| 5 | Базовый модуль № 5. Расширение множества натуральных чисел. | 15 | 100 | 150 |
| 6 | Базовый модуль № 6. Элементы алгебры. | 10 | 60 | 100 |
| 7 | Базовый модуль № 7. Геометрические фигуры и величины. | 10 | 60 | 100 |
| 8 | Дополнительный модуль | 10 | 0 | 100 |
| 9 | Итоговый модуль | 3 | 15 | 30 |
Рейтинг по дисциплине – это интегральная оценка результатов всех видов учебной деятельности студентов по дисциплине включающей: -входной рейтинг,
-рейтинг- контроль текущей работы,
-промежуточный рейтинг- контроль,
-итоговый рейтинг- контроль,
-добор баллов.
Итоговая оценка: «3» - 540-720 баллов.
«4» - 721-860 баллов.
«5» - 861-1000 баллов.
Студенты, желающие повысить свой рейтинг могут это сделать, выполнив задания из дополнительного модуля.
Входной модуль
| Форма работы | min | max |
| Контрольная работа | 12 | 20 |
Примерное содержание контрольной работы.
1.Запишите выражение для ответа на вопрос:
а) велосипедист ехал 2 часа со скоростью а км \ч , а потом еще 3 часа со скоростью в км \ч. Какое расстояние проехал велосипедист.
б) площадь прямоугольника равна с кв. м. .а его длина в м. Каков периметр прямоугольника.
2.Скорость одного пешехода х км\ч , а другого у км\ч. Объясни , что означает выражение:
а) х + у
в) 4 х
с)5 ( х+у)
3.Составь план нахождения площади фигуры.
4.Вычислить:
10 897 + 313436 : (822*106 – (3047+83 468) )
5.Решить задачу разными способами:
Базовый модуль № 1
Множества и операции над ними
Знать а) Понятия: - множество;
- элемент множества;
- характеристическое свойство элементов множества;
- подмножество;
- равные множества;
- пересечение множеств;
- объединение множеств;
- вычитание множеств;
- дополнение подмножества;
- декартово произведение множеств.
б) Обозначения: - а А, b A (для записи предложений «а принадлежит множеству А» и b не принадлежит множеству А»);
- А = {1, 2, 3, 4}( для задания множества путем перечисления всех его элементов);
- A = {x / x N, x 4} (для задания множества путем указания характеристического свойства его элементов);
- А В (для записи предложения «А подмножество В);
- А = В (для записи предложения «Множества А и В равны»;
- А В = {x / x A и x B} (для записи определения пересечения множеств А и В);
- А В = {x / x A или x B}(для записи определения объединение множеств А и В);
- А \ В = {x / x A и x B}(для записи определения разности множеств А и В);
- ВА – (для записи дополнения множества В до А);
- А В = {(x, у) / x A и у B}(для записи определения декартова произведения множеств А и В).
в) Свойства операций:
- коммутативность пересечения и объединения (А В = В А, А В = В А, А, В);
- ассоциативность пересечения и объединения ((А В) С = А (В С), (А В) С = А (В С)) А, В, С;
- дистрибутивность пересечения относительно объединения (А В) С = (А С) (В С) А, В, С;
- дистрибутивность объединения относительно пересечения (А В) С = (А В) (В С) А, В, С;
- дистрибутивность декартова произведения относительно объединения и вычитания (А В) С = (А С) (В С), (А \ В) С = (А С) \ (В С) А, В, С;
г) Правила:
- разбиения множества на классы;
- нахождение числа элементов в объединении и декартовом произведении множеств: n (А В) = n (A) + n (B) – n (А В)
n (А В) = n (A) + n (B) если А В = n (А В) = n (A) n (B).
Уметь: - задавать множества;
- выделять подмножества;
- выполнять операции объединения, пересечения, разности, декартова произведения;
- дать теоретико-множественное обоснование свойствам операций;
- разбить множество на классы.
Тематическое планирование
| Содержание | Лекции/ семинары | Лабораторные/ Практические |
| 1. Понятие множества и элементы множества. Способы задания множеств. Отношения между множествами. | 2 (лекции) | 2 |
| 2. Операции с множествами: пересечение, объединение, разность, дополнение. | 2 (лекции) | 2 |
| 3. Декартово произведение множеств. | 2 (лекции) | 2 |
| 4. Понятие разбиения множества на классы. Классификация. | 2 (семинара) | 2 2 ч (итоговая к/р) |
Рейтинг-контроль БМ 1
| | Вид контроля | Контрольные задания | Баллы |
| Модуль 1 Множества и операции над ними. | Текущий (ауд.) | 1. Конспект «Множества и операции над ними». 2. «Отношения между множествами». 3. Проверочная работа: «Объединение, пересечение множеств». 4. Зачет (теория). | 3-5 6-10 6-10 6-10 |
| | Текущий (внеауд.) | 1. Структурно-логическая схема «Множества и операции над ними». 2. Подбор заданий из учебника М 1-4 (операции с множествами). 3. Классификация объема понятий (3-5). | 9-15 6-10 9-15 |
| | Промежуточный | Контрольная работа № 1 | 15-25 |
| | | | 60-100 |
«3» - 60-72
«4» - 73-86
«5» - 86-100
Примерное содержание проверочной работы №1
«Отношения между множествами»
1. В каком отношении находится каждая пара множеств?
а) М = {a b c d} N = {b f d k e}
b) M = {a b c d} K = {b d}
c) M = {a b c d} l = {c a d b}
2. На рисунке изображены диаграммы множеств А и В. Определите, в каком отношении находятся множества. Приведите примеры множеств для каждого случая.
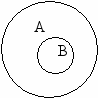





А
А
В
В
А
В
А) Б) В) Г)
3.Изобразите при помощи кругов Эйлера отношения между множествами А, В и С, где А - множество параллелограммов, В - множество ромбов, С - множество трапеций.
Примерное содержание проверочной работы № 2
«ОПЕРАЦИИ НАД МНОЖЕСТВАМИ»
1.Укажите характеристические свойства элементов множества
а) А U В∩ С и
б) (В∩ С ) \А если А = (–2; 4 ), В = ( 0 ; 5 ), С = ( 2; 8 ).
2. Х – множество цветов, К – множество цветов красного цвета, М – множество роз, Е – множество астр.
а) изобразите отношения между множествами Х, М, К, Е с помощью кругов Эйлера.
б) отметьте штриховкой множество Y = К \ (М U Е).
3. Изобразите графически декартово произведение Х Y , если Х = (2; 5 ), Y = ( -4 ; - 1 ).
Базовый модуль № 2
Отношение. Соответствия. Функции.
Требования к знаниям и умениям
Знать: а) определения понятий:
- соответствия;
- соответствие, обратное данному;
- взаимно-однозначное соответствие;
- равномощные множества;
- граф соответствия;
- график соответствия;
- счетное множество;
- бинарного отношения на множестве;
- отношение эквивалентности;
- отношение порядка.
б) свойства:
- свойства графиков взаимно-обратных соответствий;
- свойства отношений: рефлексивности, антиссиметричности, транзитивности, связности.
в)Теорему о взаимосвязи между отношением эквивалентности и на множестве Х и разбиением его на классы.
Уметь: - устанавливать соответствия между двумя множествами;
- получать соответствие, обратное данному;
- строить граф и график соответствия;
- устанавливать взаимно-однозначное соответствие;
- устанавливать свойства отношений;
- строить графы отношений.
Тематическое планирование
| Содержание | Лекции/ семинары | Лабораторные/ Практические |
| 1. Понятие отношения на множестве. Свойства отношений. Отношения эквивалентности и порядка. | 2 (лекции) | 2 |
| 2. Соответствия между двумя множествами. Взаимнооднозначные соответствия. | 2 (лекции) | 2 |
| 3. Числовые функции. | 2 (семинара) 2 ч (к/р № 2) | |
Рейтинг-контроль
по базовому модулю № 2
Отношение на множестве. Соответствия между двумя множествами
| Вид контроля | Контрольные задания | Количество балов | |
| min | max | ||
| Текущий (аудиторный) (внеаудиторный) | 1. Составление конспектов: «отношения», «соответствия». 2. Зачет (теория). 3. Проверочная работа № 1 «Отношения». 4. Тест «Соответствия». | 6 6 6 6 | 10 10 10 10 |
| 5. Подобрать задания из школьных учебников в которых устанавливаются отношения на множестве или соответствия: - между числовыми множествами; - между множествами геометрических фигур и множеством чисел; - между множеством выражений и множеством чисел; - другие. 6. Подобрать (составить) 5 заданий для учащихся начальной школы которые целесообразно решать с помощью построения графов. | 9 9 | 15 15 | |
| Промежуточный | Контрольная работа № 2 | 18 | 30 |
| | | 60 | 100 |
«3»- 60-72 балла «4»-72-85 баллов «5»-86-100 баллов.
Вопросы к зачету.
1.Определение бинарного отношения.
2.Свойство рефлексивности.
3.Ссвойство транзитивности.
4.Свойство симметричности.
5.Свойство антисимметричности.
6.Свойство связанности.
7.Отношение эквивалентности.
8.Теорема о разбиении множества на попарно- непересекающиеся подмножества.
9.Отношение порядка.
10.Определение соответствия.
11.Соответствие обратное данному.
12.Взаимно- однозначное соответствие.
13.Равномощные множества.
14.Функциональное соответствие.
Примерное содержание контрольной работы
1.На множестве Х= { 5-2, 8-5, 9-7, 5-3., 6-4, 7-2}. задано отношение R:»иметь одинаковое значение».
а) построить граф R.
б) определить свойства
в) является ли R – отношением эквивалентности,
г) назовите классы эквивалентности.
2. Можно ли упорядочить множество деревьев отношением «быть выше».
3.Х= -1, 0, 1, 2, 3. Y = R.
Соответствие М: « х больше чем у в 2 раза.
а) задайте М в виде упорядоченных пар,
б ) сформулируйте соответствие обратное данному в виде предложения с двумя переменными,
в) постройте графики соответствия и соответствия обратного данному,
г) верно ли, что 2 М 1 ; 1 М 2.
Дополнительный модуль
| № п/п | Содержание | Максимальный балл |
| 1 | Составить структурно-логическую схему по содержанию темы. | 10 |
| 2 | Составить алгоритм выполнения математического действия в виде - блок-схемы - в знаковой форме | 10 |
| 3 | Составить опорный конспект (сигнал) по теме) | 10 |
| 4 | Подборка дополнительного материала по теме. | 10 |
| 5 | Составление (подбор) дополнительных заданий по теме. | 10 |
| 6 | Самостоятельно доказать математическое утверждение. | 10 |
| 7 | Представить доказательство математического утверждения в виде - развернутого плана - блок-схемы | 10 10 |
| 8 | Написать сочинение по теме. | 10 |
| 9 | Описать сферы приложения изучаемой теории. | 10 |
Итоговый модуль
| Форма работы | min | Max |
| Экзамен | 15 | 30 |
Вопросы к экзамену
- Теоретико-множественный смысл количественного натурального числа и нуля.
- Теоретико-множественный смысл суммы целых неотрицательных чисел.
- Законы сложения целых неотрицательных чисел.
- Отношения «равно» и «меньше» на множестве целых неотрицательных чисел.
- Теоретико-множественный смысл разности целых неотрицательных чисел.
- Связь действий сложения и вычитания. Существование и единственность разности на множестве целых неотрицательных чисел.
- Правила вычитания целых неотрицательных чисел.
- Умножение целых неотрицательных чисел.
- Законы умножения целых неотрицательных чисел.
- Деление целых неотрицательных чисел.
- Существование и единственность частного. Деление с нулем на множестве целых неотрицательных чисел.
- Правила деления целых неотрицательных чисел.
- Деление с остатком.
- Свойства множества целых неотрицательных чисел.
- Смысл натурального числа – результата измерения величины.
- Смысл сложения и вычитания чисел, являющихся значениями величин.
- Смысл умножения и деления чисел, являющихся значениями величин.
- Запись чисел в десятичной системе счисления.
- Сложение многозначных чисел в десятичной системе счисления.
- Вычитание многозначных чисел в десятичной системе счисления.
- Умножение многозначных чисел в десятичной системе счисления.
- Деление многозначных чисел в десятичной системе счисления.
- Понятие отношения делимости. Свойства отношения делимости.
- Делимость суммы, разности и произведения целых неотрицательных чисел.
- Признаки делимости чисел в десятичной системе счисления.
- Наибольший общий делитель и наименьшее общее кратное. Способы нахождения НОК и НОД.
- Признаки делимости на составные числа.
- Понятие дроби и положительного рационального числа.
- Сложение и вычитание положительных рациональных чисел.
- Умножение и деление положительных рациональных чисел.
- Упорядоченность множества положительных рациональных чисел.
- Десятичные дроби.
- Понятие положительного иррационального числа.
- Действия над положительными действительными числами.
- Отрицательные числа.
- Числовые выражения и выражения с переменной. Тождественные преобразования выражений.
- Числовые равенства и неравенства, их свойства.
- Уравнения с одной переменной. Равносильность уравнений.
- Неравенства с одной переменной. Равносильность неравенств.
- Понятие величины. Понятие измерения величины.
- Длина отрезка и ее измерение.
- Площадь фигуры и ее измерение.
- Масса тела и ее измерение.
- Промежутки времени и их измерение.
Итоговая оценка:
«3» - 540 -720 баллов.
«4» - 721 – 860 баллов.
«5» - 861 - 1000 баллов.
Литература
Основная:
- Л.П. Стойлова, А.М. Пышкало. Основы начального курса математики. Учебное пособие для педагогических училищ. М., Просвещение, 1988.
- Л.П. Стойлова. Математика. Учебник для студентов высших педагогических заведений. Издательский центр «Академия», 2000.
- А.М. Пышкало, Л.П. Стойлова. Сборник задач по математике. Пособие для педучилищ. М.: Просвещение, 1979.
Дополнительная:
- Л.П. Стойлова, Н.Я Виленкин, Н.Н. Лаврова. Математика. Часть 1. Пособие для студентов-заочников факультетов подготовки учителей начальных классов.
- Н.И. Лаврова, Л.П. Стойлова. Задачник-практикум по математике. М.: Просвещение, 1985.
